Variable Step-Size Hybrid Filtered-x Affine Projection Generalized Correntropy Algorithm for Active Noise Control
Abstract
1. Introduction
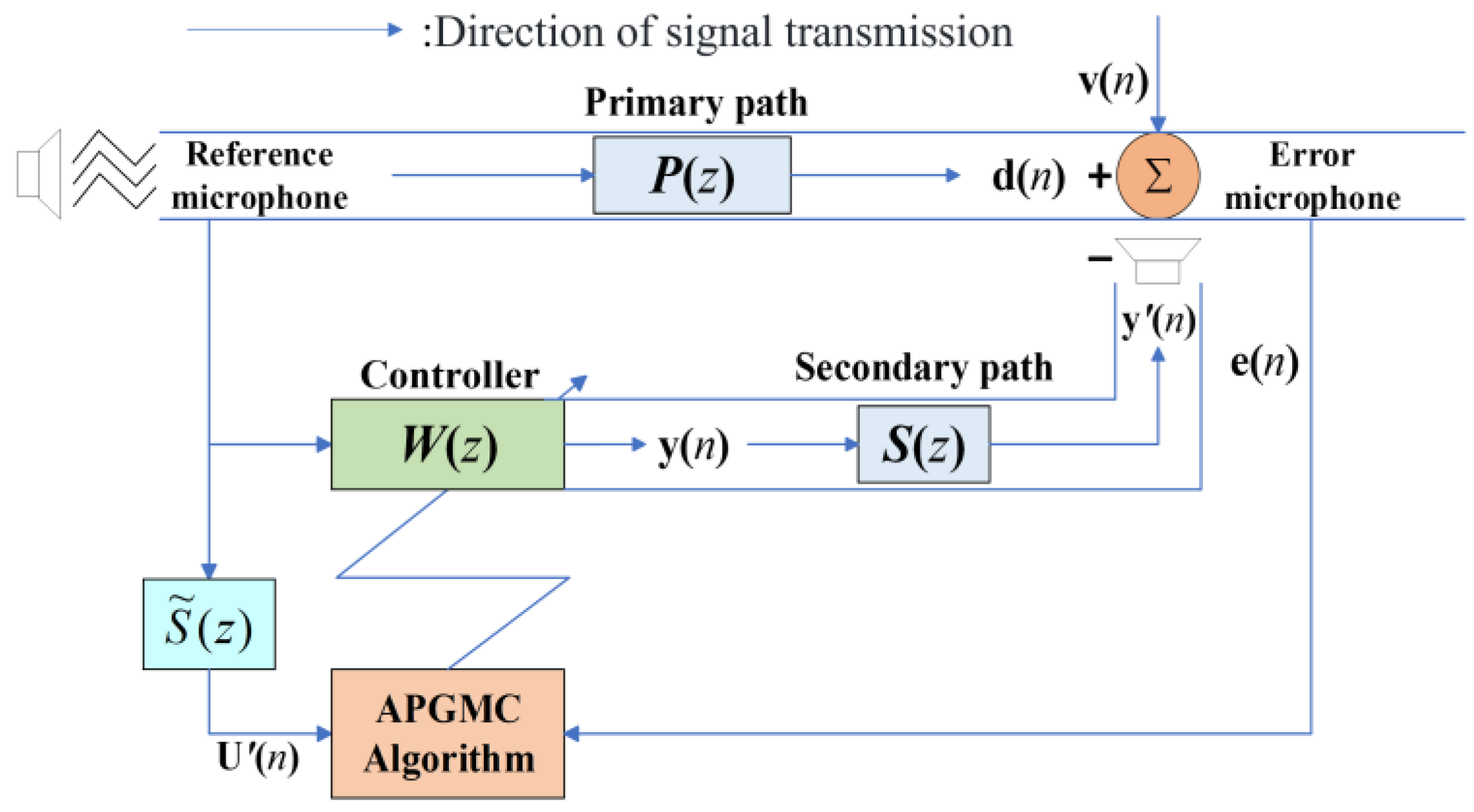
2. Algorithm and System Review
3. The Proposed Algorithm
3.1. Hybrid Scheme
3.2. The Proposed VSS-H-FxAPGMC
| Algorithm 1. Step-size reset method of VSS-H-FxAPGMC algorithm |
3.3. Stability Analysis
| Algorithm 2. VSS-H-FxAPGMC Algorithm |
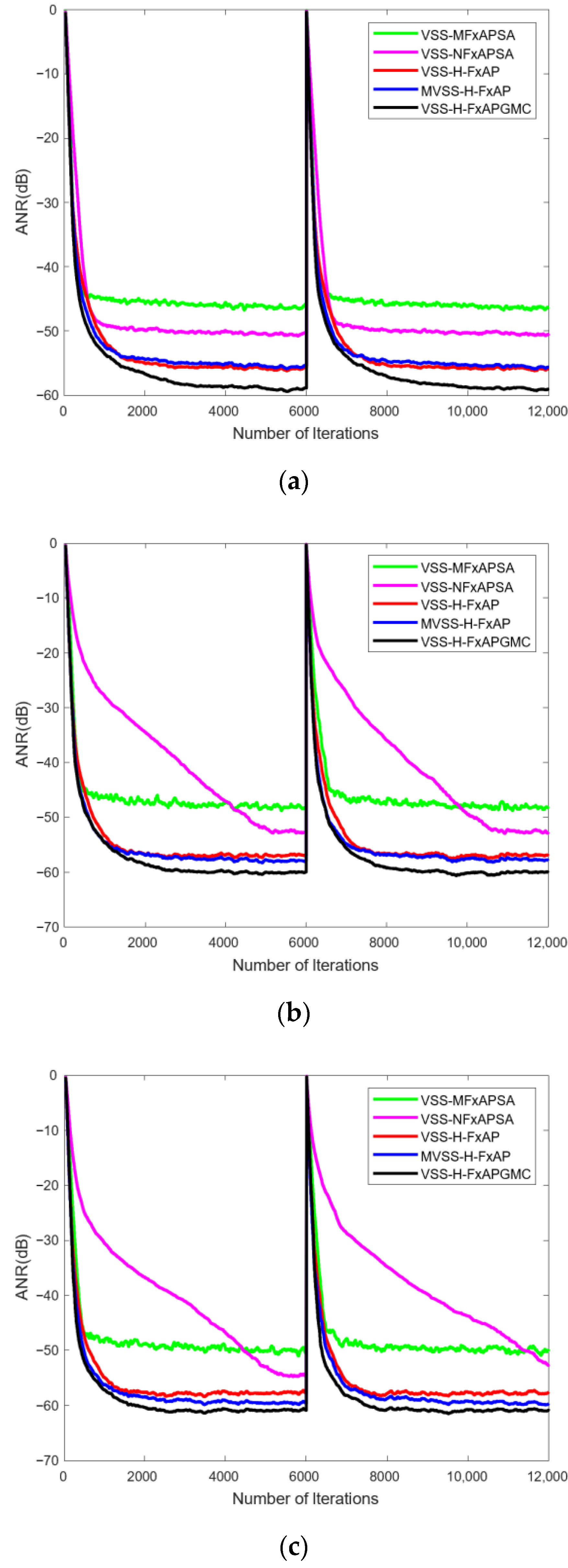
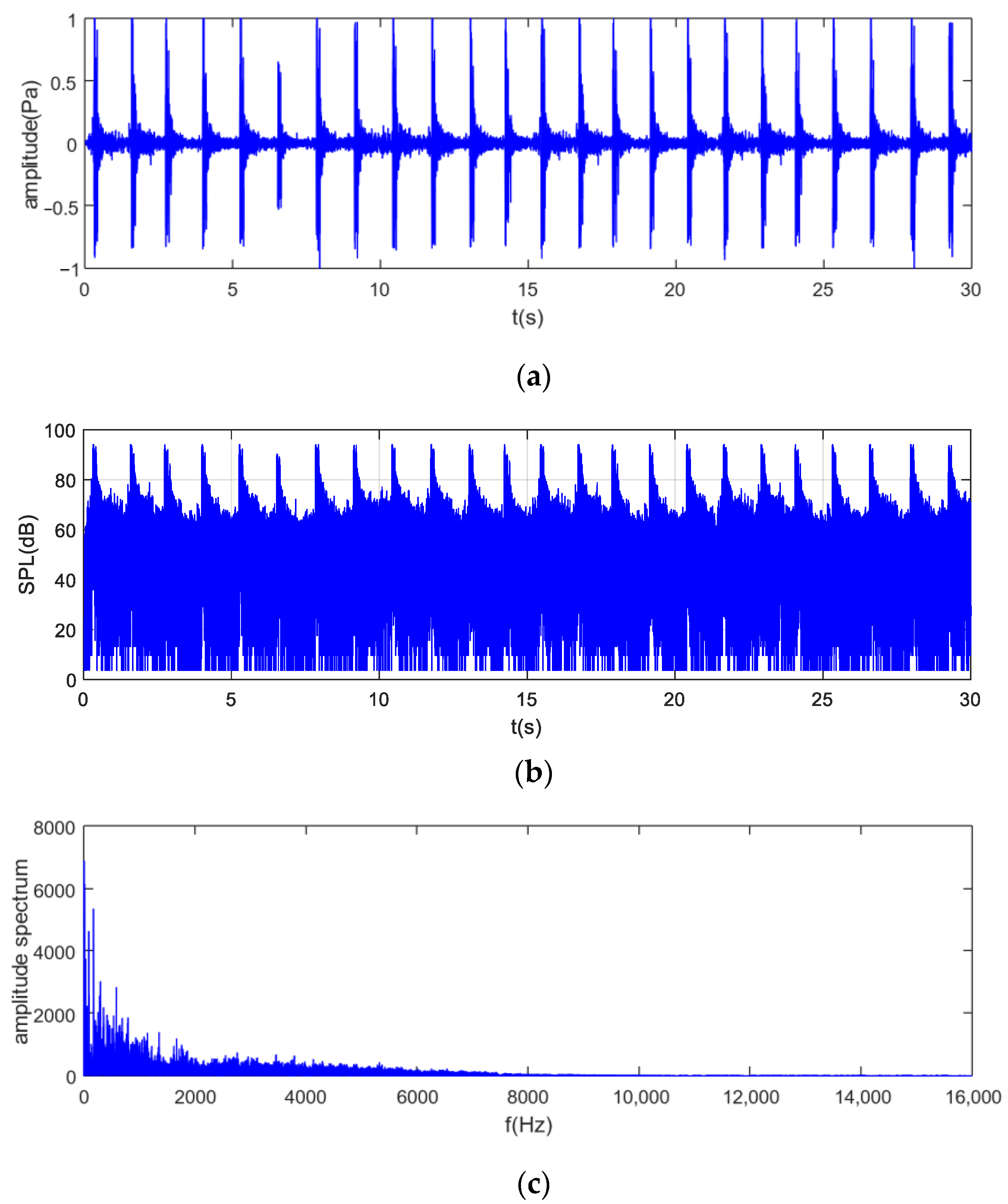
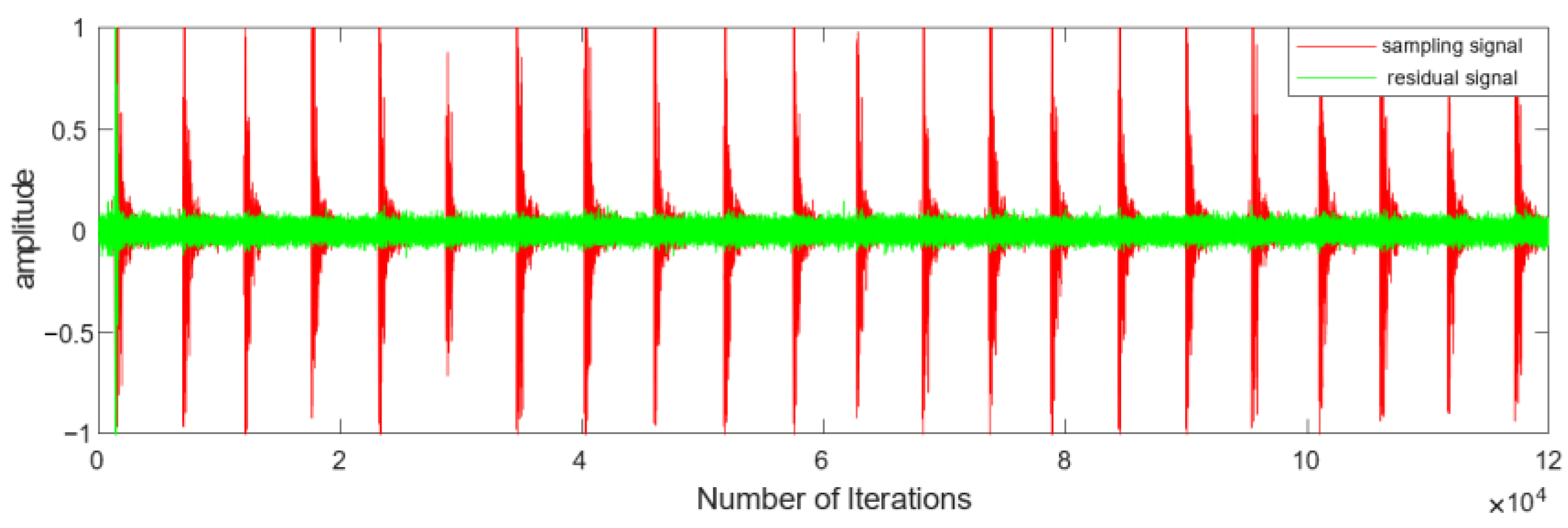
4. Experimental Results
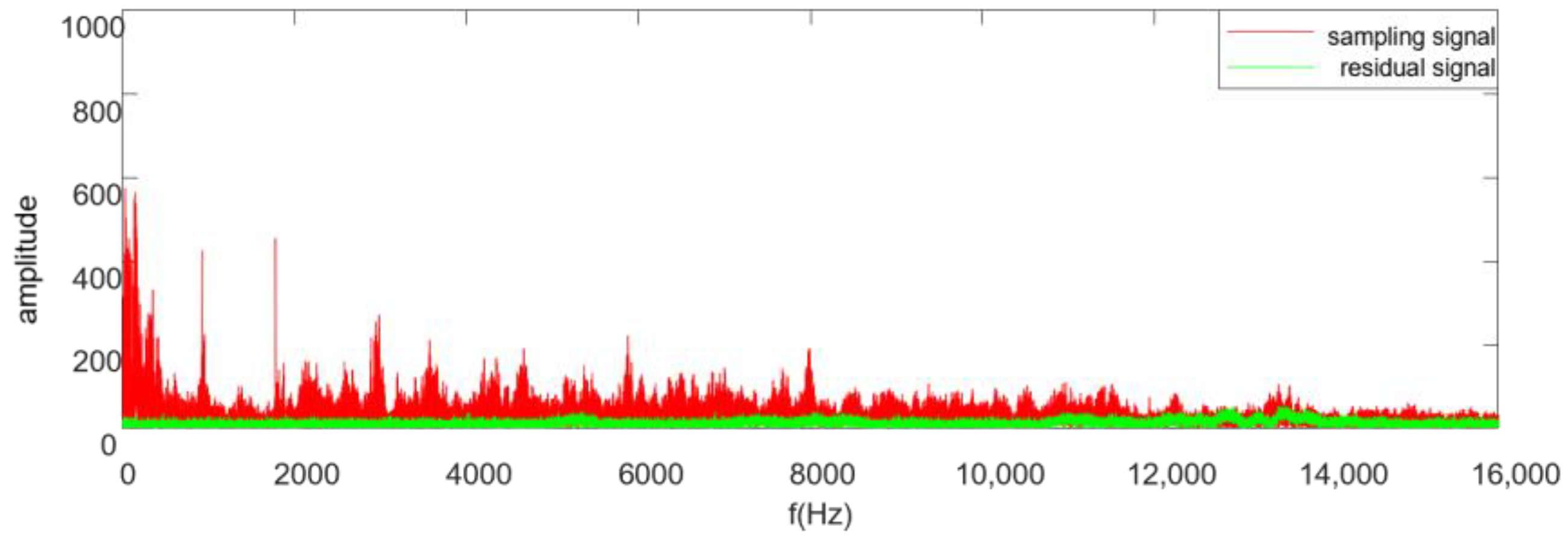
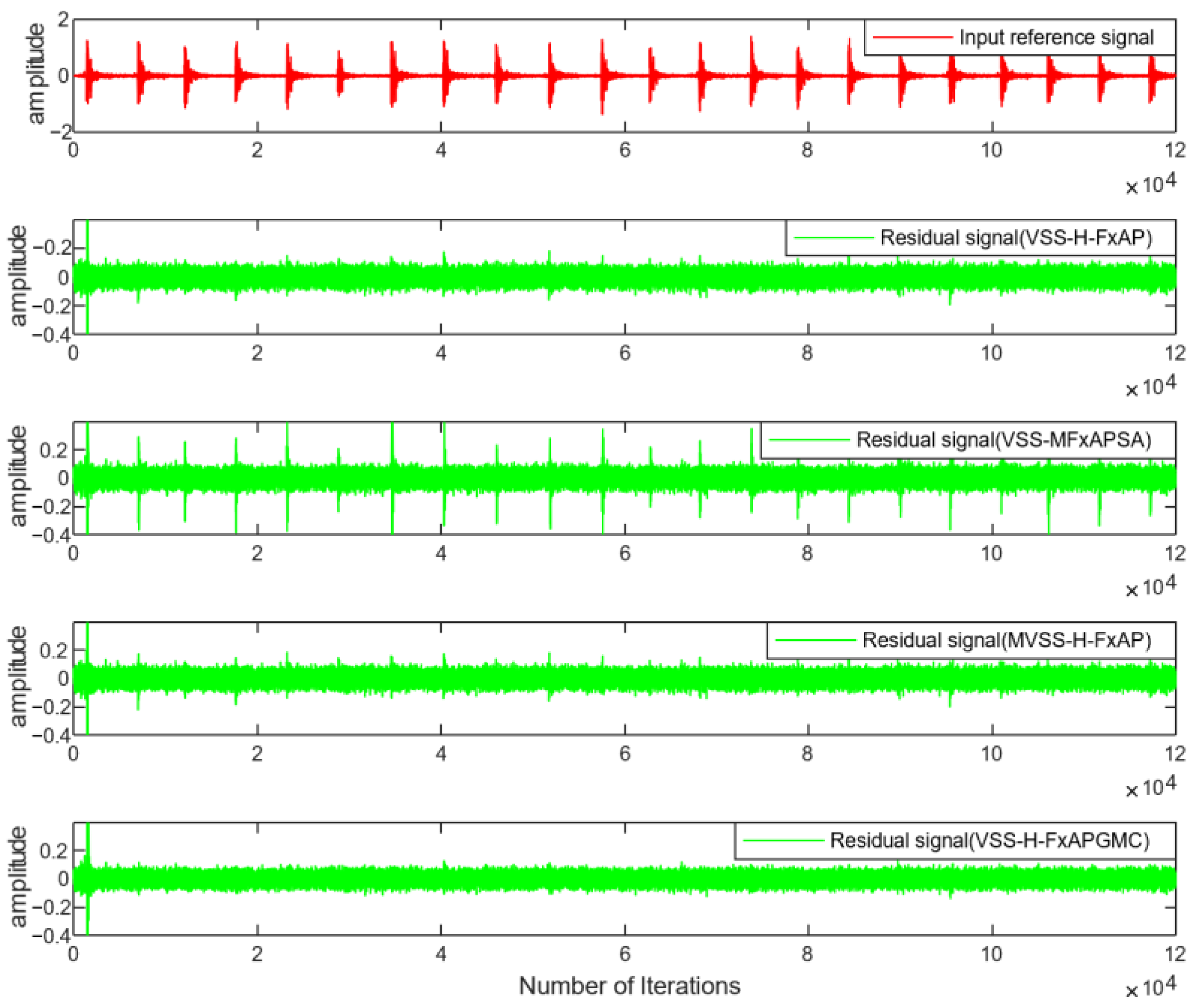
4.1. Simulated Impulse Noise
4.2. Real Industrial Noise
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Glossary
| d(n) | Desired signal. |
| P(z) | Primary path of noise propagation. |
| W(z) | ANC controller. |
| S(z) | Secondary path of noise propagation. |
| For the estimation of S(z), this paper uses an offline scheme. | |
| U(n) | Original input signal. |
| U′(n) | U(n) after filtered-x, i.e., the input signal filtered by . |
| y(n) | Response of the adaptive filter. |
| y′(n) | Noise-cancelling signal. |
| w(n) | The adaptive filter’s weight vector. |
| e(n) | The error signal. |
| v(n) | Background noise, characterized by zero-mean Gaussian noise. |
| M | The input signal’s projected order. |
| L | The length of the taps in w(n). |
| p(n) | The response of the primary path. |
| s(n) | The response of the secondary path. |
| X and Y | This pair of vectors is introduced for later analysis, and their difference between the two coincides with the e(n). |
| γ | A normalization constant for GC-loss function. |
| ϕ | A parameter that controls shape and scale for GC-loss function. |
| α | α > 0 is the shape parameter. |
| ep(n) | An estimation of e(n). |
| B(n) | A diagonal matrix formed by b(n). |
| b(n) | b(n) is a variable of the error signal e(n) which includes ϕ and α. |
| Sgn(·) | This refers to symbolic operations. |
| μ | A step size associated with the adaptive filtering algorithm, and this value is a certain amount. |
| Specific formulation for step-size inequality analysis. | |
| The largest step size that can be used without causing divergence. | |
| σ | Regularization factor. |
| Weight error vector. | |
| The optimal weight. | |
| μ(n) | The step size in the adaptive filtering algorithm, which changes with each iteration. |
| The final representation of the step size in the VSS-H-FxAPGMC algorithm. | |
| r(n) | Control items related to e(n). |
| η | Sliding parameter for e(n) weights in r(n). |
| λ | Smoothing factor. |
| Variable step-size equation in moving average method. | |
| and | Two positive integers for the reset mechanism. |
| Q | Vector related to e(n) for the reset mechanism. |
| M | A special diagonal matrix composed of 0 and 1. |
| ξ | Parameters defining the threshold for the reset mechanism. |
| in the scalar state. | |
| This is a scalar and is the first element in . | |
| B(n) | This is a scalar and is the first element in B(n). |
| in scalar form. | |
| v(n) | This is a scalar and is the first element in v(n). |
| Variable related to e(n) used for ANR as a molecule. | |
| Variable related to e(n) used for ANR as a denominator. | |
| κ | Forgetting factor for ANR. |
| ANR | Averaged noise reduction; important metrics for judging ANC algorithms. |
References
- Liu, H.; Lee, J. A Feedback Active Control Approach to Road Noise Based on a Single Microphone Sensor to Improve Automotive Cabin Sound Comfort. Sensors 2024, 24, 2515. [Google Scholar] [CrossRef]
- Watanabe, T.; Kanai, S.; Muto, H.; Kogawa, H.; Atsumi, T.; Nakadai, S. Study of Increased Wind Noise by Active Noise Cancellation Headphones. IEEJ J. Ind. Appl. 2024, 13, 208–214. [Google Scholar] [CrossRef]
- Yang, B.; Yin, J.; Ye, Z.; Yang, S.; Wang, L. Development and Testing of an Active Noise Control System for Urban Road Traffic Noise. Appl. Sci. 2024, 14, 175. [Google Scholar] [CrossRef]
- Dimino, I.; Colangeli, C.; Cuenca, J.; Vitiello, P.; Barbarino, M. Active Noise Control for Aircraft Cabin Seats. Appl. Sci. 2022, 12, 5610. [Google Scholar] [CrossRef]
- Félix, F.B.; de Castro Magalhães, M.; de Souza Papini, G. An Improved ANC Algorithm for the Attenuation of Industrial Fan Noise. J. Vib. Eng. Technol. 2021, 9, 279–289. [Google Scholar] [CrossRef]
- Lam, B.; Gan, W.-S.; Shi, D.; Nishimura, M.; Elliott, S. Ten Questions Concerning Active Noise Control in the Built Environment. Build. Environ. 2021, 200, 107928. [Google Scholar] [CrossRef]
- Bai, Y.; Gong, X.; Lu, Q.; Song, Y.; Zhu, W.; Xue, S.; Wang, D.; Peng, Z.; Zhang, Z. Application of Adaptive Filtering Algorithm to the Stability Problem for Double Crystal Monochromator. Part I: Typical Filtering Algorithms. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2023, 1048, 167924. [Google Scholar] [CrossRef]
- Zhao, H.; Gao, Y.; Zhu, Y. Robust Subband Adaptive Filter Algorithms-Based Mixture Correntropy and Application to Acoustic Echo Cancellation. IEEE/ACM Trans. Audio Speech Lang. Process. 2023, 31, 1223–1233. [Google Scholar] [CrossRef]
- Bismor, D. Leaky Partial Update LMS Algorithms in Application to Structural Active Noise Control. Sensors 2023, 23, 1169. [Google Scholar] [CrossRef]
- Shen, X.; Shi, D.; Luo, Z.; Ji, J.; Gan, W.-S. A Momentum Two-Gradient Direction Algorithm with Variable Step Size Applied to Solve Practical Output Constraint Issue for Active Noise Control. In Proceedings of the ICASSP 2023—2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar]
- Aslam, M.S.; Shi, P.; Lim, C.-C. Self-Adapting Variable Step Size Strategies for Active Noise Control Systems with Acoustic Feedback. Automatica 2021, 123, 109354. [Google Scholar] [CrossRef]
- Akhbari, A.; Ghaffari, A. The Performance Comparison of Improved Continuous Mixed P-Norm and Other Adaptive Algorithms in Sparse System Identification. Int. J. Adv. Intell. Paradig. 2020, 16, 65–74. [Google Scholar] [CrossRef]
- Yang, W.; Han, F.; Wang, G. Robust Active Noise Control: Minimum Output Variance Approach With Least Mean Lp-Norm Algorithm. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 2484–2488. [Google Scholar] [CrossRef]
- Shin, J.; Kim, J.; Kim, T.-K.; Yoo, J. p-Norm-like Affine Projection Sign Algorithm for Sparse System to Ensure Robustness against Impulsive Noise. Symmetry 2021, 13, 1916. [Google Scholar] [CrossRef]
- Wang, S.; Wang, W.; Xiong, K.; Iu, H.H.C.; Tse, C.K. Logarithmic Hyperbolic Cosine Adaptive Filter and Its Performance Analysis. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2512–2524. [Google Scholar] [CrossRef]
- Patel, V.; Bhattacharjee, S.S.; George, N.V. A Family of Logarithmic Hyperbolic Cosine Spline Nonlinear Adaptive Filters. Appl. Acoust. 2021, 178, 107973. [Google Scholar] [CrossRef]
- Hou, Y.; Li, G.; Zhang, H.; Wang, G.; Zhang, H.; Chen, J. Affine Projection Algorithms Based on Sigmoid Cost Function. Signal Process. 2024, 219, 109397. [Google Scholar] [CrossRef]
- Chen, B.; Xing, L.; Zhao, H.; Zheng, N.; Príncipe, J.C. Generalized Correntropy for Robust Adaptive Filtering. IEEE Trans. Signal Process. 2016, 64, 3376–3387. [Google Scholar] [CrossRef]
- Qian, G.; Liu, J.; Qiu, C.; Ho-Ching Iu, H.; Qian, J.; Wang, S. Minimum Total Complex Error Entropy for Adaptive Filter. Expert Syst. Appl. 2024, 237, 121522. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, D.; Lv, S. Robust Maximum Correntropy Criterion Subband Adaptive Filter Algorithm for Impulsive Noise and Noisy Input. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 604–608. [Google Scholar] [CrossRef]
- Li, G.; Wang, G.; Dai, Y.; Sun, Q.; Yang, X.; Zhang, H. Affine Projection Mixed-Norm Algorithms for Robust Filtering. Signal Process. 2021, 187, 108153. [Google Scholar] [CrossRef]
- Zhou, X.; Li, G.; Wang, Z.; Wang, G.; Zhang, H. Robust Hybrid Affine Projection Filtering Algorithm under α-Stable Environment. Signal Process. 2023, 208, 108981. [Google Scholar] [CrossRef]
- Zhou, X.; Li, G.; Zhang, H.; Cao, X. Variable Step Size Methods of the Hybrid Affine Projection Adaptive Filtering Algorithm under Symmetrical Non-Gaussian Noise. Symmetry 2023, 15, 1158. [Google Scholar] [CrossRef]
- Chien, Y.-R.; Wu, S.-T.; Tsao, H.-W.; Diniz, P.S.R. Correntropy-Based Data Selective Adaptive Filtering. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 754–766. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, S.; Lin, D.; Chen, S. Robust Affine Projection Tanh Algorithm and Its Performance Analysis. Signal Process. 2023, 202, 108749. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, H.; Zhang, J.A. Generalized Maximum Correntropy Algorithm with Affine Projection for Robust Filtering under Impulsive-Noise Environments. Signal Process. 2020, 172, 107524. [Google Scholar] [CrossRef]
- Zhong, S.; Wang, Z.; Wang, G.; Zhou, Y.; Zhou, X.; Peng, B. Robust Adaptive Filtering Based on M-Estimation-Based Minimum Error Entropy Criterion. Inf. Sci. 2024, 658, 120026. [Google Scholar] [CrossRef]
- Yoo, J.; Shin, J.; Park, P. Variable Step-Size Affine Projection Sign Algorithm. IEEE Trans. Circuits Syst. II Express Briefs 2014, 61, 274–278. [Google Scholar]
- Xiao, L.; Wu, M.; Yang, J. A New Efficient Filtered-x Affine Projection Sign Algorithm for Active Control of Impulsive Noise. Signal Process. 2016, 120, 456–461. [Google Scholar] [CrossRef]
- Wen, P.; Zhang, J. Robust Variable Step-Size Sign Subband Adaptive Filter Algorithm against Impulsive Noise. Signal Process. 2017, 139, 110–115. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, H. A New and Effective Nonparametric Variable Step-Size Normalized Least-Mean-Square Algorithm and Its Performance Analysis. Signal Process. 2023, 210, 109060. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, B.; Song, P. Variable Step-Size Affine Projection Maximum Correntropy Criterion Adaptive Filter With Correntropy Induced Metric for Sparse System Identification. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 2782–2786. [Google Scholar] [CrossRef]
- Gomathi, K.; Saravanan, V.; Santhiya kumari, N. Variable Step Size for Improving Convergence of FxLMS Algorithm. Procedia Technol. 2016, 25, 420–426. [Google Scholar] [CrossRef]
- Bershad, N.J.; Bermudez, J.C.M. A Switched Variable Step Size NLMS Adaptive Filter. Digit. Signal Process. 2020, 101, 102730. [Google Scholar] [CrossRef]
- Mohagheghian Bidgoli, Z.; Bekrani, M. A Switching-Based Variable Step-Size PNLMS Adaptive Filter for Sparse System Identification. Circuits Syst. Signal Process. 2024, 43, 568–592. [Google Scholar] [CrossRef]
- Joel, S.; Kumar, K.; George, N.V. Robust DOA Estimation Based on an Exponential Hyperbolic Cosine Adaptive Algorithm. IEEE Sens. Lett. 2023, 7, 7001904. [Google Scholar] [CrossRef]
- Mir, M.; Nasirzadeh, F.; Lee, S.; Cabrera, D.; Mills, A. Construction Noise Management: A Systematic Review and Directions for Future Research. Appl. Acoust. 2022, 197, 108936. [Google Scholar] [CrossRef]
- Thompson, R.; Smith, R.B.; Bou Karim, Y.; Shen, C.; Drummond, K.; Teng, C.; Toledano, M.B. Noise Pollution and Human Cognition: An Updated Systematic Review and meta-Analysis of Recent Evidence. Environ. Int. 2022, 158, 106905. [Google Scholar] [CrossRef] [PubMed]
- Thacher, J.D.; Poulsen, A.H.; Hvidtfeldt, U.A.; Raaschou-Nielsen, O.; Ketzel, M.; Jensen, S.S.; Brandt, J.; Valencia, V.H.; Münzel, T.; Sørensen, M. Long-Term Exposure to Transportation Noise and Risk for Atrial Fibrillation: A Danish Nationwide Cohort Study. Environ. Res. 2022, 207, 112167. [Google Scholar] [CrossRef]
- Zou, C.; Zhu, R.; Tao, Z.; Ouyang, D.; Chen, Y. Evaluation of Building Construction-Induced Noise and Vibration Impact on Residents. Sustainability 2020, 12, 1579. [Google Scholar] [CrossRef]
- Pinsonnault-Skvarenina, A.; Carrier, M.; Manolache, D.-E.; Bockstael, A.; Gagné, J.-P.; Leroux, T. Predictors of Noise Annoyance from Construction of a Large Metropolitan Highway Project. Transp. Res. Part D Transp. Environ. 2021, 94, 102787. [Google Scholar] [CrossRef]
- Silva, L.T.; Magalhães, A.; Silva, J.F.; Fonseca, F. Impacts of Low-Frequency Noise from Industrial Sources in Residential Areas. Appl. Acoust. 2021, 182, 108203. [Google Scholar] [CrossRef]
- Song, P.; Zhao, H. Filtered-x Least Mean Square/Fourth (FXLMS/F) Algorithm for Active Noise Control. Mech. Syst. Signal Process. 2019, 120, 69–82. [Google Scholar] [CrossRef]
- Huang, X.; Li, Y.; Han, X.; Tu, H. Ekblom Promoting Adaptive Algorithm for System Identification. Signal Process. 2023, 203, 108797. [Google Scholar] [CrossRef]
- Wang, X.; Ou, S.; Gao, Y. Convex Regularized Recursive Minimum Error Entropy Algorithm. Electronics 2024, 13, 992. [Google Scholar] [CrossRef]



| Performance Analysis of Each ANC Algorithm | |||
|---|---|---|---|
| Algorithm | Maximum ANR | Minimum ANR | Error |
| VSS-MFxAPSA | −22.5 dB | −37.1 dB | 14.6 dB |
| VSS-NFxAPSA | −32.9 dB | −37.0 dB | 4.1 dB |
| VSS-H-APA | −32.4 dB | −42.5 dB | 10.1 dB |
| MVSS-H-APA | −33.7 dB | −43.1 dB | 9.4 dB |
| VSS-H-FxAPGMC | −42.2 dB | −46.9 dB | 4.7 dB |
| The Contributions of the Various Literature in Addressing Pulse Noise | |
|---|---|
| Algorithm | Main Contributions |
| H-APA [22] | Proposed the application of hybrid step size in mixed-norm algorithm |
| VSS-H-APA [23] | Proposed variable step-size method for designing H-APA using MSD minimization |
| MVSS-H-APA [23] | Proposed variable step-size method for designing H-APA using modified MSD |
| VSS-H-FxAPGMC | Proposed hybrid step-size scheme for APGMC; proposed variable step-size method modified by a controlled error term |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, Z.; Gao, Y.; Guo, X.; Ou, S. Variable Step-Size Hybrid Filtered-x Affine Projection Generalized Correntropy Algorithm for Active Noise Control. Sensors 2025, 25, 1881. https://doi.org/10.3390/s25061881
Mu Z, Gao Y, Guo X, Ou S. Variable Step-Size Hybrid Filtered-x Affine Projection Generalized Correntropy Algorithm for Active Noise Control. Sensors. 2025; 25(6):1881. https://doi.org/10.3390/s25061881
Chicago/Turabian StyleMu, Zhaoqing, Ying Gao, Xinyu Guo, and Shifeng Ou. 2025. "Variable Step-Size Hybrid Filtered-x Affine Projection Generalized Correntropy Algorithm for Active Noise Control" Sensors 25, no. 6: 1881. https://doi.org/10.3390/s25061881
APA StyleMu, Z., Gao, Y., Guo, X., & Ou, S. (2025). Variable Step-Size Hybrid Filtered-x Affine Projection Generalized Correntropy Algorithm for Active Noise Control. Sensors, 25(6), 1881. https://doi.org/10.3390/s25061881






