UWB Base Station Deployment Optimization Method Considering NLOS Effects Based on Levy Flight-Improved Particle Swarm Optimizer
Abstract
1. Introduction
2. Methods
2.1. Standard PSO Algorithm
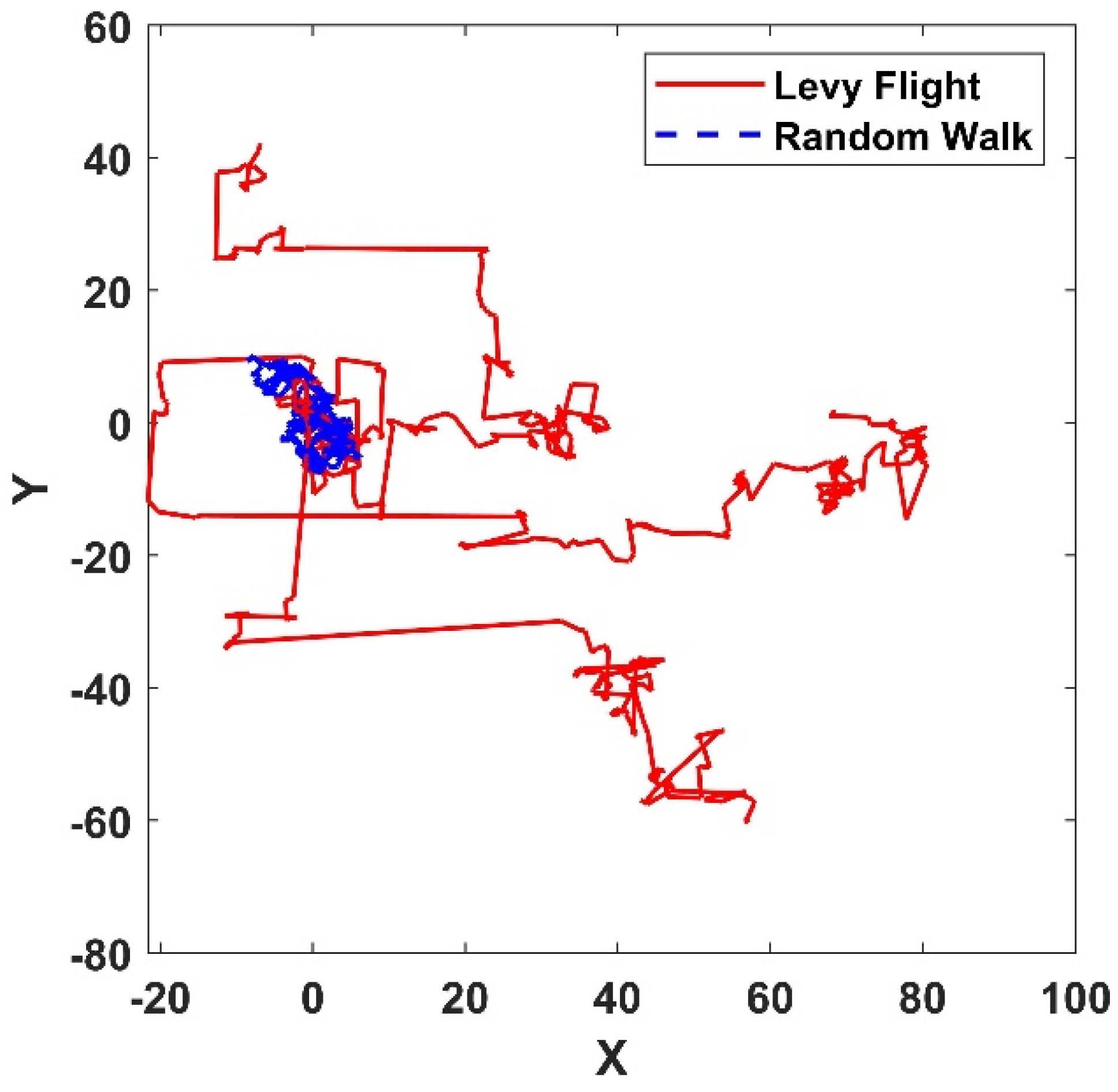
2.2. Levi’s Flight Strategy
2.3. LPSO Algorithm
- (a)
- Population initialization, which initializes the position and velocity of population particles in a randomly generated manner.
- (b)
- Calculate all particles fitness value and update the particle’s own historical best fitness value, pbest, and global best position of the whole particles, gbest.
- (c)
- Update the velocity and position of the particle according to Equation (1), and conduct transboundary processing.
- (d)
- Determine whether the particle pbest stagnation number n exceeds the threshold value 10; if so, then use Equation (3) to enter the Lévy flight mutation strategy to update the particle position, select the better particle individual, and update the particle’s pbest and gbest positions.
- (e)
- Determine whether the LPSO algorithm meets the evolutionary end condition. If yes, the optimal solution is output and the algorithm search stops; if not, return to step (b) and continue the search or evolution process.
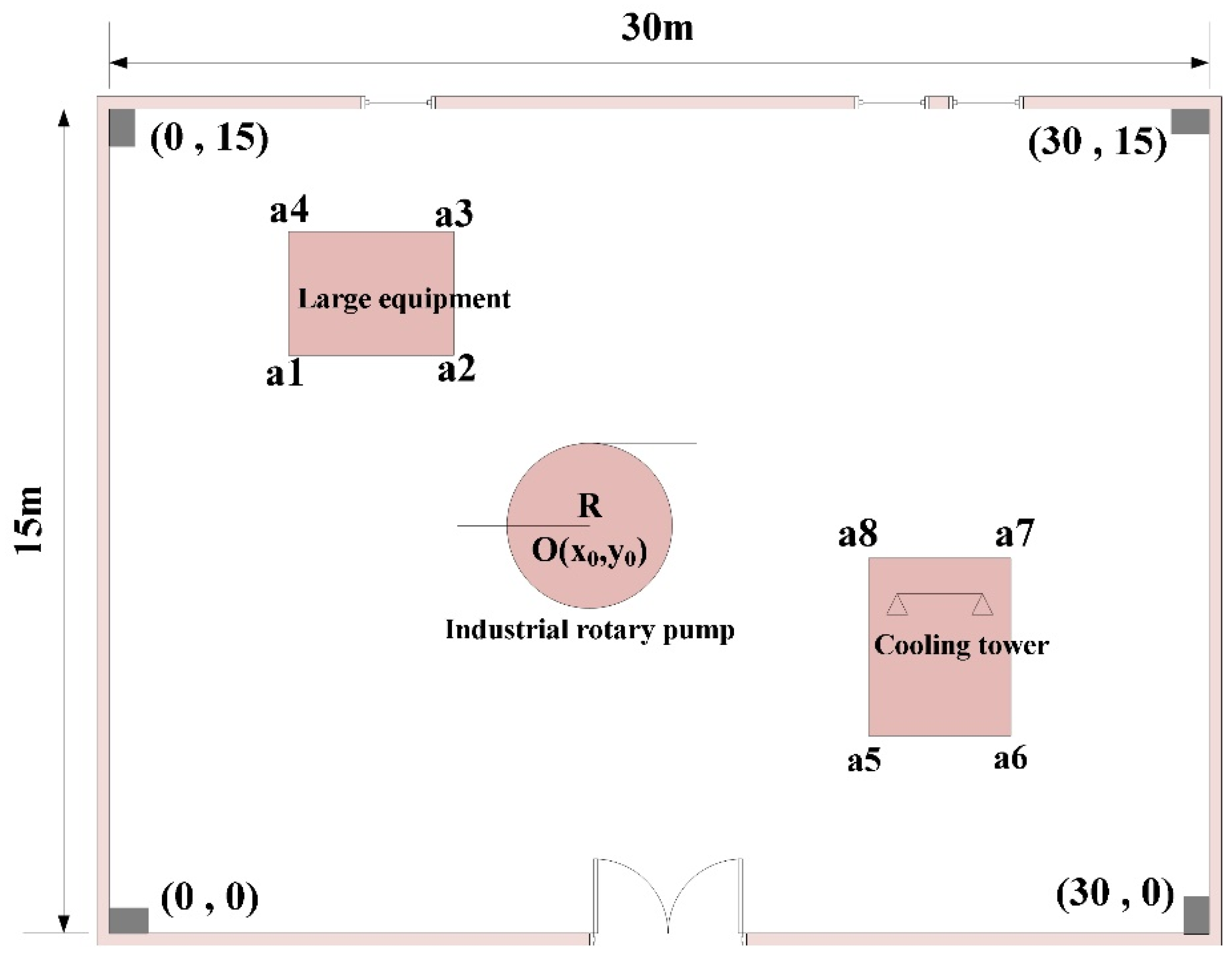
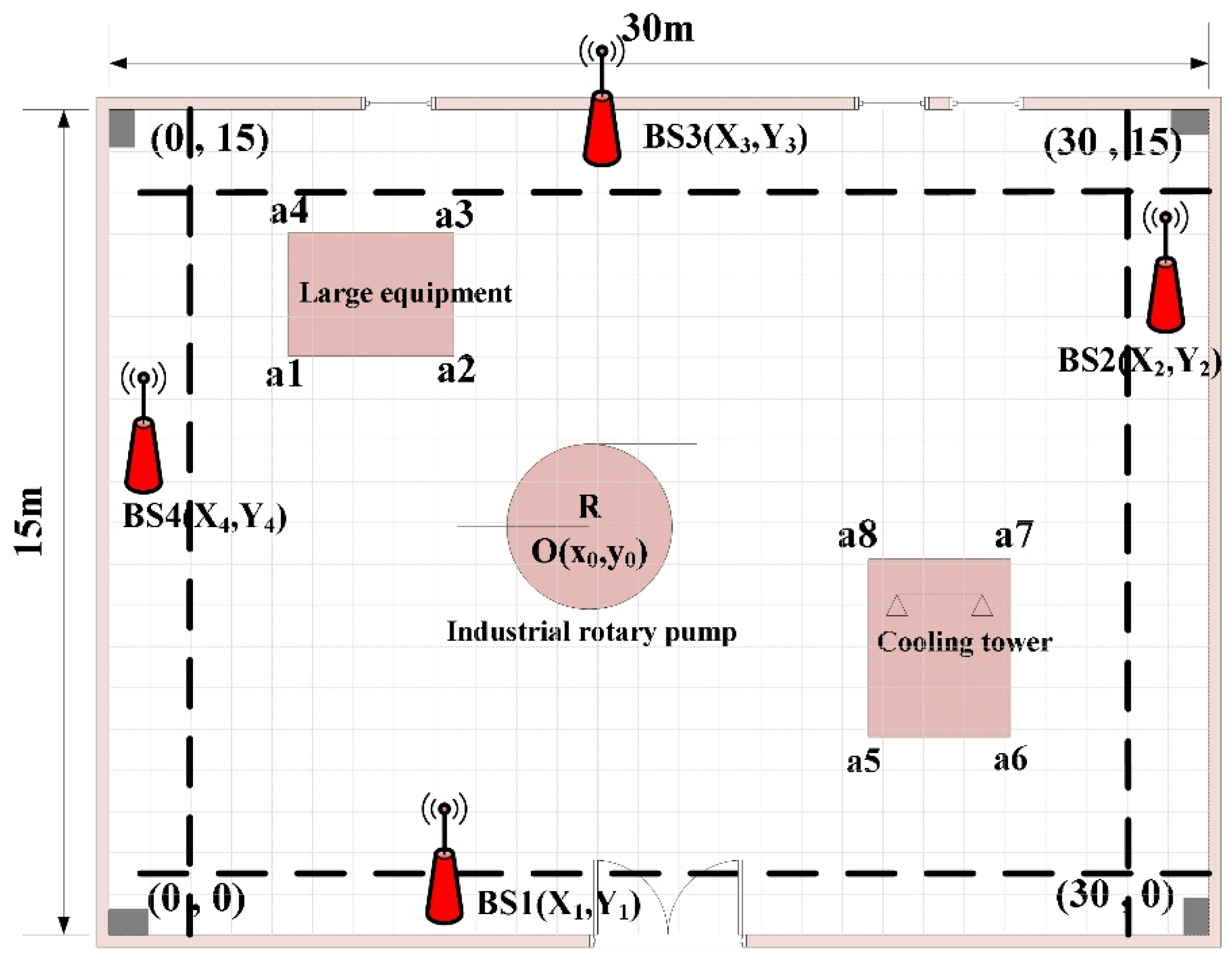
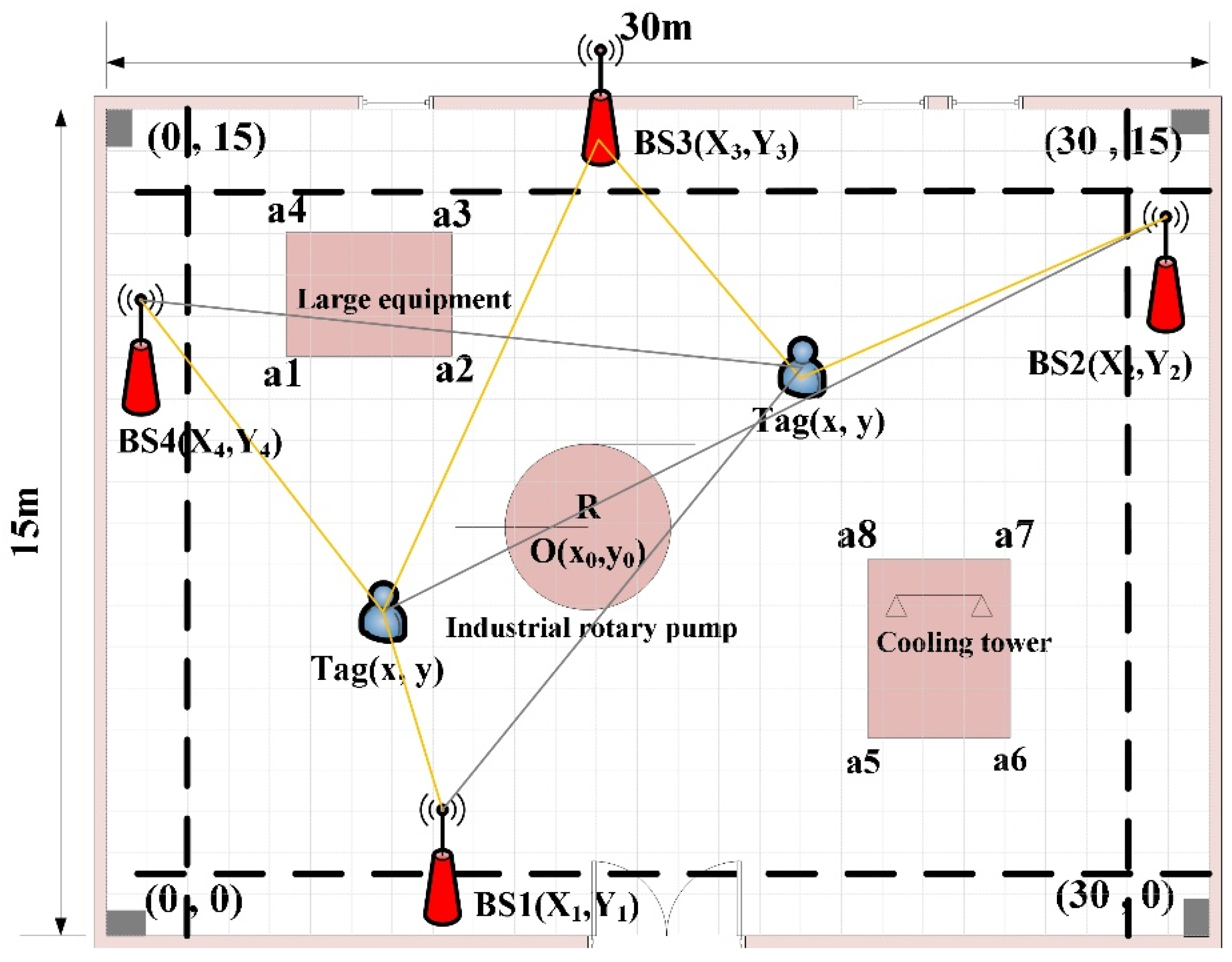
3. Fitness Function Model for UWB BS Deployment Optimization Considering NLOS Occlusion
3.1. UWB PDOP Calculation Principle
3.2. Locatable Signal Coverage Rate Calculation Model
3.3. Optimal Fitness Function Model for UWB BS Deployment
4. Result and Discussion
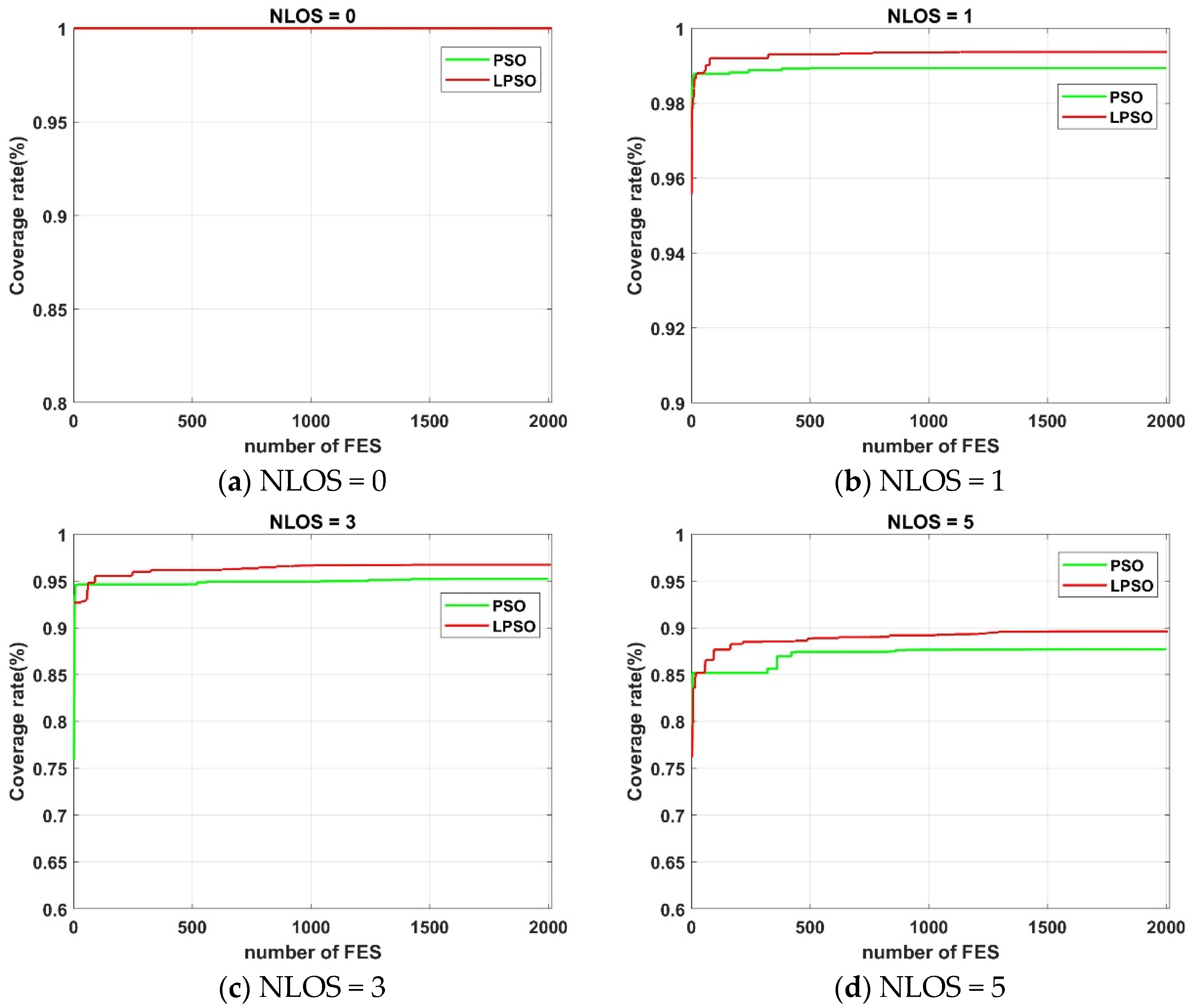
4.1. Experiment 1: Performance Verification Test
4.1.1. Simulation Experimental Data and Parameter Settings
4.1.2. Experimental Results and Analysis
4.2. Experiment 2: Deployment Experiment of UWB BS in Underground Garage
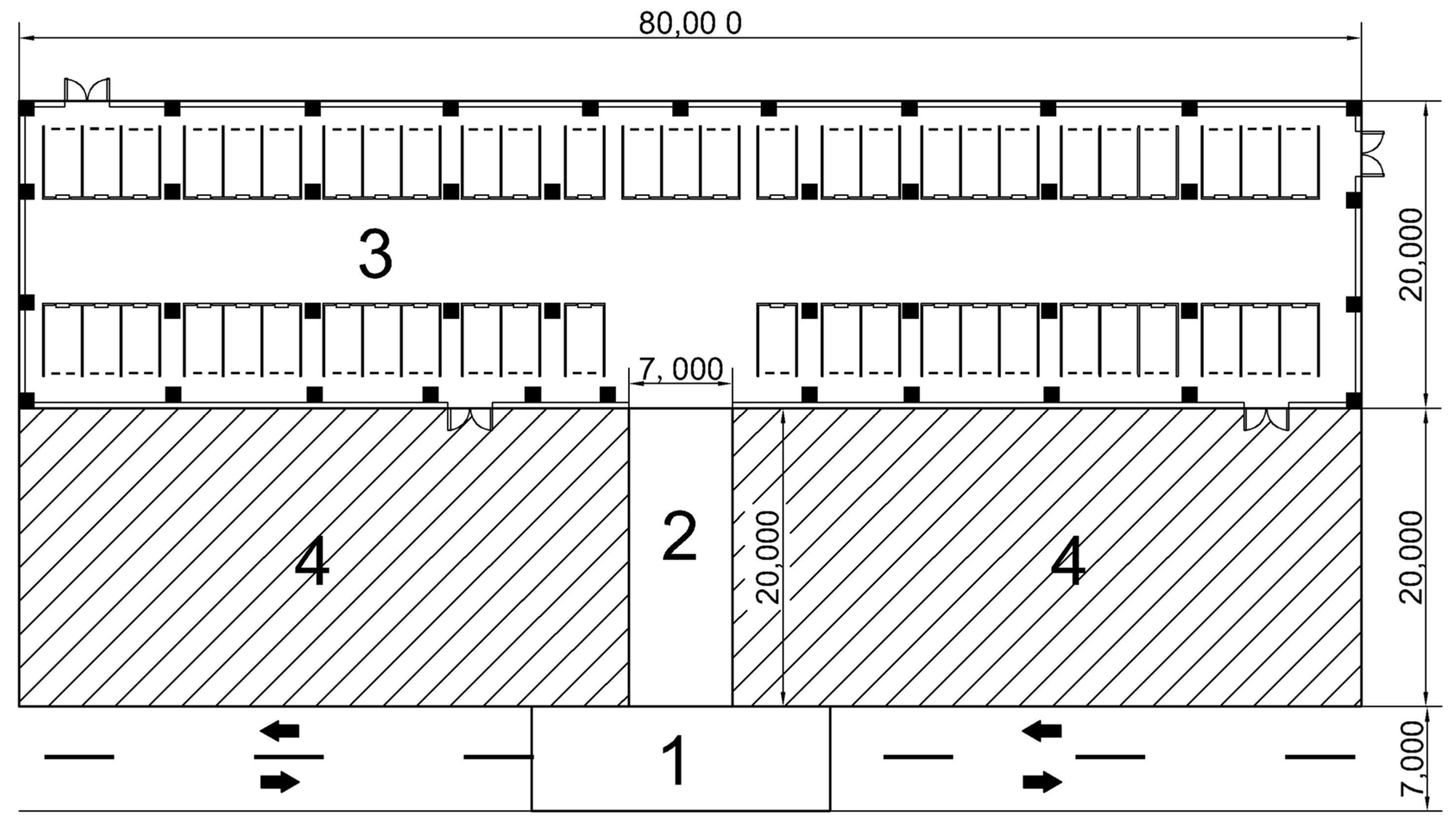
4.2.1. Parameter Setting and Layout Strategy
- (1)
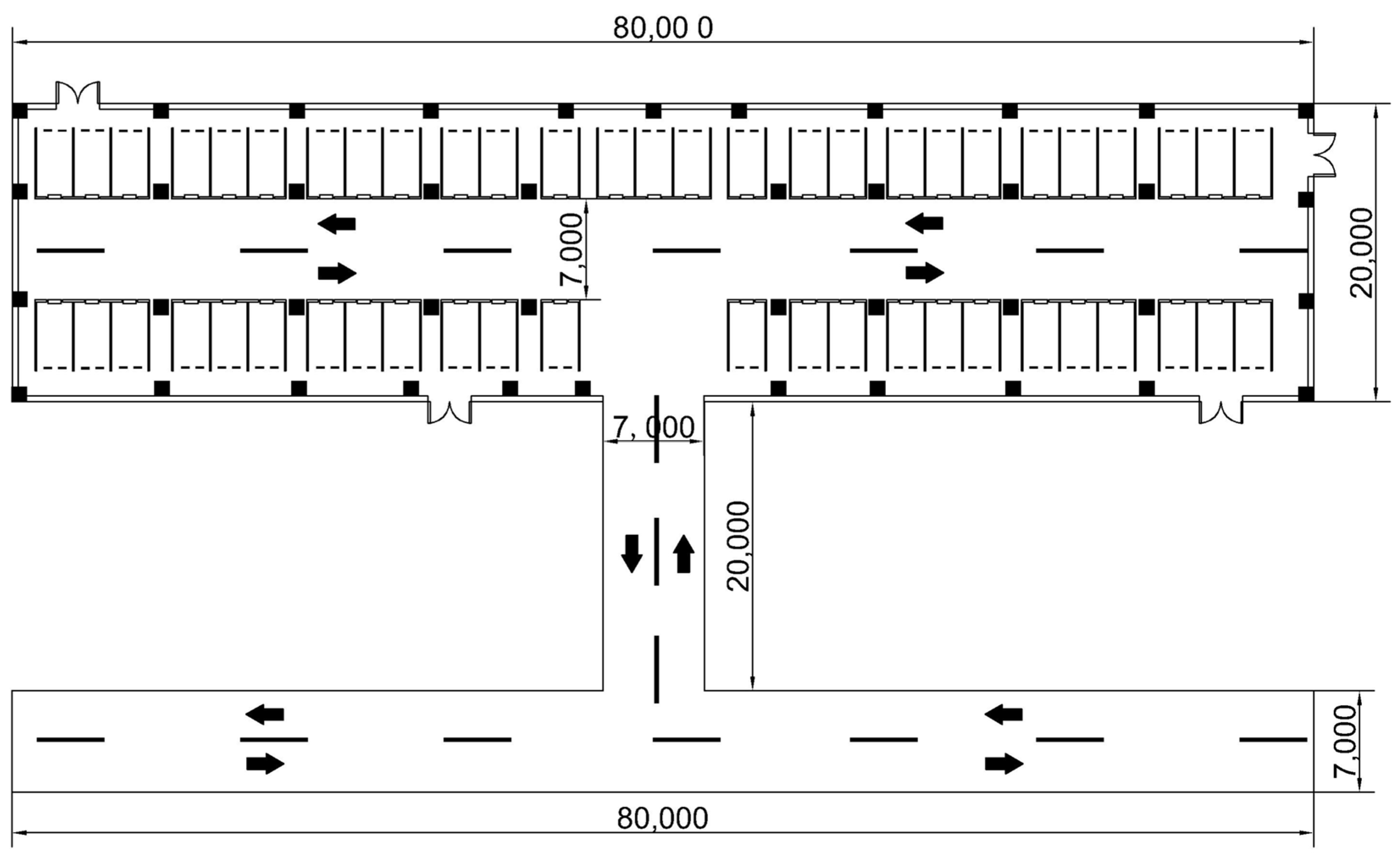
- Area 1 is the entrance and exit area of the parking lot, with a length of 20 m and a width of 7 m. It is the connection node between the urban road and the underground garage, and the vehicle driving environment is relatively complex. Based on the LPSO algorithm, the preliminary solution was used to establish that the BS layout method approximates the rectangular distribution. Considering the environmental characteristics of the large daily average vehicle flow in this region combined with the actual scene, in order to reduce the impact of the flow of personnel and vehicles and to make the wiring beautiful, a BS distribution scheme was adopted on both sides of the road, and a total of 2 pairs of 4 BSs were laid.
- (2)
- Area 2 is the entrance and exit ramp of the parking lot, with a length of 7 m and a width of 20 m. It is an area where vehicles frequently enter and exit the parking lot. At the same time, vehicles travel at a fast speed and have high positioning accuracy requirements. Similar to area 1, in order to ensure the coverage and accuracy of the BSs in this area, the HDOP value is the lowest when the BSs are uniformly placed. At the same time, considering the safety of driving and positioning equipment, the BSs are distributed in rectangles on both sides of the ramp inlet and outlet, with a total of 4.
- (3)
- Area 3 is the indoor area of the parking lot, with a relatively closed space and a complex structure. In this area, the driver needs to quickly find the parking position of the vehicle through the navigation and positioning function, which puts forward high requirements for the layout model of the UWB BS. The whole area is 80 m long and 20 m wide, which can be understood as a large rectangular area. Therefore, the LPSO algorithm proposed in this paper is adopted to optimize the BS location.
- (4)
- Area 4 is the blocked area of the concrete wall that is seriously disturbed and cannot be penetrated by the UWB BS. As such, the cocoa is set to contain two impenetrable blocks (NLOS = 2), both 35 m in length and 20 m in width.
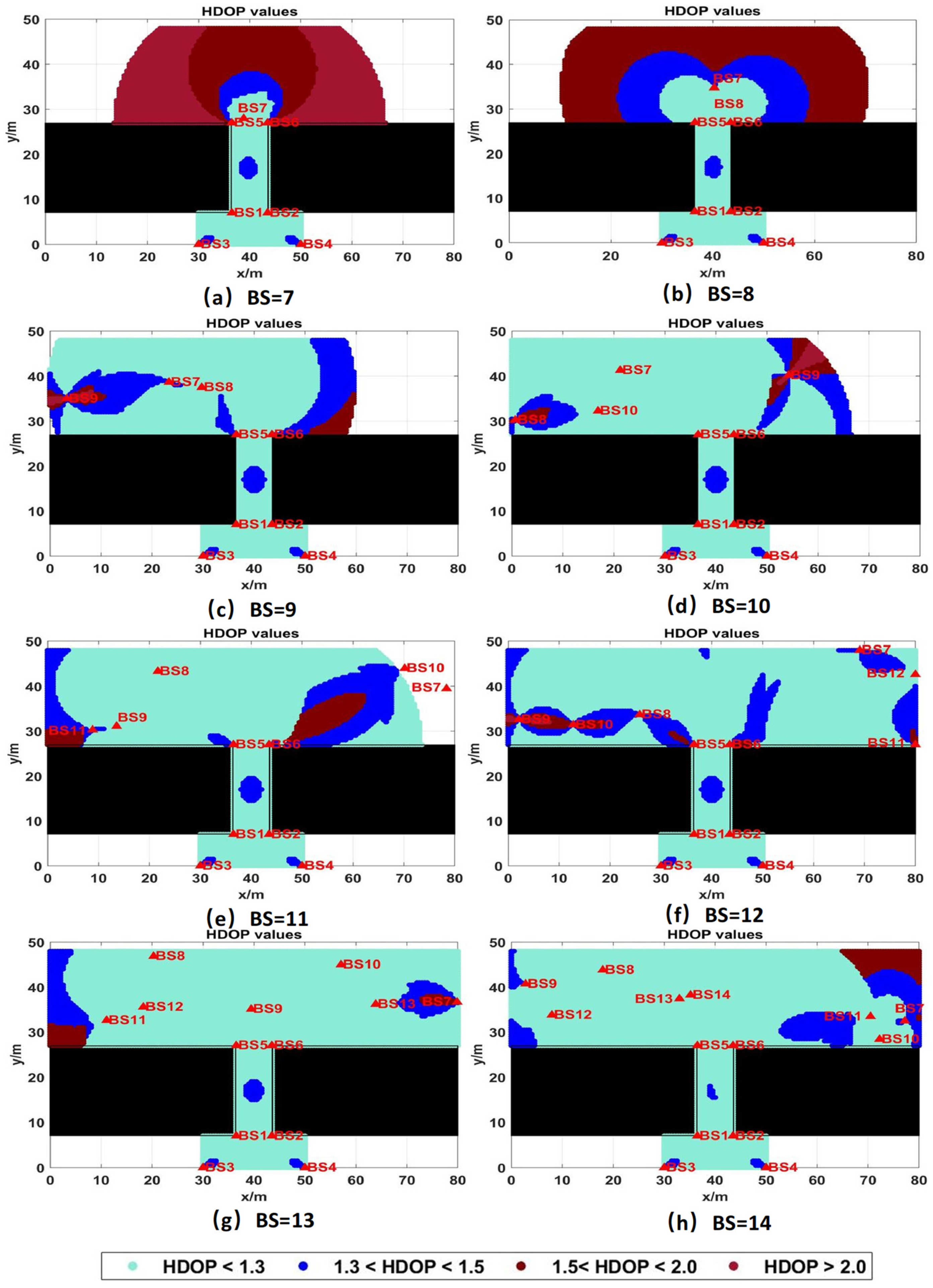
4.2.2. Evaluation of Layout Optimization Effect Under Different Number of BSs
5. Conclusions
- (1)
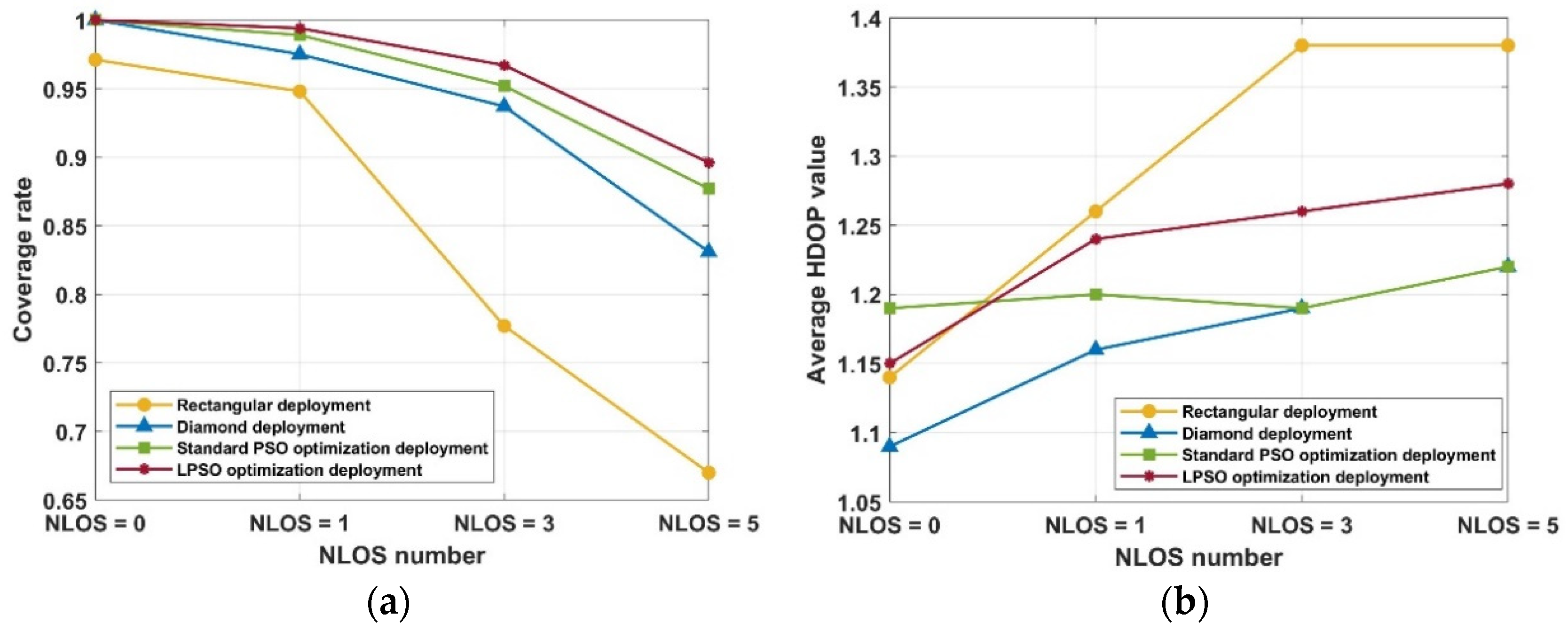
- The performance verification results show that the locatable space coverage rate of this new method is comparable to that of the diamond deployment and better than that of the rectangular deployment when there is no shading. The locatable space coverage rate of the LPSO-optimized deployment is improved by 19.0% and 22.6% compared to the rectangular deployment, and 3.0% and 6.5% compared to the diamond deployment, when the NLOS values are 3 and 5 for complex occlusion environments, respectively. Meanwhile, the LPSO deployment is better than the standard PSO deployment results and effectively decreases the blind positioning areas, while its average HDOP value is satisfactory.
- (2)
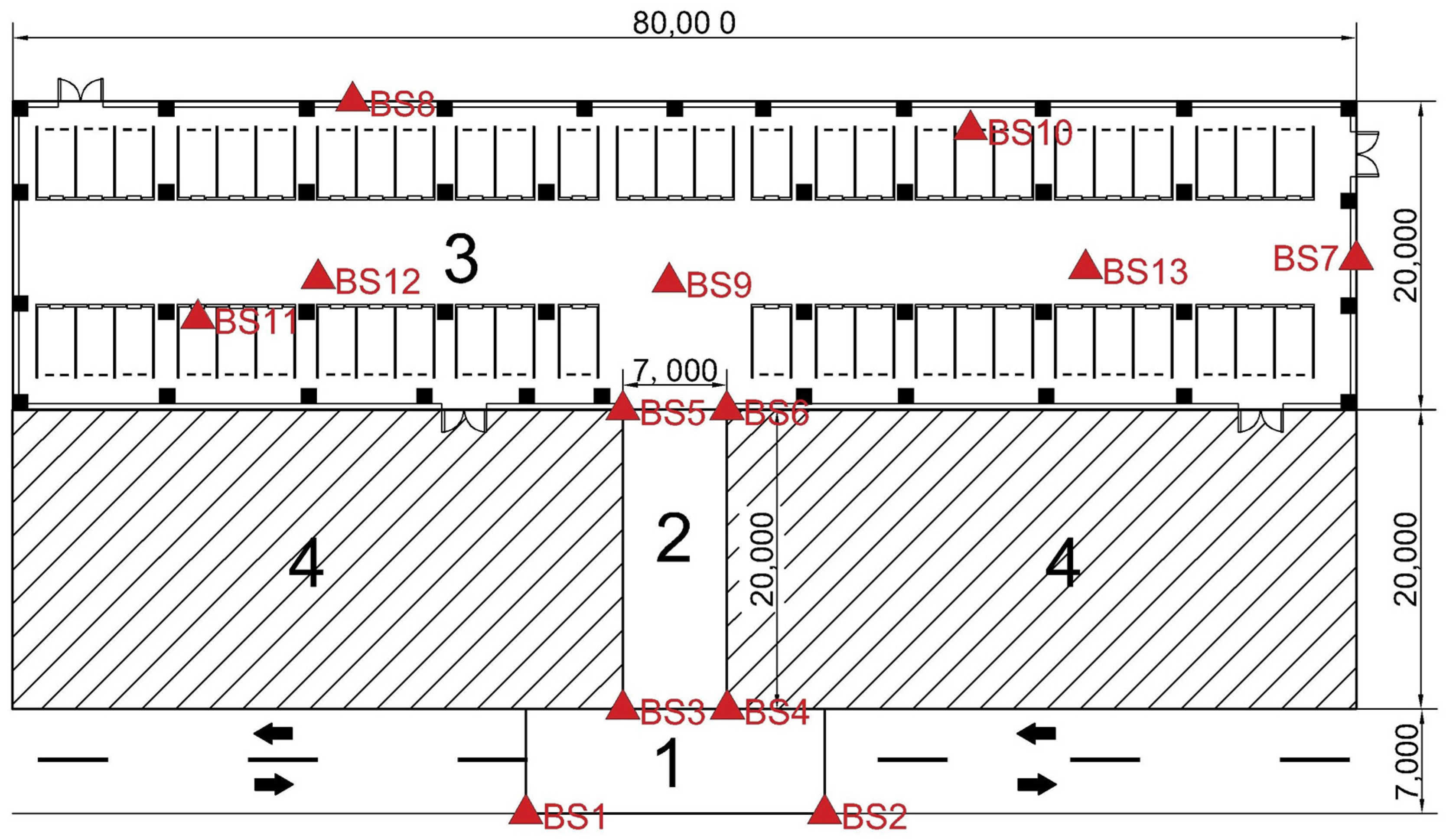
- The deployment experiment of UWB BSs in underground garage shows that compared with the 7-BS layout method with the fewest BSs, the coverage rate of the optimal 13-BS scheme is increased by 34.9%, and the HDOP value is decreased by 81.7%, which significantly improves the regional coverage rate. The comprehensive performance of the UWB layout station is greatly improved by fully taking into account the impact of the number of BSs and NLOS shielding.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, S.L.; Dong, X.S.; Liu, G.Y.; Gao, M.; Xiao, G.W.; Zhao, W.H.; Lv, D. GNSS RTK/UWB/DBA Fusion Positioning Method and Its Performance Evaluation. Remote Sens. 2022, 14, 5928. [Google Scholar] [CrossRef]
- Liu, T.; Liu, J.; Wang, J.; Zhang, H.; Zhang, B.; Ma, Y.; Sun, M.; Lv, Z.; Xu, G. Pseudolites to Support Location Services in Smart Cities: Review and Prospects. Smart Cities 2023, 6, 2081–2105. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, F.; Chen, J.X.; Ji, W. A Smart Parking System using WiFi and Wireless Sensor Network. In Proceedings of the 3rd IEEE International Conference on Consumer Electronics-Taiwan (ICCE-TW), Nantou, Taiwan, 27–29 May 2016; pp. 73–74. [Google Scholar]
- Faragher, R.; Harle, R. Location Fingerprinting with Bluetooth Low Energy Beacons. IEEE J. Sel. Areas Commun. 2015, 33, 2418–2428. [Google Scholar] [CrossRef]
- Zhuang, Y.; Yang, J.; Li, Y.; Qi, L.N.; El-Sheimy, N. Smartphone-Based Indoor Localization with Bluetooth Low Energy Beacons. Sensors 2016, 16, 596. [Google Scholar] [CrossRef]
- Khalili, B.; Abbaspour, R.A.; Chehreghan, A.; Vesali, N. A Context-Aware Smartphone-Based 3D Indoor Positioning Using Pedestrian Dead Reckoning. Sensors 2022, 22, 9968. [Google Scholar] [CrossRef]
- Piciarelli, C. Visual Indoor Localization in Known Environments. IEEE Signal Process Lett. 2016, 23, 1330–1334. [Google Scholar] [CrossRef]
- Rafian, P.; Legge, G.E. Remote Sighted Assistants for Indoor Location Sensing of Visually Impaired Pedestrians. ACM Trans. Appl. Percept. 2017, 14, 14. [Google Scholar] [CrossRef]
- Alarifi, A.; Al-Salman, A.; Alsaleh, M.; Alnafessah, A.; Al-Hadhrami, S.; Al-Ammar, M.A.; Al-Khalifa, H.S. Ultra wideband indoor positioning technologies: Analysis and recent advances. Sensors 2016, 16, 707. [Google Scholar] [CrossRef]
- Bastida-Castillo, A.; Gómez-Carmona, C.D.; De La Cruz Sánchez, E.; Pino-Ortega, J. Comparing accuracy between global positioning systems and ultra-wideband-based position tracking systems used for tactical analyses in soccer. Eur. J. Sport Sci. 2019, 19, 1157–1165. [Google Scholar] [CrossRef]
- Khosravi, F. Positioning of the Wheel Loader by Ultra Wideband Technology; Tampere University: Tampere, Finland, 2019. [Google Scholar]
- Yavari, M.; Nickerson, B.G. Ultra Wideband Wireless Positioning Systems; Faculty of Computer Science, University of New Brunswick: Fredericton, NB, Canada, 2014. [Google Scholar]
- Jourdan, D.B.; Dardari, D.; Win, M.Z. Position error bound for UWB localization in dense cluttered environments. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 613–628. [Google Scholar] [CrossRef]
- Yu, K.; Wen, K.; Li, Y.; Zhang, S.; Zhang, K. A Novel NLOS Mitigation Algorithm for UWB Localization in Harsh Indoor Environments. IEEE Trans. Veh. Technol. 2018, 68, 686–699. [Google Scholar] [CrossRef]
- Zhang, F.; Li, H.; Ding, Y.; Yang, S.H.; Yang, L. Dilution of precision for time difference of arrival with station deployment. IET Signal Proc. 2021, 15, 353–364. [Google Scholar] [CrossRef]
- Chen, W.J.; Narayanan, R.M. Antenna Placement for Minimizing Target Localization Error in UWB MIMO Noise Radar. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 135–138. [Google Scholar] [CrossRef]
- Levanon, N. Lowest GDOP in 2-D scenarios. IEE Proc.-Radar Sonar Navig. 2000, 147, 149–155. [Google Scholar] [CrossRef]
- Jiang, S.; Zhao, C.; Zhu, Y.; Wang, C.; Du, Y. A Practical and Economical Ultra-wideband Base Station Placement Approach for Indoor Autonomous Driving Systems. J. Adv. Transp. 2022, 2022, 3815306. [Google Scholar] [CrossRef]
- Wang, M.; Chen, Z.; Zhou, Z.; Fu, J.L.; Qiu, H.B. Analysis of the Applicability of Dilution of Precision in the Base Station Configuration Optimization of Ultrawideband Indoor TDOA Positioning System. IEEE Access 2020, 8, 225076–225087. [Google Scholar] [CrossRef]
- Yu, X.M.; Wang, H.Q.; Lv, H.W.; Liu, X.B.; Wu, J.Q. A fusion optimization algorithm of network element layout for indoor positioning. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 12. [Google Scholar] [CrossRef]
- Wang, S.L.; Liu, G.Y.; Gao, M.; Cao, S.L.; Guo, A.Z.; Wang, J.C. Heterogeneous comprehensive learning and dynamic multi- swarm particle swarm optimizer with two mutation operators. Inform. Sci. 2020, 540, 175–201. [Google Scholar] [CrossRef]
- Kennedy, J.; Mendes, R. Population structure and particle swarm performance. In Proceedings of the IEEE Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; IEEE: Piscataway, NJ, USA, 2002; pp. 1671–1676. [Google Scholar]
- Yang, X.S.; Deb, S. Engineering Optimisation by Cuckoo Search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330–343. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Hakli, H.; Uguz, H. A novel particle swarm optimization algorithm with Levy flight. Appl. Soft Comput. 2014, 23, 333–345. [Google Scholar] [CrossRef]
- James, J.; Caffery, J. Wireless Location in CDMA Cellular Radio Systems; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Wang, Y.C.; Tseng, Y.C. Distributed deployment schemes for mobile wireless sensor networks to ensure multilevel coverage. IEEE Trans. Parallel Distrib. Syst. 2008, 19, 1280–1294. [Google Scholar] [CrossRef]
- Ammari, H.M.; Das, S.K. Centralized and Clustered k-Coverage Protocols for Wireless Sensor Networks. IEEE Trans. Comput. 2012, 61, 118–133. [Google Scholar] [CrossRef]


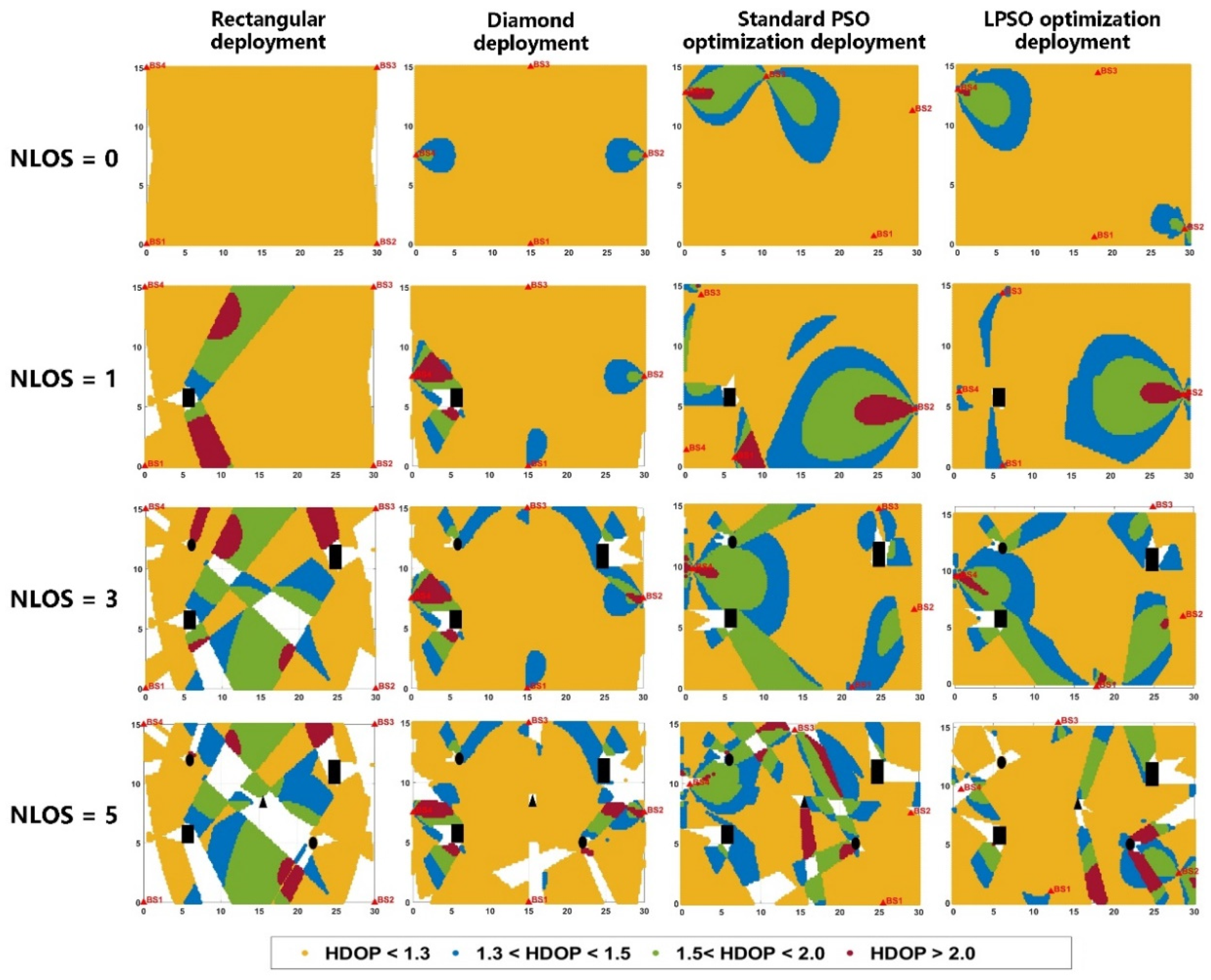
| Parameter | Occlusion Condition | Rectangular Deployment | Diamond Deployment | Standard PSO Deployment | LPSO Deployment |
|---|---|---|---|---|---|
| Coverage Rate | NLOS = 0 | 97.1% | 100% | 100% | 100% |
| NLOS = 1 | 94.8% | 97.5% | 99.0% | 99.4% | |
| NLOS = 3 | 77.7% | 93.7% | 96.4% | 96.7% | |
| NLOS = 5 | 67.0% | 83.1% | 88.3% | 89.8% | |
| Average HDOP | NLOS = 0 | 1.14 | 1.09 | 1.17 | 1.11 |
| NLOS = 1 | 1.26 | 1.16 | 1.34 | 1.24 | |
| NLOS = 3 | 1.38 | 1.19 | 1.29 | 1.21 | |
| NLOS = 5 | 1.38 | 1.22 | 1.29 | 1.24 |
| Scheme Index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Number of BSs | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Coverage Rate | 65.1% | 76.2% | 76.9% | 82.5% | 90.0% | 100% | 100% | 100% |
| Average HDOP value | 5.961 | 2.347 | 1.365 | 1.258 | 1.305 | 1.265 | 1.088 | 1.146 |
| Fitness value | 1.536 | 1.313 | 1.299 | 1.216 | 1.112 | 1.000 | 1.000 | 1.000 |
| BS | Coordinate Value/m | BS | Coordinate Value/m |
|---|---|---|---|
| BS1 | (36.5, 7) | BS8 | (20.3, 46.8) |
| BS2 | (43.5, 7) | BS9 | (39.4, 35.1) |
| BS3 | (30, 0) | BS10 | (57.1, 45.0) |
| BS4 | (50, 0) | BS11 | (11.1, 32.6) |
| BS5 | (36.5, 27) | BS12 | (18.3, 35.6) |
| BS6 | (43.5, 27) | BS13 | (63.9, 36.2) |
| BS7 | (79.9, 36.7) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Gao, M.; Li, L.; Lv, D.; Li, Y. UWB Base Station Deployment Optimization Method Considering NLOS Effects Based on Levy Flight-Improved Particle Swarm Optimizer. Sensors 2025, 25, 1785. https://doi.org/10.3390/s25061785
Wang S, Gao M, Li L, Lv D, Li Y. UWB Base Station Deployment Optimization Method Considering NLOS Effects Based on Levy Flight-Improved Particle Swarm Optimizer. Sensors. 2025; 25(6):1785. https://doi.org/10.3390/s25061785
Chicago/Turabian StyleWang, Shengliang, Ming Gao, Ling’ai Li, Dong Lv, and Yingqi Li. 2025. "UWB Base Station Deployment Optimization Method Considering NLOS Effects Based on Levy Flight-Improved Particle Swarm Optimizer" Sensors 25, no. 6: 1785. https://doi.org/10.3390/s25061785
APA StyleWang, S., Gao, M., Li, L., Lv, D., & Li, Y. (2025). UWB Base Station Deployment Optimization Method Considering NLOS Effects Based on Levy Flight-Improved Particle Swarm Optimizer. Sensors, 25(6), 1785. https://doi.org/10.3390/s25061785








