Integration of Artificial Neural Network Regression and Principal Component Analysis for Indoor Visible Light Positioning
Abstract
1. Introduction
2. System Model
2.1. Communication Model
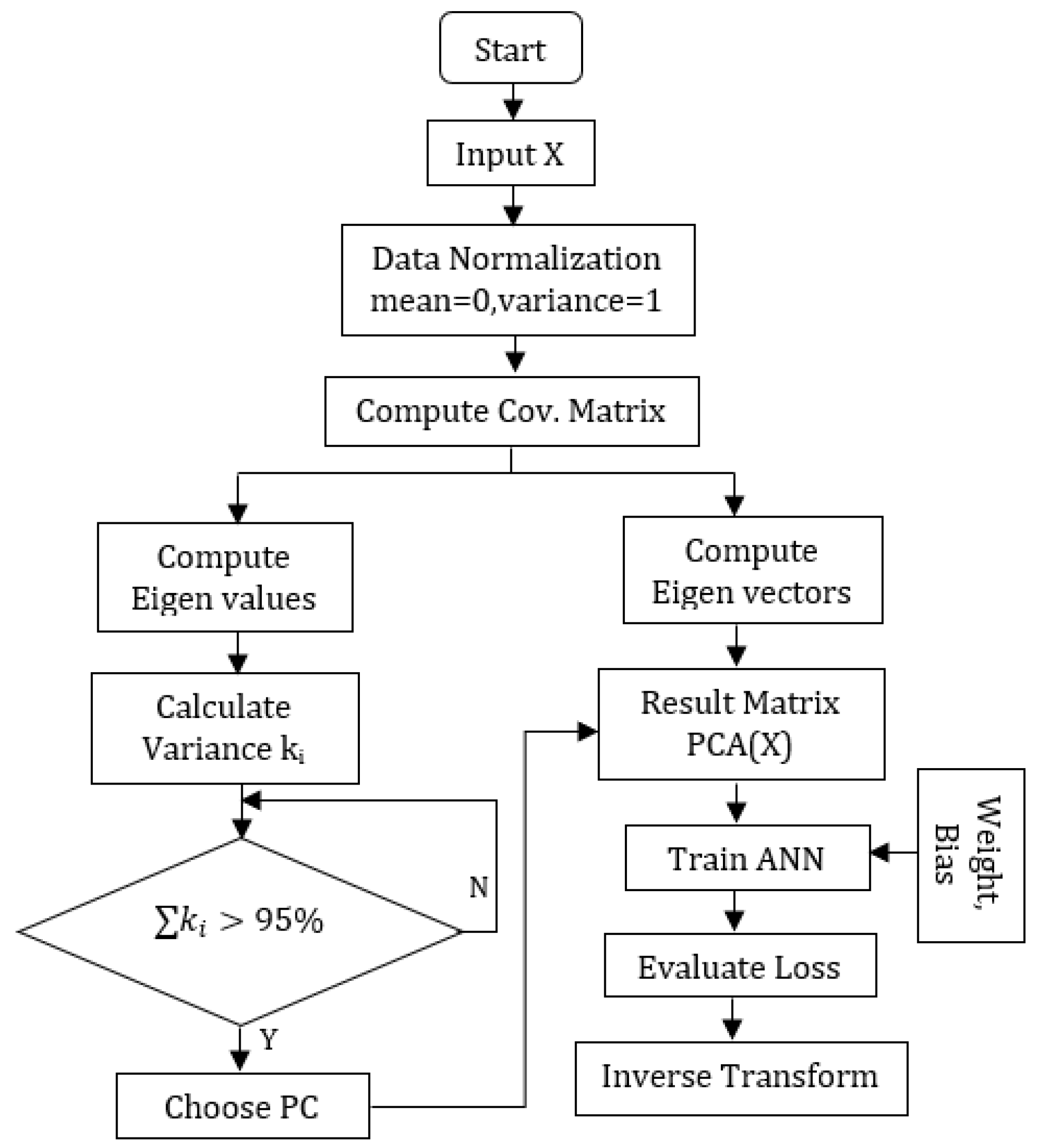
2.2. Principal Component Analysis (PCA)
| Algorithm 1:PCA-ANN Algorithm |
|
2.3. Artificial Neural Network Regression
3. Experimental Parameters
3.1. Datasets
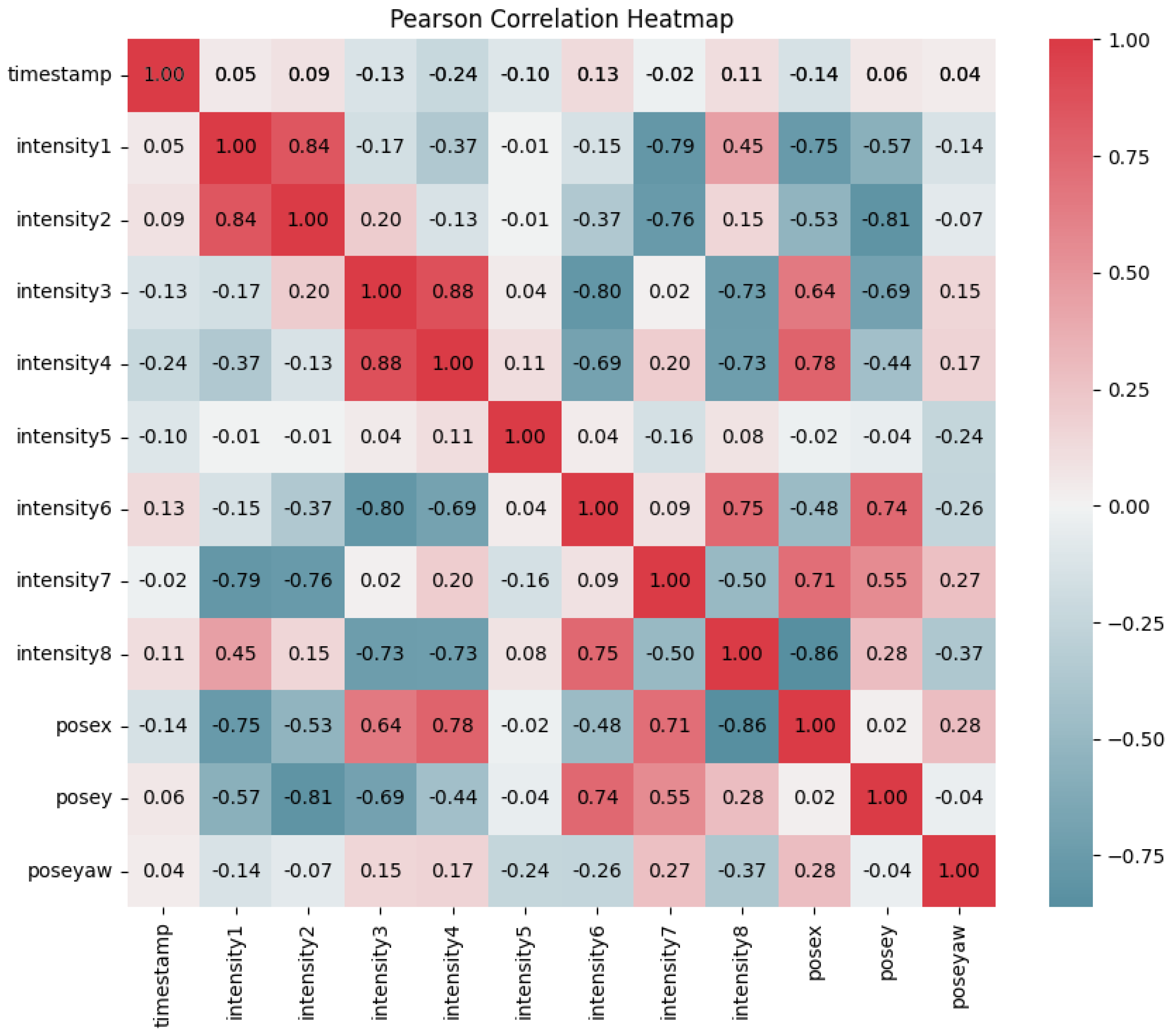
3.2. Pearson Correlation Coefficient
3.3. Performance Metrics
4. Results and Discussion
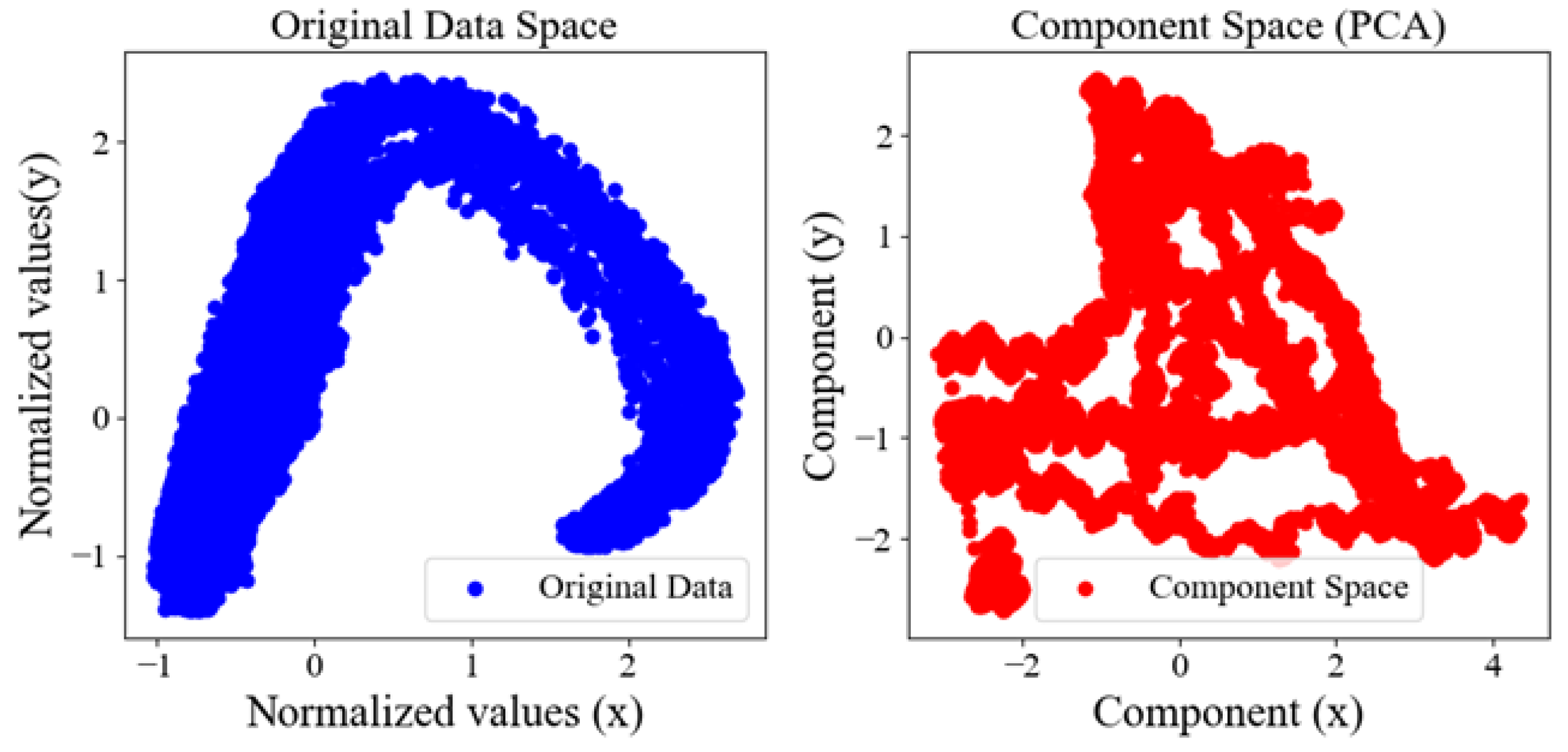
4.1. PCA Analysis
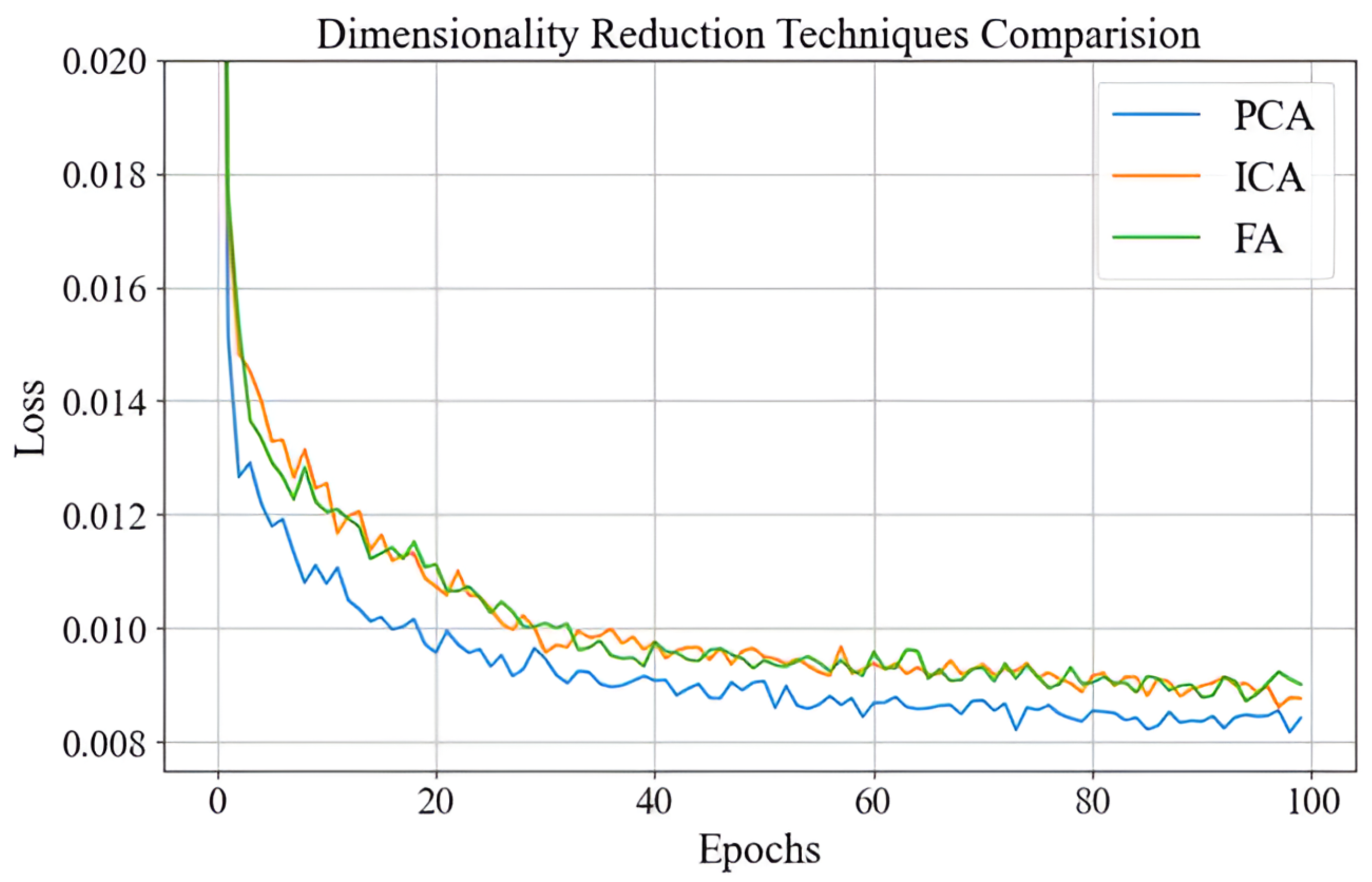
4.2. Comparison of Dimensionality Reduction Techniques
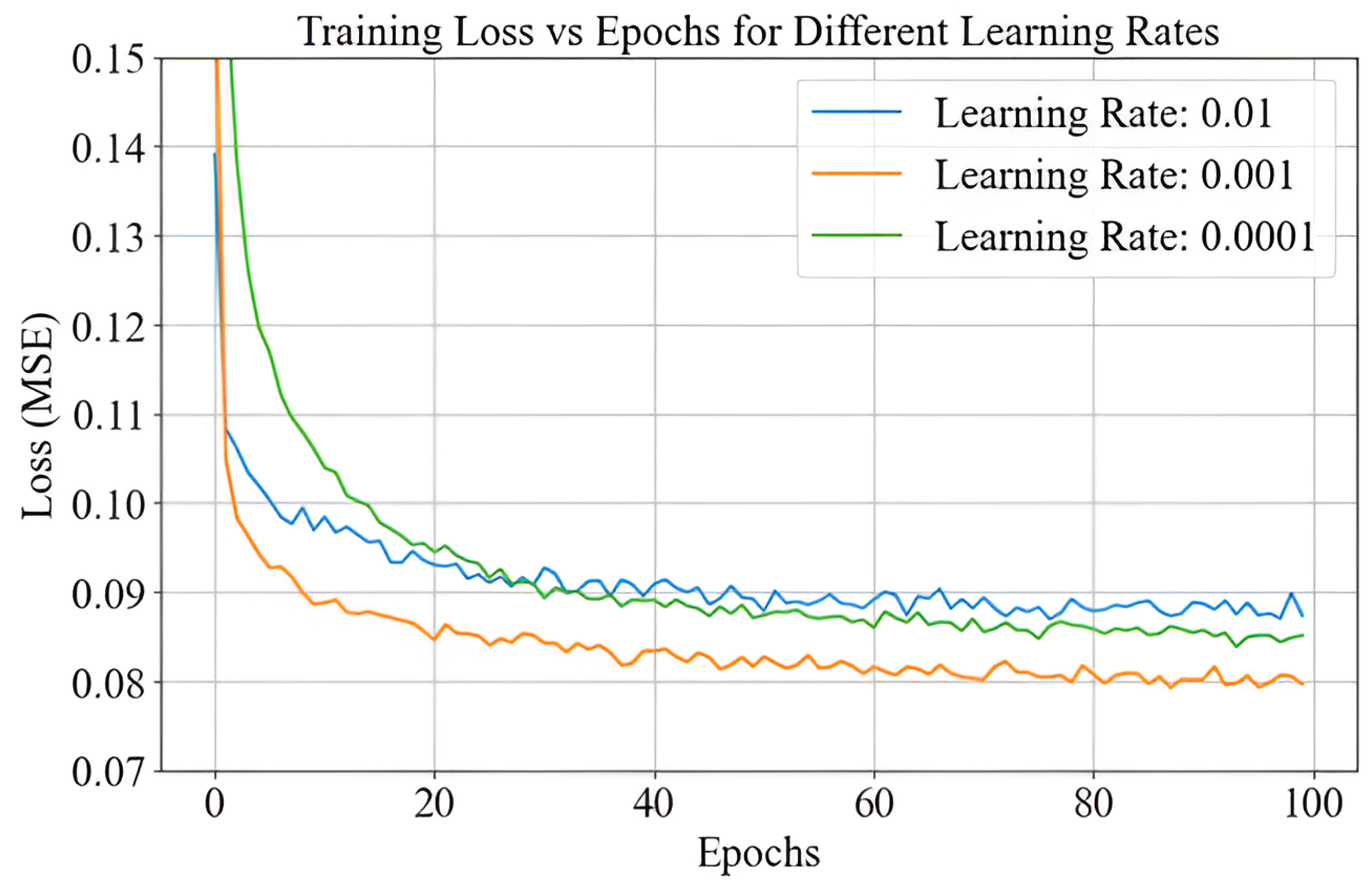
4.3. Effectiveness of PCA-ANN with Learning Rate
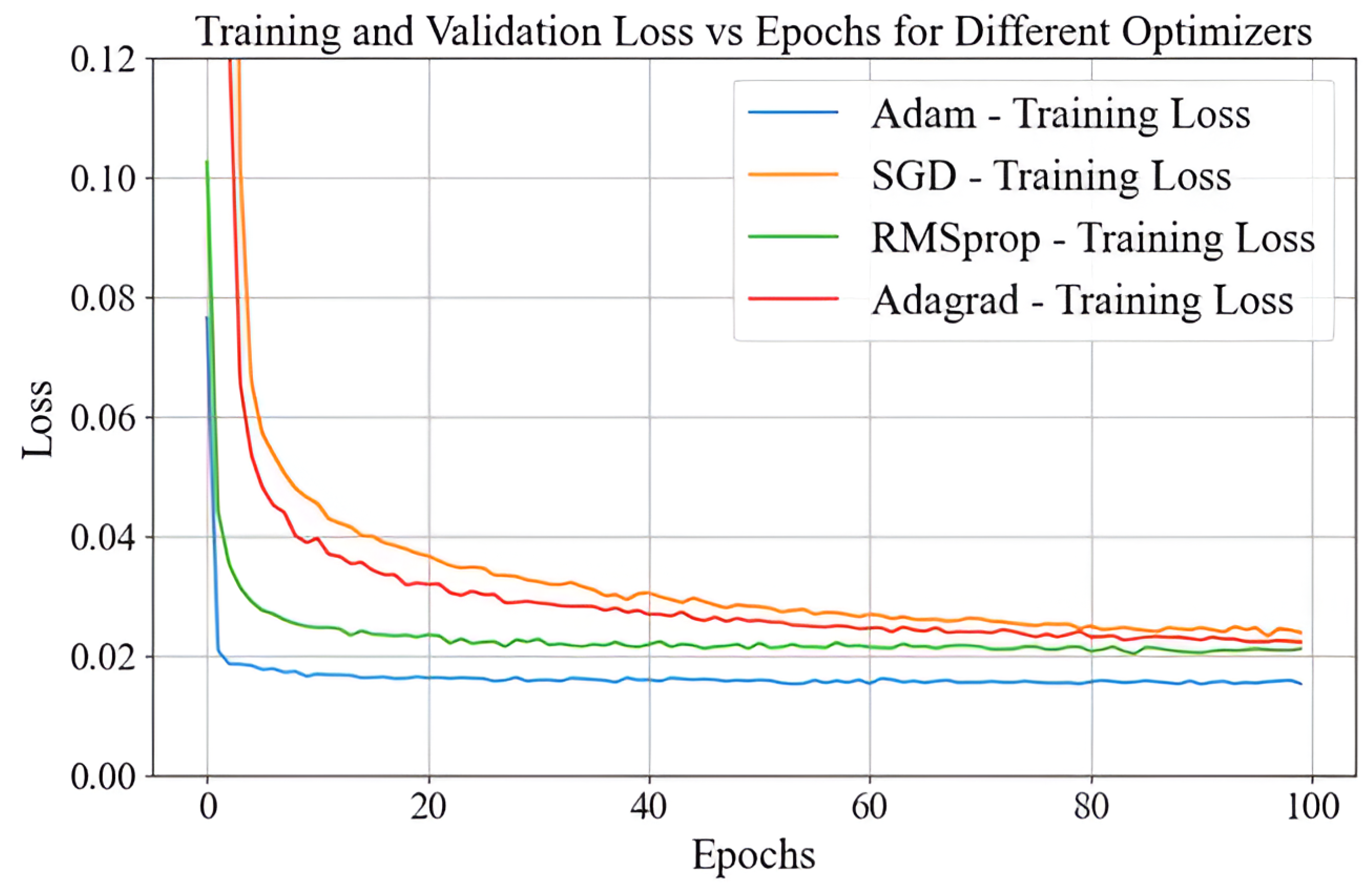
4.4. Optimizer Selection
4.5. Batch Size Impact
4.6. Selection of Optimal Dropout Rate
4.7. Hyperparameter Optimization
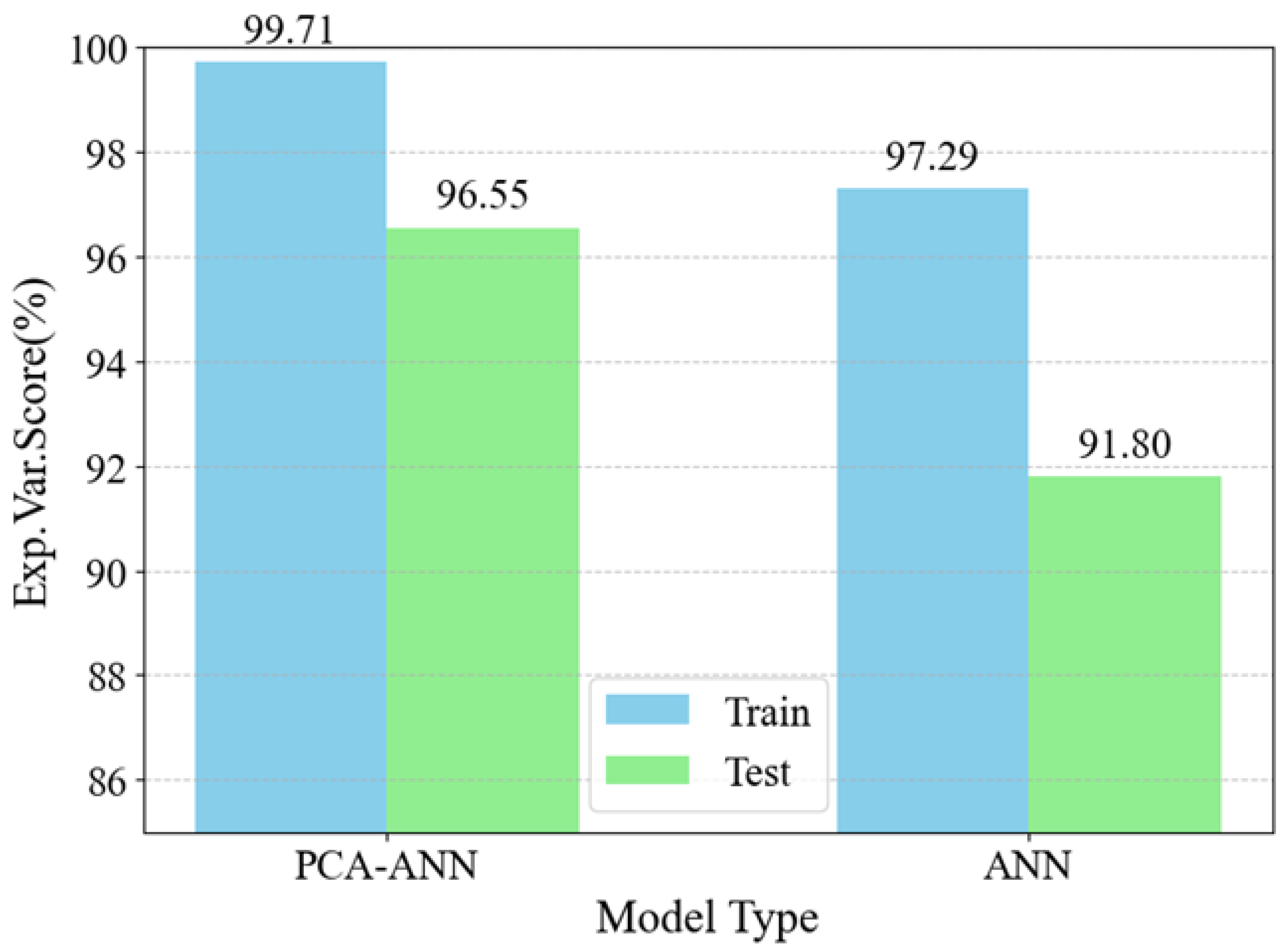
4.8. Model Evaluation
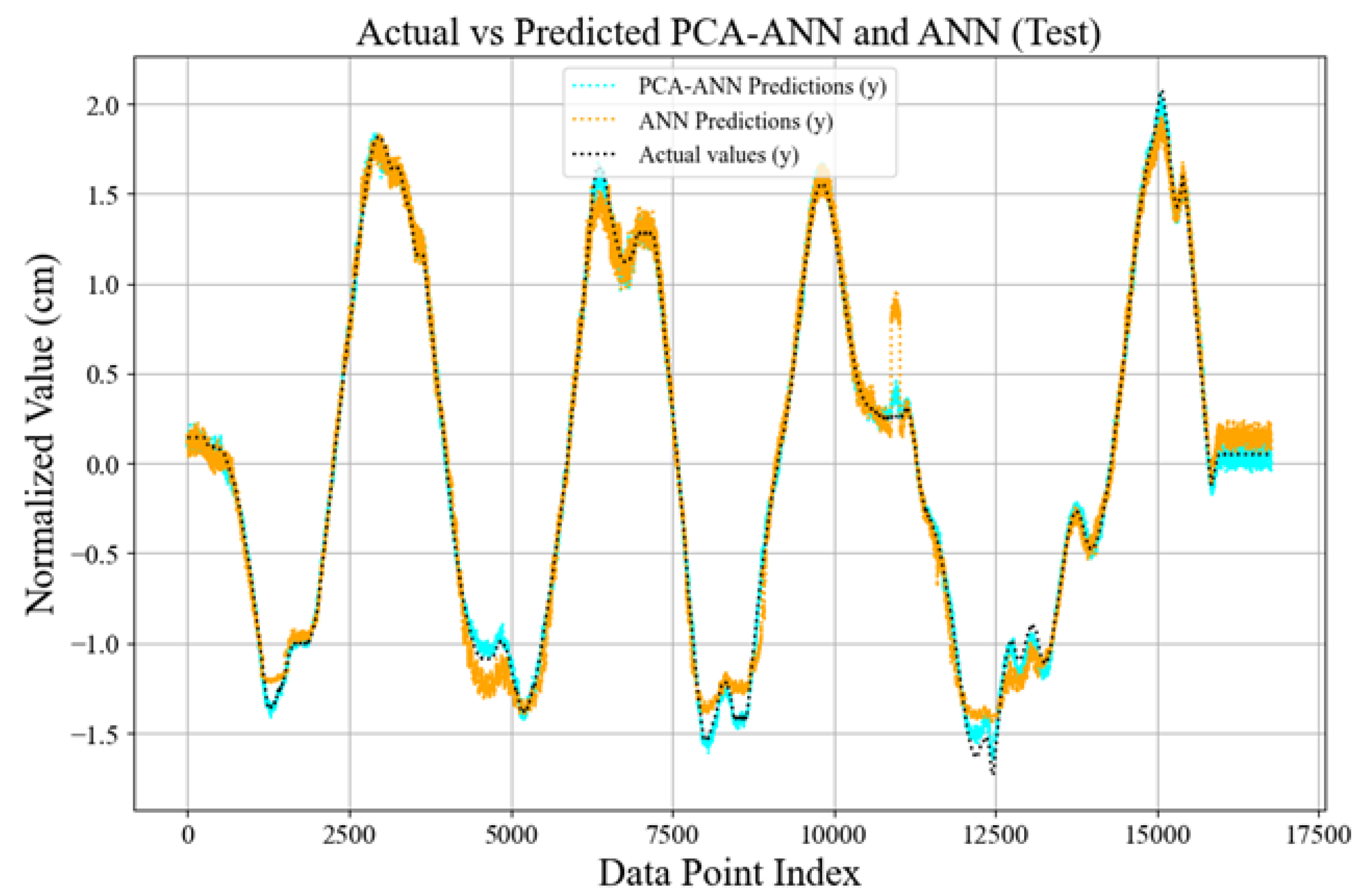
4.9. Comparison of Actual and Predicted Values
4.10. Comparison of PCA-ANN and MLP Cellular Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khan, L.U. Visible light communication: Applications, architecture, standardization and research challenges. Digit. Commun. Netw. 2017, 3, 78–88. [Google Scholar] [CrossRef]
- Steendam, H.; Wang, T.Q.; Armstrong, J. Cramer-Rao bound for indoor visible light positioning using an aperture-based angular-diversity receiver. In Proceedings of the 2016 IEEE International Conference on Communications, ICC 2016, Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Ghassemlooy, Z.; Popoola, W.; Rajbhandari, S. Optical Wireless Communications. CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar] [CrossRef]
- Borah, D.K.; Boucouvalas, A.C.; Davis, C.C.; Hranilovic, S.; Yiannopoulos, K. A review of communication-oriented optical wireless systems. Eurasip J. Wirel. Commun. Netw. 2012, 2012, 91. [Google Scholar] [CrossRef]
- Wu, Y.C.; Hsu, K.L.; Liu, Y.; Hong, C.Y.; Chow, C.W.; Yeh, C.H.; Liao, X.L.; Lin, K.H.; Chen, Y.Y. Using linear interpolation to reduce the training samples for regression based visible light positioning system. IEEE Photonics J. 2020, 12, 1–5. [Google Scholar] [CrossRef]
- Hsu, L.-S.; Chow, C.-W.; Liu, Y.; Yeh, C.-H. 3D Visible Light-Based Indoor Positioning System Using Two-Stage Neural Network (TSNN) and Received Intensity Selective Enhancement (RISE) to Alleviate Light Non-Overlap Zones. Sensors 2022, 22, 8817. [Google Scholar] [CrossRef]
- Alam, F.; Chew, M.T.; Wenge, T.; Gupta, G.S. An Accurate Visible Light Positioning System Using Regenerated Fingerprint Database Based on Calibrated Propagation Model. IEEE Trans. Instrum. Meas. 2019, 68, 2714–2723. [Google Scholar] [CrossRef]
- Long, Q.; Zhang, J.; Cao, L.; Wang, W. Indoor Visible Light Positioning System Based on Point Classification Using Artificial Intelligence Algorithms. Sensors 2023, 23, 5224. [Google Scholar] [CrossRef] [PubMed]
- Nessa, A.; Adhikari, B.; Hussain, F.; Fernando, X.N. A Survey of Machine Learning for Indoor Positioning. IEEE Access 2020, 8, 214945–214965. [Google Scholar] [CrossRef]
- Raes, W.; Knudde, N.; De Bruycker, J.; Dhaene, T.; Stevens, N. Experimental evaluation of machine learning methods for robust received signal strength-based visible light positioning. Sensors 2020, 20, 6109. [Google Scholar] [CrossRef] [PubMed]
- Raes, W.; Bruycker, J.D.; Stevens, N. A Cellular Approach for Large Scale, Machine Learning Based Visible Light Positioning Solutions. In Proceedings of the 2021 International Conference on Indoor Positioning and Indoor Navigation, IPIN 2021, Lloret de Mar, Spain, 29 November–2 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Keskin, M.F.; Gezici, S. Comparative Theoretical Analysis of Distance Estimation in Visible Light Positioning Systems. J. Light. Technol. 2016, 34, 854–865. [Google Scholar] [CrossRef]
- Naz, A.; Asif, H.M.; Umer, T.; Kim, B.S. PDOA Based Indoor Positioning Using Visible Light Communication. IEEE Access 2018, 6, 7557–7564. [Google Scholar] [CrossRef]
- Wu, Y.C.; Chow, C.W.; Liu, Y.; Lin, Y.S.; Hong, C.Y.; Lin, D.C.; Song, S.H.; Yeh, C.H. Received-Signal-Strength (RSS) Based 3D Visible-Light-Positioning (VLP) System Using Kernel Ridge Regression Machine Learning Algorithm with Sigmoid Function Data Preprocessing Method. IEEE Access 2020, 8, 214269–214281. [Google Scholar] [CrossRef]
- Chaudhary, N.; Alves, L.N.; Ghassemblooy, Z. Current trends on visible light positioning techniques. In Proceedings of the 2nd West Asian Colloquium on Optical Wireless Communications, WACOWC 2019, Tehran, Iran, 27–28 April 2019; pp. 100–105. [Google Scholar] [CrossRef]
- Sanguansat, P. Principal Component Analysis—Engineering Applications; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Dubey, S.R.; Singh, S.K.; Chaudhuri, B.B. Activation functions in deep learning: A comprehensive survey and benchmark. Neurocomputing 2022, 503, 92–108. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Hauke, J.; Kossowski, T. Comparison of values of pearson’s and spearman’s correlation coefficients on the same sets of data. Quaest. Geogr. 2011, 30, 87–93. [Google Scholar] [CrossRef]
- Rahman, M.M.; Berger, D.; Levman, J. Novel Metrics for Evaluation and Validation of Regression-based Supervised Learning. In Proceedings of the IEEE Asia-Pacific Conference on Computer Science and Data Engineering, CSDE 2022, Gold Coast, Australia, 18–20 December 2022. [Google Scholar] [CrossRef]
- Rekkas, V.P.; Sotiroudis, S.; Plets, D.; Joseph, W.; Goudos, S.K. Visible Light Positioning: A Machine Learning Approach. In Proceedings of the 7th South-East Europe Design Automation, Computer Engineering, Computer Networks and Social Media Conference, SEEDA-CECNSM 2022, Ioannina, Greece, 23–25 September 2022. [Google Scholar] [CrossRef]
- LaHuis, D.M.; Hartman, M.J.; Hakoyama, S.; Clark, P.C. Explained Variance Measures for Multilevel Models. Organ. Res. Methods 2014, 17, 433–451. [Google Scholar] [CrossRef]
- Masters, D.; Luschi, C. Revisiting Small Batch Training for Deep Neural Networks. arXiv 2017, arXiv:1804.07612v1. [Google Scholar]
- Cao, L.J.; Chua, K.S.; Chong, W.K.; Lee, H.P.; Gu, Q.M. A comparison of PCA, KPCA and ICA for dimensionality reduction in support vector machine. Neurocomputing 2003, 55, 321–336. [Google Scholar] [CrossRef]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Bengio, Y.; Goodfellow, I.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Volume 29, pp. 1–73. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]






| System Parameters | Parameter Value |
|---|---|
| Simulation Space | |
| Room dimensions | 12 m × 18 m |
| Room height | 6.81 m |
| Receiver placement height | 1.1 m |
| Distance between Tx and Rx | 5.71 m |
| Dataset taken | 5 cm inter-distance |
| Optical Transmitter | |
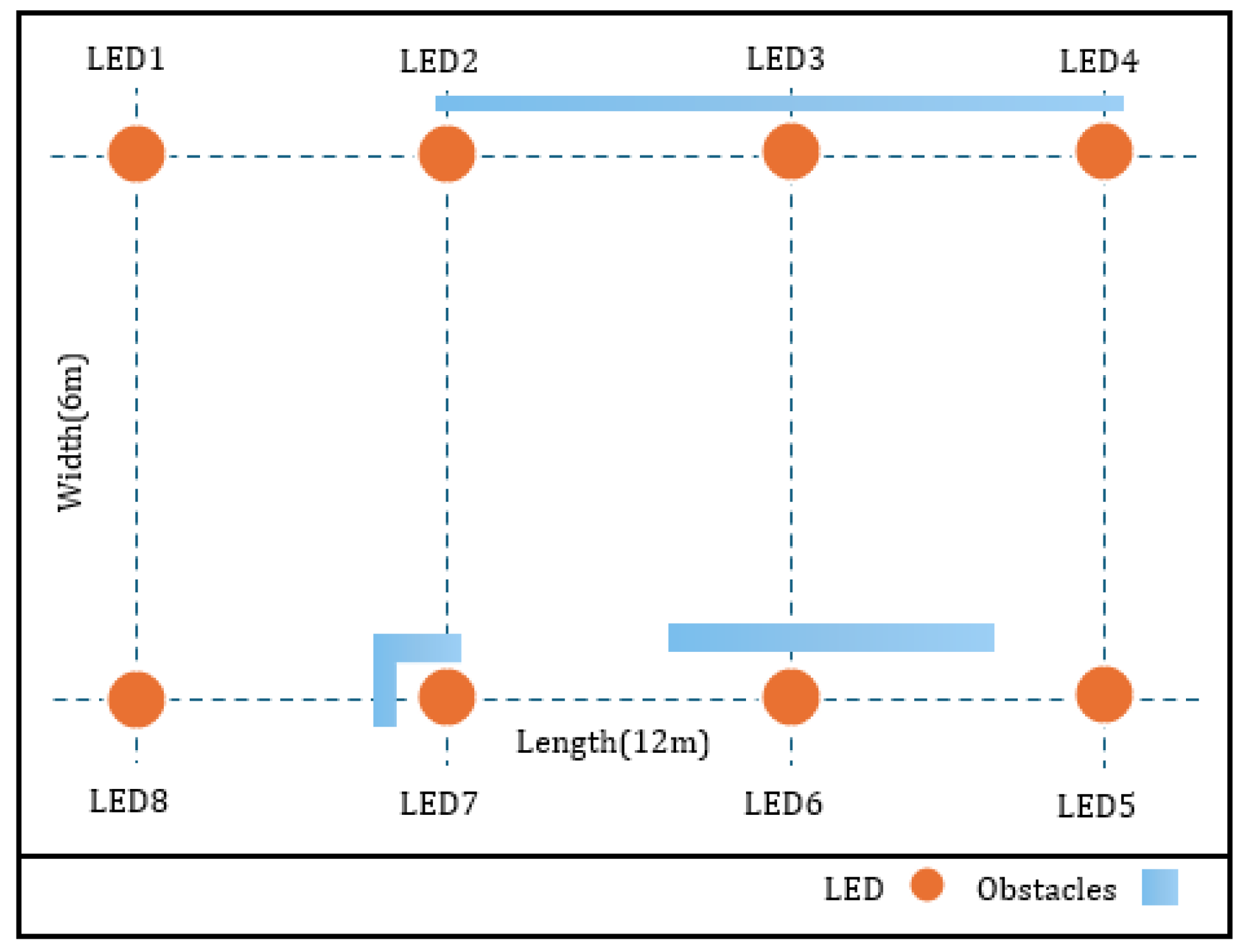
| Number of LEDs | 8 |
| Dimension of LED grid | 6 m × 12 m |
| LED power | 25 W |
| LED bandwidth | 3 MHz |
| Data rate | 2 Mbps |
| Optical Receiver | |
| Photodiode area size | 13 mm2 |
| Transimpedance gain | 40 k |
| DC-bias voltage | 1.024 V |
| Low pass filter cut-off frequency | 36 kHz |
| Sampling frequency | 128 kHz |
| ADC range | 2.048 V |
| ADC resolution | 14-bit |
| PC | Explained Variance | Eigenvalues | CR (%) | Cumulative CR (%) |
|---|---|---|---|---|
| PC1 | 0.345 | 2.757 | 35.314 | 35.314 |
| PC2 | 0.320 | 2.558 | 32.762 | 68.076 |
| PC3 | 0.169 | 1.350 | 17.294 | 85.370 |
| PC4 | 0.108 | 0.864 | 11.060 | 96.430 |
| PC5 | 0.035 | 0.279 | 3.570 | 100.000 |
| Learning Rate | Dropout Rate | Batch Size | Mean Test Score | MSE | R² Score |
|---|---|---|---|---|---|
| 0.001 | 0.1 | 64 | 0.016 | 0.006 | 0.993 |
| 0.001 | 0.2 | 64 | 0.021 | 0.008 | 0.988 |
| 0.001 | 0.1 | 32 | 0.020 | 0.010 | 0.984 |
| 0.010 | 0.1 | 64 | 0.057 | 0.095 | 0.882 |
| 0.010 | 0.1 | 32 | 0.045 | 0.013 | 0.980 |
| 0.010 | 0.2 | 64 | 0.048 | 0.018 | 0.963 |
| 0.0001 | 0.1 | 64 | 0.031 | 0.010 | 0.986 |
| 0.0001 | 0.1 | 32 | 0.028 | 0.010 | 0.986 |
| Metrics | PCA-ANN Train | ANN Train | PCA-ANN Test | ANN Test |
|---|---|---|---|---|
| R-squared (%) | 99.31 | 97.14 | 94.74 | 91.04 |
| MSE (cm) | 0.0062 | 0.0292 | 0.0456 | 0.0989 |
| MAE (cm) | 0.0532 | 0.1124 | 0.1456 | 0.1567 |
| RMSE (cm) | 0.0787 | 0.2225 | 0.1890 | 0.2850 |
| Model Property | PCA-ANN Model | MLP Cellular Model |
|---|---|---|
| Number of Inputs | 8 | 8 |
| Number of Hidden Layers | 3 | 3 |
| Nodes per Layer | 64-32-16 | 64-32-16 |
| Number of Hidden Nodes | 112 | 112 |
| Learning Type | Supervised | Supervised |
| Error Metric | Euclidean Distance | Euclidean Distance |
| Environment Size | 12 m × 18 m | 12 m × 18 m |
| Feature Source | LED Signal Intensities | LED Signal Intensities |
| LED Configuration | Rectangular Grid (8 LEDs) | Rectangular Grid (8 LEDs) |
| Receiver Device | PD based | PD based |
| Aspect | PCA-ANN Model | MLP Cellular Model | Key Advantage of PCA-ANN |
|---|---|---|---|
| Dimensionality Reduction | PCA applied | None | Simplifies data, reducing complexity and improving feature selection. |
| P50 Error (cm) | 0.49 | 4.3 | Reduces the median error by 88.3%, showing significant precision. |
| P95 Error (cm) | 1.36 | 16.6 | Reduces the worst-case error by 91.8%, improving robustness. |
| Trainable Parameters | 19,360 | 3218 | Captures intricate patterns, improving accuracy. |
| Optimizer | Adam (LR: 0.001) | Not specified | Ensures faster and stable convergence. |
| Dataset | Unified dataset | Divided by cells | Simplifies training by eliminating the need for separate datasets. |
| Classification | None | KNN (98.7%) | Removes dependency on subspace classifiers. |
| Scalability | High | Moderate | Scales better to larger or more complex setups with fewer adjustments. |
| Complexity | Simple | High | Avoids the need for cell-specific models and classifiers. |
| Overfitting Risk | Low (due to PCA) | Moderate | Reduces overfitting by emphasizing essential features. |
| Optimization Method | PCA-enhanced ANN | Direct MLP | Balances complexity and accuracy through preprocessing. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fite, N.B.; Wegari, G.M.; Steendam, H. Integration of Artificial Neural Network Regression and Principal Component Analysis for Indoor Visible Light Positioning. Sensors 2025, 25, 1049. https://doi.org/10.3390/s25041049
Fite NB, Wegari GM, Steendam H. Integration of Artificial Neural Network Regression and Principal Component Analysis for Indoor Visible Light Positioning. Sensors. 2025; 25(4):1049. https://doi.org/10.3390/s25041049
Chicago/Turabian StyleFite, Negasa Berhanu, Getachew Mamo Wegari, and Heidi Steendam. 2025. "Integration of Artificial Neural Network Regression and Principal Component Analysis for Indoor Visible Light Positioning" Sensors 25, no. 4: 1049. https://doi.org/10.3390/s25041049
APA StyleFite, N. B., Wegari, G. M., & Steendam, H. (2025). Integration of Artificial Neural Network Regression and Principal Component Analysis for Indoor Visible Light Positioning. Sensors, 25(4), 1049. https://doi.org/10.3390/s25041049







