Research on Interferometric Tilt Sensor for Vibration Isolation Platform
Abstract
1. Introduction
2. Tilt Signal Measurement Method
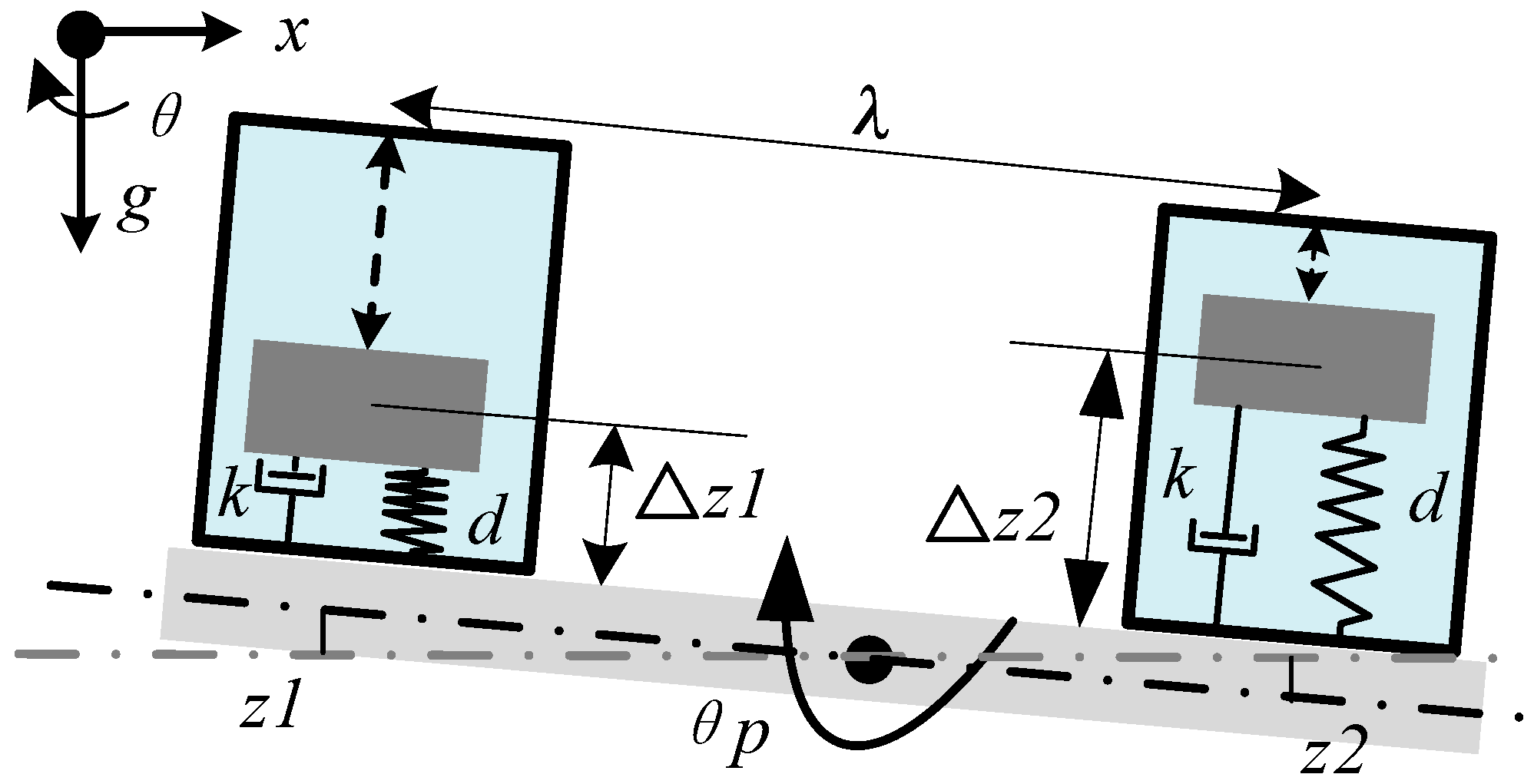
2.1. Differential-Mode Method
2.2. The Balanced Beam Method
3. Development of ITS
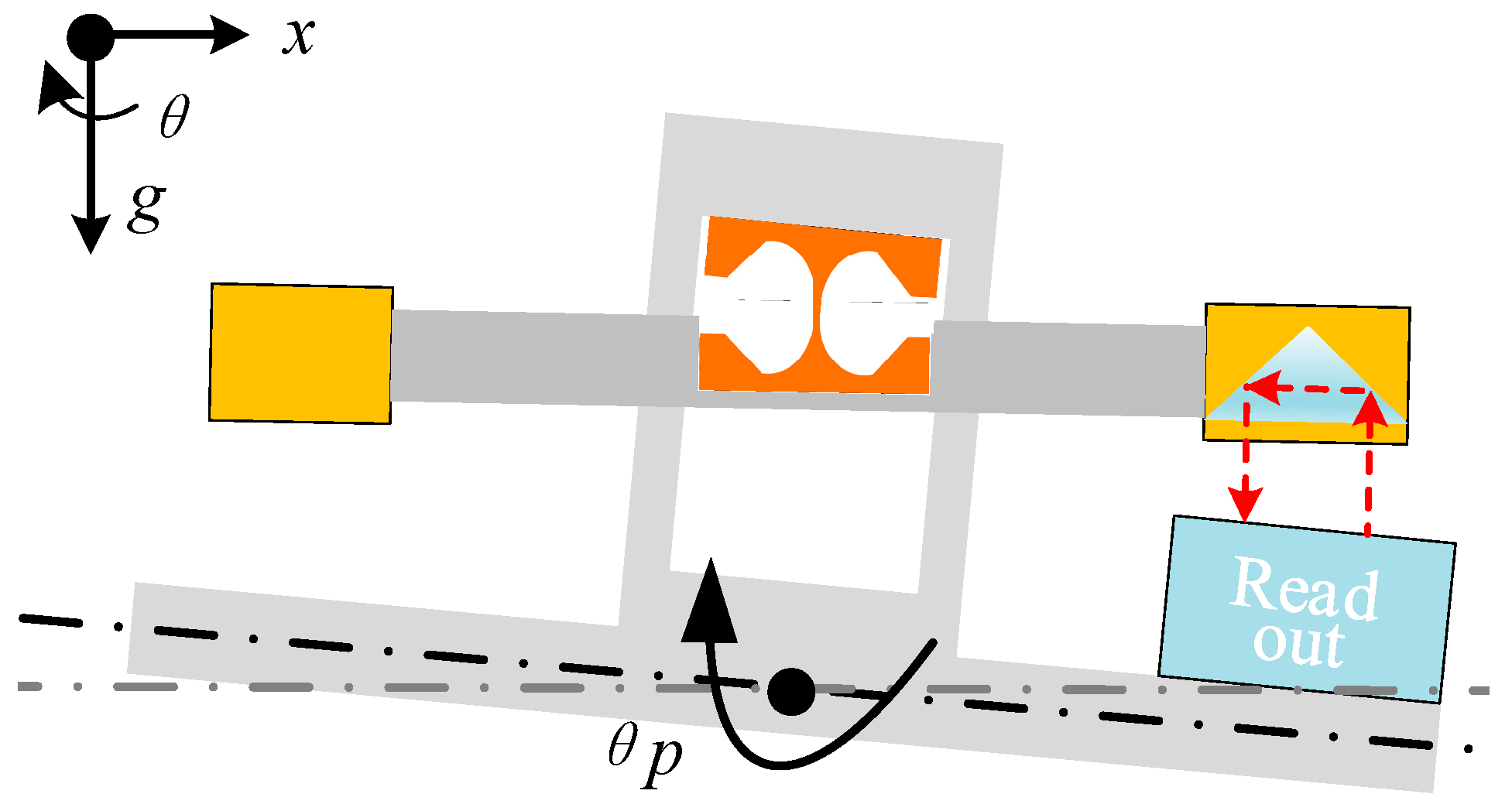
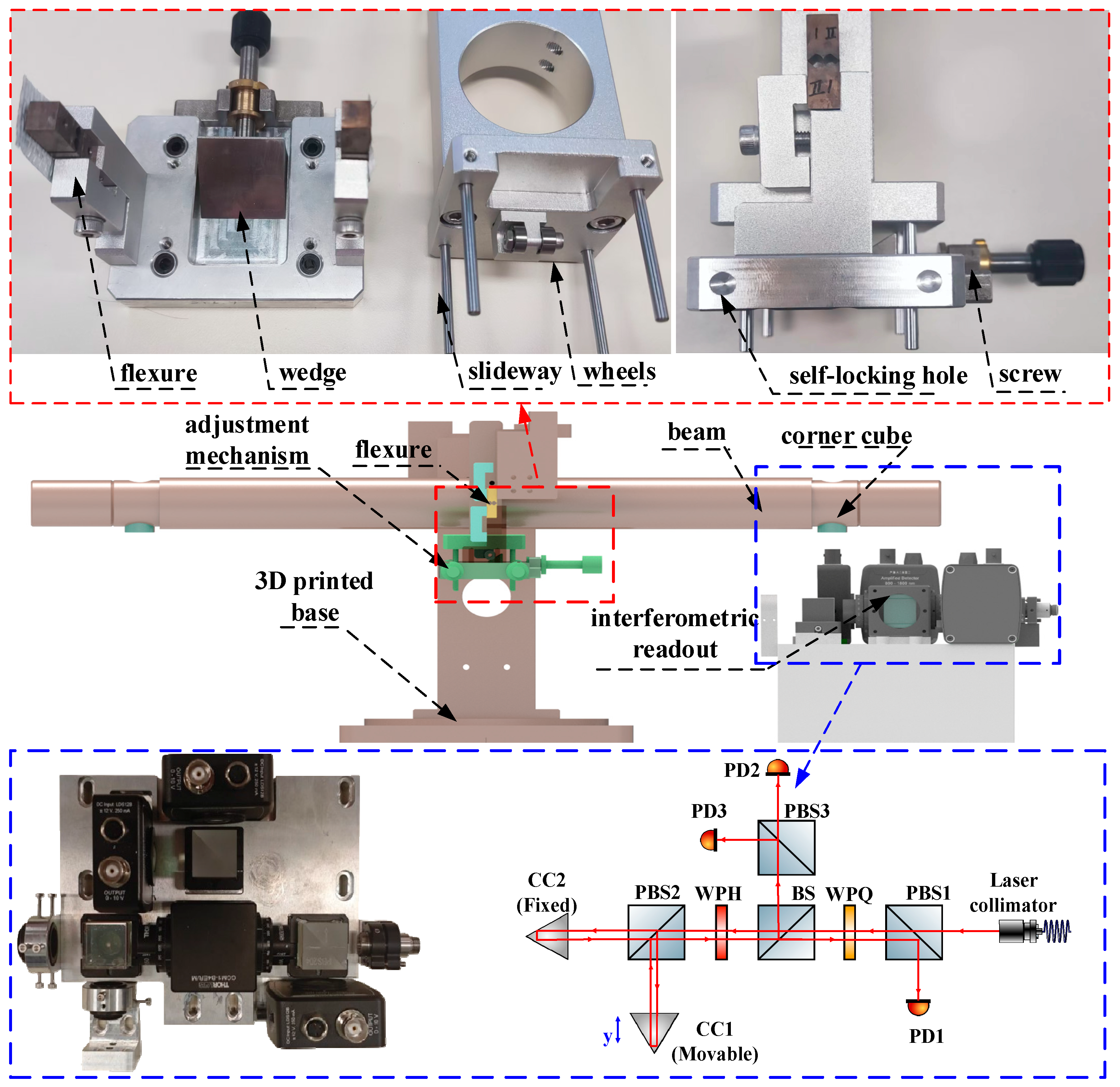
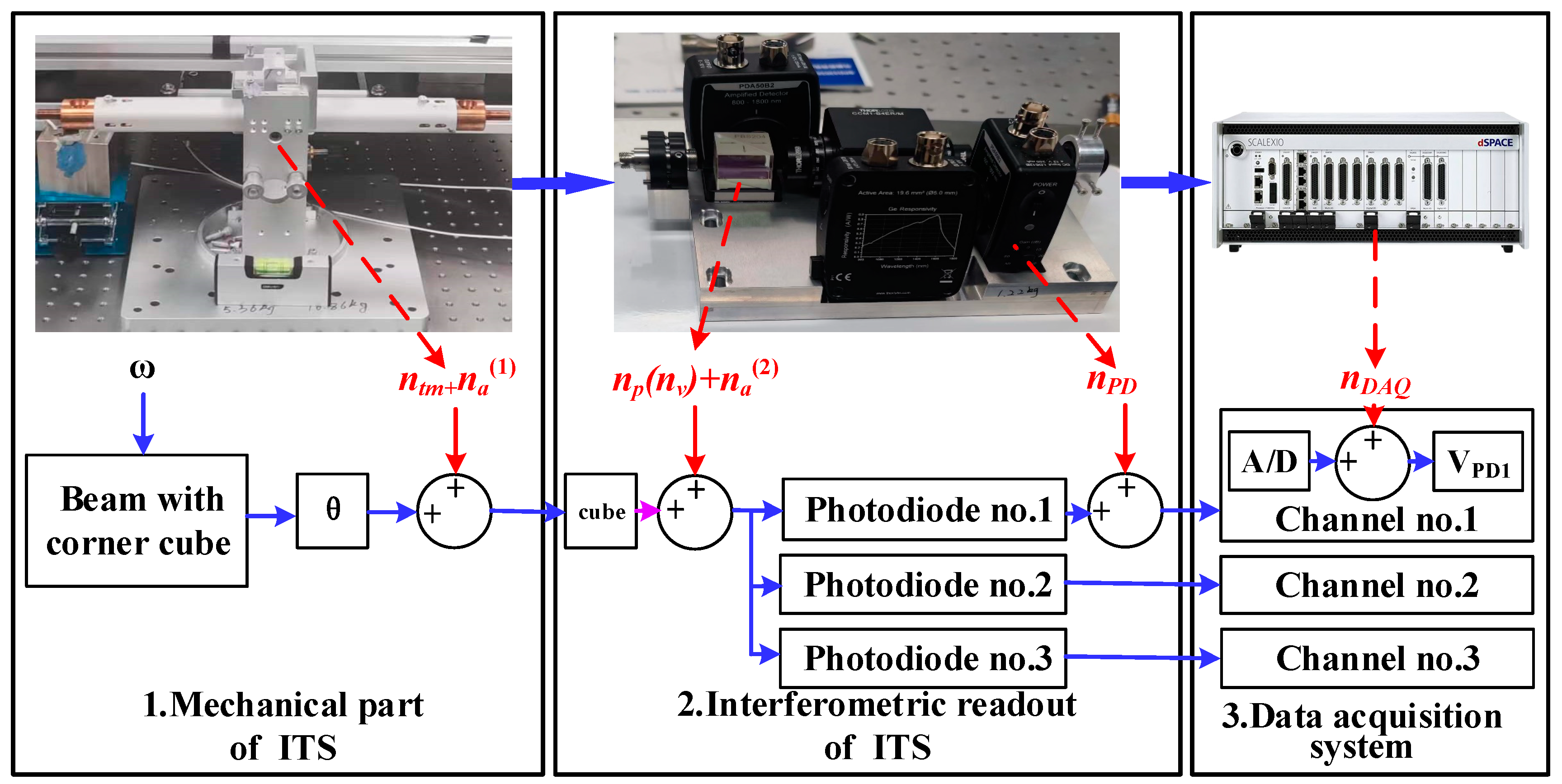
3.1. ITS Mechanics and Readout
3.2. Decoupling Adjustment Mechanism Design
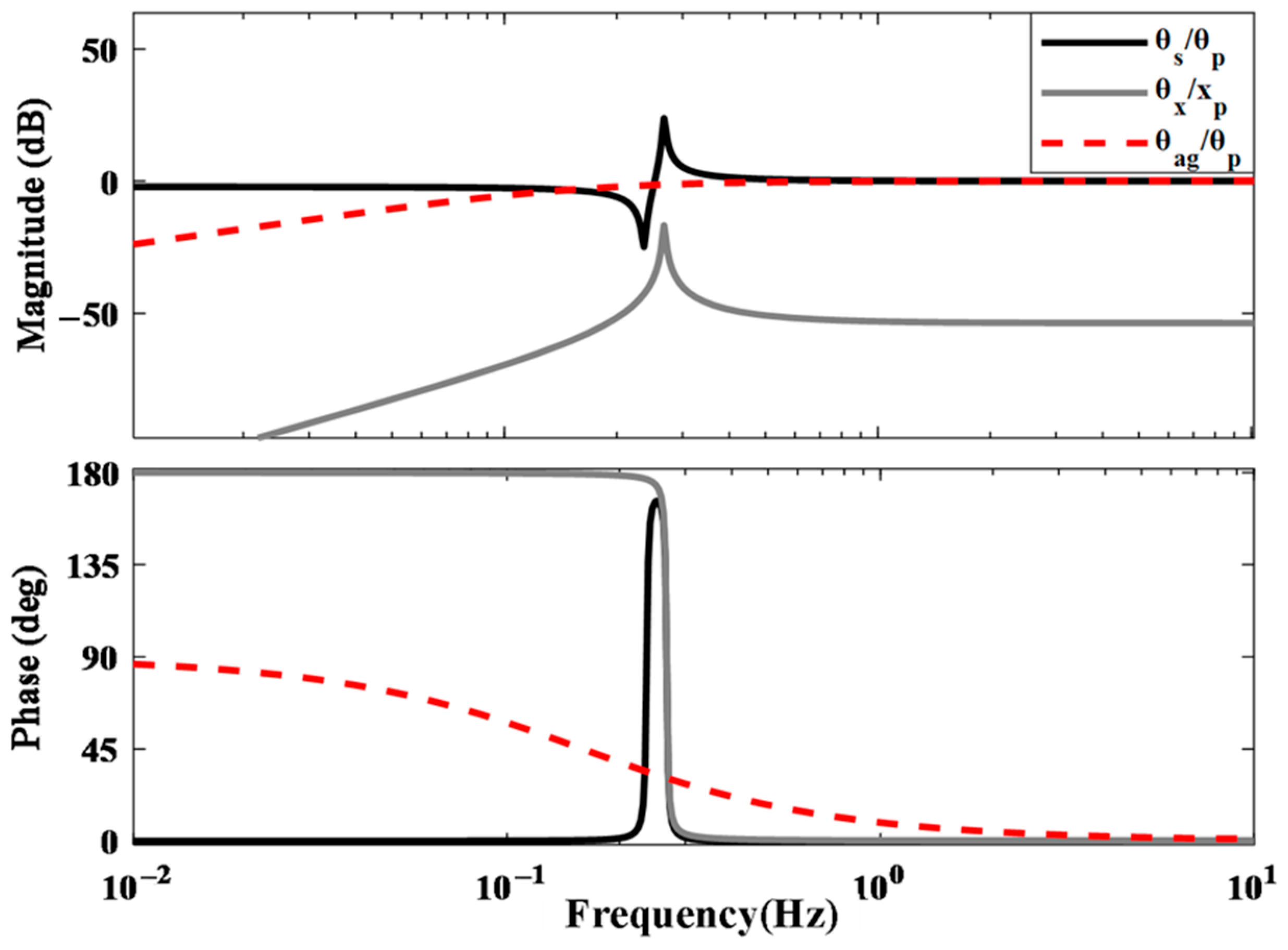
3.3. System Composition and Noise Budget
4. Experimental Verification
4.1. Huddle Test
4.2. Platform
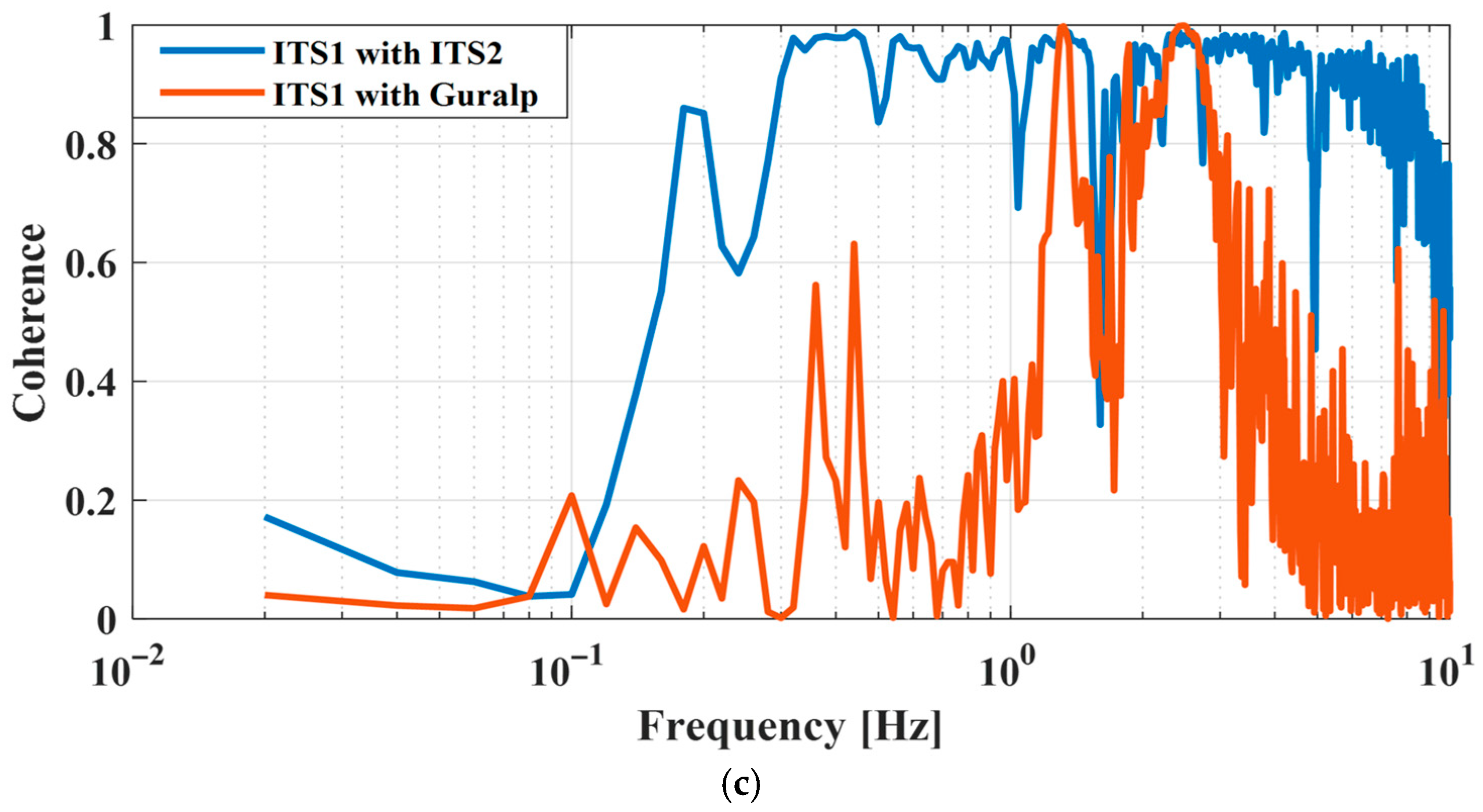
4.3. ITS Experimental Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ITS | Interferometric Tilt Sensor |
| QRS | Quartz Rotation Sensor |
| BRS | Balanced Rotational Sensor |
| LIGO | Laser Interferometer Gravitational-Wave Observatory |
| aLIGO | Advanced LIGO |
| ADC | Analog-to-digital converter |
| ASD | Amplitude Spectral Density |
| LVDTs | Linear Variable Differential Transformers |
| DAQ | Data acquisition |
| PD | Photodiode |
| PBS | Polarizing beam splitter |
| CC1 | Corner cubes |
References
- Song, Y.; Gui, C.; Huo, Z.; Lee, S.W.R.; Liu, S. Mechanical system and dynamic control in photolithography for nanoscale fabrication: A critical review. Int. J. Mech. Syst. Dyn. 2021, 1, 35–51. [Google Scholar] [CrossRef]
- Redmond, J.; Barney, P. Active vibration control of a photolithography platen for increased resolution and throughput. In Proceedings of the 37th Structure, Structural Dynamics and Materials Conference, Salt Lake City, UT, USA, 15–17 April 1996; p. 1450. [Google Scholar]
- Subrahmanyan, P.; Trumper, D. Active vibration isolation design for a photolithographic stepper. Proc. 6th Int. Symp. Magn. Bear. 1998, 10–21. [Google Scholar]
- Łacny, Ł.; Kozień, M.; Ziemiański, D. Selected overview of the impact of ground motion on the vibrations of particle accelerators. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2020; Volume 2239. [Google Scholar]
- Lersnimitthum, P.; Piccini, A.; Carra, F.; Boonyatee, T.; Wansophark, N.; Ajavakom, N. Future Circular Lepton Collider Vibrational Crosstalk. Vibration 2024, 7, 912–927. [Google Scholar] [CrossRef]
- Zhou, M.K.; Hu, Z.K.; Duan, X.C.; Sun, B.L.; Chen, L.L.; Zhang, Q.Z.; Luo, J. Performance of a cold-atom gravimeter with an active vibration isolator. Phys. Rev. A—At. Mol. Opt. Phys. 2012, 86, 043630. [Google Scholar] [CrossRef]
- Yang, B.X.; Liu, L.; Wu, S.C.; Li, H.Y.; Zhou, Z.B. A low frequency horizontal active vibration isolation bench for testing the performance of high-precision space inertial sensors. Class. Quantum Gravity 2021, 38, 175006. [Google Scholar] [CrossRef]
- Chen, D.; Li, Y.; Gong, Y.; Li, X.; Ouyang, W.; Li, X. Low frequency vibration isolation characteristics and intelligent design method of hull grillage metastructures. Mar. Struct. 2024, 94, 103572. [Google Scholar] [CrossRef]
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Advanced ligo. Class. Quantum Gravity 2015, 32, 074001. [Google Scholar]
- Sathyaprakash, B.S.; Schutz, B.F. Physics, astrophysics and cosmology with gravitational waves. Living Rev. Relativ. 2009, 12, 2. [Google Scholar] [CrossRef]
- Coccia, E. The Einstein Telescope. In Proceedings of the 38th International Cosmic Ray Conference (ICRC2023), Nagoya, Japan, 26 July–3 August 2023; p. 1591. [Google Scholar]
- Goncharov, B.; Donnay, L.; Harms, J. Inferring fundamental spacetime symmetries with gravitational-wave memory: From LISA to the Einstein Telescope. Phys. Rev. Lett. 2024, 132, 241401. [Google Scholar] [CrossRef]
- Bagnasco, S.; Bozzi, A.; Fragos, T.; Gonzalvez, A.; Hahn, S.; Hemming, G.; Lavezzi, L.; Laycock, P.; Merino, G.; Pardi, S.; et al. Computing Challenges for the Einstein Telescope project. In EPJ Web of Conferences; EDP Sciences: Les Ulis, France, 2024; Volume 295, p. 04015. [Google Scholar]
- Gath, P.F.; Weise, D.; Schulte, H.R.; Johann, U. LISA mission and system architectures and performances. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2009; Volume 154, p. 012013. [Google Scholar]
- Hu, W.R.; Wu, Y.L. The Taiji Program in Space for gravitational wave physics and the nature of gravity. Natl. Sci. Rev. 2017, 4, 685–686. [Google Scholar] [CrossRef]
- Gong, Y.; Luo, J.; Wang, B. Concepts and status of Chinese space gravitational wave detection projects. Nat. Astron. 2021, 5, 881–889. [Google Scholar] [CrossRef]
- Luo, Z.; Guo, Z.; Jin, G.; Wu, Y.; Hu, W. A brief analysis to Taiji: Science and technology. Results Phys. 2020, 16, 102918. [Google Scholar] [CrossRef]
- Luo, J.; Chen, L.S.; Duan, H.Z.; Gong, Y.G.; Hu, S.; Ji, J.; Liu, Q.; Mei, J.; Milyukov, V.; Sazhin, M.; et al. TianQin: A space-borne gravitational wave detector. Class. Quantum Gravity 2016, 33, 035010. [Google Scholar] [CrossRef]
- Luo, J.; Bai, Y.-Z.; Cai, L.; Cao, B.; Chen, W.-M.; Chen, Y.; Cheng, D.-C.; Ding, Y.-W.; Duan, H.-Z.; Gou, X.; et al. The first round result from the TianQin-1 satellite. Class. Quantum Gravity 2020, 37, 185013. [Google Scholar] [CrossRef]
- Mei, J.; Bai, Y.-Z.; Bao, J.; Barausse, E.; Cai, L.; Canuto, E.; Cao, B.; Chen, W.-M.; Chen, Y.; Ding, Y.-W.; et al. The TianQin project: Current progress on science and technology. Prog. Theor. Exp. Phys. 2021, 2021, 05A107. [Google Scholar] [CrossRef]
- Collette, C.; Janssens, S.; Fernandez-Carmona, P.; Artoos, K.; Guinchard, M.; Hauviller, C.; Preumont, A. Inertial Sensors For Low-Frequency Seismic Vibration Measurement. Bull. Seismol. Soc. Am. 2012, 102, 1289–1300. [Google Scholar] [CrossRef]
- Lantz, B.; Schofield, R.; O’reilly, B.; Clark, D.E.; DeBra, D. Requirements for a ground rotation sensor to improve advanced LIGO. Bull. Seismol. Soc. Am. 2009, 99, 980–989. [Google Scholar] [CrossRef]
- Matichard, F.; Evans, M. Tilt-free low-noise seismometry. Bull. Seismol. Soc. Am. 2015, 105, 497–510. [Google Scholar] [CrossRef]
- Allocca, A.; Avino, S.; Calloni, E.; Caprara, S.; Carpinelli, M.; D’urso, D.; De Laurentis, M.; De Rosa, R.; Errico, L.; Gagliardi, G.; et al. Picoradiant tiltmeter and direct ground tilt measurements at the Sos Enattos site. Eur. Phys. J. Plus 2021, 136, 1–8. [Google Scholar] [CrossRef]
- Venkateswara, K.; Hagedorn, C.A.; Turner, M.D.; Arp, T.; Gundlach, J.H. A high-precision mechanical absolute-rotation sensor. Rev. Sci. Instrum. 2014, 85, 015005. [Google Scholar] [CrossRef]
- McCann, J.J.; Winterflood, J.; Ju, L.; Zhao, C. A multi-orientation low-frequency rotational accelerometer. Rev. Sci. Instrum. 2021, 92, 064503. [Google Scholar] [CrossRef] [PubMed]
- Venkateswara, K.; Paros, J.; Bodin, P.; Wilcock, W.; Tobin, H.J. Quartz Rotation Sensor. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–27 May 2022; p. EGU22-13511. [Google Scholar]
- Zhao, G.; Ding, B.; Watchi, J.; Deraemaeker, A.; Collette, C. Experimental study on active seismic isolation using interferometric inertial sensors. Mech. Syst. Signal Process. 2020, 145, 106959. [Google Scholar] [CrossRef]
- Ding, B.; Zhao, G.; Watchi, J.; Sider, A.; Collette, C. An interferometric inertial sensor for low-frequency seismic isolation. Sens. Actuators A Phys. 2022, 335, 113398. [Google Scholar] [CrossRef]
- Ding, B. Development of High-Resolution Interferometric Inertial Sensors. Ph.D. Thesis, Universite Libre de Bruxelles, Ecolepolytechnique de Bruxelles—Electromecanicien, Bruxelles, Belgium, 13 January 2021. [Google Scholar]
- Ding, B.; Zhao, G.; Watchi, J.; Collette, C. Huddle test of optical inertial sensors combined with slightly damped mechanics. In Proceedings of the 28th International Conference on Noise and Vibration Engineering (ISMA2018), Leuven, Belgium, 17–19 September 2018; pp. 1471–1479. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, W.; Feng, W.; Wang, P.; Zhang, Z.; Zhao, G. Research on Interferometric Tilt Sensor for Vibration Isolation Platform. Sensors 2025, 25, 1777. https://doi.org/10.3390/s25061777
Bai W, Feng W, Wang P, Zhang Z, Zhao G. Research on Interferometric Tilt Sensor for Vibration Isolation Platform. Sensors. 2025; 25(6):1777. https://doi.org/10.3390/s25061777
Chicago/Turabian StyleBai, Weigang, Wenwu Feng, Peigen Wang, Ziliang Zhang, and Guoying Zhao. 2025. "Research on Interferometric Tilt Sensor for Vibration Isolation Platform" Sensors 25, no. 6: 1777. https://doi.org/10.3390/s25061777
APA StyleBai, W., Feng, W., Wang, P., Zhang, Z., & Zhao, G. (2025). Research on Interferometric Tilt Sensor for Vibration Isolation Platform. Sensors, 25(6), 1777. https://doi.org/10.3390/s25061777





