Time-Normalization Approach for fNIRS Data During Tasks with High Variability in Duration
Abstract
1. Introduction
2. Materials and Methods
2.1. Algorithm Description
2.2. Testing of the Algorithm
2.2.1. Participants
2.2.2. Experimental Protocol
2.2.3. Signal Acquisition and Pre-Processing
2.2.4. Statistical Analysis
3. Results
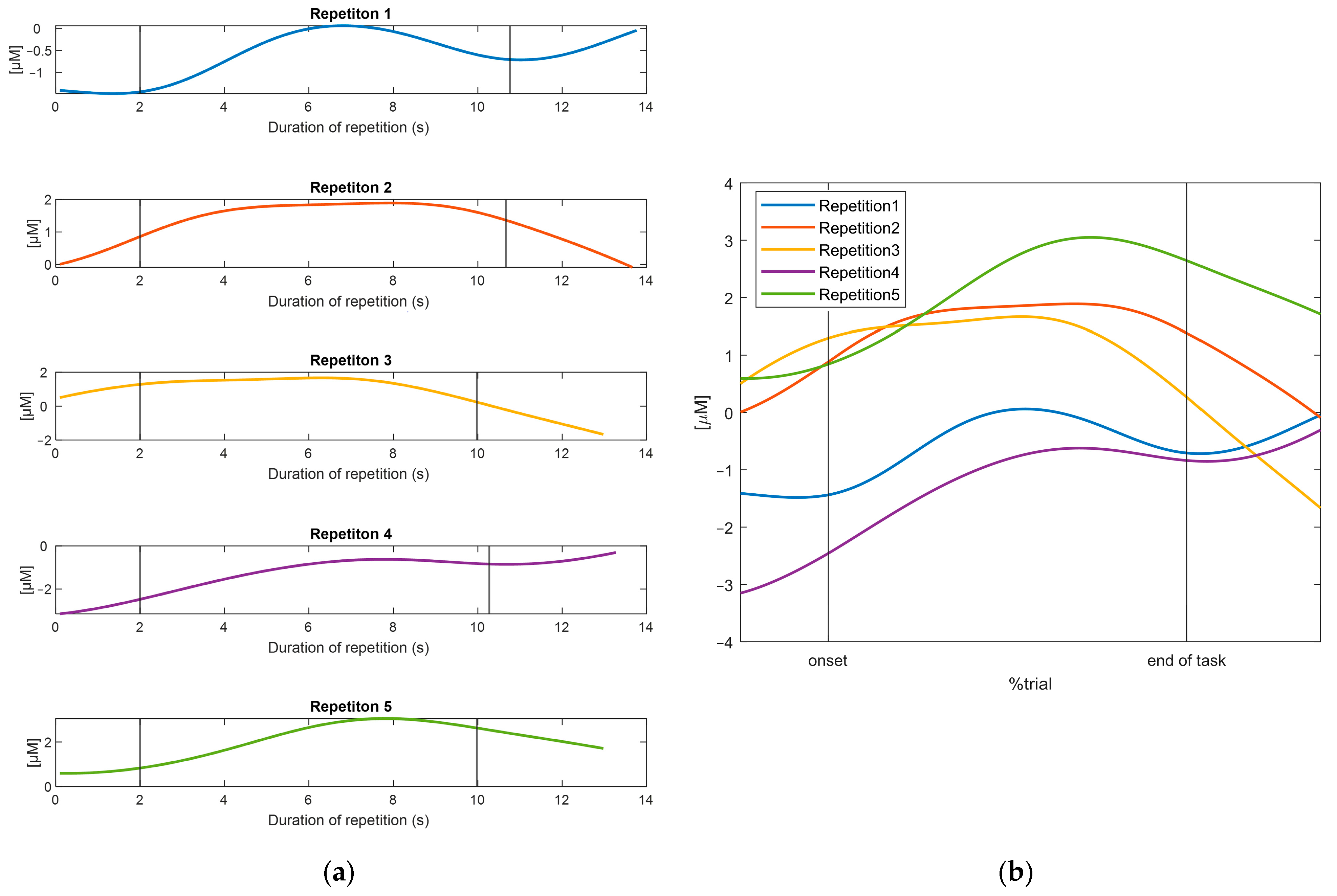
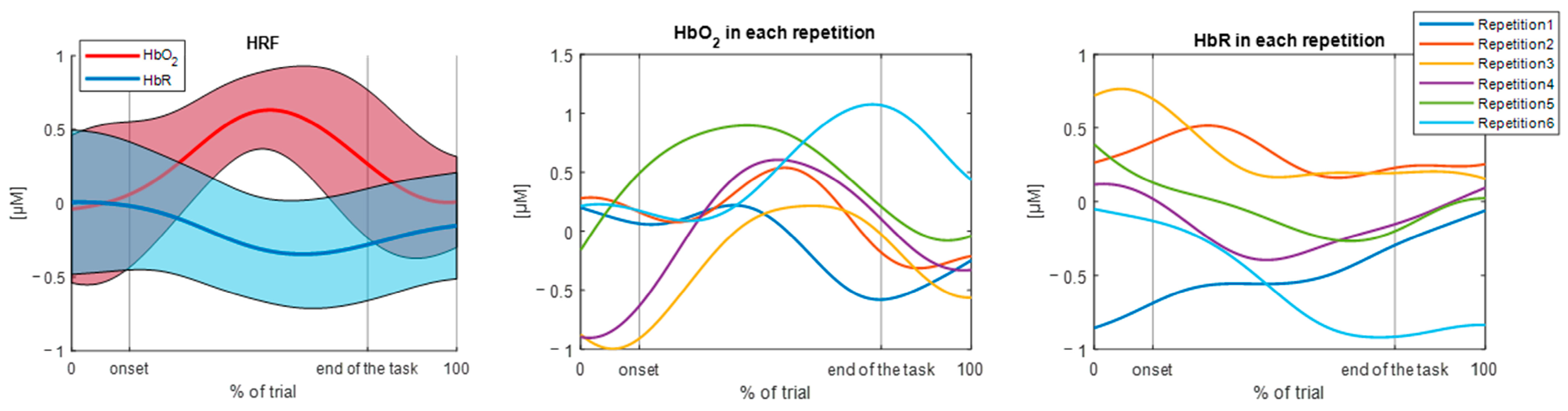
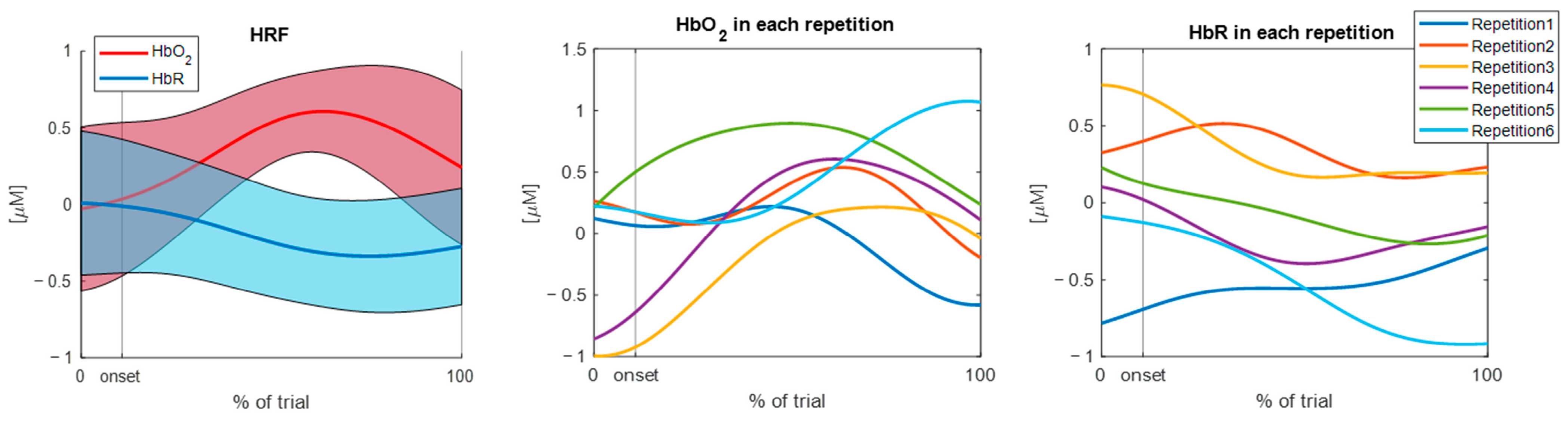
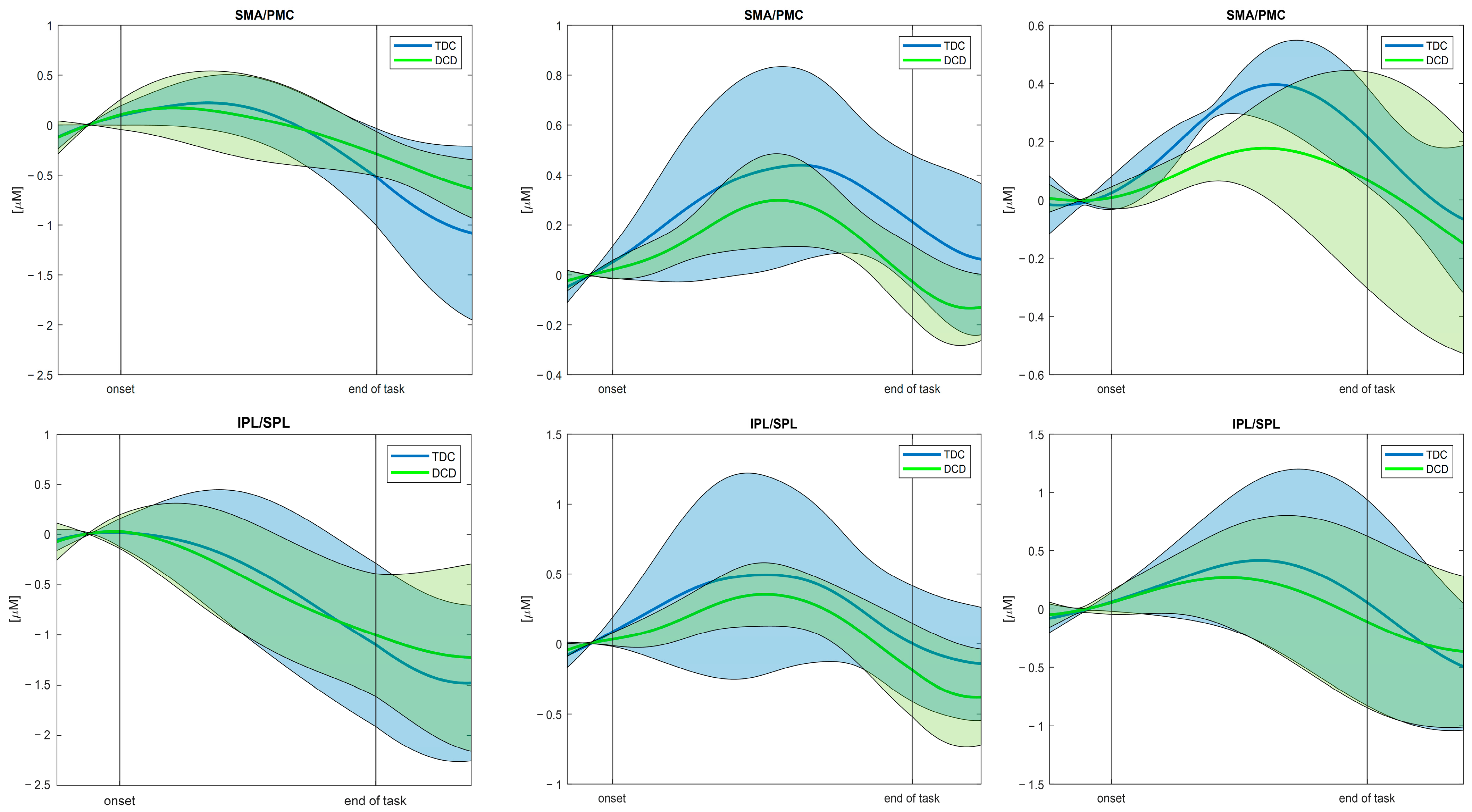
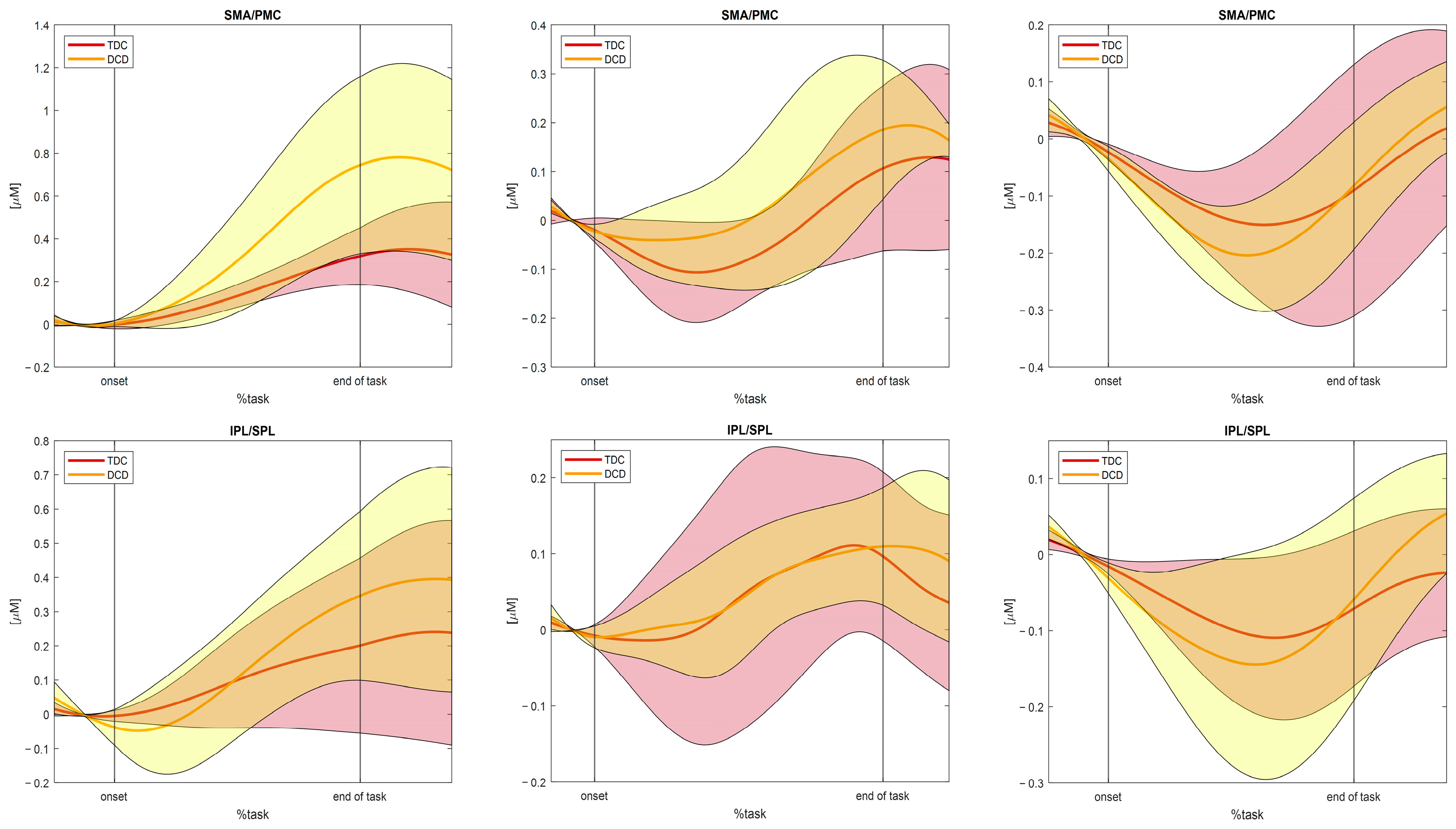
3.1. Results of the TaskNorm.m Function
3.2. Results of the Testing
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| fNIRS | functional near-infrared spectroscopy |
| HbO2 | oxyhemoglobin |
| HbR | deoxyhemoglobin |
| HT | total hemoglobin |
| fMRI | functional magnetic resonance imaging |
| EEG | electroencephalography |
| DTW | dynamic time warping |
| DCD | developmental coordination disorder |
| TD | typically developing |
| HRF | hemodynamic response function |
| EMG | electromyography |
| fOLD | fNIRS optodes locator decider |
| SMA | supplementary motor rea |
| PMC | premotor cortex |
| IPL | inferior parietal lobule |
| SPL | superior parietal lobule |
| ROI | regions of interest |
References
- Menant, J.C.; Maidan, I.; Alcock, L.; Al-Yahya, E.; Cerasa, A.; Clark, D.J.; de Bruin, E.; Fraser, S.; Gramigna, V.; Hamacher, D.; et al. A consensus guide to using functional near-infrared spectroscopy in posture and gait research. Gait Posture 2020, 82, 254–265. [Google Scholar] [CrossRef] [PubMed]
- Yücel, M.A.; Lühmann, A.V.; Scholkmann, F.; Gervain, J.; Dan, I.; Ayaz, H.; Boas, D.; Cooper, R.J.; Culver, J.; Elwell, C.E.; et al. Best practices for fNIRS publications. Neurophotonics 2021, 8, 012101. [Google Scholar] [CrossRef]
- Karim, H.; Schmidt, B.; Dart, D.; Beluk, N.; Huppert, T. Functional near-infrared spectroscopy (fNIRS) of brain function during active balancing using a video game system. Gait Posture 2012, 35, 367–372. [Google Scholar] [CrossRef]
- Hoshi, Y.; Kobayashi, N.; Tamura, M. Interpretation of near-infrared spectroscopy signals: A study with a newly developed perfused rat brain model. J. Appl. Physiol. 2001, 90, 1657–1662. [Google Scholar] [CrossRef] [PubMed]
- Kamran, M.A.; Mannan, M.M.N.; Jeong, M.Y. Cortical signal analysis and advances in functional near-infrared spectroscopy signal: A review. Front. Hum. Neurosci. 2016, 10, 261. [Google Scholar] [CrossRef]
- Pereira, J.; Direito, B.; Lührs, M.; Castelo-Branco, M.; Sousa, T. Multimodal assessment of the spatial correspondence between fNIRS and fMRI hemodynamic responses in motor tasks. Sci. Rep. 2023, 13, 2244. [Google Scholar] [CrossRef] [PubMed]
- Logothetis, N.K. What we can do and what we cannot do with fMRI. Nature 2008, 453, 869–878. [Google Scholar] [CrossRef]
- Pfeifer, M.D.; Scholkmann, F.; Labruyère, R. Signal processing in functional near-infrared spectroscopy (fNIRS): Methodological differences lead to different statistical results. Front. Hum. Neurosci. 2018, 11, 641. [Google Scholar] [CrossRef]
- Huppert, T.J.; Diamond, S.G.; Franceschini, M.A.; Boas, D.A. HomER: A review of time-series analysis methods for near-infrared spectroscopy of the brain. Appl. Opt. 2009, 48, D280–D298. [Google Scholar] [CrossRef]
- Ren, Y.; Cui, G.; Zhang, X.; Feng, K.; Yu, C.; Liu, P. The promising fNIRS: Uncovering the function of prefrontal working memory networks based on multi-cognitive tasks. Front. Psychiatry 2022, 13, 985076. [Google Scholar] [CrossRef]
- Mauri, M.; Grazioli, S.; Crippa, A.; Bacchetta, A.; Pozzoli, U.; Bertella, S.; Gatti, E.; Maggioni, E.; Rosi, E.; Diwadkar, V.; et al. Hemodynamic and behavioral peculiarities in response to emotional stimuli in children with attention deficit hyperactivity disorder: An fNIRS study. J. Affect. Disord. 2020, 277, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Grazioli, S.; Crippa, A.; Mauri, M.; Piazza, C.; Bacchetta, A.; Salandi, A.; Trabattoni, S.; Agostoni, C.; Molteni, M.; Nobile, M. Association between fatty acids profile and cerebral blood flow: An exploratory fNIRS study on children with and without ADHD. Nutrients 2019, 11, 2414. [Google Scholar] [CrossRef] [PubMed]
- Wijeakumar, S.; Huppert, T.J.; Magnotta, V.A.; Buss, A.T.; Spencer, J.P. Validating an image-based fNIRS approach with fMRI and a working memory task. Neuroimage 2017, 147, 204–218. [Google Scholar] [CrossRef]
- Lu, C.-F.; Liu, Y.-C.; Yang, Y.-R.; Wu, Y.-T.; Wang, R.-Y. Maintaining gait performance by cortical activation during dual-task interference: A functional near-infrared spectroscopy study. PLoS ONE 2015, 10, e0129390. [Google Scholar] [CrossRef] [PubMed]
- Miyai, I.; Tanabe, H.C.; Sase, I.; Eda, H.; Oda, I.; Konishi, I.; Tsunazawa, Y.; Suzuki, T.; Yanagida, T.; Kubota, K. Cortical mapping of gait in humans: A near-infrared spectroscopic topography study. Neuroimage 2001, 14, 1186–1192. [Google Scholar] [CrossRef]
- Lee, B.C.; Choi, J.; Martin, B.J. Roles of the prefrontal cortex in learning to time the onset of pre-existing motor programs. PLoS ONE 2020, 15, e0241562. [Google Scholar] [CrossRef]
- Mihara, M.; Miyai, I.; Hatakenaka, M.; Kubota, K.; Sakoda, S. Role of the prefrontal cortex in human balance control. Neuroimage 2008, 43, 329–336. [Google Scholar] [CrossRef]
- Hawkins, K.A.; Fox, E.J.; Daly, J.J.; Rose, D.K.; Christou, E.A.; McGuirk, T.E.; Otzel, D.M.; Butera, K.A.; Chatterjee, S.A.; Clark, D.J. Prefrontal over-activation during walking in people with mobility deficits: Interpretation and functional implications. Hum. Mov. Sci. 2018, 59, 46–55. [Google Scholar] [CrossRef]
- Lin, M.I.B.; Lin, K.H. Walking while performing working memory tasks changes the prefrontal cortex hemodynamic activations and gait kinematics. Front. Behav. Neurosci. 2016, 10, 92. [Google Scholar] [CrossRef]
- de Lima-Pardini, A.C.; Zimeo Morais, G.A.; Balardin, J.B.; Coelho, D.B.; Azzi, N.M.; Teixeira, L.A.; Sato, J.R. Measuring cortical motor hemodynamics during assisted stepping–An fNIRS feasibility study of using a walker. Gait Posture 2017, 56, 112–118. [Google Scholar] [CrossRef]
- Mirelman, A.; Maidan, I.; Bernad-Elazari, H.; Nieuwhof, F.; Reelick, M.; Giladi, N.; Hausdorff, J.M. Increased frontal brain activation during walking while dual tasking: An fNIRS study in healthy young adults. J. Neuroeng. Rehabil. 2014, 11, 85. [Google Scholar] [CrossRef]
- Clark, D.J.; Rose, D.K.; Ring, S.A.; Porges, E.C. Utilization of central nervous system resources for preparation and performance of complex walking tasks in older adults. Front. Aging Neurosci. 2014, 6, 217. [Google Scholar] [CrossRef]
- McKendrick, R.; Mehta, R.; Ayaz, H.; Scheldrup, M.; Parasuraman, R. Prefrontal Hemodynamics of Physical Activity and Environmental Complexity during Cognitive Work. Hum. Factors 2017, 59, 147–162. [Google Scholar] [CrossRef]
- Pinti, P.; Aichelburg, C.; Lind, F.; Power, S.; Swingler, E.; Merla, A.; Hamilton, A.; Gilber, S.; Burgess, P.; Tachtsidis, I. Using fiberless, wearable fnirs to monitor brain activity in real-world cognitive tasks. J. Vis. Exp. 2015, 2015, e53336. [Google Scholar] [CrossRef]
- Balardin, J.B.; Zimeo Morais, G.A.; Furucho, R.A.; Trambaiolli, L.; Vanzella, P.; Biazoli, C.; Sato, J.R. Imaging brain function with functional near-infrared spectroscopy in unconstrained environments. Front. Hum. Neurosci. 2017, 11, 258. [Google Scholar] [CrossRef]
- Liu, Z.; Shore, J.; Wang, M.; Yuan, F.; Buss, A.; Zhao, X. A systematic review on hybrid EEG/fNIRS in brain-computer interface. Biomed. Signal Process. Control 2021, 68, 102595. [Google Scholar] [CrossRef]
- Llopis-Albert, C.; Toro, W.R.V.; Farhat, N.; Zamora-Ortiz, P.; Del Pozo, Á.F.P. A new method for time normalization based on the continuous phase: Application to neck kinematics. Mathematics 2021, 9, 3138. [Google Scholar] [CrossRef]
- Wagner, J.; Solis-Escalante, T.; Scherer, R.; Neuper, C.; Müller-Putz, G. It’s how you get there: Walking down a virtual alley activates premotor and parietal areas. Front. Hum. Neurosci. 2014, 8, 93. [Google Scholar] [CrossRef]
- Gwin, J.T.; Gramann, K.; Makeig, S.; Ferris, D.P. Electrocortical activity is coupled to gait cycle phase during treadmill walking. Neuroimage 2011, 54, 1289–1296. [Google Scholar] [CrossRef]
- Wagner, J.; Solis-Escalante, T.; Grieshofer, P.; Neuper, C.; Müller-Putz, G.; Scherer, R. Level of participation in robotic-assisted treadmill walking modulates midline sensorimotor EEG rhythms in able-bodied subjects. Neuroimage 2012, 63, 1203–1211. [Google Scholar] [CrossRef]
- Zhu, L.; Najafizadeh, L. Dynamic time warping-based averaging framework for functional near-infrared spectroscopy brain imaging studies. J. Biomed. Opt. 2017, 22, 066011. [Google Scholar] [CrossRef]
- Müller, M. Dynamic Time Warping. In Information Retrieval for Music and Motion; Springer: Berlin/Heidelberg, Germany, 2007; pp. 69–84. ISBN 978-3-540-74048-3. [Google Scholar]
- Sakoe, H.; Chiba, S. Dynamic Programming Algorithm Optimization for Spoken Word Recognition. IEEE Trans. Acoust. 1978, 26, 43–49. [Google Scholar] [CrossRef]
- Li, H.; Liu, J.; Yang, Z.; Liu, R.W.; Wu, K.; Wan, Y. Adaptively constrained dynamic time warping for time series classification and clustering. Inf. Sci. 2020, 534, 97–116. [Google Scholar] [CrossRef]
- Blank, R.; Barnett, A.L.; Cairney, J.; Green, D.; Kirby, A.; Polatajko, H.; Rosenblum, S.; Smits-Engelsman, B.; Sugden, D.; Wilson, P.; et al. International clinical practice recommendations on the definition, diagnosis, assessment, intervention, and psychosocial aspects of developmental coordination disorder. Dev. Med. Child Neurol. 2019, 61, 242–285. [Google Scholar] [CrossRef]
- American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders: DSM-5TM, 5th ed.; American Psychiatric Publishing, Inc.: Arlington, VA, USA, 2013. [Google Scholar] [CrossRef]
- Verbecque, E.; Johnson, C.; Rameckers, E.; Thijs, A.; van der Veer, I.; Meyns, P.; Smits-Engelsman, B.; Klingels, K. Balance control in individuals with developmental coordination disorder: A systematic review and meta-analysis. Gait Posture 2021, 83, 268–279. [Google Scholar] [CrossRef]
- Subara-Zukic, E.; Cole, M.H.; McGuckian, T.B.; Steenbergen, B.; Green, D.; Smits-Engelsman, B.C.M.; Lust, J.M.; Abdollahipour, R.; Domellöf, E.; Deconinck, F.J.A.; et al. Behavioral and Neuroimaging Research on Developmental Coordination Disorder (DCD): A Combined Systematic Review and Meta-Analysis of Recent Findings. Front. Psychol. 2022, 13, 809455. [Google Scholar] [CrossRef]
- Al-Yahya, E.; Esser, P.; Weedon, B.D.; Joshi, S.; Liu, Y.-C.; Springett, D.N.; Salvan, P.; Meaney, A.; Collett, J.; Inacio, M.; et al. Motor learning in developmental coordination disorder: Behavioral and neuroimaging study. Front. Neurosci. 2023, 17, 1187790. [Google Scholar] [CrossRef]
- Joshi, S.; Weedon, B.D.; Esser, P.; Liu, Y.C.; Springett, D.N.; Meaney, A.; Inacio, M.; Delextrat, A.; Kemp, S.; Ward, T.; et al. Neuroergonomic assessment of developmental coordination disorder. Sci. Rep. 2022, 12, 10239. [Google Scholar] [CrossRef]
- Caçola, P.; Getchell, N.; Srinivasan, D.; Alexandrakis, G.; Liu, H. Cortical activity in fine-motor tasks in children with Developmental Coordination Disorder: A preliminary fNIRS study. Int. J. Dev. Neurosci. 2018, 65, 83–90. [Google Scholar] [CrossRef] [PubMed]
- Dewar, R.; Claus, A.P.; Tucker, K.; Ware, R.; Johnston, L.M. Reproducibility of the Balance Evaluation Systems Test (BESTest) and the Mini-BESTest in school-aged children. Gait Posture 2017, 55, 68–74. [Google Scholar] [CrossRef] [PubMed]
- Piazza, C.; Bacchetta, A.; Crippa, A.; Mauri, M.; Grazioli, S.; Reni, G.; Nobile, M.; Bianchi, A.M. Preprocessing Pipeline for fNIRS Data in Children BT-XV Mediterranean Conference on Medical and Biological Engineering and Computing–MEDICON 2019; Henriques, J., Neves, N., de Carvalho, P., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 235–244. [Google Scholar]
- Whiteman, A.C.; Santosa, H.; Chen, D.F.; Perlman, S.; Huppert, T. Investigation of the sensitivity of functional near-infrared spectroscopy brain imaging to anatomical variations in 5- to 11-year-old children. Neurophotonics 2017, 5, 011009. [Google Scholar] [CrossRef]
- Hu, X.-S.; Arredondo, M.M.; Gomba, M.; Confer, N.; DaSilva, A.F.; Johnson, T.D.; Shalinsky, M.; Kovelman, I. Comparison of motion correction techniques applied to functional near-infrared spectroscopy data from children. J. Biomed. Opt. 2015, 20, 126003. [Google Scholar] [CrossRef]
- Molavi, B.; Dumont, G.A. Wavelet-based motion artifact removal for functional near-infrared spectroscopy. Physiol. Meas. 2012, 33, 259–270. [Google Scholar] [CrossRef]
- Lim, S.B.; Louie, D.R.; Peters, S.; Liu-Ambrose, T.; Boyd, L.A.; Eng, J.J. Brain activity during real-time walking and with walking interventions after stroke: A systematic review. J. Neuroeng. Rehabil. 2021, 18, 8. [Google Scholar] [CrossRef]

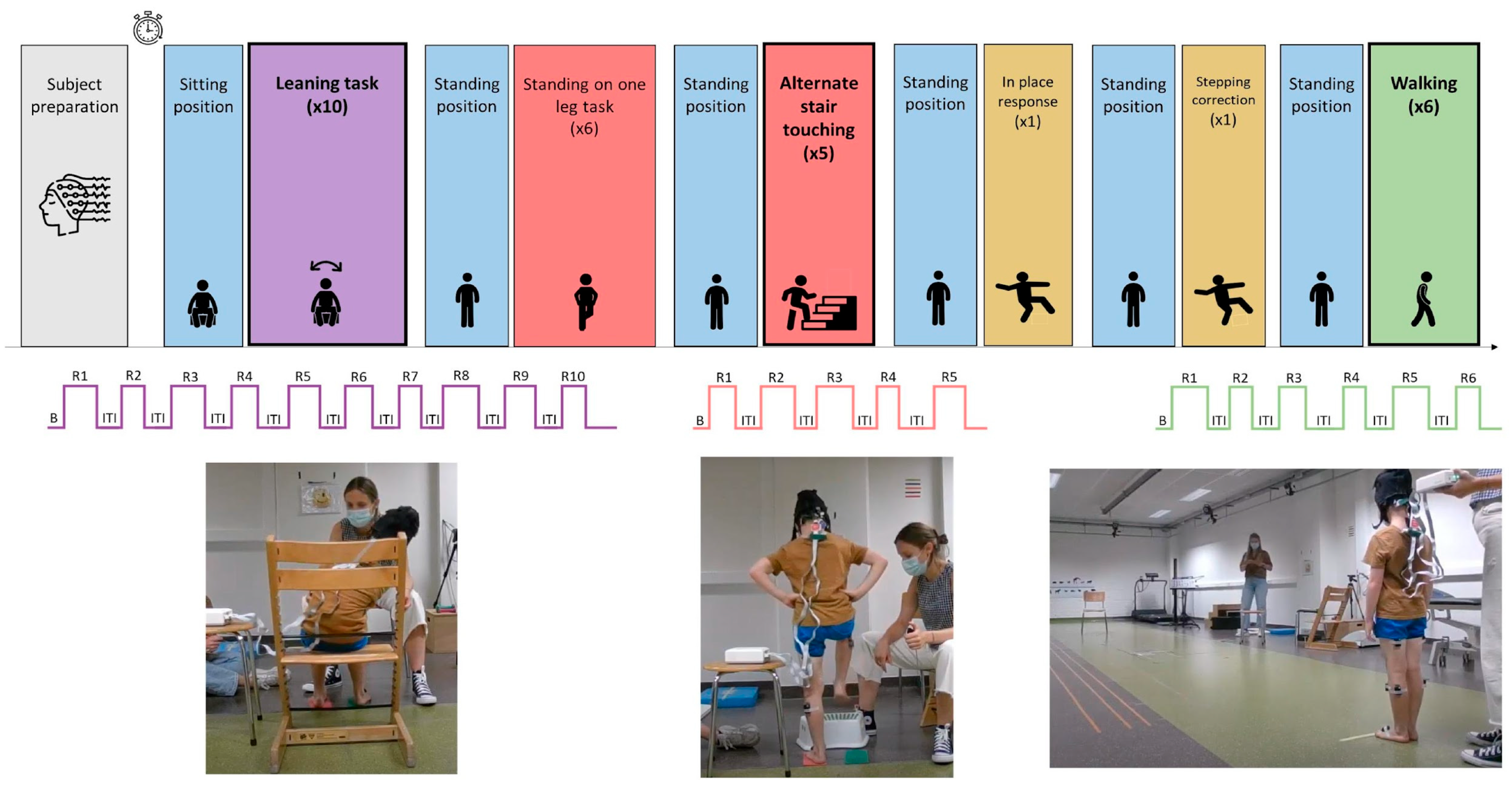
| Task | Baseline/Rest Position | Repetitions | ||||
|---|---|---|---|---|---|---|
| Kids-BEST Test Section | Name | Explanation | Description | Intra-Trial Mean Duration (SD) [s] | N | Mean Duration (SD) [s] |
| Anticipatory postural adjustment | Alternate stair touching | The child taps with their feet on a stool in front of them alternately with the left and right foot as fast and as controlled as possible. | Standing on two feet | 12.70 (4.11) | 5 times | 7.81 (1.46) |
| Stability limits | Leaning left and right while seated | The child leans as far and as stable as possible sidewards while seated, without falling and keeping their feet on the ground. Arms are crossed at the chest. | Sitting | 12.59 (12.16) | 10 times | 12.87 (2.25) |
| Stability in gait | Walking | The child walks 6 m over level ground as fluently as possible. | Standing on two feet | 11.3 (6.91) | 6 times | 6.60 (1.30) |
| Anticipatory postural adjustment | Standing on one leg | The child stands on one leg for as long as possible. This exercise is then repeated with the other leg. | Standing on two feet | 60.56 (22) | 6 times | 18.88 (11.21) |
| Reactive postural responses | In place response—backward | The therapist holds the child, who resists. When the therapist suddenly releases the child, he/she should keep balancewithout taking a step. | Standing on two feet | - | 1 time | 0.1 (0) |
| Reactive postural responses | Compensatory stepping correction—backward | The child leans beyond theirbackward limits against the therapist’s hands. When the therapist suddenly releases the child, he/she should be able to avoid falling, perhaps even taking a step. | Standing on two feet | - | 1 time | 0.1 (0) |
| First Version | Second Version | |||||
|---|---|---|---|---|---|---|
| Task | ID Code | Mean Duration (SD) | %Mean Onset (SD) | %Mean Offset (SD) | %Mean Onset (SD) | %Mean Offset (SD) |
| Walking | DCD_1 | 8.38 (1.26) | 15.15 (0) | 76.97 (0) | 14.95 (1.26) | 76.89 (2.02) |
| Walking | DCD_2 | 5.16 (0.94) | 19.72 (0) | 70.02 (0) | 19.64 (1.78) | 69.54 (2.79) |
| Walking | DCD_3 | 6.76 (0.47) | 16.42 (0) | 75.04 (0) | 17.03 (0.69) | 73.79 (1.07) |
| Walking | DCD_4 | 6.27 (0.66) | 17.92 (0) | 72.76 (0) | 17.85 (1.04) | 72.53 (1.67) |
| Walking | TD_1 | 6.25 (0.5) | 17.92 (0) | 72.76 (0) | 17.67 (0.75) | 72.56 (1.16) |
| Walking | TD_2 | 5.34 (0.37) | 19.72 (0) | 70.02 (0) | 19.24 (0.7) | 70.14 (1.09) |
| Walking | TD_3 | 6.31 (0.42) | 17.92 (0) | 72.76 (0) | 17.67 (0.69) | 72.86 (1.03) |
| Walking | TD_4 | 8.32 (0.35) | 15.15 (0) | 76.97 (0) | 14.95 (0.34) | 76.89 (0.55) |
| Alternate stair touching | DCD_1 | 10.21 (0.96) | 13.12 (0) | 80.05 (0) | 13.08 (0.77) | 79.71 (1.24) |
| Alternate stair touching | DCD_2 | 6.89 (1.07) | 16.42 (0) | 75.04 (0) | 16.69 (1.39) | 74.12 (2.2) |
| Alternate stair touching | DCD_3 | 7.63 (0.93) | 15.15 (0) | 76.97 (0) | 15.87 (1.2) | 75.5 (1.86) |
| Alternate stair touching | DCD_4 | 9.09 (0.99) | 14.06 (0) | 78.62 (0) | 14.16 (0.93) | 78.11 (1.5) |
| Alternate stair touching | TD_1 | 6.89 (1.17) | 16.42 (0) | 75.04 (0) | 16.86 (1.61) | 73.96 (2.61) |
| Alternate stair touching | TD_2 | 6.24 (0.28) | 17.92 (0) | 72.76 (0) | 17.85 (0.49) | 72.5 (0.79) |
| Alternate stair touching | TD_3 | 7.23 (0.28) | 16.42 (0) | 75.04 (0) | 16.36 (0.3) | 74.79 (0.52) |
| Alternate stair touching | TD_4 | 8.3 (0.37) | 15.15 (0) | 76.97 (0) | 14.95 (0.43) | 76.89 (0.66) |
| Leaning | DCD_1 | 12.87 (1.22) | 10.93 (0) | 83.39 (0) | 11.23 (0.8) | 82.65 (1.23) |
| Leaning | DCD_2 | 11.12 (1.43) | 12.3 (0) | 81.3 (0) | 12.39 (1.2) | 80.85 (1.9) |
| Leaning | DCD_3 | 13.17 (1.44) | 10.93 (0) | 83.39 (0) | 11.01 (0.85) | 82.98 (1.32) |
| Leaning | DCD_4 | 11.45 (1.05) | 12.3 (0) | 81.3 (0) | 12.14 (0.74) | 81.23 (1.15) |
| Leaning | TD_1 | 13.28 (1.23) | 10.93 (0) | 83.39 (0) | 10.9 (0.69) | 83.09 (1.08) |
| Leaning | TD_2 | 12.65 (1.21) | 10.93 (0) | 83.39 (0) | 11.35 (0.78) | 82.54 (1.22) |
| Leaning | TD_3 | 11.37 (0.79) | 12.3 (0) | 81.3 (0) | 12.14 (0.6) | 81.23 (0.89) |
| Leaning | TD_4 | 17.09 (2.45) | 8.93 (0) | 86.42 (0) | 9.1 (0.94) | 85.99 (1.48) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falivene, A.; Johnson, C.; Klingels, K.; Meyns, P.; Verbecque, E.; Hallemans, A.; Biffi, E.; Piazza, C.; Crippa, A. Time-Normalization Approach for fNIRS Data During Tasks with High Variability in Duration. Sensors 2025, 25, 1768. https://doi.org/10.3390/s25061768
Falivene A, Johnson C, Klingels K, Meyns P, Verbecque E, Hallemans A, Biffi E, Piazza C, Crippa A. Time-Normalization Approach for fNIRS Data During Tasks with High Variability in Duration. Sensors. 2025; 25(6):1768. https://doi.org/10.3390/s25061768
Chicago/Turabian StyleFalivene, Anna, Charlotte Johnson, Katrijn Klingels, Pieter Meyns, Evi Verbecque, Ann Hallemans, Emilia Biffi, Caterina Piazza, and Alessandro Crippa. 2025. "Time-Normalization Approach for fNIRS Data During Tasks with High Variability in Duration" Sensors 25, no. 6: 1768. https://doi.org/10.3390/s25061768
APA StyleFalivene, A., Johnson, C., Klingels, K., Meyns, P., Verbecque, E., Hallemans, A., Biffi, E., Piazza, C., & Crippa, A. (2025). Time-Normalization Approach for fNIRS Data During Tasks with High Variability in Duration. Sensors, 25(6), 1768. https://doi.org/10.3390/s25061768






