Study on Vibration Characteristics of Functionally Graded Material Composite Spherical Piezoelectric Transducer
Abstract
1. Introduction
2. Structure and Principle
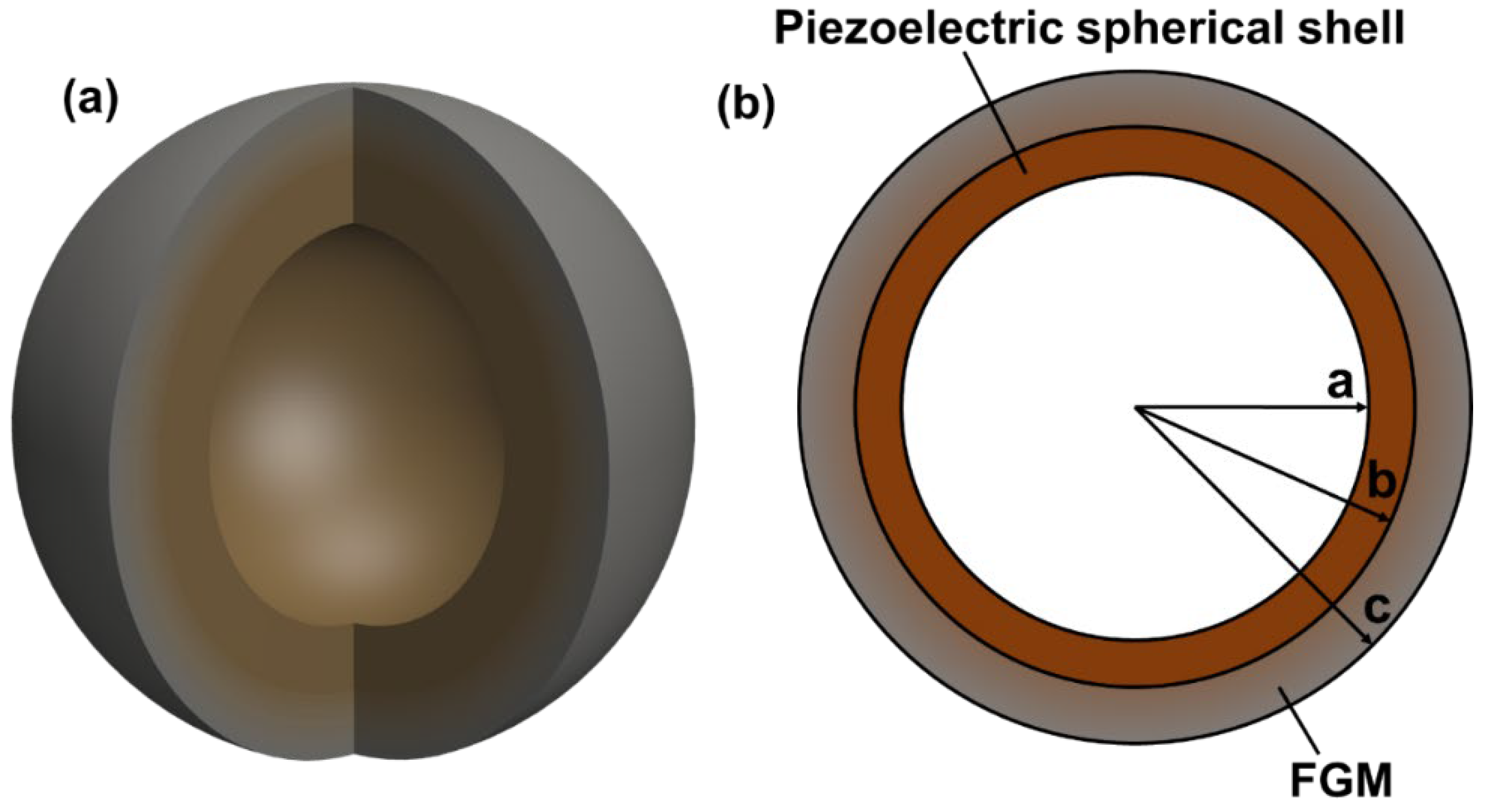
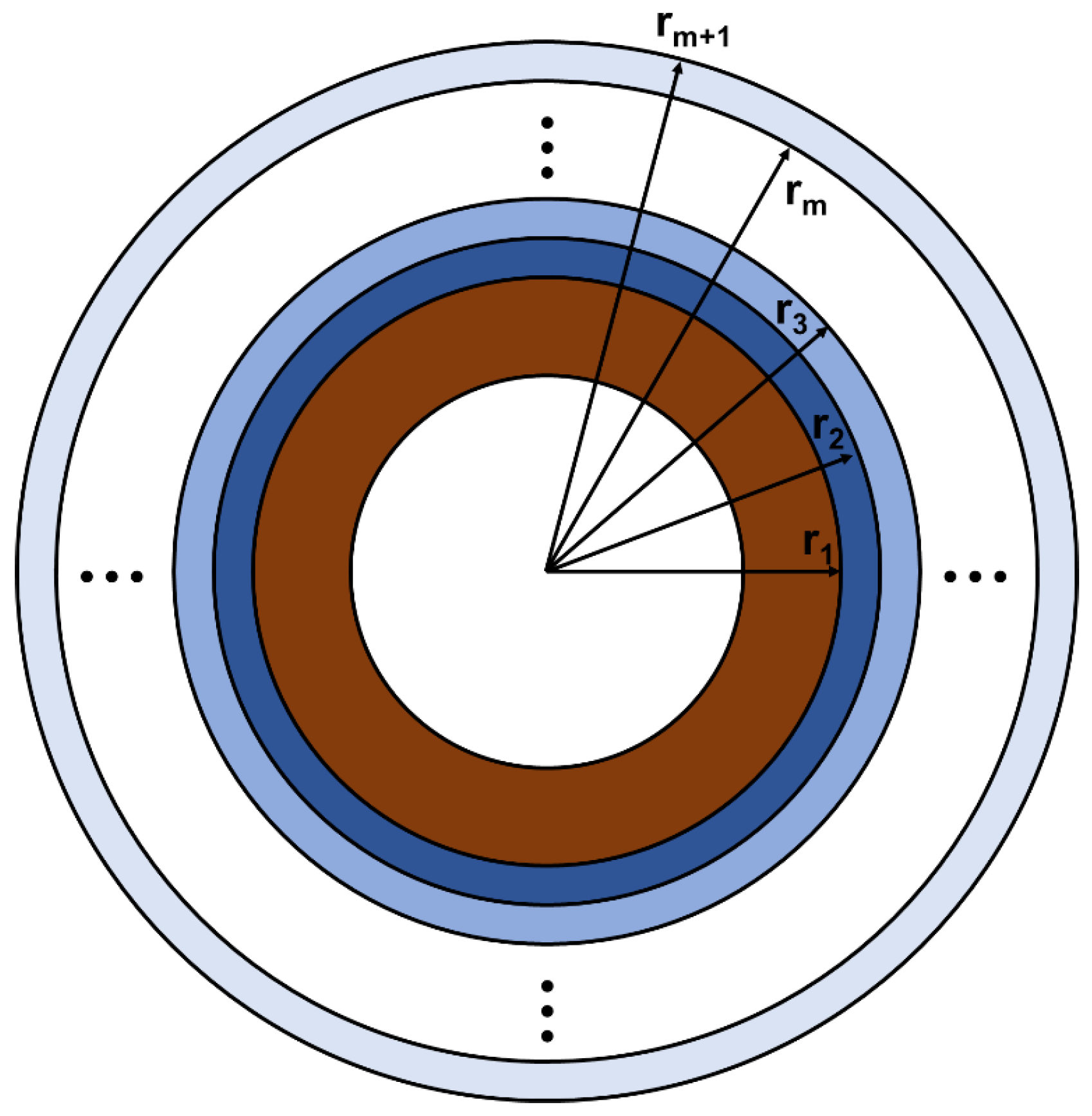
2.1. Structure of FGM-cSPT
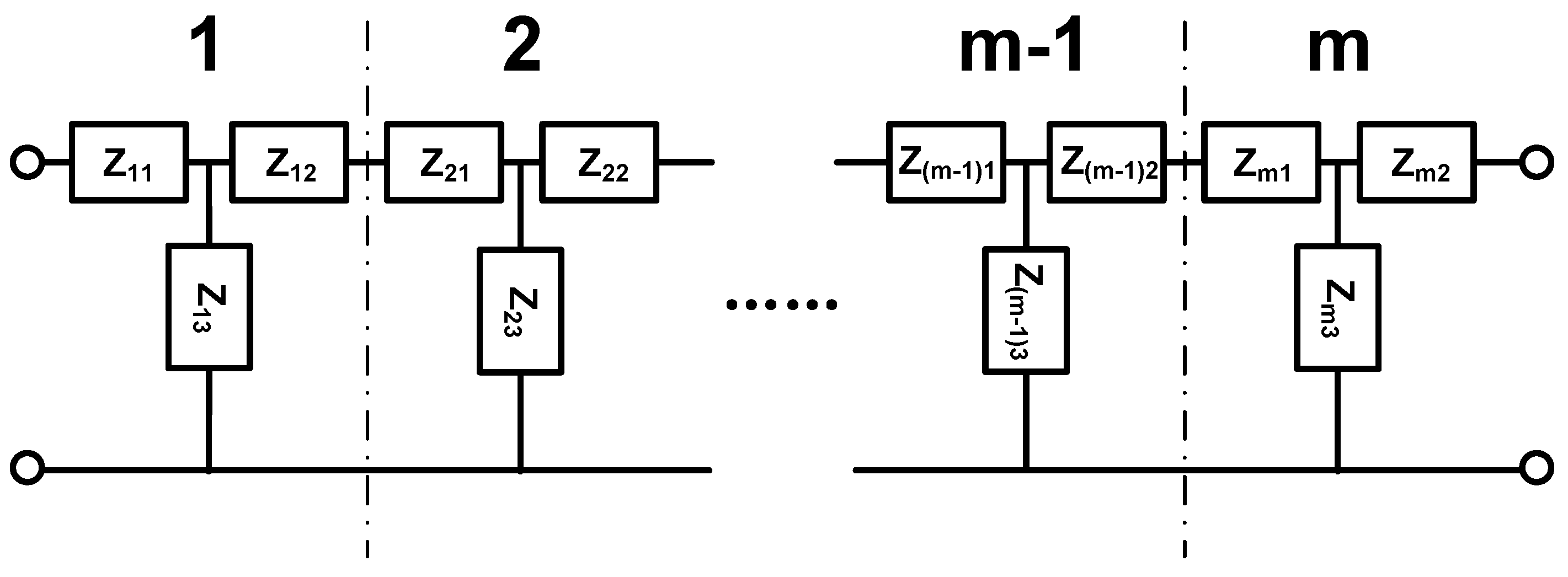
2.2. EECM for FGM-cSPT
3. Results and Discussion
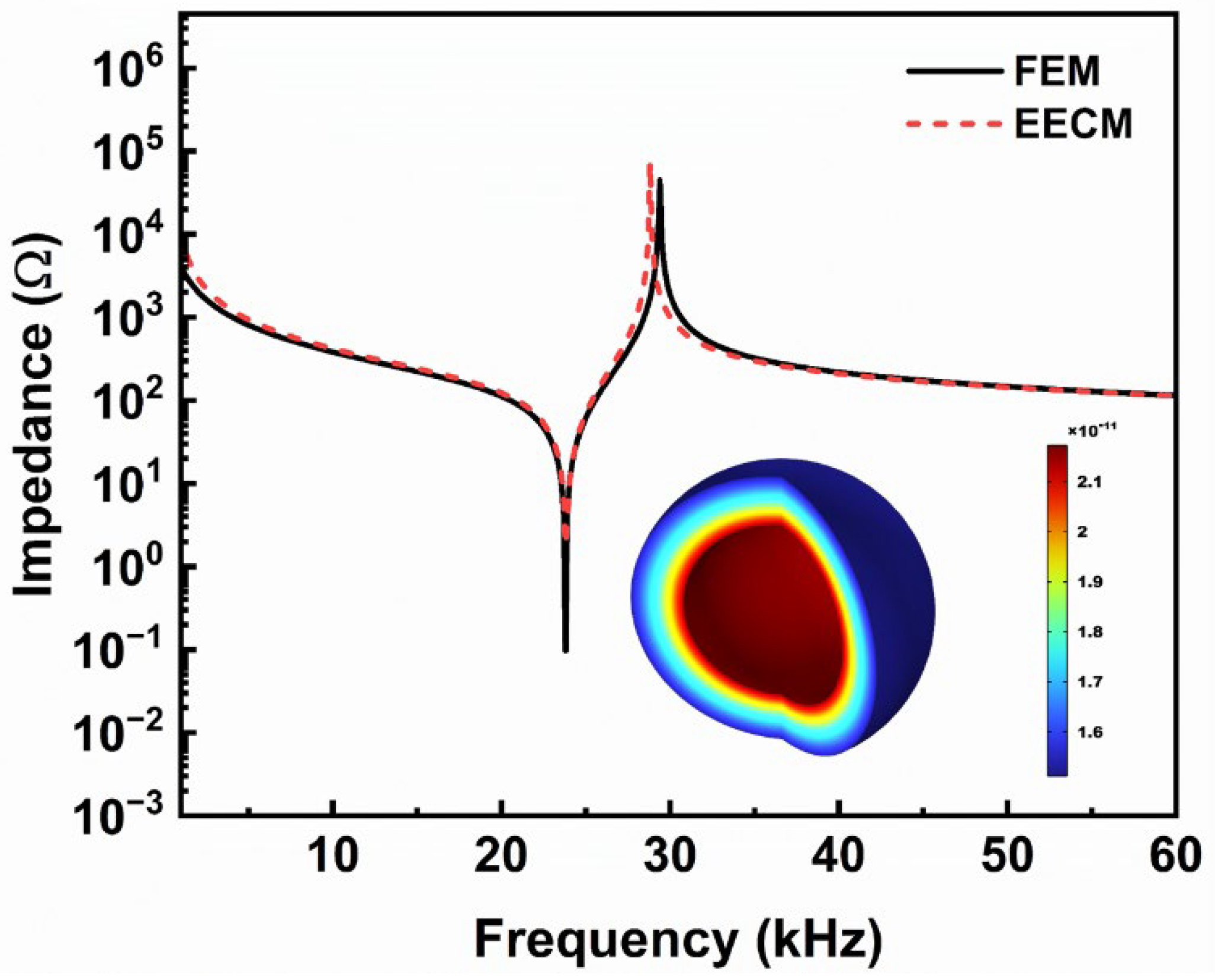
3.1. Vibration Modes and Admittance
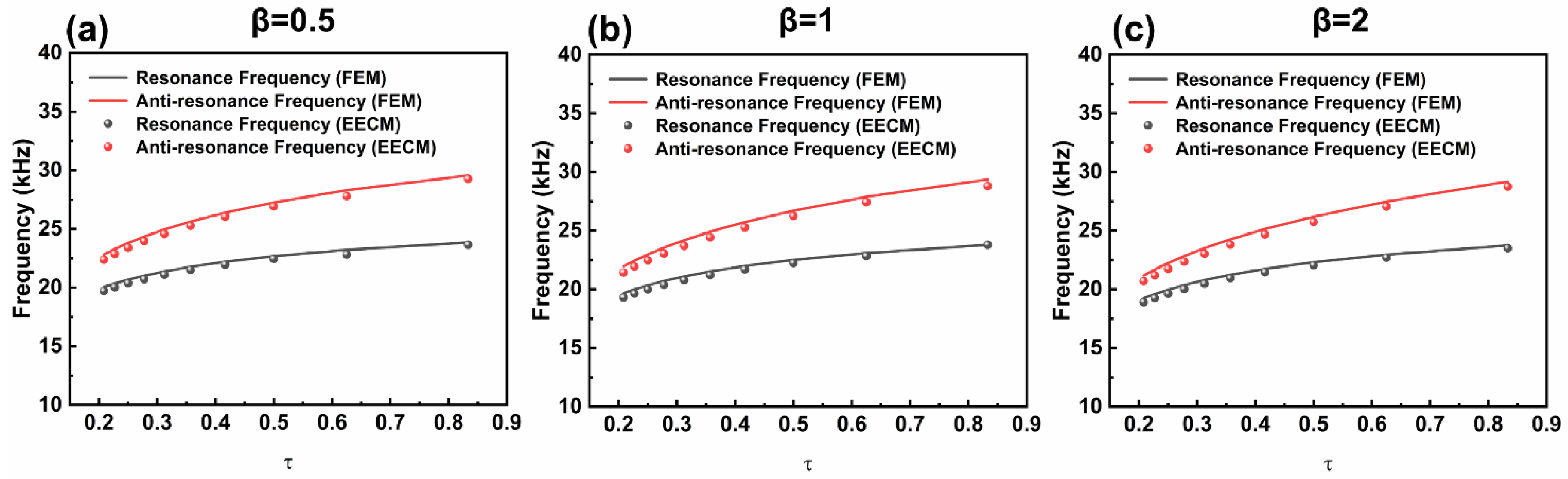
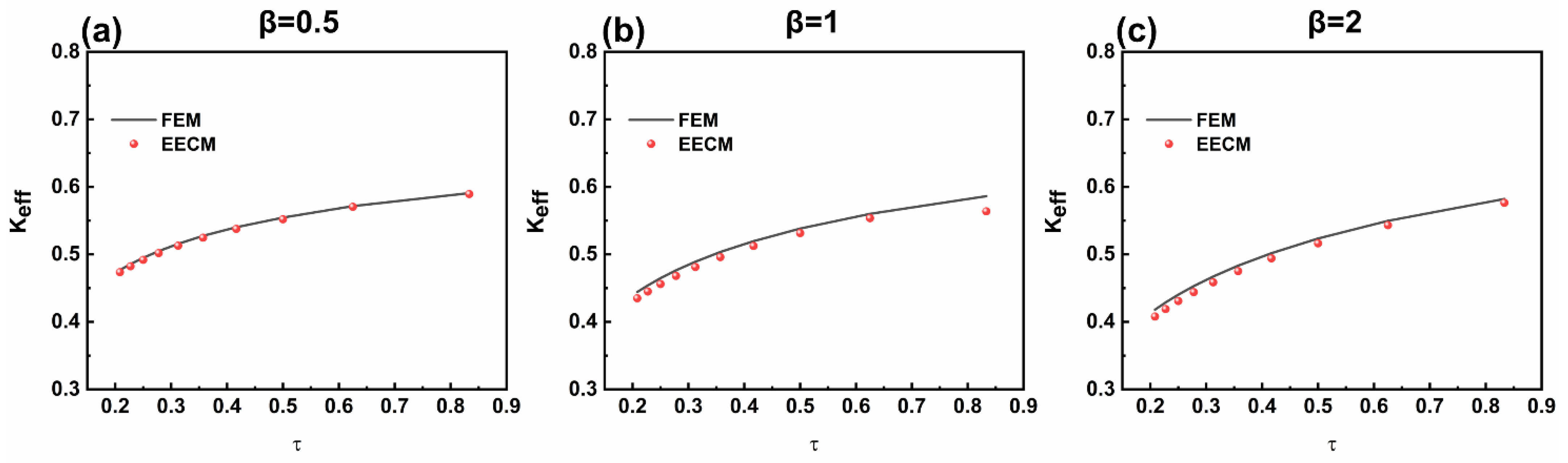
3.2. Effect of FGM on Vibration Characteristics of FGM-cSPT
3.3. Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FEM | Finite element method |
| EECM | Electromechanical equivalent circuit method |
| FGM | Functionally graded material |
| FGM-cSPT | Functionally graded material composite spherical PZT-5A piezoelectric transducer |
Appendix A
- Density: ρc+(ρw−ρc)×((((R^2+Z^2)^0.5-a)/(b-a))^β)
- Young’s modulus: Ec+(Ew-Ec)×((((R^2+Z^2)^0.5-a)/(b-a))^β)
- Poisson’s ratio: vc+(vw-vc)×((((R^2+Z^2)^0.5-a)/(b-a))^β)
References
- Zhang, Y.J.; Wang, L.K.; Qin, L.; Zhong, C.; Hao, S.H. Spherical–Omnidirectional Piezoelectric Composite Transducer for High Frequency Underwater Acoustics. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 1791–1796. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.F.; Chen, C.; Wang, C.H.; Lin, S.Y. A universal analysis method for an omnidirectional broadband spherical transducer based on 1-3-2 piezoelectric composite. Mech. Syst. Signal. Prac. 2024, 224, 111996. [Google Scholar] [CrossRef]
- Ma, K.J.; Chen, H.Y.; Wu, Z.Y.; Hao, X.L.; Ya, G.; Li, W.B.; Shao, L.; Meng, G.; Zhang, W.M. A wave-confining metasphere beamforming acoustic sensor for superior human-machine voice interaction. Sci. Adv. 2022, 8, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Lin, S.Y. A novelly universal theory: Toward accurately evaluating radial vibration characteristics for radially sandwiched spherical piezoelectric transducer. Ultrasonics 2021, 11, 106299. [Google Scholar] [CrossRef]
- Wang, S.; Lin, S.Y. An Exact and Practical Analyzing Model for Radial Vibration of Piezoelectric Spherical Transducers With Arbitrary Wall Thickness. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 760–766. [Google Scholar] [CrossRef]
- Tang, Y.F.; Chen, C.; Tian, H.; Lin, S.Y. Radial vibration analysis for piezoceramic shell-stacked spherical transducer with thick walls. Smart Mater. Struct. 2024, 33, 035002. [Google Scholar] [CrossRef]
- Tang, Y.F.; Lin, S.Y. Systematic design and experimental realization of a radially cascaded spherical piezoelectric transducer. J. Acoust. Soc. Am. 2023, 154, 1838–1849. [Google Scholar] [CrossRef] [PubMed]
- Kong, Q.Z.; Fan, S.L.; Bai, X.L.; Mo, Y.L.; Song, G.B. A novel embeddable spherical smart aggregate for structural health monitoring: Part I. Fabrication and electrical characterization. Smart Mater. Struct. 2017, 26, 095050. [Google Scholar] [CrossRef]
- Kong, Q.Z.; Fan, S.L.; Mo, Y.L.; Song, G.B. A novel embeddable spherical smart aggregate for structural health monitoring: Part II. Numerical and experimental verifications Smart Mater. Struct. 2017, 26, 095051. [Google Scholar] [CrossRef]
- Dong, E.Q.; Song, Z.C.; Zhang, Y.; Mosanenzadeh, S.G.; He, Q.; Zhao, X.H.; Fang, N.X. Bioinspired metagel with broadband tunable impedance matching. Sci. Adv. 2020, 6, 44. [Google Scholar] [CrossRef]
- Bian, J.C.; Wang, Y.; Liu, Z.J.; Shen, M.J.; Zhao, H.; Sun, Y.L.; Zhu, J.J. Ultra-wideband underwater acoustic transducer with a gradient impedance matching layer. Appl. Acoust. 2021, 175, 107789. [Google Scholar] [CrossRef]
- Ji, H.W.; Qi, A.Q.; Yang, F.; Wu, X.; Lv, B.; Ni, J. Design of acoustic impedance gradient matching layers. Appl. Acoust. 2023, 211, 109549. [Google Scholar] [CrossRef]
- Zhang, Y.W.; Chen, W.J.; Ni, Z.Y.; Zang, J.; Hou, S. Supersonic aerodynamic piezoelectric energy harvesting performance of functionally graded beams. Compos. Struct. 2020, 233, 111537. [Google Scholar] [CrossRef]
- Larkin, K.; Abdelkefi, A. Neutral axis modeling and effectiveness of functionally graded piezoelectric energy harvesters. Compos. Struct. 2019, 213, 25–36. [Google Scholar] [CrossRef]
- Foroutan, M.; Mohammadi, F.; Alihemati, J.; Soltanimaleki, A. Dynamic analysis of functionally graded piezoelectric cylindrical panels by a three-dimensional mesh-free model. J. Intel. Mat. Syst. Str. 2017, 28, 2516–2527. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.G.; Xiong, H.L.; Sun, S.T.; Ling, Z.C.; Shen, G.D.; Zhao, X.; Chen, B.J.; Meng, G. Design and experimental validation of a broadband multi-modal coupled capsule-shaped transducer for underwater acoustics. Sens. Actuators A Phys. 2024, 373, 115393. [Google Scholar] [CrossRef]
- Naghdi, M.; Zhang, H.F.; Sreedharan, S.V.; Ju, S.; Desai, M.H. A new FEM-based approach on the modeling of stress-induced velocity shift of piezoelectric surface acoustic wave resonators. Ultrasonics 2024, 148, 107521. [Google Scholar] [CrossRef] [PubMed]
- Yamada, K.; Ieiri, S.; Itoh, S.; Kasashima, T.; Morita, T. Rayleigh wave excitation with an elliptical reflector for high-power ultrasound. Sens. Actuators A Phys. 2024, 370, 115253. [Google Scholar] [CrossRef]
- Yang, T.Y.; Zhu, Y.F.; Li, S.Y.; An, D.W.; Yao, M.; Cao, W.W. Dielectric loss and thermal effect in high power piezoelectric systems. Sens. Actuators A Phys. 2020, 303, 111724. [Google Scholar] [CrossRef]
- Maadi, M.; Zemp, R.A. Nonlinear Lumped Equivalent Circuit Model for a Single Uncollapsed Square CMUT Cell. J. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 66, 1340–1351. [Google Scholar] [CrossRef]
- Shim, H.; Roh, Y. Development of an equivalent circuit of a cymbal transducer. IEEE Sens. J. 2021, 21, 13146–13155. [Google Scholar] [CrossRef]
- Chen, D.D.; Zhao, J.X.; Fei, C.L.; Li, D.; Zhu, Y.B.; Li, Z.X.; Guo, R.; Lou, L.F.; Feng, W.; Yang, Y.T. Particle Swarm Optimization Algorithm-Based Design Method for Ultrasonic Transducers. Micromachines 2020, 11, 715. [Google Scholar] [CrossRef] [PubMed]
- Pyo, S.; Lim, Y.; Roh, Y. Analysis of the transmitting characteristics of an acoustic conformal array of multimode tonpilz transducers by the equivalent circuit method. Sens. Actuators A Phys. 2021, 318, 112507. [Google Scholar] [CrossRef]
- Hasheminejad, S.M.; Malakooti, S.; Akbarzadeh, H.M. Acoustic radiation from a submerged hollow FGM sphere. Arch. Appl. Mech. 2011, 81, 1889–1902. [Google Scholar] [CrossRef]
- Hasheminejad, S.M.; Gudarzi, M. Active sound radiation control of a submerged piezocomposite hollow sphere. J. Intell. Mater. Syst. Struct. 2015, 26, 2073–2091. [Google Scholar] [CrossRef]
- Wang, S.; Chen, C.; Hu, L.Q.; Lin, S.Y. Spherical piezoelectric transducers of functionally graded materials. J Acoust. Soc. Am. 2022, 152, 193–200. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Shan, J.J.; Lin, S.Y. Radial vibration analysis for functionally graded ring piezoelectric transducers based on electromechanical equivalent circuit method. Ultrasonics 2022, 120, 106640. [Google Scholar] [CrossRef]
- Wang, H.M.; Luo, D.S. Exact analysis of radial vibration of functionally graded piezoelectric ring transducers resting on elastic foundation. Appl. Math. Model 2015, 40, 2549–2559. [Google Scholar] [CrossRef]




| Parameters | Value | |
|---|---|---|
| PZT-5A | ||
| 7750 | ||
| 12.1 | ||
| 7.54 | ||
| 7.52 | ||
| 11.1 | ||
| −5.4 | ||
| 15.8 | ||
| 7.35 | ||
| Parameters | Value | |
| Ceramic | Hydrogel | |
| 7700 | 1070 | |
| E (N/m2) | 53.2 × 109 | 790 |
| σ | 0.26 | 0.44 |
| Experiment | FEM | EECM | |||||||
|---|---|---|---|---|---|---|---|---|---|
| fre (Hz) | fae (Hz) | frf (Hz) | Δf1% | faf (Hz) | Δf2% | frt (Hz) | Δt1% | fat (Hz) | Δt2% |
| 105,333 | 119,717 | 109,980 | 4.41 | 125,080 | 4.48 | 109,854 | 4.29 | 125,500 | 4.83 |
| Parameters | Value |
|---|---|
| PZT-4 | |
| 7500 | |
| 13.9 | |
| 7.78 | |
| 7.43 | |
| 11.5 | |
| −5.2 | |
| 15.1 | |
| 5.62 | |
| Parameters | Value |
| Aluminum | |
| 2700 | |
| E (N/m2) | 69 × 109 |
| σ | 0.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Shan, J. Study on Vibration Characteristics of Functionally Graded Material Composite Spherical Piezoelectric Transducer. Sensors 2025, 25, 1514. https://doi.org/10.3390/s25051514
Wang S, Shan J. Study on Vibration Characteristics of Functionally Graded Material Composite Spherical Piezoelectric Transducer. Sensors. 2025; 25(5):1514. https://doi.org/10.3390/s25051514
Chicago/Turabian StyleWang, Sha, and Junjie Shan. 2025. "Study on Vibration Characteristics of Functionally Graded Material Composite Spherical Piezoelectric Transducer" Sensors 25, no. 5: 1514. https://doi.org/10.3390/s25051514
APA StyleWang, S., & Shan, J. (2025). Study on Vibration Characteristics of Functionally Graded Material Composite Spherical Piezoelectric Transducer. Sensors, 25(5), 1514. https://doi.org/10.3390/s25051514






