Lightweight Explicit 3D Human Digitization via Normal Integration
Abstract
1. Introduction
- We propose an innovative human reconstruction method incorporating an innovative loss function designed to optimize the training process. This loss function significantly enhances the accuracy and detail of reconstructions, as evidenced by the promising results achieved in our experiments;
- We also introduce a lightweight generative network designed to produce high-quality surface normal maps of the human body. This network employs efficient architectural designs to capture intricate geometric details effectively. Experimental results confirm the robustness and efficiency of our approach in generating accurate and realistic surface normal maps;
- Extensive experiments were conducted to evaluate our proposed method comprehensively. These assessments, comprising both quantitative and qualitative analyses, underscore the superiority of our approach. The results demonstrate consistent performance across diverse scenarios, highlighting its robustness and effectiveness in reconstructing detailed human models.
2. Related Works
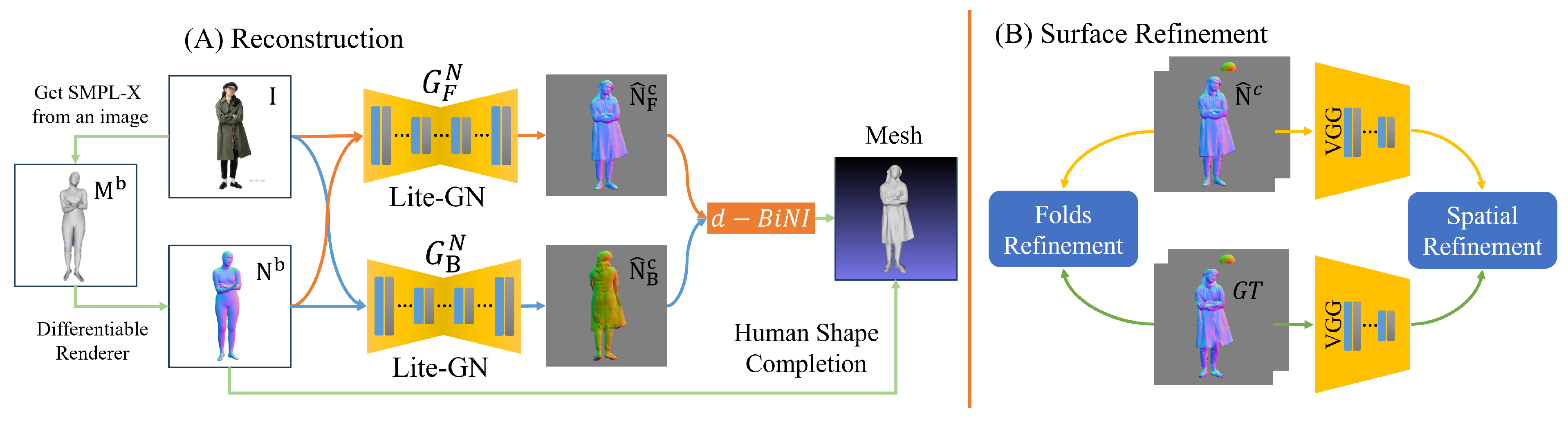
3. Methods
3.1. Human Models Reconstruction
3.2. The Proposed Framework: Lite-GN
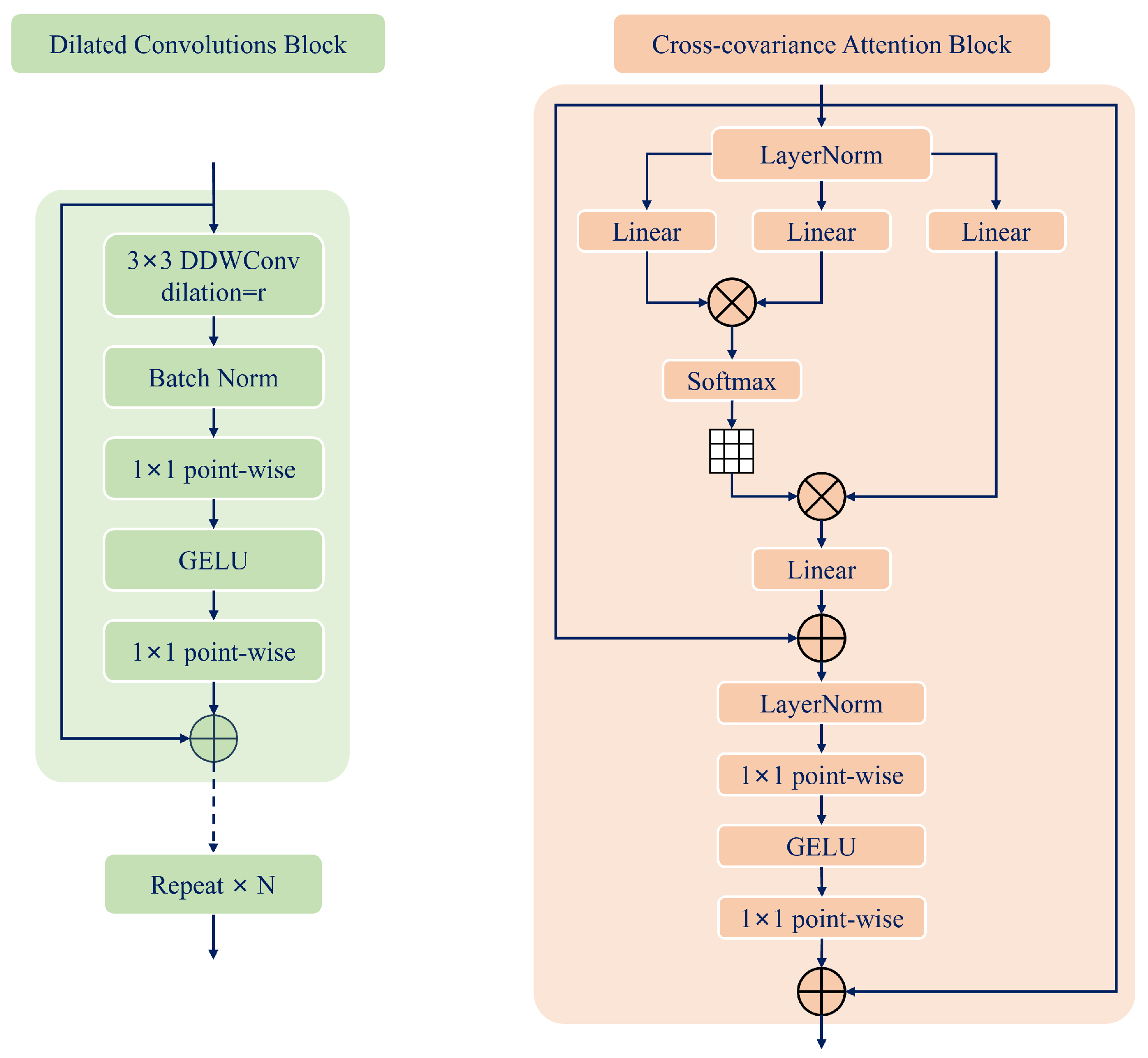
3.2.1. Dilated Convolutions Block
3.2.2. Cross-Covariance Attention Block
3.3. Surface Refinement
4. Experiments and Results
4.1. Implementation Details
4.2. Evaluation Metrics
4.3. Evaluation
4.3.1. Quantitative Evaluation
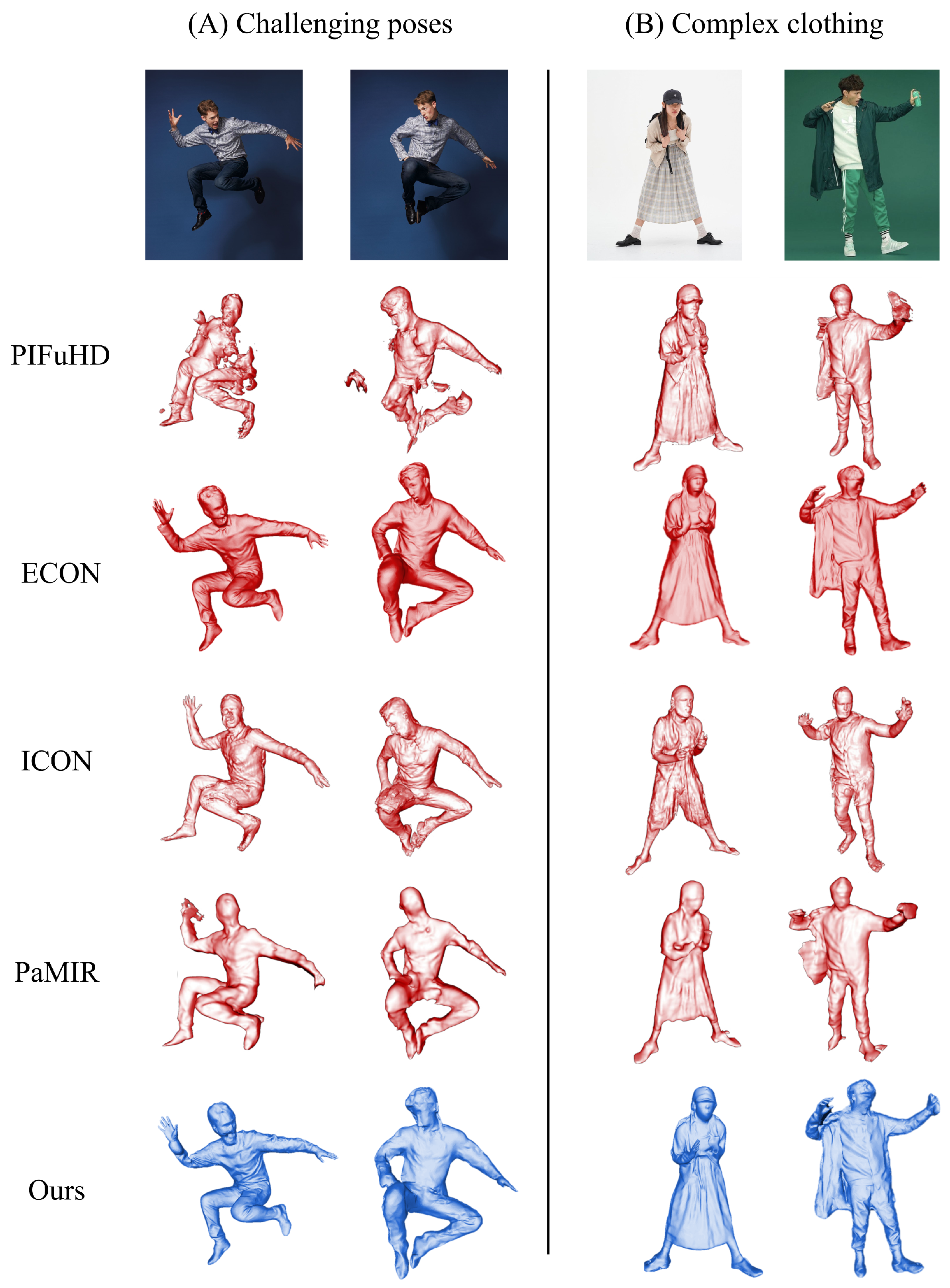
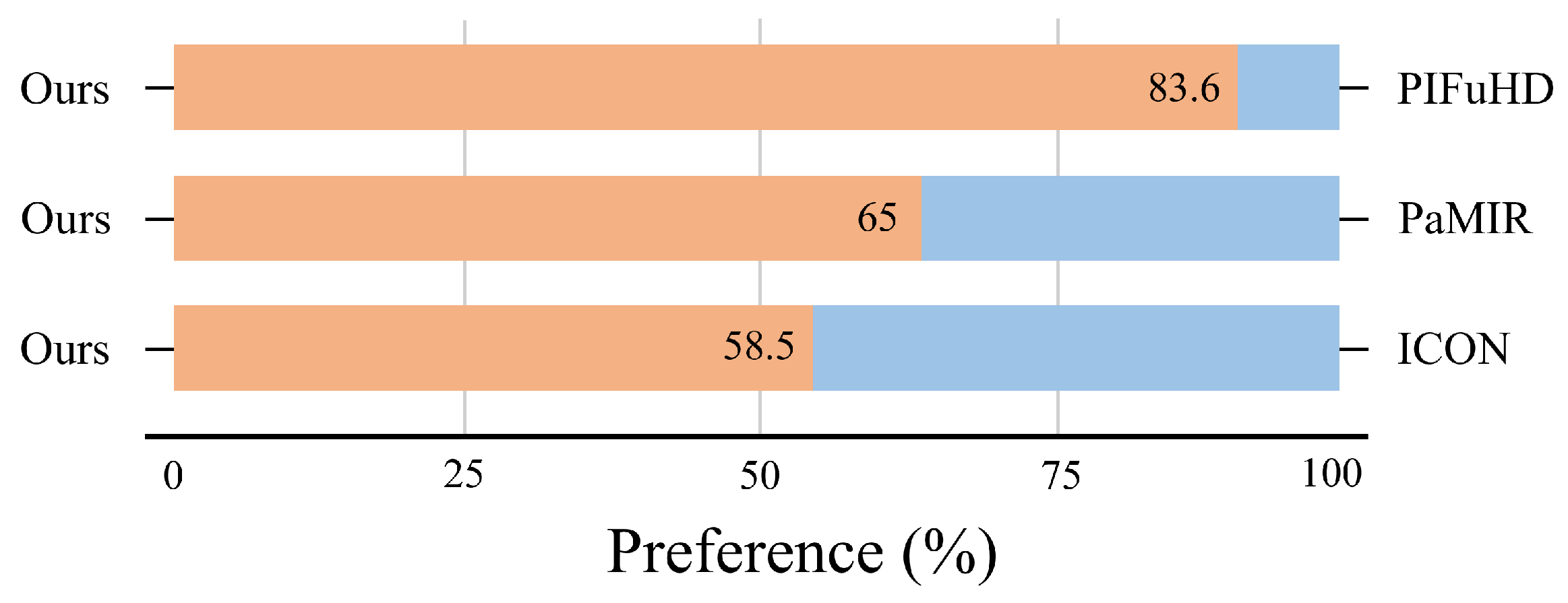
4.3.2. Qualitative Comparison
4.4. Ablation Study
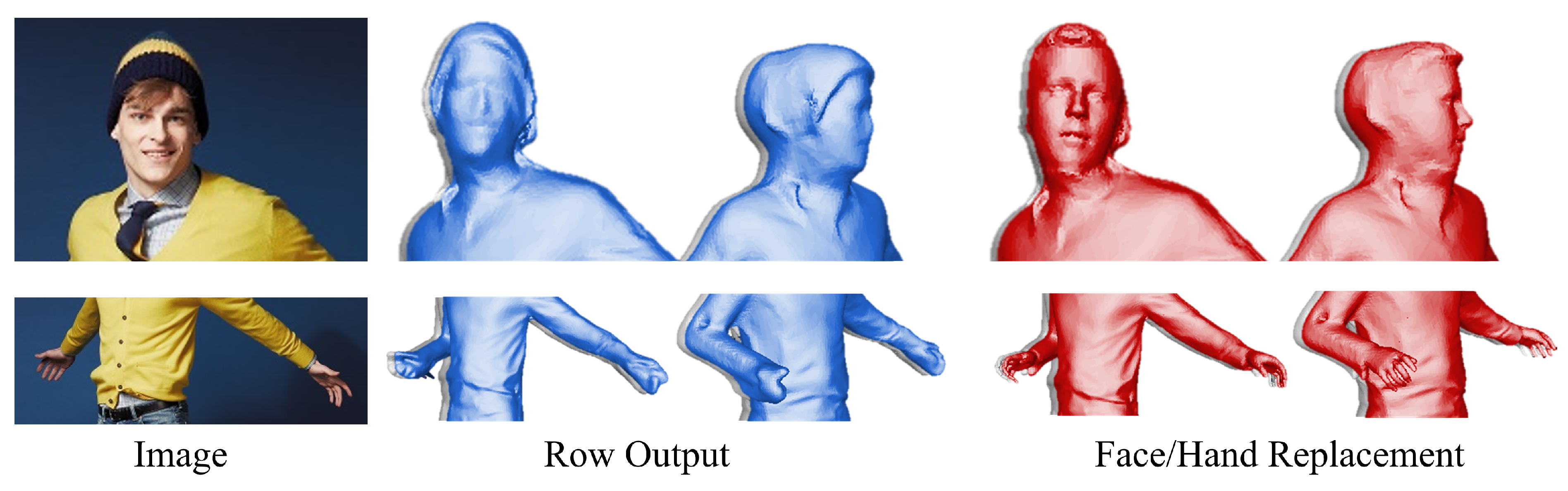
4.5. Facial and Hand Refinement Attempts
4.6. Text-Driven Texture Generation
4.7. Animatable Avatar Creation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rymov, D.A.; Svistunov, A.S.; Starikov, R.S.; Shifrina, A.V.; Rodin, V.G.; Evtikhiev, N.N.; Cheremkhin, P.A. 3D-CGH-Net: Customizable 3D-hologram generation via deep learning. Opt. Lasers Eng. 2025, 184, 108645. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, H.; Che, F.; Chen, X.L.Z.; Zhang, Q. Dynamic 3D shape reconstruction under complex reflection and transmission conditions using multi-scale parallel single-pixel imaging. Light Adv. Manuf. 2024, 5, 373. [Google Scholar] [CrossRef]
- Puliti, C.S. Structure from Motion Photogrammetry in Forestry: A Review. Curr. For. Rep. 2019, 5, 155–168. [Google Scholar]
- Rossol, N.; Cheng, I.; Basu, A. A Multisensor Technique for Gesture Recognition Through Intelligent Skeletal Pose Analysis. IEEE Trans. Hum.-Mach. Syst. 2016, 46, 350–359. [Google Scholar] [CrossRef]
- Chua, J.; Ong, L.Y.; Leow, M.C. Telehealth Using PoseNet-Based System for In-Home Rehabilitation. Future Internet 2021, 13, 173. [Google Scholar] [CrossRef]
- Dai, Q.; Ma, C.; Zhang, Q. Advanced Hyperspectral Image Analysis: Superpixelwise Multiscale Adaptive T-HOSVD for 3D Feature Extraction. Sensors 2024, 24, 4072. [Google Scholar] [CrossRef]
- Sharma, P.; Shah, B.B.; Prakash, C. A Pilot Study on Human Pose Estimation for Sports Analysis. In Pattern Recognition and Data Analysis with Applications; Gupta, D., Goswami, R.S., Banerjee, S., Tanveer, M., Pachori, R.B., Eds.; Springer: Singapore, 2022; pp. 533–544. [Google Scholar]
- Rabosh, E.V.; Balbekin, N.S.; Petrov, N.V. Analog-to-digital conversion of information archived in display holograms: I. discussion. J. Opt. Soc. Am. A 2023, 40, B47–B56. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Liu, Z.; Gu, X.; Wang, D. Three-Dimensional Reconstruction of Road Structural Defects Using GPR Investigation and Back-Projection Algorithm. Sensors 2025, 25, 162. [Google Scholar] [CrossRef]
- Liu, H.; Hellín, C.J.; Tayebi, A.; Calles, F.; Gómez, J. Vertex-Oriented Method for Polyhedral Reconstruction of 3D Buildings Using OpenStreetMap. Sensors 2024, 24, 7992. [Google Scholar] [CrossRef]
- Pan, H.; Cai, Y.; Yang, J.; Niu, S.; Gao, Q.; Wang, X. HandFI: Multilevel Interacting Hand Reconstruction Based on Multilevel Feature Fusion in RGB Images. Sensors 2025, 25, 88. [Google Scholar] [CrossRef] [PubMed]
- Saito, S.; Huang, Z.; Natsume, R.; Morishima, S.; Li, H.; Kanazawa, A. PIFu: Pixel-Aligned Implicit Function for High-Resolution Clothed Human Digitization. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision, ICCV 2019, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 2304–2314. [Google Scholar] [CrossRef]
- Saito, S.; Simon, T.; Saragih, J.M.; Joo, H. PIFuHD: Multi-Level Pixel-Aligned Implicit Function for High-Resolution 3D Human Digitization. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2020, Seattle, WA, USA, 13–19 June 2020; pp. 81–90. [Google Scholar] [CrossRef]
- Zheng, Z.; Yu, T.; Liu, Y.; Dai, Q. PaMIR: Parametric Model-Conditioned Implicit Representation for Image-Based Human Reconstruction. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 3170–3184. [Google Scholar] [CrossRef]
- Loper, M.; Mahmood, N.; Romero, J.; Pons-Moll, G.; SMPL, M.B. SMPL: A skinned multi-person linear model. ACM Trans. Graph. (TOG) 2015, 34, 1–16. [Google Scholar] [CrossRef]
- Kovács, L.; Bódis, B.M.; Benedek, C. LidPose: Real-Time 3D Human Pose Estimation in Sparse Lidar Point Clouds with Non-Repetitive Circular Scanning Pattern. Sensors 2024, 24, 3427. [Google Scholar] [CrossRef]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. arXiv 2016, arXiv:1511.07122. [Google Scholar]
- Ali, A.; Touvron, H.; Caron, M.; Bojanowski, P.; Douze, M.; Joulin, A.; Laptev, I.; Neverova, N.; Synnaeve, G.; Verbeek, J.; et al. XCiT: Cross-Covariance Image Transformers. arXiv 2021, arXiv:2106.09681. [Google Scholar]
- Xiu, Y.; Yang, J.; Cao, X.; Tzionas, D.; Black, M.J. ECON: Explicit Clothed humans Optimized via Normal integration. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 512–523. [Google Scholar] [CrossRef]
- Pavlakos, G.; Choutas, V.; Ghorbani, N.; Bolkart, T.; Osman, A.A.; Tzionas, D.; Black, M.J. Expressive body capture: 3d hands, face, and body from a single image. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10975–10985. [Google Scholar]
- Johnson, J.; Alahi, A.; Li, F.-F. Perceptual Losses for Real-Time Style Transfer and Super-Resolution; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Huber, P.J. Robust Estimation of a Location Parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Anguelov, D.; Srinivasan, P.; Koller, D.; Thrun, S.; Rodgers, J.; Davis, J. SCAPE: Shape completion and animation of people. ACM Trans. Graph. (TOG) 2005, 24, 408–416. [Google Scholar] [CrossRef]
- Hasler, N.; Stoll, C.; Sunkel, M.; Rosenhahn, B.; Seidel, H. A Statistical Model of Human Pose and Body Shape. Comput. Graph. Forum 2009, 28, 337–346. [Google Scholar] [CrossRef]
- James, D.L.; Twigg, C.D. Skinning mesh animations. ACM Trans. Graph. 2005, 24, 399–407. [Google Scholar] [CrossRef]
- Allen, B.; Curless, B.; Popović, Z. Articulated body deformation from range scan data. ACM Trans. Graph. (TOG) 2002, 21, 612–619. [Google Scholar] [CrossRef]
- Bogo, F.; Kanazawa, A.; Lassner, C.; Gehler, P.V.; Romero, J.; Black, M.J. Keep It SMPL: Automatic Estimation of 3D Human Pose and Shape from a Single Image. In Proceedings of the Computer Vision-ECCV 2016-14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Volume 9909, pp. 561–578. [Google Scholar] [CrossRef]
- Kanazawa, A.; Black, M.J.; Jacobs, D.W.; Malik, J. End-to-end recovery of human shape and pose. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7122–7131. [Google Scholar]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Kolotouros, N.; Pavlakos, G.; Black, M.J.; Daniilidis, K. Learning to Reconstruct 3D Human Pose and Shape via Model-fitting in the Loop. In Proceedings of the ICCV, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- He, T.; Collomosse, J.; Jin, H.; Soatto, S. Geo-pifu: Geometry and pixel aligned implicit functions for single-view human reconstruction. Adv. Neural Inf. Process. Syst. 2020, 33, 9276–9287. [Google Scholar]
- Li, Z.; Yu, T.; Pan, C.; Zheng, Z.; Liu, Y. Robust 3d self-portraits in seconds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1344–1353. [Google Scholar]
- Dong, Z.; Guo, C.; Song, J.; Chen, X.; Geiger, A.; Hilliges, O. Pina: Learning a personalized implicit neural avatar from a single rgb-d video sequence. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 20470–20480. [Google Scholar]
- Yang, Z.; Wang, S.; Manivasagam, S.; Huang, Z.; Ma, W.; Yan, X.; Yumer, E.; Urtasun, R. S3: Neural Shape, Skeleton, and Skinning Fields for 3D Human Modeling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2021, Virtual, 19–25 June 2021; pp. 13284–13293. [Google Scholar] [CrossRef]
- Zheng, Y.; Shao, R.; Zhang, Y.; Yu, T.; Zheng, Z.; Dai, Q.; Liu, Y. Deepmulticap: Performance capture of multiple characters using sparse multiview cameras. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 6239–6249. [Google Scholar]
- Huang, Z.; Xu, Y.; Lassner, C.; Li, H.; Tung, T. ARCH: Animatable Reconstruction of Clothed Humans. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2020, Seattle, WA, USA, 13–19 June 2020; pp. 3090–3099. [Google Scholar] [CrossRef]
- He, T.; Xu, Y.; Saito, S.; Soatto, S.; Tung, T. ARCH++: Animation-Ready Clothed Human Reconstruction Revisited. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision, ICCV 2021, Montreal, QC, Canada, 11–17 October 2021; pp. 11026–11036. [Google Scholar] [CrossRef]
- Liao, T.; Zhang, X.; Xiu, Y.; Yi, H.; Liu, X.; Qi, G.J.; Zhang, Y.; Wang, X.; Zhu, X.; Lei, Z. High-fidelity clothed avatar reconstruction from a single image. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 8662–8672. [Google Scholar]
- Xiu, Y.; Yang, J.; Tzionas, D.; Black, M.J. ICON: Implicit Clothed humans Obtained from Normals. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2022, New Orleans, LA, USA, 18–24 June 2022; pp. 13286–13296. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Zhou, Z.; Fan, X.; Shi, P.; Xin, Y. R-MSFM: Recurrent Multi-Scale Feature Modulation for Monocular Depth Estimating. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision, ICCV 2021, Montreal, QC, Canada, 10–17 October 2021; pp. 12757–12766. [Google Scholar] [CrossRef]
- Zhang, N.; Nex, F.; Vosselman, G.; Kerle, N. Lite-Mono: A Lightweight CNN and Transformer Architecture for Self-Supervised Monocular Depth Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2023, Vancouver, BC, Canada, 17–24 June 2023; pp. 18537–18546. [Google Scholar] [CrossRef]
- Bae, J.; Moon, S.; Im, S. Deep Digging into the Generalization of Self-Supervised Monocular Depth Estimation. In Proceedings of the Thirty-Seventh AAAI Conference on Artificial Intelligence, AAAI 2023, Thirty-Fifth Conference on Innovative Applications of Artificial Intelligence, IAAI 2023, Thirteenth Symposium on Educational Advances in Artificial Intelligence, EAAI 2023, Washington, DC, USA, 7–14 February 2023; pp. 187–196. [Google Scholar] [CrossRef]
- Deng, B.; Lewis, J.P.; Jeruzalski, T.; Pons-Moll, G.; Hinton, G.; Norouzi, M.; Tagliasacchi, A. Nasa neural articulated shape approximation. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; pp. 612–628. [Google Scholar]
- Feng, Y.; Choutas, V.; Bolkart, T.; Tzionas, D.; Black, M.J. Collaborative regression of expressive bodies using moderation. In Proceedings of the 2021 International Conference on 3D Vision (3DV), London, UK, 1–3 December 2021; pp. 792–804. [Google Scholar]
- Rembg: A Tool to Remove Images Background. 2022. Available online: https://github.com/danielgatis/rembg (accessed on 26 January 2024).
- Kazhdan, M.; Bolitho, M.; Hoppe, H. Poisson surface reconstruction. In Proceedings of the Fourth Eurographics Symposium on Geometry Processing, Cagliari, Italy, 26–28 June 2006; Volume 7. [Google Scholar]
- Godard, C.; Aodha, O.M.; Firman, M.; Brostow, G.J. Digging Into Self-Supervised Monocular Depth Estimation. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision, ICCV 2019, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3827–3837. [Google Scholar] [CrossRef]
- Zhou, H.; Greenwood, D.; Taylor, S. Self-Supervised Monocular Depth Estimation with Internal Feature Fusion. arXiv 2021, arXiv:2110.09482. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2021, arXiv:2010.11929. [Google Scholar]
- Hendrycks, D.; Gimpel, K.; Gimpel, K. Bridging Nonlinearities and Stochastic Regularizers with Gaussian Error Linear Units. arXiv 2016, arXiv:1606.08415. Available online: https://api.semanticscholar.org/CorpusID:2359786 (accessed on 20 February 2025).
- Ba, L.J.; Kiros, J.R.; Hinton, G.E. Layer Normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian error linear units (gelus). arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Yu, T.; Zheng, Z.; Guo, K.; Liu, P.; Dai, Q.; Liu, Y. Function4d: Real-time human volumetric capture from very sparse consumer rgbd sensors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 5746–5756. [Google Scholar]
- Ma, Q.; Yang, J.; Ranjan, A.; Pujades, S.; Pons-Moll, G.; Tang, S.; Black, M.J. Learning to dress 3d people in generative clothing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 6469–6478. [Google Scholar]
- RenderPeople. 2018. Available online: https://renderpeople.com (accessed on 20 October 2024).
- Charles, R.Q.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar] [CrossRef]
- Richardson, E.; Metzer, G.; Alaluf, Y.; Giryes, R.; Cohen-Or, D. TEXTure: Text-Guided Texturing of 3D Shapes. In Proceedings of the ACM SIGGRAPH 2023 Conference Proceedings, SIGGRAPH 2023, Los Angeles, CA, USA, 6–10 August 2023; pp. 54:1–54:11. [Google Scholar] [CrossRef]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10684–10695. [Google Scholar]
- Saito, S.; Yang, J.; Ma, Q.; Black, M.J. SCANimate: Weakly Supervised Learning of Skinned Clothed Avatar Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2021, Virtual, 19–25 June 2021; pp. 2886–2897. [Google Scholar] [CrossRef]

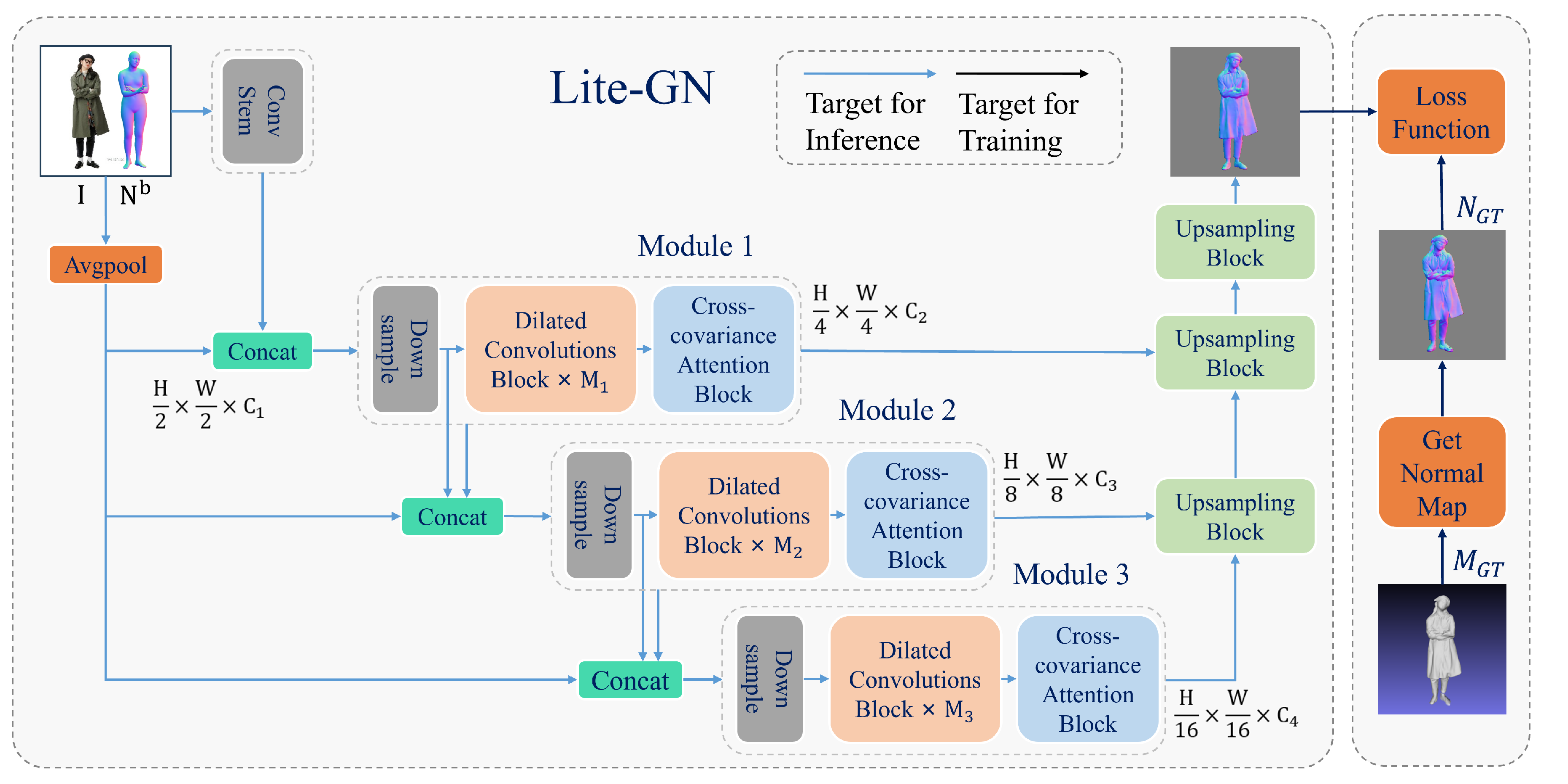



| Output Size | Stage | Layer |
|---|---|---|
| 512 × 512 × 6 | Input | |
| 256 × 256 × 64 | Stem | [3 × 3] × 4 |
| [3 × 3] × 2 | ||
| 128 × 128 × 64 | Stage 1 | Dilated Convolutions Block × 6 |
| Cross-Covariance Attention Block × 1 | ||
| [3 × 3] × 2 | ||
| 64 × 64 × 128 | Stage 2 | Dilated Convolutions Block × 6 |
| Cross-Covariance Attention Block × 1 | ||
| [3 × 3] × 2 | ||
| 32 × 32 × 224 | Stage 3 | Dilated Convolutions Block × 18 |
| Cross-Covariance Attention Block × 1 |
| Equipment | Computer Configuration Parameters |
|---|---|
| Operating system | Linux |
| RAM | 32 G |
| Type of operating system | Ubuntu20.04 |
| CPU | Intel Core i7-12700K |
| GPU | RTX 4090(24 GB) × 1 |
| Development language | Python 3.8 |
| Deep learning framework | PyTorch 1.12.1 |
| Methods | Chamfer ↓ | P2S ↓ | Normals ↓ | Weight Size ↓ |
|---|---|---|---|---|
| PIFuHD [13] | 3.767 | 3.591 | 0.0994 | 1.4 GB |
| PaMIR [14] | 0.989 | 0.992 | 0.0422 | 472 MB |
| ICON [39] | 0.971 | 0.909 | 0.0409 | 1.38 GB |
| ECON-IF [19] | 0.996 | 0.967 | 0.0413 | 1.49 GB |
| ECON-EX [19] | 0.926 | 0.917 | 0.0367 | 1.35 GB |
| Ours | 0.965 | 0.930 | 0.0472 | 201.6 MB |
| Methods | Model Size ↓ | Weight Size ↓ | Speed (ms) ↓ |
|---|---|---|---|
| ICON [39] | 345.6 M | 1.35 GB | 22.8 ms |
| ECON [19] | 345.6 M | 1.35 GB | 23.6 ms |
| Ours | 50 M | 201.6 MB | 12.8 ms |
| Methods | Chamfer ↓ | P2S ↓ | Normals ↓ |
|---|---|---|---|
| PIFuHD [13] | 1.946 | 1.983 | 0.0658 |
| PaMIR [14] | 1.296 | 1.430 | 0.0518 |
| ICON [39] | 1.373 | 1.522 | 0.0566 |
| ECON-IF [19] | 1.401 | 1.422 | 0.0516 |
| ECON-EX [19] | 1.342 | 1.458 | 0.0478 |
| Ours | 1.353 | 1.430 | 0.0452 |
| Methods | Chamfer | P2S | Normals |
|---|---|---|---|
| Cross-Covariance Attention Block | 1.074 | 0.994 | 0.0535 |
| Dilated Convolutions Block | 1.139 | 1.087 | 0.0569 |
| VGG Loss | 1.560 | 1.607 | 0.0662 |
| Huber Loss | 1.917 | 1.973 | 0.0546 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Wu, J.; Jing, R.; Yu, H.; Liu, J.; Song, L. Lightweight Explicit 3D Human Digitization via Normal Integration. Sensors 2025, 25, 1513. https://doi.org/10.3390/s25051513
Liu J, Wu J, Jing R, Yu H, Liu J, Song L. Lightweight Explicit 3D Human Digitization via Normal Integration. Sensors. 2025; 25(5):1513. https://doi.org/10.3390/s25051513
Chicago/Turabian StyleLiu, Jiaxuan, Jingyi Wu, Ruiyang Jing, Han Yu, Jing Liu, and Liang Song. 2025. "Lightweight Explicit 3D Human Digitization via Normal Integration" Sensors 25, no. 5: 1513. https://doi.org/10.3390/s25051513
APA StyleLiu, J., Wu, J., Jing, R., Yu, H., Liu, J., & Song, L. (2025). Lightweight Explicit 3D Human Digitization via Normal Integration. Sensors, 25(5), 1513. https://doi.org/10.3390/s25051513







