Abstract
This paper aims to design the modulation strategy of SiC motor controller for vehicles with low EMI, low device loss and low voltage/current ripple. The equivalent evaluation model of input voltage, output current and switching loss of the inverter under periodic spread spectrum modulation strategy is constructed, and the quantitative relationship between each parameter of spread spectrum modulation and the three indicators is established. The input/output performance and loss level of the inverter under different spread spectrum modulation strategies are evaluated. On this basis, based on the carrier frequency distribution characteristics of periodic signal spread spectrum modulation, a “secondary frequency modulation” strategy is proposed to reduce the inverter-conducted EMI to a greater extent under the limited spread spectrum range. Experimental results show that compared with the single periodic signal spread spectrum modulation, the “secondary frequency modulation” strategy can reduce the peak value of inverter-conducted EMI to a greater extent without increasing the ripple and loss of the inverter.
1. Introduction
As a third-generation semiconductor material, SiC has excellent characteristics such as high temperature resistance, high voltage resistance, high switching frequency and low loss, which makes it useful in electric vehicle motor controllers. However, the high-frequency switching operation of SiC MOSFETs is prone to deteriorate the electromagnetic compatibility characteristics of the controller, and it is of great significance to make full use of the advantages brought about by the high-frequency characteristics of SiC, while suppressing its negative impacts to enhance the performance of electric vehicle motor controllers.
Because of the characteristic of “dispersing the energy spikes”, spread spectrum modulation strategy is widely used to reduce the conducted electromagnetic interference (EMI) in motor controllers. The principle is to change the carrier wave, so that the energy of the concentrated part of the system can be dispersed to a wider frequency range. According to Parseval’s theorem, if the energy distribution of a signal in the time domain is unchanged, the energy of the signal in the frequency domain is also unchanged. Therefore, under the precondition that the signal energy in the frequency domain remains unchanged, spread spectrum modulation realizes the beneficial effect of reducing signal spikes in a wider frequency range by expanding the bandwidth of the signal energy distribution [1]. Common spread spectrum modulation strategies can be divided into two main categories: periodic (PWM) [1,2,3,4] and random (PWM) [4,5,6,7], which are realized by injecting periodic or random signals into the carrier, respectively. Common periodic signals include: sinusoidal signals, triangular signals, sawtooth signals, etc. [6,8]. Random signals are usually replaced by chaotic signals, and common chaotic sequences include: logistic sequences, cubic sequences, and so on. Of these two types of methods, the principle of periodic PWM is relatively simple, has less impact on the dynamic performance of the motor system, and is easily realized in engineering, which makes it an important solution to improve the inverter conduction EMI problem [9]. Existing research on EMI reduction of spread spectrum modulation mainly focuses on the influence of different modulation parameters on the spread spectrum effect, for example, the effects of different random signal types, periodic signal types, frequency and spreading width of periodic signals and other parameters on the spreading effect [8,10,11].
However, in addition to conducted EMI, the design of modulation strategies and the performance evaluation of inverters usually consider the following aspects: the input/output performance of the inverter [12,13], the volume and weight of the inverter [12,14,15,16], and the overall efficiency of the inverter [14,15,16]. The input/output performance of the inverter is mainly determined by the modulation technology and the topology structure of the inverter [13,15,16]. The performance can be improved by adding auxiliary devices to the topology structure or optimizing the modulation technology. For example, the coupled reactor and hybrid modulation technology are adopted in literature [12], and impedance network is adopted in literature [13], to achieve better modulation effects. When the topology structure and modulation technology are determined, the volume, weight and overall efficiency of the inverter are usually affected by the power device itself [14,16]. For example, reference [14] includes experimental studies on two kinds of inverters with full SiC and Si power devices. The results show that the application of SiC devices can help to provide higher efficiency and smaller heat sink volume. Reference [16] reports experimental studies on two kinds of high-power three-phase two-level voltage source inverters of SiC and Si respectively, and finally shows that the weight of the inverter component designed based on SiC was reduced by about 39%.
Therefore, specifically, the indicators that need to be considered for the modulation strategy also include input-side DC voltage ripple [17], output current ripple [18,19], and switching losses. The input voltage ripple affects the output voltage waveform quality and the design of the DC side support capacitor, and excessive voltage ripple has higher requirements for the design of the support capacitor [17], which is not conducive to the miniaturization and lightweighting of the inverter. The output current ripple directly affects the efficiency of the loaded motor, and it will also lead to the reduction of the control accuracy of the motor controller. The magnitude of switching loss directly affects the overall efficiency of the inverter. For these indicators, there is a lack of a comprehensive analysis of the impact brought by spread spectrum modulation, which is not conducive to further improving the performance of motor controllers through the optimization of modulation strategies.
This paper aims to design a modulation strategy for electric vehicle motor controllers with low EMI, low device loss, and low voltage/current ripple. Based on the waveform characteristics of the periodic signals, this paper intends to analyze the spectral distribution characteristics of the conducted EMI; and based on the calculation of voltage ripple and flux fluctuation amount, this paper establishes an equivalent analysis model for the input voltage ripple and the output current ripple. This paper further evaluates the level of inverter loss by analyzing the number of carrier waves per unit of time for different spread spectrum modulation strategies, so that a comprehensive analysis of the inverter input and output performance under the spread spectrum modulation strategy is realized. Based on the conclusions of the analysis, a new modulation strategy of “secondary frequency modulation” is proposed, and a comparative experimental study is carried out between the proposed strategy and the existing spread-spectrum modulation strategies in terms of voltage/current ripple, loss, and conducted EMI spikes.
2. Traditional Spread Spectrum Modulation Strategy
2.1. Inverter Topology
Figure 1 shows the three-phase two-level inverter topology adopted by electric vehicle motor controllers, which also includes the Line Impedance Stabilization Network (LISN), which is used to test the conducted EMI of switching circuits according to CISPR 25 standard. The three-phase reference voltage of the inverter is defined as:
where Uref = m·Udc/1.732 is the reference phase voltage amplitude; m is the modulation index; ω = 2πf1 is the reference angular frequency; f1 is the fundamental frequency; φ0 is the initial phase. Set sa, sb and sc as switching functions, and their values are 1 when the corresponding upper bridge arm is opened, and 0 when it is closed. The inverter output phase voltage can be expressed as:
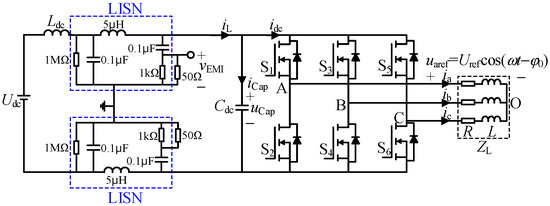
Figure 1.
Topology of two-level three-phase system with LISN.
Since the output side of the inverter is connected to inductive load, the output current waveforms are in the form of sine, and their expressions are:
where Io is the amplitude of output phase current; φL is the load power factor angle; the expression for the DC input current idc is:
2.2. Implementation Process of Traditional Spread Spectrum Modulation Strategy
The implementation process of traditional spread spectrum modulation is shown in Figure 2. Compared with the fixed-carrier-frequency SVPWM modulation, the two methods are the same in the calculation of the action time of each vector, but there are differences in the carrier.
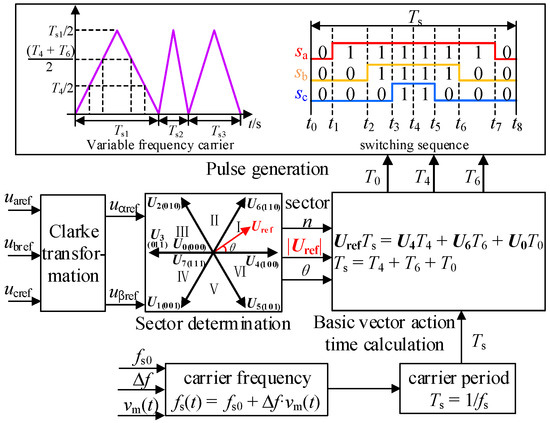
Figure 2.
Implementation process of traditional periodic spread spectrum modulation.
Spread spectrum modulation adopts carriers with varying frequencies, and its frequency expression can be uniformly written as:
where fs(t) is the carrier frequency; fs0 is the carrier center frequency; Δf is the maximum carrier frequency deviation. vm(t) is a periodic signal, and the expressions of sine, triangle and sawtooth three periodic signals are:
where fm is the frequency of the periodic signal and Tm = 1/fm is the period value of the periodically modulated signal.
3. Performance Analysis of Spread Spectrum Modulation Strategy
In order to achieve the modulation optimization under multi-objective, this section analyzes the effects of periodic signal waveform characteristics on EMI, inverter switching loss, and voltage/current ripple. Based on the analysis method of each indicator under fixed carrier frequency modulation, the relevant conclusions of ripple and loss under spread spectrum modulation strategy are obtained.
3.1. Conducted EMI Analysis of the Inverter Under Spread Spectrum Modulation
The factors that affect the peak of the conducted EMI spectrum are mainly the characteristics of the carrier frequency. It is manifested in the following two points:
① When spread spectrum modulation is adopted, the peak of EMI spectrum at hfs0 will be mainly dispersed in the range of [h(fs0 − Δf), h(fs0 + Δf)] [5], h = 1, 2, 3…. As shown in Figure 3, the main factor affecting the diffusion degree of the EMI spectrum is Δf; the larger Δf is, the wider the diffusion degree of EMI spectrum is, and the more it can weaken the EMI spectrum peak to a greater extent. However, only increasing Δf to reduce the EMI peak may lead to the phenomenon of “spectrum overlap” [20]; that is, the originally disjoint frequency bands overlap after the spread spectrum, making the EMI energy of some frequency bands rise, as shown in Figure 3b,c.
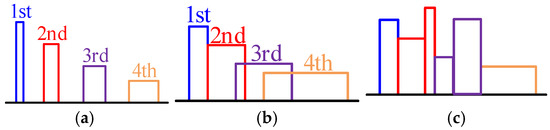
Figure 3.
Diffusion of each frequency band for different Δf: (a) Spread spectrum in a small area; (b) Spread spectrum over a wide area; (c) Spectrum overlap.
② For periodic signal vm(t), the distribution of carrier frequency in different frequency bands is affected by the gradient of periodic signal [21], which affects the spectrum distribution of EMI. Take the sinusoidal signal as an example: as shown in Figure 4, the absolute value of the gradient of the sinusoidal signal at the value of 0 is the largest, the carrier frequency value is fs0, and the action time of fs0 and its nearby frequency bands is the shortest. The gradient of the sinusoidal signal at the extreme value is 0, and the carrier frequency value is fs0 ± Δf; fs0 ± Δf and its nearby frequency band have the longest action time. Therefore, when vm(t) is the sinusoidal signal, the frequency distribution of the carrier will present a trend of “high on both sides and low in the middle”.
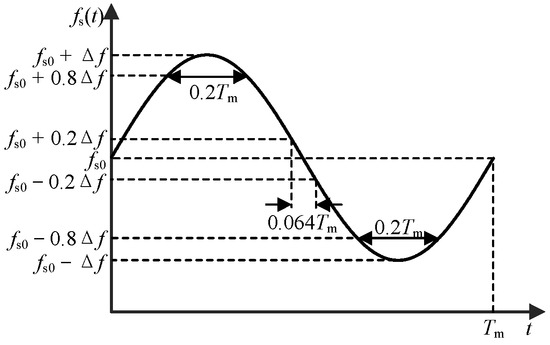
Figure 4.
The duration of different frequency bands when vm(t) is sinusoidal signal.
The voltage on the output impedance of LISN (i.e., vEMI in Figure 1) is analyzed by DFT, and its voltage spectrum is used to replace the EMI spectrum to analyze the influence of carrier frequency characteristics on EMI. At Δf = 2 kHz, m = 0.9, fs0 = 10 kHz, f1 = 50 Hz, fm = 30 Hz. When vm(t) are sine, triangle and sawtooth, the simulation results are shown in Figure 5. The figure shows the carrier frequency ratio and the corresponding EMI spectrum distribution.
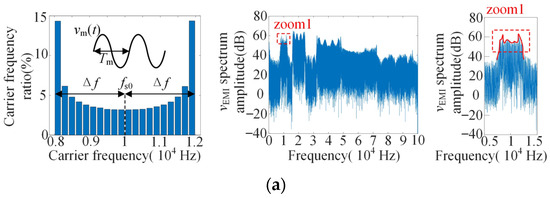
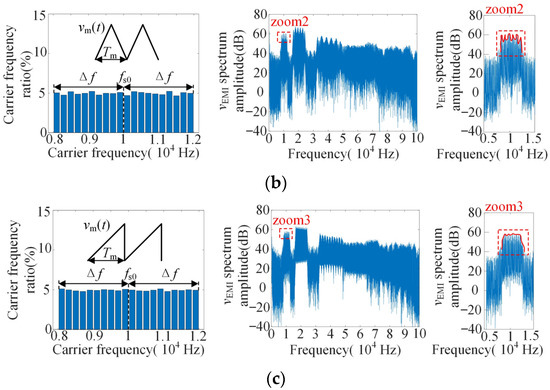
Figure 5.
Carrier frequency distribution and DFT spectrum of vEMI under different vm(t) waveforms: (a) vm(t)-sine; (b) vm(t)-triangle; (c) vm(t)-sawtooth.
As shown in the Figure 5, the distribution characteristics of vEMI spectrum at the frequency band [fs0 − Δf, fs0 + Δf] is similar to that of the carrier frequency ratio.
3.2. Equivalent Analysis of Voltage and Current Ripple Under Spread Spectrum Modulation
3.2.1. DC Side Voltage Ripple
According to Equation (2), the fluctuation of DC voltage at the input side will, on the one hand, affect the stability of output voltage. On the other hand, the higher voltage ripple has higher requirements for the design of DC support capacitor Cdc [17], which will increase the volume and weight of the controller. Therefore, it is necessary to establish a quantitative model for the influence of the spread spectrum modulation strategy on input voltage ripple.
According to the current relationship in the inverter topology in Figure 1, the capacitor current iCap, the inductor current iL and the DC input side current idc satisfy iCap = iL − idc. The current is decomposed into the sum form of the average value and the fluctuation value:
where ICap, IL and Idc represent the average current value of capacitor Cdc, the stray inductor Ldc, and idc, respectively. iCap_rip, iL_rip and idc_rip represent the corresponding current ripple components. Among them, the relationship of current ripple components satisfies iCap_rip = iL_rip − idc_rip. When the DC filter capacitor is large enough, almost all the ripple components of the input current of the inverter flow through the capacitor, and the ripple current iL_rip is negligible compared with the ripple current idc_rip [17], obtaining:
where uCap_r is the input voltage ripple.
It can be seen from Equation (11) that the ripple is the integral of the fluctuation quantity with respect to time. Under the spread spectrum modulation, the change of carrier period will affect the input and output waveform ripple.
According to Equations (3) and (4), idc is determined by ia, ib and ic, and is a cosine function with amplitude Io, denoted idc as Io·cos[α(t)], and α(t) is the phase of the cosine function with time, which is determined by ia, ib and ic. Ideally, Io satisfies , where R and L are the resistance and inductance in the load impedance ZL, respectively; therefore, Equation (11) can be expanded as:
The average value of idc is expressed as:
So that the voltage ripple expression can be obtained.
According to Equation (11), the DC voltage ripple at the input side can be calculated theoretically, and the quantitative relationship between voltage ripple and each modulation parameter can be established. According to Equation (12), the factors affecting voltage ripple are the integration time Ts and the amplitude of the integration current. Here, Ts = 1/fs(t) = 1/[fs0 + Δf·vm(t)], and the amplitude of the integrated current is related to m and f1. Therefore, according to the above derivation process, the modulation parameters affecting voltage ripple are fs0, Δf, vm(t) (including fm), m and f1, respectively.
3.2.2. AC Side Output Current Ripple
In this section, in order to achieve fast and accurate evaluation of inverter output waveform quality under different modulation methods, the effective value model of motor stator flux fluctuation under the spread spectrum modulation strategy is constructed, which is equivalent to the sum of three-phase output current fluctuation, and can be used to analyze and compare the influence of different periodic signals and spread spectrum modulation parameters on inverter output waveform quality. The steps are as follows: in the vector synthesis process, there is an error voltage vector between the basic vector and the reference vector at any time [18,19], and the reference voltage vector is defined as Uref. Without loss of generality, when the reference vector Uref is located in sector I, the corresponding error voltage vectors are U4_err and U6_err. When the basic voltage vectors U4 and U6 act is shown in Figure 6.
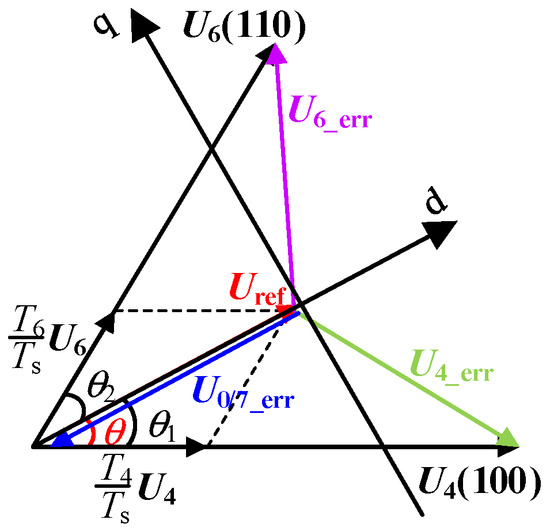
Figure 6.
Schematic diagram of voltage error vector in sector I.
The expressions of the error voltage vectors U4_err, U6_err and U0_err are:
The direction of the reference vector Uref is defined as the d-axis, and the direction of the leading d-axis π/2 is defined as the q-axis. The error voltage vectors U4_err, U6_err and U0_err are decomposed into the d-axis and the q-axis:
Define ud0~ud2 and uq1~uq2 as:
According to the motor voltage equation, the integral of the error voltage vector with respect to time within the carrier period Ts is the stator flux fluctuation ψrip, as shown in the following equation:
Among them, ud and uq are error voltage components of d-axis and q-axis in different time periods, and their values in different time periods can be represented by ud0~ud2 and uq1~uq2 respectively, as shown in Equation (16).
Furthermore, the effective value ψrip_rms of the flux fluctuation quantity in time T can be calculated as:
Among them, to ensure that fs(t) and i(t) contained in the selected time period are all integer periods, T should take at minimum the least common multiple of 1/fm and 1/f1.
According to Equations (16) and (17), the amplitude of flux fluctuation is affected by modulation parameters similar to input voltage ripple, which is mainly determined by the integration time Ts (Ts = 1/[fs0 + Δf·vm(t)]) and the amplitude of the integral component. According to Equation (16), the integral components ud and uq are mainly determined by the amplitude |Uref|, since the modulation parameters affecting ψrip_rms are fs0, Δf, vm(t) (including fm) and m, respectively.
3.2.3. Analysis of the Influence of Spread Spectrum Modulation Parameters on Ripple
In this section, under the conditions of Udc = 600 V, R = 2.75 Ω, L = 1 mH, Cdc = 1680 μF, the input voltage ripple and flux fluctuation are calculated according to the derived expressions.
The initial values of the five modulation parameters affecting the two indicators are set as follows: fs0 = 10 kHz, Δf = 0 kHz, f1 = 50 Hz, m = 0.9 and fm = 30 Hz, and any two of the five parameters are changed to present the calculation results in the form of a 3D surface graph.
When vm(t) is the sawtooth signal, the calculation results are shown in Figure 7. The results are highly similar when vm(t) is sinusoidal signal or triangular signal. Among them, m = 0.05:0.05:1 means that the modulation index m starts from 0.05 and changes in the amplitude of 0.05 each time until m = 1, and the other parameters are expressed in the same way. The integration time T for calculating the effective value of flux fluctuation quantity in Equation (18) is 1 s. According to the results shown in Figure 7a–c, the voltage ripple and flux fluctuation are mainly affected by the four parameters of m, f1, Δf and fs0, and are not significantly affected by fm. According to the above results, the variation rules of input voltage ripple and flux fluctuation with each parameter are shown in Table 1.
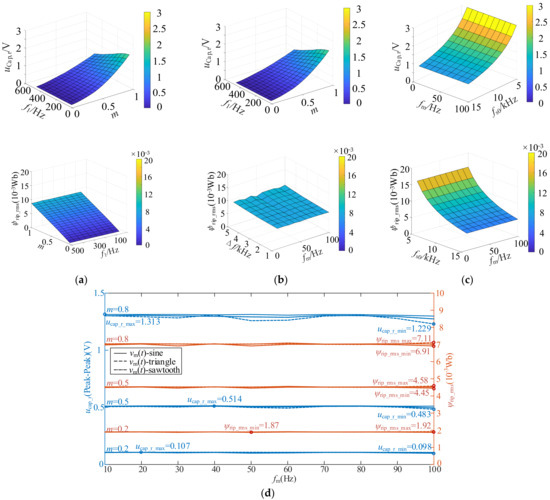
Figure 7.
Variation trend of voltage ripple and stator flux fluctuation with different parameters: (a) m = 0.05:0.05:1, f1 = 50:50:500 Hz; (b) Δf = 1 k:0.5 k:5 kHz, fm = 10:10:100 Hz; (c) fs0 = 5 k:1 k:15 kHz, fm = 10:10:100 Hz; (d) Voltage ripple and flux fluctuation values corresponding to different vm(t) and fm conditions under three modulation index.

Table 1.
Variations of voltage ripple and flux fluctuation when different parameters increase.
In practical applications, the carrier center frequency fs0 is usually fixed, and the modulation index m and fundamental frequency f1 usually change with the change of load conditions. Therefore, the only degrees of freedom that can be changed are Δf and the type of periodic signal vm(t) (including fm).
The influence of the types of periodic signals vm(t) and fm on the input voltage ripple and flux fluctuation is further quantitatively analyzed according to the above derived formula, under the three modulation indexes of m of 0.2 (low modulation index), 0.5 (medium modulation index) and 0.8 (high modulation index), the voltage ripple and flux fluctuation of three periodic signals of sine, triangle and sawtooth under 10 sets of parameters of fm = 10:10:100 Hz; that is, 30 sets of calculation results correspond to each modulation condition. Two sets of results and corresponding conditions for the minimum and maximum values of input voltage ripple and flux fluctuation were compared from the 30 sets of results. The other calculated conditions were fs0 = 10 kHz, Δf = 1 kHz and f1 = 50 Hz, and the specific results are shown in Figure 7d.
Therefore, by comparing the results in Figure 7, it can be seen that when the four parameters m, fs0, Δf and f1 are all determined, vm(t) and fm have little influence on the input voltage ripple and flux fluctuation. According to Figure 7d, when the waveform characteristics of vm(t) change, the voltage ripple is basically around 1 V, which is very limited compared to the vehicle voltage platform of 800 V. For the flux ripple, which is basically equivalent to the current ripple, its order of magnitude is 10−3 Wb, which is 1~2 orders of magnitude different from the permanent magnet flux amplitude of the vehicle motor. Therefore, it can be analyzed that in the vehicle scenario, the waveform characteristics of the periodic signal have little influence on the DC side voltage ripple of the inverter, and the influence on the AC side current ripple is relatively limited. When optimizing the modulation strategy, the influence of vm(t) waveform characteristics on ripple can be temporarily ignored or less considered.
3.3. Loss Analysis Under Spread Spectrum Modulation
The loss of power switching devices includes switching loss and conduction loss, and switching loss is the main one. Switching loss can be fitted as a quadratic function related to current [22]:
where, i(t) is the current flowing through the switch tube at time t, and the parameters A1, B1 and C1 can be obtained by curve fitting with double-pulse experimental data. The total loss is usually determined by the single turn-on and turn-off loss of the switch tube and the total switching times per unit time [22]. In a carrier cycle, the upper and lower switches of the same bridge arm are turned on and off once, so the switching loss can be evaluated equivalently by analyzing the number of carriers included in the corresponding modulation strategy per unit time. The number of carriers included in different modulation strategies within 1 s is shown in Table 2.

Table 2.
Number of carriers within 1 s for different modulation strategies.
As can be seen from Table 2, under different Δf for different periodic signals, since fs always fluctuates periodically around fs0, the number of carriers included in unit time is almost the same, and compared with the fixed carrier frequency condition, the number of carriers is not significantly increased, so it can be considered that the spread spectrum modulation strategy has almost no effect on the switching loss of the inverter. Therefore, based on the above analysis, the influence of modulation strategy on switching loss can be less considered when designing periodic spread spectrum modulation strategy.
3.4. Summary
In summary, for the three parameters of periodic signals, vm(t), fm and Δf, that need to be considered in the design of spread spectrum modulation strategy, it can be concluded that vm(t) and fm have no significant influence on ripple and loss through the mathematical model. Under the premise of weighing multiple indicators, when designing a new spread spectrum modulation strategy, it only needs to focus on limiting Δf to ensure that under the same conditions, compared with the traditional spread spectrum modulation strategy, the conducted EMI is reduced to a greater extent.
4. “Secondary Frequency Modulation” Spread Spectrum Modulation Strategy
According to the above analysis, this paper further proposes a “secondary frequency modulation (secondary FM)” spread spectrum modulation strategy based on sinusoidal signal waveform characteristics, which can reduce the peak value of conducted EMI to a greater extent than single periodic signal spread spectrum modulation within the same frequency fluctuation range, and does not increase additional ripple and loss. The schematic diagram of the spectrum dispersion effect is shown in Figure 8a. The main idea is explained as follows: on the basis of the spread spectrum modulation of vm(t) for sinusoidal signal, the concentrated part of the uneven frequency band of high-frequency and low-frequency is dispersed, so as to further reduce the conducted EMI peak. The spread spectrum modulation of a single sinusoidal signal is denoted as “primary frequency modulation”, and the modulation strategy of dispersing a specific frequency band based on the “primary frequency modulation” is denoted as “secondary FM”. The schematic diagram of carrier frequency change after secondary FM is shown in Figure 8c, and the design basis of the parameters in the figure is explained as follows:
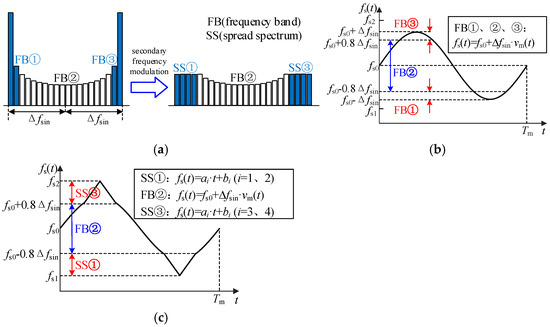
Figure 8.
“Secondary FM” principle and implementation process: (a) ”Secondary FM” principle; (b) ”Primary frequency modulation” carrier frequency variation law and expression; (c) ”Secondary FM” carrier frequency variation law and expression.
4.1. Determine the Frequency Band and Diffusion Mode for Secondary Diffusion Based on the Waveform Characteristics of Periodic Signals
According to Figure 5a, when vm(t) is a sinusoidal signal, part of the frequency bands with uneven carrier frequency distribution are mainly concentrated on both sides of the full frequency band, and the proportion content of the other frequency bands is significantly lower than that of the triangular signal and sawtooth signal. The frequency bands are defined as follows: [fs0 − Δf, fs0 − 0.8Δf] for frequency band ①(FB①), [fs0 − 0.8Δf, fs0 + 0.8Δf] for frequency band ②(FB②), and [fs0 + 0.8Δf, fs0 + Δf] for frequency band ③(FB③). Through the simulation analysis, the EMI peaks of sinusoidal, triangular and sawtooth signals in different frequency bands and adjacent bands are shown in the following table. The parameters of the simulation are: fs0 = 10 kHz, m = 0.9, fm = 30, f1 = 50 Hz, Δf =3 kHz.
As can be seen from Table 3, when vm(t) is a sinusoidal signal, the peak of the vEMI spectrum is mainly distributed in narrow FB① and FB③, and the EMI spectrum peak in FB② is significantly lower than when vm(t) is a triangular signal or a sawtooth signal. Based on this feature, the FB① and FB③ are further spread to further reduce the conducted EMI peak.

Table 3.
vEMI spectrum peak of each band under different conditions (unit: dB).
In order to distinguish it from the Δf of the spread spectrum modulation of a single periodic signal, the frequency deviation variable of the “primary frequency modulation” of the sinusoidal signal in the “secondary FM” strategy is denoted as Δfsin. The frequency component in the original FB① is diffused to the frequency band [fs1, fs0 − 0.8Δfsin], and [fs1, fs0 − 0.8Δfsin] is denoted as spread spectrum ①(SS①). FB② remains unchanged. The FB③ is spread to [fs0 + 0.8Δfsin, fs2] band, [fs0 + 0.8Δfsin, fs2] is denoted as spread spectrum ③(SS③). fs1 and fs2 are the lower and upper limits of the fundamental carrier frequency band of “secondary FM”, respectively. According to Figure 8c, after “secondary FM”, the variation law of the carrier in the two parts of the SS① and SS③ is a piecewise primary function, and ai and bi represent the slope and intercept of the carrier frequency expression in different periods, respectively.
4.2. Determine the Value of Δfsin
The selection principle of Δfsin is to fully realize the spread spectrum effect of “primary frequency modulation” and reduce the problem of “spectrum overlap” as much as possible. When vm(t) is a sinusoidal signal, and the value of Δfsin is 1, 2 and 3 kHz, the other parameters of the simulation are set as: fs0 = 10 kHz, m = 0.9, fm = 30, f1 = 50 Hz. The distribution and characteristic analysis of the EMI peak in the simulation are shown in Table 4.

Table 4.
Distribution of EMI spikes in each frequency band under different Δfsin when vm(t) is a sinusoidal signal.
Based on the distribution characteristics of the conducted EMI spectrum under different conditions, Δfsin = 2 kHz is finally selected as the basis of the “secondary FM”.
4.3. Determine the Value Range of fs1 and fs2
According to Figure 5a, FB① and FB③ of the uneven part account for about 20% of the full frequency band, respectively, and the proportion of each component in FB② is less than 5% at most. Therefore, from the perspective of carrier frequency dispersion, the proportion of each component in the dispersed FB① and FB③ (within the length of 0.1Δfsin band) should not exceed 5%, so as to ensure that the EMI peak value of the dispersed frequency band is not higher than that of other frequency bands. The width of the frequency band before dispersion is 0.2Δfsin, then the width of the frequency band after dispersion should be satisfied:
i.e., fs1 ≤ fs0 − 1.2Δfsin; fs2 ≥ fs0 + 1.2Δfsin
The lower and upper limits of the fundamental carrier frequency change are defined as fsmin and fsmax, respectively. In order to reduce the overlap between “SS① double frequency” and “primary frequency modulation” original frequency band [fs0 − Δfsin, fs0 + Δfsin], as shown in Figure 9, 2 fs1 ≥ fs0 + Δfsin should be satisfied. For fsmax, it is determined according to |fsmin − fs0| = |fsmax − fs0|, i.e.,:
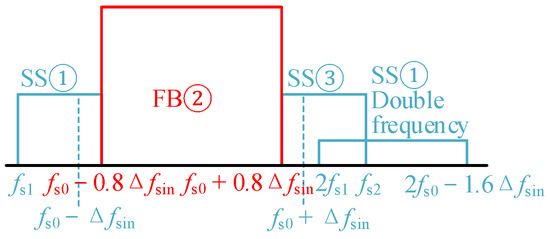
Figure 9.
Schematic diagram of different frequency bands.
Under the condition of Δfsin = 2 kHz, according to Equations (20) and (21), the variation range of fs1 is determined to be [6 kHz,7.6 kHz], and the variation range of fs2 is determined to be [12.4 kHz,14 kHz].
5. Experimental Results and Analysis
In this section, the “secondary FM” strategy and single periodic signal spread spectrum modulation are experimentally studied, and the effect of the traditional spread spectrum modulation strategy and the “secondary FM” on reducing the conducted EMI is analyzed. The input voltage ripple, output current and controller loss under different modulation strategies or different modulation parameters are measured.
The experimental parameters are shown in Table 5, and the experimental platform is shown in Figure 10. The chip model of the control system is DSP28379, the model of the power semiconductor module is BSM600D12P3G001 SiC module, the DC side is powered by the battery simulator as the DC power supply and connected to the inverter through the NNHV 8123-800 high-voltage LISN of Rhode&Schwartz (Munich, Germany). The LISN load end is connected to the ESW8 receiver for testing the conducted EMI spectrum. The voltage and current ripple are measured by Yokogawa oscilloscope. The loss test is divided into two parts: the double-pulse test for measuring the characteristics of the inverter switch tube, and the loss test for measuring the efficiency of the inverter. The double-pulse test is completed by the Edison DPT2K04B (Dongguan, China) power device dynamic parameter measurement instrument, and the loss test is completed by the Yokogawa (Tokyo, Japan) WT5000 power analyzer.

Table 5.
Experimental parameter settings.

Figure 10.
Schematic diagram of the experimental platform.
5.1. Experimental Parameter Design of “Secondary FM” Modulation Strategy
The EMI spectrum distribution characteristics of a single sinusoidal signal with spread spectrum modulation in three cases of Δfsin = 1, 2 and 3 kHz are tested experimentally, and the results are shown in Figure 11.
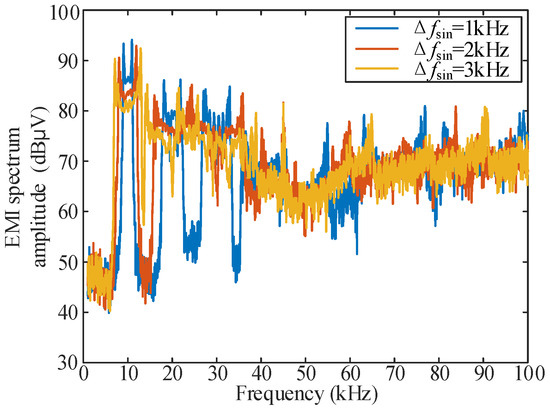
Figure 11.
Corresponding EMI spectrum of vm(t)-sine with different Δfsin.
According to Figure 11, for Δfsin = 1, 2, 3 kHz, the lowest amplitude of the EMI spectrum of the spread spectrum modulation of the sine signal in [fs0 − Δfsin, fs0 + Δfsin] band is shown in Table 6. The spectrum distribution characteristics under the three conditions in Figure 11 are highly similar to the analysis in Table 4, and according to the results shown in Figure 11 and Table 6, it can be seen that the selection of Δfsin = 2 kHz as the basic condition of “secondary FM” is still reasonable in the actual experiment.

Table 6.
For Δfsin = 1, 2, 3 kHz, the lowest EMI amplitude of the spread spectrum modulation of the sine signal in [fs0 − Δfsin, fs0 + Δfsin].
5.2. Comparison of EMI Experimental Results
In this section, the traditional period spread spectrum modulation strategy and the “secondary FM” strategy proposed in this paper are tested, to verify and compare the effects of different strategies on reducing the conducted EMI peak.
5.2.1. EMI Results of Spread Spectrum Modulation of Single Periodic Signal
In order to verify the effect of spread spectrum modulation of a single periodic signal on reducing the conducted EMI spike, the EMI spectrum of fixed carrier frequency modulation and vm(t)-sine, vm(t)-triangle, vm(t)-sawtooth spread spectrum modulation at Δf = 1 kHz was tested, and the results are shown in Figure 12.
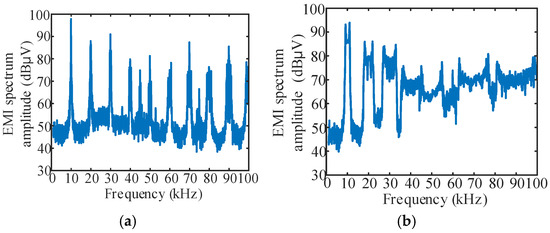
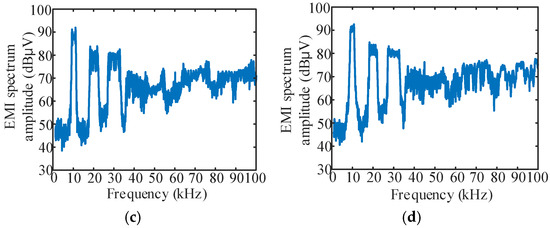
Figure 12.
EMI spectrum of fixed carrier frequency modulation and spread spectrum modulation at Δf = 1 kHz: (a) The carrier frequency is fixed at 10 kHz; (b) vm(t)-sine, Δf = 1 kHz; (c) vm(t)-triangle, Δf = 1 kHz; (d) vm(t)-sawtooth, Δf = 1 kHz.
It can be seen from the figure that the peak value of conducted EMI under a fixed carrier frequency of 10 kHz is 98.03 dBμV, and the peak value of conducted EMI corresponding to sine, triangle and sawtooth signals under Δf = 1 kHz is 94.11 dBμV, 92.1 dBμV and 92.52 dBμV, respectively, which are lower than those under a fixed carrier frequency modulation.
In order to analyze the influence of vm(t) and Δf on conducted EMI, vm(t)-sine, vm(t)-triangle, vm(t)-sawtooth spread spectrum modulation were tested, respectively, and the conducted EMI peak values corresponding to different conditions of Δf = 1 kHz:0.1 kHz:4 kHz (that is, all cases of carrier frequency fluctuation in the range of 6 kHz to 14 kHz) were measured. A total of 93 groups of data were collected. The measurement results are shown in Figure 13, where the lowest peak value of conducted EMI and the corresponding Δf under spread spectrum modulation are also marked.
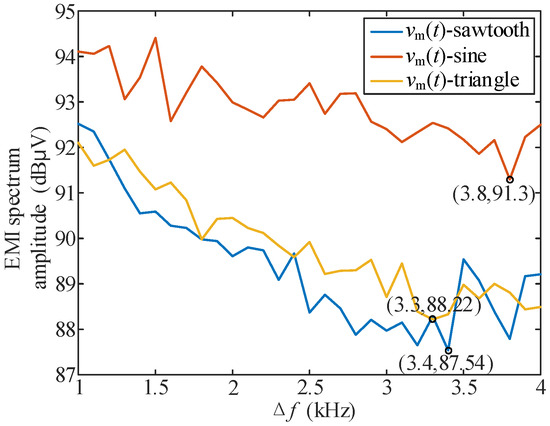
Figure 13.
EMI spectrum peaks corresponding to different types of periodic signals at different Δf.
Figure 13 shows that the EMI peak does not decrease monotonically with the increase of Δf, corresponding to the “spectrum overlap” phenomenon analyzed; therefore, the purpose of reducing the conducted EMI peak cannot be achieved by simply increasing Δf.
5.2.2. Analysis of EMI Experimental Results of “Secondary FM” Spread Spectrum Modulation Strategy
At Δfsin = 2 kHz, the FB① and FB③ were dispersed as described in Section 4. That is, the frequency band of the sinusoidal signal is [8.4 kHz, 11.6 kHz], the [8 kHz, 8.4 kHz] frequency band is separately dispersed into [fs1, 8.4 kHz], and the [11.6 kHz, 12 kHz] frequency band is dispersed into the [11.6 kHz, fs2] frequency band. The results under different combinations of fs1 and fs2 parameters were tested, and partial results are shown in Figure 14.
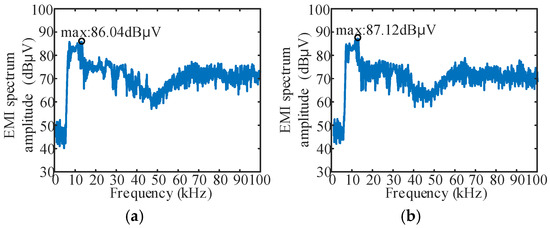
Figure 14.
“Secondary FM” results: (a) fs1 = 6.5 kHz, fs2 = 13.9 kHz; (b) fs1 = 6.7 kHz, fs2 = 13.3 kHz.
By comparing the results of Figure 13 and Figure 14a, the “secondary FM” strategy can achieve a better EMI peak reduction effect than the single periodic signal spread spectrum modulation in the fs range of 6 k~14 kHz. The optimal effect of the “secondary FM” method is reduced by an additional 1.5 dBμV on the basis of 87.54 dBμV in Figure 13. The comparison of results in Figure 13 and Figure 14b shows that with the same or lower Δf, “secondary FM” can also achieve better EMI peak reduction effect.
5.3. Input Voltage and Output Current Ripple
In this section, the input voltage ripple and output current of different modulation strategies are tested, respectively, and the results are shown in Figure 15. It can be seen from the figure that for input voltage ripple, the maximum difference of voltage ripple under different conditions is only 1.2 V, which is not much different from the input voltage ripple under fixed carrier frequency. Compared with 600 V DC bus voltage, the increase of ripple is only 0.2%.
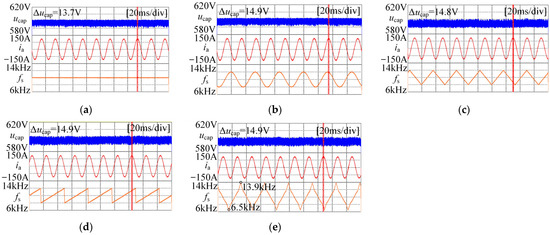
Figure 15.
Input DC voltage, output current and corresponding carrier frequency variation waveforms under different conditions: (a) The carrier frequency is fixed at 10 kHz; (b) vm(t)-sine, Δf = 2 kHz; (c) vm(t)-triangle, Δf = 2 kHz; (d) vm(t)-sawtooth, Δf = 2 kHz; (e) fs1 = 6.5 kHz, fs2 = 13.9 kHz, secondary FM.
As for the output current, it can be seen from Figure 15 that there is no obvious distortion of the output phase current, indicating that the spread spectrum modulation strategy will not significantly affect the quality of the output current.
5.4. Loss Testing
In this section, the double-pulse experiment is carried out to test the switching tube loss data under 12 different switching currents, starting from 50 A and increasing by 50 A until 600 A each time. The relationship between the corresponding current and switching loss is shown in Figure 16.
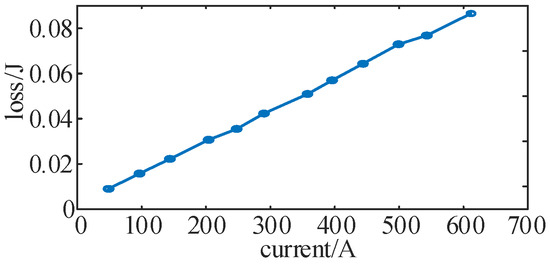
Figure 16.
Changing trend of switching loss with current.
According to the results shown in Figure 16, each parameter in Equation (19) is identified and obtained:
Under the experimental parameters shown in Table 5, combined with Equations (3) and (22), the expression of switching loss in a single carrier cycle at different times and different currents can be obtained as:
The total switching loss of the inverter per unit time can be obtained by accumulating the switching loss at different times. Taking the Δf = 1 kHz condition as an example, the numerical theoretical evaluation of switching loss within 1 s for different modulation strategies is shown in Table 7.

Table 7.
Number of carriers and switching losses within 1 s for different modulation strategies.
When vm(t) is three kinds of periodic signals, the input and output power, efficiency and loss under different Δf are measured by the power analyzer, and the results are shown in Figure 17. The figure contains the experimental data of three kinds of periodic signals under the condition of Δf = 1 kHz:0.1 kHz:4 kHz.
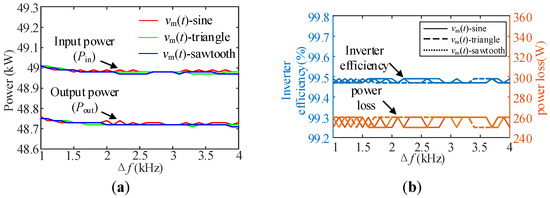
Figure 17.
Inverter input and output power, efficiency and loss under different conditions: (a) The corresponding inverter input and output power of different periodic signals at different Δf; (b) Inverter efficiency and power loss corresponding to different period signals at different Δf.
In addition, the loss test results of three typical modulation strategies are selected for presentation, as shown in Figure 18. Figure 17 and Figure 18 show that there is almost no difference between different types of spread spectrum modulation strategies and fixed carrier frequency modulation in terms of loss and efficiency. In addition, the loss results tested by the power analyzer are very close to the loss evaluation results fitted based on the two-pulse experiment in Table 7, which verifies the effectiveness of the method of indirectly evaluating switching loss through the number of carriers included in the unit time in the spread spectrum modulation strategy. Therefore, in general, when designing the spread spectrum modulation strategy, its impact on the loss can be ignored under the premise that the average carrier frequency does not change much.
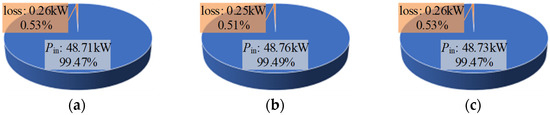
Figure 18.
Loss results under three typical modulation strategies: (a) Fixed carrier frequency modulation strategy, fs = 10 kHz; (b) vm(t)-sine, Δf = 1 kHz; (c) Secondary FM, fs1 = 6.5 kHz, fs2 = 13.9 kHz.
6. Conclusions
In this paper, the factors affecting the conducted EMI of the motor controller are analyzed, and the impact level of the spread spectrum modulation strategy on the input DC voltage ripple, output AC current ripple, and controller loss is theoretically evaluated. On this basis, a “secondary FM” spread spectrum modulation strategy is further proposed. Research shows that:
(1) In the single periodic signal spread spectrum modulation, the sawtooth signal has the best suppression effect on EMI peak;
(2) When fs0 is fixed, the influence of spread spectrum modulation on input voltage ripple and stator flux fluctuation mainly depends on Δf. The larger Δf is, the larger input voltage ripple and stator flux fluctuation are, while the type of periodic signal and fm have little effect on them.
(3) The influence of spread spectrum modulation strategy on controller loss is negligible.
(4) In the limited range of carrier frequency variation, compared with the traditional period spread spectrum modulation strategy, the “secondary FM” strategy can further reduce the conducted EMI of the motor controller, the reduced amplitude of conducted EMI is 1.5 dBμV, and this method does not have significant impact on the ripple, loss and other indicators.
Compared with the existing research, the influence of spread spectrum modulation strategy on the input/output performance and loss of the inverter is theoretically analyzed in this paper. The existing research on these indicators under the spread spectrum modulation strategy is usually directly through the experiment, which lacks theoretical analysis. This paper theoretically makes up for this deficiency.
Author Contributions
The formulation of overarching research goals was explored by T.S., Y.Y., J.S. and Y.C. The main innovation point was explored by Y.C. The design of methodology was developed by Y.C., J.S. and Y.Y. The implementation of the software code was completed by J.S. and Z.L. Validation of the proposed method was made by Y.Y. and Z.L. The original draft and pictures were completed by both J.S. and Y.Y. The review and editing were completed by Y.C. and T.S. All the authors have made contributions to the revision and improvement of the paper. The provision of instrumentation was supported by T.S. Y.Y. and T.S. led and managed the research execution, and T.S. had the oversight responsibility for the research. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Key Research and Development Project of China (2022YFB2502803); Zhejiang Provincial “Pioneer” and “Leading Goose” R&D Program of China (2023C01134); Zhejiang Provincial Major Program of Natural Science Foundation of China (LD24E070001).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Acknowledgments
This work has been supported by the Zhejiang University Advanced Electrical Equipment Innovation Center in terms of instrumentation and equipment provision.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| Variable | Comment | Variable | Comment |
| Udc | DC bus voltage | Ldc | Stray inductance |
| iL | Current of stray inductor branch | Uref | Reference voltage vector |
| iCap | Capacitance current | uCap | DC side input voltage |
| idc | DC side input current | Cdc | DC side support capacitance |
| sa, sb, sc | Switching state of the three-phase bridge arm | ω | Angular frequency of reference voltage |
| ia, ib, ic | Three-phase load current | m | Modulation index |
| uCap_r | DC side voltage ripple | R, L | Load resistance and inductance |
| ZL | Load impedance | f1 | Output fundamental frequency |
| φ0 | Initial phase of the phase A voltage | Io | Amplitude of output phase current |
| φL | Power factor angle of load | fm | Frequency of periodic signal |
| ud, uq | Voltage component of d and q-axis | ψrip_rms | Effective value of flux fluctuation |
| fs | Carrier frequency | fs0 | Centre carrier frequency |
| vm(t) | Periodic signal | Ts | Carrier cycle |
| Δfs | Maximum offset frequency of single signal periodic spread spectrum modulation strategy | θ | The angle between the voltage reference vector Uref and the α axis |
| Δfsin | “Primary frequency modulation” spread width | ψrd, ψrq | Flux fluctuation component of d and q-axis |
| U0~U7 | SVPWM basic vector | Tm | Signal period |
References
- Qiu, Z.; Chen, Y.; Cheng, H.Q.; Liu, X.; Gu, F. Periodic Harmonic Spread Spectrum Modulation for High-Frequency Sideband Vibro-Acoustic Suppression in Permanent Magnet Synchronous Motor. Trans. China Electrotech. Soc. 2022, 37, 2459–2468. [Google Scholar] [CrossRef]
- Huang, J.; Li, K. Suppressing the Maximum EMI Spectral Peak Through Asynchronous Carriers in the Three-Phase Inverter with the Periodic CFM. IEEE Trans. Power Electron. 2022, 37, 3702–3707. [Google Scholar] [CrossRef]
- Chen, J.; Jiang, D.; Sun, W.; Shen, Z.; Zhang, Y. A Family of Spread-Spectrum Modulation Schemes Based on Distribution Characteristics to Reduce Conducted EMI for Power Electronics Converters. IEEE Trans. Ind. Appl. 2020, 56, 5142–5157. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, Y.; Zhang, W.; Zou, J. Hybrid RPWM Technique Based on Modified SVPWM to Reduce the PWM Acoustic Noise. IEEE Trans. Power Electron. 2019, 34, 5667–5674. [Google Scholar] [CrossRef]
- Qi, C.; Chen, X.; Mou, X. A Hybrid Spread Spectrum Modulation Technique for PWM Inverters. Proc. CSEE 2012, 32, 8. [Google Scholar] [CrossRef]
- Gamoudi, R.; Chariag, D.E.; Sbita, L. A Review of Spread-Spectrum-Based PWM Techniques—A Novel Fast Digital Implementation. IEEE Trans. Power Electron. 2018, 33, 10292–10307. [Google Scholar] [CrossRef]
- Mina, K.; Hwa-Pyeong, P.; Jee-Hoon, J. Spread Spectrum Technique with Random-Linear Modulation for EMI Mitigation and Audible Noise Elimination in IH Appliances. IEEE Trans. Ind. Electron. 2022, 69, 8589–8593. [Google Scholar] [CrossRef]
- Xu, Y.; Yuan, Q.; Zou, J.; Li, Y. Analysis of Triangular Periodic Carrier Frequency Modulation on Reducing Electromagnetic Noise of Permanent Magnet Synchronous Motor. IEEE Trans. Magn. 2012, 48, 4424–4427. [Google Scholar] [CrossRef]
- Shan, Y.; Pei, X.; Sun, T.; Zhang, M.; Zhou, P.; Jiang, D. Space Spread-Spectrum Strategy for MMC to Reduce the Conducted EMI. IEEE Trans. Ind. Electron. 2022, 69, 10807–10818. [Google Scholar] [CrossRef]
- Lee, K.; Shen, G.; Yao, W.; Lu, Z. Performance Characterization of Random Pulse Width Modulation Algorithms in Industrial and Commercial Adjustable-Speed Drives. IEEE Trans. Ind. Appl. 2017, 53, 1078–1087. [Google Scholar] [CrossRef]
- Kumar, A.C.B.; Narayanan, G. Variable-Switching Frequency PWM Technique for Induction Motor Drive to Spread Acoustic Noise Spectrum with Reduced Current Ripple. IEEE Trans. Ind. Appl. 2016, 52, 3927–3938. [Google Scholar] [CrossRef]
- Szwarc, K.J.; Szczepankowski, P.; Nieznanski, J.; Swinarski, C.; Usoltsev, A.; Strzelecki, R. Hybrid Modulation for Modular Voltage Source Inverters with Coupled Reactors. Energies 2020, 13, 4450. [Google Scholar] [CrossRef]
- Kapil, P.N.; Sant, A.V. Comparison of Various Modulation Techniques for Conventional, Quasi and Switched Inductor Z-Source Inverter Topologies. In Proceedings of the 2023 IEEE 2nd Industrial Electronics Society Annual On-Line Conference (ONCON), Online, 8–10 December 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Stepenko, S.; Husev, O.; Vinnikov, D.; Roncero-Clemente, C.; Pimentel, S.P.; Santasheva, E. Experimental Comparison of Two-Level Full-SiC and Three-Level Si-SiC Quasi-Z-Source Inverters for PV Applications. Energies 2019, 12, 2509. [Google Scholar] [CrossRef]
- Stepenko, S.; Husev, O.; Vinnikov, D.; Fesenko, A.; Matiushkin, O. Feasibility Study of Interleaving Approach for Quasi-Z-Source Inverter. Electronics 2020, 9, 277. [Google Scholar] [CrossRef]
- Fuentes, C.D.; Müller, M.; Bernet, S.; Kouro, S. SiC-MOSFET or Si-IGBT: Comparison of Design and Key Characteristics of a 690 V Grid-Tied Industrial Two-Level Voltage Source Converter. Energies 2021, 14, 3054. [Google Scholar] [CrossRef]
- Pei, X.; Chen, C.; Kang, Y. Analysis of Voltage Ripple and Design for DC-Link Capacitor in Three-Phase Voltage Source Inverters. Trans. China Electrotech. Soc. 2014, 29, 269. [Google Scholar] [CrossRef]
- Casadei, D.; Serra, G.; Tani, A.; Zarri, L. Theoretical and experimental analysis for the RMS current ripple minimization in induction motor drives controlled by SVM technique. IEEE Trans. Ind. Electron. 2004, 51, 1056–1065. [Google Scholar] [CrossRef]
- Casadei, D.; Serra, G.; Tani, A.; Zarri, L. Optimal Use of Zero Vectors for Minimizing the Output Current Distortion in Matrix Converters. IEEE Trans. Ind. Electron. 2009, 56, 326–336. [Google Scholar] [CrossRef]
- Chen, J.; Jiang, D.; Shen, Z.; Sun, W.; Fang, Z. Uniform Distribution Pulsewidth Modulation Strategy for Three-Phase Converters to Reduce Conducted EMI and Switching Loss. IEEE Trans. Ind. Electron. 2020, 67, 6215–6226. [Google Scholar] [CrossRef]
- Johnson, S.; Zane, R. Custom Spectral Shaping for EMI Reduction in High-Frequency Inverters and Ballasts. IEEE Trans. Power Electron. 2005, 20, 1499–1505. [Google Scholar] [CrossRef]
- Li, J.; Dang, E.; Fan, Y.; Dong, H.; Liu, J. A Hybrid Three-Level Active-Neutral-Point-Clamped Zero-Voltage Transition Soft-Switching Converter with Silicon Carbide and Silicon Devices. Trans. China Electrotech. Soc. 2024, 39, 2496–2510. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).