Path Planning Trends for Autonomous Mobile Robot Navigation: A Review
Abstract
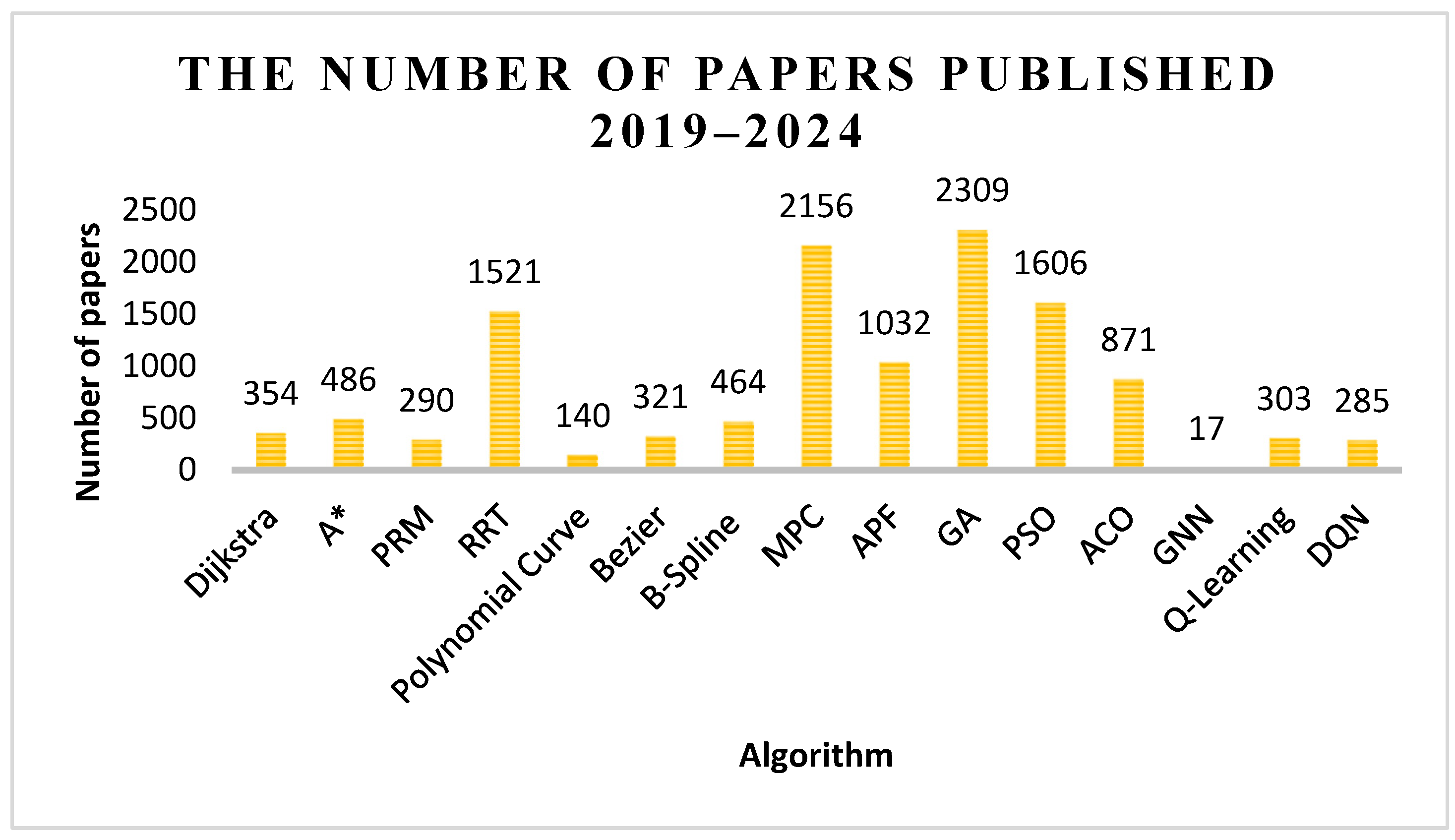
1. Introduction
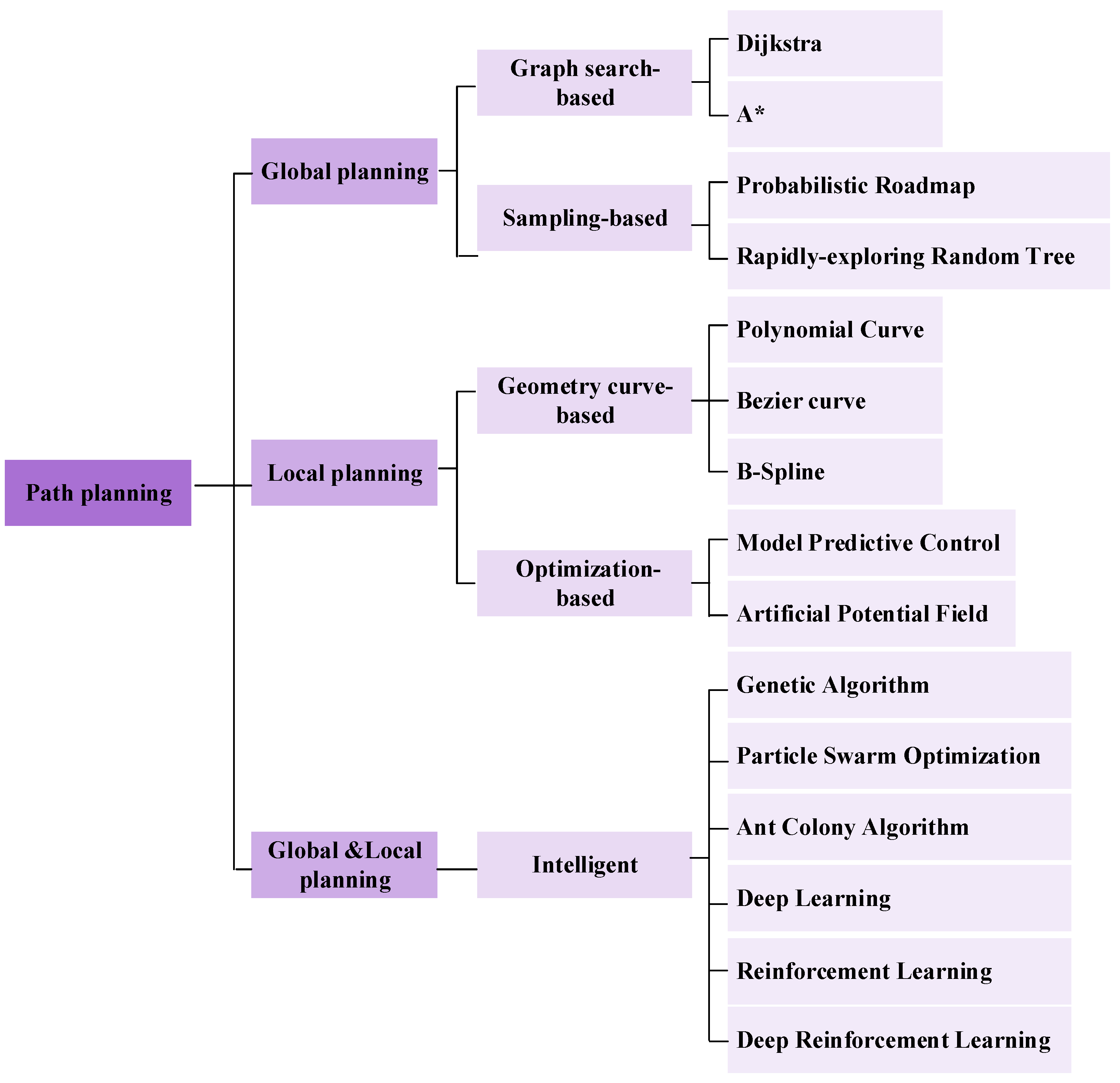
2. Graph Search-Based Planning Algorithms
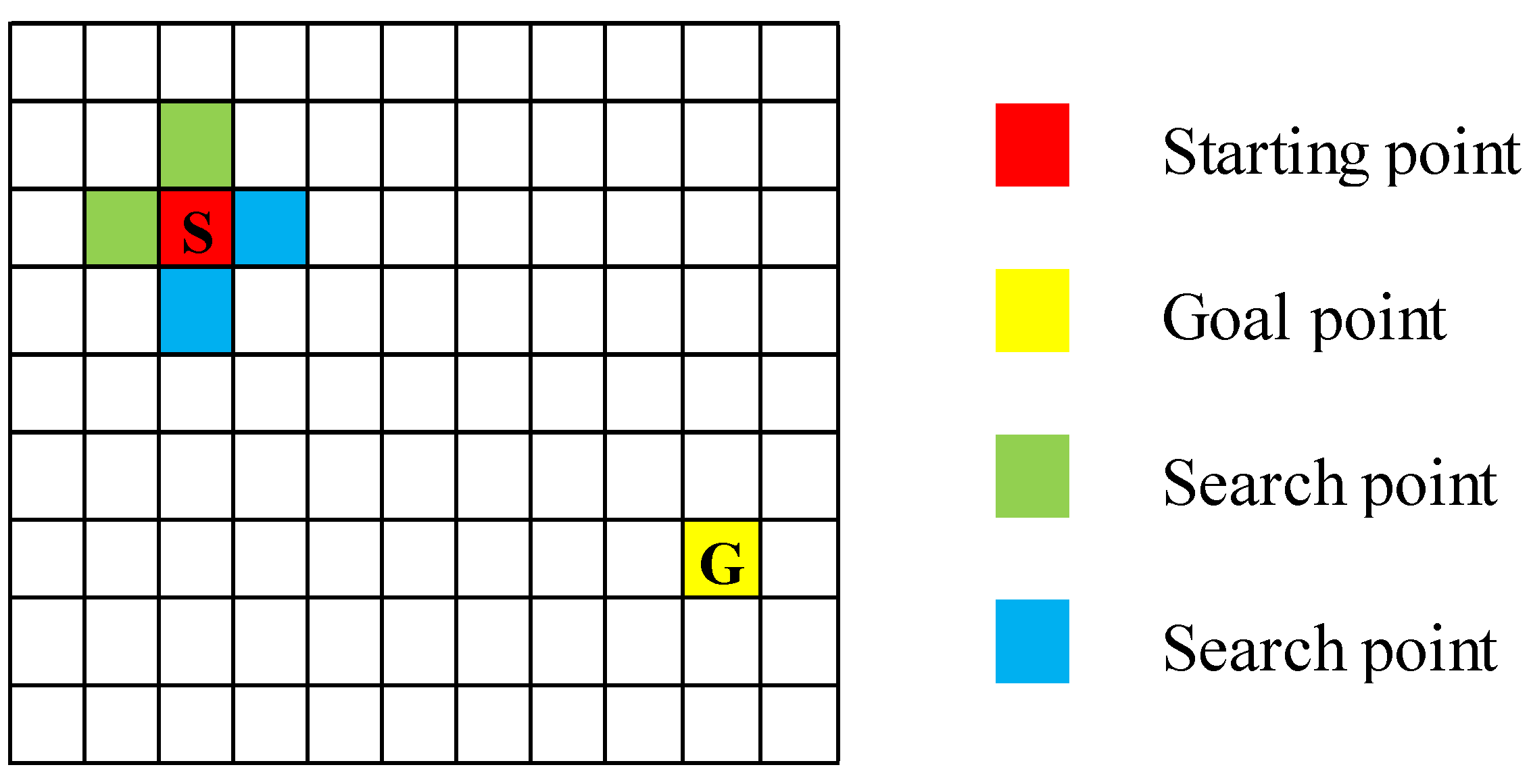
2.1. Dijkstra Algorithm
2.2. A* Algorithm
2.3. Summary
3. Sampling-Based Planning Algorithms
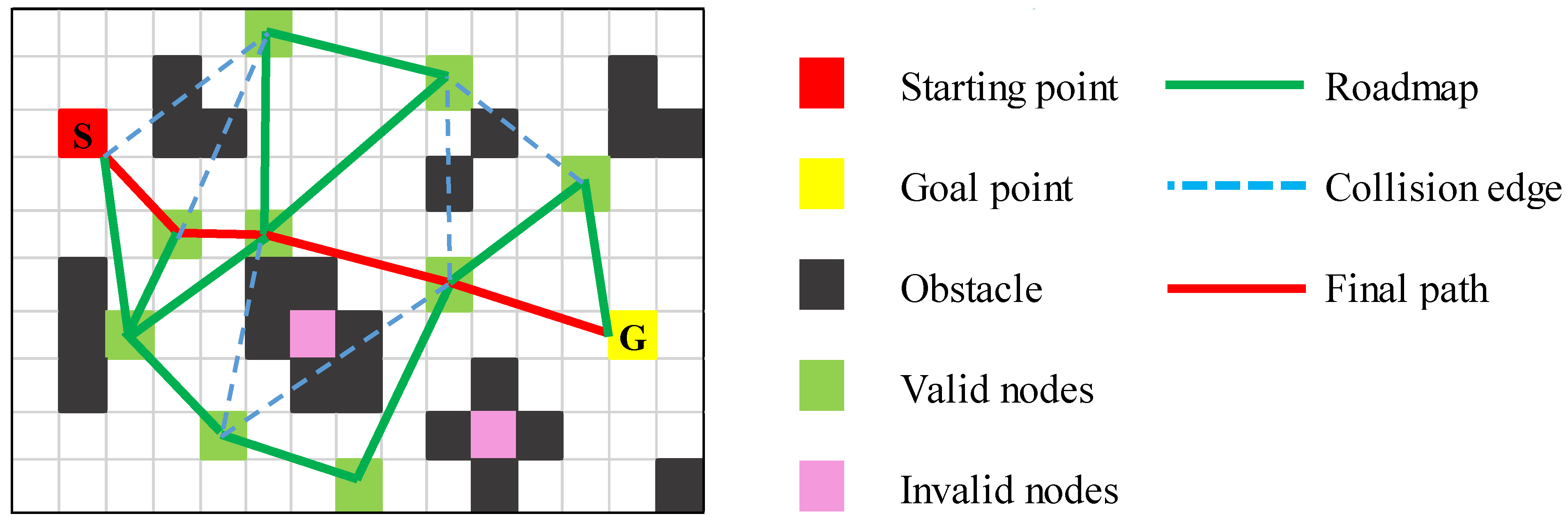
3.1. Probabilistic Roadmap (PRM)
3.1.1. For Low Sampling Efficiency
3.1.2. For Narrow Passages
3.1.3. Hybrid Algorithm
3.2. Rapidly-Exploring Random Tree (RRT)
3.3. Summary
4. Geometry Curve-Based Planning Algorithms
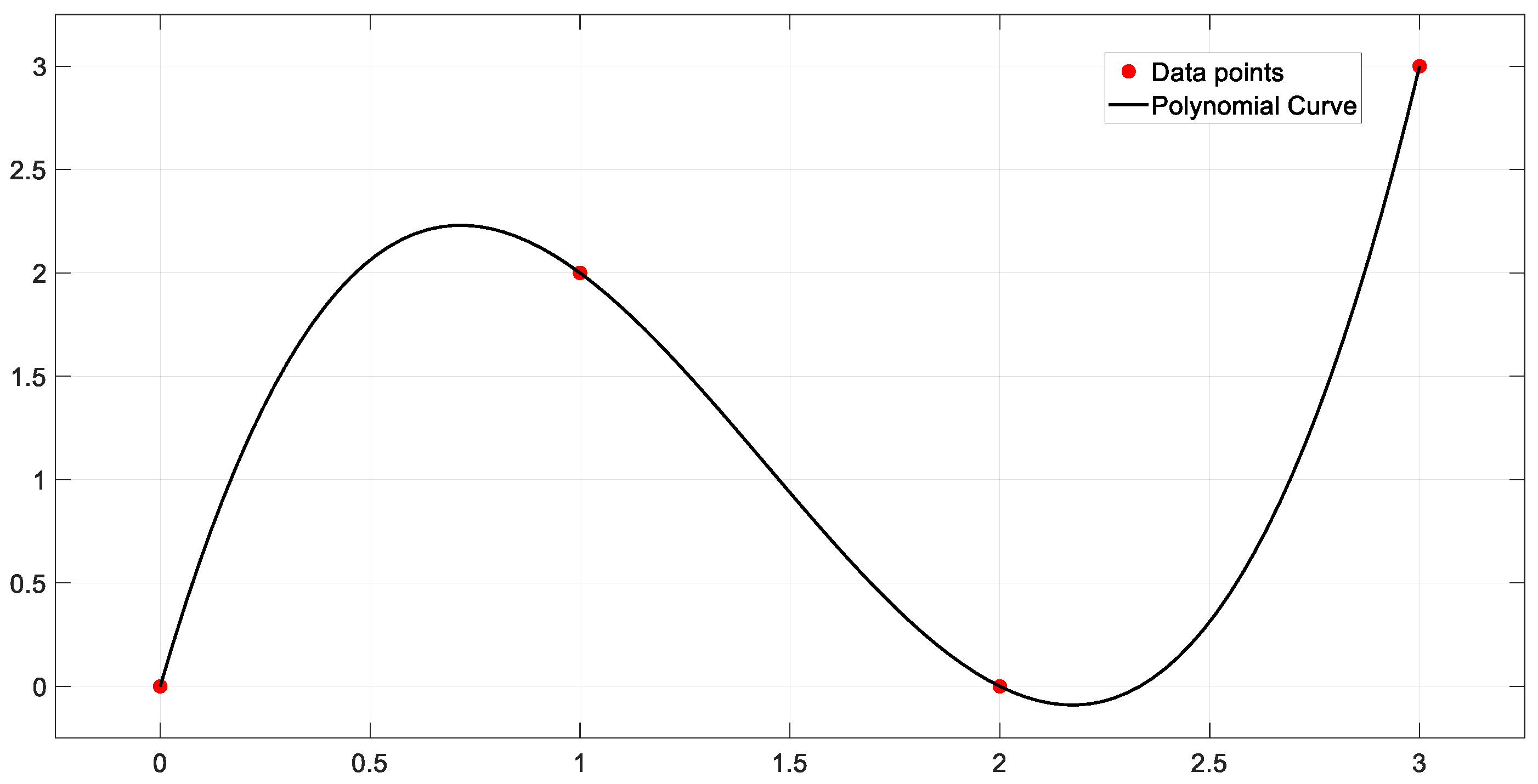
4.1. Polynomial Curve
4.2. Bezier Curve
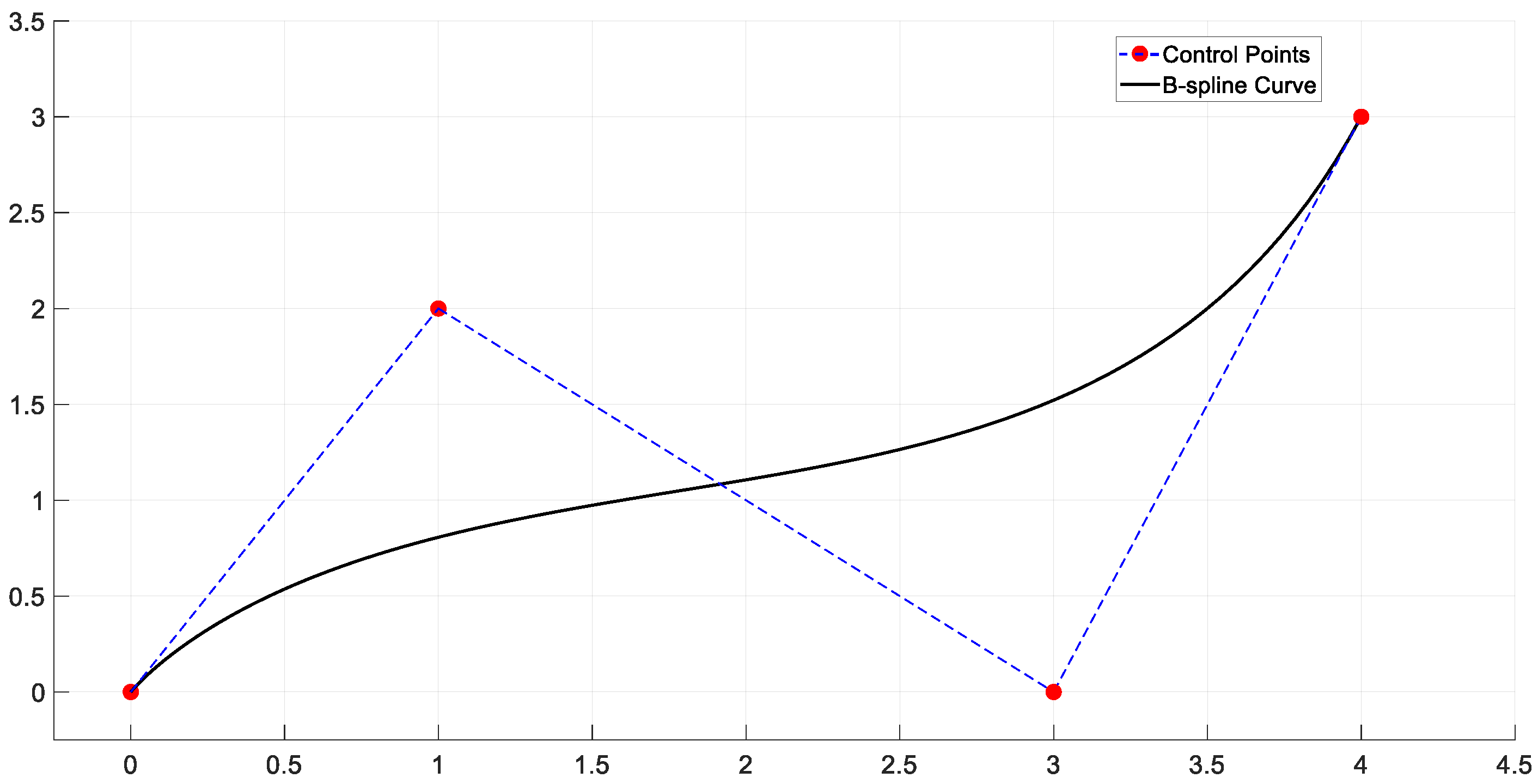
4.3. B-Spline
4.4. Summary
5. Optimization-Based Planning Algorithms
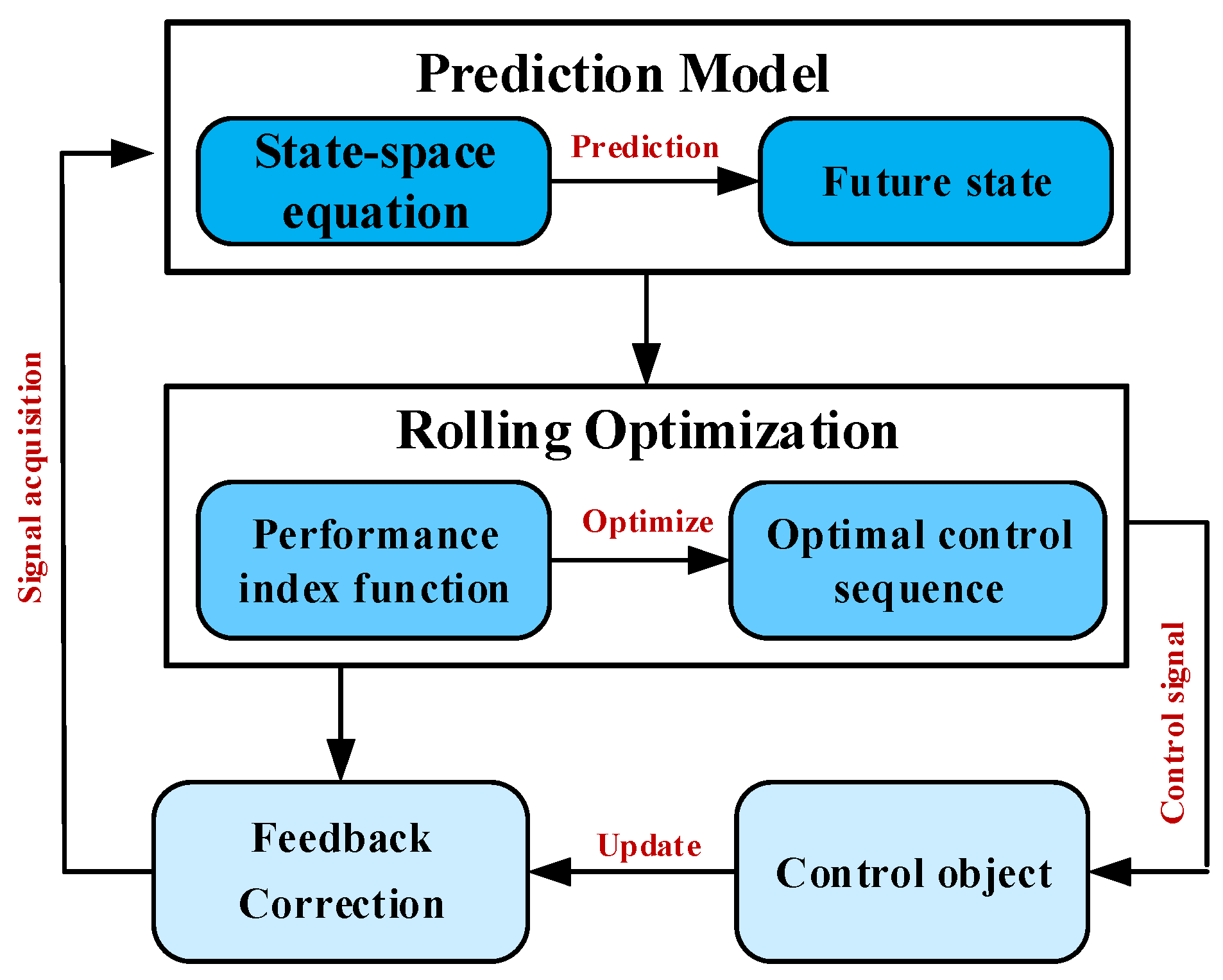
5.1. Model Predictive Control (MPC)
5.1.1. Improving Model
5.1.2. Introduction of Layered Architecture
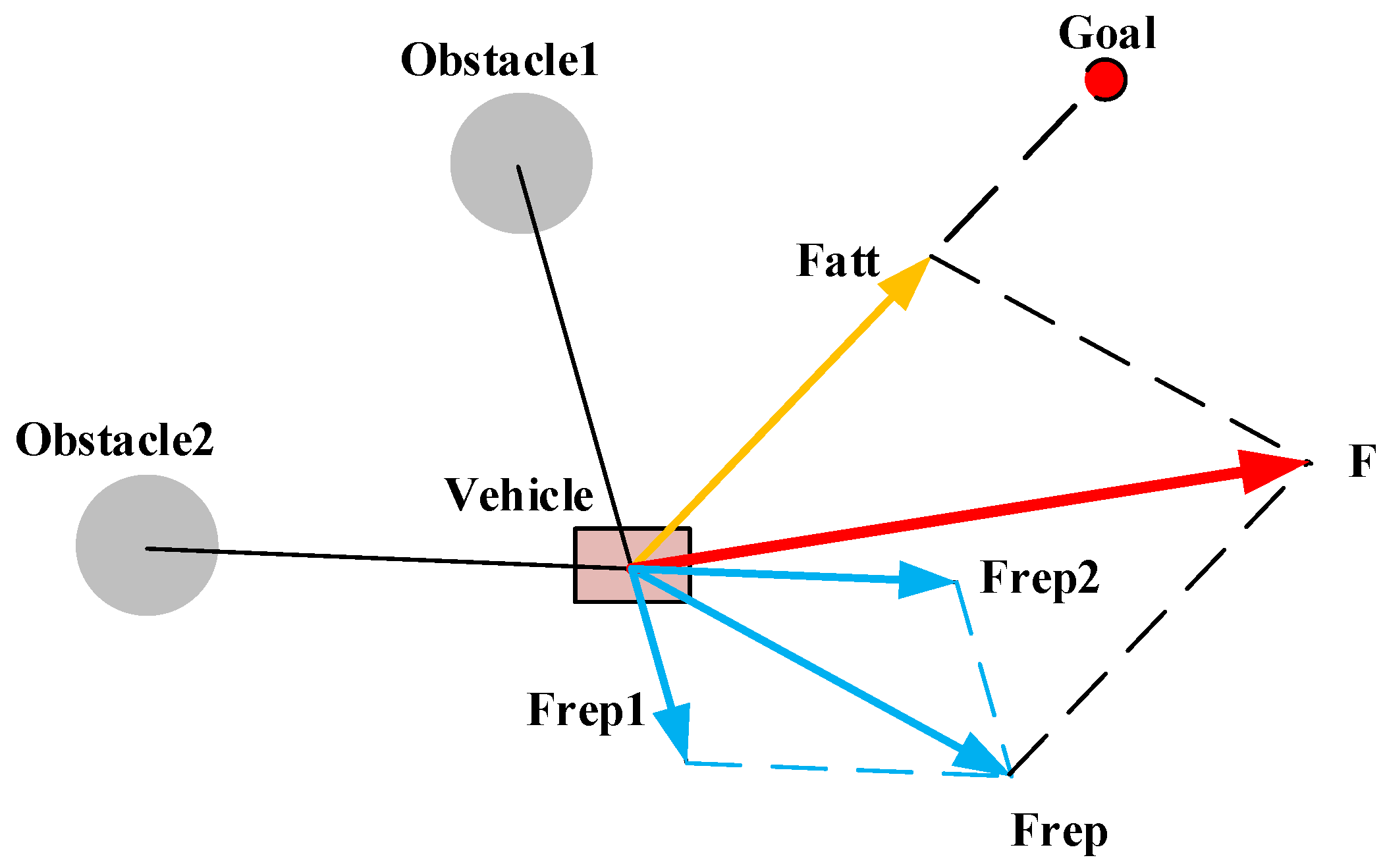
5.2. Artificial Potential Field (APF)
5.2.1. Improving the Repulsive Force Function
5.2.2. Improving the Potential Field Distribution
5.2.3. Integrating Other Path Planning Algorithms
5.3. Summary
6. Intelligent Algorithms
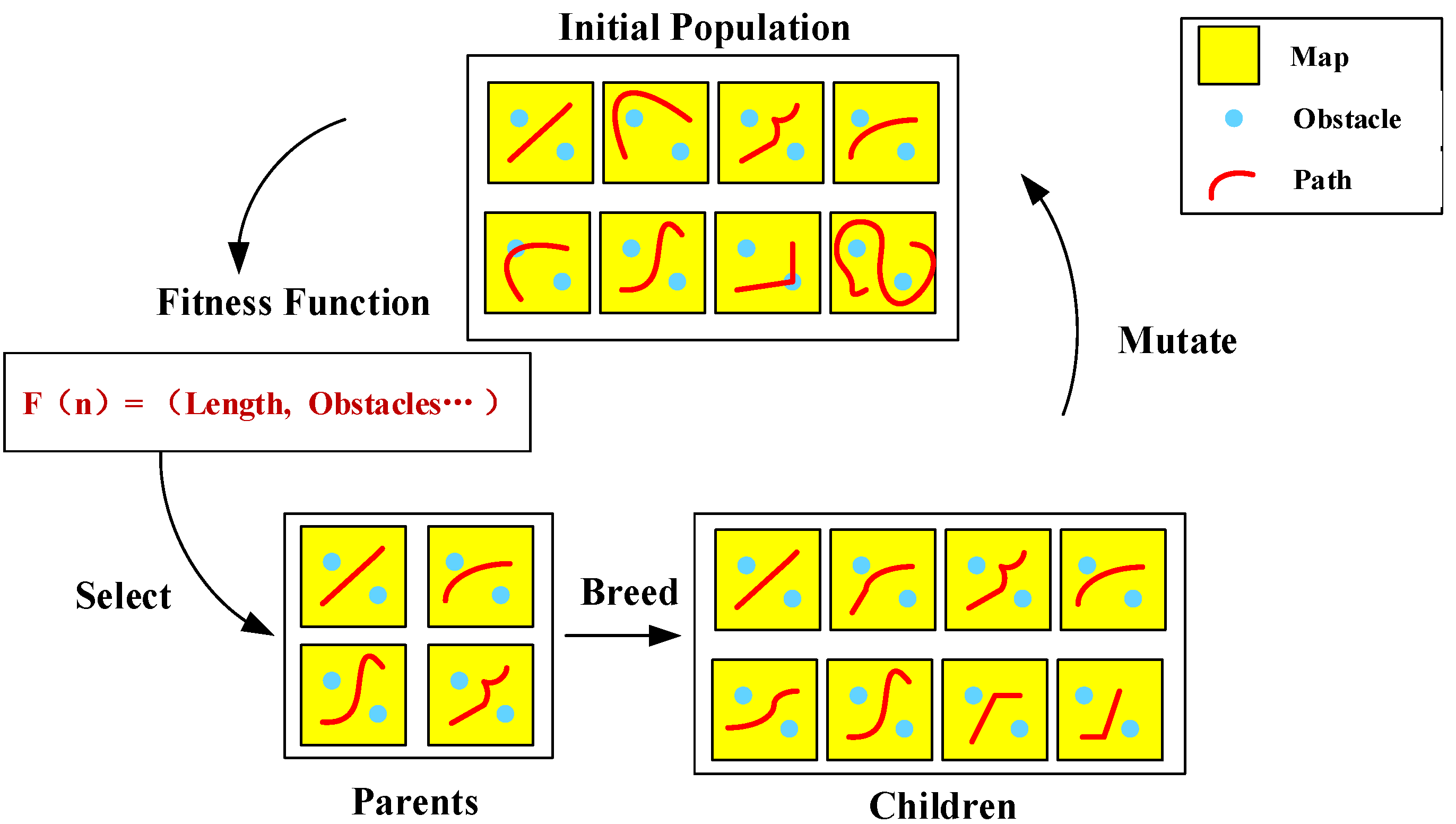
6.1. Genetic Algorithm (GA)
6.1.1. Improving the Initial Population
6.1.2. Improving Convergence Speed
6.1.3. Enhancing Local Search Capability
6.1.4. Hybrid Algorithm
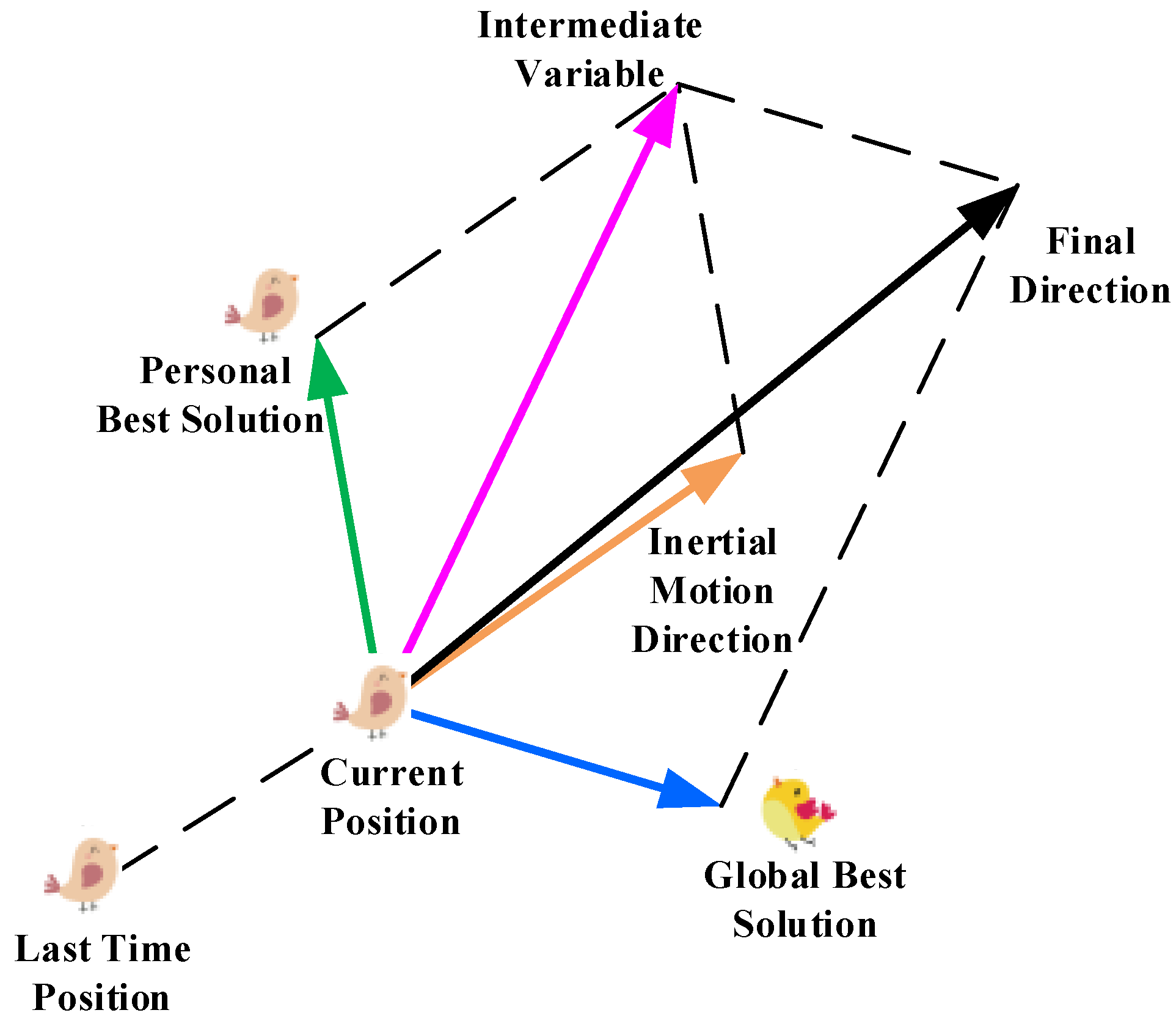
6.2. Particle Swarm Optimization (PSO)
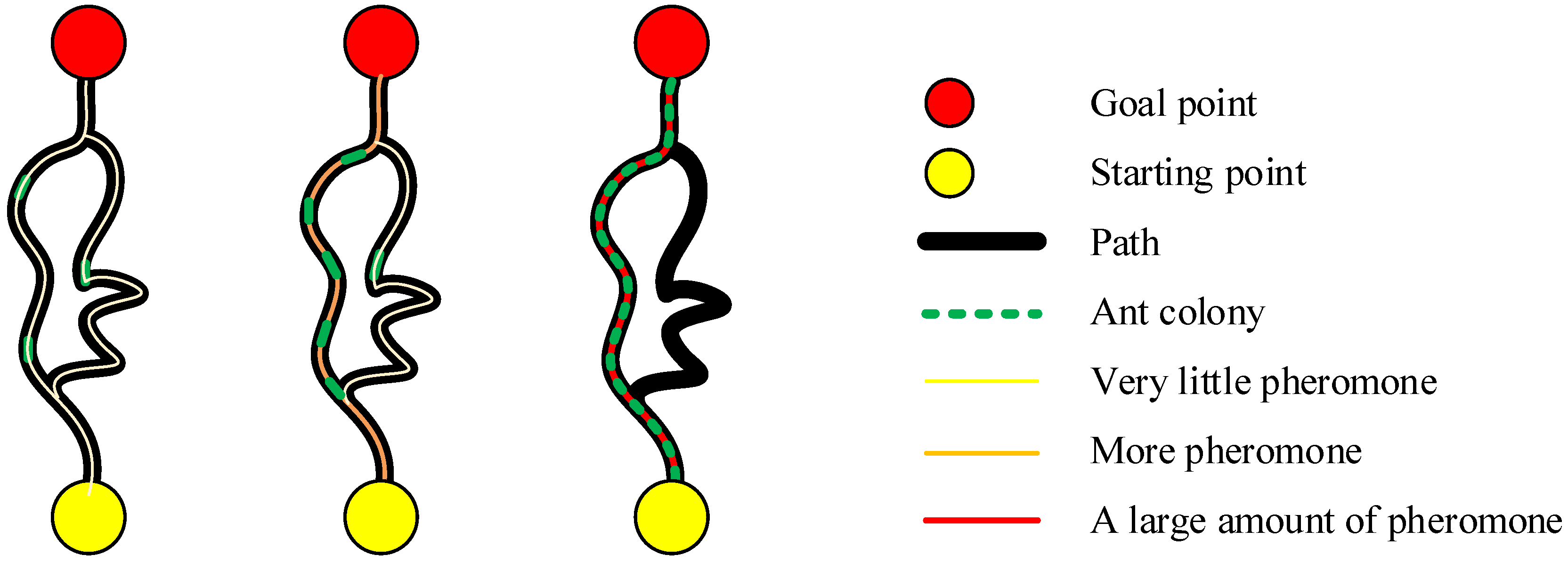
6.3. Ant Colony Optimization (ACO)
6.3.1. Addressing the Issue of Initial Pheromone Deficiency
6.3.2. Addressing the Issue of Slow Convergence
6.3.3. Addressing the Issue of Local Optima
6.3.4. Hybrid Algorithm
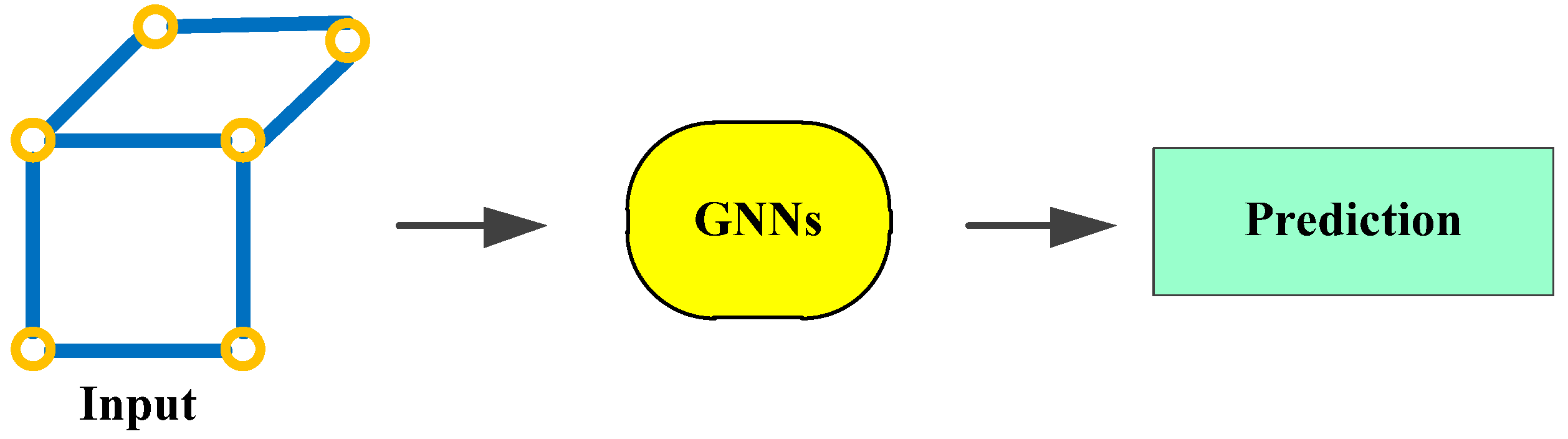
6.4. Deep Learning (DL)
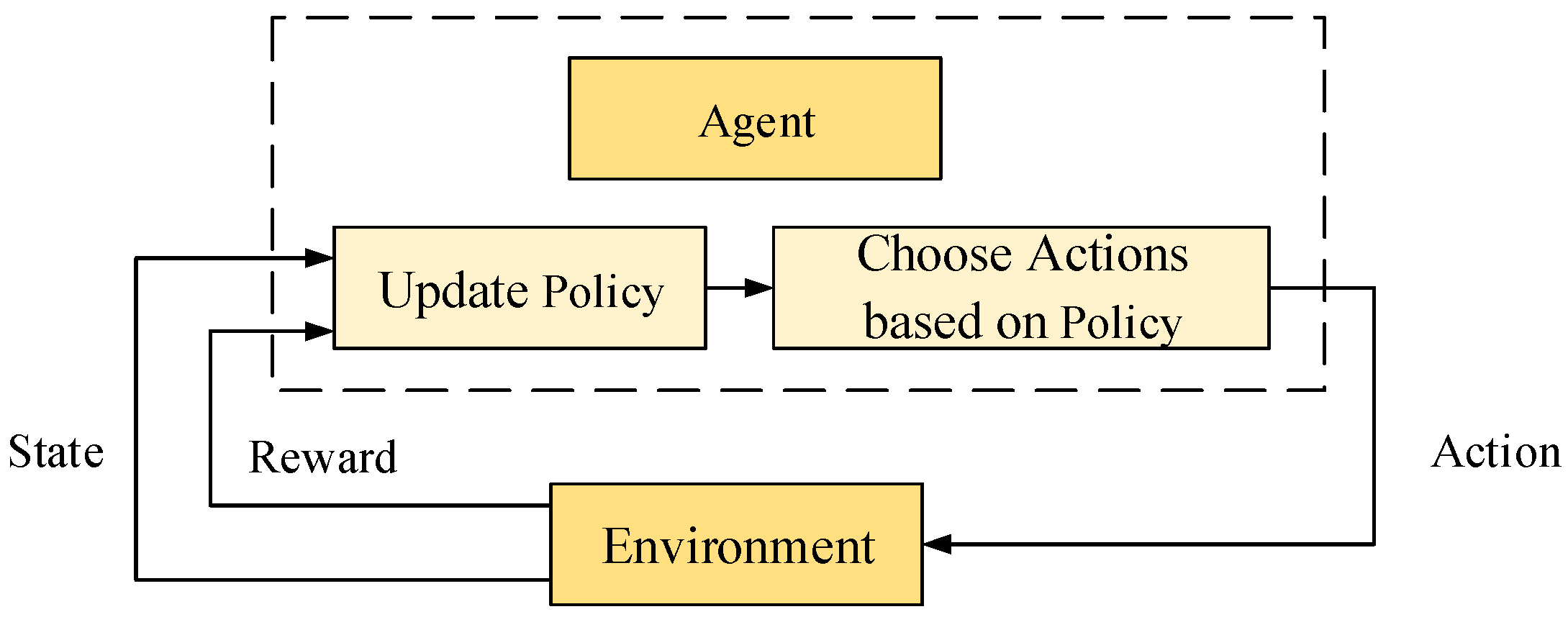
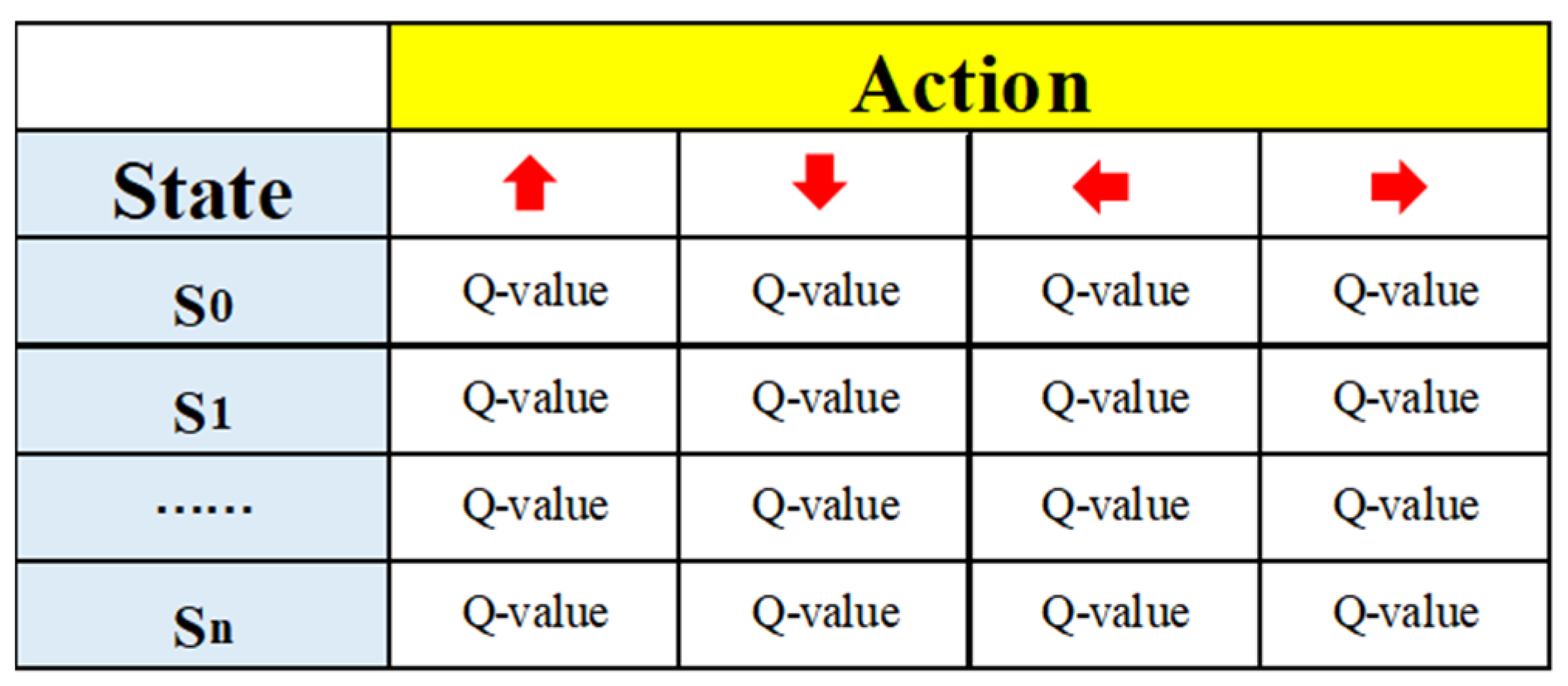
6.5. Reinforcement Learning (RL)
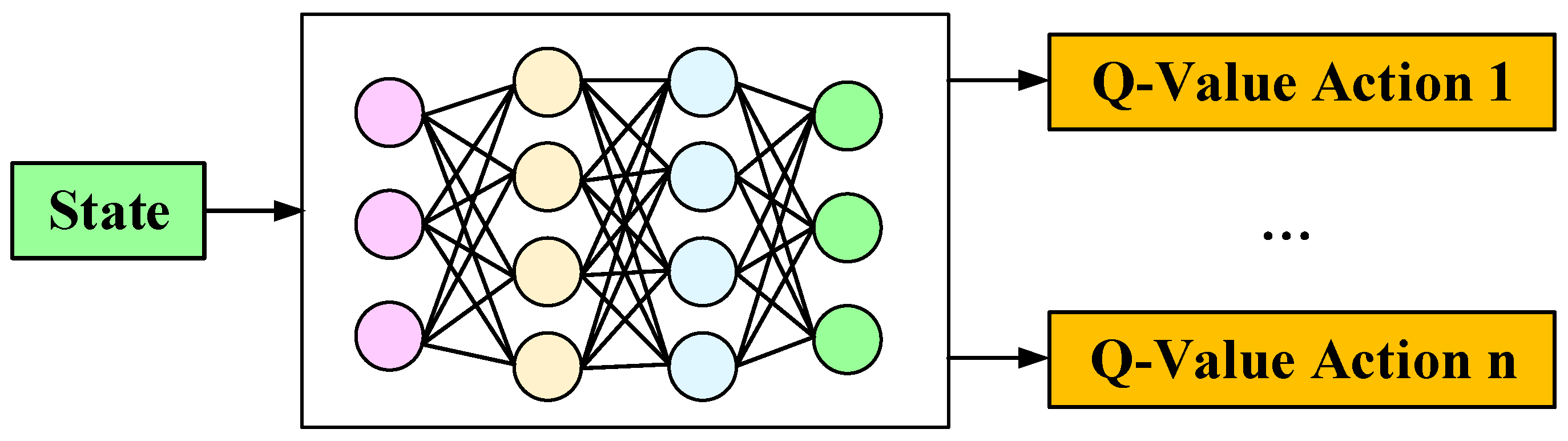
6.6. Deep Reinforcement Learning (DRL)
6.6.1. Regarding the Slow Convergence Speed
6.6.2. Regarding the Low Sample Efficiency
6.6.3. Hybrid Algorithm
6.7. Summary
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baek, M.; Mun, J.; Kim, W.; Choi, D.; Yim, J.; Lee, S. Driving Environment Perception Based on the Fusion of Vehicular Wireless Communications and Automotive Remote Sensors. Sensors 2021, 21, 1860. [Google Scholar] [CrossRef] [PubMed]
- Garrido, F.; Resende, P. Review of Decision-Making and Planning Approaches in Automated Driving. IEEE Access 2022, 10, 100348–100366. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Lin, W.M.; Chen, A.X. Path Planning for the Mobile Robot: A Review. Symmetry 2018, 10, 450. [Google Scholar] [CrossRef]
- Song, X.; Gao, H.; Ding, T.; Gu, Y.; Liu, J.; Tian, K. A Review of the Motion Planning and Control Methods for Automated Vehicles. Sensors 2023, 23, 6140. [Google Scholar] [CrossRef] [PubMed]
- Hardy, J.; Campbell, M. Contingency Planning Over Probabilistic Obstacle Predictions for Autonomous Road Vehicles. IEEE Trans. Robot. 2013, 29, 913–929. [Google Scholar] [CrossRef]
- Wang, N.; Xu, H. Dynamics-Constrained Global-Local Hybrid Path Planning of an Autonomous Surface Vehicle. IEEE Trans. Veh. Technol. 2020, 69, 6928–6942. [Google Scholar] [CrossRef]
- Sánchez-Ibáñez, J.R.; Pérez-del-Pulgar, C.J.; García-Cerezo, A. Path Planning for Autonomous Mobile Robots: A Review. Sensors 2021, 21, 7898. [Google Scholar] [CrossRef] [PubMed]
- Qin, H.; Shao, S.; Wang, T.; Yu, X.; Jiang, Y.; Cao, Z. Review of Autonomous Path Planning Algorithms for Mobile Robots. Drones 2023, 7, 211. [Google Scholar] [CrossRef]
- Javaid, A. Understanding Dijkstra’s Algorithm. Telecommun. Netw. Models Ejournal 2013. [Google Scholar] [CrossRef]
- Singal, P.; Dijkstra, R.C. Shortest Path Algorithm Using Global Position System. Int. J. Comput. Appl. 2014, 101, 12–18. [Google Scholar] [CrossRef]
- Bing, H.; Lai, L. Improvement and Application of Dijkstra Algorithms. Acad. J. Comput. Inf. Sci. 2022, 5, 97–102. [Google Scholar] [CrossRef]
- Sun, Y.; Fang, M.; Su, Y. AGV Path Planning Based on Improved Dijkstra Algorithm. J. Phys. Conf. Ser. 2021, 1746, 012052. [Google Scholar] [CrossRef]
- Wayahdi, M.R.; Ginting, S.H.N.; Syahputra, D. Greedy, A-Star, and Dijkstra’s Algorithms in Finding Shortest Path. Int. J. Adv. Data Inf. Syst. 2021, 2, 45–52. [Google Scholar] [CrossRef]
- Hansen, E.; Zhou, R. Anytime Heuristic Search. J. Artif. Intell. Res. 2011, 28, 267–297. [Google Scholar] [CrossRef]
- Chen, C.; Cai, J.; Wang, Z.; Chen, F.; Yi, W. An Improved A* Algorithm for Searching the Minimum Dose Path in Nuclear Facilities. Prog. Nucl. Energy 2020, 126, 103394. [Google Scholar] [CrossRef]
- Wang, H.; Qi, X.; Lou, S.; Jing, J.; He, H.; Liu, W. An Efficient and Robust Improved A* Algorithm for Path Planning. Symmetry 2021, 13, 2213. [Google Scholar] [CrossRef]
- Liu, S.; Ma, Y. Research for Bidirectional Path Planning Based on An Improved A* Algorithm. In Proceedings of the 2020 IEEE International Conference on Advances in Electrical Engineering and Computer Applications (AEECA), Dalian, China, 25–27 August 2020; pp. 1036–1039. [Google Scholar]
- Li, K.; Zhang, Y.; Huang, C.; Huang, B.; Chen, W. Two-Dimensional Path Planning on Improved A* Algorithm. In Proceedings of the 2019 IEEE 3rd Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 11–13 October 2019; pp. 1328–1332. [Google Scholar]
- Wang, R.; Lu, Z.; Jin, Y.; Liang, C. Application of A* Algorithm in Intelligent Vehicle Path Planning. Math. Models Eng. 2022, 8, 82–90. [Google Scholar] [CrossRef]
- Wang, P.; Liu, Y.; Yao, W.; Yu, Y. Improved A-Star Algorithm Based on Multivariate Fusion Heuristic Function for Autonomous Driving Path Planning. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 237, 1527–1542. [Google Scholar] [CrossRef]
- Lai, R.; Wu, Z.; Liu, X.; Zeng, N. Fusion Algorithm of the Improved A* Algorithm and Segmented Bézier Curves for the Path Planning of Mobile Robots. Sustainability 2023, 15, 2483. [Google Scholar] [CrossRef]
- Wang, H.; Lou, S.; Jing, J.; Wang, Y.; Liu, W.; Liu, T. The EBS-A* Algorithm: An Improved A* Algorithm for Path Planning. PLoS ONE 2022, 17, e0263841. [Google Scholar] [CrossRef] [PubMed]
- Miao, J.; Yao, X.; Liu, Y.; Liu, T.; Zhang, Y. Global Path Planning for Unmanned Vehicles Based on Improved A* Algorithm. In Proceedings of the Third International Conference on Artificial Intelligence and Electromechanical Automation (AIEA 2022), Changsha, China, 7 September 2022. [Google Scholar]
- Cao, M.; Li, B.; Shi, M. The Dynamic Path Planning of Indoor Robot Fusing B-Spline and Improved Anytime Repairing A* Algorithm. IEEE Access 2023, 11, 92416–92423. [Google Scholar] [CrossRef]
- Tang, G.; Tang, C.; Claramunt, C.; Hu, X.; Zhou, P. Geometric A-Star Algorithm: An Improved A-Star Algorithm for AGV Path Planning in a Port Environment. IEEE Access 2021, 9, 59196–59210. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Liu, J. Mobile Robot Path Planning Based on an Improved A* Algorithm. In Proceedings of the Conference on Computer Graphics, Artificial Intelligence, and Data Processing, Guangzhou, China, 23 May 2023. [Google Scholar]
- Li, Y.; Jin, R.; Xu, X.; Qian, Y.; Wang, H.; Xu, S.-S.; Wang, Z. A Mobile Robot Path Planning Algorithm Based on Improved A* Algorithm and Dynamic Window Approach. IEEE Access 2022, 10, 57736–57747. [Google Scholar] [CrossRef]
- Li, Z.; Shi, R.; Zhao, Z. A New Path Planning Method Based on Sparse A* Algorithm with Map Segmentation. Trans. Inst. Meas. Control 2021, 44, 916–925. [Google Scholar]
- Maniar, P.A. AI Path Prediction & Planning for Autonomous Vehicles. Interantional J. Sci. Res. Eng. Manag. 2023. [Google Scholar] [CrossRef]
- Sun, Z.; Hsu, D.; Jiang, T.; Kurniawati, H.; Reif, J.H. Reif Narrow Passage Sampling for Probabilistic Roadmap Planning. IEEE Trans. Robot. 2005, 21, 1105–1115. [Google Scholar] [CrossRef]
- Alarabi, S.; Luo, C.; Santora, M. A PRM Approach to Path Planning with Obstacle Avoidance of an Autonomous Robot. Proceeding of the 2022 8th International Conference on Automation, Robotics and Applications (ICARA), Prague, Czech Republic, 18–20 February 2022. [Google Scholar]
- Li, Q.; Xu, Y.; Bu, S.; Yang, J. Smart Vehicle Path Planning Based on Modified PRM Algorithm. Sensors 2022, 22, 6581. [Google Scholar] [CrossRef]
- Ma, X.; Gong, R.; Tan, Y.; Mei, H.; Li, C. Path Planning of Mobile Robot Based on Improved PRM Based on Cubic Spline. Wirel. Commun. Mob. Comput. 2022, 2022, 1632698. [Google Scholar] [CrossRef]
- Sandström, R.; Uwacu, D.; Denny, J.; Amato, N.M. Topology-Guided Roadmap Construction With Dynamic Region Sampling. IEEE Robot. Autom. Lett. 2020, 5, 6161–6168. [Google Scholar] [CrossRef]
- Ahmed, E.M.; Munim, H.E.A.E.; Bedour, H.M.S. An Accelerated Path Planning Approach. In Proceedings of the 2018 13th International Conference on Computer Engineering and Systems (ICCES), Cairo, Egypt, 18–19 December 2018; pp. 15–20. [Google Scholar]
- Ravankar, A.A.; Ravankar, A.; Emaru, T.; Kobayashi, Y. HPPRM: Hybrid Potential Based Probabilistic Roadmap Algorithm for Improved Dynamic Path Planning of Mobile Robots. IEEE Access 2020, 8, 221743–221766. [Google Scholar] [CrossRef]
- Li, W.; Wang, L.; Zou, A.; Cai, J.; He, H.; Tan, T. Path Planning for UAV Based on Improved PRM. Energies 2022, 15, 7267. [Google Scholar] [CrossRef]
- Cao, K.; Cheng, Q.; Gao, S.; Chen, Y.; Chen, C. Improved PRM for Path Planning in Narrow Passages. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 4–7 August 2019; pp. 45–50. [Google Scholar]
- Liu, C.; Xie, S.; Sui, X.; Huang, Y.; Ma, X.; Guo, N.; Yang, F. PRM-D* Method for Mobile Robot Path Planning. Sensors 2023, 23, 3512. [Google Scholar] [CrossRef] [PubMed]
- Cui, J. The Combination of Searching Algorithms with Sample-Based Planner in Solving 2D Robot Navigation Problems. In Proceedings of the 2021 3rd International Conference on Machine Learning, Big Data and Business Intelligence (MLBDBI), Taiyuan, China, 35 December 2021; pp. 504–509. [Google Scholar]
- Qiao, L.; Luo, X.; Luo, Q. An Optimized Probabilistic Roadmap Algorithm for Path Planning of Mobile Robots in Complex Environments with Narrow Channels. Sensors 2022, 22, 8983. [Google Scholar] [CrossRef]
- LaValle, S. Rapidly-Exploring Random Trees: A New Tool for Path Planning. Annu. Res. Rep. 1998, 18, 1001–1024. [Google Scholar]
- Véras, L.G.D.; Medeiros, F.L.; Guimaráes, L.N. Systematic Literature Review of Sampling Process in Rapidly-Exploring Random Trees. IEEE Access 2019, 7, 50933–50953. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Zheng, J.; Yu, J. Path Planning of Industrial Robot Based on Improved RRT Algorithm in Complex Environments. IEEE Access 2018, 6, 53296–53306. [Google Scholar] [CrossRef]
- Guo, X.; Cao, Y.; Zhou, J.; Huang, Y.; Li, B. HDM-RRT: A Fast HD-Map-Guided Motion Planning Algorithm for Autonomous Driving in the Campus Environment. Remote. Sens. 2023, 15, 487. [Google Scholar] [CrossRef]
- Kiani, F.; Seyyedabbasi, A.; Aliyev, R.; Gulle, M.U.; Basyildiz, H.; Shah, M.A. Adapted-RRT: Novel Hybrid Method to Solve Three-Dimensional Path Planning Problem Using Sampling and Metaheuristic-Based Algorithms. Neural Comput. Appl. 2021, 33, 15569–15599. [Google Scholar] [CrossRef]
- Li, X.; Tong, Y. Path Planning of a Mobile Robot Based on the Improved RRT Algorithm. Appl. Sci. 2023, 14, 25. [Google Scholar] [CrossRef]
- Jermyn, J. A Comparison of the Effectiveness of the RRT, PRM, and Novel Hybrid RRT-PRM Path Planners. Int. J. Res. Appl. Sci. Eng. Technol. 2021, 9, 600–611. [Google Scholar] [CrossRef]
- Al-Ansarry, S.; Al-Darraji, S. Hybrid RRT-A*: An Improved Path Planning Method for an Autonomous Mobile Robots. J. Electr. Electron. Eng. 2021, 17, 1–9. [Google Scholar] [CrossRef]
- Qin, T.; Xin, S. Path Planning Algorithm Based on Improved Bidirectional RRT. J. Phys. Conf. Ser. 2022, 2396, 012055. [Google Scholar] [CrossRef]
- Boryga, M.; Kołodziej, P.; Gołacki, K. The Use of Asymmetric Polynomial Profiles for Planning a Smooth Trajectory. Appl. Sci. 2022, 12, 2284. [Google Scholar] [CrossRef]
- Li, S.; Wang, J. Parallel Parking Path Planning in Narrow Space Based on a Three-Stage Curve Interpolation Method. IEEE Access 2023, 11, 93841–93851. [Google Scholar] [CrossRef]
- Zhang, Z.; Wei, C.; Ma, B.; Hu, L.; Zhao, B.; Lv, M. An Optimization-Based Trajectory Planning Method with Polynomial Curves. In Proceedings of the 2023 IEEE International Conference on Unmanned Systems (ICUS), Hefei, China, 13–15 October 2023; pp. 1–6. [Google Scholar]
- Boryga, M.; Kołodziej, P.; Gołacki, K. Application of Polynomial Transition Curves for Trajectory Planning on the Headlands. Agriculture 2020, 10, 144. [Google Scholar] [CrossRef]
- Huang, J.; Yang, Y.; Ding, D.; Li, Y.; He, Y. Automatic Parking Paths Planning Research Based on Scattering Points Six-Degree Polynomial and Easement Curve. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 237, 529–543. [Google Scholar] [CrossRef]
- Vu, T.M.; Moezzi, R.; Cyrus, J.; Hlava, J.; Petru, M. Feasible Trajectories Generation for Autonomous Driving Vehicles. Appl. Sci. 2021, 11, 1143. [Google Scholar] [CrossRef]
- Kawabata, K.; Ma, L.; Xue, J.; Zhu, C.; Zheng, N. A Path Generation for Automated Vehicle Based on Bezier Curve and Via-Points. Robot. Auton. Syst. 2015, 74, 243–252. [Google Scholar] [CrossRef]
- Fan, F. A 5-Degree Bézier Curve Shape Adjusting Method. J. Tonghua Norm. Univ. 2015. [Google Scholar] [CrossRef]
- Zheng, L.; Zeng, P.; Yang, W.; Li, Y.; Zhan, Z. Bézier Curve-Based Trajectory Planning for Autonomous Vehicles with Collision Avoidance. IET Intell. Transp. Syst. 2020, 14, 1882–1891. [Google Scholar] [CrossRef]
- Vinayak, A.; Zakaria, M.A.; Baarath, K.; Majeed, A.P.A. Novel Bezier Curve Control Point Search Algorithm for Autonomous Navigation Using N-Order Polynomial Search with Boundary Conditions. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 3884–3889. [Google Scholar]
- Bae, I.; Kim, J.H.; Moon, J.; Kim, S. Lane Change Maneuver Based on Bezier Curve Providing Comfort Experience for Autonomous Vehicle Users. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 2272–2277. [Google Scholar]
- Li, H.; Luo, Y.; Wu, J. Collision-Free Path Planning for Intelligent Vehicles Based on Bézier Curve. IEEE Access 2019, 7, 123334–123340. [Google Scholar] [CrossRef]
- Chiaravalli, D.; Califano, F.; Biagiotti, L.; De Gregorio, D.; Melchiorri, C. Physical-Consistent Behavior Embodied in B-Spline Curves for Robot Path Planning. IFAC-PapersOnLine 2018, 51, 306–311. [Google Scholar] [CrossRef]
- Xie, Q.; Huang, Y. A Class of Generalized Quadratic B-Splines with Local Controlling Functions. AIMS Math. 2023, 8, 23472–23499. [Google Scholar] [CrossRef]
- Cao, H.; Zoldy, M. Implementing B-Spline Path Planning Method Based on Roundabout Geometry Elements. IEEE Access 2022, 10, 81434–81446. [Google Scholar] [CrossRef]
- Wang, P.; Yang, J.; Zhang, Y.; Wang, Q.; Sun, B.; Guo, D. Obstacle-Avoidance Path-Planning Algorithm for Autonomous Vehicles Based on B-Spline Algorithm. World Electr. Veh. J. 2022, 13, 233. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, P.; Cui, K.; Zhou, H.; Yang, J.; Kong, X. An Obstacle Avoidance Path Planning and Evaluation Method for Intelligent Vehicles Based on the B-Spline Algorithm. Sensors 2023, 23, 8151. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, X.; Xu, C.; Gao, F. Geometrically Constrained Trajectory Optimization for Multicopters. IEEE Trans. Robot. 2021, 38, 3259–3278. [Google Scholar] [CrossRef]
- Tang, L.; Yan, F.; Zou, B.; Wang, K.; Lv, C. An Improved Kinematic Model Predictive Control for High-Speed Path Tracking of Autonomous Vehicles. IEEE Access 2020, 8, 51400–51413. [Google Scholar] [CrossRef]
- Huang, Y.; Ding, H.; Zhang, Y.; Wang, H.; Cao, D.; Xu, N.; Hu, C. A Motion Planning and Tracking Framework for Autonomous Vehicles Based on Artificial Potential Field Elaborated Resistance Network Approach. IEEE Trans. Ind. Electron. 2020, 67, 1376–1386. [Google Scholar] [CrossRef]
- Schwenzer, M.; Ay, M.; Bergs, T.; Abel, D. Review on Model Predictive Control: An Engineering Perspective. Int. J. Adv. Manuf. Technol. 2021, 117, 1327–1349. [Google Scholar] [CrossRef]
- Ammour, M.; Orjuela, R.; Basset, M. A MPC Combined Decision Making and Trajectory Planning for Autonomous Vehicle Collision Avoidance. IEEE Trans. Intell. Transp. Syst. 2022, 23, 24805–24817. [Google Scholar] [CrossRef]
- Franzè, G.; Fedele, G.; Bono, A.; D’Alfonso, L. Reference Tracking for Multiagent Systems Using Model Predictive Control. IEEE Trans. Control Syst. Technol. 2023, 31, 1884–1891. [Google Scholar] [CrossRef]
- Batkovic, I.; Gupta, A.; Zanon, M.; Falcone, P. Experimental Validation of Safe MPC for Autonomous Driving in Uncertain Environments. IEEE Trans. Control Syst. Technol. 2023, 31, 2027–2042. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, X. Path Planning for Intelligent Vehicle Collision Avoidance of Dynamic Pedestrian Using Att-LSTM, MSFM, and MPC at Unsignalized Crosswalk. IEEE Trans. Ind. Electron. 2022, 69, 4285–4295. [Google Scholar] [CrossRef]
- Shi, Q.; Zhao, J.; Kamel, A.E.; López-Juárez, I. MPC Based Vehicular Trajectory Planning in Structured Environment. IEEE Access 2021, 9, 21998–22013. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X.; Li, C.; Song, R.; Li, Y.; Meng, M.Q.-H. Chase and Track: Toward Safe and Smooth Trajectory Planning for Robotic Navigation in Dynamic Environments. IEEE Trans. Ind. Electron. 2023, 70, 604–613. [Google Scholar] [CrossRef]
- Li, Y.; Tian, B.; Yang, Y.; Li, C. Path Planning of Robot Based on Artificial Potential Field Method. In Proceedings of the 2022 IEEE 6th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 4–6 March 2022; Volume 6, pp. 91–94. [Google Scholar]
- Xia, X.; Li, T.; Sang, S.; Cheng, Y.; Ma, H.; Zhang, Q.; Yang, K. Path Planning for Obstacle Avoidance of Robot Arm Based on Improved Potential Field Method. Sensors 2023, 23, 3754. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.; Guo, Y.; Liu, H.; Wei, B.; Lyu, W. Improved Artificial Potential Field Method Applied for AUV Path Planning. Math. Probl. Eng. 2020, 2020, 6523158. [Google Scholar] [CrossRef]
- Tian, J.; Bei, S.; Li, B.; Hu, H.; Quan, Z.J.; Zhou, D.; Zhou, X.; Tang, H. Research on Active Obstacle Avoidance of Intelligent Vehicles Based on Improved Artificial Potential Field Method. World Electr. Veh. J. 2022, 13, 97. [Google Scholar] [CrossRef]
- Liu, Z.; Yuan, X.; Huang, G.; Wang, Y.; Zhang, X. Two Potential Fields Fused Adaptive Path Planning System for Autonomous Vehicle under Different Velocities. ISA Trans. 2021, 112, 176–185. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, K.; Gao, F.; Zhao, F. Research on Path Planning and Path Tracking Control of Autonomous Vehicles Based on Improved APF and SMC. Sensors 2023, 23, 7918. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Tan, C.; Mo, R.; Zhang, H.; Cai, G.; Li, H. Research on Path Planning of Three-Neighbor Search A* Algorithm Combined with Artificial Potential Field. Int. J. Adv. Robot. Syst. 2021, 18, 17298814211026449. [Google Scholar] [CrossRef]
- Sang, H.; You, Y.; Sun, X.J.; Ying, Z.; Liu, F. The Hybrid Path Planning Algorithm Based on Improved A* and Artificial Potential Field for Unmanned Surface Vehicle Formations. Ocean Eng. 2021, 223, 108709. [Google Scholar] [CrossRef]
- Diao, Q.; Zhang, J.; Liu, M.; Yang, J. A Disaster Relief UAV Path Planning Based on APF-IRRT* Fusion Algorithm. Drones 2023, 7, 323. [Google Scholar] [CrossRef]
- Abdel-Rahman, A.S.; Zahran, S.; Elnaghi, B.E.; Nafea, S.F. Enhanced hybrid path planning algorithm based on apf and a-star. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, 48, 867–873. [Google Scholar] [CrossRef]
- Yuan, Q.; Yi, J.; Sun, R.; Bai, H. Path Planning of a Mechanical Arm Based on an Improved Artificial Potential Field and a Rapid Expansion Random Tree Hybrid Algorithm. Algorithms 2021, 14, 321. [Google Scholar] [CrossRef]
- Fan, Q.; Cui, G.; Zhao, Z.; Shen, J. Obstacle Avoidance for Microrobots in Simulated Vascular Environment Based on Combined Path Planning. IEEE Robot. Autom. Lett. 2022, 7, 9801–9808. [Google Scholar] [CrossRef]
- Ke, Y. Comparative Analysis of Path Planning Algorithms and Prospects for Practical Application. Highlights Sci. Eng. Technol. 2023, 52, 202–207. [Google Scholar] [CrossRef]
- Hao, B.; Zhao, J.; Wang, Q. A Review of Intelligence-Based Vehicles Path Planning. SAE Int. J. Commer. Veh. 2023, 16, 329–339. [Google Scholar] [CrossRef]
- Varma, A.P.T. Self-Driving Car Simulation Using Genetic Algorithm. Int. J. Res. Appl. Sci. Eng. Technol. 2020. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A Review on Genetic Algorithm: Past, Present, and Future. Multimed. Tools Appl. 2020, 80, 8091–8126. [Google Scholar] [CrossRef]
- Li, K.; Hu, Q.; Liu, J. Path Planning of Mobile Robot Based on Improved Multiobjective Genetic Algorithm. Wirel. Commun. Mob. Comput. 2021, 2021, 8836615:1–8836615:12. [Google Scholar] [CrossRef]
- Hao, K.; Zhao, J.; Yu, K.; Li, C.; Wang, C. Path Planning of Mobile Robots Based on a Multi-Population Migration Genetic Algorithm. Sensors 2020, 20, 5873. [Google Scholar] [CrossRef]
- Hao, K.; Zhao, J.; Wang, B.; Liu, Y.; Wang, C. The Application of an Adaptive Genetic Algorithm Based on Collision Detection in Path Planning of Mobile Robots. Comput. Intell. Neurosci. 2021, 2021, 5536574. [Google Scholar] [CrossRef] [PubMed]
- Receveur, J.-B.; Victor, S.; Melchior, P. Autonomous Car Decision Making and Trajectory Tracking Based on Genetic Algorithms and Fractional Potential Fields. Intell. Serv. Robot. 2020, 13, 315–330. [Google Scholar] [CrossRef]
- Wang, Z.; Fu, Z. Unified Modeling of Path Planning and Tracking Control Based on Improved Genetic Algorithm. In Proceedings of the 2022 IEEE 8th International Conference on Computer and Communications (ICCC), Chengdu, China, 9–12 December 2022; pp. 2352–2356. [Google Scholar]
- Wang, M.; Chen, J.; Yang, H.; Wu, X.; Ye, L. Path Tracking Method Based on Model Predictive Control and Genetic Algorithm for Autonomous Vehicle. Math. Probl. Eng. 2022, 2022, 4661401. [Google Scholar] [CrossRef]
- Nazarahari, M.; Khanmirza, E.; Doostie, S. Multi-Objective Multi-Robot Path Planning in Continuous Environment Using an Enhanced Genetic Algorithm. Expert Syst. Appl. 2019, 115, 106–120. [Google Scholar] [CrossRef]
- Sahoo, S.P.; Das, D.B.; Pati, B.B.; Márquez, F.P.G.; Ramírez, I.S. Hybrid Path Planning Using a Bionic-Inspired Optimization Algorithm for Autonomous Underwater Vehicles. J. Mar. Sci. Eng. 2023, 11, 761. [Google Scholar] [CrossRef]
- Freitas, D.; Lopes, L.G.; Dias, F.M. Particle Swarm Optimisation: A Historical Review Up to the Current Developments. Entropy 2020, 22, 362. [Google Scholar] [CrossRef]
- Fang, J.; Liu, W.; Chen, L.; Lauria, S.; Miron, A.D.; Liu, X. A Survey of Algorithms, Applications and Trends for Particle Swarm Optimization. Int. J. Netw. Dyn. Intell. 2023, 2, 24–50. [Google Scholar] [CrossRef]
- Abdallaoui, S.; Aglzim, E.-H.; Chaibet, A.; Kribèche, A. Thorough Review Analysis of Safe Control of Autonomous Vehicles: Path Planning and Navigation Techniques. Energies 2022, 15, 1358. [Google Scholar] [CrossRef]
- Abed, M.; Lutfy, O.; Al-Doori, Q. A Review on Path Planning Algorithms for Mobile Robots. Eng. Technol. J. 2021, 39, 804–820. [Google Scholar] [CrossRef]
- van Zyl, J.-P.; Engelbrecht, A.P. Set-Based Particle Swarm Optimisation: A Review. Mathematics 2023, 11, 2980. [Google Scholar] [CrossRef]
- Chu, H.-S.; Yi, J.; Yang, F. Chaos Particle Swarm Optimization Enhancement Algorithm for UAV Safe Path Planning. Appl. Sci. 2022, 12, 8977. [Google Scholar] [CrossRef]
- Thammachantuek, I.; Ketcham, M. Path Planning for Autonomous Mobile Robots Using Multi-Objective Evolutionary Particle Swarm Optimization. PLoS ONE 2022, 17, e0271924. [Google Scholar] [CrossRef]
- Wang, Z.; Li, G.; Ren, J. Dynamic Path Planning for Unmanned Surface Vehicle in Complex Offshore Areas Based on Hybrid Algorithm. Comput. Commun. 2021, 166, 49–56. [Google Scholar] [CrossRef]
- Abhishek, B.; Ranjit, S.; Shankar, T.; Eappen, G.; Sivasankar, P.; Rajesh, A. Hybrid PSO-HSA and PSO-GA Algorithm for 3D Path Planning in Autonomous UAVs. SN Appl. Sci. 2020, 2, 1–16. [Google Scholar] [CrossRef]
- Deng, L.; Chen, H.; Zhang, X.; Liu, H. Three-Dimensional Path Planning of UAV Based on Improved Particle Swarm Optimization. Mathematics 2023, 11, 1987. [Google Scholar] [CrossRef]
- Huang, C. A Novel Three-Dimensional Path Planning Method for Fixed-Wing UAV Using Improved Particle Swarm Optimization Algorithm. Int. J. Aerosp. Eng. 2021, 2021, 7667173. [Google Scholar] [CrossRef]
- Yuan, Q.; Sun, R.; Du, X. Path Planning of Mobile Robots Based on an Improved Particle Swarm Optimization Algorithm. Processes 2022, 11, 26. [Google Scholar] [CrossRef]
- Huang, C.; Zhao, Y.; Zhang, M.; Yang, H. APSO: An A*-PSO Hybrid Algorithm for Mobile Robot Path Planning. IEEE Access 2023, 11, 43238–43256. [Google Scholar] [CrossRef]
- Yu, Z.; Si, Z.; Li, X.; Wang, D.; Song, H.H. A Novel Hybrid Particle Swarm Optimization Algorithm for Path Planning of UAVs. IEEE Internet Things J. 2022, 9, 22547–22558. [Google Scholar] [CrossRef]
- Song, B.; Wang, Z.; Zou, L. An Improved PSO Algorithm for Smooth Path Planning of Mobile Robots Using Continuous High-Degree Bezier Curve. Appl. Soft Comput. 2021, 100, 106960. [Google Scholar] [CrossRef]
- Doerner, K.F.; Merkle, D.; Stützle, T. Special Issue on Ant Colony Optimization. Swarm Intell. 2009, 3, 1–2. [Google Scholar] [CrossRef][Green Version]
- Sattari, M.R.J.; Malakooti, H.; Noor, R.M.; Anuar, N.B.; Khamis, N.B. Ant Colony Optimisation for Vehicle Traffic Systems: Applications and Challenges. Int. J. Bio Inspired Comput. 2014, 6, 32–56. [Google Scholar]
- Hamad, I.I.; Hasan, M.S. A Review: On Using ACO Based Hybrid Algorithms for Path Planning of Multi-Mobile Robotics. Int. J. Interact. Mob. Technol. 2020, 14, 145–156. [Google Scholar] [CrossRef]
- Qawqzeh, Y.K.; Alharbi, M.T.; Jaradat, A.; Sattar, K.N.A. A Review of Swarm Intelligence Algorithms Deployment for Scheduling and Optimization in Cloud Computing Environments. PeerJ Comput. Sci. 2021, 7, e696. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Zhu, C.; Wang, F.; Li, T.; Zhang, X. Multi-Factor of Path Planning Based on an Ant Colony Optimization Algorithm. Ann. GIS 2020, 26, 101–112. [Google Scholar] [CrossRef]
- Xiong, N.; Zhou, X.; Yang, X.; Xiang, Y.; Ma, J. Mobile Robot Path Planning Based on Time Taboo Ant Colony Optimization in Dynamic Environment. Front. Neurorobotics 2021, 15, 642733. [Google Scholar] [CrossRef]
- Ajeil, F.H.; Ibraheem, I.K.; Azar, A.T.; Humaidi, A.J. Grid-Based Mobile Robot Path Planning Using Aging-Based Ant Colony Optimization Algorithm in Static and Dynamic Environments. Sensors 2020, 20, 1880. [Google Scholar] [CrossRef]
- Wang, L.; Wang, H.; Yang, X.-H.; Gao, Y.; Cui, X.; Wang, B. Research on Smooth Path Planning Method Based on Improved Ant Colony Algorithm Optimized by Floyd Algorithm. Front. Neurorobotics 2022, 16, 955179. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Li, B.; Qi, Z.; Li, J.; Wu, J. Optimized APF-ACO Algorithm for Ship Collision Avoidance and Path Planning. J. Mar. Sci. Eng. 2023, 11, 1177. [Google Scholar] [CrossRef]
- Chen, Y.; Bai, G.; Zhan, Y.; Hu, X.; Liu, J. Path Planning and Obstacle Avoiding of the USV Based on Improved ACO-APF Hybrid Algorithm With Adaptive Early-Warning. IEEE Access 2021, 9, 40728–40742. [Google Scholar] [CrossRef]
- Hu, J.; Er, M.J.; Liu, T.; Wang, S. A Hybrid Algorithm Based on Ant Colony and Genetic Algorithm for AUV Path Planning. In Proceedings of the 2023 2nd Conference on Fully Actuated System Theory and Applications (CFASTA), Qingdao, China, 14–16 July 2023; pp. 888–893. [Google Scholar]
- Shi, K.; Huang, L.; Jiang, D.; Sun, Y.; Tong, X.; Xie, Y.; Fang, Z. Path Planning Optimization of Intelligent Vehicle Based on Improved Genetic and Ant Colony Hybrid Algorithm. Front. Bioeng. Biotechnol. 2022, 10, 905983. [Google Scholar] [CrossRef] [PubMed]
- Châari, I.; Koubâa, A.; Trigui, S.; Bennaceur, H.; Ammar, A.; Al-Shalfan, K. SmartPATH: An Efficient Hybrid ACO-GA Algorithm for Solving the Global Path Planning Problem of Mobile Robots. Int. J. Adv. Robot. Syst. 2014, 11, 94. [Google Scholar] [CrossRef]
- Song, Q.; Li, S.; Yang, J.; Bai, Q.; Hu, J.; Zhang, X.; Zhang, A. Intelligent Optimization Algorithm-Based Path Planning for a Mobile Robot. Comput. Intell. Neurosci. 2021, 2021, 8025730. [Google Scholar] [CrossRef]
- Pohan, M.A.R.; Trilaksono, B.R.; Santosa, S.P.; Syaichu-Rohman, A. Path Planning Algorithm Using the Hybridization of the Rapidly-Exploring Random Tree and Ant Colony Systems. IEEE Access 2021, 9, 153599–153615. [Google Scholar] [CrossRef]
- Yu, X.; Chen, W.; Gu, T.; Yuan, H.; Zhang, H.; Zhang, J. ACO-A*: Ant Colony Optimization Plus A* for 3-D Traveling in Environments With Dense Obstacles. IEEE Trans. Evol. Comput. 2019, 23, 617–631. [Google Scholar] [CrossRef]
- Zhao, B.; Huo, M.; Li, Z.; Yu, Z.; Qi, N. Clustering-Based Hyper-Heuristic Algorithm for Multi-Region Coverage Path Planning of Heterogeneous UAVs. Neurocomputing 2024, 610, 128528. [Google Scholar] [CrossRef]
- Yu, X.; Liu, F.; Ou, L. A Multi-Agent Path Planning Method Based on Graph Neural Network. Gaojishu Tongxin/Chin. High Technol. Lett. 2024, 34, 1081–1090. [Google Scholar] [CrossRef]
- Diao, X.; Chi, W.; Wang, J. Graph Neural Network Based Method for Robot Path Planning. Biomim. Intell. Robot. 2024, 4, 100147. [Google Scholar] [CrossRef]
- Almazrouei, K.S.; Kamel, I.; Rabie, T. Dynamic Obstacle Avoidance and Path Planning through Reinforcement Learning. Appl. Sci. 2023, 13, 8174. [Google Scholar] [CrossRef]
- Zhu, C. Intelligent Robot Path Planning and Navigation Based on Reinforcement Learning and Adaptive Control. J. Logist. Inform. Serv. Sci. 2023, 10, 235–248. [Google Scholar]
- Jang, B.; Kim, M.; Harerimana, G.; Kim, J.W. Q-Learning Algorithms: A Comprehensive Classification and Applications. IEEE Access 2019, 7, 133653–133667. [Google Scholar] [CrossRef]
- Ibrahim, M.M.S.; Atia, M.R.A.; Fakhr, M.W. Autonomous Vehicle Path Planning Using Q-Learning. J. Phys. Conf. Ser. 2021, 2128, 012018. [Google Scholar] [CrossRef]
- Hao, B.; Du, H.; Zhao, J.; Zhang, J.-M.; Wang, Q. A Path-Planning Approach Based on Potential and Dynamic Q-Learning for Mobile Robots in Unknown Environment. Comput. Intell. Neurosci. 2022, 2022, 2540546. [Google Scholar] [CrossRef] [PubMed]
- Ma, T.; Lyu, J.-M.; Yang, J.; Xi, R.; Li, Y.; An, J.; Li, C. CLSQL: Improved Q-Learning Algorithm Based on Continuous Local Search Policy for Mobile Robot Path Planning. Sensors 2022, 22, 5910. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Lu, H.; Yang, S.; Guo, F. The Experience-Memory Q-Learning Algorithm for Robot Path Planning in Unknown Environment. IEEE Access 2020, 8, 47824–47844. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, K.; Zhang, J. Improved Reinforcement Learning Path Planning Algorithm Integrating Prior Knowledge. PLoS ONE 2023, 18, e0284942. [Google Scholar] [CrossRef] [PubMed]
- Du, H.; Hao, B.; Zhao, J.; Zhang, J.-M.; Wang, Q.; Yuan, Q. A Path Planning Approach for Mobile Robots Using Short and Safe Q-Learning. PLoS ONE 2022, 17, e0275100. [Google Scholar] [CrossRef]
- Orozco-Rosas, U.; Picos, K.; Pantrigo, J.J.; Montemayor, A.S.; Cuesta-Infante, A. Mobile Robot Path Planning Using a QAPF Learning Algorithm for Known and Unknown Environments. IEEE Access 2022, 10, 84648–84663. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Fan, J.; Geng, Y. A Novel Q-Learning Algorithm Based on Improved Whale Optimization Algorithm for Path Planning. PLoS ONE 2022, 17, e0279438. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Yin, W.; Wong, W.E.; Jian, M.; Chau, M. Quality-Oriented Hybrid Path Planning Based on A* and Q-Learning for Unmanned Aerial Vehicle. IEEE Access 2022, 10, 7664–7674. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Peng, L. Multi-Robot Path Planning Based on a Deep Reinforcement Learning DQN Algorithm. CAAI Trans. Intell. Technol. 2020, 5, 177–183. [Google Scholar] [CrossRef]
- Singh, R.; Ren, J.; Lin, X. A Review of Deep Reinforcement Learning Algorithms for Mobile Robot Path Planning. Vehicles 2023, 5, 1423–1451. [Google Scholar] [CrossRef]
- Han, H.; Wang, J.; Kuang, L.; Han, X.; Xue, H. Improved Robot Path Planning Method Based on Deep Reinforcement Learning. Sensors 2023, 23, 5622. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.; Huang, X.; Huang, R.N. Efficient Deep Reinforcement Learning for Optimal Path Planning. Electronics 2022, 11, 3628. [Google Scholar] [CrossRef]
- Zheng, J.; Mao, S.; Wu, Z.; Kong, P.; Qiang, H. Improved Path Planning for Indoor Patrol Robot Based on Deep Reinforcement Learning. Symmetry 2022, 14, 132. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, P.; Ni, C.; Cheng, N. Deep Q Network Algorithm Based on Sample Screening. In Proceedings of the International Conference on Computer Application and Information Security (ICCAIS 2021), Wuhan, China, 18–19 December 2021. [Google Scholar]
- Guan, M.; Yang, F.X.; Jiao, J.C.; Chen, X. Research on Path Planning of Mobile Robot Based on Improved Deep Q Network. J. Phys. Conf. Ser. 2021, 1820, 012024. [Google Scholar] [CrossRef]
- Kong, F.; Wang, Q.; Gao, S.; Yu, H. B-APFDQN: A UAV Path Planning Algorithm Based on Deep Q-Network and Artificial Potential Field. IEEE Access 2023, 11, 44051–44064. [Google Scholar] [CrossRef]
- Wang, J.; Lei, G.; Zhang, J. Study of UAV Path Planning Problem Based on DQN and Artificial Potential Field Method. In Proceedings of the 2023 4th International Symposium on Computer Engineering and Intelligent Communications (ISCEIC), Nanjing, China, 18–20 August 2023; pp. 175–182. [Google Scholar]
- Zhang, F.; Gu, C.; Yang, F. An Improved Algorithm of Robot Path Planning in Complex Environment Based on Double DQN. In Advances in Guidance, Navigation and Control; Springer: Singapore, 2021. [Google Scholar]



| Ref. | Disadvantage | Improvement | Method Description |
|---|---|---|---|
| [16,17,18,19,20,21] | Excessive redundant nodes | Optimization of the heuristic function | Construct a new evaluation function to reduce the number of nodes during the search. |
| [16,17,22,23] | Slow planning speed | Bidirectional search | Conduct searches simultaneously from both the starting point and the endpoint. |
| [16,19,22] | Excessive inflection points | Path smoothing | Reduce the number of turning points and right-angle turns. |
| [21,23,24,25] | Excessive inflection points | Hybrid algorithm | Combining polynomial curves, Bezier curves-spline curves for smooth path planning. |
| [16,22] | High collisionrisk | Extended distance | Expand a certain distance outward from the edge of obstacles to form a safety buffer. |
| Comparison | Dijkstra | A* |
|---|---|---|
| Search Method | Only considers path cost | Combines path cost and heuristic function |
| Heuristic Information | No heuristic information | Requires a heuristic function h(n) |
| Application | Network routing | Autonomous driving |
| Memory Consumption | High (traverse all nodes) | High (maintain open list and closed list) |
| Optimality | Find the optimal solution | Can find the optimal solution with suitable h(n) |
| Dynamic Environments | Not suitable | Not suitable |
| Computational Efficiency | Low (needs to traverse all paths) | High (when optimized by the heuristic function) |
| Ref. | Hybrid | Solved Problem | Method Description |
|---|---|---|---|
| [39] | D* | Improve search efficiency | The D* algorithm is employed to conduct a secondary search for nodes that cannot be directly connected in the PRM construction phase. |
| [40] | A* | Improve search efficiency while managing dynamic obstacles | PRM constructs a global roadmap, A* algorithm is used for local search. |
| [41] | APF | Increase the density of sampling points in narrow passages | Using PRM for global planning, the Artificial Potential Field is used to optimize obstacle points. |
| Ref. | Hybrid | Solved Problem | Method Description |
|---|---|---|---|
| [46] | GWO | Shorten path length | Use Grey Wolf Optimization to determine the optimal length and direction for each movement. |
| [47] | Dijkstra | Improve search efficiency | Adjustable probability strategies dynamically adjust the target biasing probability based on the state of the search tree. The Dijkstra algorithm is used to prune the initial path and eliminate redundant nodes. |
| [48] | RPM Dijkstra | Improve path planning efficiency and shorten path length | RPM and RRT each generate a path. Resampling and roadmap construction are carried out within the convex hull area defined by the outer points of the two paths. Finally, Dijkstra’s algorithm is used to find the optimal path. |
| [49] | A* | Improve convergence speed | RRT generates an initial path, and the A* algorithm is used for local optimization in the area near the initial path. |
| [50] | APF | Improve search efficiency | Bi-directional RRT generates an initial path, while the Artificial Potential Field method is responsible for real-time obstacle avoidance and trajectory smoothing. |
| Comparison | PRM | RRT |
|---|---|---|
| Planning method | Offline roadmap construction | Online real-time expansion |
| Environment | Static environment | Dynamic environment |
| Application | Complex and high-dimensional spaces | Real-time planning and narrow passage |
| Path quality | Better paths | Require post-processing |
| Reuse | Roadmaps can be reused multiple times | The tree needs to be rebuilt for each query |
| Narrow passage | Poor | Good |
| Comparison | Polynomial Curves | Bezier Curves | B-Spline |
|---|---|---|---|
| Definition | Single polynomial equation | Control points | Control points and knot vector |
| Local control | NO(global changes) | No (global changes) | Yes (only affects the local area) |
| Complexity | Low | Medium | High |
| Smoothness | High-order polynomials may be unstable | Smooth but complex with a large number of control points | Very smooth, supporting high-order continuity |
| Application | Short-range path planning, dynamic constraint control | Local path optimization, high-precision path planning | Complex path planning, parking, and obstacle avoidance |
| Ref. | Hybrid | Improvement | Method Description |
|---|---|---|---|
| [86] | IRRT* | RRT: Introduces adaptive step size and search range, along with path-cutting optimization | For each expanded node, attraction and repulsion functions are constructed to enable the search tree to move more effectively toward the target point under the combined force. |
| [87] | A* | APF: Adds oscillation detection and local minimum detection A*: Adds local minimum boundary detection | A fusion manager is introduced to receive the results returned by the APF and determine whether to initiate the A* based on those results. |
| [88] | RRT Bezier | APF: Proposes a heuristic method based on the number of adjacent obstacles RRT: Introduces a triangular nearest neighbor node selection strategy | When the distance to obstacles is greater than twice the step size, the improved APF is used for rapid path expansion; otherwise, the improved RRT is employed for obstacle avoidance, and finally, the path is smoothed using Bezier curves. |
| [89] | RRT | APF: Improves the force fields RRT: Generates constrained nodes to enhance safety, extracts key nodes to reduce redundancy | The improved RRT is used for global path planning, and the path is divided into multiple sub-path segments. Each sub-path segment is then optimized using the improved APF. |
| Ref. | Hybrid | Improvement | Method Description |
|---|---|---|---|
| [100] | APF | APF: Adopts a time-efficient deterministic approach to optimize potential value assignment and path search processes. GA: Customizes crossover and mutation operators and optimizes path representation and encoding. | Using the improved APF, all initial paths are found and encoded as the initial population. The improved GA is then employed for path optimization. |
| [101] | GWO | No | GA is used to provide stable initial solutions, while GWO leverages these initial solutions for global optimization. |
| Ref. | Hybrid | Improvement | Method Description |
|---|---|---|---|
| [109] | APF | APF: Introducing relative velocity and relative acceleration to improve the repulsive force field PSO: Incorporating the Opposing Base Learning strategy, with adaptive adjustment of inertia weight and step size | Using the improved PSO for global path planning and the improved APF for dynamic obstacle avoidance |
| [110] | HSA | No | PSO conducts a global search, while the Harmony Search Algorithm performs a fine-tuning search around the potential optimal areas identified by PSO |
| GA | No | PSO performs a global search, and GA conducts a local search | |
| [111] | GA B-spline | PSO: Adaptive dynamic inertia weight | PSO is responsible for quickly locating potential high-quality solutions in the search space, while GA further optimizes these solutions. Finally, a cubic B-spline curve is used to smooth the path |
| [112] | DC A* | PSO: Adaptive dynamic inertia weight and chaotic mutation | The optimal solution is selected based on the DC strategy. The A* algorithm is used to generate a path that participates in the evolution process of PSO as a particle |
| [113] | IDE | PSO: Introducing the concept of corporate governance, optimizing the PSO update formula through adaptive adjustment of weight and acceleration coefficients | The improved PSO is responsible for global search and initial optimization, generating an elite population. Improved Differential Evolution further optimizes and feedback to PSO |
| [114] | A* | A*: Introducing a strategy for removing redundant nodes PSO: Proposing random inertia weight and random opposing base learning strategy | A* is used to calculate the initial path and key nodes are extracted as the initial particles for the PSO algorithm, which is then optimized using the improved PSO |
| [115] | SA | PSO: Proposing a global optimal solution update strategy: introducing a dimensional learning strategy | In each iteration, the Simulated Annealing algorithm is used to update the global optimal solution of the PSO algorithm |
| [116] | Bezier | PSO: Introducing adaptive fractional-order velocity, with dynamic adjustment of acceleration coefficients and inertia weight. | Continuous high-degree Bezier curves are used to generate smooth paths, and the improved PSO algorithm is employed to optimize the control points of these curves |
| Ref. | Hybrid | Improvement | Method Description |
|---|---|---|---|
| [125] | APF | APF: Optimize the potential field model and construct a dynamic APF gradient ACO: Introduce improved strategies | Using the improved ACO algorithm for global path planning and the enhanced APF algorithm to address collision issues |
| [126] | APF | APF: Establish a dynamic early warning obstacle avoidance model, redefine the potential field function, and dynamically adjust the step size ACO: Improve the heuristic function and pheromone update rules and introduce a dynamic pheromone evaporation factor | |
| [127] | GA | GA: Optimize the adjustment of the evaluation function | The initial path generated by ACO is used as the initial population for the GA algorithm |
| [128] | GA | GA: Introduce the deletion operator to remove unnecessary nodes | |
| [129] | GA | ACO: Improve the pheromone update rules and transition probability rules and introduce heuristic distance information probability | |
| [130] | GA | GA: Optimize the fitness function and genetic operation methods. ACO: Optimize the pheromone update strategy and introduce a penalty function to establish a dead-end table. | Utilize multiple optimized paths generated by the GA as the initial pheromones for the ACO. |
| [131] | RRT | No | A pseudorandom rule determines each iteration’s process: expanding the search tree via RRT for exploration or selecting nodes based on pheromone for exploitation. |
| [132] | A* | A*: Optimize the heuristic function. ACO: Develop a Representative-Based Estimation (RBE) strategy | ACO determines the target visit order using the cost map, while A* plans the path to each target in that order. |
| Ref. | Hybrid | Improvement | Method Description |
|---|---|---|---|
| [133] | RL | A hyper-heuristic algorithm is proposed | The heuristic space is parameterized by GNNs |
| [134] | Convolutional Neural Network (CNN) | GNN: A new reward structure | Features are collected from local observations using CNN, and these data are transmitted among agents by GNN |
| [135] | The greedy algorithm. | NO | The GNN outputs a set of guidance values for the neighbor set, and then the greedy algorithm is used to select the next vertex based on these guidance values |
| Ref. | Hybrid | Improvement | Method Description |
|---|---|---|---|
| [144] | APF | Q-Learning: Dynamic Q-Learning | Utilizing APF to initialize the Q-table based on the positional information of obstacles and target points in the environment |
| [145] | APF | Q-Learning: Introducing APF Weighting in the Decision-Making Process | Selecting the optimal action using Q-values and guiding the robot’s movement direction through APF weighting |
| [146] | WOA | Q-Learning: New Exploration Strategy with Dynamic Value Adjustment | Employing the Whale Optimization Algorithm (WOA) to generate the Q-table |
| [147] | A* | A*: Dynamically Adjusting Weights of Actual and Estimated Costs, Introducing Bidirectional Search Strategy Q-Learning: Designing State Space and Action Space, Optimizing Reward Mechanism, Introducing Dynamic Exploration Factor ε | Utilizing an improved A* algorithm for global path planning and an improved Q-learning algorithm for local dynamic path adjustment |
| Ref. | Hybrid | Improvement | Method Description |
|---|---|---|---|
| [154] | A*,APF | DQN: Proposes an improved ε-greedy strategy and designs a heuristic reward function using A* and APF | Incorporate the improved ε-greedy adaptive exploration strategy and heuristic reward function into the DQN algorithm |
| [155] | APF B-spline | DQN: A multi-output neural network structure is adopted, and an adaptive SA-ε-greedy algorithm is proposed | Utilize prior knowledge provided by APF to accelerate the DQN learning process and apply cubic B-spline for path smoothing |
| [156] | APF | DQN: A reward function based on an artificial potential field is introduced | Optimize the training process of DQN by introducing a reward function based on APF |
| [157] | A*,RRT | DQN: An improved Double DQN. | By integrating the concepts of the A* algorithm and RRT algorithm into the DDQN algorithm, improve the initialization strategy and reward function design of DDQN |
| Software | Path Planning Algorithms |
|---|---|
| Autoware Universe (release/v1.0 beta) | Dijkstra, A*,MPC, Hybrid A*, Frenet Frame, RRT, RRT*, B-Spline, QP (Quadratic Programming), RL, DNN |
| Apollo v8.0 | Dijkstra, A*, Hybrid A*, Frenet Frame, MPC, QP, RPM, RRT, RL, DQN |
| OpenPilot v0.8.5 | Polynomial Path Planning, MPC |
| ROS 1.0 (Noetic) | It does not directly provide path-planning algorithms but supports the implementation and integration of various path-planning algorithms. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Zakaria, M.A.; Younas, M. Path Planning Trends for Autonomous Mobile Robot Navigation: A Review. Sensors 2025, 25, 1206. https://doi.org/10.3390/s25041206
Tang Y, Zakaria MA, Younas M. Path Planning Trends for Autonomous Mobile Robot Navigation: A Review. Sensors. 2025; 25(4):1206. https://doi.org/10.3390/s25041206
Chicago/Turabian StyleTang, Yuexia, Muhammad Aizzat Zakaria, and Maryam Younas. 2025. "Path Planning Trends for Autonomous Mobile Robot Navigation: A Review" Sensors 25, no. 4: 1206. https://doi.org/10.3390/s25041206
APA StyleTang, Y., Zakaria, M. A., & Younas, M. (2025). Path Planning Trends for Autonomous Mobile Robot Navigation: A Review. Sensors, 25(4), 1206. https://doi.org/10.3390/s25041206





