ZPTM: Zigzag Path Tracking Method for Agricultural Vehicles Using Point Cloud Representation
Abstract
1. Introduction
2. Materials and Methods
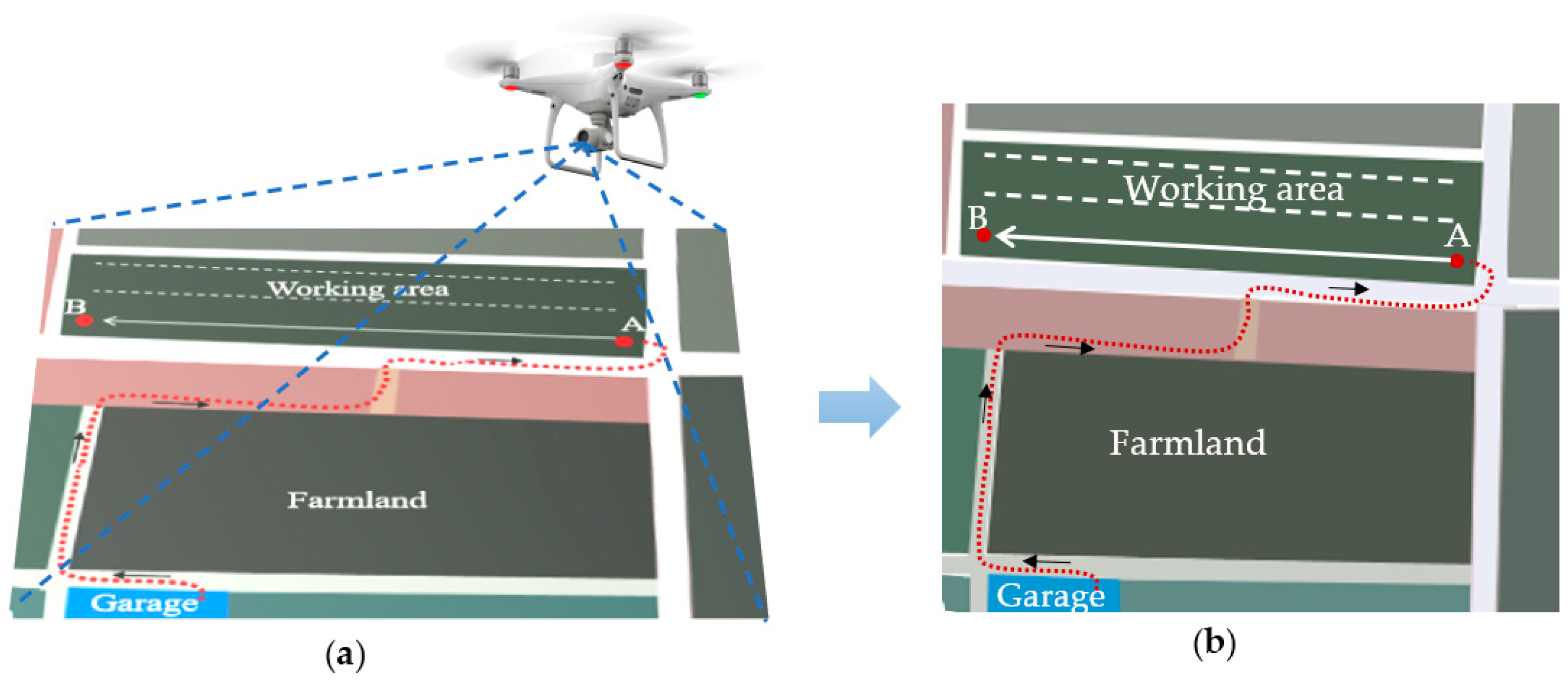
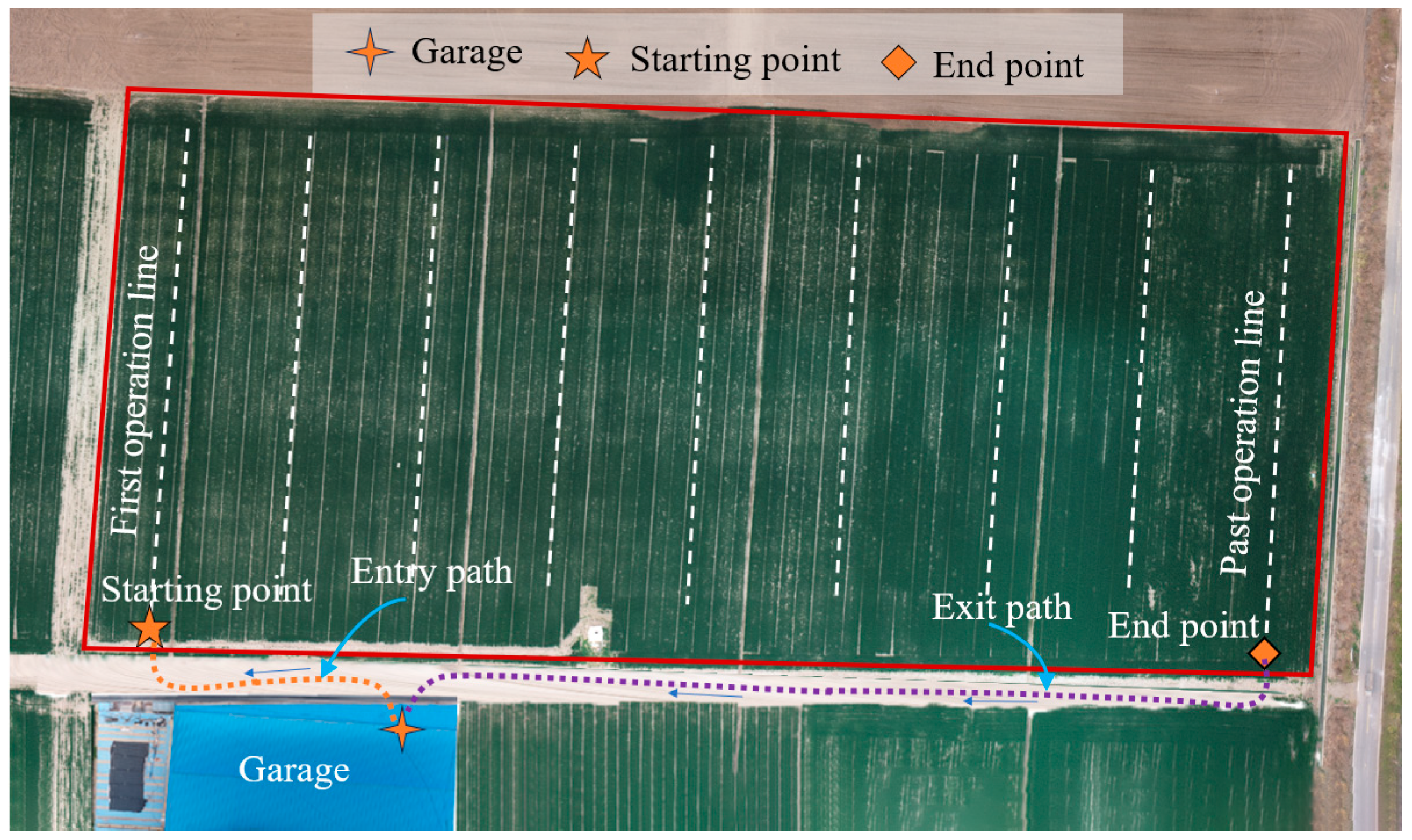
2.1. Path Planning
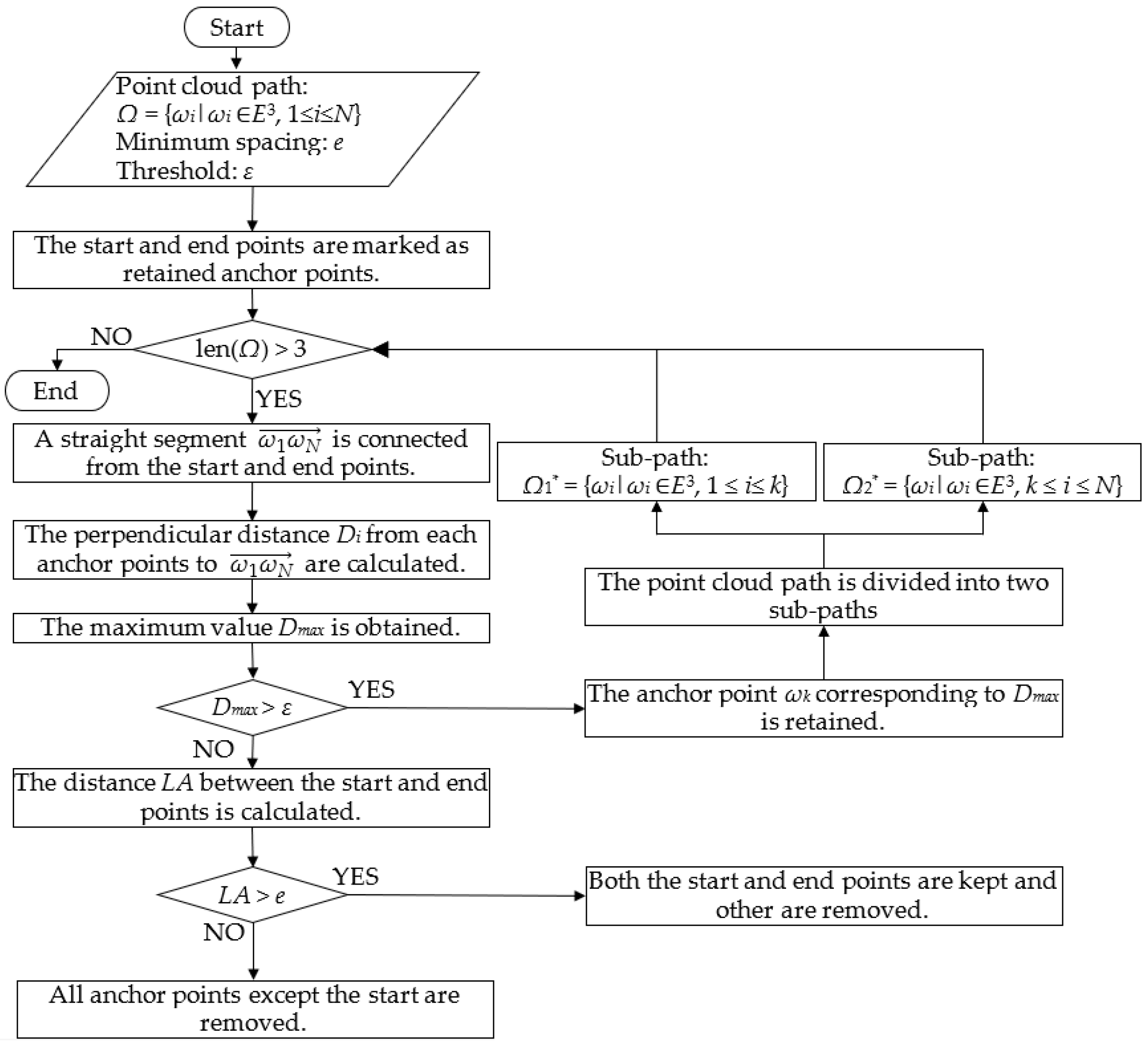
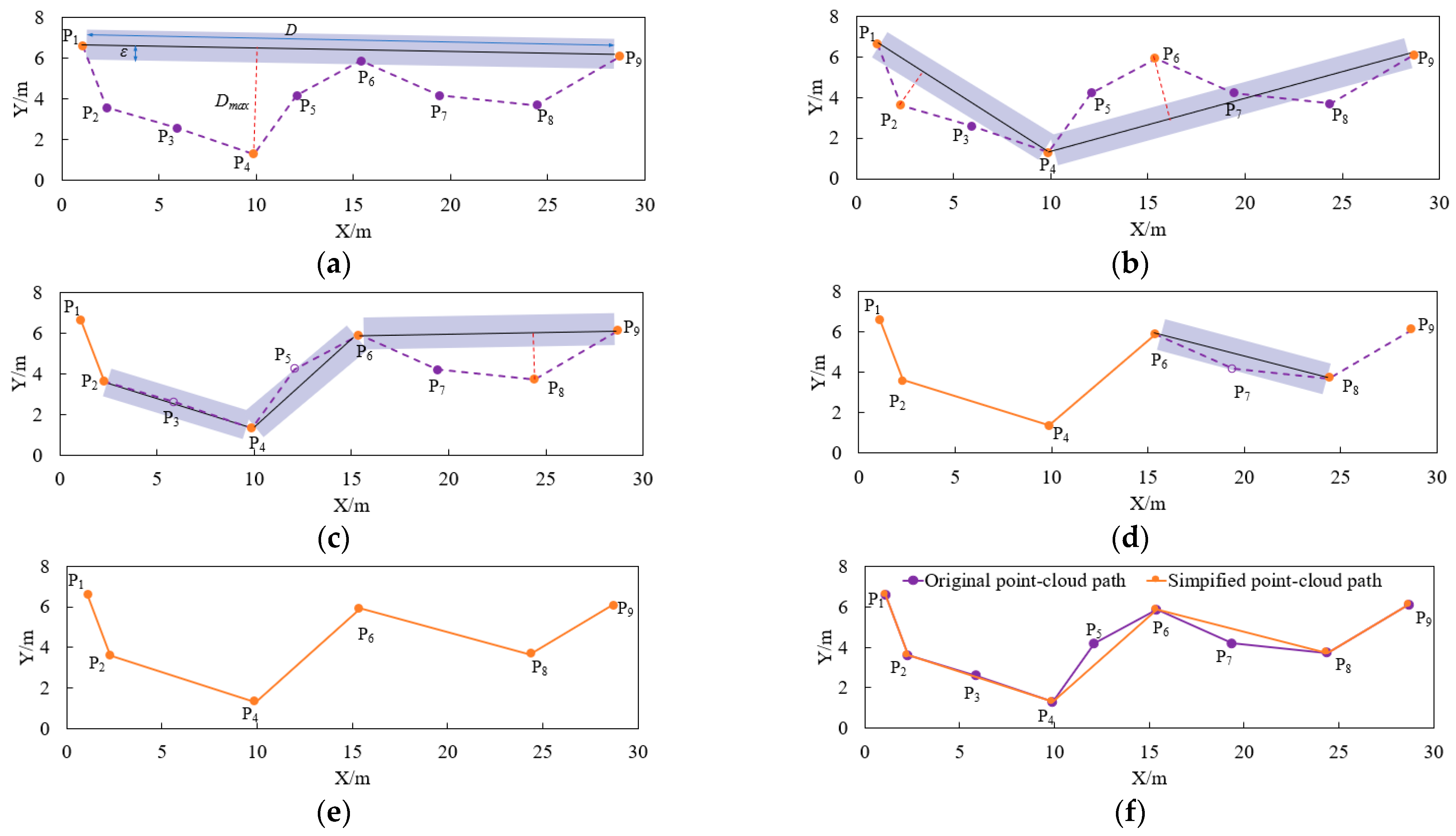
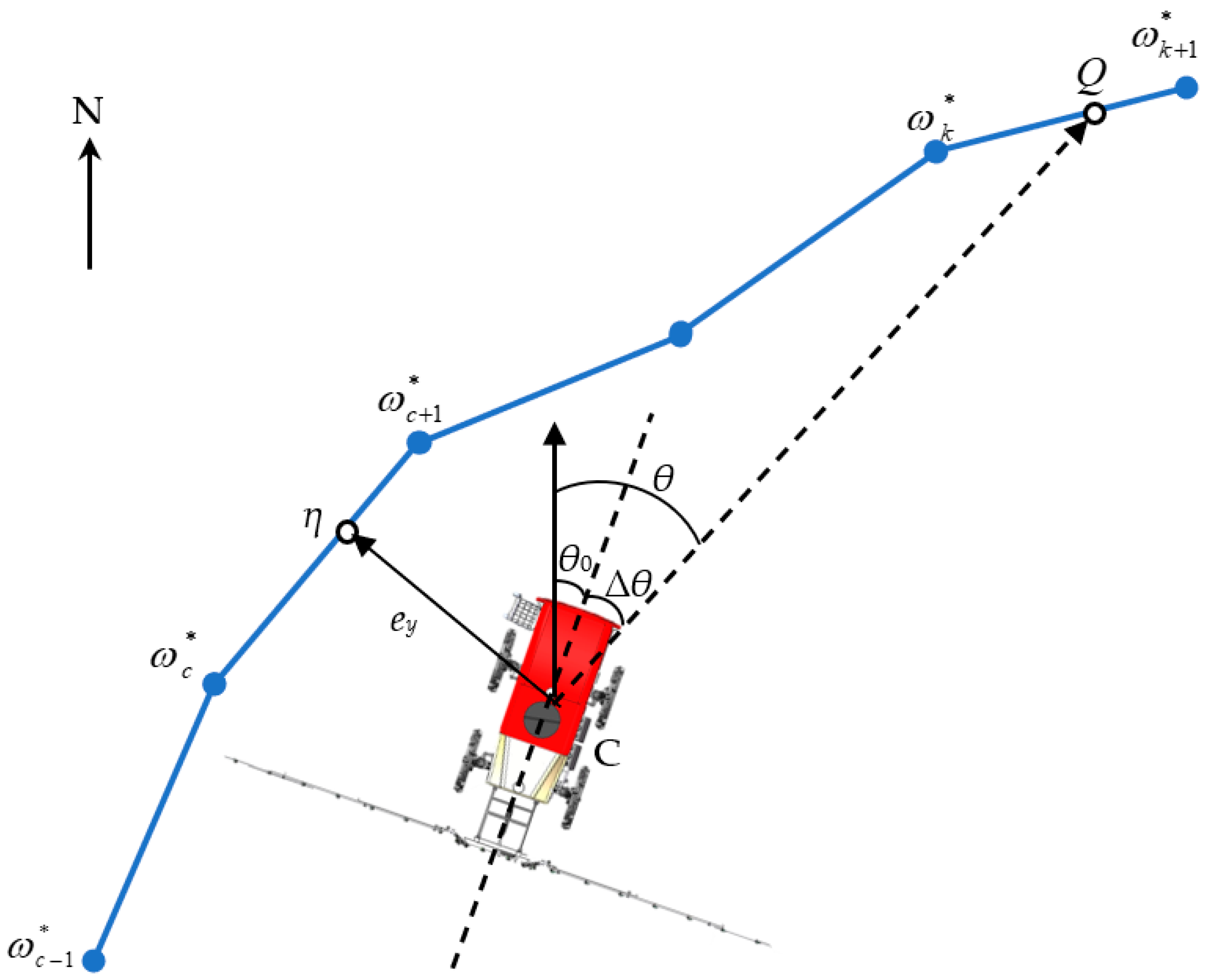
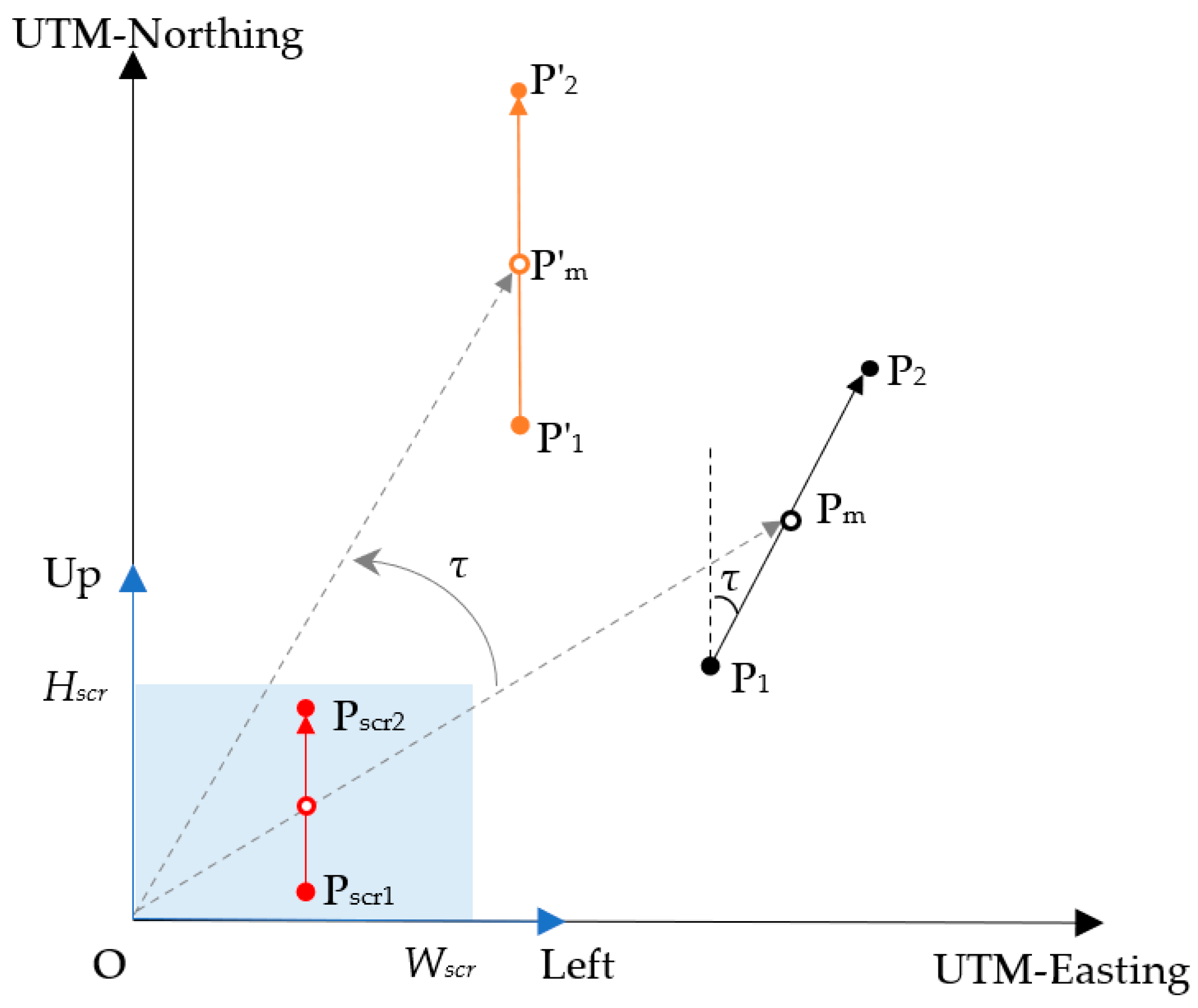
2.2. Point Cloud Path Tracking
2.3. Design of the GUI
2.4. Optimization of Zigzag Path Tracking Parameters
3. Results and Discussion
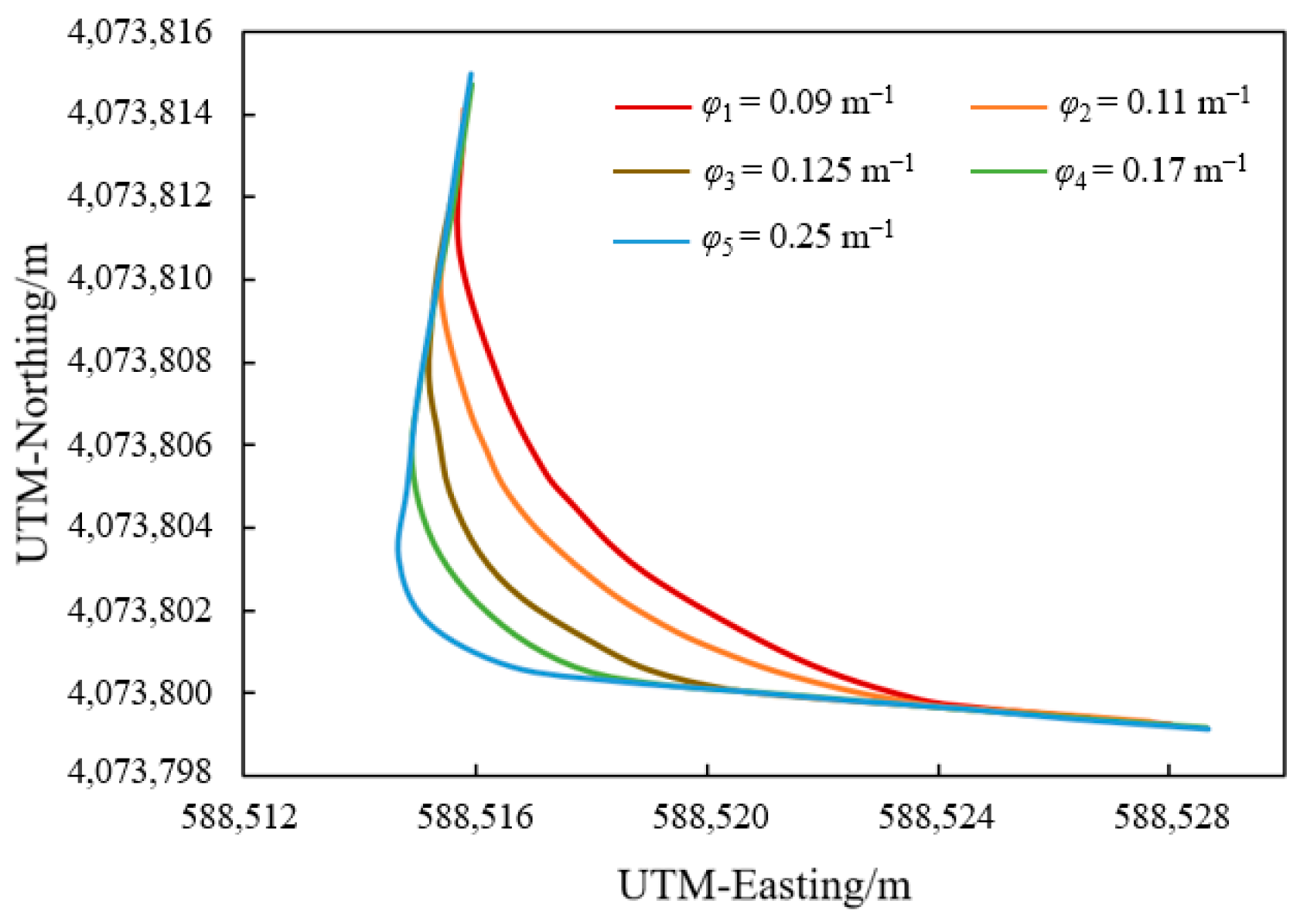
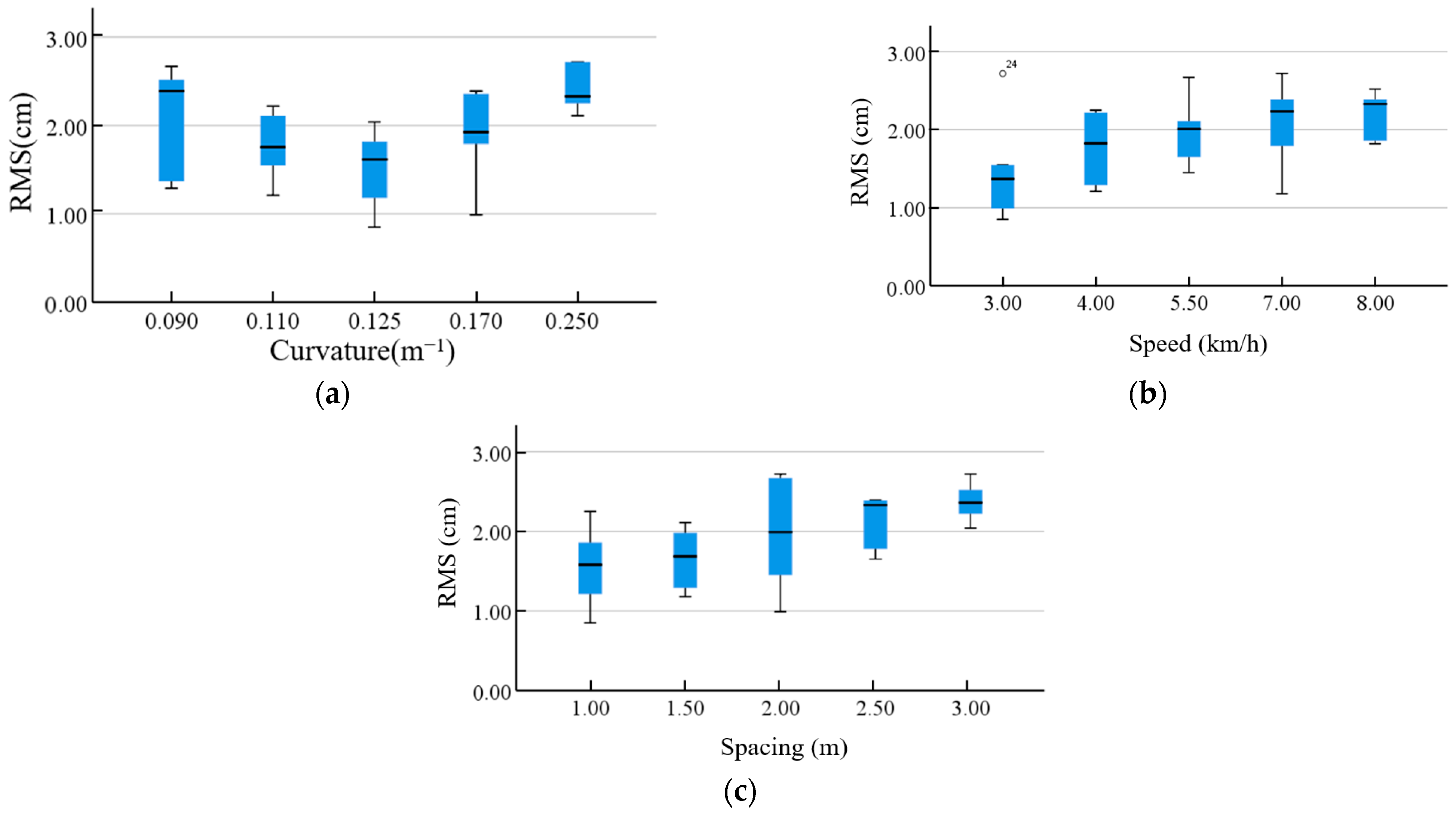
3.1. Determination of Optimal Navigation Parameters
3.2. Tests in the Field
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Fountas, S.; Mylonas, N.; Malounas, I.; Rodias, E.; Hellmann Santos, C.; Pekkeriet, E. Agricultural Robotics for Field Operations. Sensors 2020, 20, 2672. [Google Scholar] [CrossRef] [PubMed]
- Kutyrev, A.I.; Kiktev, N.A.; Smirnov, I.G. Laser Rangefinder Methods: Autonomous-Vehicle Trajectory Control in Horticultural Plantings. Sensors 2024, 24, 982. [Google Scholar] [CrossRef]
- Wang, N.; Yang, X.; Wang, T.; Xiao, J.; Zhang, M.; Wang, H.; Li, H. Collaborative path planning and task allocation for multiple agricultural machines. Comput. Electron. Agric. 2023, 213, 108218. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, J.Y.; Du, Y.F.; Zhu, Z.X.; Mao, E.R.; Song, Z.H. Method on automatic navigation control of tractor based on speed adaptation. Trans. Chin. Soc. Agric. Eng. 2017, 33, 48–55. [Google Scholar]
- Xie, B.B.; Jin, Y.C.; Faheem, M.; Gao, W.J.; Liu, J.Z.; Jiang, H.K.; Cai, L.J.; Li, Y.X. Research progress of autonomous navigation technology for multi-agricultural scenes. Comput. Electron. Agric. 2023, 211, 107963. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, K.; Wu, S.; Wen, L.; Chen, Z.; Dong, L.; Sun, M.; Wu, C. An obstacle avoidance path planner for an autonomous tractor using the minimum snap algorithm. Comput. Electron. Agric. 2023, 207, 107738. [Google Scholar] [CrossRef]
- Kim, W.-S.; Lee, D.-H.; Kim, T.; Kim, H.; Sim, T.; Kim, Y.-J. Weakly Supervised Crop Area Segmentation for an Autonomous Combine Harvester. Sensors 2021, 21, 4801. [Google Scholar] [CrossRef]
- Ye, L.; Wu, F.Y.; Zou, X.J.; Li, J. Path planning for mobile robots in unstructured orchard environments: An improved kinematically constrained bi-directional RRT approach. Comput. Electron. Agric. 2023, 215, 108453. [Google Scholar] [CrossRef]
- Urrea, C.; Muñoz, J. Path Tracking of Mobile Robot in Crops. J. Intell. Robot. Syst. 2015, 80, 193–205. [Google Scholar] [CrossRef]
- Liu, W.L.; Guo, R.; Zhao, J.Y. Predictive control method for the path tracking of agricultural machinery based on preview model. Trans. CSAE 2023, 39, 39–50. [Google Scholar]
- Sun, J.L.; Li, Q.S.; Ding, S.H.; Xing, G.Y.; Chen, L.P. Fixed-time generalized super-twisting control for path tracking of autonomous agricultural vehicles considering wheel slipping. Comput. Electron. Agric. 2023, 213, 108231. [Google Scholar] [CrossRef]
- Zhang, X.; Fu, Y.; Li, J.; Wei, Y.; Li, Y.; Zheng, L. Research on Combined Localization Algorithm Based on Active Screening–Kalman Filtering. Sensors 2024, 24, 2372. [Google Scholar] [CrossRef]
- Ji, P.; Duan, Z.; Xu, W. A Combined UWB/IMU Localization Method with Improved CKF. Sensors 2024, 24, 3165. [Google Scholar] [CrossRef] [PubMed]
- Takai, R.; Yang, L.L.; Noguchi, N. Development of a crawler-type robot tractor using RTK-GPS and IMU. Eng. Agric. Environ. Food 2014, 7, 143–147. [Google Scholar] [CrossRef]
- Li, S.; Zhang, M.; Ji, Y.H.; Zhang, Z.Q.; Cao, R.Y.; Chen, B.; Li, H.; Yin, Y.X. Agricultural machinery GNSS/IMU-integrated navigation based on fuzzy adaptive finite impulse response Kalman filtering algorithm. Comput. Electron. Agric. 2021, 191, 106524. [Google Scholar] [CrossRef]
- Jing, Y.P.; Li, Q.; Ye, W.S.; Liu, G. Development of a GNSS/INS-based automatic navigation land levelling system. Comput. Electron. Agric. 2023, 213, 108187. [Google Scholar] [CrossRef]
- Ou, Y.; Fan, Y.; Zhang, X.; Lin, Y.; Yang, W. Improved A* Path Planning Method Based on the Grid Map. Sensors 2022, 22, 6198. [Google Scholar] [CrossRef] [PubMed]
- You, Z.; Shen, K.; Huang, T.; Liu, Y.; Zhang, X. Application of A* Algorithm Based on Extended Neighborhood Priority Search in Multi-Scenario Maps. Electronics 2023, 12, 1004. [Google Scholar] [CrossRef]
- Wu, B.; Chi, X.; Zhao, C.; Zhang, W.; Lu, Y.; Jiang, D. Dynamic Path Planning for Forklift AGV Based on Smoothing A* and Improved DWA Hybrid Algorithm. Sensors 2022, 22, 7079. [Google Scholar] [CrossRef] [PubMed]
- Jeon, C.W.; Kim, H.J.; Yun, C.; Guang, M.S.; Han, X. An entry-exit path planner for an autonomous tractor in a paddy field. Comput. Electron. Agric. 2021, 191, 106548. [Google Scholar] [CrossRef]
- Xu, X.; Zeng, J.Z.; Zhao, Y.; Lv, X.S. Research on global path planning algorithm for mobile robots based on improved A*. Expert Syst. Appl. 2024, 243, 122922. [Google Scholar] [CrossRef]
- Ahn, J.; Shin, S.; Kim, M.; Park, J. Accurate Path Tracking by Adjusting Look-Ahead Point in Pure Pursuit Method. Int. J. Automot. Technol. 2021, 22, 119–129. [Google Scholar] [CrossRef]
- Nguyen, P.T.T.; Yan, S.W.; Liao, J.F.; Kuo, C.H. Autonomous Mobile Robot Navigation in Sparse LiDAR Feature Environments. Appl. Sci. 2021, 11, 5963. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.; Wen, X.; Zhang, G.; Ma, Q.; Cheng, S.; Qi, J.; Xu, L.; Chen, L. An optimal goal point determination algorithm for automatic navigation of agricultural machinery: Improving the tracking accuracy of the Pure Pursuit algorithm. Comput. Electron. Agric. 2022, 194, 106760. [Google Scholar] [CrossRef]
- Wu, C.C.; Wu, S.X.; Wen, L.; Chen, Z.B.; Yang, W.Z.; Zhai, W.X. Variable curvature path tracking control for the automatic navigation of tractors. Trans. Chin. Soc. Agric. Eng. 2022, 38, 1–7. [Google Scholar]
- He, Y.Q.; Zhou, J.; Sun, J.W.; Jia, H.B.; Liang, Z.A.; Awuah, E. An adaptive control system for path tracking of crawler combine harvester based on paddy ground conditions identification. Comput. Electron. Agric. 2023, 210, 107948. [Google Scholar] [CrossRef]
- Lamini, C.; Benhlima, S.; Elbekri, A. Genetic algorithm based approach for autonomous mobile robot path planning. Procedia Comput. Sci. 2018, 127, 180–189. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Zheng, H.; Li, Q.; Tian, Q. A spherical vector-based adaptive evolutionary particle swarm optimization for UAV path planning under threat conditions. Sci. Rep. 2025, 15, 2116. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Dong, A.; Li, Q.; Wei, W.; Zhang, Y.; Ye, Z. Application of ant colony optimization algorithm based on farthest point optimization and multi-objective strategy in robot path planning. Appl. Soft Comput. 2024, 167, 112433. [Google Scholar] [CrossRef]
- Khan, A.H.; Li, S.; Chen, D.; Liao, L. Tracking control of redundant mobile manipulator: An RNN based metaheuristic approach. Neurocomputing 2020, 400, 272–284. [Google Scholar] [CrossRef]
- Zhao, C.; Wu, D.; He, J.; Dai, C. A Visual Positioning Method of UAV in a Large-Scale Outdoor Environment. Sensors 2023, 23, 6941. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Yi, W. Composite Improved Algorithm Based on Jellyfish, Particle Swarm and Genetics for UAV Path Planning in Complex Urban Terrain. Sensors 2024, 24, 7679. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.Y.; Wu, W.B.; Zhou, J.P.; Dai, M.L.; Sun, Q.; Sun, X.G.; Chan, Z.; Gu, X.H. A spectral index for estimating grain filling rate of winter wheat using UAV-based hyperspectral images. Comput. Electron. Agric. 2024, 223, 109059. [Google Scholar] [CrossRef]
- Yang, J.K.; Zhai, Z.Q.; Li, Y.L.; Duan, H.W.; Cai, F.J.; Lv, J.D.; Zhang, R.Y. Design and research of residual film pollution monitoring system based on UAV. Comput. Electron. Agric. 2024, 217, 108608. [Google Scholar] [CrossRef]
- Wu, S.L.; Chen, Z.G.; Bangura, K.; Jiang, J.; Ma, X.G.; Li, J.Y.; Peng, B.; Meng, X.B.; Qi, L. A navigation method for paddy field management based on seedlings coordinate information. Comput. Electron. Agric. 2023, 215, 108436. [Google Scholar] [CrossRef]
- Sun, Q.L.; Zhang, R.R.; Chen, L.P.; Zhang, L.H.; Zhang, H.M.; Zhao, C.J. Semantic segmentation and path planning for orchards based on UAV images. Comput. Electron. Agric. 2022, 200, 107222. [Google Scholar] [CrossRef]
- Yin, X.; An, J.H.; Wang, Y.X.; Wang, Y.K.; Jin, C.Q. Development and experiments of the autonomous driving system for high-clearance spraying machines. Trans. Chin. Soc. Agric. Eng. 2021, 37, 22–30. [Google Scholar]
- Song, W.; Wang, C.; Dong, T.; Wang, Z.; Wang, C.; Mu, X.; Zhang, H. Hierarchical extraction of cropland boundaries using Sentinel-2 time-series data in fragmented agricultural landscapes. Comput. Electron. Agric. 2023, 212, 108097. [Google Scholar] [CrossRef]
- Lee, W.; Cho, S.-W. AIS Trajectories Simplification Algorithm Considering Topographic Information. Sensors 2022, 22, 7036. [Google Scholar] [CrossRef] [PubMed]
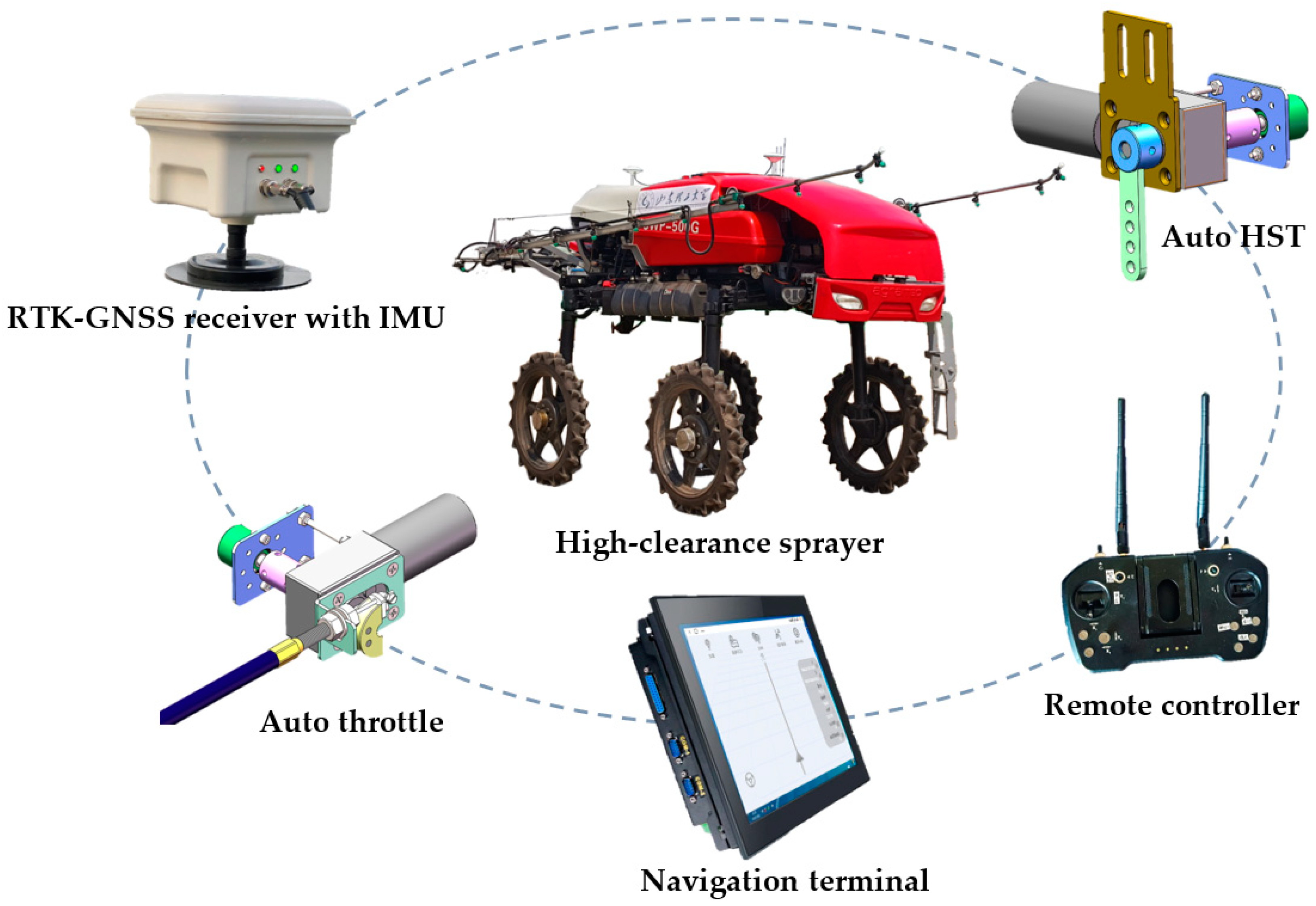



| Technical Parameter | Value |
|---|---|
| Motor power/kW | 20 |
| Tank volume/L | 500 |
| Wheelbase × Tread/m × m | 1.5 × 1.5 |
| Sprinkling width/m | 12 |
| Traving speed/km/h | 0–10 |
| Ground clearance/m | 1.2 |
| Minimum turn radius/m | 3.5 |
| Number | Curvature (m−1) | Speed (km/h) | Spacing (m) | Maximum (cm) | Average (cm) | RMS (cm) |
|---|---|---|---|---|---|---|
| 1 | 0.09 | 3 | 1 | 3.7 | 1.42 | 1.37 |
| 2 | 0.09 | 4 | 1.5 | 3.3 | 1.32 | 1.29 |
| 3 | 0.09 | 5.5 | 2 | 3.1 | 1.46 | 2.67 |
| 4 | 0.09 | 7 | 2.5 | 4.3 | 2.02 | 2.39 |
| 5 | 0.09 | 8 | 3 | 4.8 | 2.24 | 2.52 |
| 6 | 0.11 | 4 | 1 | 4.2 | 1.37 | 1.21 |
| 7 | 0.11 | 8 | 1 | 3.2 | 1.33 | 1.86 |
| 8 | 0.11 | 3 | 1.5 | 3.6 | 1.43 | 1.55 |
| 9 | 0.11 | 7 | 2 | 4.4 | 1.76 | 2.11 |
| 10 | 0.11 | 5.5 | 2.5 | 3.5 | 1.64 | 1.65 |
| 11 | 0.11 | 4 | 3 | 4.4 | 1.84 | 2.22 |
| 12 | 0.125 | 3 | 1 | 2.1 | 0.84 | 0.85 |
| 13 | 0.125 | 7 | 1.5 | 3.9 | 1.53 | 1.18 |
| 14 | 0.125 | 8 | 1.5 | 2.8 | 1.23 | 1.82 |
| 15 | 0.125 | 5.5 | 2 | 2.2 | 0.94 | 1.45 |
| 16 | 0.125 | 4 | 2.5 | 3.9 | 1.57 | 1.78 |
| 17 | 0.125 | 5.5 | 3 | 3.3 | 1.84 | 2.04 |
| 18 | 0.17 | 7 | 1 | 4.3 | 2.02 | 1.79 |
| 19 | 0.17 | 5.5 | 1.5 | 3.7 | 1.67 | 1.98 |
| 20 | 0.17 | 4 | 2 | 5.2 | 1.69 | 1.87 |
| 21 | 0.17 | 8 | 2 | 3.5 | 1.43 | 0.99 |
| 22 | 0.17 | 3 | 2.5 | 3.7 | 1.76 | 2.39 |
| 23 | 0.17 | 7 | 3 | 5 | 2.24 | 2.36 |
| 24 | 0.25 | 3 | 1 | 4.1 | 1.73 | 2.25 |
| 25 | 0.25 | 5.5 | 1.5 | 6.8 | 2.24 | 2.11 |
| 26 | 0.25 | 7 | 2 | 4.2 | 1.72 | 2.72 |
| 27 | 0.25 | 8 | 2.5 | 6.3 | 2.49 | 2.33 |
| 28 | 0.25 | 4 | 3 | 6.5 | 2.65 | 2.72 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 4.40 | 4 | 1.10 | 8.06 | 0.0003 | significant |
| v-Speed | 0.8022 | 1 | 0.8022 | 5.88 | 0.0236 | \ |
| d-Spacing | 1.68 | 1 | 1.68 | 12.31 | 0.0019 | \ |
| φv | 0.7287 | 1 | 0.7287 | 5.34 | 0.0301 | \ |
| φ2 | 1.38 | 1 | 1.38 | 10.10 | 0.0042 | \ |
| Path | Maximum (cm) | Average (cm) | RMS (cm) |
|---|---|---|---|
| Turn at the starting point | 3.30 | 1.86 | 2.14 |
| Turn at the end point | 2.40 | 1.75 | 1.98 |
| Entry path | 3.30 | 2.04 | 2.27 |
| Exit path | 2.40 | 1.82 | 2.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Zhang, E.; Liu, Y.; Du, J.; Yin, X. ZPTM: Zigzag Path Tracking Method for Agricultural Vehicles Using Point Cloud Representation. Sensors 2025, 25, 1110. https://doi.org/10.3390/s25041110
Yang S, Zhang E, Liu Y, Du J, Yin X. ZPTM: Zigzag Path Tracking Method for Agricultural Vehicles Using Point Cloud Representation. Sensors. 2025; 25(4):1110. https://doi.org/10.3390/s25041110
Chicago/Turabian StyleYang, Shuang, Engen Zhang, Yufei Liu, Juan Du, and Xiang Yin. 2025. "ZPTM: Zigzag Path Tracking Method for Agricultural Vehicles Using Point Cloud Representation" Sensors 25, no. 4: 1110. https://doi.org/10.3390/s25041110
APA StyleYang, S., Zhang, E., Liu, Y., Du, J., & Yin, X. (2025). ZPTM: Zigzag Path Tracking Method for Agricultural Vehicles Using Point Cloud Representation. Sensors, 25(4), 1110. https://doi.org/10.3390/s25041110







