Semi-Supervised Burn Depth Segmentation Network with Contrast Learning and Uncertainty Correction
Abstract
1. Introduction
- (1)
- We introduce two additional decoders based on our previous work LTB-Net [22] to form a three-branch decoder structure. One decoder concatenates features directly to introduce network perturbations, while the other employs feature edge enhancement to introduce feature-level perturbations. Consistency constraints are applied between the probability outputs and soft pseudo-labels generated by these perturbations, significantly improving the model’s robustness.
- (2)
- Based on the multi-branch decoder, we propose a contrastive learning strategy that models features in regions where predictions from the edge enhancement branch diverge from those of other branches. By reducing the discrepancy between predictions in these regions within the feature space, the strategy enhances segmentation performance, particularly in challenging areas such as burn edges.
- (3)
- We developed an uncertainty correction mechanism that calculates the deviation between each branch’s prediction and the mean prediction, determining uncertainty with a single forward pass. This mechanism adaptively weights the consistency loss based on branch uncertainty, reducing the influence of unreliable predictions and better guiding the model’s training process.
- (4)
- We evaluated our model on burn datasets with varying proportions of labeled and unlabeled data, and we compared its performance against several state-of-the-art (SOTA) methods. Experimental results demonstrate that SBCU-Net achieves superior performance in burn depth segmentation, surpassing existing SOTA approaches.
2. Related Works
2.1. Main Models in the Field of Burn Image Segmentation
2.2. Semi-Supervised Learning
3. Materials and Methods
3.1. Preliminaries
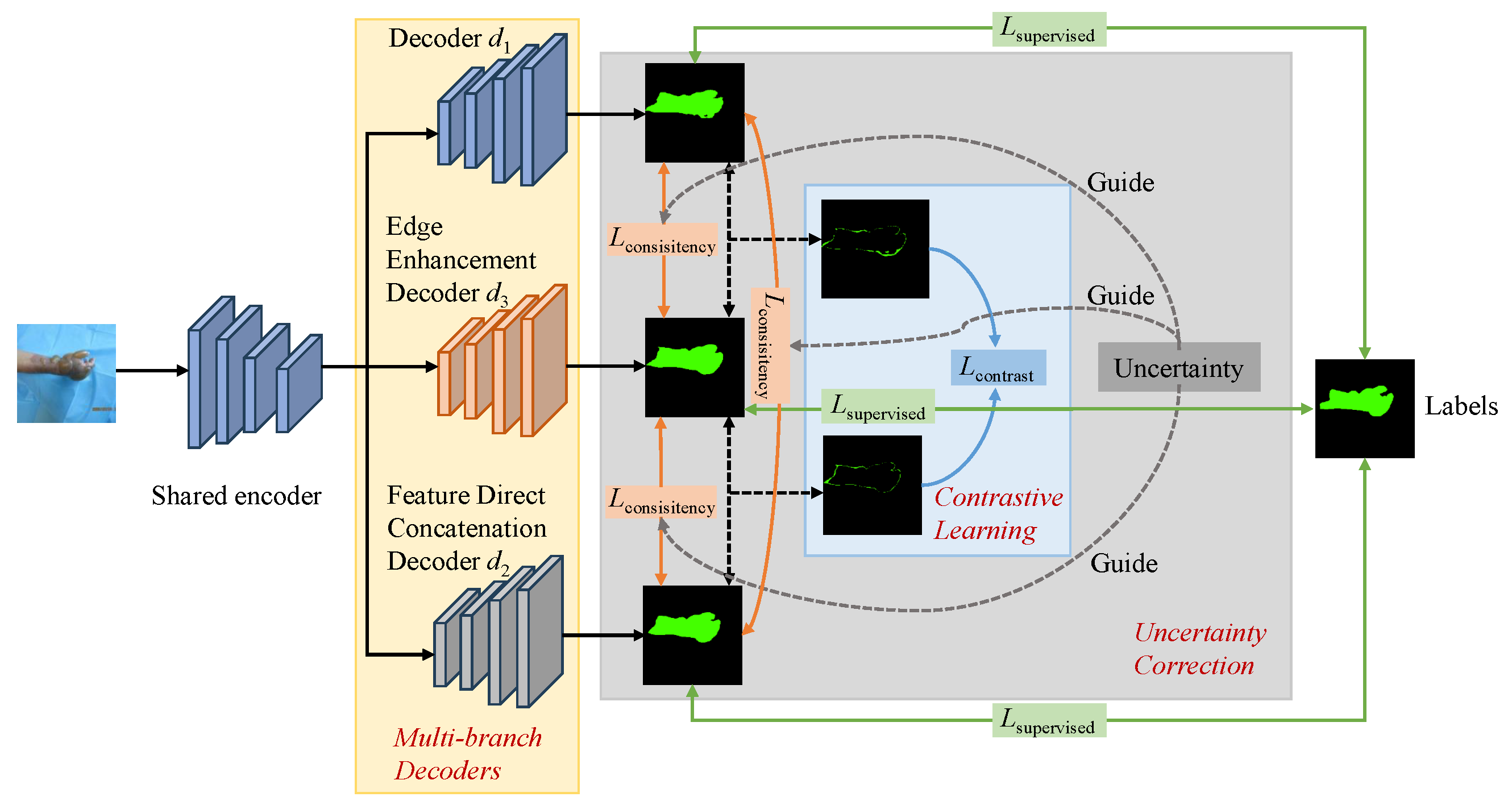
3.2. Framework Overview
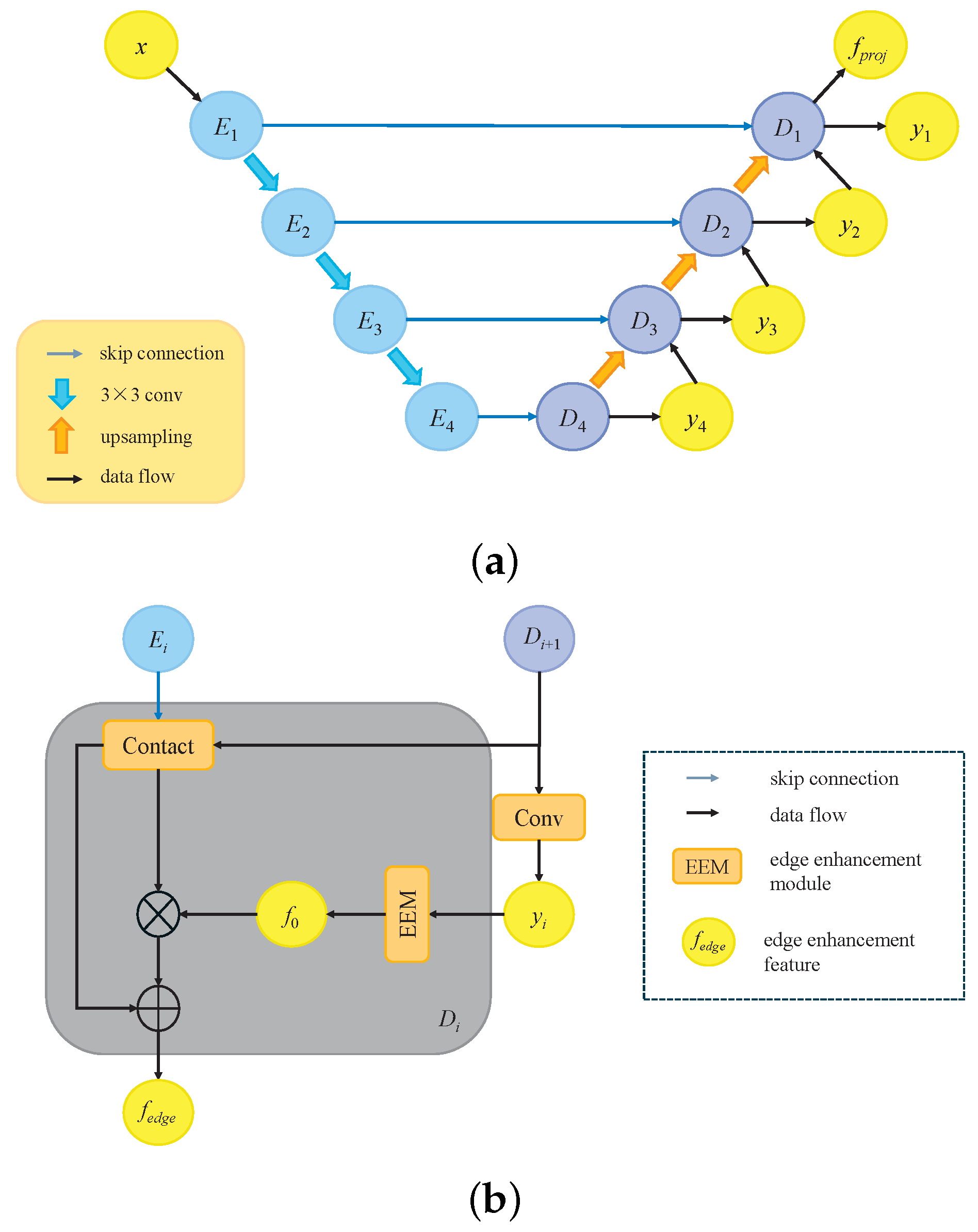
3.3. Multi-Branch Decoders
3.3.1. Feature Direct Concatenation Decoder
3.3.2. Edge Enhancement Decoder
3.4. Contrastive Learning Strategy
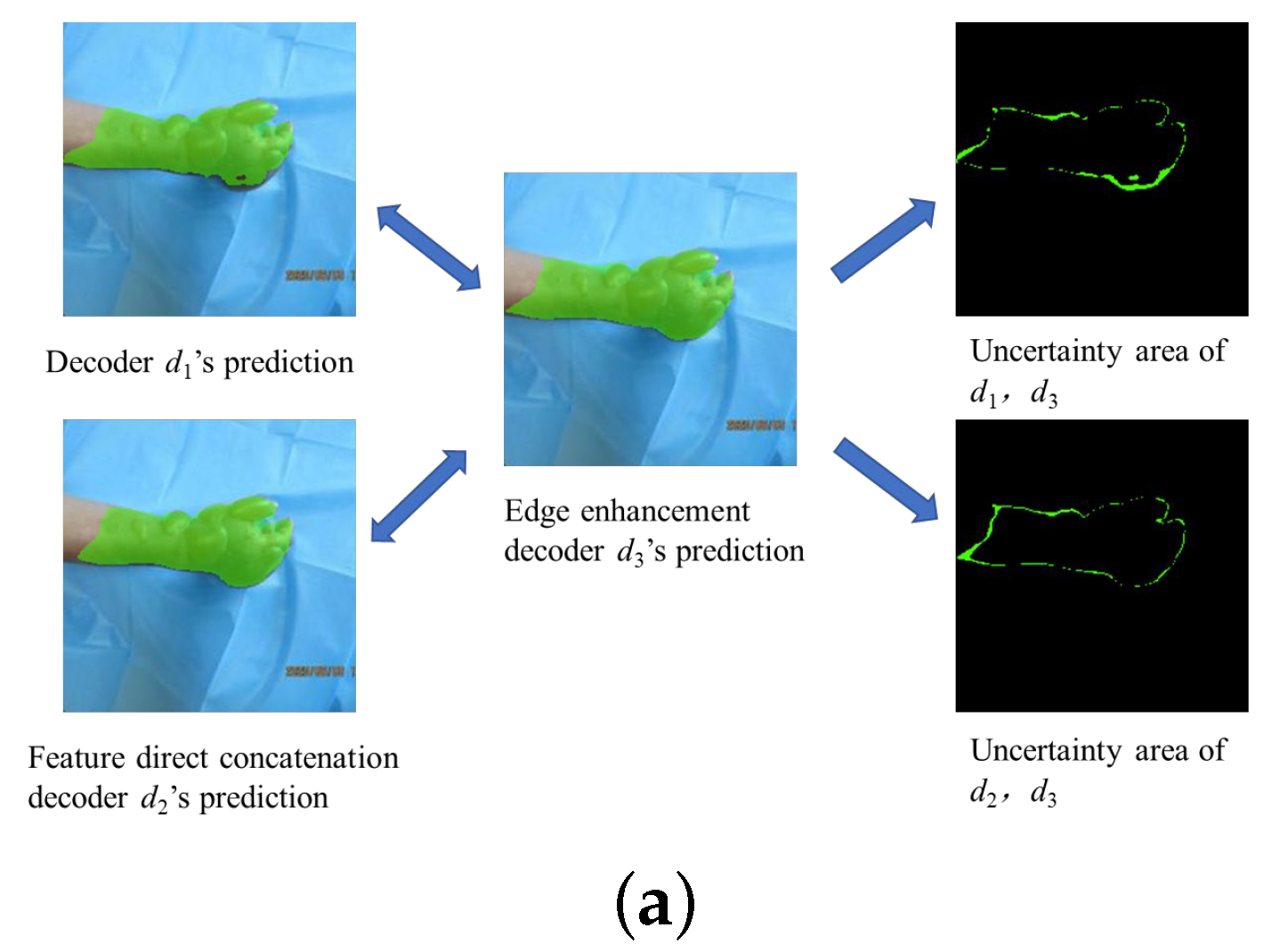
3.5. Uncertainty Correction
3.6. Loss Function
4. Experiments
4.1. Dataset
4.2. Experimental Environment
4.3. Experimental Results Analysis
4.3.1. Comparative Experiments with 50% Labeled Data
4.3.2. Comparative Experiments with 10% Labeled Data
4.4. Ablation Study
4.4.1. Module Ablation Experiment
4.4.2. Ablation Experiment on Decoder Branches
5. Discussion
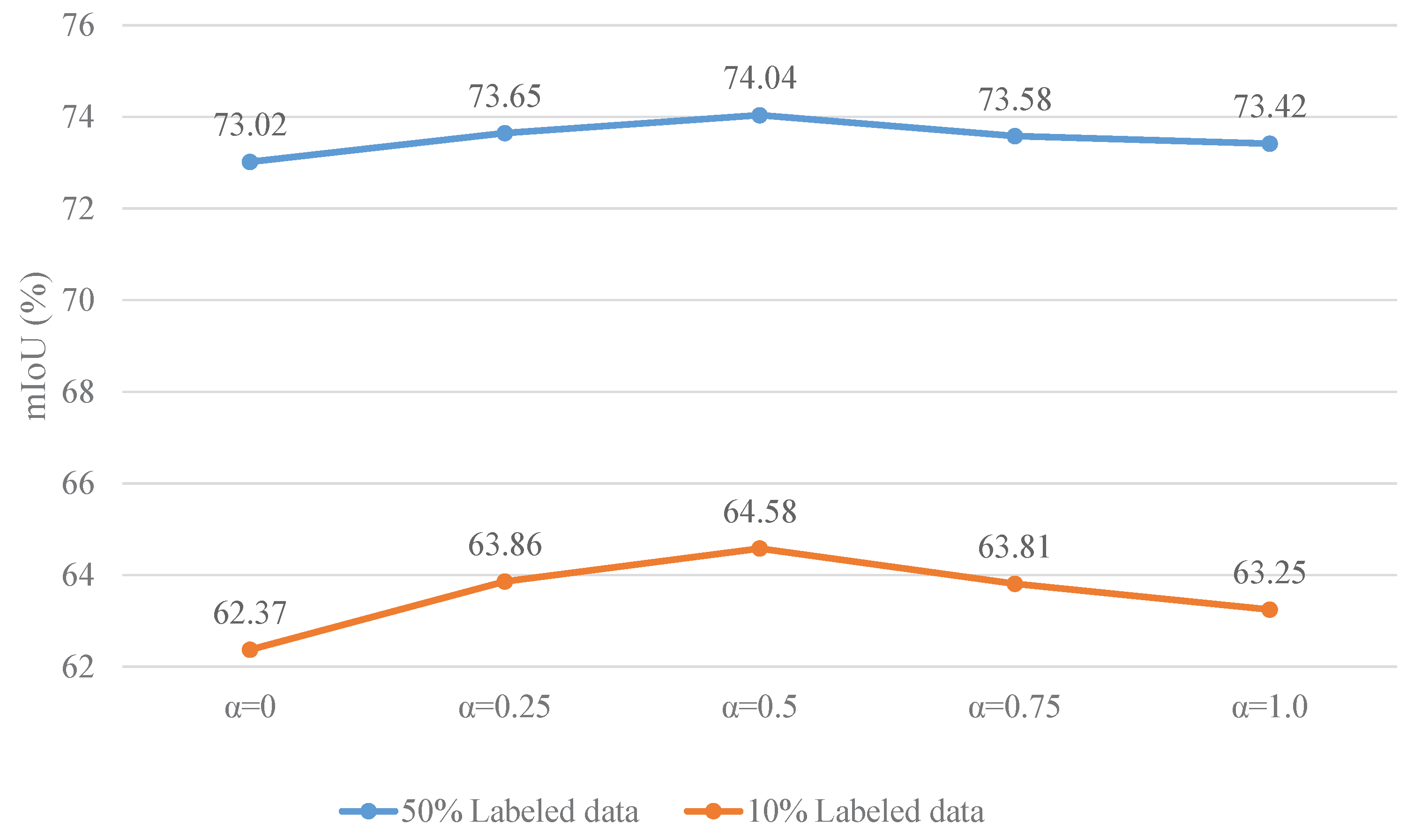
5.1. Effects of Hyperparameter
5.2. Future Works
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jeschke, M.G.; van Baar, M.E.; Choudhry, M.A.; Chung, K.K.; Gibran, N.S.; Logsetty, S. Burn injury. Nat. Rev. Dis. Prim. 2020, 6, 11. [Google Scholar] [CrossRef] [PubMed]
- Greenhalgh, D.G. Sepsis in the burn patient: A different problem than sepsis in the general population. Burns Trauma 2017, 5, 23. [Google Scholar] [CrossRef] [PubMed]
- Parvizi, A.; Haddadi, S.; Atrkar Roshan, Z.; Kafash, P. Haemoglobin changes before and after packed red blood cells transfusion in burn patients: A retrospective cross-sectional study. Int. Wound J. 2023, 20, 2269–2275. [Google Scholar] [CrossRef] [PubMed]
- Zaboli Mahdiabadi, M.; Farhadi, B.; Shahroudi, P.; Shahroudi, P.; Hekmati Pour, N.; Hojjati, H.; Najafi, M.; Farzan, R.; Salehi, R. Prevalence of anxiety and its risk factors in burn patients: A systematic review and meta-analysis. Int. Wound J. 2024, 21, e14705. [Google Scholar] [CrossRef]
- Al-dolaimy, F.; Abdul-Reda Hussein, U.; Hadi Kzar, M.; Saud, A.; Abed Jawad, M.; Yaseen Hasan, S.; Alhassan, M.S.; Hussien Alawadi, A.; Alsaalamy, A.; Farzan, R. Relationship between body mass index and mortality of burns patients: A systematic review and meta-analysis. Int. Wound J. 2024, 21, e14358. [Google Scholar] [CrossRef]
- Miri, S.; Hosseini, S.J.; Ghorbani Vajargah, P.; Firooz, M.; Takasi, P.; Mollaei, A.; Ramezani, S.; Tolouei, M.; Emami Zeydi, A.; Osuji, J.; et al. Effects of massage therapy on pain and anxiety intensity in patients with burns: A systematic review and meta-analysis. Int. Wound J. 2023, 20, 2440–2458. [Google Scholar] [CrossRef]
- Resch, T.R.; Drake, R.M.; Helmer, S.D.; Jost, G.D.; Osland, J.S. Estimation of burn depth at burn centers in the United States: A survey. J. Burn. Care Res. 2014, 35, 491–497. [Google Scholar] [CrossRef]
- Watts, A.; Tyler, M.; Perry, M.; Roberts, A.; McGrouther, D. Burn depth and its histological measurement. Burns 2001, 27, 154–160. [Google Scholar] [CrossRef]
- Shin, J.Y.; Yi, H.S. Diagnostic accuracy of laser Doppler imaging in burn depth assessment: Systematic review and meta-analysis. Burns 2016, 42, 1369–1376. [Google Scholar] [CrossRef]
- Medina-Preciado, J.D.; Kolosovas-Machuca, E.S.; Velez-Gomez, E.; Miranda-Altamirano, A.; González, F.J. Noninvasive determination of burn depth in children by digital infrared thermal imaging. J. Biomed. Opt. 2013, 18, 061204. [Google Scholar] [CrossRef]
- Li, H.; Bu, Q.; Shi, X.; Xu, X.; Li, J. Non-invasive medical imaging technology for the diagnosis of burn depth. Int. Wound J. 2024, 21, e14681. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.W.; Ho, C.Y.; Lai, F.; Christian, M.; Huang, S.C.; Chang, D.H.; Chen, Y.S. Application of multiple deep learning models for automatic burn wound assessment. Burns 2023, 49, 1039–1051. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; proceedings, part III 18. Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Liu, H.; Yue, K.; Cheng, S.; Li, W.; Fu, Z. A framework for automatic burn image segmentation and burn depth diagnosis using deep learning. Comput. Math. Methods Med. 2021, 2021, 5514224. [Google Scholar] [CrossRef] [PubMed]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep high-resolution representation learning for human pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5693–5703. [Google Scholar]
- Tarvainen, A.; Valpola, H. Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results. In Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 1195–1204. [Google Scholar]
- Wu, Y.; Xu, M.; Ge, Z.; Cai, J.; Zhang, L. Semi-supervised left atrium segmentation with mutual consistency training. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Strasbourg, France, 27 September–1 October 2021; proceedings, part II 24. Springer: Berlin/Heidelberg, Germany, 2021; pp. 297–306. [Google Scholar]
- Yu, L.; Wang, S.; Li, X.; Fu, C.W.; Heng, P.A. Uncertainty-aware self-ensembling model for semi-supervised 3D left atrium segmentation. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2019: 22nd International Conference, Shenzhen, China, 13–17 October 2019; proceedings, part II 22. Springer: Berlin/Heidelberg, Germany, 2019; pp. 605–613. [Google Scholar]
- Xie, J.; Li, H.; Li, J.; Xu, X. LTB-Net: A Lightweight Transformer-based Burn Depth Segmentation Network. In Proceedings of the BIBE 2024; The 7th International Conference on Biological Information and Biomedical Engineering, Hohhot, China, 13–15 August 2024; pp. 234–239. [Google Scholar]
- Zunair, H.; Hamza, A.B. Sharp U-Net: Depthwise convolutional network for biomedical image segmentation. Comput. Biol. Med. 2021, 136, 104699. [Google Scholar] [CrossRef]
- Liang, J.; Li, R.; Wang, C.; Zhang, R.; Yue, K.; Li, W.; Li, Y. A spiking neural network based on retinal ganglion cells for automatic burn image segmentation. Entropy 2022, 24, 1526. [Google Scholar] [CrossRef]
- Chauhan, J.; Goyal, P. Convolution neural network for effective burn region segmentation of color images. Burns 2021, 47, 854–862. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Vaswani, A. Attention is all you need. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2017; pp. 5998–6008. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 213–229. [Google Scholar]
- Alexey, D. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Zheng, S.; Lu, J.; Zhao, H.; Zhu, X.; Luo, Z.; Wang, Y.; Fu, Y.; Feng, J.; Xiang, T.; Torr, P.H.; et al. Rethinking semantic segmentation from a sequence-to-sequence perspective with transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 6881–6890. [Google Scholar]
- Chen, J.; Lu, Y.; Yu, Q.; Luo, X.; Adeli, E.; Wang, Y.; Lu, L.; Yuille, A.L.; Zhou, Y. Transunet: Transformers make strong encoders for medical image segmentation. arXiv 2021, arXiv:2102.04306. [Google Scholar]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-unet: Unet-like pure transformer for medical image segmentation. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 205–218. [Google Scholar]
- Wang, J.; Wei, L.; Wang, L.; Zhou, Q.; Zhu, L.; Qin, J. Boundary-aware transformers for skin lesion segmentation. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Strasbourg, France, 27 September–1 October 2021; Proceedings, Part I 24; Springer: Berlin/Heidelberg, Germany, 2021; pp. 206–216. [Google Scholar]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7794–7803. [Google Scholar]
- Xu, X.; Bu, Q.; Xie, J.; Li, H.; Xu, F.; Li, J. On-site burn severity assessment using smartphone-captured color burn wound images. Comput. Biol. Med. 2024, 182, 109171. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, H.; Hu, Q. Transfuse: Fusing transformers and cnns for medical image segmentation. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Strasbourg, France, 27 September–1 October 2021; proceedings, Part I 24; Springer: Berlin/Heidelberg, Germany, 2021; pp. 14–24. [Google Scholar]
- Wu, H.; Chen, S.; Chen, G.; Wang, W.; Lei, B.; Wen, Z. FAT-Net: Feature adaptive transformers for automated skin lesion segmentation. Med. Image Anal. 2022, 76, 102327. [Google Scholar] [CrossRef]
- Nie, D.; Gao, Y.; Wang, L.; Shen, D. ASDNet: Attention based semi-supervised deep networks for medical image segmentation. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2018: 21st International Conference, Granada, Spain, 16–20 September 2018; Proceedings, Part IV 11; Springer: Berlin/Heidelberg, Germany, 2018; pp. 370–378. [Google Scholar]
- Tang, Y.; Wang, S.; Qu, Y.; Cui, Z.; Zhang, W. Consistency and adversarial semi-supervised learning for medical image segmentation. Comput. Biol. Med. 2023, 161, 107018. [Google Scholar] [CrossRef] [PubMed]
- Bai, W.; Oktay, O.; Sinclair, M.; Suzuki, H.; Rajchl, M.; Tarroni, G.; Glocker, B.; King, A.; Matthews, P.M.; Rueckert, D. Semi-supervised learning for network-based cardiac MR image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention- MICCAI 2017: 20th International Conference, Quebec City, QC, Canada, 11–13 September 2017; Proceedings, Part II 20; Springer: Berlin/Heidelberg, Germany, 2017; pp. 253–260. [Google Scholar]
- Peng, J.; Estrada, G.; Pedersoli, M.; Desrosiers, C. Deep co-training for semi-supervised image segmentation. Pattern Recognit. 2020, 107, 107269. [Google Scholar] [CrossRef]
- Wu, Y.; Ge, Z.; Zhang, D.; Xu, M.; Zhang, L.; Xia, Y.; Cai, J. Mutual consistency learning for semi-supervised medical image segmentation. Med. Image Anal. 2022, 81, 102530. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Wu, Z.; Wu, Q.; Ge, Z.; Cai, J. Exploring smoothness and class-separation for semi-supervised medical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Singapore, 18-22 September 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 34–43. [Google Scholar]
- Zhong, Y.; Yuan, B.; Wu, H.; Yuan, Z.; Peng, J.; Wang, Y.X. Pixel contrastive-consistent semi-supervised semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 7273–7282. [Google Scholar]
- Zhao, X.; Fang, C.; Fan, D.J.; Lin, X.; Gao, F.; Li, G. Cross-level contrastive learning and consistency constraint for semi-supervised medical image segmentation. In Proceedings of the 2022 IEEE 19th International Symposium on Biomedical Imaging (ISBI), Kolkata, India, 28–31 March 2022; pp. 1–5. [Google Scholar]
- Alonso, I.; Sabater, A.; Ferstl, D.; Montesano, L.; Murillo, A.C. Semi-supervised semantic segmentation with pixel-level contrastive learning from a class-wise memory bank. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 8219–8228. [Google Scholar]
- Lai, X.; Tian, Z.; Jiang, L.; Liu, S.; Zhao, H.; Wang, L.; Jia, J. Semi-supervised semantic segmentation with directional context-aware consistency. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 1205–1214. [Google Scholar]
- Zheng, Z.; Yang, Y. Rectifying pseudo label learning via uncertainty estimation for domain adaptive semantic segmentation. Int. J. Comput. Vis. 2021, 129, 1106–1120. [Google Scholar] [CrossRef]
- Lee, D.H. Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks. In Proceedings of the Workshop on Challenges in Representation Learning, ICML, Daegu, Republic of Korea, 3–7 November 2013; Volume 3, p. 896. [Google Scholar]
- Xie, Q.; Dai, Z.; Hovy, E.; Luong, T.; Le, Q. Unsupervised data augmentation for consistency training. Adv. Neural Inf. Process. Syst. 2020, 33, 6256–6268. [Google Scholar]
- Cao, X.; Chen, H.; Li, Y.; Peng, Y.; Wang, S.; Cheng, L. Uncertainty aware temporal-ensembling model for semi-supervised abus mass segmentation. IEEE Trans. Med. Imaging 2020, 40, 431–443. [Google Scholar] [CrossRef]
- Jiao, C.; Su, K.; Xie, W.; Ye, Z. Burn image segmentation based on Mask Regions with Convolutional Neural Network deep learning framework: More accurate and more convenient. Burns Trauma 2019, 7, 1–14. [Google Scholar] [CrossRef]
- Rahman, S.; Faezipour, M.; Ribeiro, G.A.; Ridelman, E.; Klein, J.D.; Angst, B.A.; Shanti, C.M.; Rastgaar, M. Inflammation assessment of burn wound with deep learning. In Proceedings of the 2022 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 14–16 December 2022; pp. 1792–1795. [Google Scholar]
- Torralba, A.; Russell, B.C.; Yuen, J. Labelme: Online image annotation and applications. Proc. IEEE 2010, 98, 1467–1484. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Li, J.; Socher, R.; Hoi, S.C. Dividemix: Learning with noisy labels as semi-supervised learning. arXiv 2020, arXiv:2002.07394. [Google Scholar]





| Method | PA | mIoU | DC | 95HD | DC (ST) | DC (DT) | DC (FT) |
|---|---|---|---|---|---|---|---|
| LTB-Net [22] | 93.98 | 68.60 | 79.84 | 12.34 | 78.25 | 83.28 | 61.16 |
| MT [19] | 93.48 | 70.27 | 81.64 | 11.58 | 70.17 | 80.78 | 77.94 |
| UA-MT [21] | 93.96 | 71.61 | 82.68 | 10.26 | 74.42 | 83.59 | 75.16 |
| MC-Net [20] | 93.97 | 70.98 | 82.16 | 12.15 | 74.37 | 83.60 | 72.99 |
| MC-Net++ [42] | 93.80 | 72.32 | 83.24 | 10.67 | 74.76 | 82.63 | 77.95 |
| SS-Net [43] | 93.25 | 72.16 | 83.14 | 8.32 | 73.42 | 80.33 | 81.57 |
| SBCU-Net | 94.32 | 74.04 | 84.51 | 7.17 | 78.68 | 83.03 | 78.59 |
| Method | PA | mIoU | DC | 95HD | DC (ST) | DC (DT) | DC (FT) |
|---|---|---|---|---|---|---|---|
| LTB-Net [22] | 90.16 | 58.08 | 71.35 | 23.74 | 63.02 | 73.67 | 52.78 |
| MT [19] | 90.72 | 59.55 | 72.67 | 20.51 | 64.38 | 75.13 | 54.94 |
| UA-MT [21] | 91.04 | 60.23 | 73.35 | 19.68 | 62.16 | 74.46 | 60.09 |
| MC-Net [20] | 90.18 | 60.48 | 73.66 | 21.54 | 58.22 | 74.74 | 65.70 |
| MC-Net++ [42] | 91.10 | 62.35 | 75.28 | 20.61 | 60.60 | 76.53 | 67.83 |
| SS-Net [43] | 90.21 | 61.02 | 74.00 | 15.32 | 53.79 | 74.77 | 71.91 |
| SBCU-Net | 92.10 | 64.58 | 76.95 | 15.18 | 72.54 | 80.17 | 58.73 |
| Baseline Method | Feature Direct Concatenation Decoder | Edge Enhancement Decoder | Contrastive Learning | Uncertainty Correction | PA | mIoU | DC | 95HD |
|---|---|---|---|---|---|---|---|---|
| ✔ | 93.97 | 70.98 | 82.16 | 12.15 | ||||
| ✔ | 93.81 | 71.82 | 82.87 | 11.98 | ||||
| ✔ | ✔ | 94.02 | 72.86 | 83.64 | 10.24 | |||
| ✔ | ✔ | ✔ | 94.25 | 73.63 | 84.19 | 7.86 | ||
| ✔ | ✔ | ✔ | ✔ | 94.32 | 74.04 | 84.51 | 7.17 |
| Baseline Method | Feature Direct Concatenation Decoder | Edge Enhancement Decoder | Contrastive Learning | Uncertainty Correction | PA | mIoU | DC | 95HD |
|---|---|---|---|---|---|---|---|---|
| ✔ | 90.18 | 60.48 | 73.66 | 21.54 | ||||
| ✔ | 90.72 | 61.50 | 74.42 | 21.17 | ||||
| ✔ | ✔ | 90.85 | 62.48 | 75.43 | 19.36 | |||
| ✔ | ✔ | ✔ | 91.57 | 63.12 | 75.89 | 17.19 | ||
| ✔ | ✔ | ✔ | ✔ | 92.10 | 64.58 | 76.95 | 15.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Xie, J. Semi-Supervised Burn Depth Segmentation Network with Contrast Learning and Uncertainty Correction. Sensors 2025, 25, 1059. https://doi.org/10.3390/s25041059
Zhang D, Xie J. Semi-Supervised Burn Depth Segmentation Network with Contrast Learning and Uncertainty Correction. Sensors. 2025; 25(4):1059. https://doi.org/10.3390/s25041059
Chicago/Turabian StyleZhang, Dongxue, and Jingmeng Xie. 2025. "Semi-Supervised Burn Depth Segmentation Network with Contrast Learning and Uncertainty Correction" Sensors 25, no. 4: 1059. https://doi.org/10.3390/s25041059
APA StyleZhang, D., & Xie, J. (2025). Semi-Supervised Burn Depth Segmentation Network with Contrast Learning and Uncertainty Correction. Sensors, 25(4), 1059. https://doi.org/10.3390/s25041059





