Strain Decay Monitoring and Analytical Prediction of RC Columns Using Brillouin Optical Technology and Time-Dependent Deterioration Factor
Abstract
1. Introduction
2. Experimental Program
2.1. Design of Column Specimens
- t = 28 days testing: establishes baseline performance, capturing initial strength and stiffness of RC columns under early-age concrete conditions.
- t = 360 days testing: evaluates intermediate effects of aging, highlighting the influence of creep and shrinkage on strain distribution and structural response.
- t = 720 days testing: assesses long-term performance, validating the “time-dependent deterioration factor” by capturing significant strain reduction and material degradation.
2.2. Materials Used
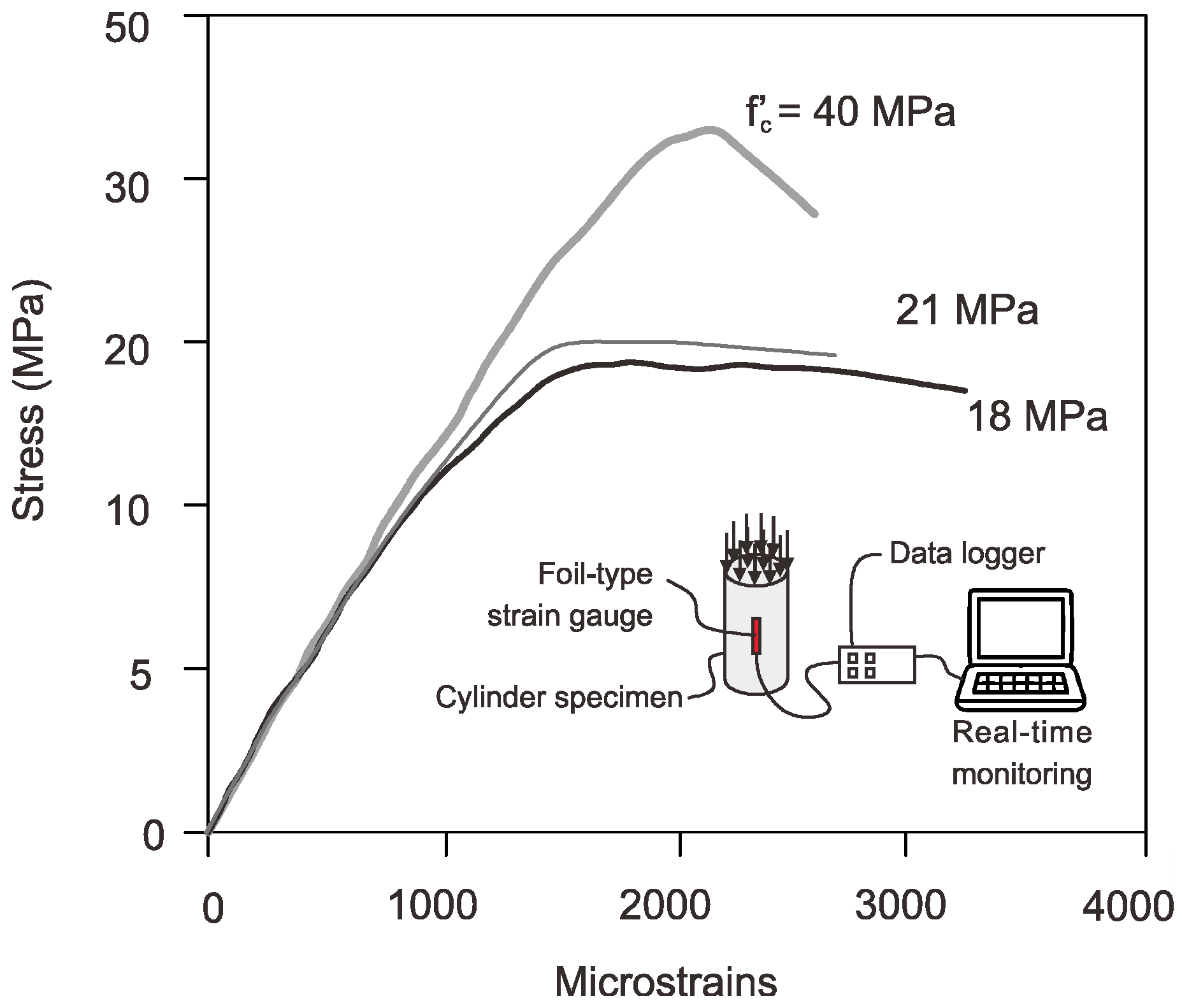
2.2.1. Concrete
2.2.2. Reinforcement Bars
2.3. Test Setup and Instrumentation
2.3.1. Loading Arrangement and Procedure
2.3.2. Deflection Measurement
2.3.3. Strain Measurement and Installation
3. Results and Discussion
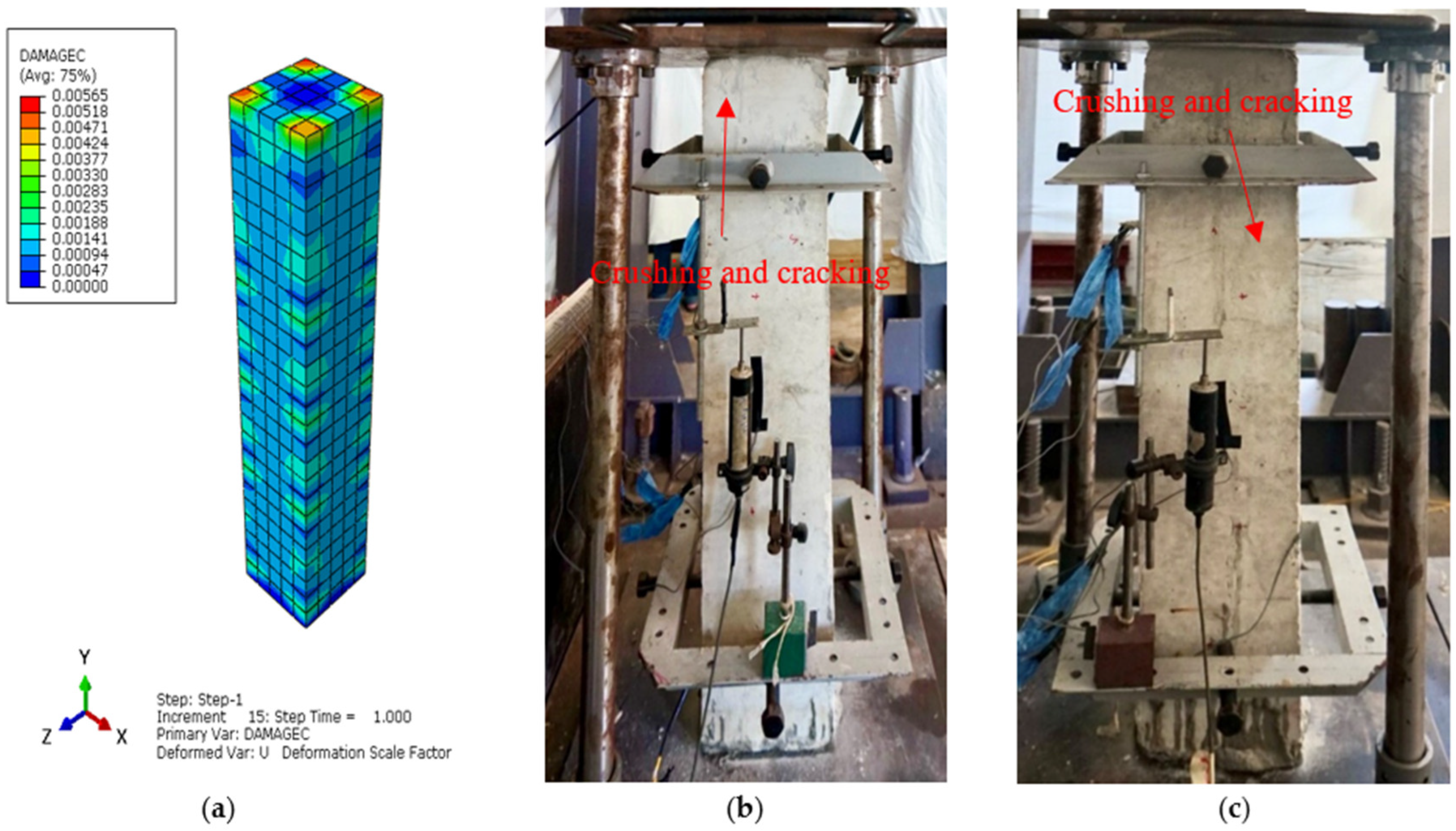
3.1. Ultimate Capacity and Failure Behaviors
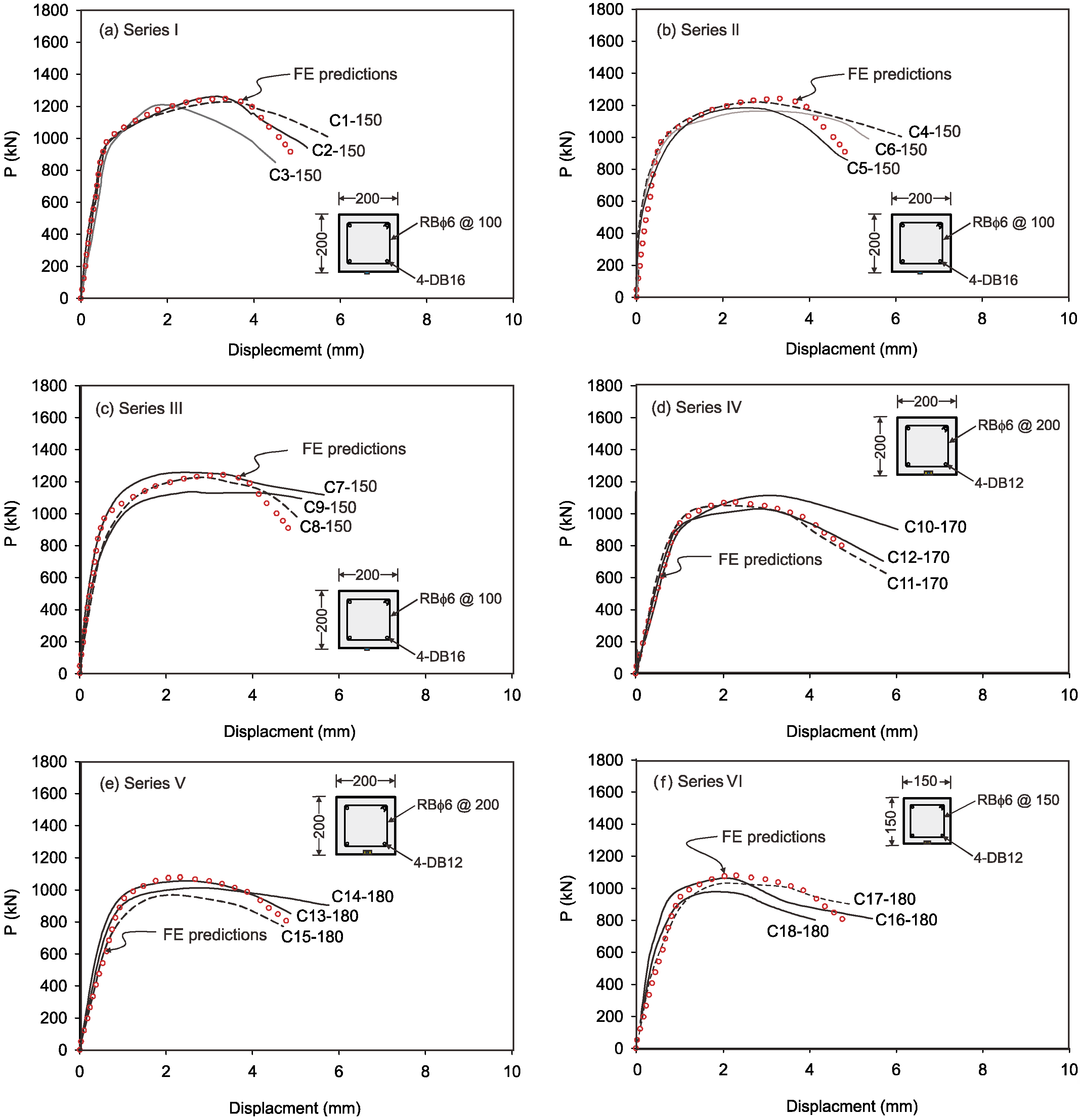
3.2. Load vs. Displacement Curves
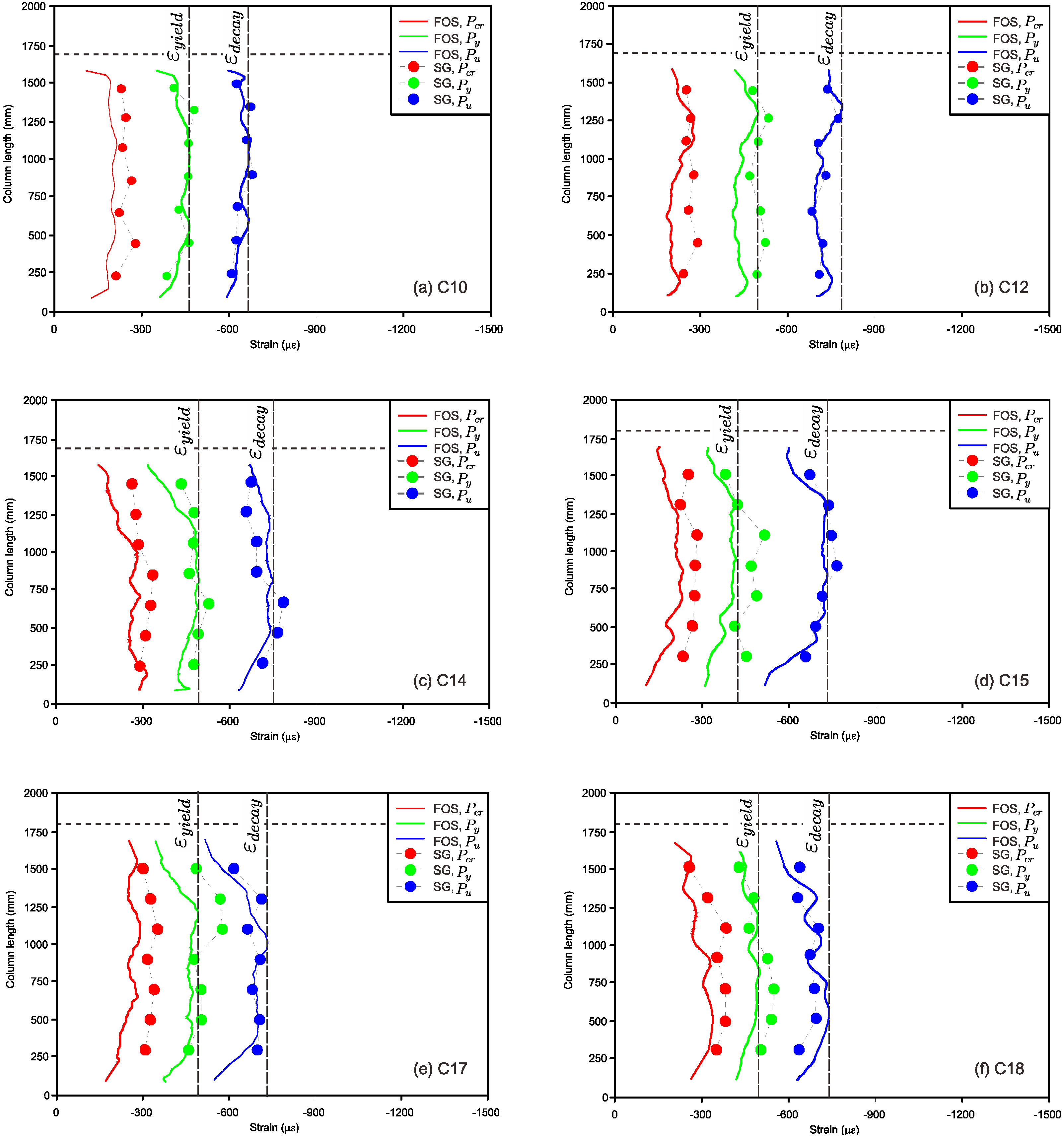
3.3. Strain Measurement from BOTDA FOS and Strain Gauge
4. Numerical Study
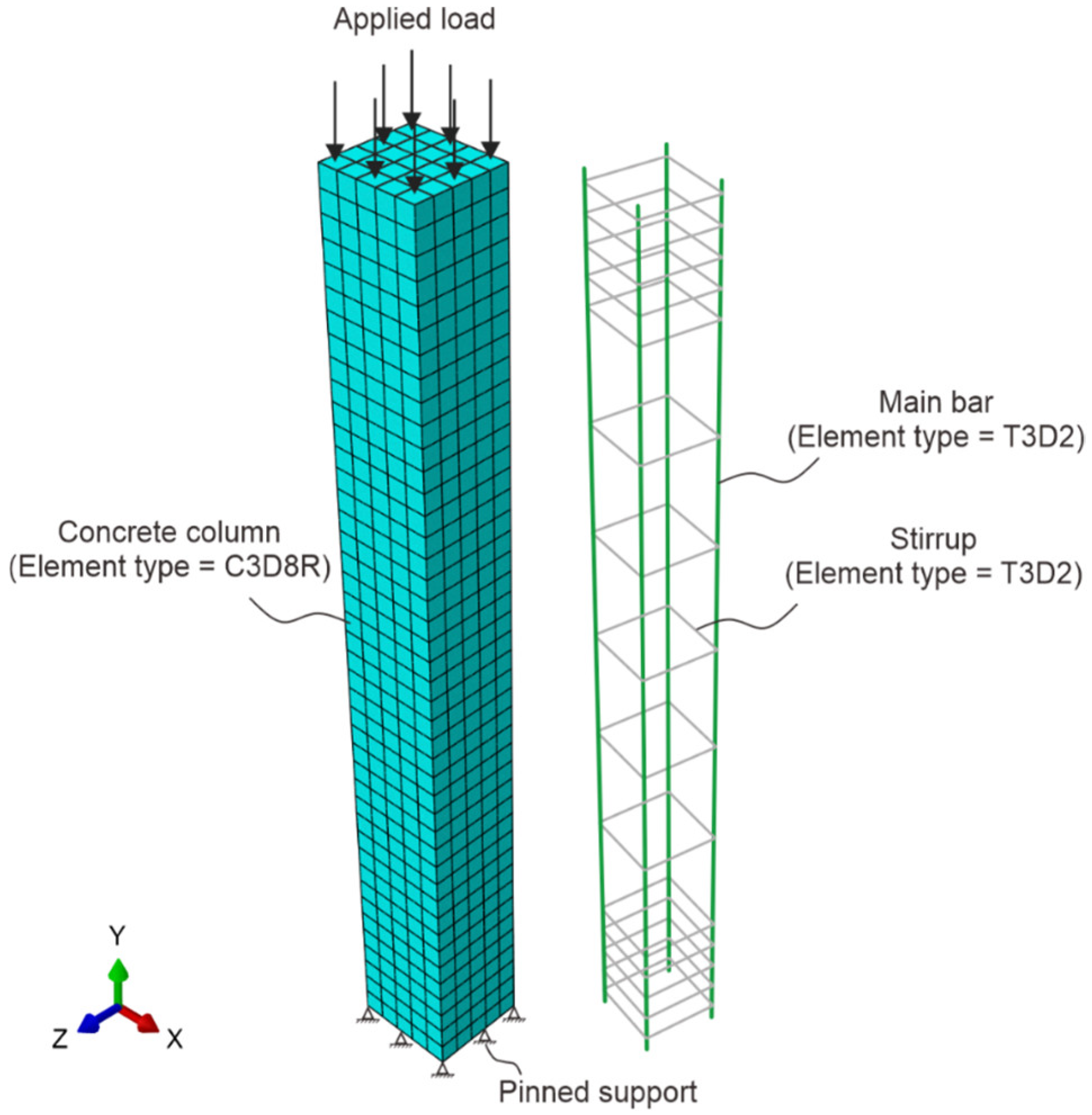
4.1. Geometry, FE Model and Boundary Conditions
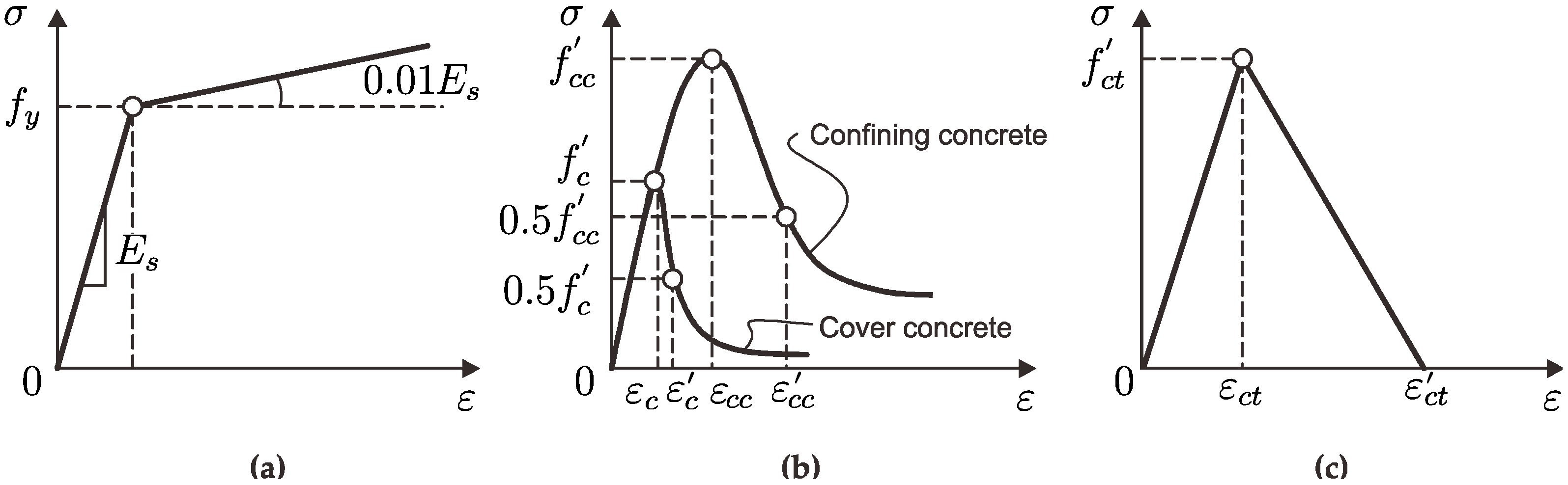
4.2. Concrete Damage Plascticity Model and Applied Loading
4.3. Comparison of the FE Predictions and Experimental Results
5. Modified ACI and Eurocode Equations for Predicting Column Strength
5.1. ACI 318 Equation
5.2. Eurocode 2 Equation
5.3. Proposed Modifications to the ACI and Eurocode 2 Equations
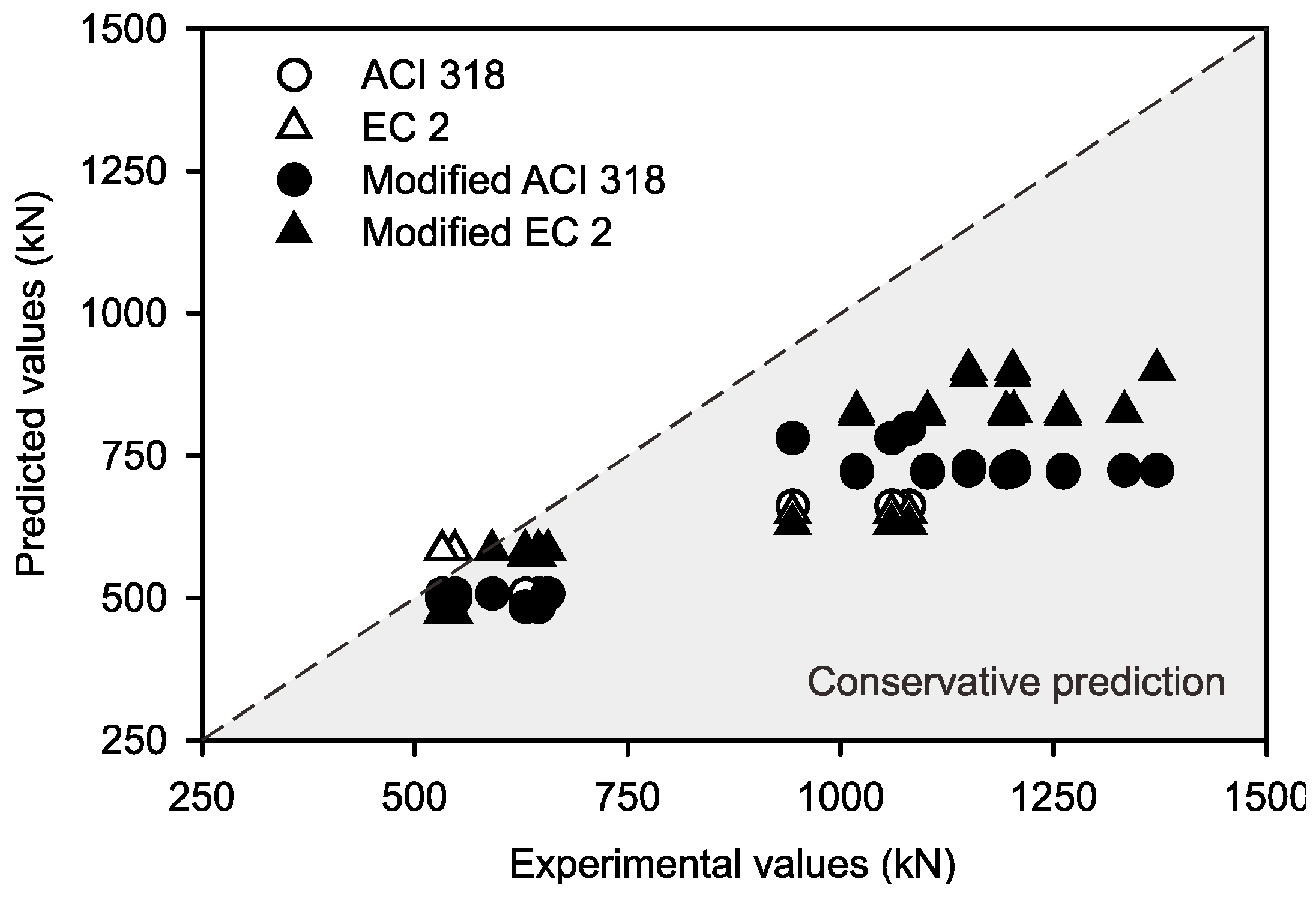
5.4. Comparison of the Modified Code Equations and Experimental Values
6. Summary and Conclusions
- From the experimental investigations, the load values at the cracking, yield, and ultimate points decreased with the increase in the number of days for all series of all columns, which implied that the deformation plays a vital role over time in terms of environmental, creep, shrinkage, and microcrack factors.
- This experimental study evaluated the strain’s variational behavior through the conventional strain gauges and BOTDA FOS, which can be used for evaluation of the strain decay factor to improve the service life predictions of RC columns.
- Finite element analyses (Abaqus) were performed to predict the experimental column damage using the CDP model, which also proves that the experimental and validation values were in good agreement.
- ηdecay was introduced into model strain reduction from creep and shrinkage, enhancing prediction accuracy by 3% for long-term performance.
- The ultimate load values were also predicted for all the tested columns through the ACI 318 and Eurocode 2 guidelines to ensure that the experimental values conservatively predicted values for specimens tested at t = 720 days.
- Findings were validated through experiments and simulations, ensuring 5% improvements in reliability for durable and sustainable existing low-strength RC columns.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Zhou, X.Q.; Huang, B.G.; Wang, X.Y.; Xia, Y. Deep learning-based rapid damage assessment of RC columns under blast loading. Eng. Struct. 2022, 271, 114949. [Google Scholar] [CrossRef]
- Lee, D.H.; Lee, J.H.; Kim, D.J.; Kim, J. Experimental evaluation on the seismic performance of reinforced concrete bridge columns with high strength reinforcement. Struct. Infrastruct. Eng. 2022, 18, 1365–1375. [Google Scholar] [CrossRef]
- Gupta, P.; Gupta, C. Seismic performance evaluation of reinforced concrete flat slab buildings using ETABS. Asian J. Civ. Eng. 2024, 18, 4995–5007. [Google Scholar] [CrossRef]
- Patel, P.V.; Joshi, D.D.; Makawana, R.V. Experimental assessment of stainless-steel wire mesh (SSWM) strengthened wet precast beam-column connections. Results Eng. 2024, 22, 102325. [Google Scholar] [CrossRef]
- Yuan, F.; Wu, Y.F.; Zhao, X.Y. Effect of internal stirrups on the eccentric compression behavior of FRP-confined RC columns based on finite-element analysis. J. Compos. Constr. 2022, 26, 04021069. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, L.; Elchalakani, M.; Cai, J. Cyclic loading test for reinforced concrete columns strengthened with high-strength engineered cementitious composite jacket. Eng. Struct. 2023, 278, 115571. [Google Scholar] [CrossRef]
- Tiwary, A.K.; Singh, S.; Chohan, J.S.; Kumar, R.; Sharma, S.; Chattopadhyaya, S.; Abed, F.; Stepinac, M. Behavior of RC beam–column joints strengthened with modified reinforcement techniques. Sustainability 2022, 14, 1918. [Google Scholar] [CrossRef]
- Chen, R.P.; Ma, Q.L.; Zhang, Y.; Wu, H.N.; Liu, Y.; Lu, L. Experimental study on the mechanical behaviour of eccentric compression short column strengthened by ultra-high-performance fibre-reinforced concrete. Structures 2021, 33, 508–522. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Z.; Li, Y.; Zhu, W.; Zheng, H.; Zheng, S. Exploring the shear performance and predictive shear capacity of corroded RC columns utilizing the modified compression-field theory: An investigative study. Eng. Struct. 2024, 302, 117390. [Google Scholar] [CrossRef]
- Bado, M.F.; Casas, J.R. A review of recent distributed optical fiber sensors applications for civil engineering structural health monitoring. Sensors 2021, 21, 1818. [Google Scholar] [CrossRef]
- Liu, Y.; Li, W.; He, J.; Liu, S.; Cai, L.; Cheng, G. Application of Brillouin optical time domain reflectometry to dynamic monitoring of overburden deformation and failure caused by underground mining. Int. J. Rock Mech. Min. Sci. 2018, 106, 133–143. [Google Scholar] [CrossRef]
- Mohamad, H.; Kueh, A.B.; Rashid, A.S. Distributed optical-fibre strain sensing in reinforced concrete structures. J. Teknol. 2015, 74, 93–97. [Google Scholar] [CrossRef][Green Version]
- Wu, J.; Liu, H.; Yang, P.; Tang, B.; Wei, G. Quantitative strain measurement and crack opening estimate in concrete structures based on OFDR technology. Opt. Fiber Technol. 2020, 60, 102354. [Google Scholar] [CrossRef]
- Bao, Y.; Hoehler, M.S.; Smith, C.M.; Bundy, M.; Chen, G. Measuring three-dimensional temperature distributions in steel–concrete composite slabs subjected to fire using distributed fiber optic sensors. Sensors 2020, 20, 5518. [Google Scholar] [CrossRef]
- Bao, Y.; Chen, G. High-temperature measurement with Brillouin optical time domain analysis of an annealed fused-silica single-mode fiber. Opt. Lett. 2016, 41, 3177–3180. Available online: https://opg.optica.org/ol/abstract.cfm?URI=ol-41-14-3177 (accessed on 30 January 2024). [CrossRef]
- Bao, Y.; Chen, Y.; Hoehler, M.S.; Smith, C.M.; Bundy, M.; Chen, G. Experimental analysis of steel beams subjected to fire enhanced by Brillouin scattering-based fiber optic sensor data. J. Struct. Eng. 2017, 143, 04016143. [Google Scholar] [CrossRef]
- Baoa, Y.; Hoehlerb, M.S.; Smithb, C.M.; Bundyb, M.; Chena, G. Temperature Measurement and Damage Detection in Concrete Beams Exposed to Fire Using PPP-BOTDA Based Fiber Optic Sensors. Smart Mater. Struct. 2017, 26, 105034. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, S.; Coulibaly, A.A.; Cheng, J.; DeJong, M.J. Monitoring reinforced concrete cracking behavior under uniaxial tension using distributed fiber-optic sensing technology. J. Struct. Eng. 2021, 147, 04021212. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, Y.; Li, D.; Zhang, J. Two-step detection of concrete internal condition using array ultrasound and deep learning. NDT E Int. 2023, 139, 102945. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, C.; Xie, X.; Yousefi, A.M.; Zhang, G.; Li, J.; Samali, B. Compressive strength evaluation of cement-based materials in sulphate environment using optimized deep learning technology. Dev. Built Environ. 2023, 16, 100298. [Google Scholar] [CrossRef]
- Guo, J.; Liu, P.; Xiao, B.; Deng, L.; Wang, Q.; 2024. Surface defect detection of civil structures using images: Review from data perspective. Autom. Constr. 2023, 158, 105186. [Google Scholar] [CrossRef]
- ACI 318-19; Building Code Requirements for Structural Concrete. American Concrete Institute: Farmington Hills, MI, USA, 2022.
- Eurocode 2-2004; European Standard Code for Design of Concrete Structures—General Rules and Rules for Buildings. Management Centre: Brussels, Belgium, 2004.
- ACI PRC-211.1-91; Standard Practice for Selecting Proportions for Normal, Heavyweight, and Mass Concrete. ACI Committee 211: Farmington Hills, MI, USA, 1991.
- Imjai, T.; Aosai, P.; Garcia, R.; Raman, S.N.; Chaudhary, S. Deflections of high-content recycled aggregate concrete beams reinforced with GFRP bars and steel fibres. Eng. Struct. 2024, 312, 118247. [Google Scholar] [CrossRef]
- Henault, J.M.; Quiertant, M.; Delepine-Lesoille, S.; Salin, J.; Moreau, G.; Taillade, F.; Benzarti, K. Quantitative strain measurement and crack detection in RC structures using a truly distributed fiber optic sensing system. Constr. Build. Mater. 2012, 37, 916–923. [Google Scholar] [CrossRef]
- Mehdi Mirzazadeh, M.; Green, M.F. Fiber optic sensors and digital image correlation for measuring deformations in reinforced concrete beams. J. Bridge Eng. 2018, 23, 04017144. [Google Scholar] [CrossRef]
- Fernandez, I.; Berrocal, C.G.; Rempling, R. Long-term performance of distributed optical fiber sensors embedded in reinforced concrete beams under sustained deflection and cyclic loading. Sensors 2021, 21, 6338. [Google Scholar] [CrossRef]
- Kaklauskas, G.; Sokolov, A.; Ramanauskas, R.; Jakubovskis, R. Reinforcement strains in reinforced concrete tensile members recorded by strain gauges and FBG sensors: Experimental and numerical analysis. Sensors 2019, 19, 200. [Google Scholar] [CrossRef]
- Gheorghiu, C.; Labossiére, P.; Proulx, J. Fiber optic sensors for strain measurement of CFRP-strengthened RC beams. Struct. Health Monit. 2005, 4, 67–80. [Google Scholar] [CrossRef]
- ABAQUS. FEA Software and User’s Manual Version 6.14; Hibbitt, Karlsson & Sorensen Inc.: Providence, RI, USA, 2014. [Google Scholar]
- Légeron, F.; Paultre, P. Uniaxial confinement model for normal-and high-strength concrete columns. J. Struct. Eng. 2003, 129, 241–252. [Google Scholar] [CrossRef]
- Tuo, L.; Boquan, L.; Feng, L. Development and application of material constitutive models based on ABAQUS/Standard beam elements. J. Cent. South Univ. Sci. Technol. 2013, 8, 3503–3511. [Google Scholar] [CrossRef]
- Ayazian, R.; Abdolhosseini, M.; Firouzi, A.; Li, C.Q. Reliability-based optimization of external wrapping of CFRP on reinforced concrete columns considering decayed diffusion. Eng. Fail. Anal. 2021, 128, 105592. [Google Scholar] [CrossRef]
- Mwafy, A.M.; Elnashai, A.S. Calibration of force reduction factors of RC buildings. J. Earthq. Eng. 2002, 6, 239–273. [Google Scholar] [CrossRef]











| Series | Specimen | b (mm) | H (mm) | f’c (MPa) | ρϕ (%) | Shear Reinforcement | FOS | Load Test (t), Days | |
|---|---|---|---|---|---|---|---|---|---|
| I | C1-150 | 200 × 200 | 1500 | 26.0 | 24 | 2.0% | ϕ6 mm @ 100 | A | 28 |
| C2-150 | 200 × 200 | 1500 | 26.0 | 24 | 2.0% | ϕ6 mm @ 100 | A | 360 | |
| C3-150 | 200 × 200 | 1500 | 26.0 | 24 | 2.0% | ϕ6 mm @ 100 | A | 720 | |
| II | C4-150 | 200 × 200 | 1500 | 26.0 | 24 | 2.0% | ϕ6 mm @ 100 | B | 28 |
| C5-150 | 200 × 200 | 1500 | 26.0 | 24 | 2.0% | ϕ6 mm @ 100 | B | 360 | |
| C6-150 | 200 × 200 | 1500 | 26.0 | 24 | 2.0% | ϕ6 mm @ 100 | B | 720 | |
| III | C7-150 | 200 × 200 | 1500 | 26.0 | 24 | 2.0% | ϕ6 mm @ 100 | C | 28 |
| C8-150 | 200 × 200 | 1500 | 26.0 | 24 | 2.0% | ϕ6 mm @ 100 | C | 360 | |
| C9-150 | 200 × 200 | 1500 | 26.0 | 24 | 2.0% | ϕ6 mm @ 100 | C | 720 | |
| IV | C10-170 | 200 × 200 | 1700 | 29.4 | 18 | 1.13% | ϕ6 mm @ 200 | D | 28 |
| C11-170 | 200 × 200 | 1700 | 29.4 | 18 | 1.13% | ϕ6 mm @ 200 | D | 360 | |
| C12-170 | 200 × 200 | 1700 | 29.4 | 18 | 1.13% | ϕ6 mm @ 200 | D | 720 | |
| V | C13-180 | 200 × 200 | 1800 | 29.4 | 18 | 1.13% | ϕ6 mm @ 200 | D | 28 |
| C14-180 | 200 × 200 | 1800 | 29.4 | 18 | 1.13% | ϕ6 mm @ 200 | D | 360 | |
| C15-180 | 200 × 200 | 1800 | 29.4 | 18 | 1.13% | ϕ6 mm @ 200 | D | 720 | |
| VI | C16-180 | 150 × 150 | 1800 | 41.6 | 40 | 1.13% | ϕ6 mm @ 150 | D | 28 |
| C17-180 | 150 × 150 | 1800 | 41.6 | 40 | 1.13% | ϕ6 mm @ 150 | D | 360 | |
| C18-180 | 150 × 150 | 1800 | 41.6 | 40 | 1.13% | ϕ6 mm @ 150 | D | 720 |
| Mixture ID | CEM I (kg) | Fine Aggegates (kg) | Coarse Aggegates (kg) | Water + SP (kg) | Slump (mm) |
|---|---|---|---|---|---|
| M18 | 284 | 698 | 1257 | 173 | 95 |
| M24 | 305 | 740 | 1140 | 165 | 90 |
| M40 | 370 | 792 | 1084 | 157 | 85 |
| Mixture ID | Modulus of Rupture | |||||
|---|---|---|---|---|---|---|
| Mean (MPa) | SD (MPa) | Mean (MPa) | SD (MPa) | Mean (MPa) | SD (MPa) | |
| M18 | 19.1 | 2.1 | 2.1 | 2.2 | 2.8 | 2.6 |
| M24 | 24.5 | 2.3 | 3.8 | 2.6 | 4.2 | 3.1 |
| M40 | 42.2 | 3.2 | 4.2 | 4.1 | 5.4 | 4.2 |
| ID | Pcr | Δcr | Py | Pu | Δmax | Δy (mm) | Δf (mm) | µu | µf | Se | ζ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (kN) | (mm) | (kN) | (kN) | (mm) | (kN/mm) | (kN.mm) | |||||
| C1-150 | 590.64 | 0.33 | 961.24 | 1215.61 | 3.17 | 0.64 | 6.71 | 4.95 | 0.10 | 1789.82 | 7800 |
| C2-150 | 566.10 | 0.29 | 910.65 | 1104.26 | 2.75 | 0.29 | 3.58 | 9.48 | 0.08 | 8087.14 | 3950 |
| C3-150 | 529.37 | 0.26 | 891.93 | 1006.59 | 2.31 | 0.71 | 4.01 | 3.25 | 0.18 | 1459.92 | 4250 |
| C4-150 | 573.03 | 0.35 | 965.43 | 1187.53 | 2.93 | 0.62 | 5.23 | 4.73 | 0.12 | 2072.39 | 4350 |
| C5-150 | 469.37 | 0.29 | 925.32 | 1094.38 | 2.55 | 0.10 | 5.48 | 25.50 | 0.02 | 18,979.00 | 5900 |
| C6-150 | 374.67 | 0.26 | 893.67 | 984.21 | 3.00 | 0.75 | 5.08 | 4.00 | 0.15 | 1040.75 | 4200 |
| C7-150 | 599.55 | 0.43 | 984.26 | 1203.45 | 2.51 | 1.50 | 5.8 | 1.67 | 0.26 | 1131.23 | 4550 |
| C8-150 | 468.13 | 0.38 | 916.12 | 1094.53 | 4.21 | 1.32 | 5.71 | 3.19 | 0.23 | 968.76 | 4400 |
| C9-150 | 467.73 | 0.27 | 853.56 | 959.28 | 3.92 | 0.31 | 5.86 | 12.65 | 0.05 | 3339.59 | 5950 |
| C10-170 | 549.52 | 0.73 | 846.46 | 1053.12 | 1.83 | 1.75 | 1.95 | 1.05 | 0.90 | 436.90 | 560 |
| C11-170 | 445.26 | 0.61 | 814.28 | 946.26 | 3.56 | 3.33 | 3.87 | 1.07 | 0.86 | 729.93 | 850 |
| C12-170 | 352.38 | 0.56 | 791.26 | 884.35 | 3.58 | 2.31 | 3.21 | 1.55 | 0.72 | 677.98 | 1050 |
| C13-180 | 593.49 | 0.35 | 891.59 | 989.25 | 3.77 | 2.78 | 3.95 | 1.36 | 0.70 | 3289.93 | 1280 |
| C14-180 | 514.87 | 0.28 | 869.53 | 884.63 | 2.33 | 2.26 | 3.68 | 1.17 | 0.54 | 1838.82 | 1550 |
| C15-180 | 451.26 | 0.24 | 842.58 | 865.38 | 4.50 | 4.42 | 5.89 | 1.13 | 0.68 | 337.79 | 2230 |
| C16-180 | 521.93 | 0.32 | 795.86 | 1079.65 | 1.06 | 0.64 | 1.15 | 1.66 | 0.56 | 1631.03 | 360 |
| C17-180 | 483.57 | 0.27 | 761.24 | 942.51 | 1.52 | 1.54 | 1.55 | 0.99 | 0.99 | 711.13 | 700 |
| C18-180 | 416.39 | 0.25 | 749.19 | 892.47 | 1.68 | 1.86 | 1.49 | 0.90 | 1.24 | 615.68 | 790 |
| Specimen ID | Experiment Value (E), kN | Predicted Column Strength (P), kN | Exp/ Equation (2) | Exp/ Equation (3) | Exp/ Equation (5) | Exp/ Equation (9) | |||
|---|---|---|---|---|---|---|---|---|---|
| Equation (2) | Equation (3) | Equation (5) | Equation (9) | ||||||
| C1-150 | 1333.0 | 723.9 | 827.1 | 723.9 | 827.1 | 1.84 | 1.61 | 1.84 | 1.61 |
| C2-150 | 1261.0 | 723.9 | 827.1 | 720.1 | 820.5 | 1.74 | 1.52 | 1.75 | 1.54 |
| C3-150 | 1102.0 | 723.9 | 827.1 | 720.1 | 820.5 | 1.52 | 1.33 | 1.53 | 1.34 |
| C4-150 | 1371.0 | 723.9 | 900.0 | 723.9 | 900.0 | 1.89 | 1.52 | 1.89 | 1.52 |
| C5-150 | 1202.0 | 723.9 | 900.0 | 730.0 | 890.0 | 1.66 | 1.34 | 1.65 | 1.35 |
| C6-150 | 1150.0 | 723.9 | 900.0 | 730.0 | 890.0 | 1.59 | 1.28 | 1.58 | 1.29 |
| C7-150 | 1203.5 | 723.9 | 827.1 | 723.9 | 827.1 | 1.66 | 1.46 | 1.66 | 1.46 |
| C8-150 | 1194.5 | 723.9 | 827.1 | 720.0 | 820.1 | 1.65 | 1.44 | 1.66 | 1.46 |
| C9-150 | 1019.0 | 723.9 | 827.1 | 720.0 | 820.1 | 1.41 | 1.23 | 1.42 | 1.24 |
| C10-170 | 656.0 | 554.4 | 631.1 | 554.4 | 631.1 | 1.18 | 1.04 | 1.18 | 1.04 |
| C11-170 | 645.0 | 554.4 | 631.1 | 531.8 | 620.0 | 1.16 | 1.02 | 1.21 | 1.04 |
| C12-170 | 630.0 | 554.4 | 631.1 | 531.8 | 620.0 | 1.14 | 1.00 | 1.18 | 1.02 |
| C13-180 | 591.0 | 554.4 | 631.1 | 554.4 | 631.1 | 1.07 | 0.94 | 1.07 | 0.94 |
| C14-180 | 547.0 | 554.4 | 631.1 | 546.2 | 520.0 | 0.99 | 0.87 | 1.00 | 1.05 |
| C15-180 | 532.0 | 554.4 | 631.1 | 546.2 | 520.0 | 0.96 | 0.84 | 0.97 | 1.02 |
| C16-180 | 1079.7 | 661.5 | 649.6 | 797.0 | 630.0 | 1.63 | 1.66 | 1.35 | 1.71 |
| C17-180 | 1059.5 | 661.5 | 649.6 | 780.1 | 630.0 | 1.60 | 1.63 | 1.36 | 1.68 |
| C18-180 | 943.6 | 661.5 | 649.6 | 780.1 | 630.0 | 1.43 | 1.45 | 1.21 | 1.50 |
| Mean (E/P) | 1.45 | 1.32 | 1.42 | 1.29 | |||||
| STD. | 0.30 | 0.25 | 0.29 | 0.27 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pasityothin, I.; Thansirichaisree, P.; Buatik, A.; Imjai, T.; Sridhar, R.; Garcia, R.; Noguchi, T. Strain Decay Monitoring and Analytical Prediction of RC Columns Using Brillouin Optical Technology and Time-Dependent Deterioration Factor. Sensors 2025, 25, 741. https://doi.org/10.3390/s25030741
Pasityothin I, Thansirichaisree P, Buatik A, Imjai T, Sridhar R, Garcia R, Noguchi T. Strain Decay Monitoring and Analytical Prediction of RC Columns Using Brillouin Optical Technology and Time-Dependent Deterioration Factor. Sensors. 2025; 25(3):741. https://doi.org/10.3390/s25030741
Chicago/Turabian StylePasityothin, Ittipon, Phromphat Thansirichaisree, Apichat Buatik, Thanongsak Imjai, Radhika Sridhar, Reyes Garcia, and Takafumi Noguchi. 2025. "Strain Decay Monitoring and Analytical Prediction of RC Columns Using Brillouin Optical Technology and Time-Dependent Deterioration Factor" Sensors 25, no. 3: 741. https://doi.org/10.3390/s25030741
APA StylePasityothin, I., Thansirichaisree, P., Buatik, A., Imjai, T., Sridhar, R., Garcia, R., & Noguchi, T. (2025). Strain Decay Monitoring and Analytical Prediction of RC Columns Using Brillouin Optical Technology and Time-Dependent Deterioration Factor. Sensors, 25(3), 741. https://doi.org/10.3390/s25030741








