A Bio-Inspired Vibration Energy Harvesting System with Internal Resonance and Slapping Mechanism for Enhanced Low-Frequency Power Generation
Abstract
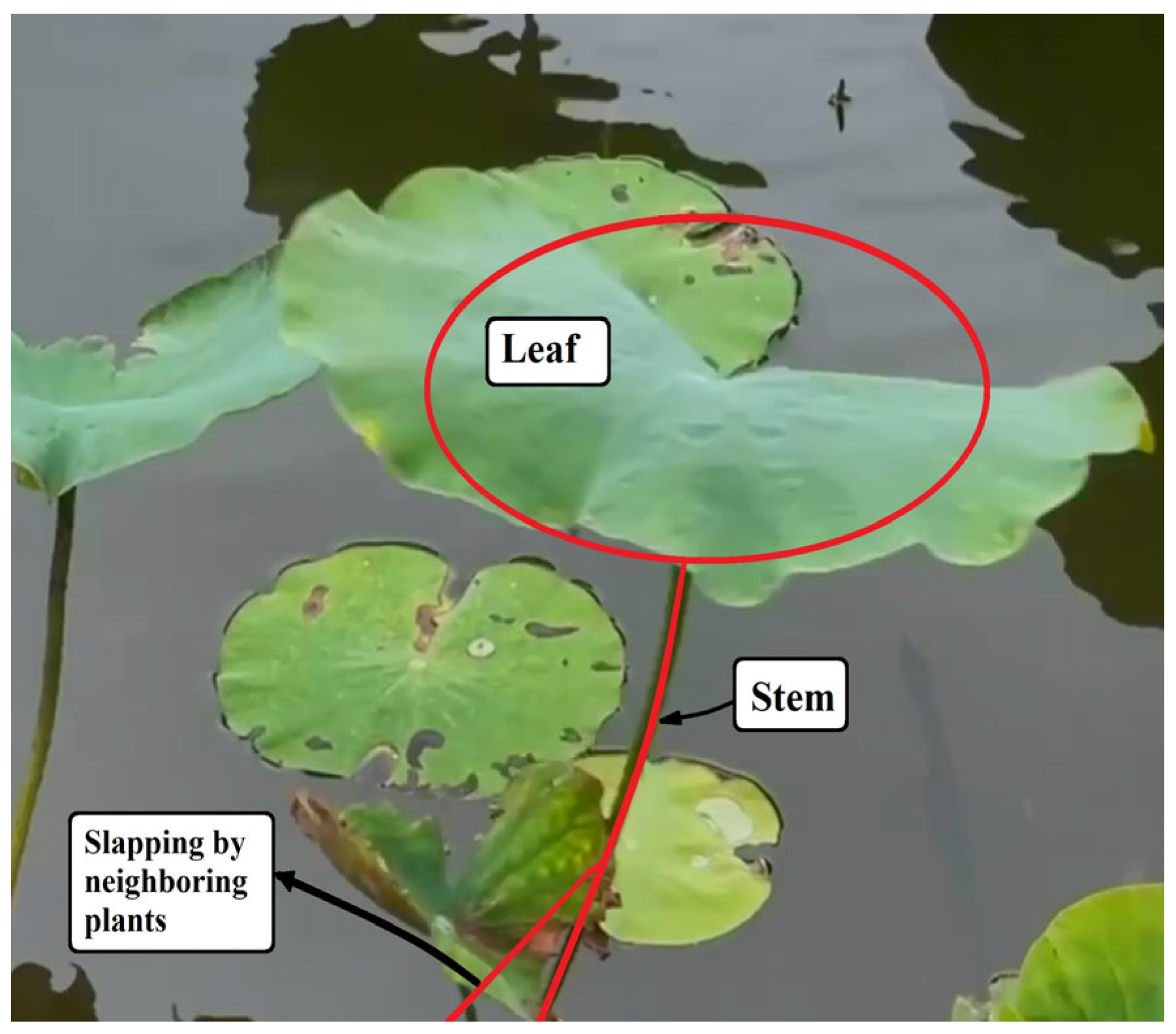
1. Introduction
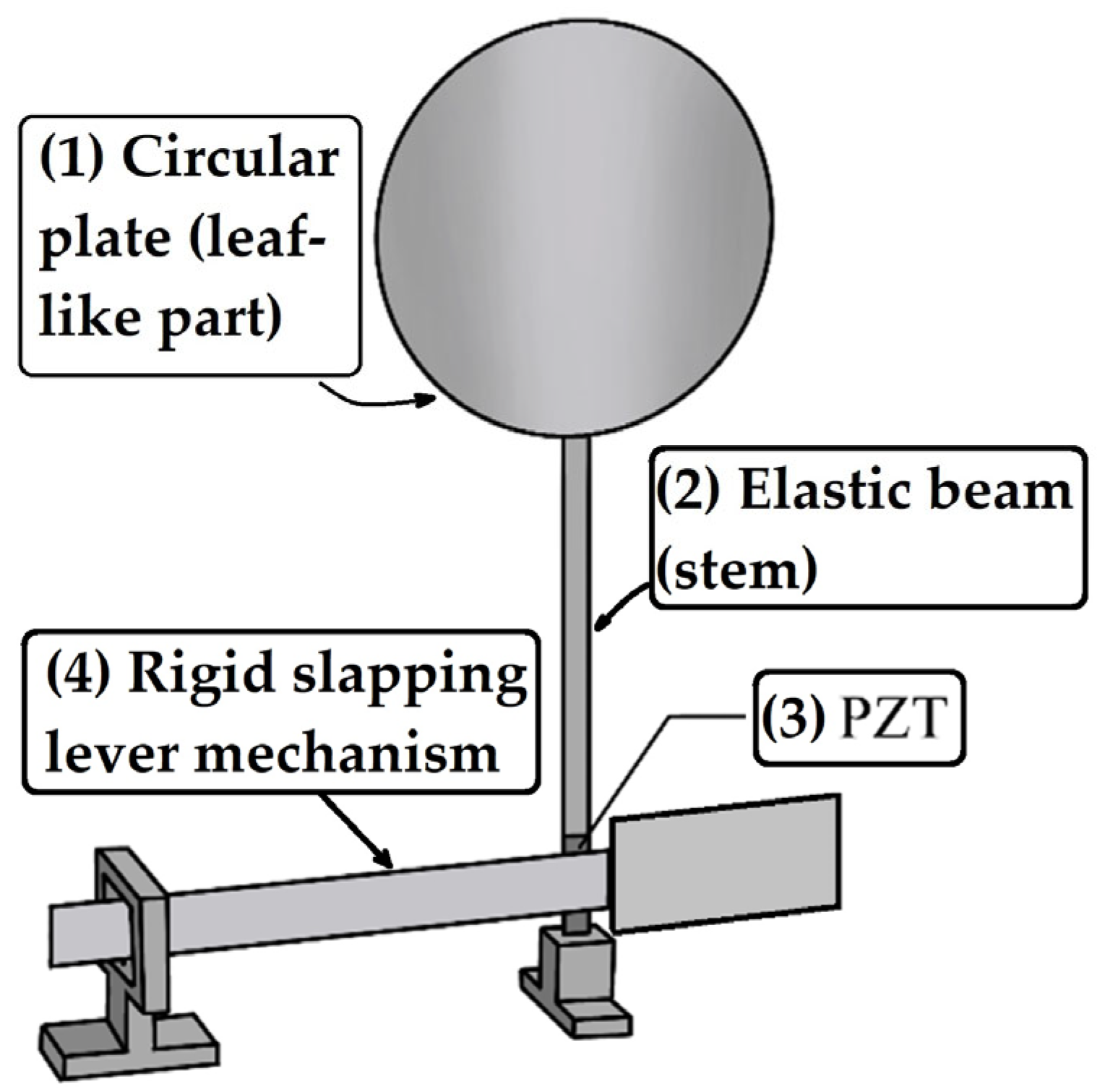
2. Establishment of Theoretical Model
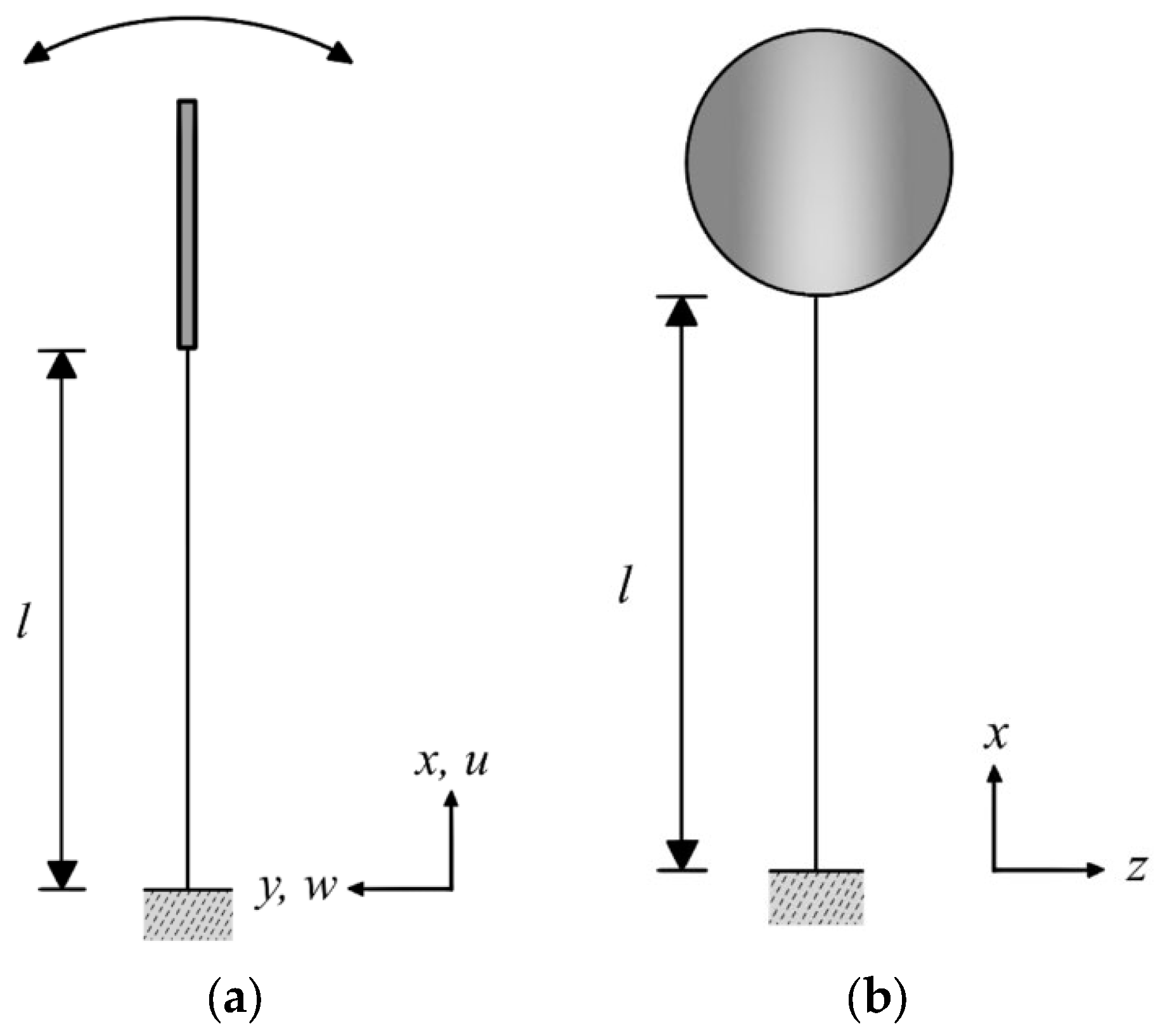
2.1. Derivation of Nonlinear Equations of Motion
- u-direction:
- w-direction:
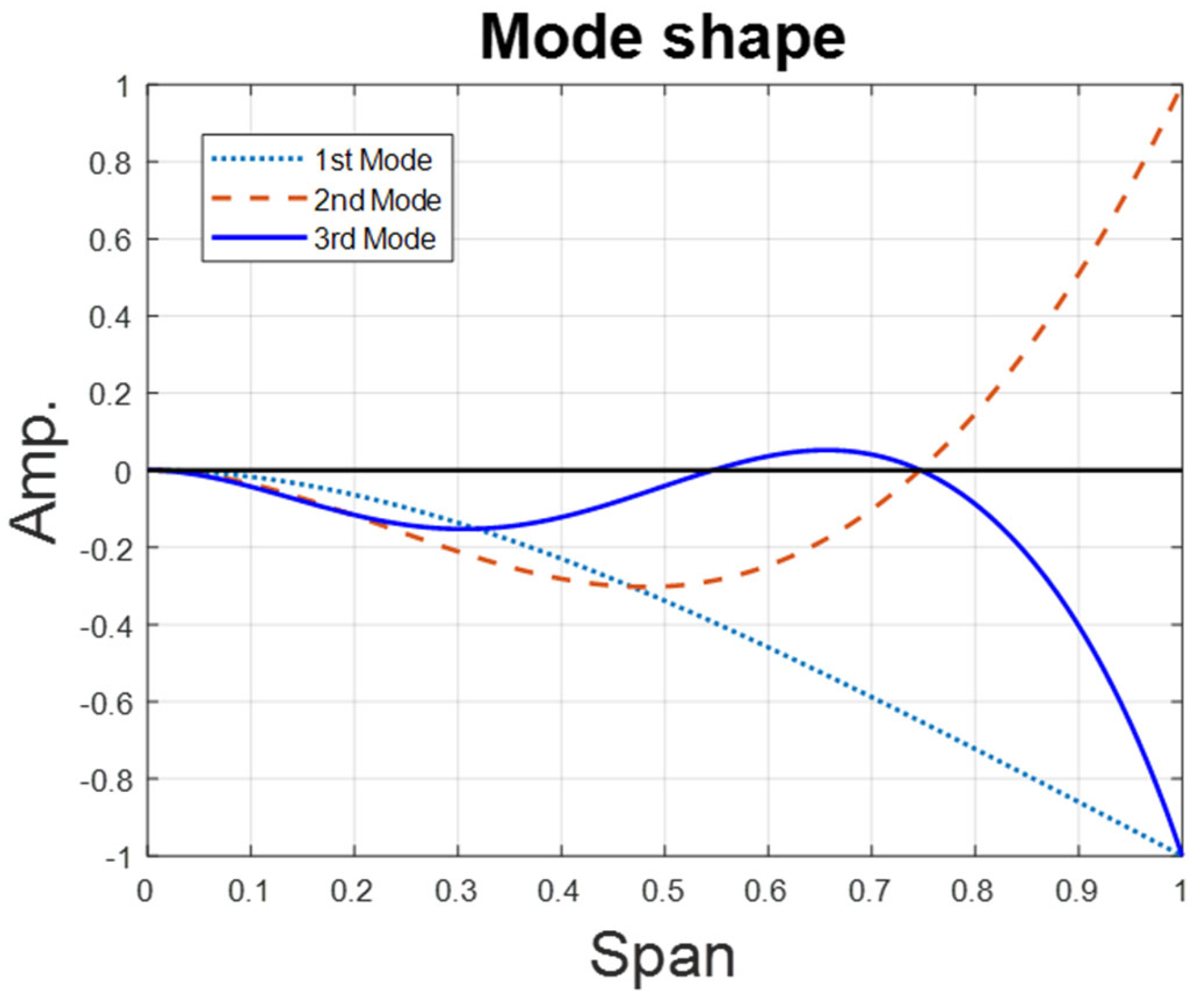
2.2. Natural Frequency
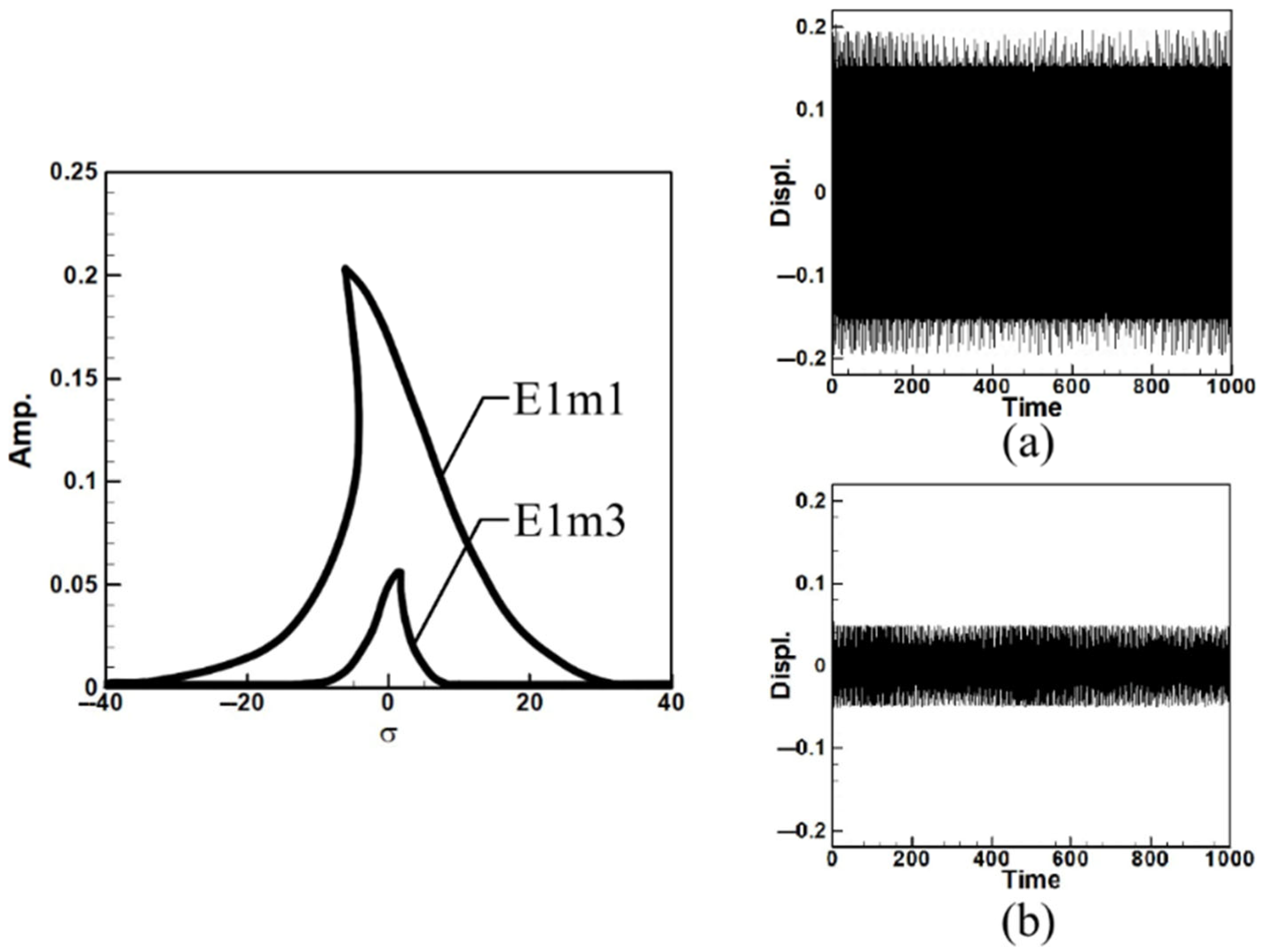
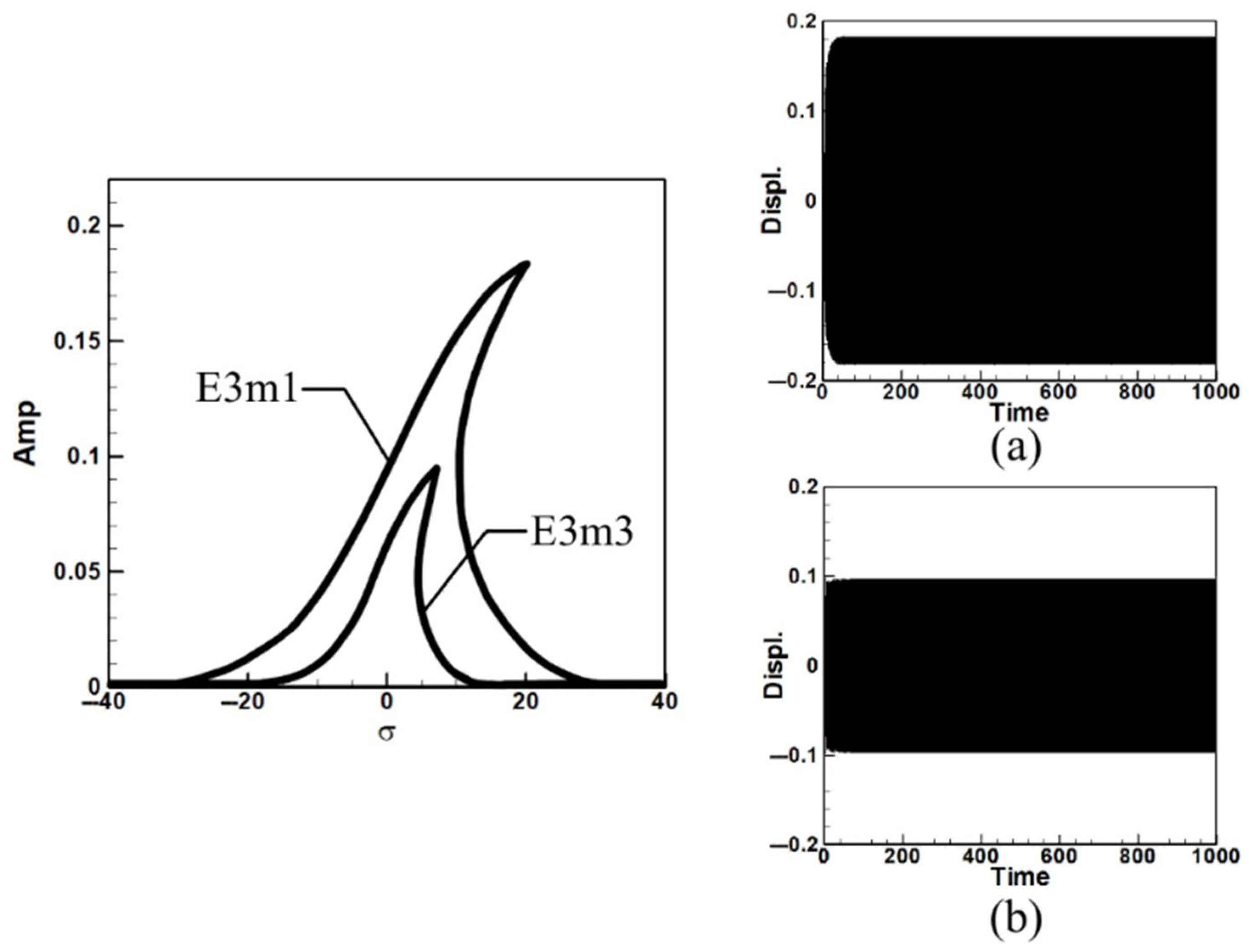
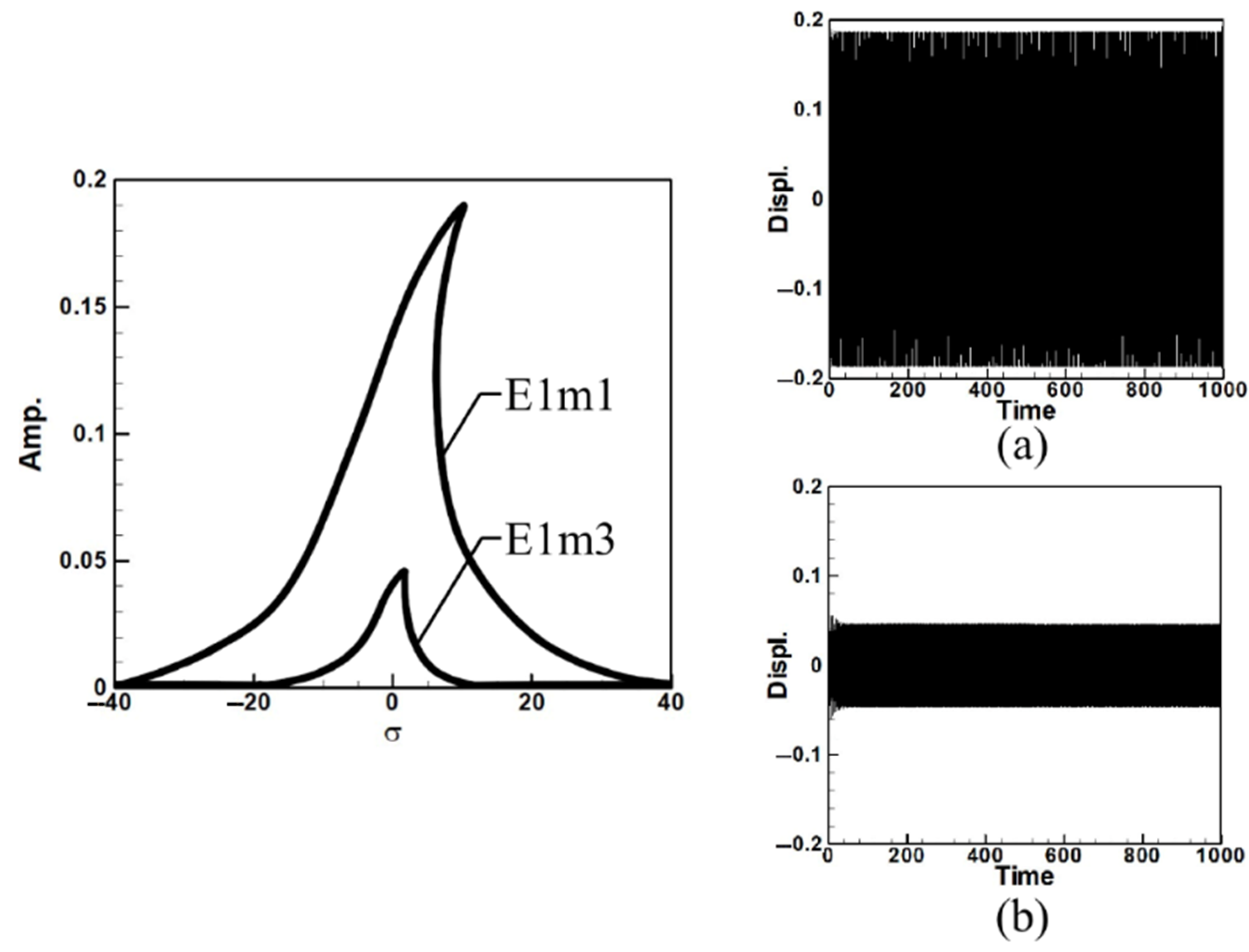
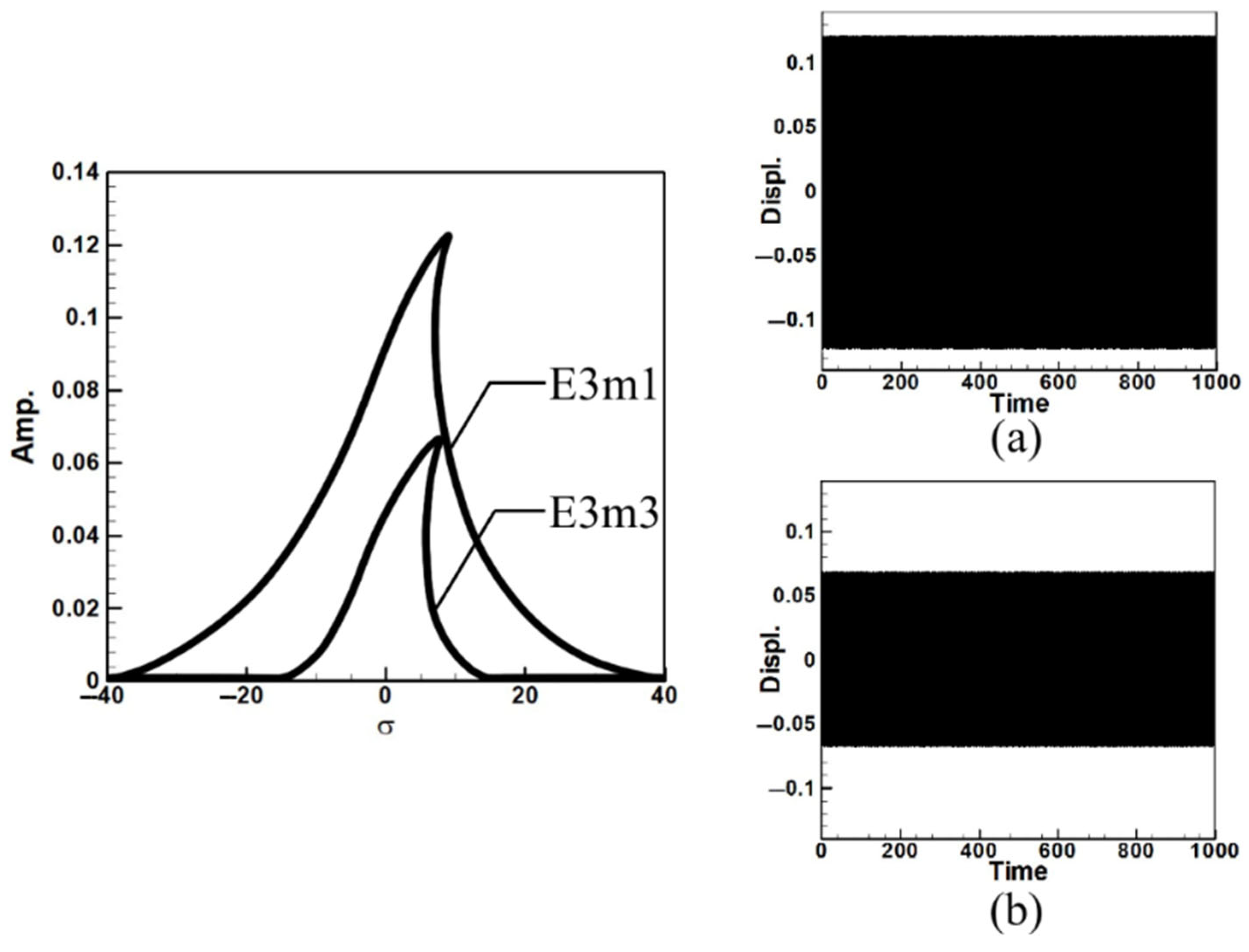
2.3. Frequency Response Analysis
2.4. Piezoelectric Equations
2.5. Simulation of Slapping Force
3. Theoretical Energy Harvesting Efficiency Analysis
4. Experimental Setup
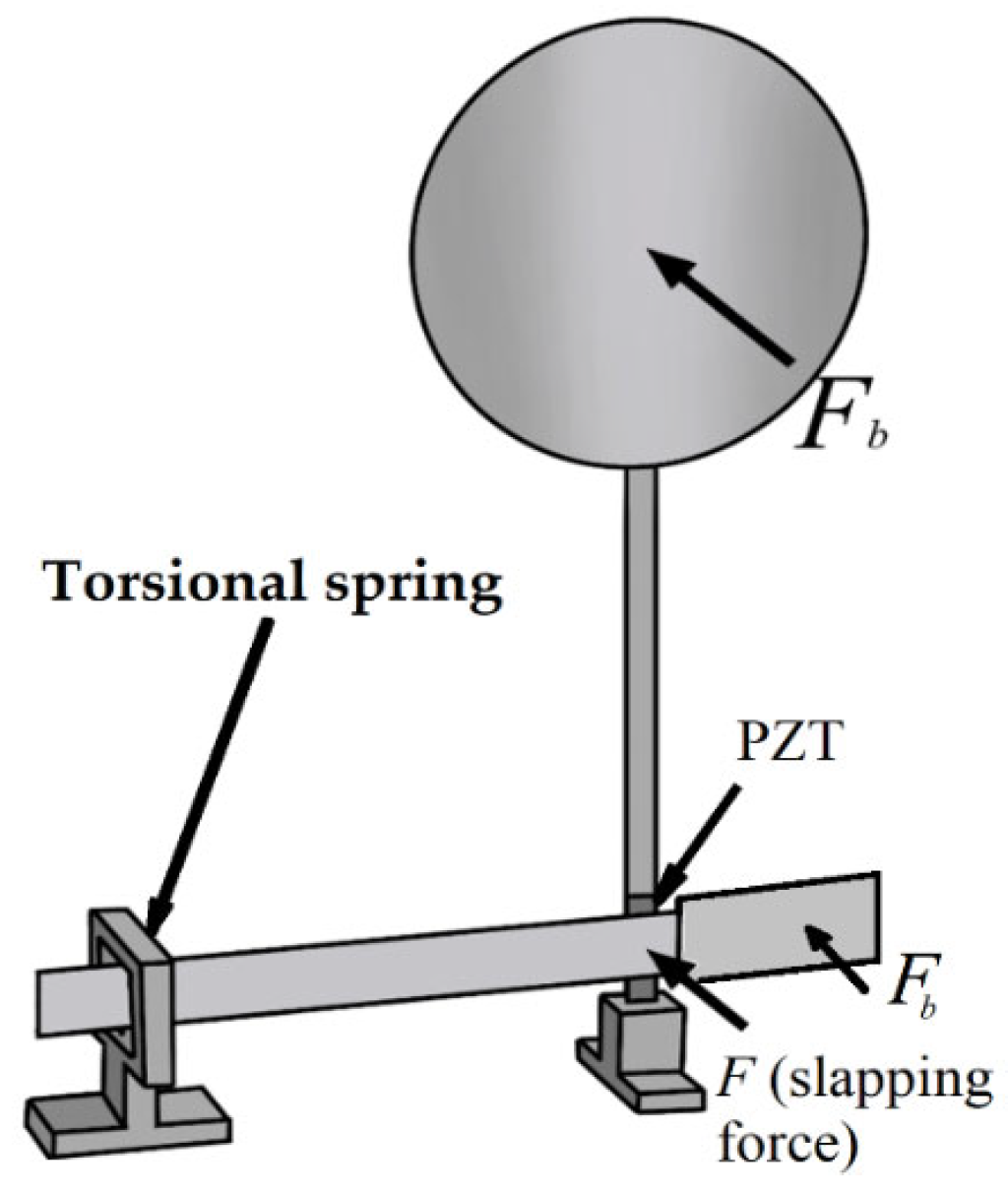
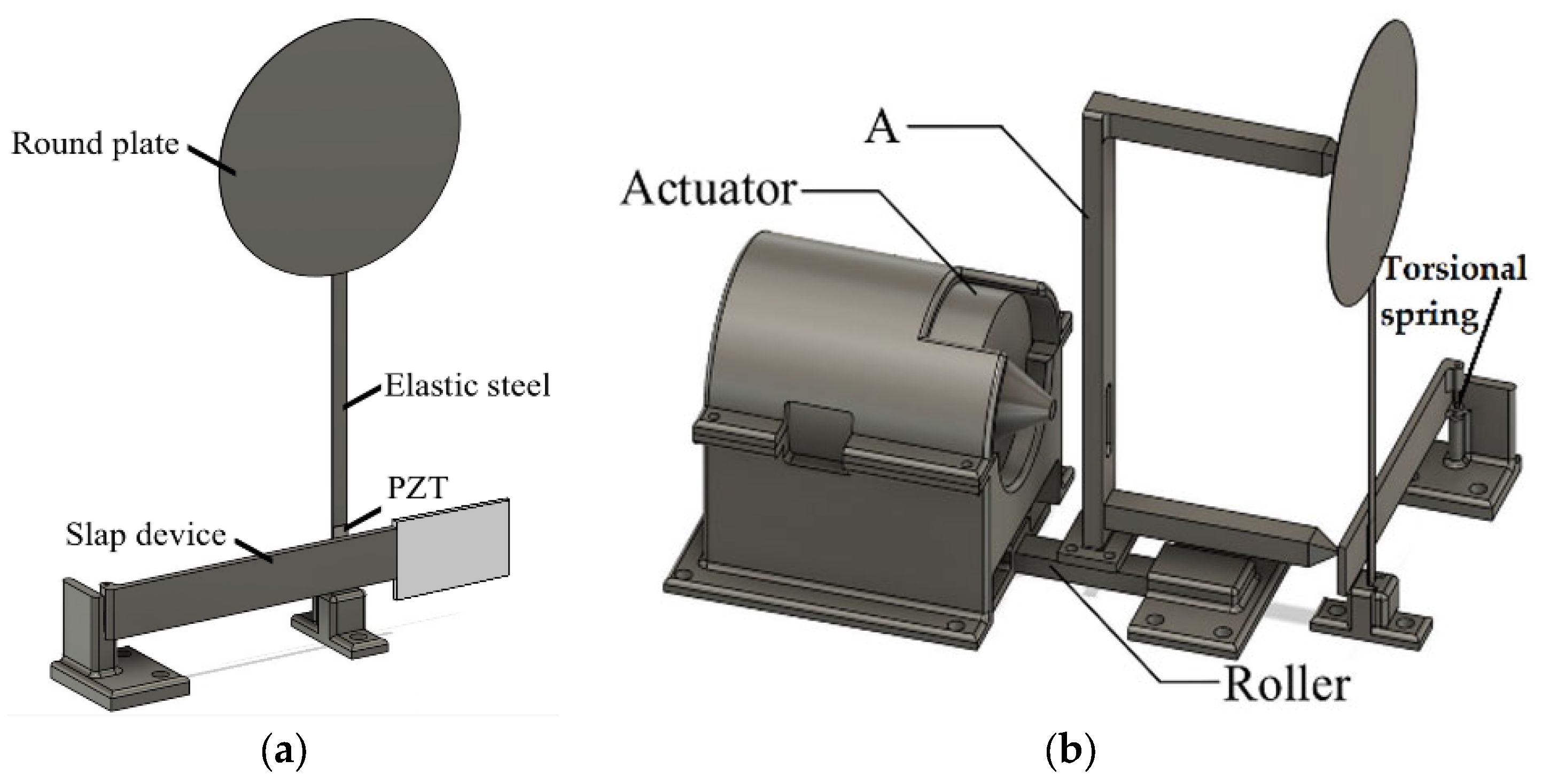
4.1. Experimental Model
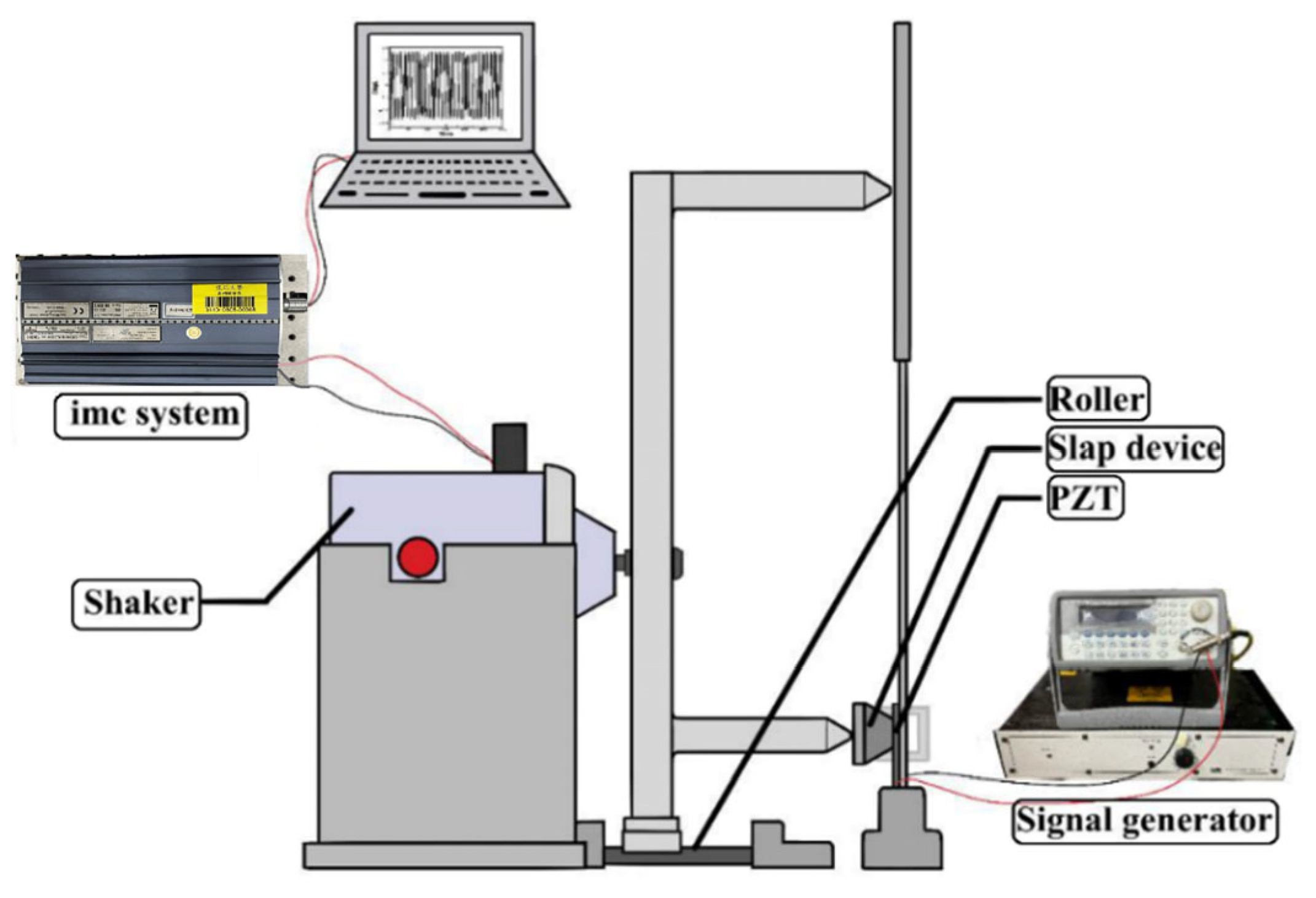
4.2. External Setup
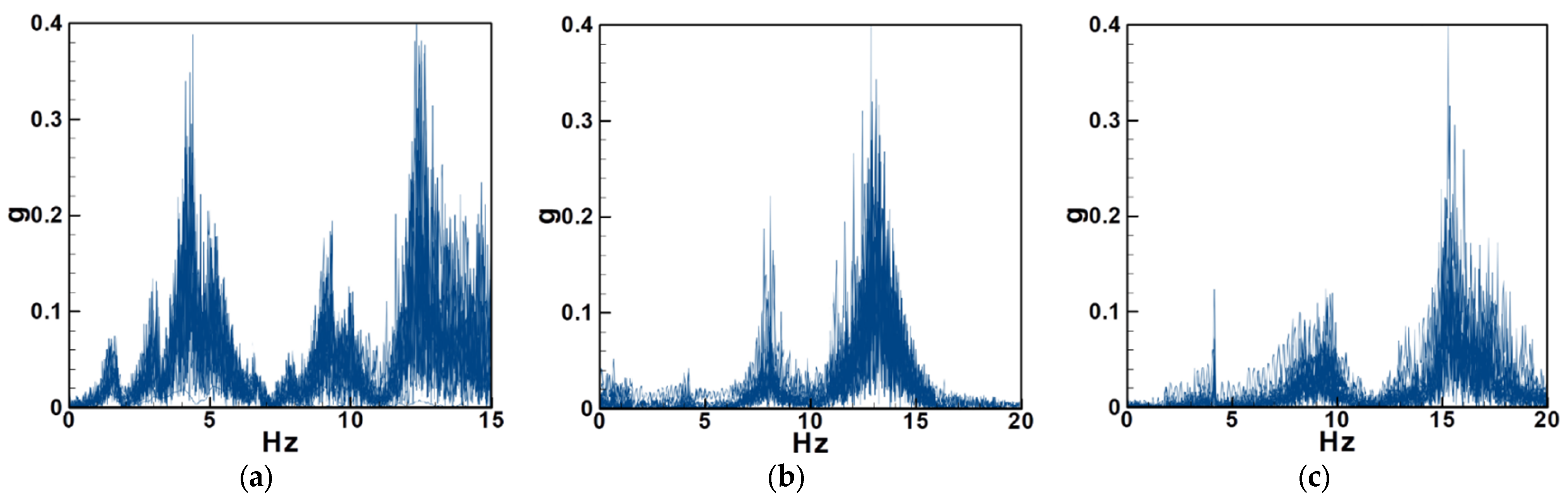
4.2.1. Experimental and Theoretical Validation of the System’s Natural Frequencies
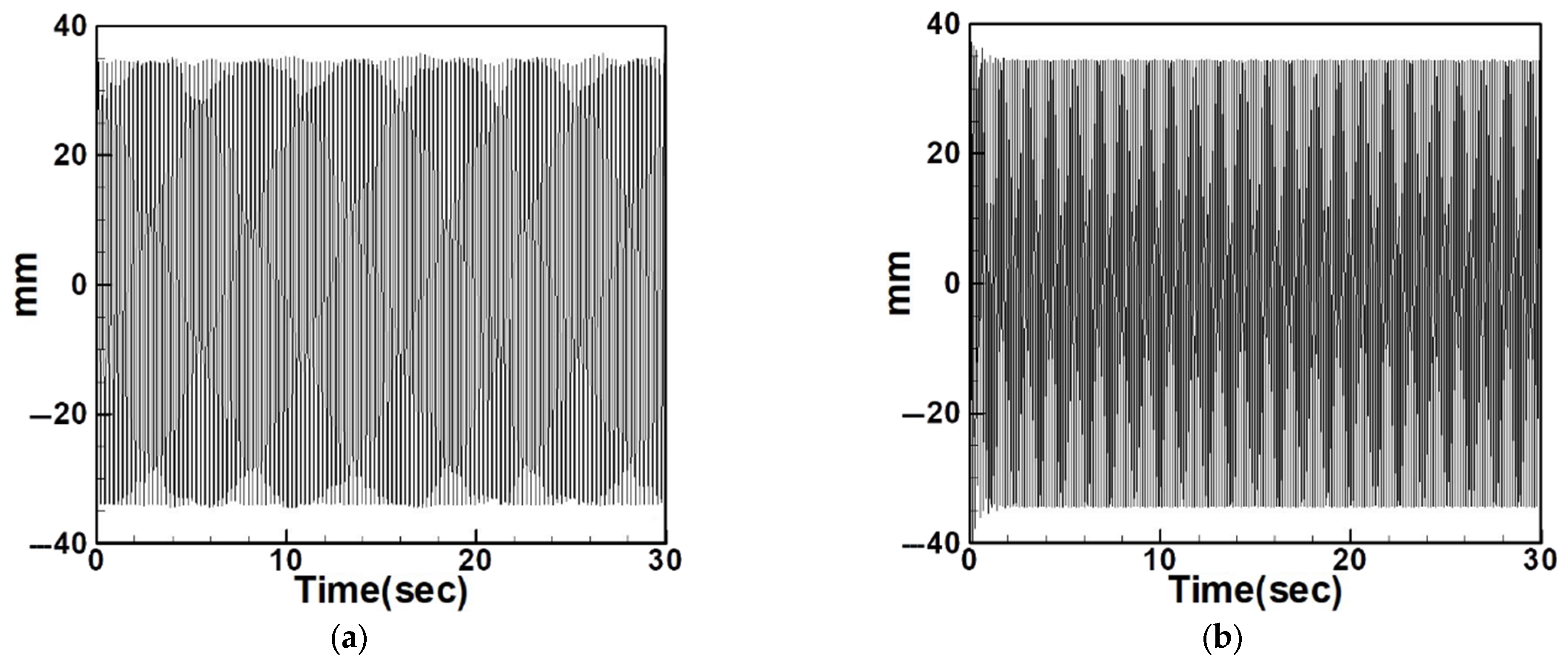
4.2.2. Experimental and Theoretical Validation of the System’s Displacements
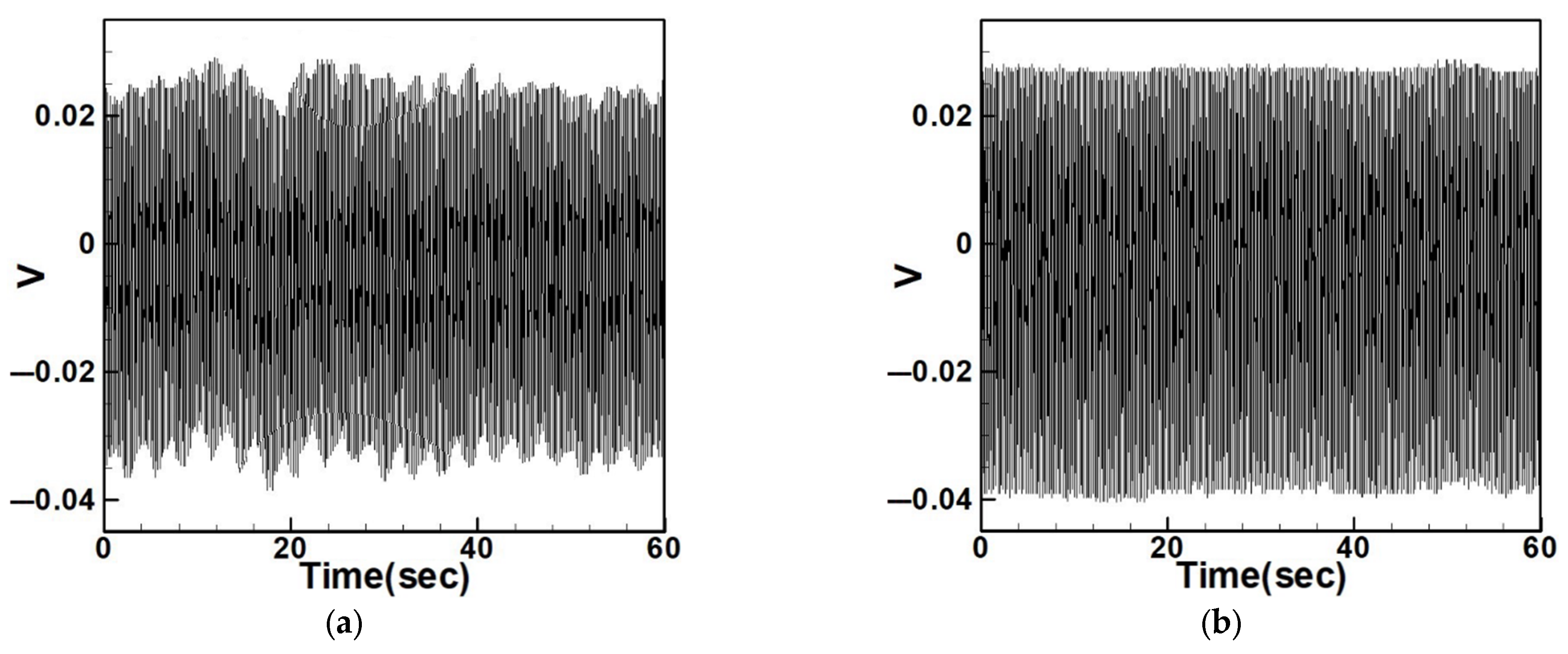
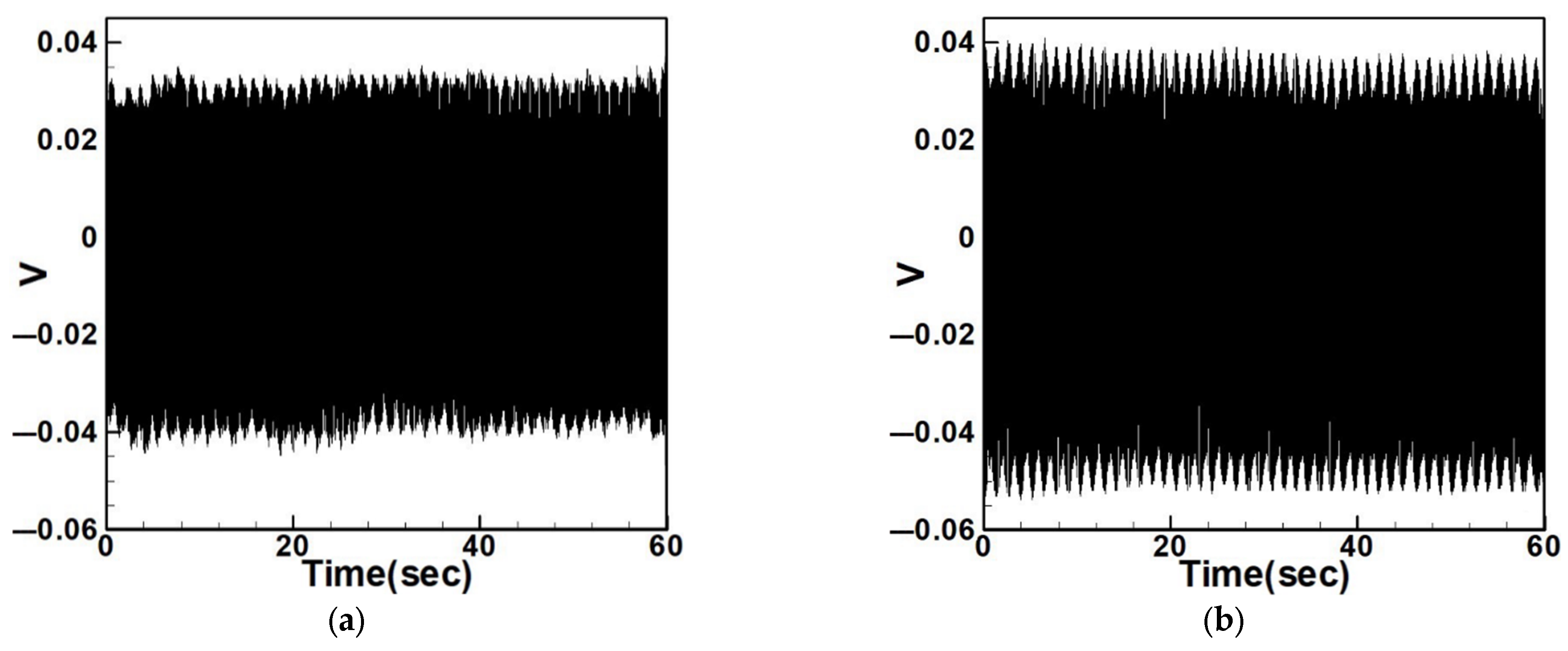
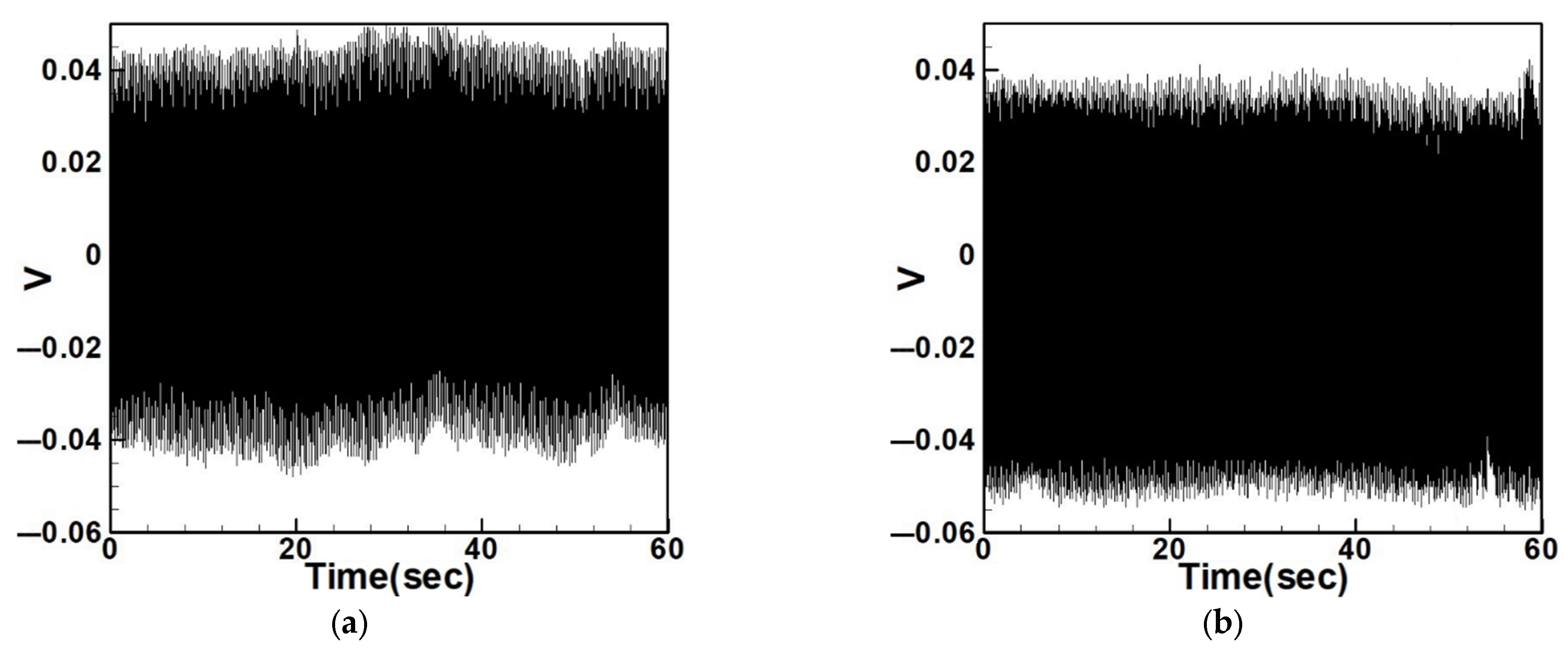
4.2.3. Experimental and Theoretical Validation of the System’s Voltage Output
5. Discussion and Analysis of Experimental Results
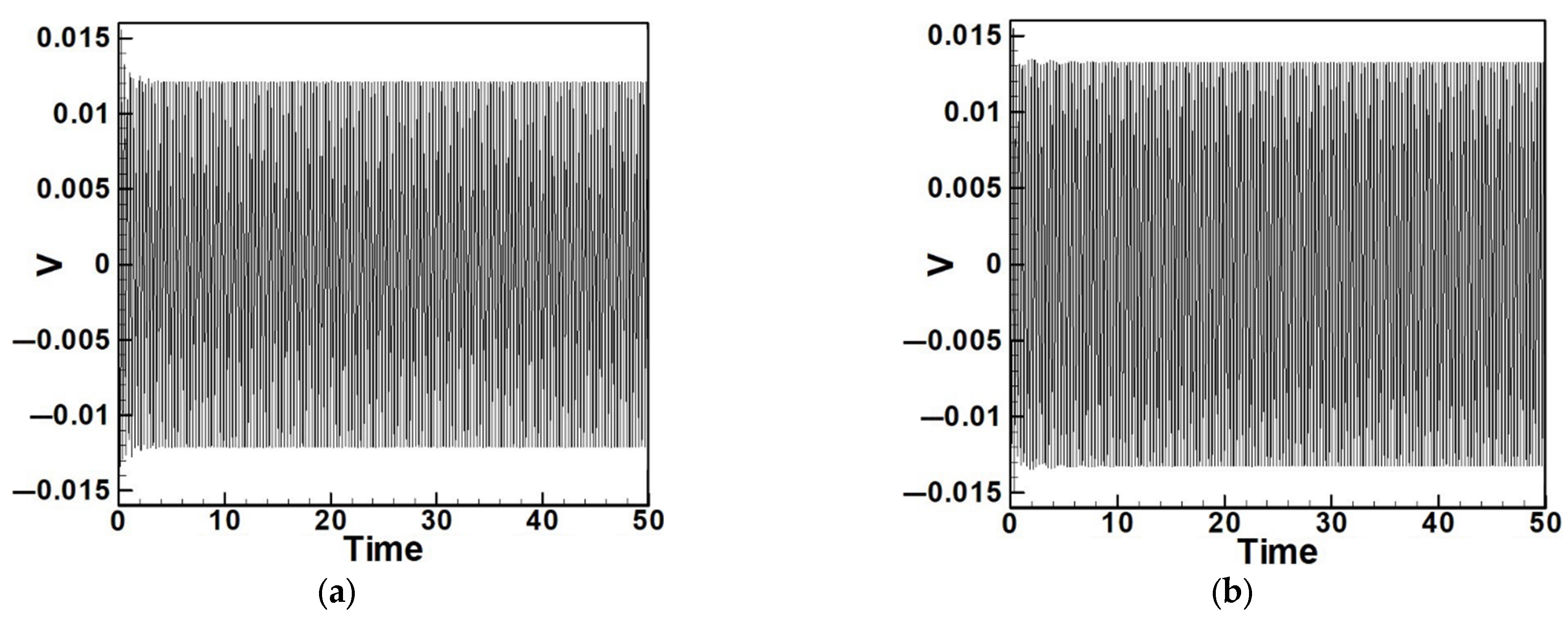
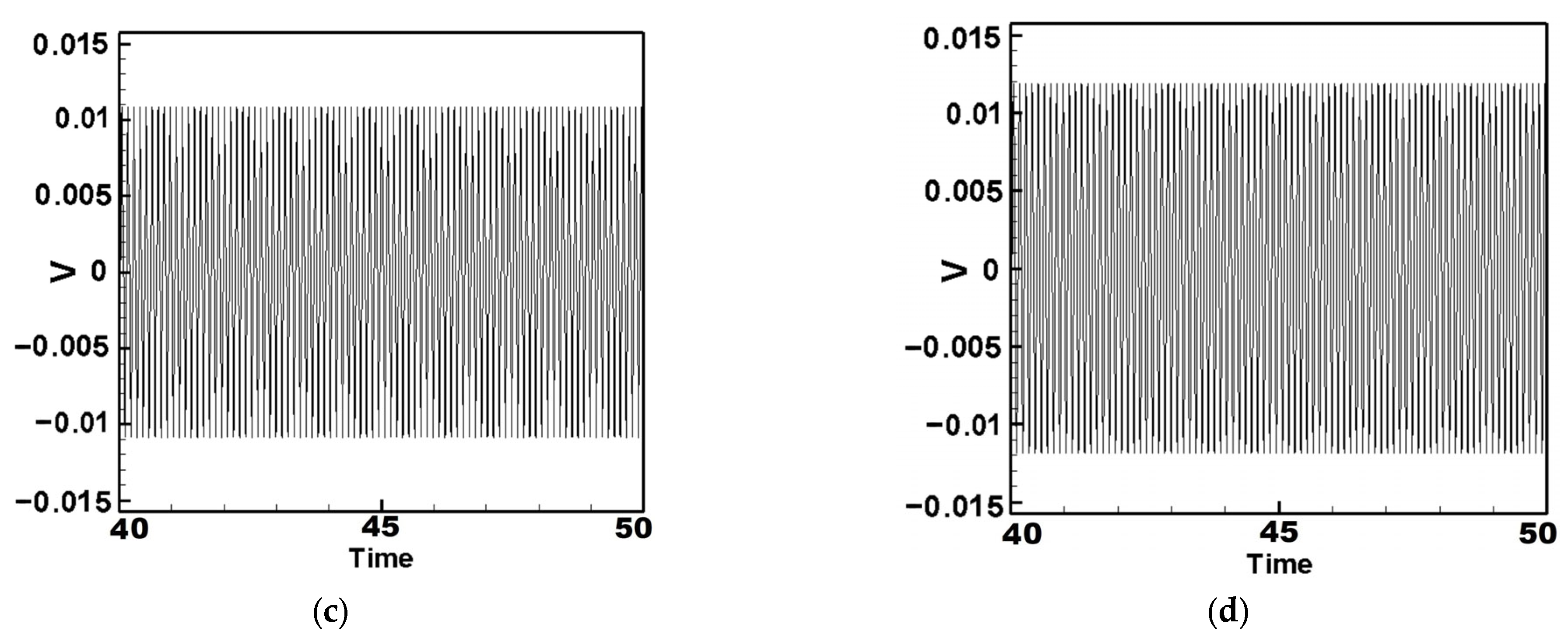
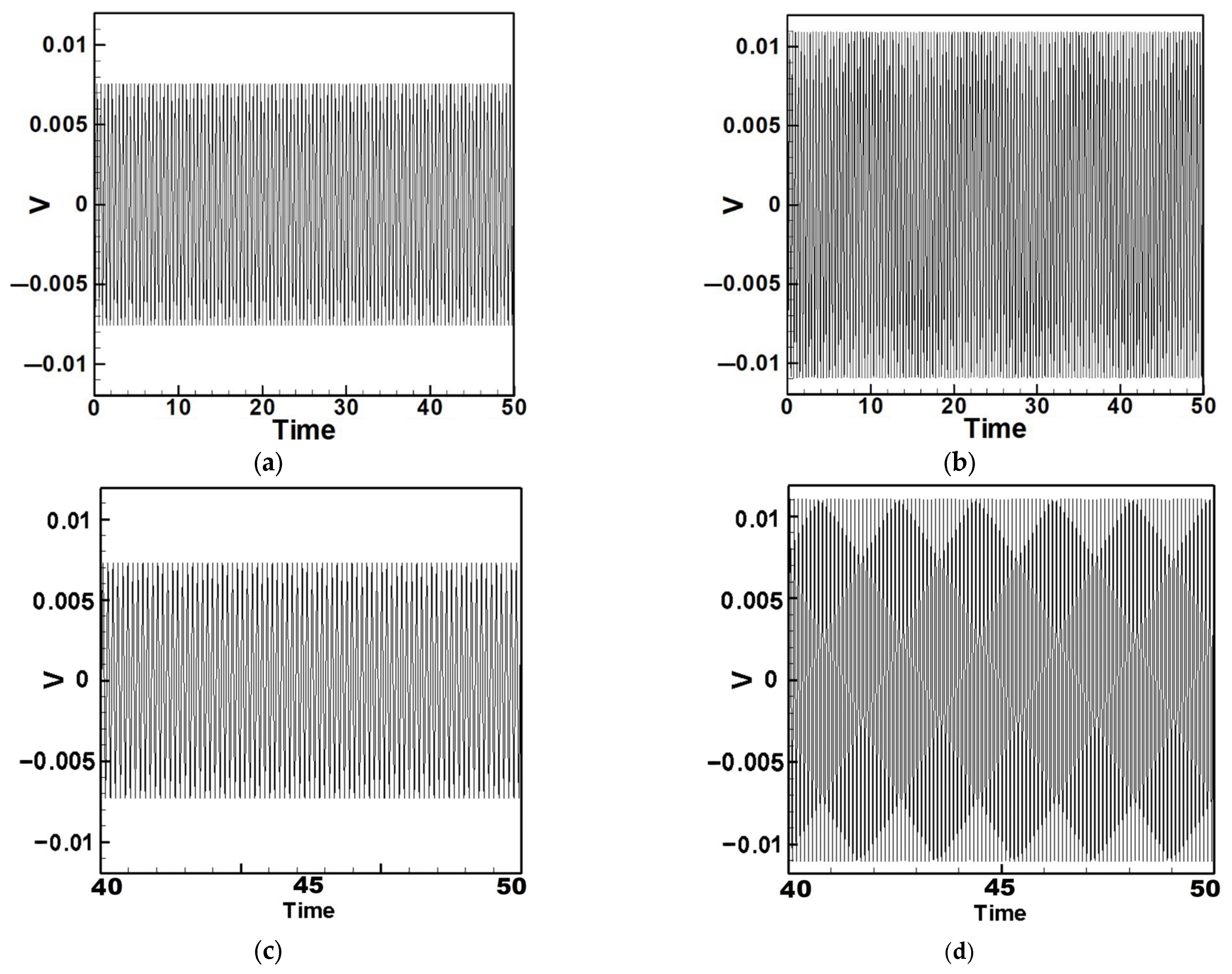
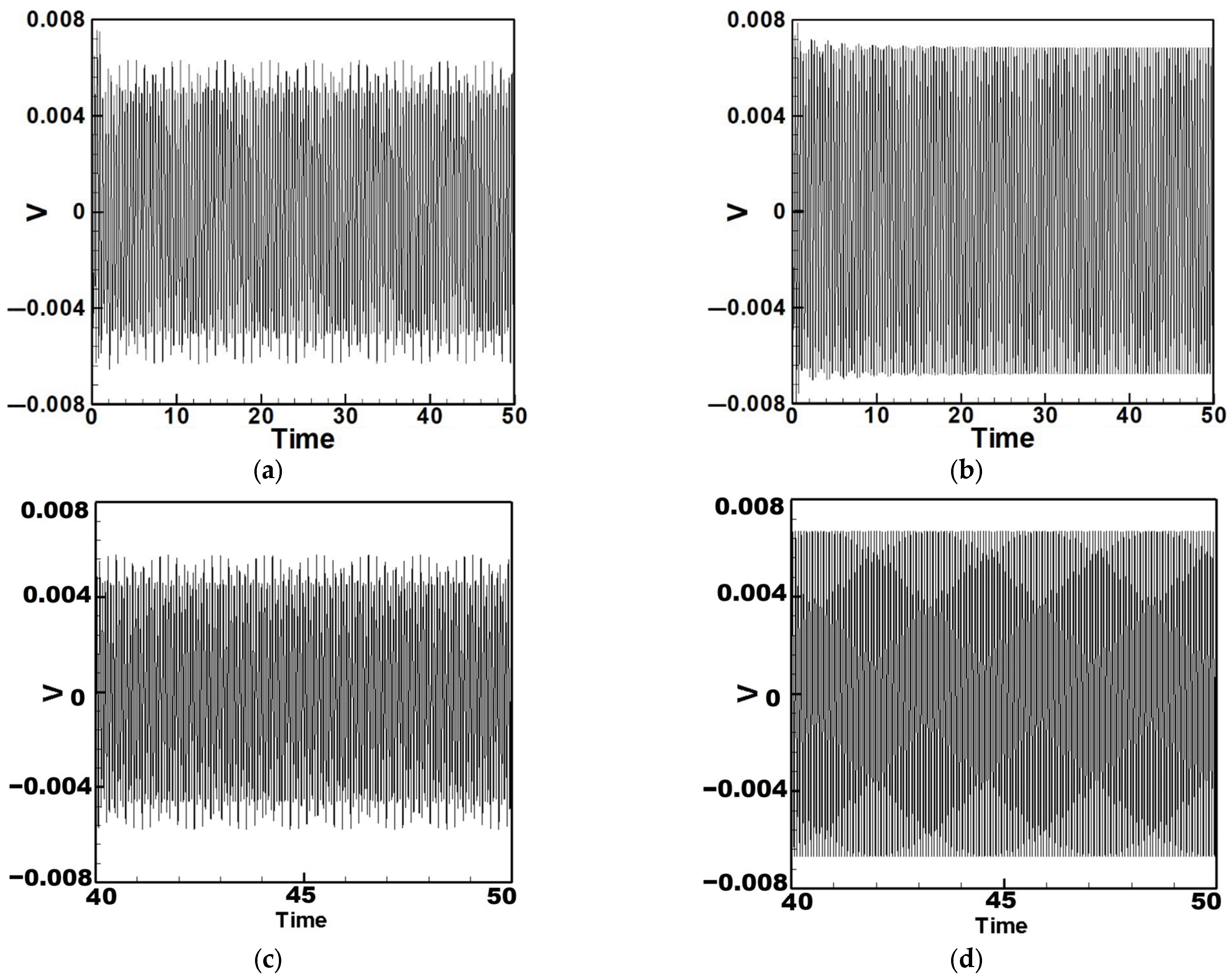
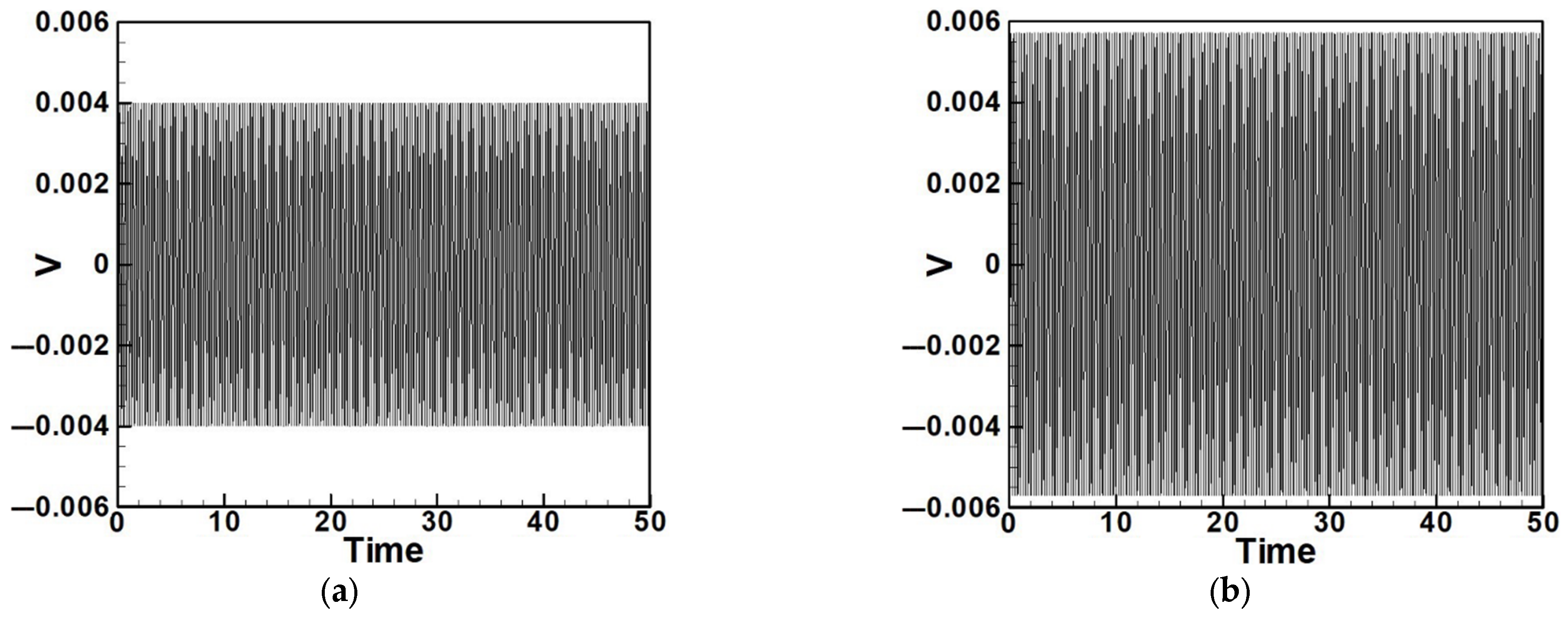
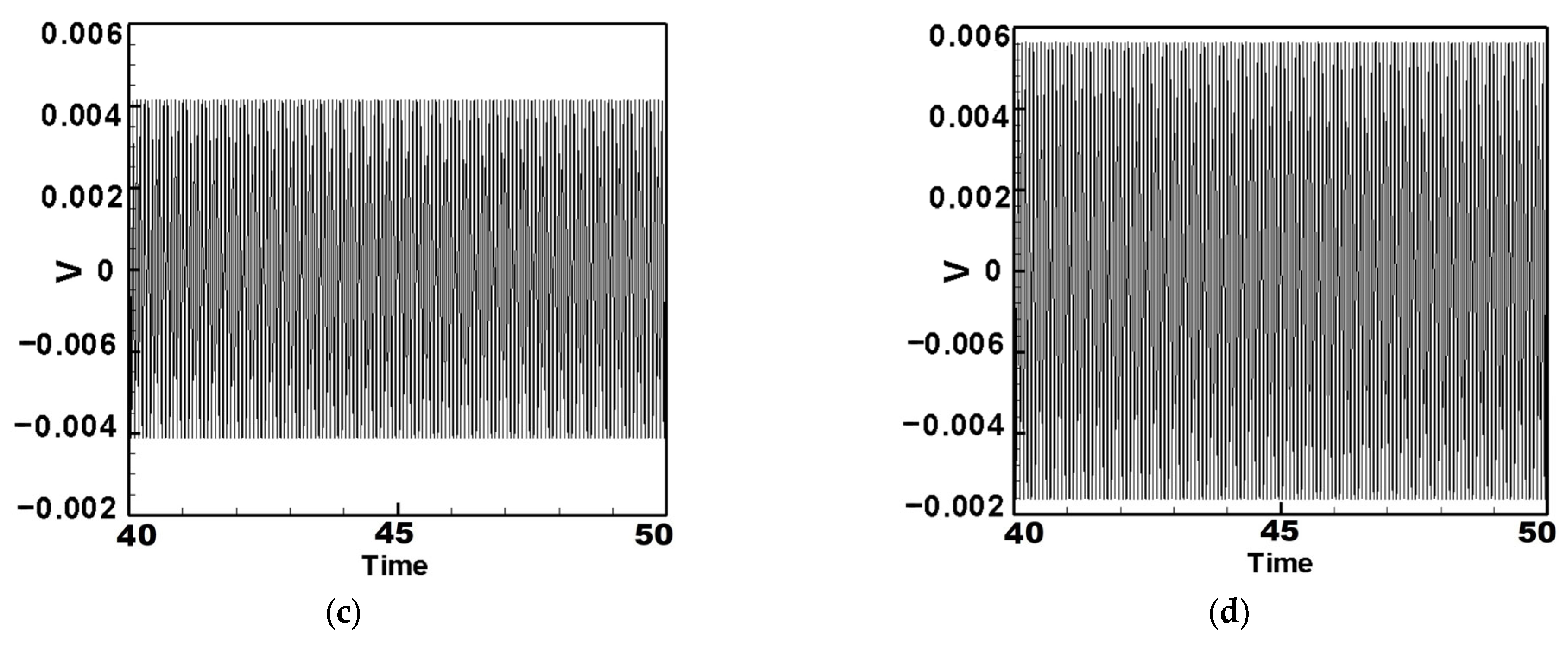
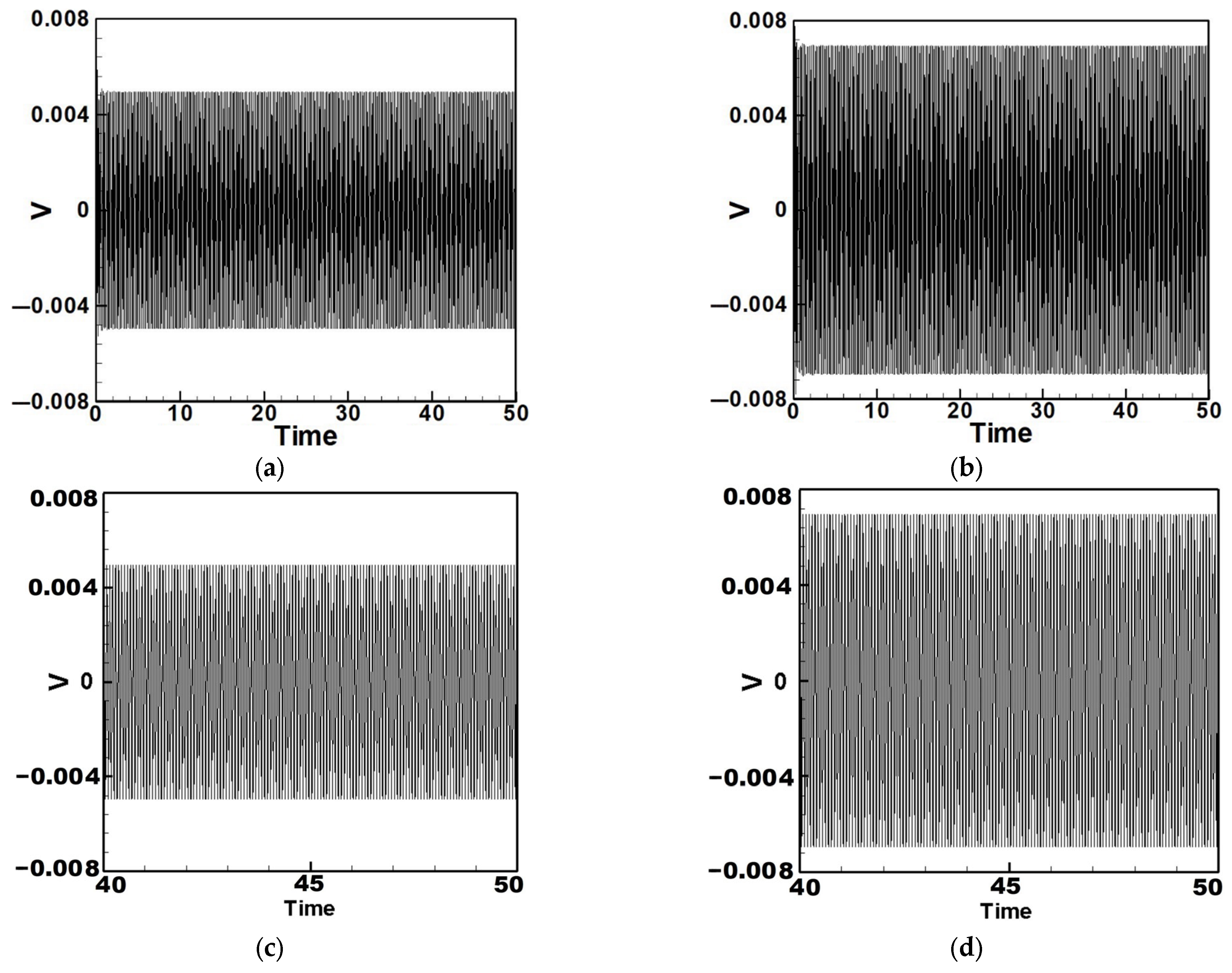
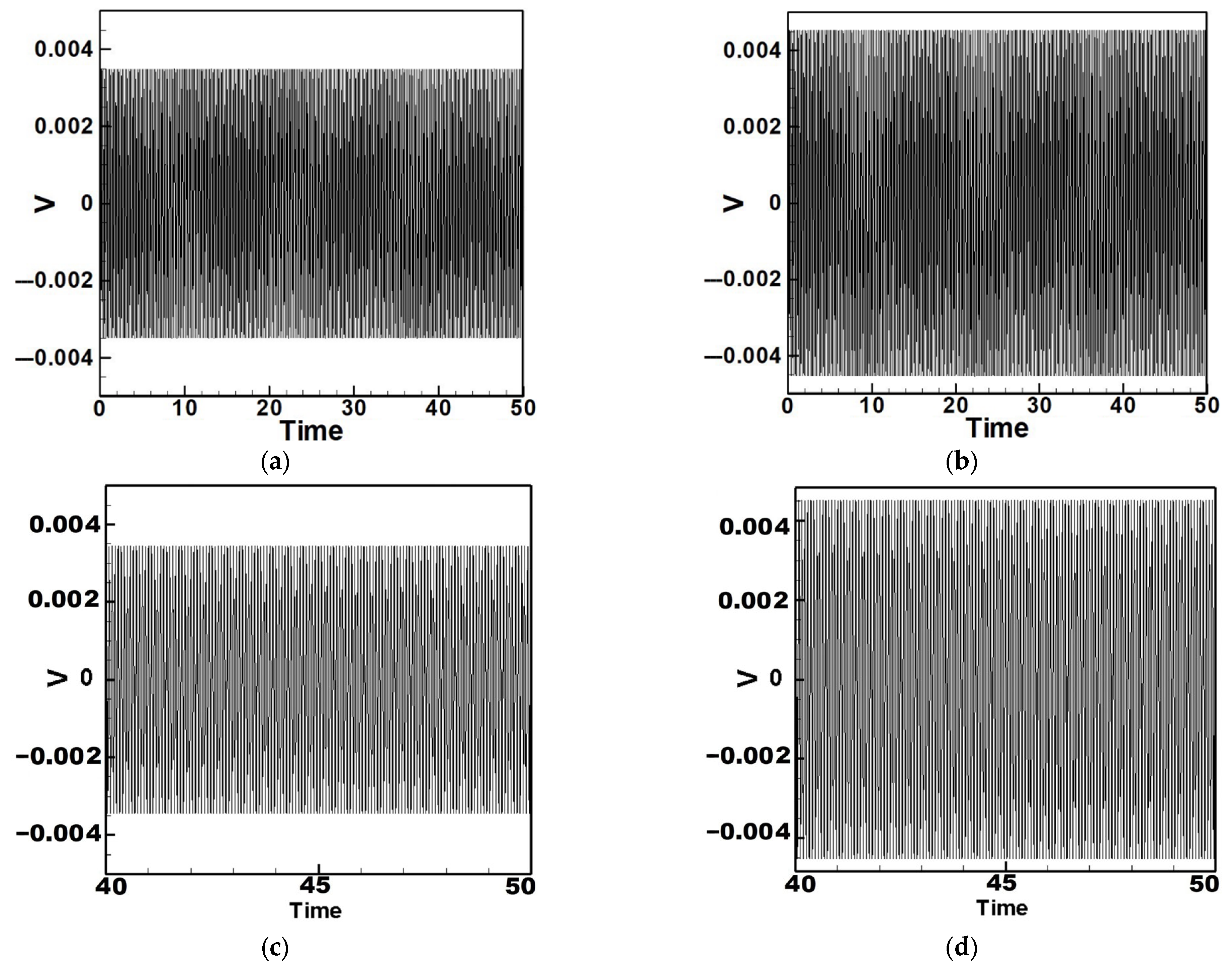
5.1. Quantitative Discussion and Comparison with Experimental Results
- (1)
- Internal Resonance Case
- (2)
- Non-Resonant Case
5.2. Physical Discussion and Mechanism Interpretation
- (1)
- Energy transfer and internal resonance effects.
- (2)
- Voltage enhancement through slapping mechanism.
- (3)
- Error sources and system sensitivity.
- (4)
- Application potential and optimization.
- (5)
- Mechanism of Energy Transfer and Slapping Interaction.
5.3. Sensitivity Discussion of Key Parameters
5.4. Future Perspectives
6. Conclusions
- Validation of theoretical modeling.
- 2.
- Influence of internal resonance.
- 3.
- Role of the slapping mechanism.
- 4.
- Experimental verification and robustness.
- 5.
- Practical significance and applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description |
| A | Circle plate (leaf) cross-sectional area |
| Ab | beam cross-sectional area |
| Cp | Capacitance of the PZT |
| Cf | Piezoelectric coupling coefficient |
| Young’s modulus of the elastic beam | |
| F | Slapping force (acting on the root of the main structure) |
| Fb | Wind force acting on both the circular plate and the rectangular plate. |
| Beam area moment of inertia | |
| Dimensionless mass moment of inertia of the circle plate (leaf) | |
| Dimensionless beam mass moment of inertia | |
| Length of beam | |
| Mass ratio of the circle plate to the beam | |
| mb | beam mass |
| q | distributed external force |
| Dimensionless distributed external force | |
| T | Slapping period |
| Dimensionless slapping period | |
| t | Dimensional time |
| V | Voltage |
| Eigenvalue of nth mode | |
| Time scale of small perturbations. | |
| Von Kármán nonlinear strain | |
| Dimensionless damping coefficient | |
| Generalized coordinate (time-dependent variable) | |
| Dimensionless voltage | |
| Density | |
| Dimensionless time | |
| Mode shape of nth mode | |
| Tuned frequency | |
| The nth mode phase | |
| Natural frequency of nth mode |
Appendix A
Appendix B
Appendix C
| Parameter | Symbol | Dimensionless/Normalized Value | Description |
|---|---|---|---|
| Beam length | 1.0 | Reference length for normalization | |
| Circular-plate diameter | 0.4–0.8 | Diameter ratio | |
| Equivalent stiffness | 1.0 | Baseline stiffness for normalization | |
| Plate mass | 0.12–0.25 | Normalized mass relative to beam mass | |
| Piezoelectric patch length | 0.16 | ratio | |
| Piezoelectric coupling coefficient | 0.002 | Dimensionless coupling between mechanical strain and electric field (from PZT-5H properties) |
References
- Cheng, T.H.; Ching, K.B.; Uttraphan, C.; Heong, Y.M. A Review on Energy Harvesting Potential from Living Plants: Future Energy Resource. Int. J. Renew. Energy Res. 2018, 8, 2598–2614. [Google Scholar] [CrossRef]
- Yan, G.; Zou, H.-X.; Wang, S.; Zhao, L.-C.; Wu, Z.-Y.; Zhang, W.-M. Bio-Inspired Vibration Isolation: Methodology and Design. Appl. Mech. Rev. 2021, 73, 020801. [Google Scholar] [CrossRef]
- Huang, Z.; Shi, X.; Mu, D.; Huang, X.; Tong, W. Performance and Optimization of a Dual-Stage Vibration Isolation System Using Bio-Inspired Vibration Isolators. Appl. Sci. 2022, 12, 11387. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, D.; Hou, B.; Ren, Z. Vibration isolation performance analysis of a bilateral supported bio-inspired anti-vibration control system. Appl. Math. Mech. 2023, 44, 759–772. [Google Scholar] [CrossRef]
- Choo, Y.Y.; Dayou, J. A method to harvest electrical energy from living plants. J. Sci. Technol. 2013, 5, 79–90. [Google Scholar]
- Ying, C.Y.; Dayou, J. MODELLING OF THE ELECTRICITY GENERATION FROM LIVING PLANTS. J. Teknol. 2016, 78, 29–33. [Google Scholar] [CrossRef]
- Pechsiri, T.; Puengsungwan, S. Energy Harvesting Based on Living Plants For Smart Farming. ASEAN J. Sci. Eng. 2022, 3, 47–56. [Google Scholar] [CrossRef]
- Greenman, J.; Thorn, R.; Willey, N.; Ieropoulos, I. Energy harvesting from plants using hybrid microbial fuel cells; potential applications and future exploitation. Front. Bioeng. Biotechnol. 2024, 12, 1276176. [Google Scholar] [CrossRef]
- Wang, W.; He, X.; Wang, X.; Wang, M.; Xue, K. A bioinspired structure modification of piezoelectric wind energy harvester based on the prototype of leaf veins. Sens. Actuators A Phys. 2018, 279, 467–473. [Google Scholar] [CrossRef]
- Qian, F.; Hajj, M.R.; Zuo, L. Bio-inspired bi-stable piezoelectric harvester for broadband vibration energy harvesting. Energy Convers. Manag. 2020, 222, 113174. [Google Scholar] [CrossRef]
- Lenci, S.; Clementi, F.; Warminski, J. Nonlinear free dynamics of a two-layer composite beam with different boundary conditions. Meccanica 2014, 50, 675–688. [Google Scholar] [CrossRef]
- Kharazan, M.; Irani, S.; Salimi, M.R. Nonlinear vibration analysis of a cantilever beam with a breathing crack and bilinear behavior. J. Vib. Control 2021, 28, 2653–2665. [Google Scholar] [CrossRef]
- Chouvion, B. Vibration analysis of beam structures with localized nonlinearities by a wave approach. J. Sound Vib. 2019, 439, 344–361. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; Wiley-Interscience: New York, NY, USA, 1995. [Google Scholar]
- Thai, T.Q.; Zhuang, X.; Rabczuk, T. Curved flexoelectric and piezoelectric micro-beams for nonlinear vibration analysis of energy harvesting. Int. J. Solids Struct. 2022, 264, 112096. [Google Scholar] [CrossRef]
- Sahoo, B. Nonlinear Vibration Analysis of a Hinged–Clamped Beam Moving with Pulsating Speed and Subjected to Internal Resonance. Int. J. Struct. Stab. Dyn. 2021, 21, 2150117. [Google Scholar] [CrossRef]
- Wang, Y.-R.; Chen, P.-T. Energy harvesting analysis of the magneto-electric and fluid-structure interaction parametric excited system. J. Sound Vib. 2023, 569, 118087. [Google Scholar] [CrossRef]
- Sofi, A.; Muscolino, G.; Di Paola, M. Reliability analysis of structures controlled by external fractional viscoelastic dampers with interval parameters. Acta Mech. Sin. 2023, 39, 722486. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, Z.; Wei, Y.; Xiong, Y. Nonlinear electromagnetic vibration energy harvester comprising dual helical-plane springs and multiple halbach arrays for low-frequency and small-amplitude vibrations. Energy Rep. 2024, 11, 1363–1375. [Google Scholar] [CrossRef]
- Clementi, G.; Neri, I.; Cottone, F.; Di Michele, A.; Mattarelli, M.; Sforna, L.; Chiappalupi, S.; Sorci, G.; Michelucci, A.; Catacuzzeno, L.; et al. Self-Powered Temperature Sensors Harnessing Membrane Potential of Living Cells. Nano Energy 2024, 121, 109211. [Google Scholar] [CrossRef]
- Guo, X.; Wang, L.; Jin, Z.; Lee, C. A multifunctional hydrogel with multimodal self-powered sensing capability and stable direct-current output for outdoor plant monitoring systems. Nano-Micro Lett. 2025, 17, 76. [Google Scholar] [CrossRef]
- Qu, G.; Xia, H.; Liang, Q.; Liu, Y.; Ming, S.; Zhao, J.; Xia, Y.; Wu, J. Current research status and future trends of vibration energy harvesters. Micromachines 2024, 15, 1109. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-R.; Chu, M.-C. Analysis of Double Elastic Steel Wind Driven Magneto-Electric Vibration Energy Harvesting System. Sensors 2021, 21, 7364. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-R.; Wong, M.-S.; Chen, B.-Y. Analytical and Experimental Studies of Double Elastic Steel Sheet (DESS) Vibration Energy Harvester System. Energies 2020, 13, 1793. [Google Scholar] [CrossRef]
- Wang, Y.-R.; Hung, C.-C.; Tseng, J.-T. Transverse Vibration Energy Harvesting of Double Elastic Steel. Int. J. Struct. Stab. Dyn. 2021, 21, 2150113. [Google Scholar] [CrossRef]
- Rajora, A.; Dwivedi, A.; Vyas, A.; Gupta, S.; Tyagi, A. Energy Harvesting Estimation from the Vibration of a Simply Supported Beam. Int. J. Acoust. Vib. 2017, 22, 186–193. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Li, R.; Dai, L.; Wang, W.; Yang, K. Internal resonance of a two-degree-of-freedom tuned bistable electromagnetic actuator. Chaos Solitons Fractals 2021, 143, 110612. [Google Scholar] [CrossRef]
- Li, N.; Yang, F.; Luo, T.; Qin, L. Design and Experimental Investigation of an Ultra-Low Frequency, Low-Intensity, and Multidirectional Piezoelectric Energy Harvester with Liquid as the Energy-Capture Medium. Micromachines 2023, 14, 369. [Google Scholar] [CrossRef]
- Zhang, Q.; Yan, Y.; Han, J.; Hao, S.; Wang, W. Dynamic Design of a Quad-Stable Piezoelectric Energy Harvester via Bifurcation Theory. Sensors 2022, 22, 8453. [Google Scholar] [CrossRef]
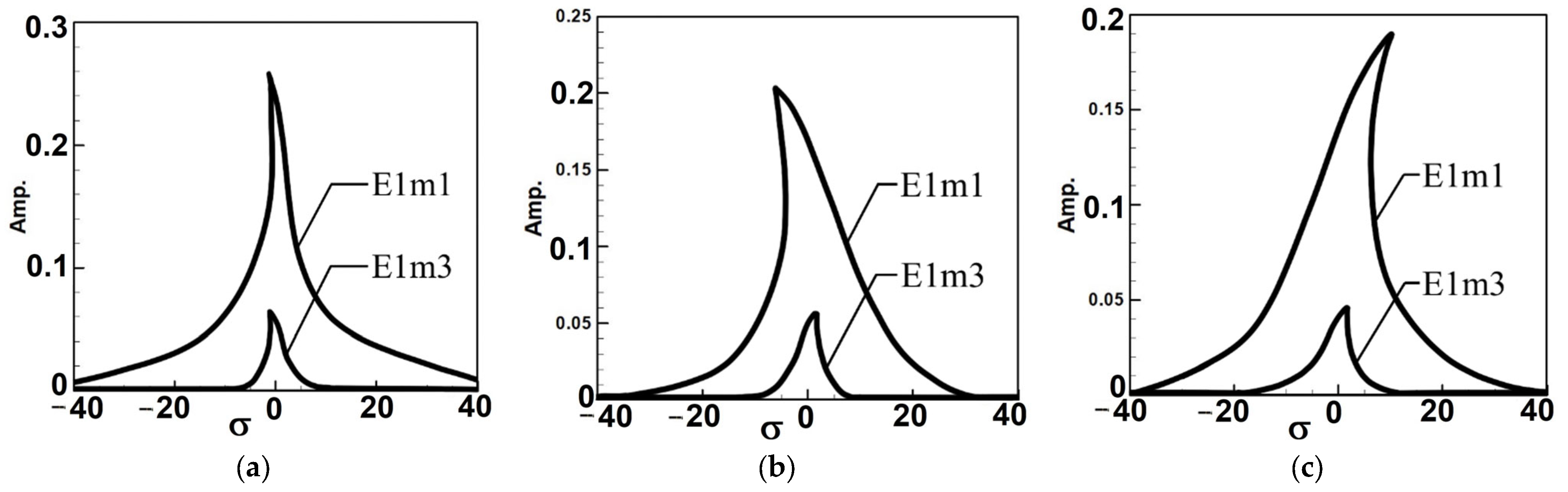
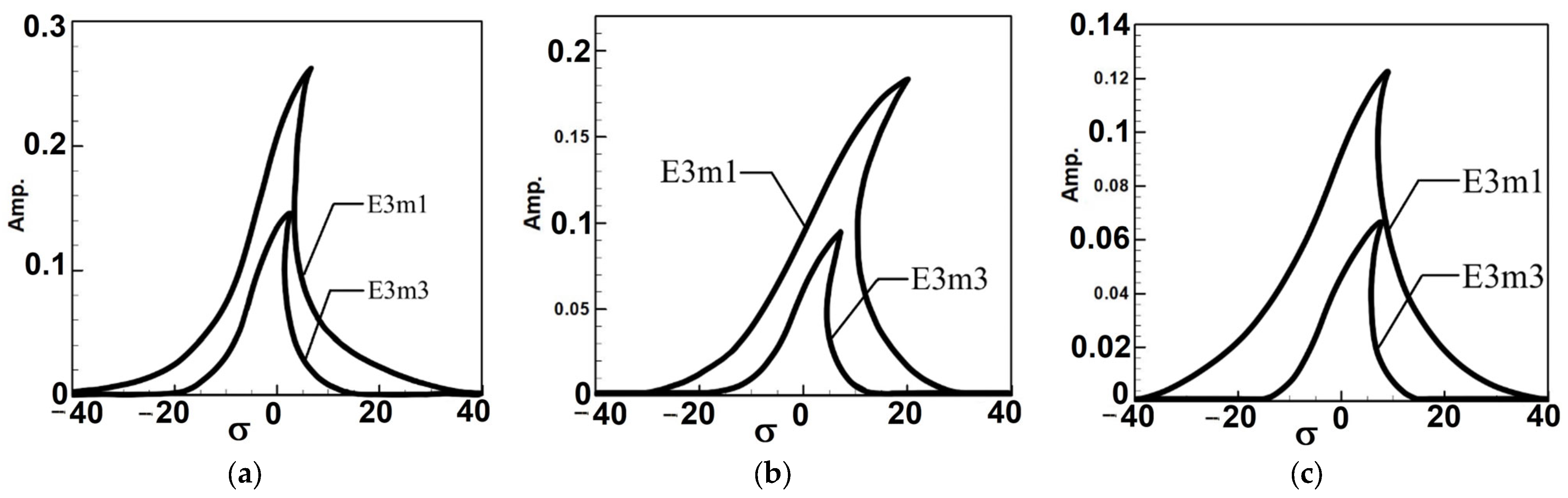
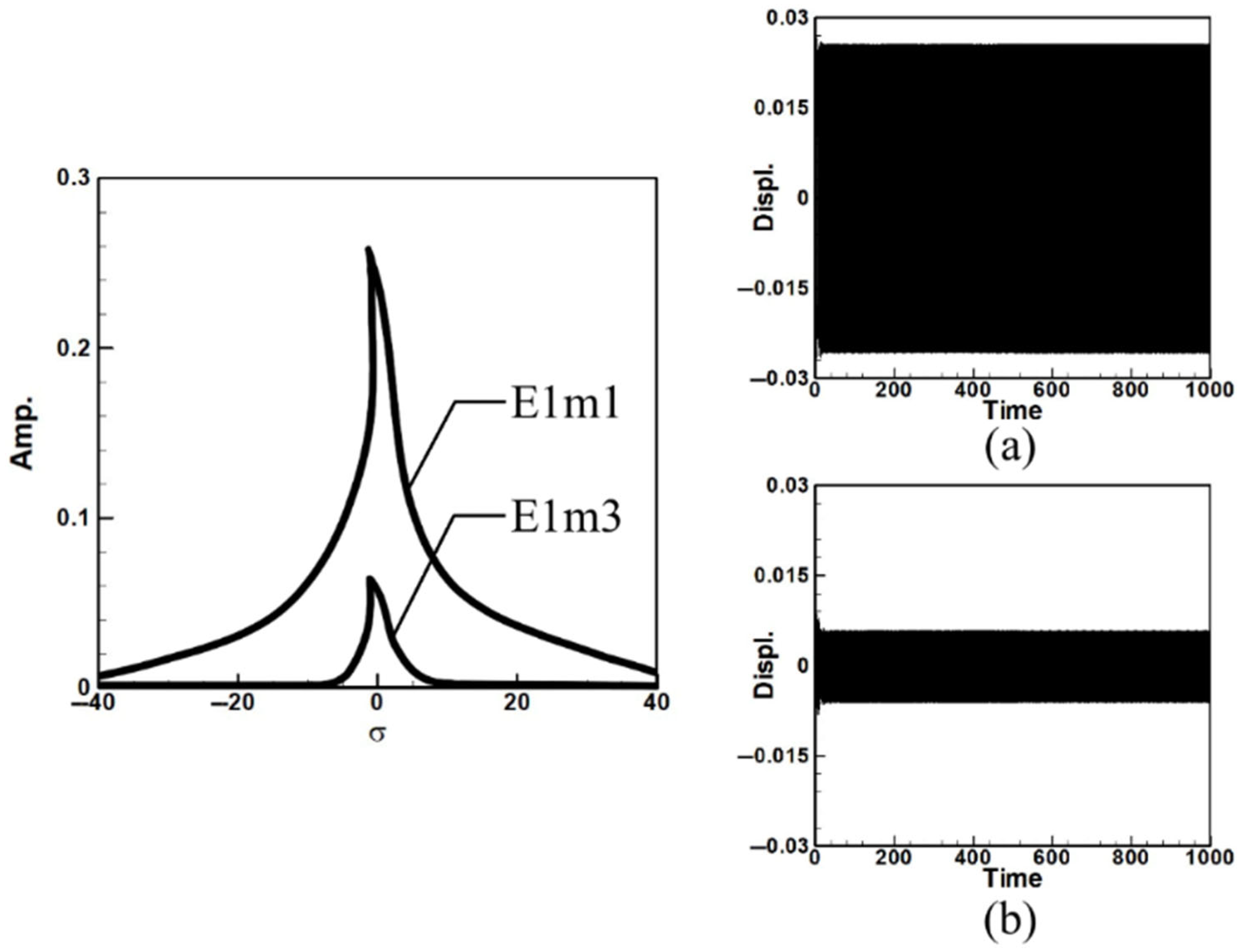
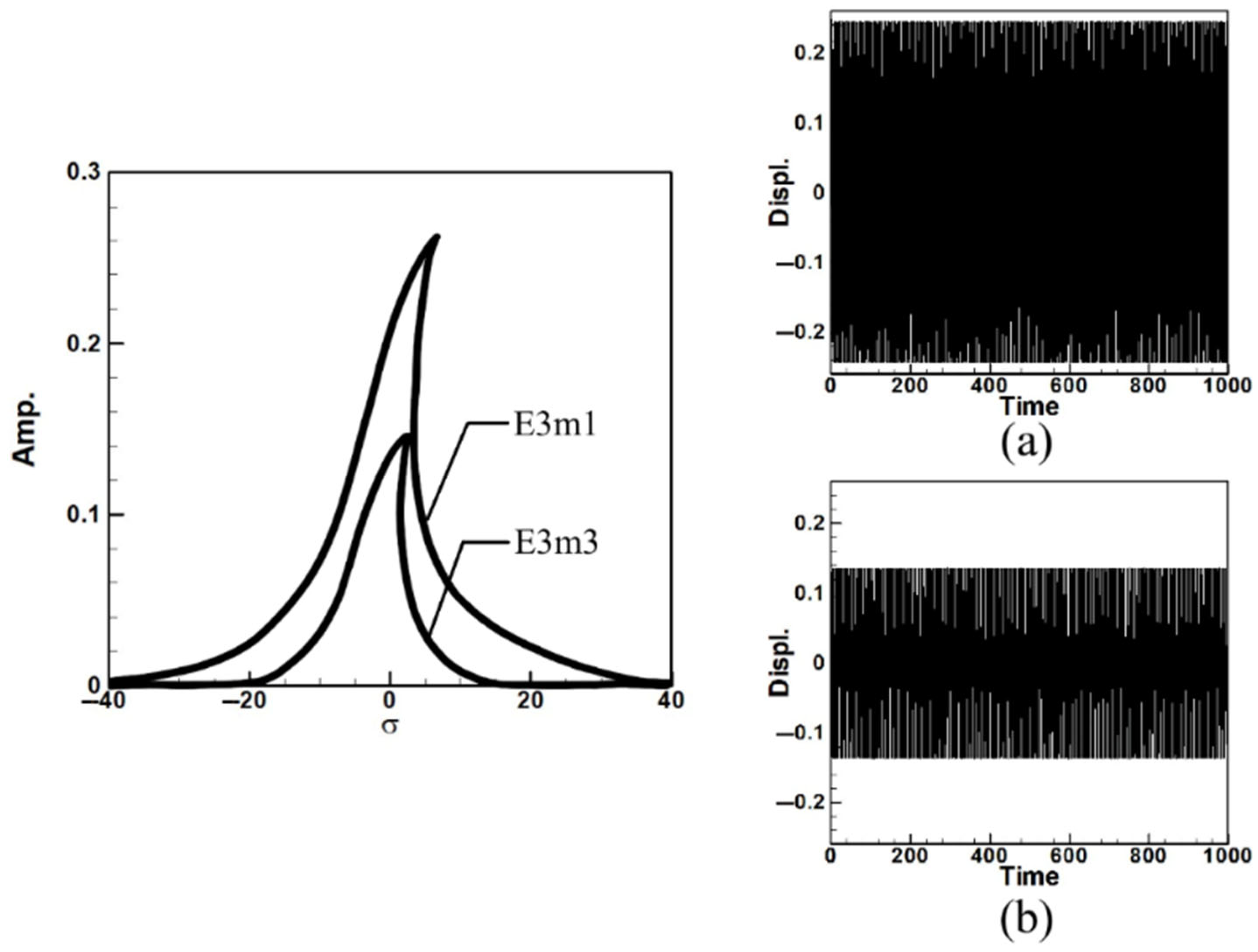
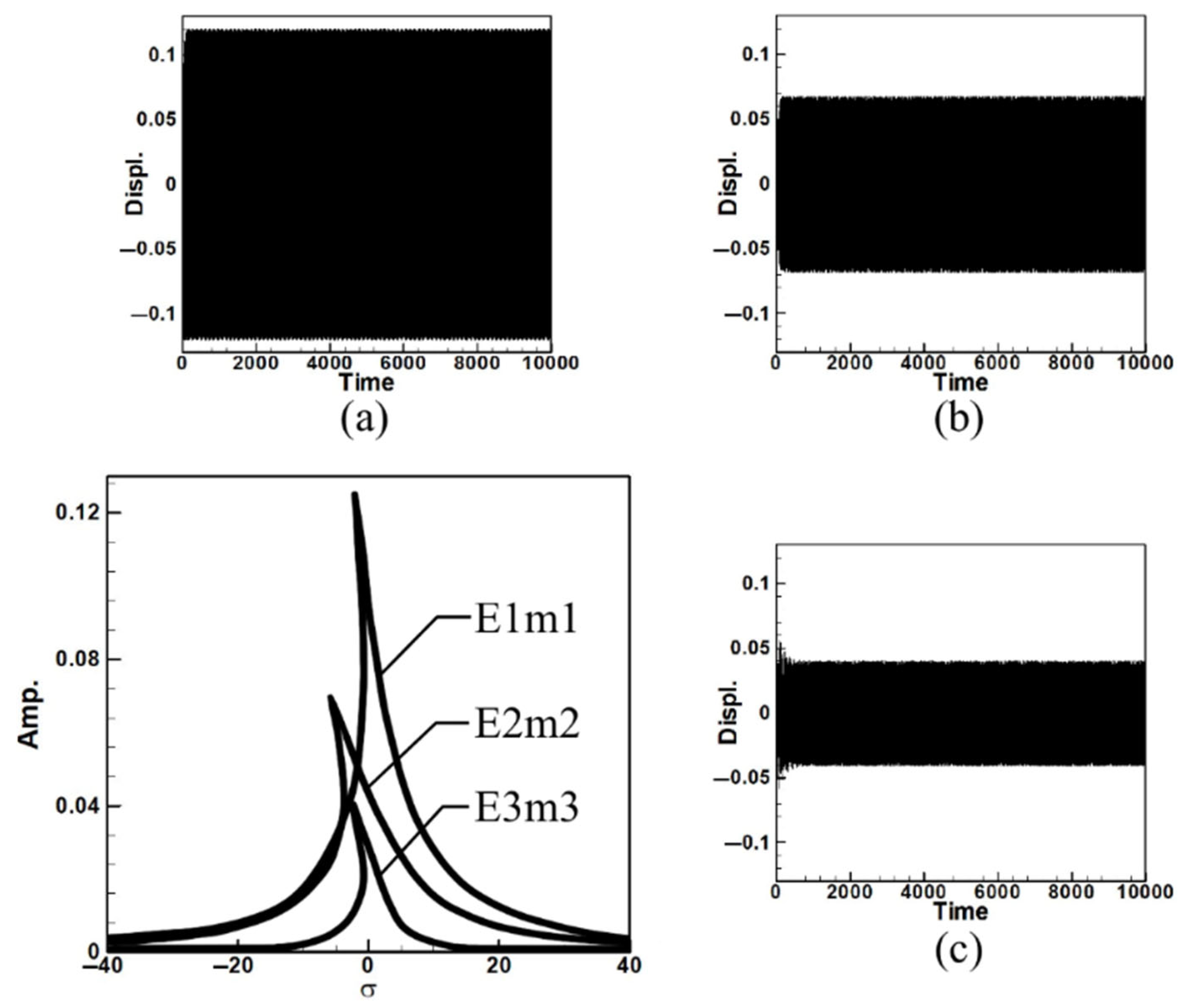
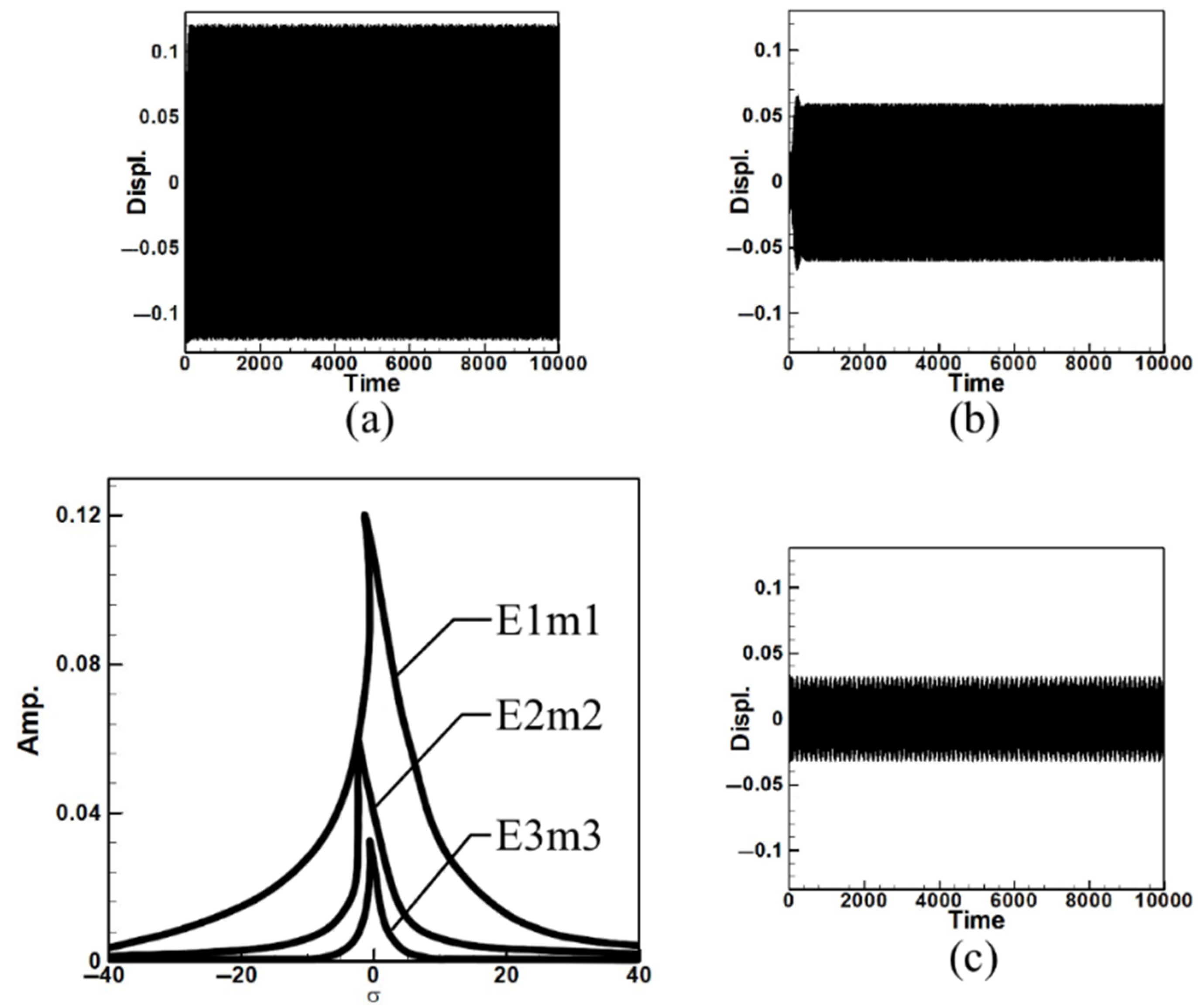
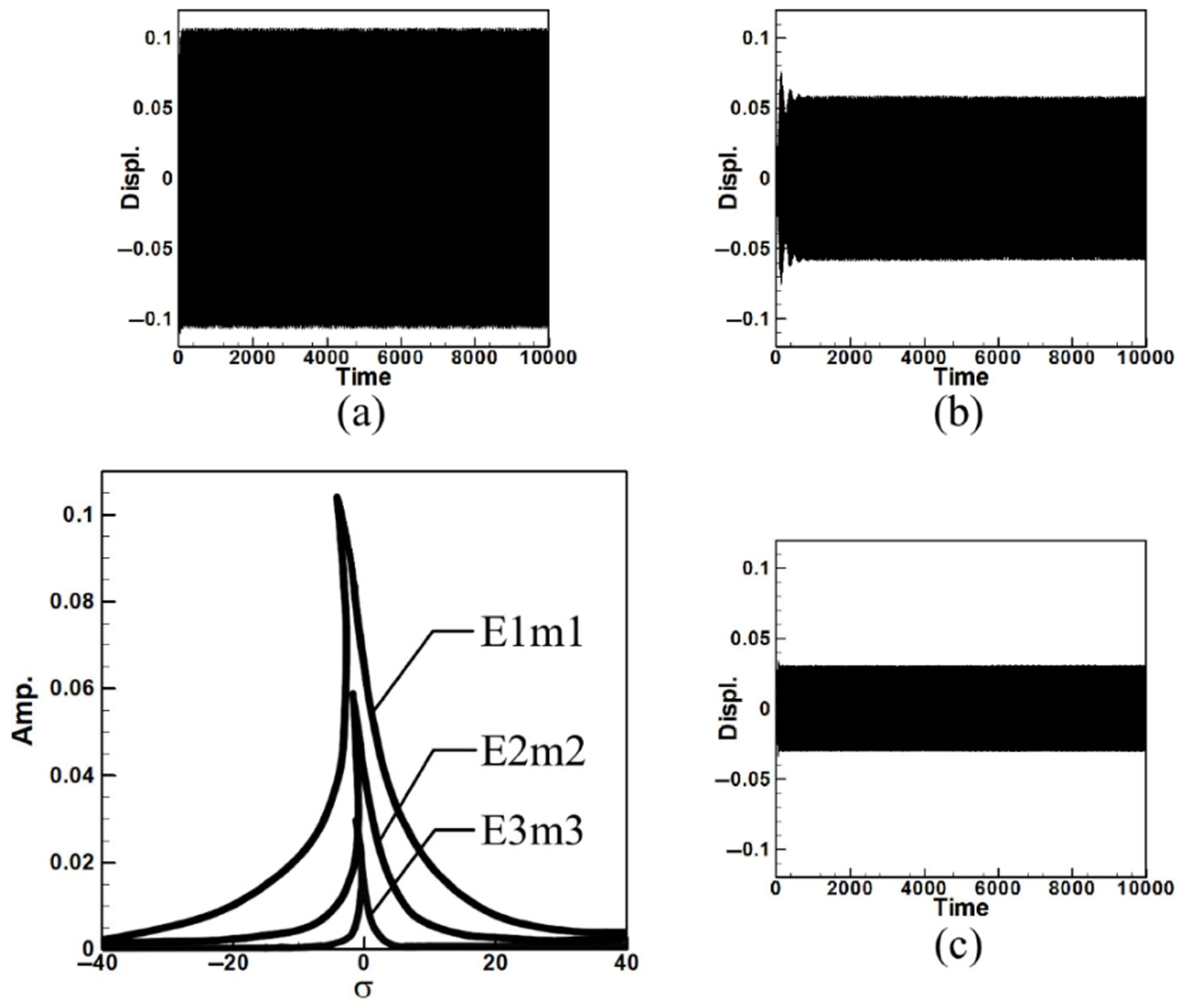

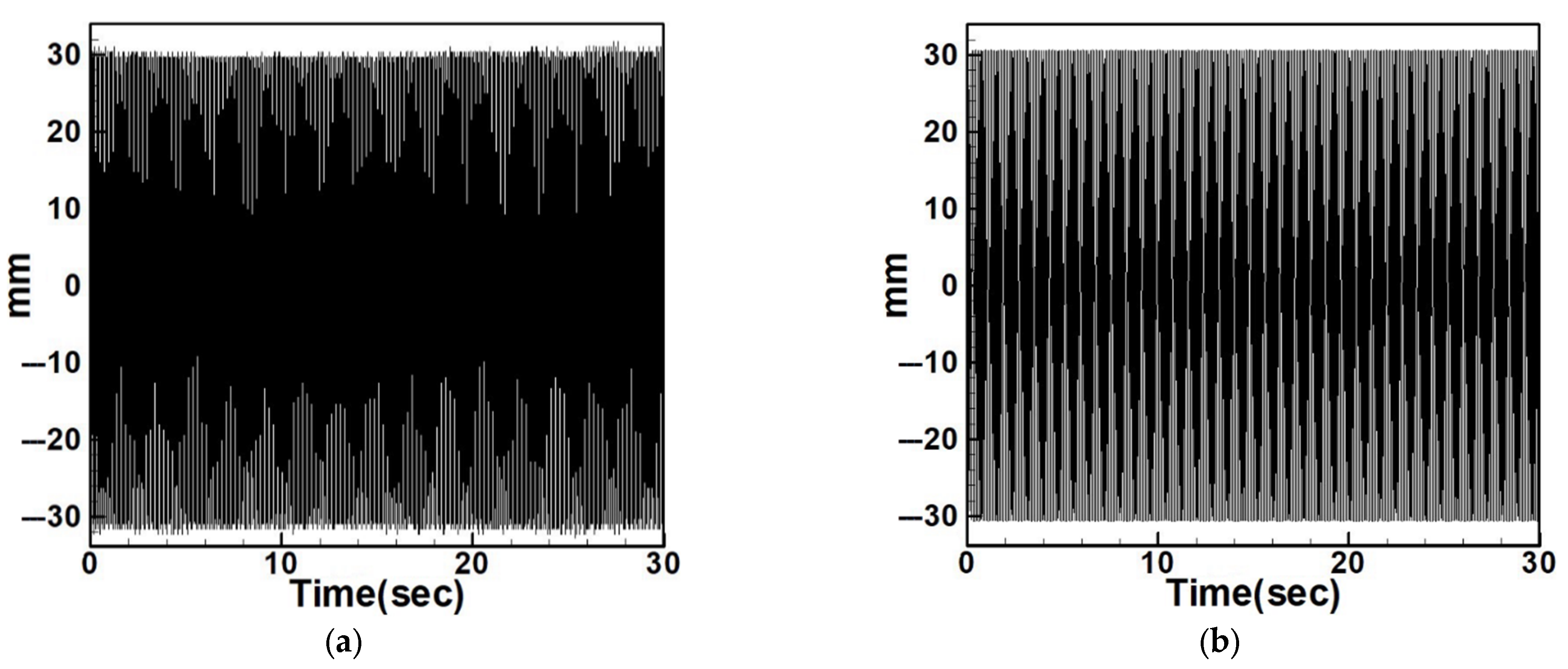
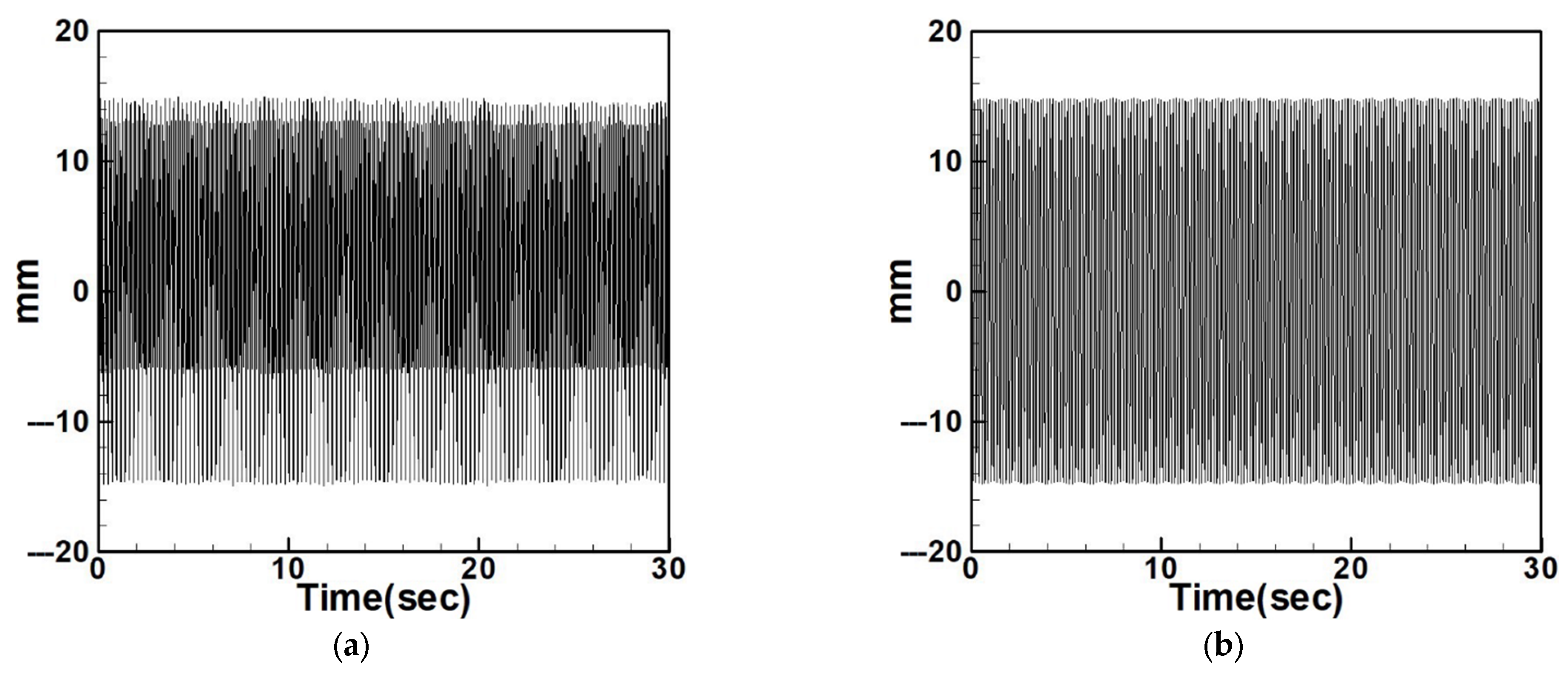

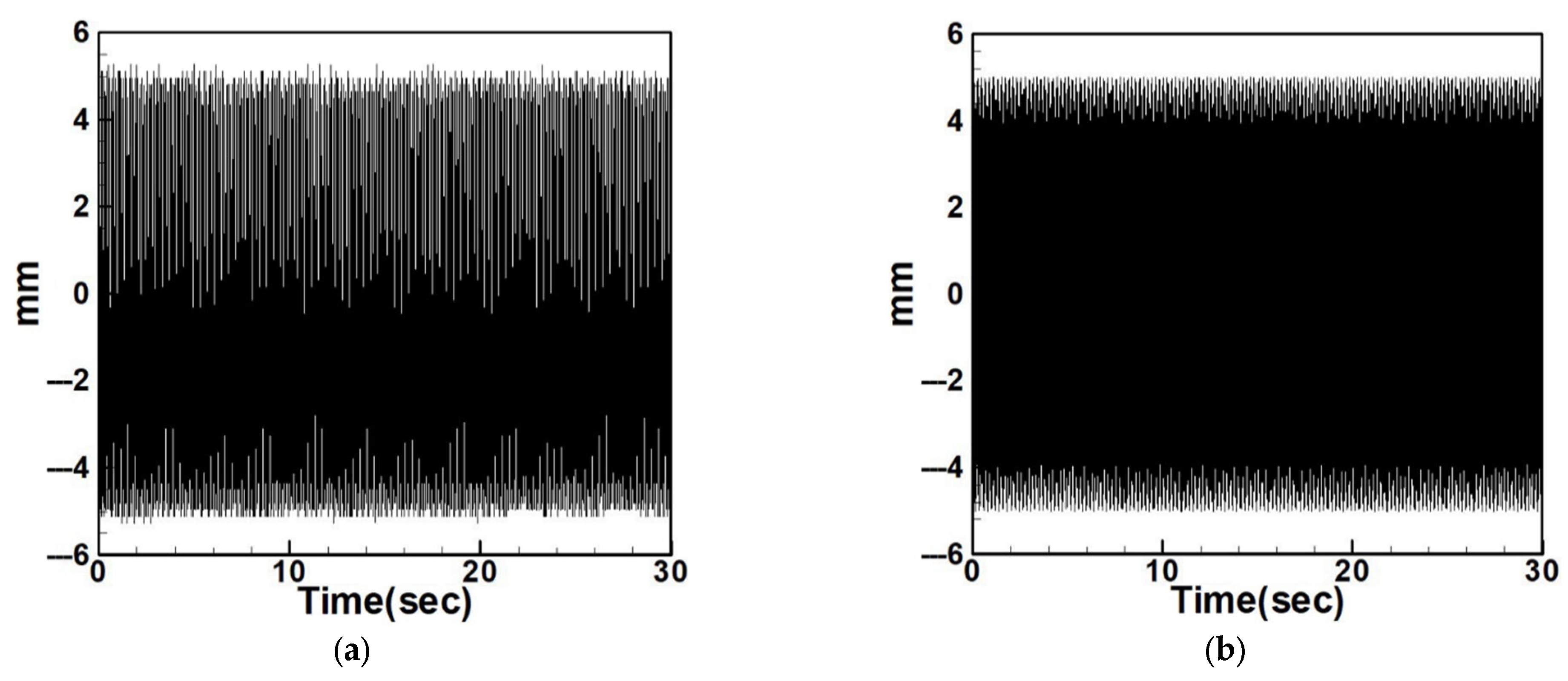
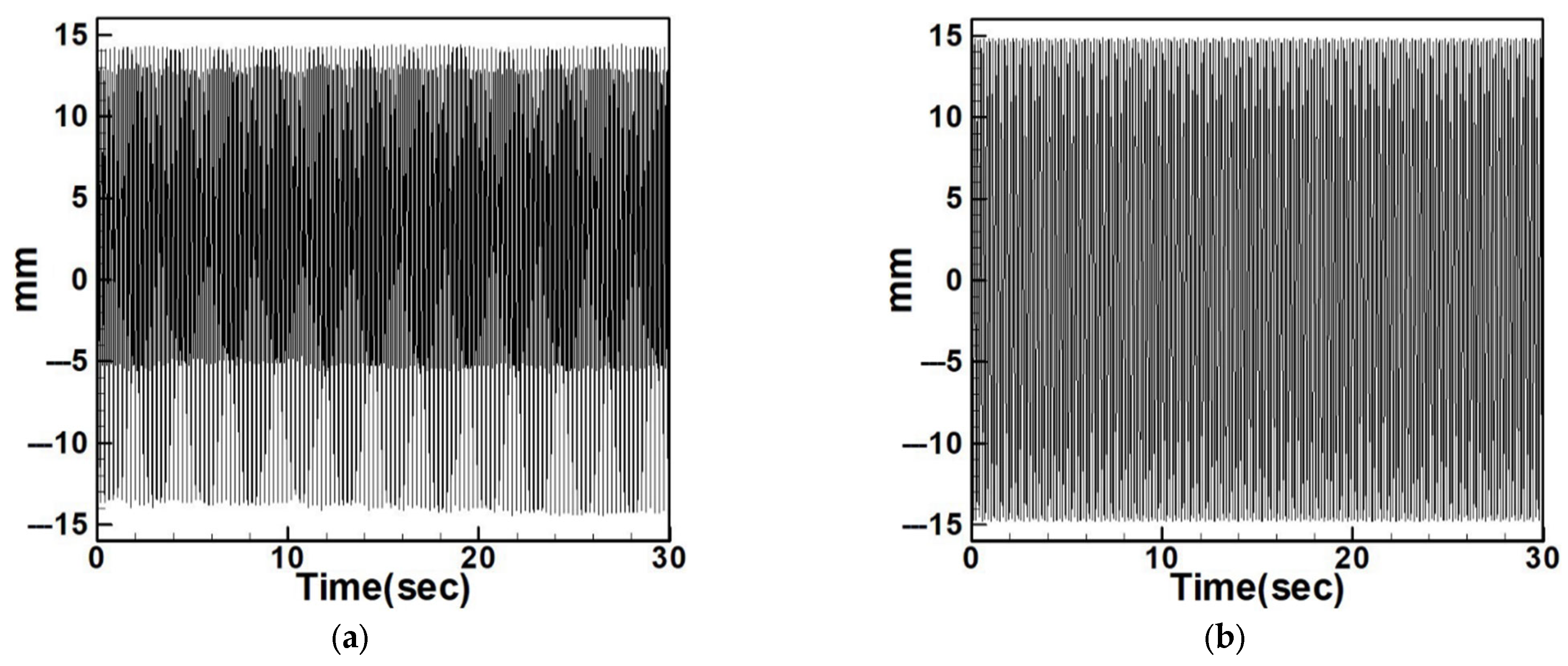
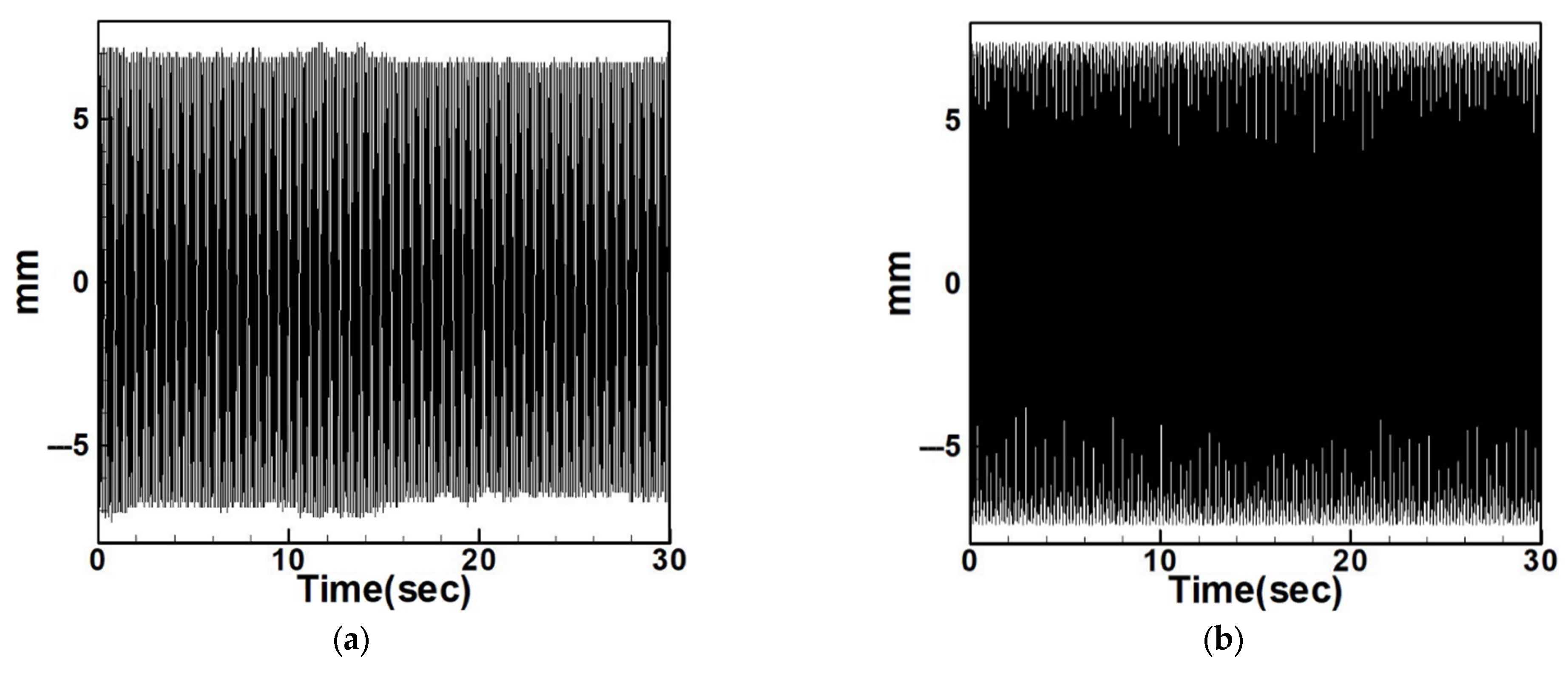
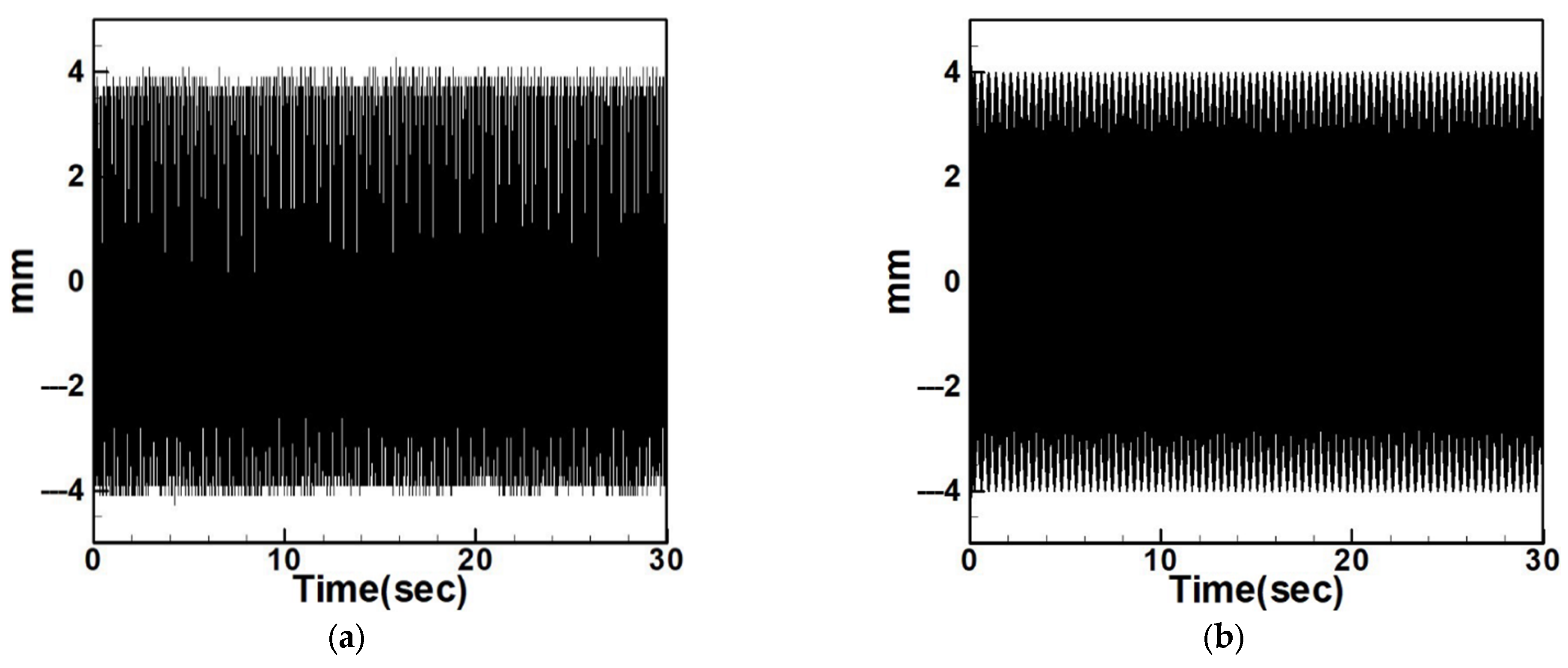
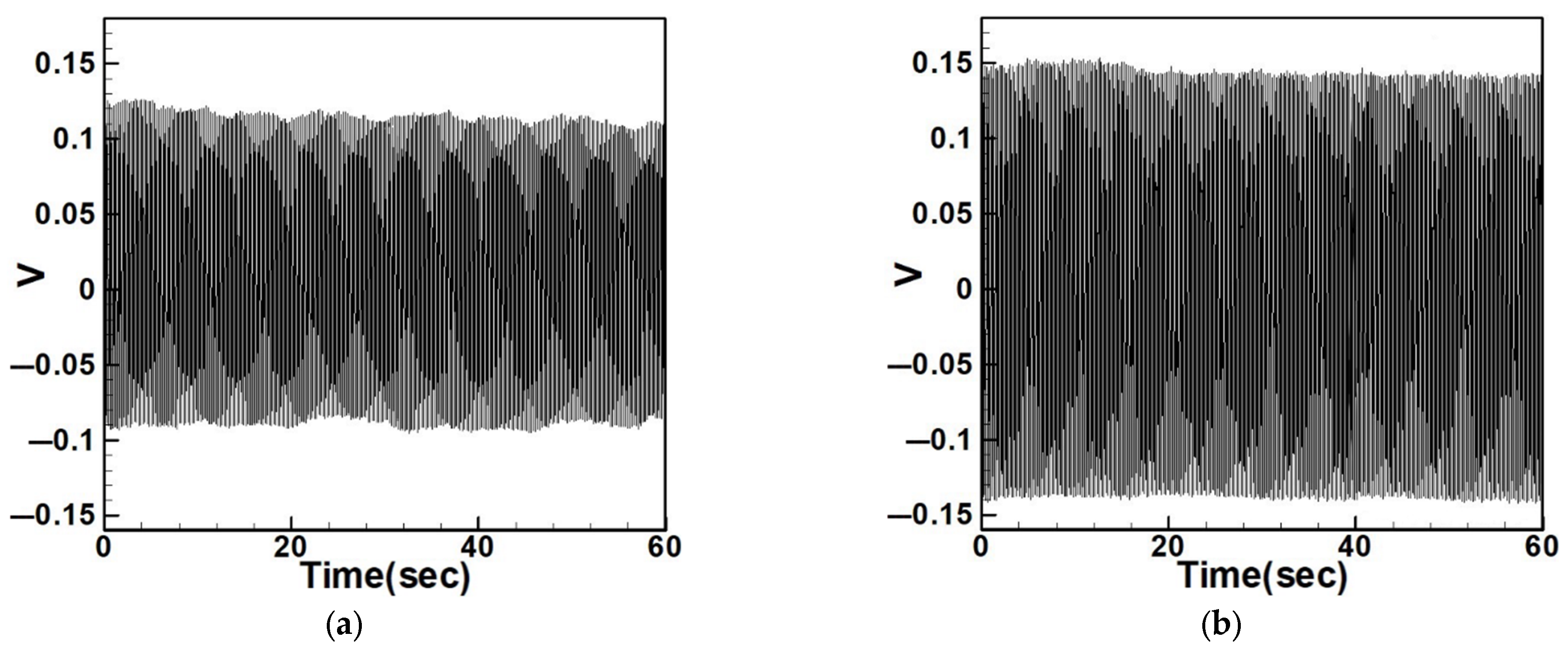
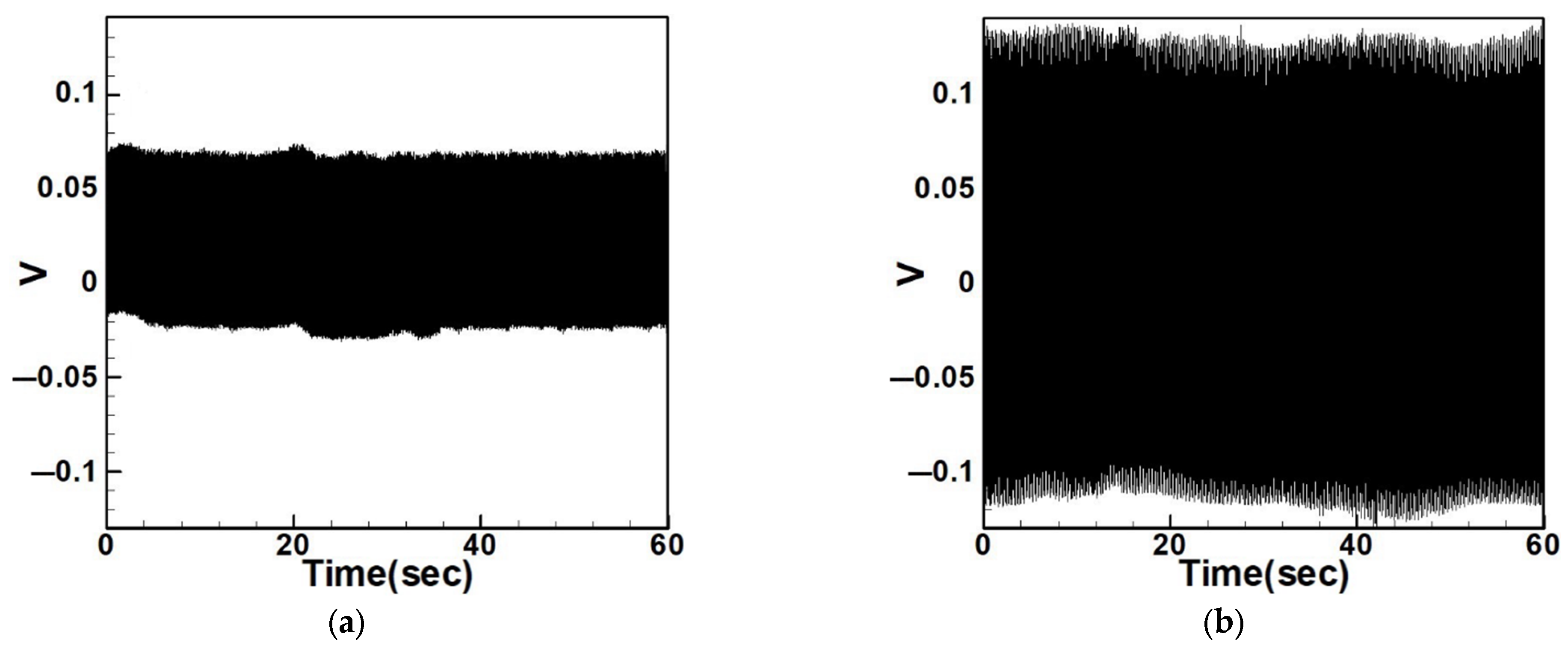



| Circular Plate Dimensionless Diameters | |||
|---|---|---|---|
| 0.4 | 0.19294 | 0.15584 | 0.46751 |
| 0.8 | 0.12930 | 0.13630 | 0.40891 |
| 1.2 | 0.12431 | 0.12595 | 0.37784 |
| D = 0.4 | D = 0.8 | D = 1.2 | ||||
|---|---|---|---|---|---|---|
| Excite 1st Mode | Excite 3rd Mode | Excite 1st Mode | Excite 3rd Mode | Excite 1st Mode | Excite 3rd Mode | |
| Mode 1 | 0.27612 | 0.24564 | 0.1966 | 0.1838 | 0.188 | 0.1232 |
| Mode 3 | 0.06524 | 0.1368 | 0.04972 | 0.0978 | 0.0474 | 0.06828 |
| D = 0.4 | D = 0.8 | D = 1.2 | |
|---|---|---|---|
| Excite 1st mode | 0.11912 | 0.11832 | 0.10664 |
| Excite 2nd mode | 0.06736 | 0.05888 | 0.05808 |
| Excite 3rd mode | 0.04016 | 0.03224 | 0.03056 |
| Diameter Ratio | D = 0.4 | D = 0.8 | D = 1.2 | |||
|---|---|---|---|---|---|---|
| Mode excited | 1st | 3rd | 1st | 3rd | 1st | 3rd |
| VNo Slp | 0.00694 | 0.00475 | 0.00361 | 0.00292 | 0.00313 | 0.00240 |
| Vslp | 0.00872 | 0.00674 | 0.00489 | 0.00451 | 0.00460 | 0.00346 |
| Diameter Ratio | D = 0.4 | D = 0.8 | D = 1.2 | |
|---|---|---|---|---|
| VNo Slp | Excite 1st mode | 0.00160 | 0.00148 | 0.00122 |
| Excite 2nd mode | 0.00183 | 0.00171 | 0.00141 | |
| Excite 3rd mode | 0.00193 | 0.00186 | 0.00152 | |
| Vslp | Excite 1st mode | 0.00192 | 0.00177 | 0.00146 |
| Excite 2nd mode | 0.00203 | 0.00199 | 0.00161 | |
| Excite 3rd mode | 0.00219 | 0.00209 | 0.00180 |
| Excite 1st | Excite 3rd | |
|---|---|---|
| Theo. | 4.36 | 13.08 |
| Exp. | 4.25 | 12.45 |
| Error (%) | 2.52 | 4.82 |
| D = 5 cm | D = 10 cm | |||||
|---|---|---|---|---|---|---|
| Excite 1st | Excite 2nd | Excite 3rd | Excite 1st | Excite 2nd | Excite 3rd | |
| Theo. | 4.41 | 8.51 | 13.56 | 4.02 | 9.87 | 15.83 |
| Exp. | 4.15 | 8.19 | 13.15 | 4.07 | 9.57 | 15.65 |
| Error (%) | 5.90 | 3.76 | 3.02 | 1.24 | 3.04 | 1.14 |
| Excite 1st Mode | Excite 3rd Mode | |
|---|---|---|
| Theo. | 19.684126 | 20.27122 |
| Exp. | 22.351167 | 22.420755 |
| Error (%) | 13.549196 | 10.603875 |
| D = 5 cm | D = 10 cm | |||||
|---|---|---|---|---|---|---|
| Excite 1st Mode | Excite 2nd Mode | Excite 3rd Mode | Excite 1st Mode | Excite 2nd Mode | Excite 3rd Mode | |
| Theo. | 10.5639 | 5.9358 | 3.5290 | 10.5425 | 5.2164 | 2.7329 |
| Exp. | 9.9936 | 5.8203 | 3.3733 | 10.1664 | 4.9504 | 2.6161 |
| Error (%) | 5.3987 | 1.9450 | 4.4114 | 3.5676 | 5.0997 | 4.2755 |
| Excite 1st Mode | Excite 3rd Mode | |
|---|---|---|
| Theo. (V) | 0.086796 | 0.059363 |
| Exp. (V) | 0.074732 | 0.050280 |
| Error (%) | 13.898451 | 15.299765 |
| Excite 1st Mode | Excite 3rd Mode | |
|---|---|---|
| Theo. (V) | 0.108962 | 0.084209 |
| Exp. (V) | 0.104095 | 0.0865736 |
| Error (%) | 4.466694811 | 2.808013395 |
| D = 5 cm | D = 10 cm | |||||
|---|---|---|---|---|---|---|
| Excite 1st Mode | Excite 2nd Mode | Excite 3rd Mode | Excite 1st Mode | Excite 2nd Mode | Excite 3rd Mode | |
| Theo. (V) | 0.01999 | 0.02291 | 0.02408 | 0.01846 | 0.02142 | 0.02330 |
| Exp. (V) | 0.01944 | 0.02317 | 0.02527 | 0.01847 | 0.02110 | 0.02406 |
| Error (%) | 2.71795 | 1.14112 | 4.92878 | 0.00649 | 1.49383 | 3.26509 |
| D = 5 cm | D = 10 cm | |||||
|---|---|---|---|---|---|---|
| Excite 1st Mode | Excite 2nd Mode | Excite 3rd Mode | Excite 1st Mode | Excite 2nd Mode | Excite 3rd Mode | |
| Theo. (V) | 0.02394 | 0.02533 | 0.02742 | 0.02218 | 0.02490 | 0.02610 |
| Exp. (V) | 0.02383 | 0.02506 | 0.02872 | 0.02136 | 0.02500 | 0.02626 |
| Error (%) | 0.48824 | 1.06535 | 4.75635 | 3.68407 | 0.40882 | 0.62182 |
| Excited Mode | Vno slapping (V) | Vwith slapping (V) | ΔV (%) | Pslap/Pno | ΔP (%) |
|---|---|---|---|---|---|
| 1st mode | 0.07473 | 0.10409 | 39.3 | 1.94 | 94.0 |
| 3rd mode | 0.05028 | 0.08657 | 72.2 | 2.96 | 196.5 |
| Plate Dia. | Excited Mode | (V) | (V) | ΔV (%) | ΔP (%) | |
|---|---|---|---|---|---|---|
| 5 cm | 1st | 0.01944 | 0.02383 | 22.6 | 1.50 | 50.3 |
| 5 cm | 2nd | 0.02317 | 0.02506 | 8.2 | 1.17 | 17.0 |
| 5 cm | 3rd | 0.02527 | 0.02872 | 13.7 | 1.29 | 29.2 |
| 10 cm | 1st | 0.01847 | 0.02136 | 15.6 | 1.34 | 33.7 |
| 10 cm | 2nd | 0.02110 | 0.02500 | 18.5 | 1.40 | 40.4 |
| 10 cm | 3rd | 0.02406 | 0.02626 | 9.1 | 1.19 | 19.1 |
| System/Reference | Frequency Range (Hz) | RMS Voltage/Power Trend | Key Mechanism | Remarks |
|---|---|---|---|---|
| Proposed BIS-VEHS (with slapping) | 5~20 | 0.104 V (RMS), ≈1.9× higher power than no-slap case | Internal resonance + slapping impact | High efficiency at low frequency; bio-inspired design |
| Piezoelectric (liquid-coupled cantilever), Li et al., Micromachines 2023, [28] | <3 | ≈0.07 V RMS (~51 µW at 0.03 g) | Liquid-medium energy capture | Ultra-low-frequency multidirectional harvesting |
| Quad-stable PEH, Zhang et al., Sensors 2022, [29] | ~5–17 Hz | ~0.1 V RMS (≈1 mW peak) | Geometric nonlinear piezoelectric harvester (bifurcation-based) | Broadband low-frequency, geometric nonlinearity, magnet-free design |
| Electromagnetic, tristable, Chen et al., Energy Reports 2024, [19] | 20~30 | 0.1 V RMS | Dual helical spring stiffness + Halbach arrays | Broadband, small-amplitude low-frequency operation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.-R.; Chen, S.-H.; Ma, S.-S. A Bio-Inspired Vibration Energy Harvesting System with Internal Resonance and Slapping Mechanism for Enhanced Low-Frequency Power Generation. Sensors 2025, 25, 7222. https://doi.org/10.3390/s25237222
Wang Y-R, Chen S-H, Ma S-S. A Bio-Inspired Vibration Energy Harvesting System with Internal Resonance and Slapping Mechanism for Enhanced Low-Frequency Power Generation. Sensors. 2025; 25(23):7222. https://doi.org/10.3390/s25237222
Chicago/Turabian StyleWang, Yi-Ren, Shian-Hsuan Chen, and Su-Sheng Ma. 2025. "A Bio-Inspired Vibration Energy Harvesting System with Internal Resonance and Slapping Mechanism for Enhanced Low-Frequency Power Generation" Sensors 25, no. 23: 7222. https://doi.org/10.3390/s25237222
APA StyleWang, Y.-R., Chen, S.-H., & Ma, S.-S. (2025). A Bio-Inspired Vibration Energy Harvesting System with Internal Resonance and Slapping Mechanism for Enhanced Low-Frequency Power Generation. Sensors, 25(23), 7222. https://doi.org/10.3390/s25237222







