High-Precision Centroid Measurement Method Based on 3D Scanning and Hooke’s Law
Abstract
1. Introduction
2. Materials and Methods
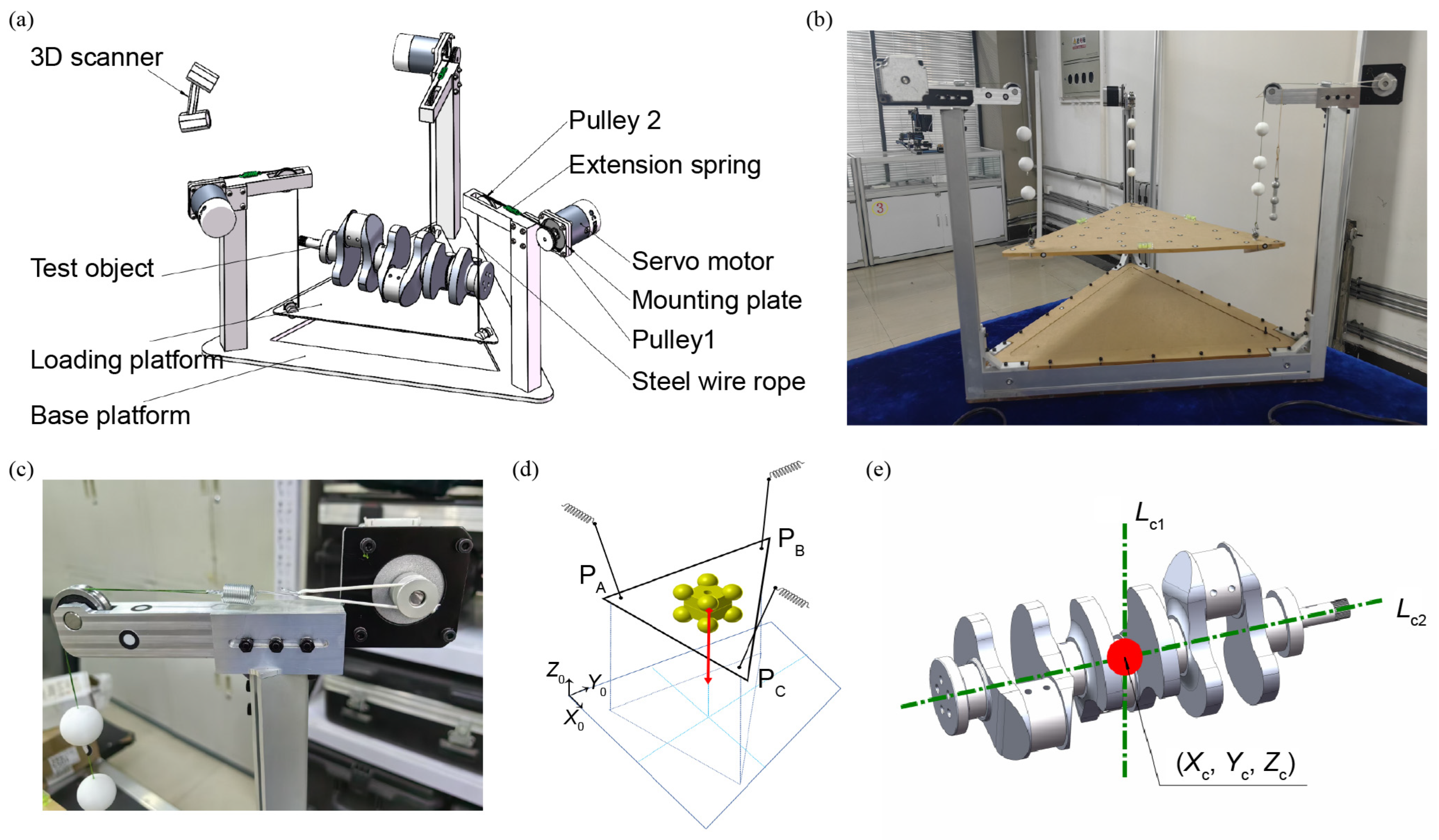
2.1. Overall Design of Centroid Measurement System
2.2. Modeling the Centroid Measurement System
3. Results
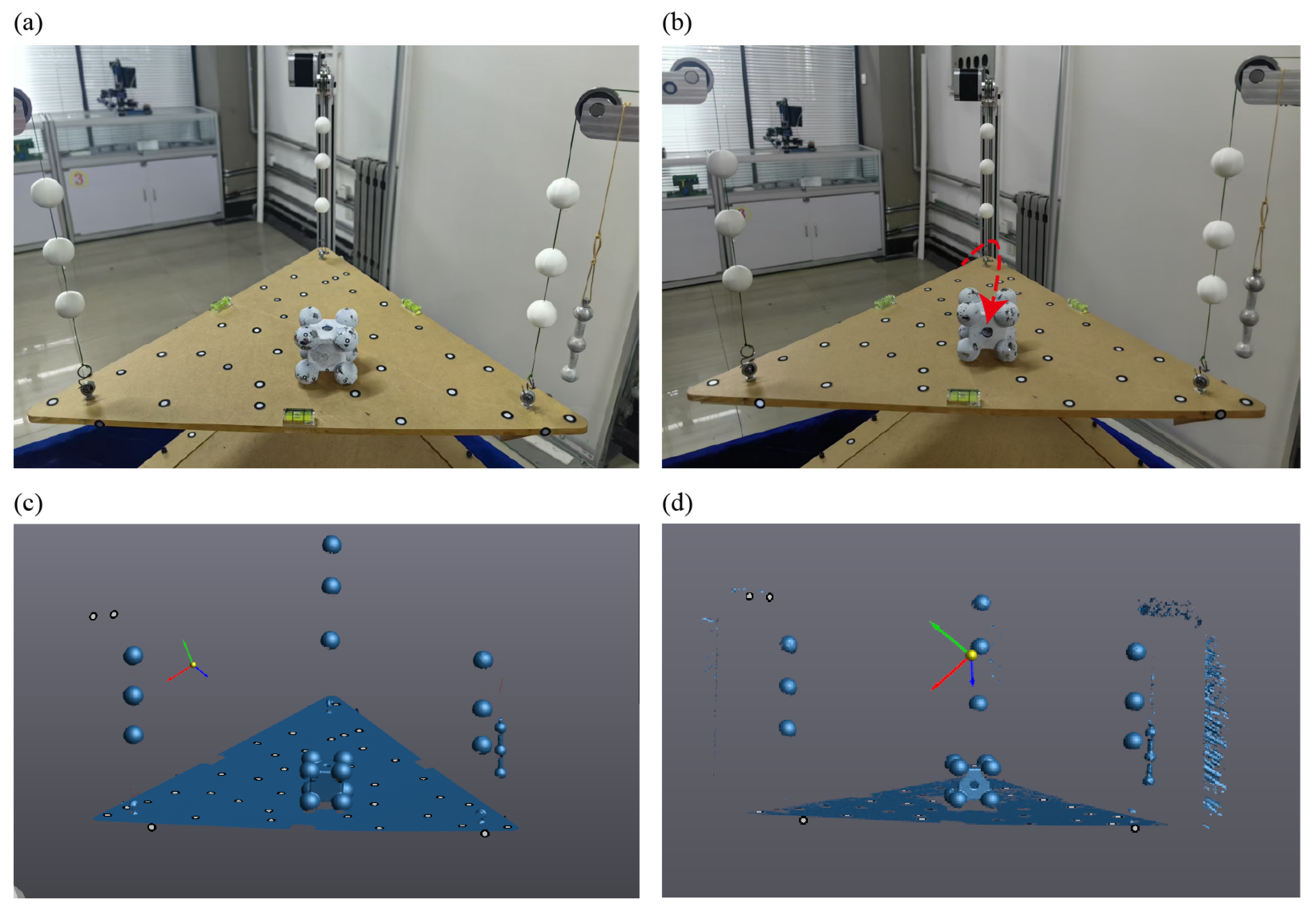
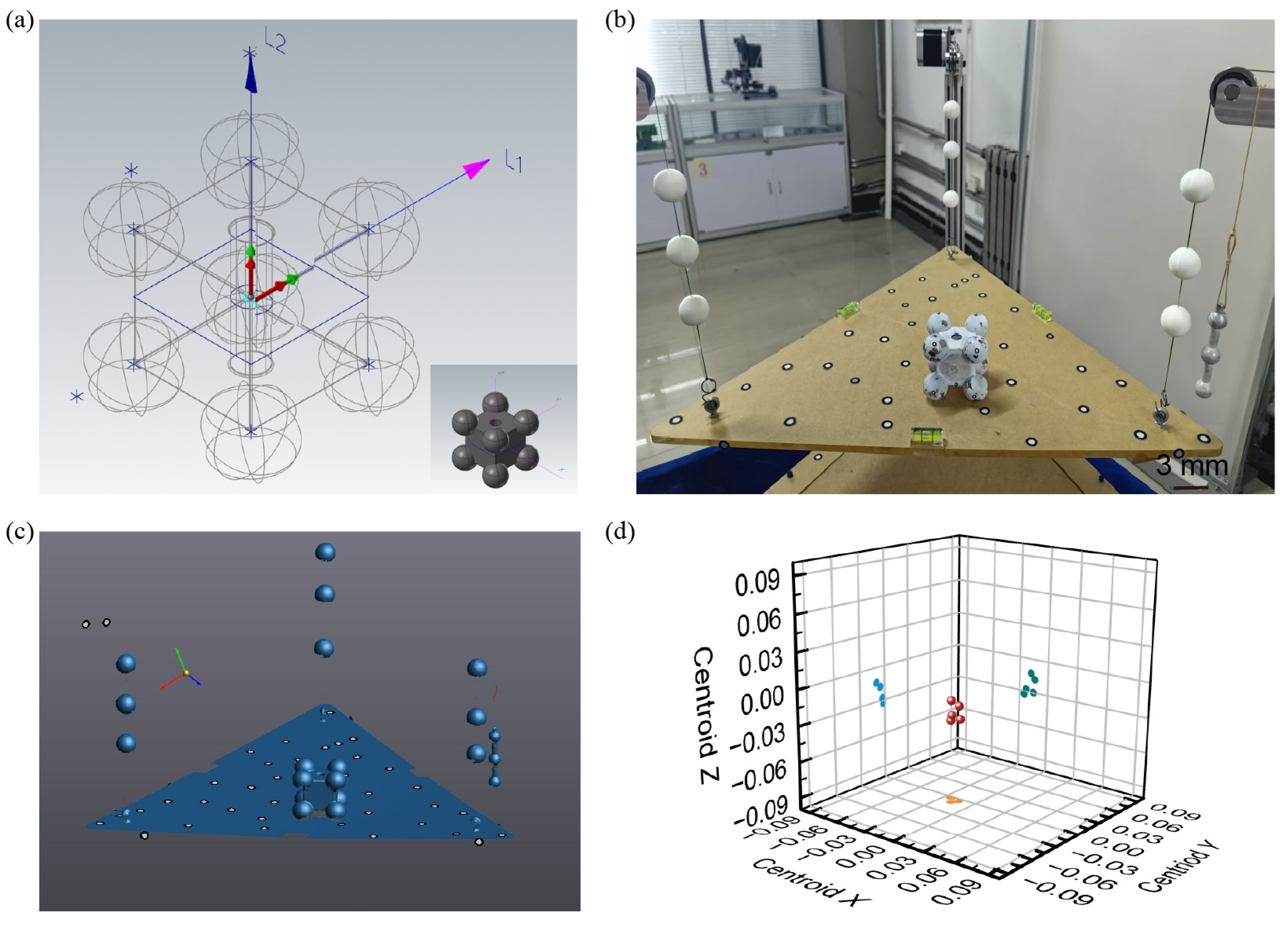
3.1. Accuracy Test with Standard Parts
3.2. Measurement System Validation on Representative Models
3.3. Error Analysis of Centroid Measurement
3.3.1. Measurement Error of 3D Scanner
3.3.2. Sphere Center Localization Error
3.3.3. Measurement Error of Spring Stiffness
3.3.4. Thermal Drift
3.3.5. Alignment and Leveling Error
3.3.6. Evaluation of the Combined Uncertainty
3.4. Centroid Measurement of Special-Shaped Mass Blocks
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bacaro, M.; Cianetti, F.; Alvino, A. Device for measuring the inertia properties of space payloads. Mech. Mach. Theory 2014, 74, 134–153. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, Y.; Wu, Y.; Hu, W.; Jin, G. The Taiji program: A concise overview. Prog. Theor. Exp. Phys. 2021, 2021, 05A108. [Google Scholar] [CrossRef]
- Tang, L.; Shangguan, W.-B. An improved pendulum method for the determination of the center of gravity and inertia tensor for irregular-shaped bodies. Measurement 2011, 44, 1849–1859. [Google Scholar] [CrossRef]
- Li, T.; Shangguan, W.-B.; Yin, Z. Error analysis of inertia parameters measurement for irregular-shaped rigid bodies using suspended trifilar pendulum. Measurement 2021, 174, 108956. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, D.; Liu, Y. Recent progress in precision measurement and assembly optimization methods of the aero-engine multistage rotor: A comprehensive review. Measurement 2024, 235, 114990. [Google Scholar] [CrossRef]
- Li, S.; Chu, W.; Huang, X. Measurement method of aircraft barycenter based on multi posture. Sens. Rev. 2020, 40, 217–226. [Google Scholar] [CrossRef]
- Modenini, D.; Curzi, G.; Tortora, P. Experimental Verification of a Simple Method for Accurate Center of Gravity Determination of Small Satellite Platforms. Int. J. Aerosp. Eng. 2018, 2018, 3582508. [Google Scholar] [CrossRef]
- Li, R.; Liu, Y.; Tan, J. Determination of COG Based on Propagation of Positioning and Orientation Errors in Aero-Engine Rotors. IEEE Trans. Instrum. Meas. 2022, 71, 1004611. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, M.; Li, D.; Tao, M.; Zhu, C.; Zheng, Y.; Tian, Y. A disturbance suppression micro-Newton force sensor based on shadow method. ISA Trans. 2023, 134, 442–450. [Google Scholar] [CrossRef] [PubMed]
- Mondal, N.; Acharyya, S.; Saha, R.; Sanyal, D.; Majumdar, K. Optimum design of mounting components of a mass property measurement system. Measurement 2016, 78, 309–321. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, X.; Tang, W.; Wang, J. A Structure for Accurately Determining the Mass and Center of Gravity of Rigid Bodies. Appl. Sci. 2019, 9, 2532. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, M.; Tang, W.; Wang, J. A flexible measurement technique for testing the mass and center of gravity of large-sized objects. Meas. Sci. Technol. 2020, 31, 015006. [Google Scholar] [CrossRef]
- Sun, L.; Wang, S.; Wang, H.; Zhao, W.; Li, J.; Dong, L. Mass and 3D centroid test and error analysis of small UAV. Vibroeng. Procedia 2022, 42, 106–111. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, H.; Tang, W.; Wang, J. General Mass Property Measurement Equipment for Large-Sized Aircraft. Sensors 2022, 22, 3912. [Google Scholar] [CrossRef] [PubMed]
- Gonzalo, O.; Seara, J.M.; Chekh, B.A.; Berreteaga, I.; Marrocu, M.; Rotondi, E. A method for the 3D identification of the center of gravity of an aircraft. Measurement 2023, 220, 113398. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, X.; Wang, Z.; Tang, W.; Wang, J. Research on the Pose Error Compensation Technology for the Mass and Centroid Measurement of Large-Sized Aircraft Based on Kinematics. Sensors 2023, 23, 701. [Google Scholar] [CrossRef] [PubMed]



| Number | L1 (mm) | L2 (mm) | Centroid (mm) |
|---|---|---|---|
| 1 | (−0.097, 0.02, −50) | (0.039, 50, −0.07) | (−0.025, −0.002, −0.033) |
| (−0.054, −0.03, 50) | (0.012, −50, −0.06) | ||
| 2 | (−0.081, 0.02, −50) | (0.041, 50, −0.01) | (−0.018, −0.01, −0.013) |
| (−0.042, −0.02, 50) | (0.010, −50, −0.04) | ||
| 3 | (−0.085, 0.01, −50) | (0.025, 50, −0.05) | (−0.023, −0.003, −0.028) |
| (−0.050, −0.02, 50) | (0.017, −50, −0.06) | ||
| 4 | (−0.081, 0.02, −50) | (0.048, 50, −0.06) | (−0.015, −0.002, −0.03) |
| (−0.031, −0.03, 50) | (0.004, −50, −0.06) | ||
| 5 | (−0.078, 0.01, −50) | (0.039, 50, −0.05) | (−0.014, −0.005, −0.018) |
| (−0.029, −0.03, 50) | (0.012, −50, −0.02) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Li, Z.; Pan, X.; Yang, Y. High-Precision Centroid Measurement Method Based on 3D Scanning and Hooke’s Law. Sensors 2025, 25, 7210. https://doi.org/10.3390/s25237210
He X, Li Z, Pan X, Yang Y. High-Precision Centroid Measurement Method Based on 3D Scanning and Hooke’s Law. Sensors. 2025; 25(23):7210. https://doi.org/10.3390/s25237210
Chicago/Turabian StyleHe, Xin, Zhen Li, Xin Pan, and Yong Yang. 2025. "High-Precision Centroid Measurement Method Based on 3D Scanning and Hooke’s Law" Sensors 25, no. 23: 7210. https://doi.org/10.3390/s25237210
APA StyleHe, X., Li, Z., Pan, X., & Yang, Y. (2025). High-Precision Centroid Measurement Method Based on 3D Scanning and Hooke’s Law. Sensors, 25(23), 7210. https://doi.org/10.3390/s25237210






