Intelligent Debonding Detection in GFRP Rock Bolts via Piezoelectric Time Reversal and CNN-SVM Model
Abstract
1. Introduction
2. Methodology and Theoretical Framework
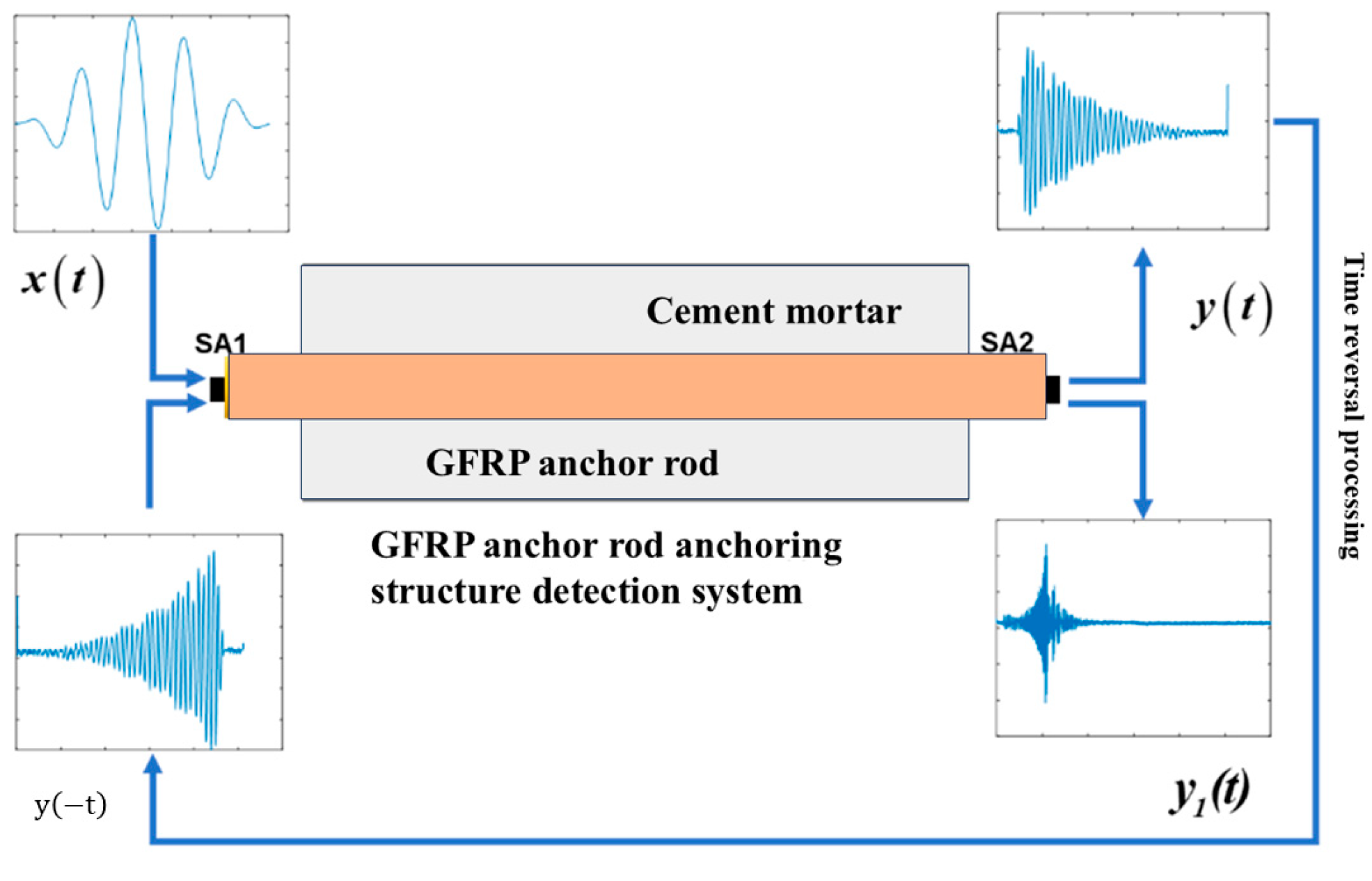
2.1. Time Reversal Method
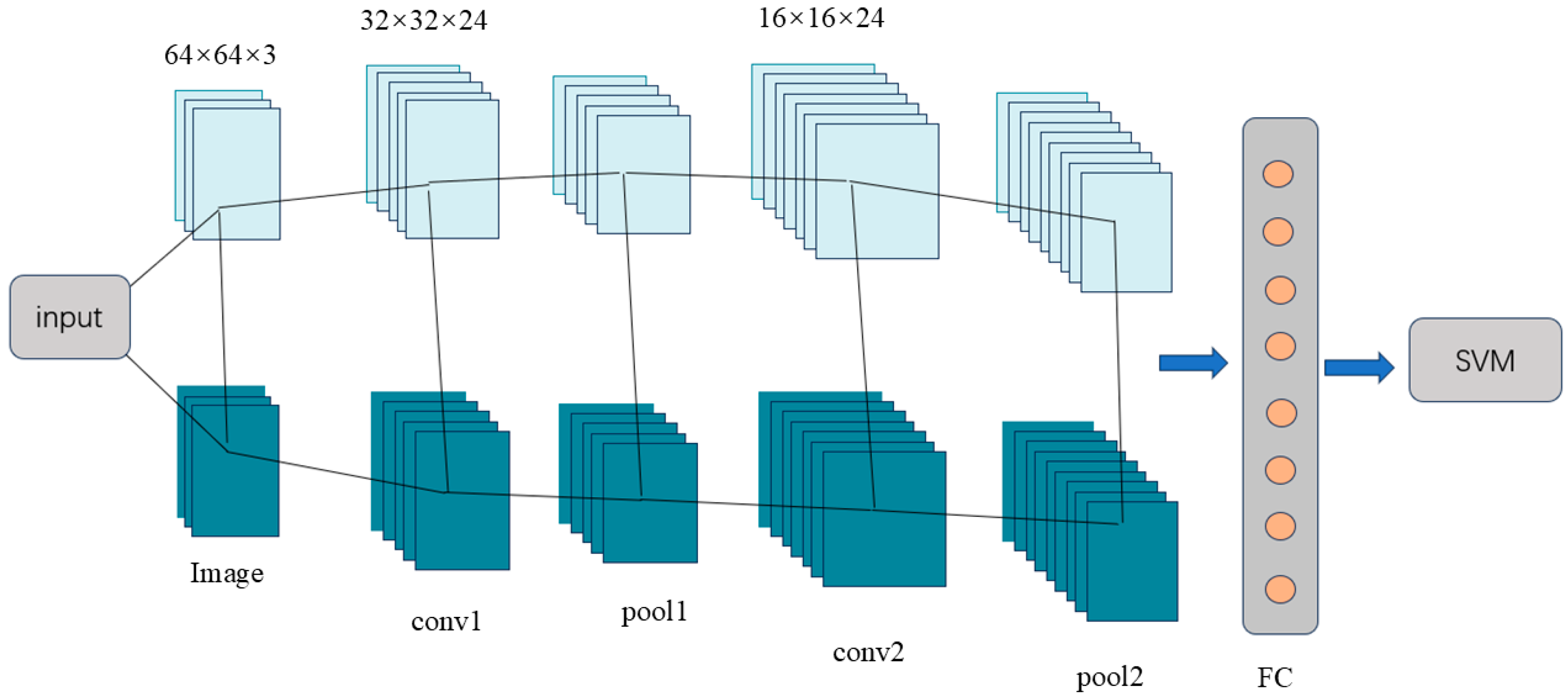
2.2. CNN-SVM Model
- (1)
- (2)
- Pooling layer [47]
- (3)
- (4)
- Support vector machines (SVMs) [50]
2.3. Experimental Design
3. Finite Element Modeling and Numerical Analysis
3.1. Multiphysics Model Setup and Material Properties
3.2. Boundary Conditions and Mesh Sensitivity Analysis
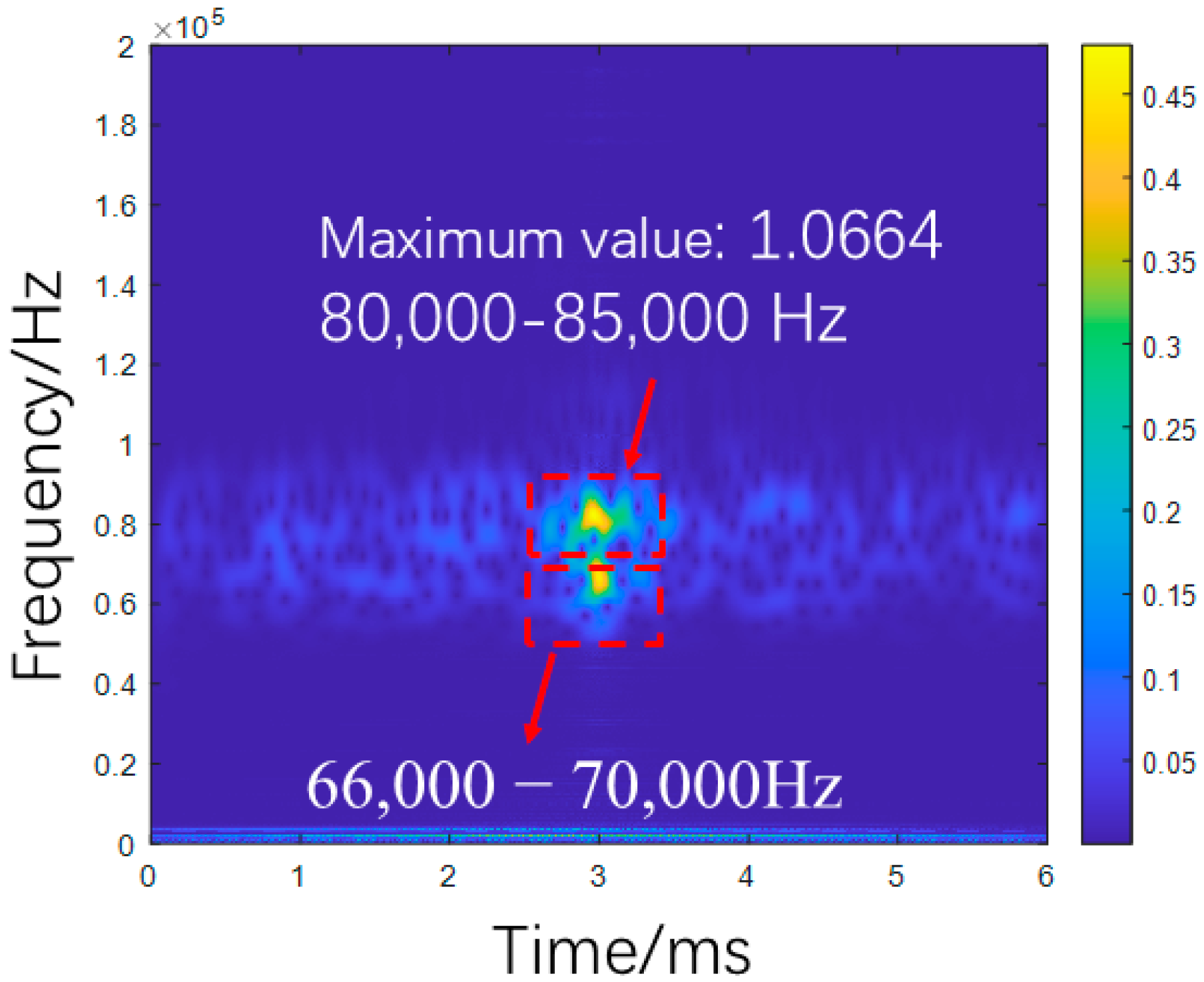
3.3. Parametric Study of Debonding Effects on Wave Propagation
- (1)
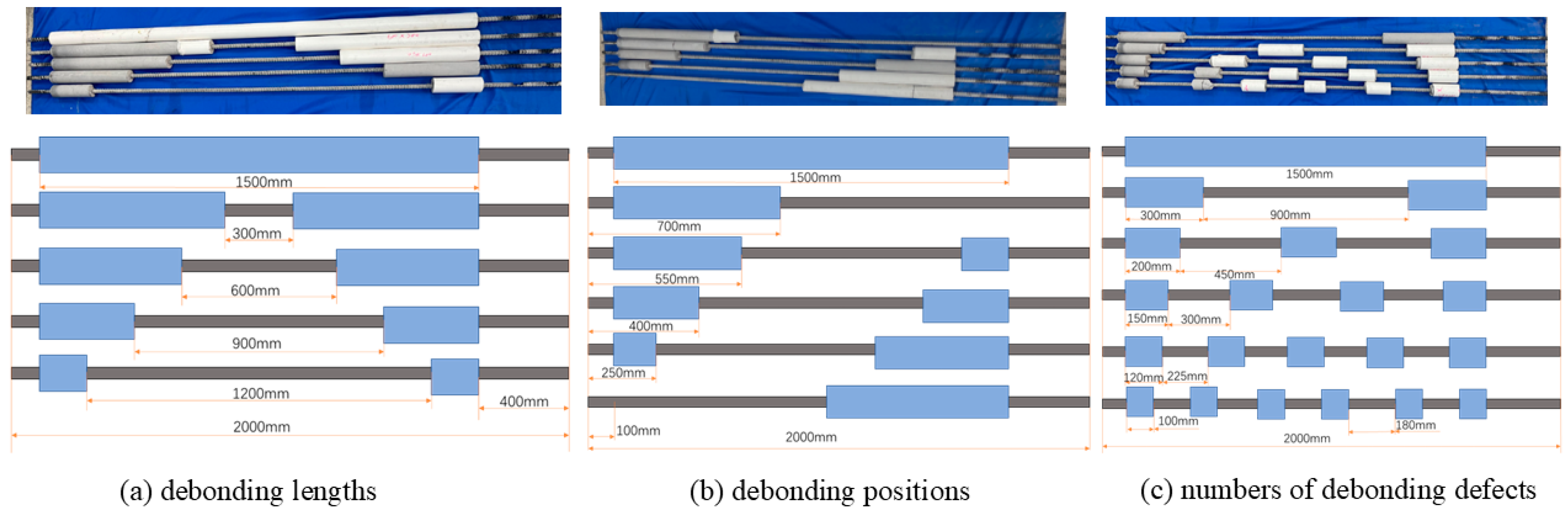
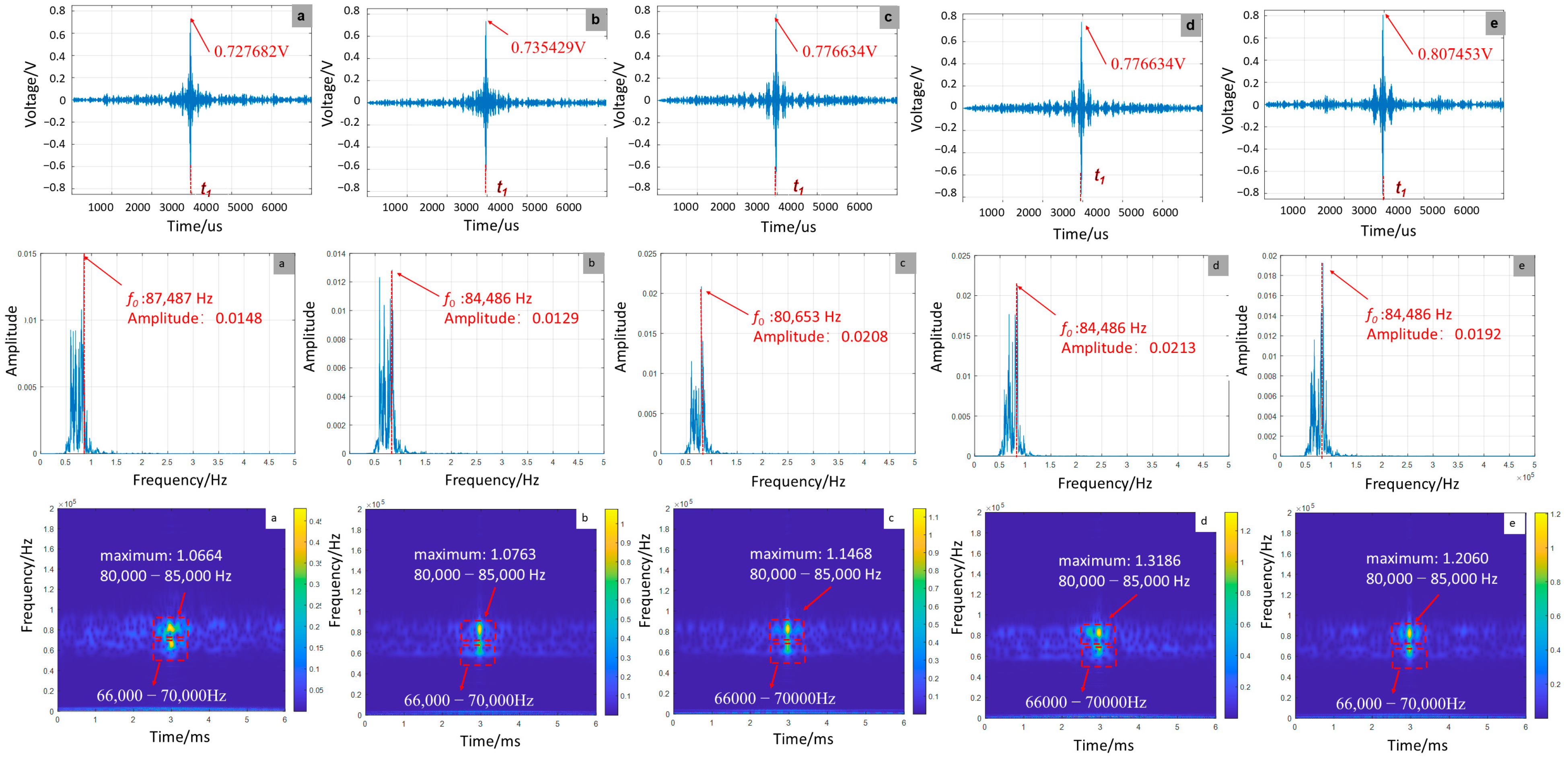
- Effect of debonding defect length on focused signal
- (2)
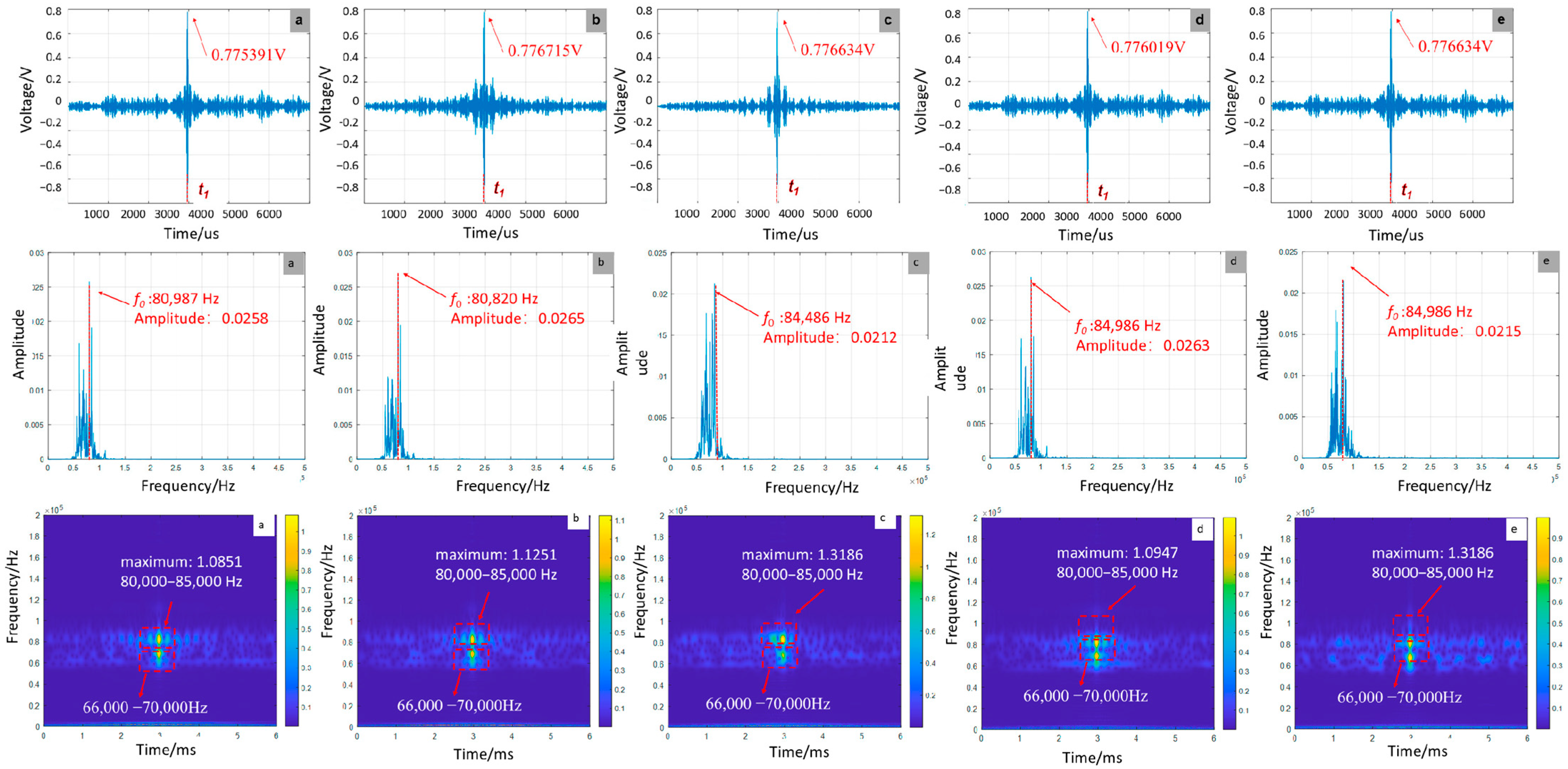
- Effect of delamination defect location on focused signal
- (3)
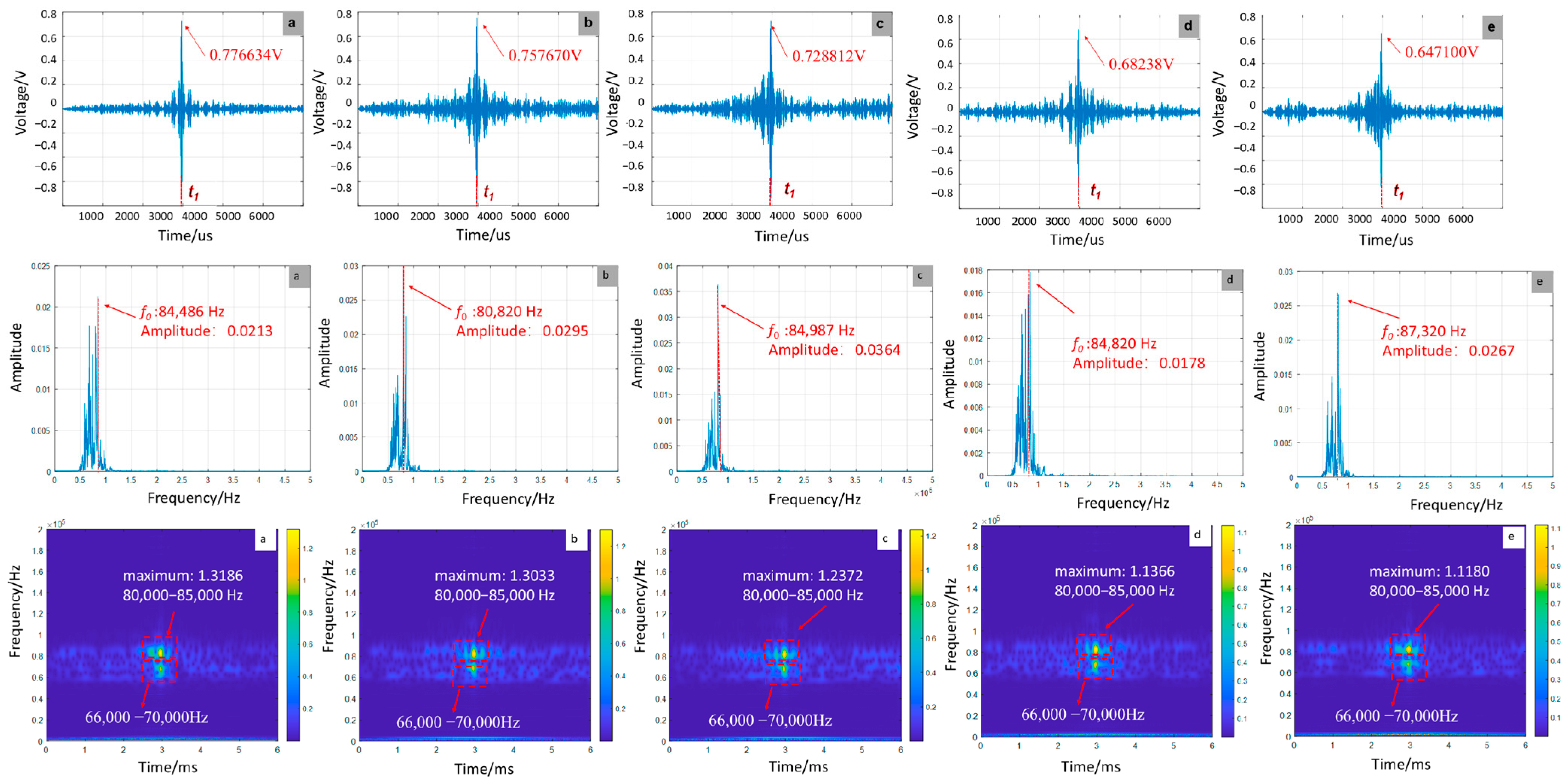
- Effect of the number of debonding defects on the focus signal
4. Experimental Validation and Signal Characterization
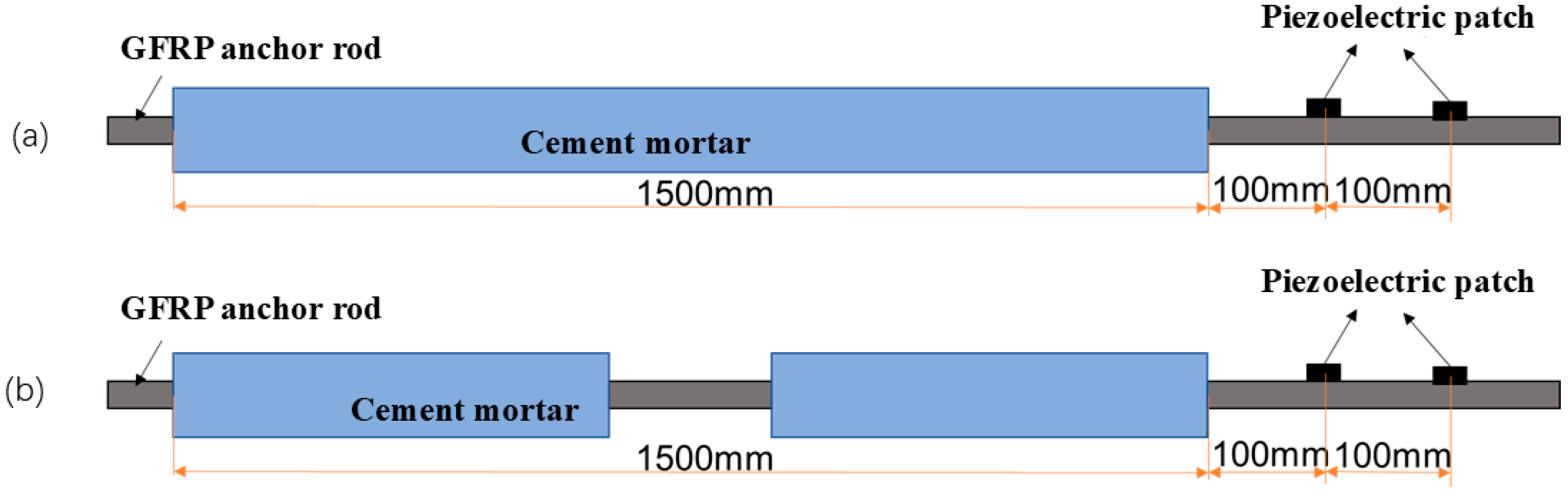
4.1. Fabrication of GFRP Anchorage Specimens with Controlled Defects
4.2. Piezoelectric Sensing System and Data Acquisition Protocol
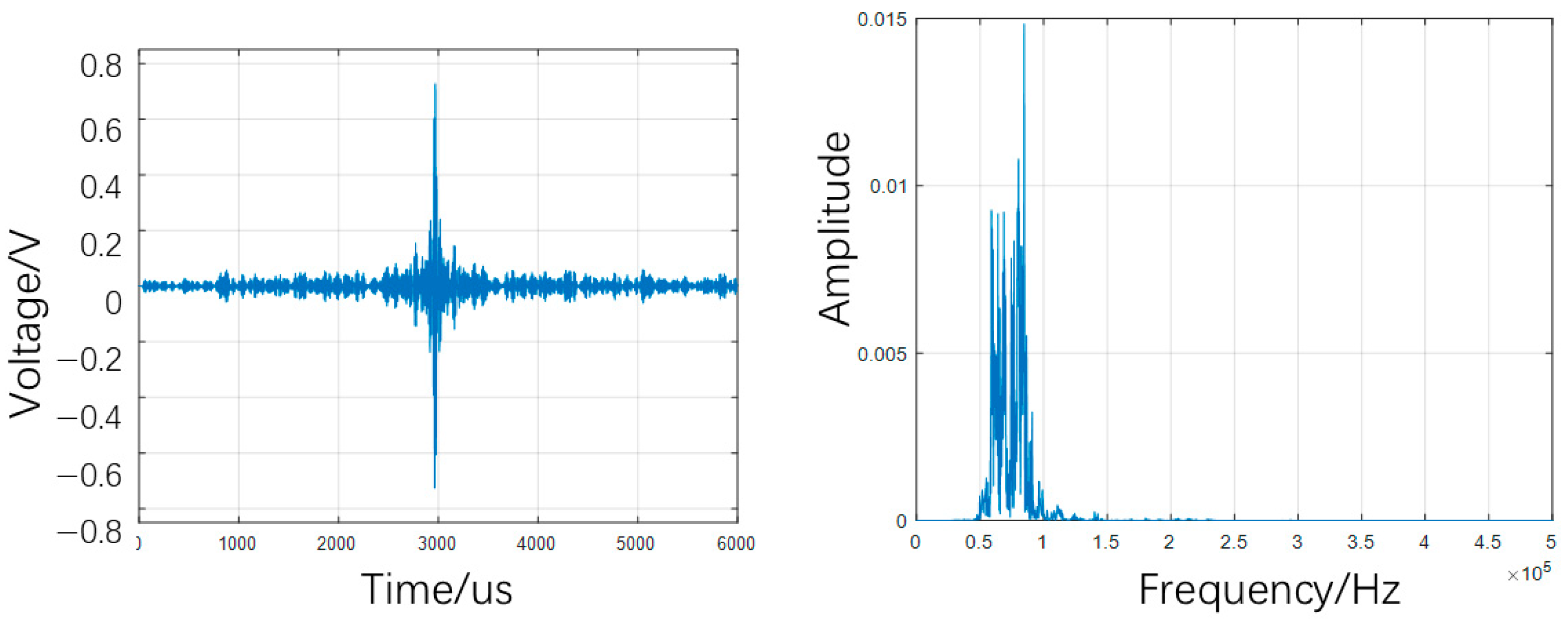
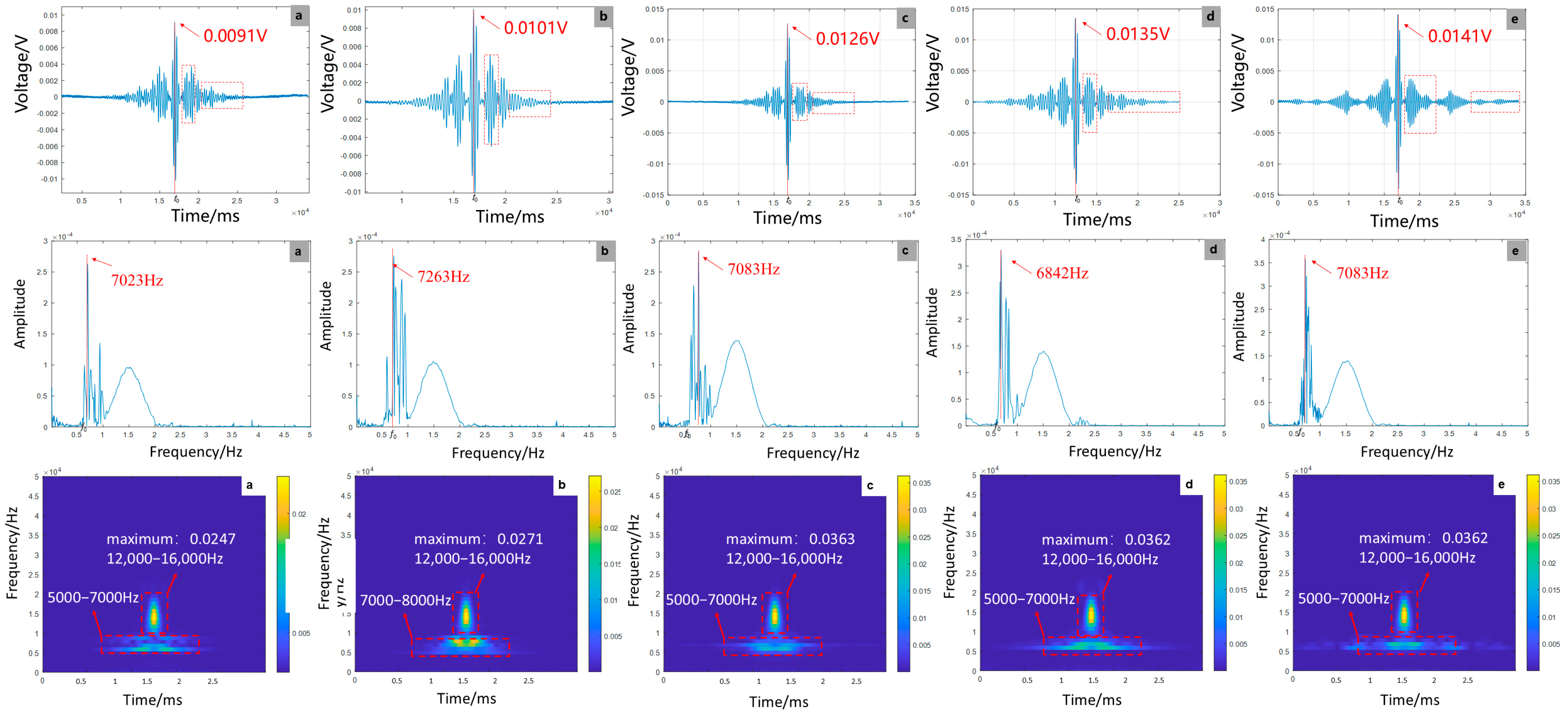
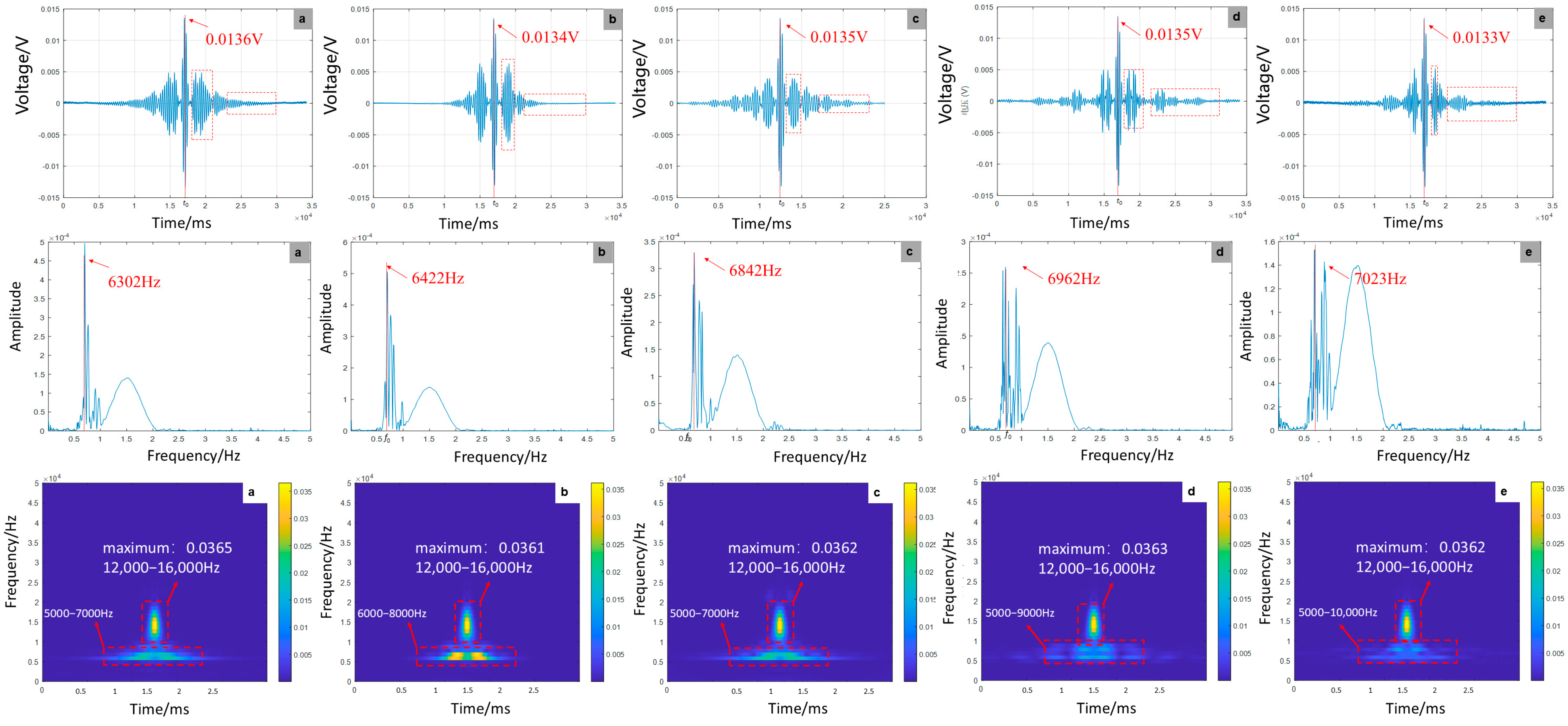
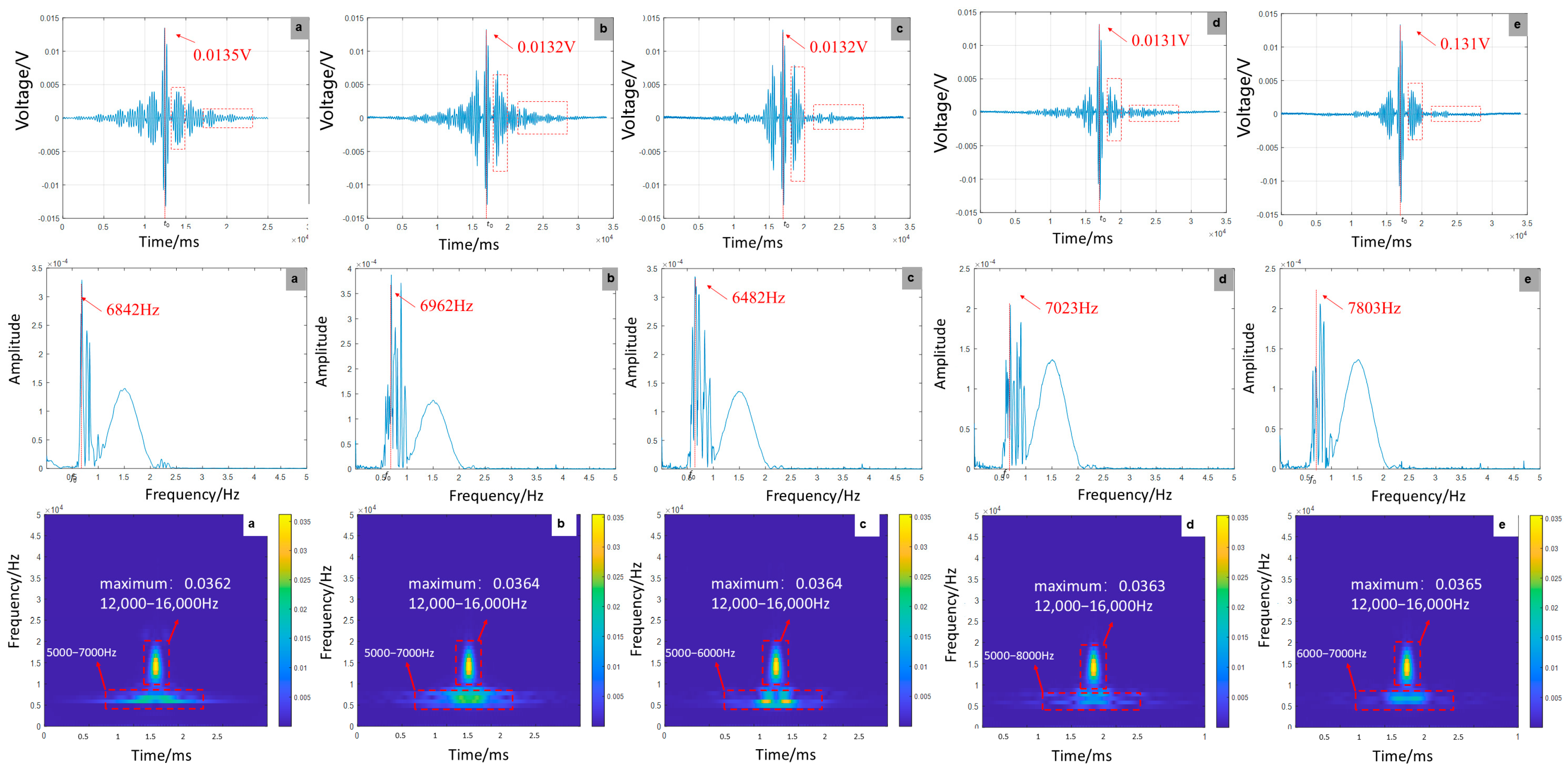
4.3. Time–Frequency Signal Response to Debonding Variants
- (1)
- Effect of debonding defect length on signal characteristics
- (2)
- Effect of delamination defect location on signal characteristics
- (3)
- Effect of the number of debonding defects on signal characteristics
5. Intelligent Defect Identification via CNN-SVM
5.1. Model Parameter Settings and Preprocessing
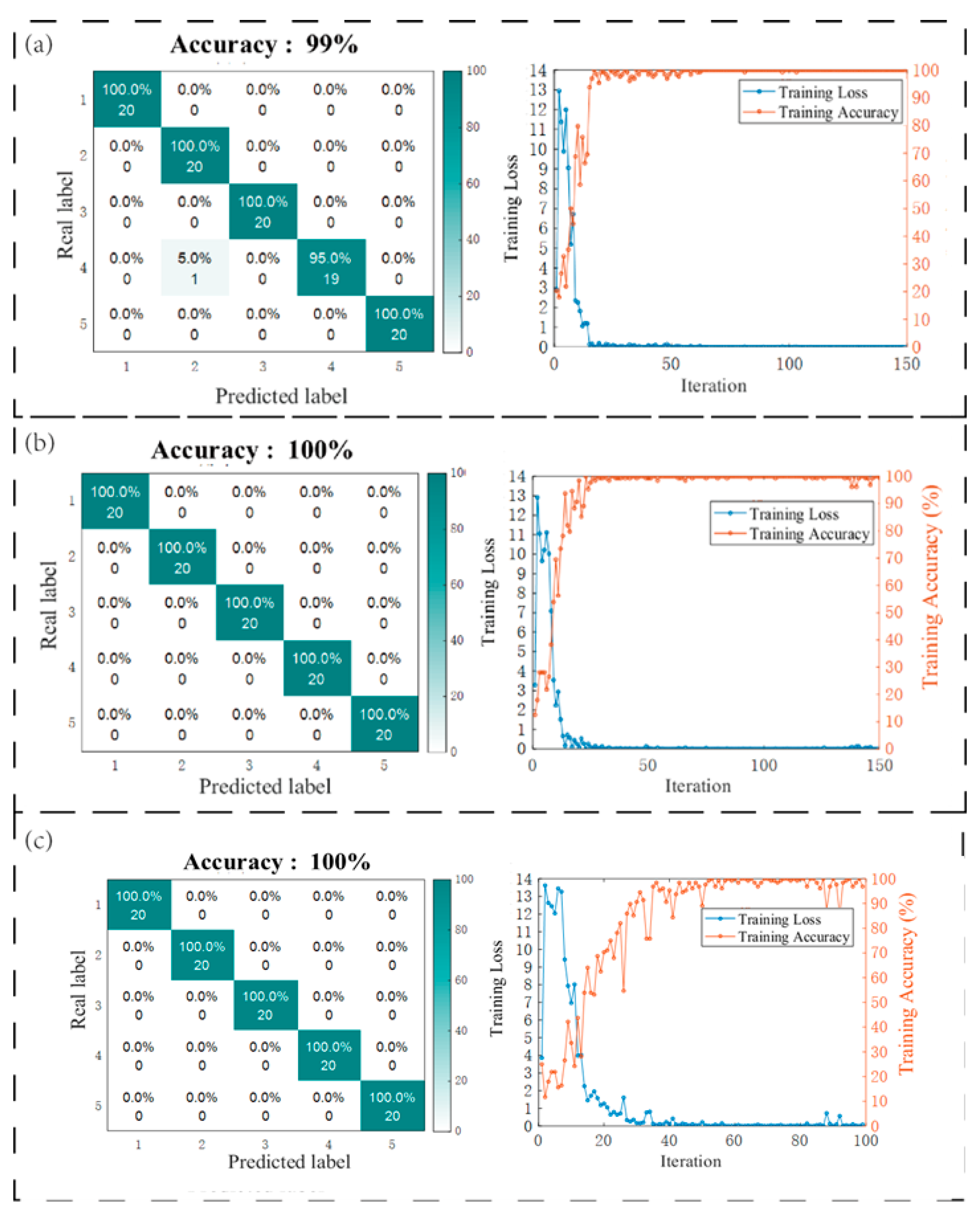
5.2. Analysis of Classification Results
6. Conclusions
- (1)
- Numerical simulations reveal distinct debonding patterns: Increasing defect length raises signal amplitude by 10.96% (from 0.727682 V to 0.807453 V), reduces peak frequency to 84,486 Hz, and intensifies energy concentration (peak energy: 1.3186). Variations in defect position maintain stable amplitude (±0.15%) while increasing peak frequency (from 80,987 Hz to 84,986 Hz) and energy. More defects reduce amplitude by 16.68%, elevate peak frequency to 87,320 Hz, and redistribute energy.
- (2)
- Experimental tests confirm these trends: Longer defects enhance amplitude by 54.9%, increase energy concentration by 13.1%, but reduce peak frequency to 7083 Hz while worsening waveform distortion. Changes in defect location preserve amplitude stability (±1.19%) but elevate peak frequency and energy. Multiple defects decrease amplitude by 3.0%, increase peak frequency to 7803 kHz, and maintain stable energy despite intensified aliasing.
- (3)
- A CNN-SVM model was developed to evaluate debonding conditions, using time–frequency representations of experimental signals as input. The model achieved exceptional accuracy rates of 99%, 100%, and 100% across three test scenarios, all surpassing the 95% reliability threshold. These results demonstrate the model’s robust capability for precise defect assessment in GFRP anchorage systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guan, Y.; Yang, Y.; Fahmy, M.F.; Du, W.; Cui, J.; Wu, B. Study on the shear performance and damage mechanics model of the joint surface of prestressed GFRP bolts. Constr. Build. Mater. 2025, 476, 141269. [Google Scholar] [CrossRef]
- Benmokrane, B.; Xu, H.; Bellavance, E. Bond strength of cement grouted glass fibre reinforced plastic (GFRP) anchor bolts. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1996, 33, 455–465. [Google Scholar] [CrossRef]
- Sun, G.; Yan, N.; Bai, X.; Liu, J.; Hou, D.; Sang, S.; Zhang, M.; Wang, P.; Jing, D. Laboratory full-scale test on the bond property of GFRP anchor to concrete. Constr. Build. Mater. 2023, 396, 132216. [Google Scholar] [CrossRef]
- Ngo, T.T.; Pham, T.M.; Hao, H.; Chen, W.; Ha, N.S. Proposed new dry and hybrid concrete joints with GFRP bolts and GFRP reinforcement under cyclic loading: Testing and analysis. J. Build. Eng. 2022, 49, 104033. [Google Scholar] [CrossRef]
- Chen, J.; Lv, X.; Kang, J.; Liu, G.; Zhou, Y. Experimental study on the anchoring mechanism and performance of BFRP bolt-anchorage system in supporting clay slopes. Polym. Test. 2025, 147, 108822. [Google Scholar] [CrossRef]
- Pedrosa, B.; Farahani, B.V.; Rebelo, C.F.; Santos, R.F.; Correia, J. Fatigue mechanisms and crack strain field measurements on bolt hole detail. J. Constr. Steel Res. 2025, 233, 109664. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, H.; Zhao, H.; Song, L. Characterization of transverse vibration response of resin-anchored bolt under axial tension and life cycle health assessment of anchorage debonding. Measurement 2025, 256, 118273. [Google Scholar] [CrossRef]
- Guo, C.C.; Moore, K.; Vlachopoulos, N. Investigating the effects of geothermally active temperature conditions on fully grouted rock bolts with distributed fiber optic sensors. J. Rock Mech. Geotech. Eng. 2025, in press.
- Jiang, S.H.; Li, D.Q.; Zhang, L.M.; Zhou, C.B. Time-dependent system reliability of anchored rock slopes considering rock bolt corrosion effect. Eng. Geol. 2014, 175, 1–8. [Google Scholar] [CrossRef]
- Panaitescu, I.; Koch, T.; Archodoulaki, V.M. Effects of temperature, humidity and automotive fluids exposure on glass fiber/polyurethane composites. Polym. Compos. 2019, 40, 2357–2367. [Google Scholar] [CrossRef]
- Zou, Y.; Ji, Y. Research on coupled erosion damage model of FRP bonded concrete beams subjected to Lemaitre assumption. Polym. Compos. 2024, 45, 151–168. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Q.; Zhou, G.; Zhu, K.; Jing, B.; Zhu, K.; Shi, J.; Li, C. Effects of hygrothermal condition on water diffusion and flexural properties of carbon–glass hybrid fiber-reinforced epoxy polymer winding pipes. Polymers 2024, 16, 3433. [Google Scholar] [CrossRef]
- Huang, L.; Hu, J.; Zeng, B.; Wei, Y.; Zhou, Z. Investigation on the failure mechanism of friction-based self-centering timber beam-column joint considering bolt bearing effect: Experimental study and theoretical analyses. J. Build. Eng. 2024, 98, 110974. [Google Scholar] [CrossRef]
- Zhang, S.; Luan, H.; Jiang, Y.; Wang, Y.; Li, B.; Liu, Z.; Jiang, T.; Li, X. Study on the Load Transfer and Damage Evolution Characteristics of the Bolt-Grout Interface concerning Bolt Rib Parameters: Based on a Finite-Discrete Numerical Method. Comput. Geotech. 2025, 179, 107010. [Google Scholar] [CrossRef]
- Grindheim, B.; Li, C.C.; Høien, A.H. Full-scale pullout tests of rock anchors in a limestone quarry focusing on bond failure at the anchor-grout and grout-rock interfaces. J. Rock Mech. Geotech. Eng. 2023, 15, 2264–2279. [Google Scholar] [CrossRef]
- He, Z.; Zhang, N.; Xie, Z.; Ma, C.; Han, C.; Zhang, F.; Wang, H.; Alarifi, S.S. Study on stress corrosion behavior and failure mechanism of galvanized bolts in complex coal mine environments. J. Mater. Res. Technol. 2025, 34, 1759–1776. [Google Scholar] [CrossRef]
- Cui, K.; Wang, D.; Yu, X.; Wu, G. Performance and mechanism of bolt and slurry bonds in anchor systems for earthen sites. Proc. Inst. Civ. Eng. Geotech. Eng. 2020, 173, 485–499. [Google Scholar] [CrossRef]
- Li, B.; Zhan, Y.; Cui, J.; Yan, K. Mechanical performance of a new stiffened PFRP-steel bolted connection: Experimental and numerical investigations. J. Build. Eng. 2024, 95, 110229. [Google Scholar] [CrossRef]
- Rahman, M.M.; Cope, C.T., III; Abavisani, I.; D’Antino, T.; Focacci, F.; Carloni, C. Comprehensive study of GFRP bar-concrete bond behavior using pull-out and three-point bending tests. J. Build. Eng. 2025, 108, 112819. [Google Scholar] [CrossRef]
- Rojas, G.; Domingo, M.; Kanstad, T. Fiber distribution and orientation in full scale walls investigated from drilled cores using the inductive method and the Montevideo splitting test. Constr. Build. Mater. 2025, 489, 142347. [Google Scholar] [CrossRef]
- Yang, W.S.; Chiang, C.C.; Hsu, H.C. Monitoring torque in bolts using an embedded fiber Bragg grating sensor. Optik 2023, 291, 171294. [Google Scholar] [CrossRef]
- Li, Z.; Yu, J.; Liu, Y.; Zhang, X.; Zhang, B.; Elmaimouni, L. Determination of fractional order for layered viscoelastic materials in cement grouted resin anchor bolt by using guided wave technology. Mech. Syst. Signal Process. 2025, 224, 112101. [Google Scholar] [CrossRef]
- Debnath, P.P.; Ning, W.; Chan, T.M. Experimental, numerical, and analytical assessment for static performance of concrete-filled steel tube T-stub connections with group of high-strength blind-bolts. Eng. Struct. 2025, 338, 120586. [Google Scholar] [CrossRef]
- Sepehry, N.; Amindavar, H.; Qalehsari, E.Q.; Zahrai, S.M. Proposing a Time–frequency Analysis Method Using Nonlinear Wave Modulation for Machine Learning-Based Detection of Bolt Looseness in Non-Gaussian Noise Environment. J. Ind. Inf. Integr. 2025, 47, 100877. [Google Scholar] [CrossRef]
- Huang, P.; Qiu, Z.; Zheng, F.; Zhang, X.; Shi, M.; Yang, L.; Su, Y.; Ma, L.; Li, Y.; Li, Y.; et al. An improved multi-frequency eddy current array sensor for detecting micro-defects of welding seam in metal plates. Sens. Actuators A Phys. 2024, 374, 115459. [Google Scholar] [CrossRef]
- Zhou, D.; Chen, F.; Liang, J.; Zhang, Y.; Zheng, W.; Li, X. Battery defect detection using ultrasonic guided waves and a convolutional neural network model. J. Energy Storage 2025, 119, 116352. [Google Scholar] [CrossRef]
- Li, Z.; Yu, J.; Zhang, X.; Elmaimouni, L. Study on propagation characteristics of ultrasonic guided wave and detection of the defect in resin bolts. Appl. Acoust. 2022, 195, 108843. [Google Scholar] [CrossRef]
- Shi, Z.M.; Liu, L.; Peng, M.; Liu, C.C.; Tao, F.J.; Liu, C.S. Non-destructive testing of full-length bonded rock bolts based on HHT signal analysis. J. Appl. Geophys. 2018, 151, 47–65. [Google Scholar] [CrossRef]
- Sinha, S.; Walton, G. Investigation of pillar damage mechanisms and rock-support interaction using Bonded Block Models. Int. J. Rock Mech. Min. Sci. 2021, 138, 104652. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, W.; Xie, Y. A leak sensing method for offshore oil pipeline using acoustic emission signals and machine learning. Ocean Eng. 2025, 336, 121768. [Google Scholar] [CrossRef]
- Zhu, L.; Wu, G.; Tang, G. Acoustic source localization of anisotropic CFRP plate based on time-reversal method and improved Geiger iteration. Measurement 2025, 246, 116684. [Google Scholar] [CrossRef]
- Wei, L.; Shen, L.; Cao, M.; Wang, J.; Wang, Z.; Ostachowicz, W. Corrosion damage identification in concrete underwater based on time reversal of stress waves. Mech. Syst. Signal Process. 2023, 194, 110281. [Google Scholar] [CrossRef]
- Zhou, L.; Zheng, Y.; Song, G.; Chen, D.; Ye, Y. Identification of the structural damage mechanism of BFRP bars reinforced concrete beams using smart transducers based on time reversal method. Constr. Build. Mater. 2019, 220, 615–627. [Google Scholar] [CrossRef]
- Du, F.; Tian, Z.; Nan, Y.; Zhang, X.; Xu, C.; Wang, S.; Su, Z. A modified virtual time reversal method for enhancing monitoring sensitivity of bolt preloads based on ultrasonic guided waves. J. Sound Vib. 2024, 585, 118475. [Google Scholar] [CrossRef]
- Wang, F.; Song, G. Bolt early looseness monitoring using modified vibro-acoustic modulation by time-reversal. Mech. Syst. Signal Process. 2019, 130, 349–360. [Google Scholar] [CrossRef]
- Aras, S.; Aras, E.; Gedikli, E.; Kahraman, H.T. Multi-Objective CNN Optimization: A Robust Framework for Automated Model Design. Inf. Sci. 2025, 719, 122468. [Google Scholar] [CrossRef]
- Ning, F.; Cheng, Z.; Meng, D.; Wei, J. A framework combining acoustic features extraction method and random forest algorithm for gas pipeline leak detection and classification. Appl. Acoust. 2021, 182, 108255. [Google Scholar] [CrossRef]
- Cheng, X.; Wu, X.; Wu, Z.; Zheng, K.; Li, H.; Hu, X. Ultrasonic detection of porosity in composites based on wavelet packet transform and convolutional neural network. Measurement 2025, 253, 117695. [Google Scholar] [CrossRef]
- Kannusamy, M.; Kapuria, S.; Sasmal, S. An efficient Lamb wave-based virtual refined time-reversal method for damage localization in plates using broadband measurements. Ultrasonics 2022, 124, 106767. [Google Scholar] [CrossRef]
- Gangadharan, R.; Murthy, C.R.L.; Gopalakrishnan, S.; Bhat, M.R. Time reversal technique for health monitoring of metallic structure using Lamb waves. Ultrasonics 2009, 49, 696–705. [Google Scholar] [CrossRef]
- Chang, S.H.; Rogacheva, N.N.; Chou, C.C. Analysis of methods for determining electromechanical coupling coefficients of piezoelectric elements. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1995, 42, 630–640. [Google Scholar] [CrossRef]
- Chen, S.; Lu, Y.; Sriramadasu, R.C. An energy based enhanced imaging method for debonding evaluation in tile panels using Lamb wave time reversal with limited sensor numbers. Ultrasonics 2025, 155, 107732. [Google Scholar] [CrossRef]
- Shu, Z.; He, J.; Hu, M.; Zhou, C.; Sun, X. Damage location of plate structures based on the exchanging-element time-reversal method by using Lamb waves. J. Sound Vib. 2023, 565, 117907. [Google Scholar] [CrossRef]
- Xu, J.; Zhou, S.; Xu, A.; Ye, J.; Zhao, A. Automatic scoring of postures in grouped pigs using depth image and CNN-SVM. Comput. Electron. Agric. 2022, 194, 106746. [Google Scholar] [CrossRef]
- Vasilache, M.M.; Tretiak, I.; Tayong, R.B.; Velisavljevic, V. Using Convolution Neural Network Methods for the Ultrasound Characterization of Porosity across Carbon Fiber Reinforced Polymer Layers. Results Eng. 2025, 26, 105517. [Google Scholar] [CrossRef]
- Li, X.; Liu, X. Accelerated analysis on the triple momentum method for a two-layer ReLU neural network. J. King Saud Univ. Comput. Inf. Sci. 2024, 36, 102016. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Y.; Ke, D.; Su, K. PLDE: A lightweight pooling layer for spoken language recognition. Speech Commun. 2024, 158, 103055. [Google Scholar] [CrossRef]
- Mondal, A.; Shrivastava, V.K. A novel Parametric Flatten-p Mish activation function based deep CNN model for brain tumor classification. Comput. Biol. Med. 2022, 150, 106183. [Google Scholar] [CrossRef]
- Zhao, L.; Yin, L. Fully-connected layers-embedded self-attention optimizer based on quantum-inspired and fuzzy logic for smart household energy management. Sustain. Comput. Inform. Syst. 2025, 47, 101151. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, H.; Tang, X.; Lv, J.; Zhang, R. Research on computer multi feature fusion SVM model based on remote sensing image recognition and low energy system. Results Eng. 2025, 26, 104861. [Google Scholar] [CrossRef]
- de Oliveira Nogueira, T.; Palacio, G.B.A.; Braga, F.D.; Maia, P.P.N.; de Moura, E.P.; de Andrade, C.F.; Rocha, P.A.C. Imbalance classification in a scaled-down wind turbine using radial basis function kernel and support vector machines. Energy 2022, 238, 122064. [Google Scholar] [CrossRef]
- Ding, X.; Liu, J.; Yang, F.; Cao, J. Random radial basis function kernel-based support vector machine. J. Frankl. Inst. 2021, 358, 10121–10140. [Google Scholar] [CrossRef]
- Wael, M.; Abd El Latif, E.; Lotfy, E.; Hosny, S. Analytical models of horizontal shear stress and failure mode for reinforced concrete beam-column joints externally retrofitted with FRP sheets and steel anchor bolts. Eng. Struct. 2025, 332, 120058. [Google Scholar] [CrossRef]
- Wu, T.; Huang, F.; Zhang, D.; An, Y. Anchorage failure mechanism and uplift bearing capacity of L-& J-anchor bolts in plain concrete. Eng. Fail. Anal. 2024, 159, 107991. [Google Scholar]
- Shi, H.; Song, L.; Zhang, H.; Chen, W.; Lin, H.; Li, D.; Wang, G.; Zhao, H. Experimental and numerical studies on progressive debonding of grouted rock bolts. Int. J. Min. Sci. Technol. 2022, 32, 63–74. [Google Scholar] [CrossRef]

| Material | E/GPa | G/GPa | ν | ρ/(kg·m−3) |
|---|---|---|---|---|
| GFRP Bolts | (41, 25, 25) | (29.95, 29.95, 29.95) | (0.22, 0.22, 0.22) | 2500 |
| Rock mass | 40 | — | 0.25 | 2700 |
| Layers | Kemel Size | Number of Kernels | Stride |
|---|---|---|---|
| Convolution_1 | (3, 3) | 10 | (1, 1) |
| Max_pooling_1 | (2, 2) | 10 | (2, 2) |
| Convolution_2 | (5, 5) | 24 | (1, 1) |
| Max_pooling_2 | (2, 1) | 24 | (2, 2) |
| Dense_1 | 64 | (1, 1) | |
| Dense_2 | 32 | (1, 1) | |
| Dense_3 | numClasses | (1, 1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Liu, Y.; Bai, Y.; Si, J.; Zhang, Z.; Tu, S. Intelligent Debonding Detection in GFRP Rock Bolts via Piezoelectric Time Reversal and CNN-SVM Model. Sensors 2025, 25, 7208. https://doi.org/10.3390/s25237208
Zhang Z, Liu Y, Bai Y, Si J, Zhang Z, Tu S. Intelligent Debonding Detection in GFRP Rock Bolts via Piezoelectric Time Reversal and CNN-SVM Model. Sensors. 2025; 25(23):7208. https://doi.org/10.3390/s25237208
Chicago/Turabian StyleZhang, Zhenyu, Yang Liu, Yixuan Bai, Jianfeng Si, Zhaolong Zhang, and Shengwu Tu. 2025. "Intelligent Debonding Detection in GFRP Rock Bolts via Piezoelectric Time Reversal and CNN-SVM Model" Sensors 25, no. 23: 7208. https://doi.org/10.3390/s25237208
APA StyleZhang, Z., Liu, Y., Bai, Y., Si, J., Zhang, Z., & Tu, S. (2025). Intelligent Debonding Detection in GFRP Rock Bolts via Piezoelectric Time Reversal and CNN-SVM Model. Sensors, 25(23), 7208. https://doi.org/10.3390/s25237208





