Advancing Three-Photon-Excited Rydberg RF Sensing: Fluorescence Readout for Wide-Dynamic-Range Characterization and Spatial Resolution Beyond Transmission
Abstract
1. Introduction
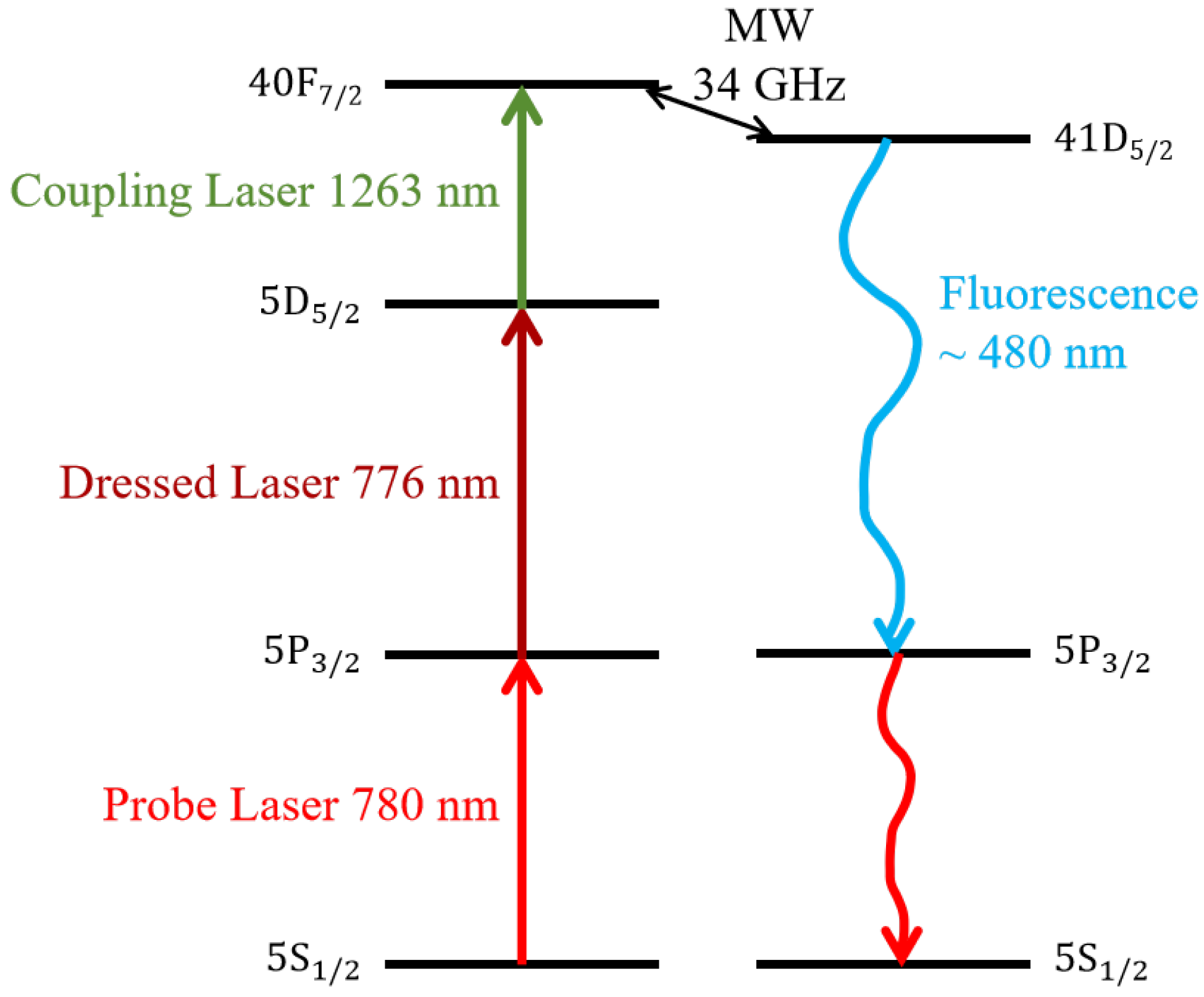
2. Theoretical Model
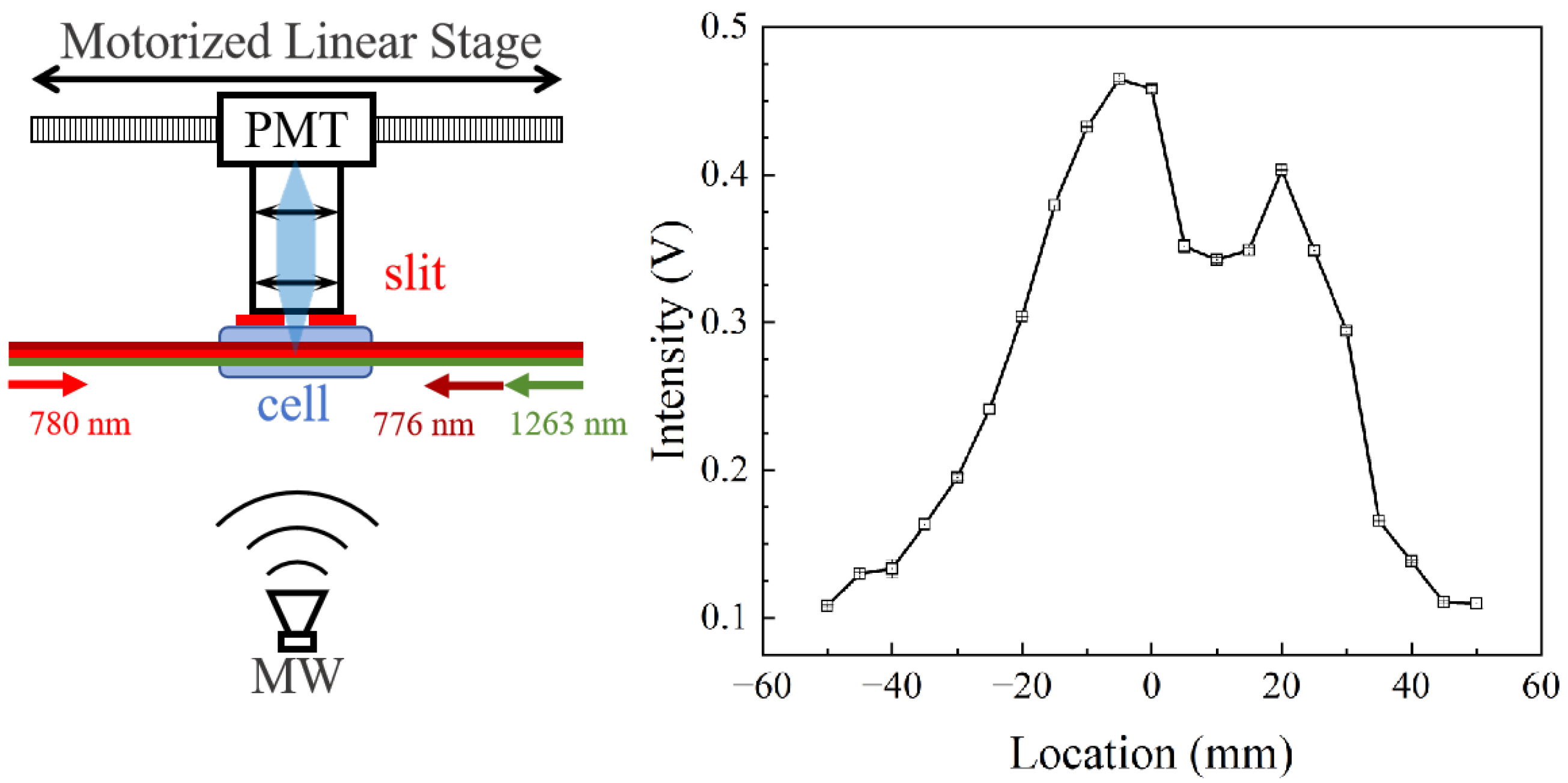
3. Experimental Setup
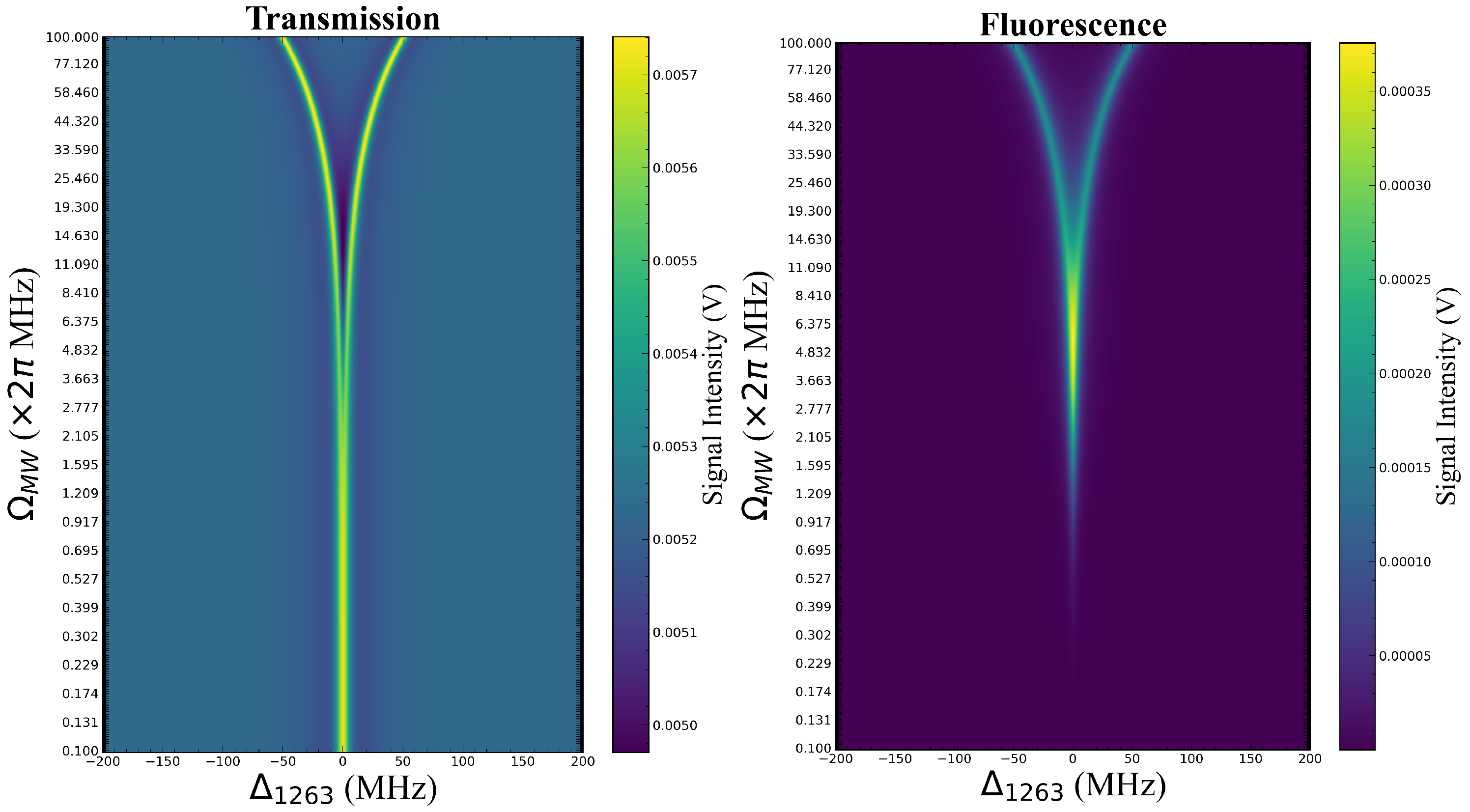
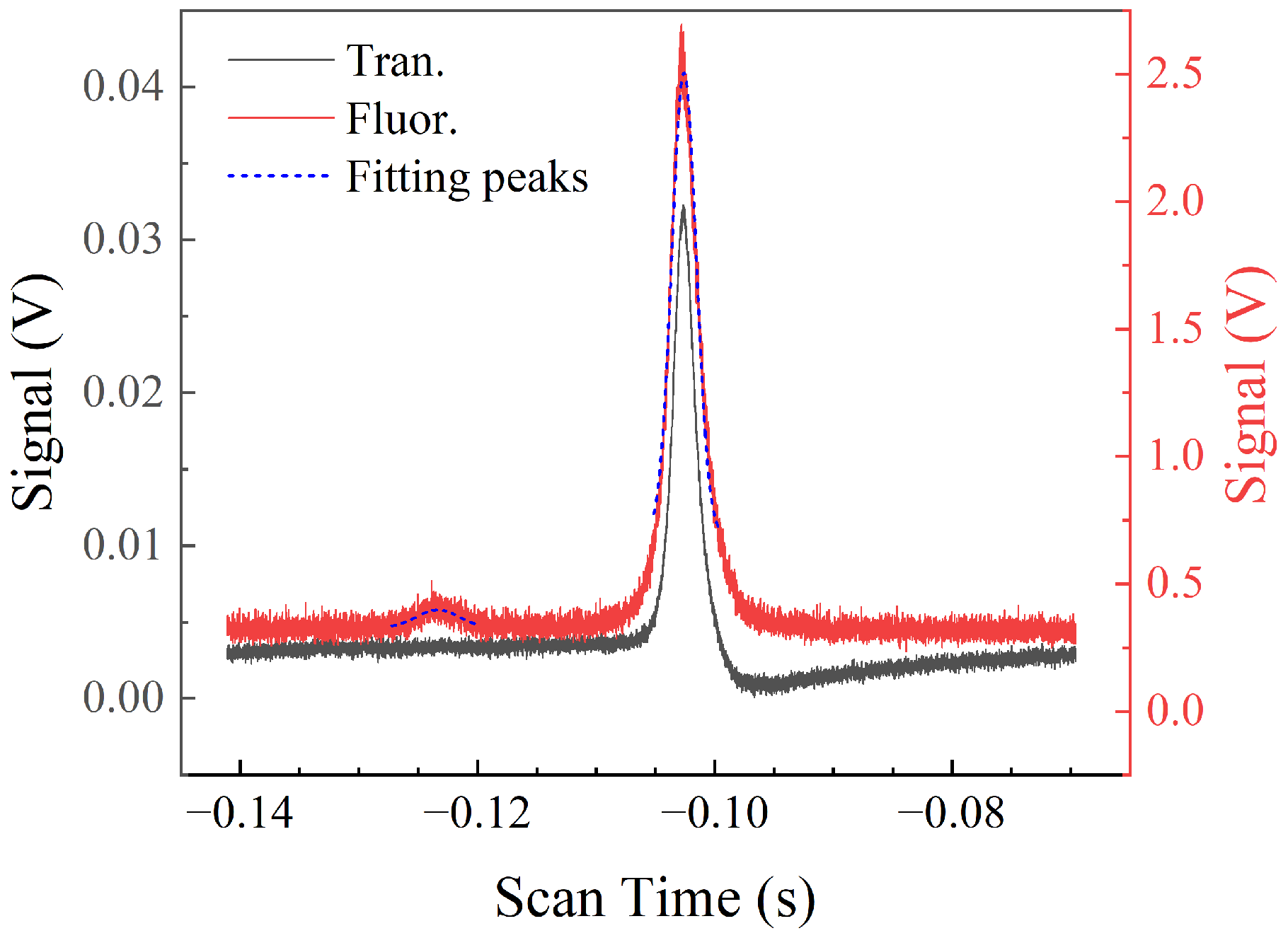
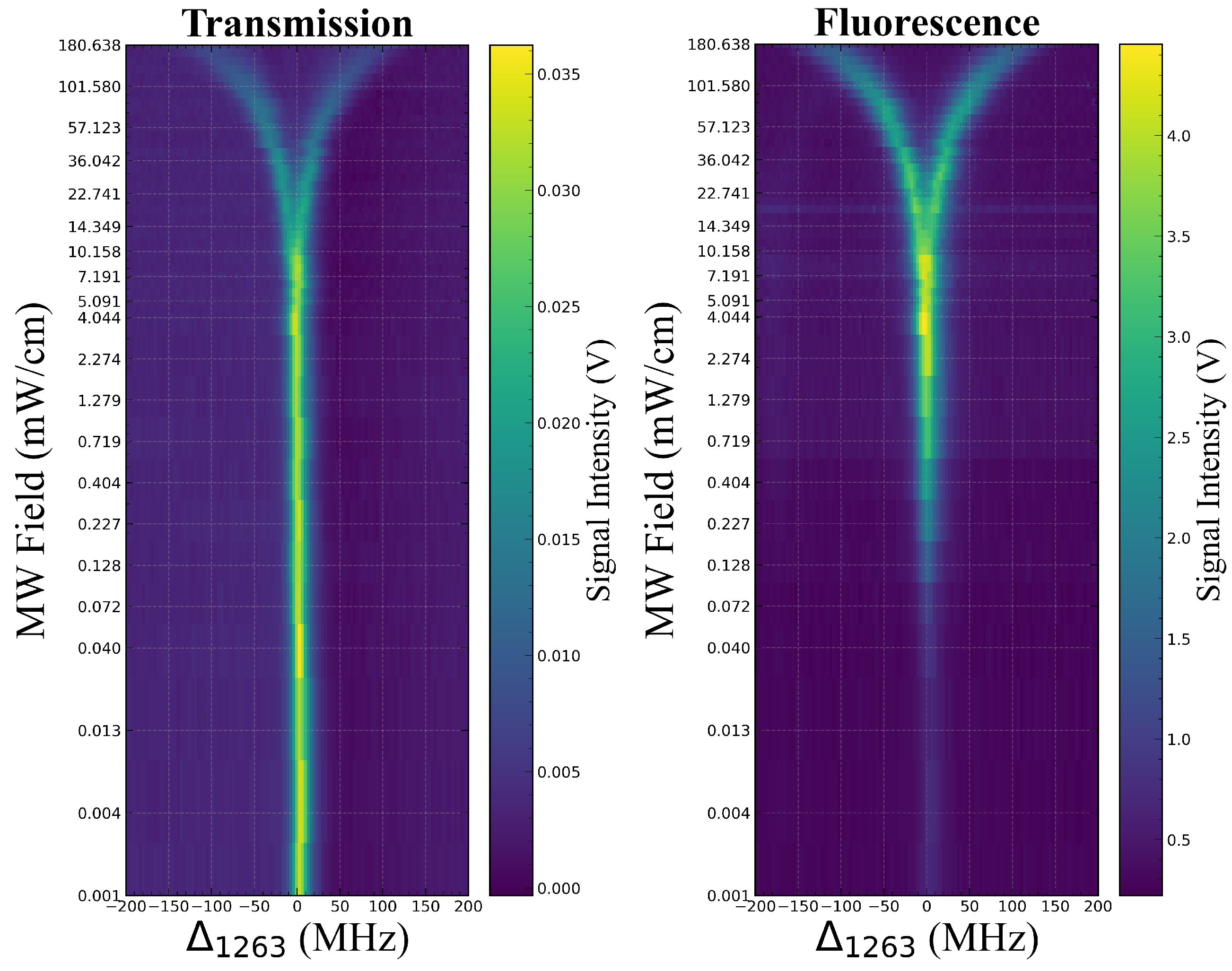
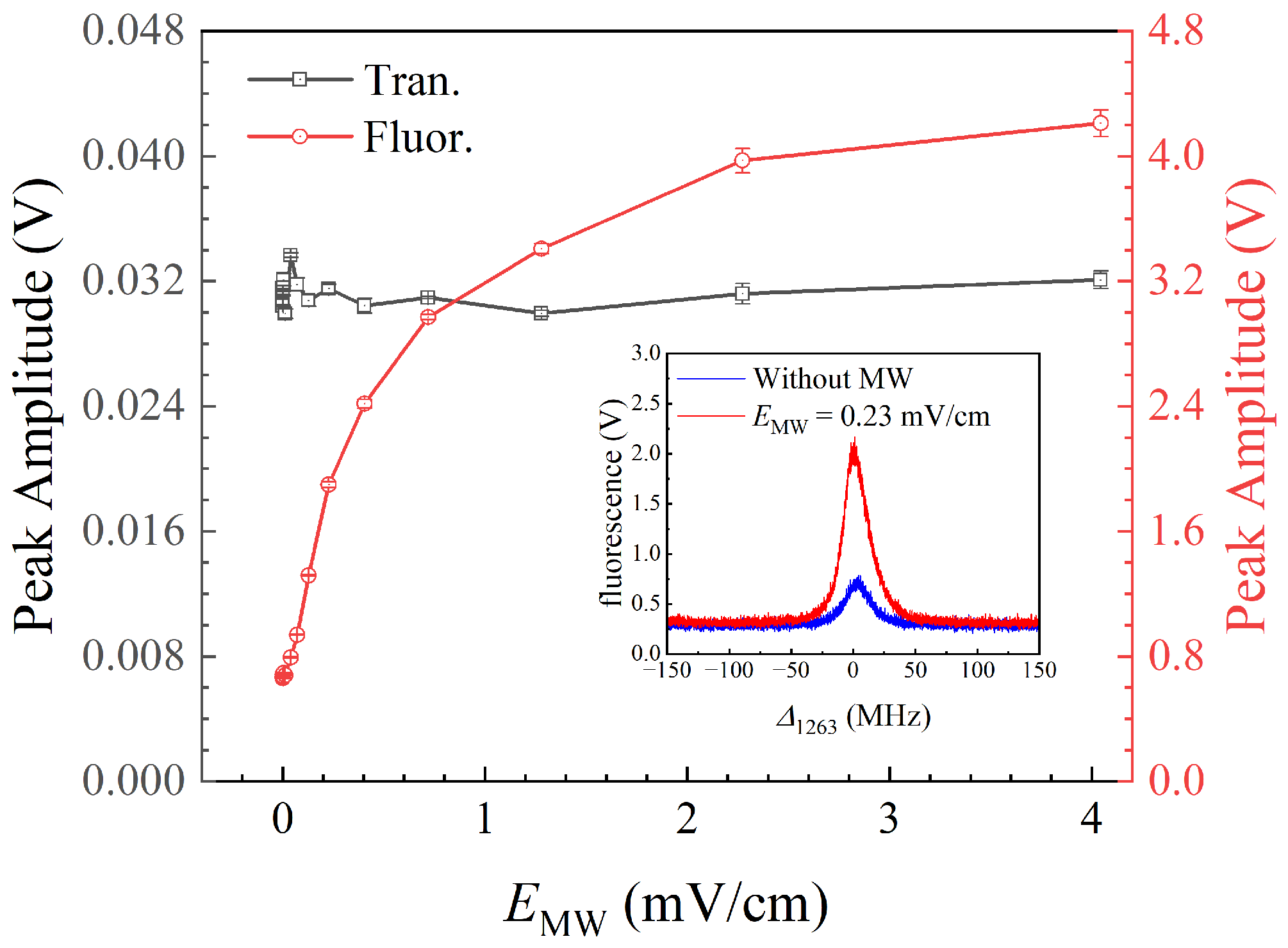
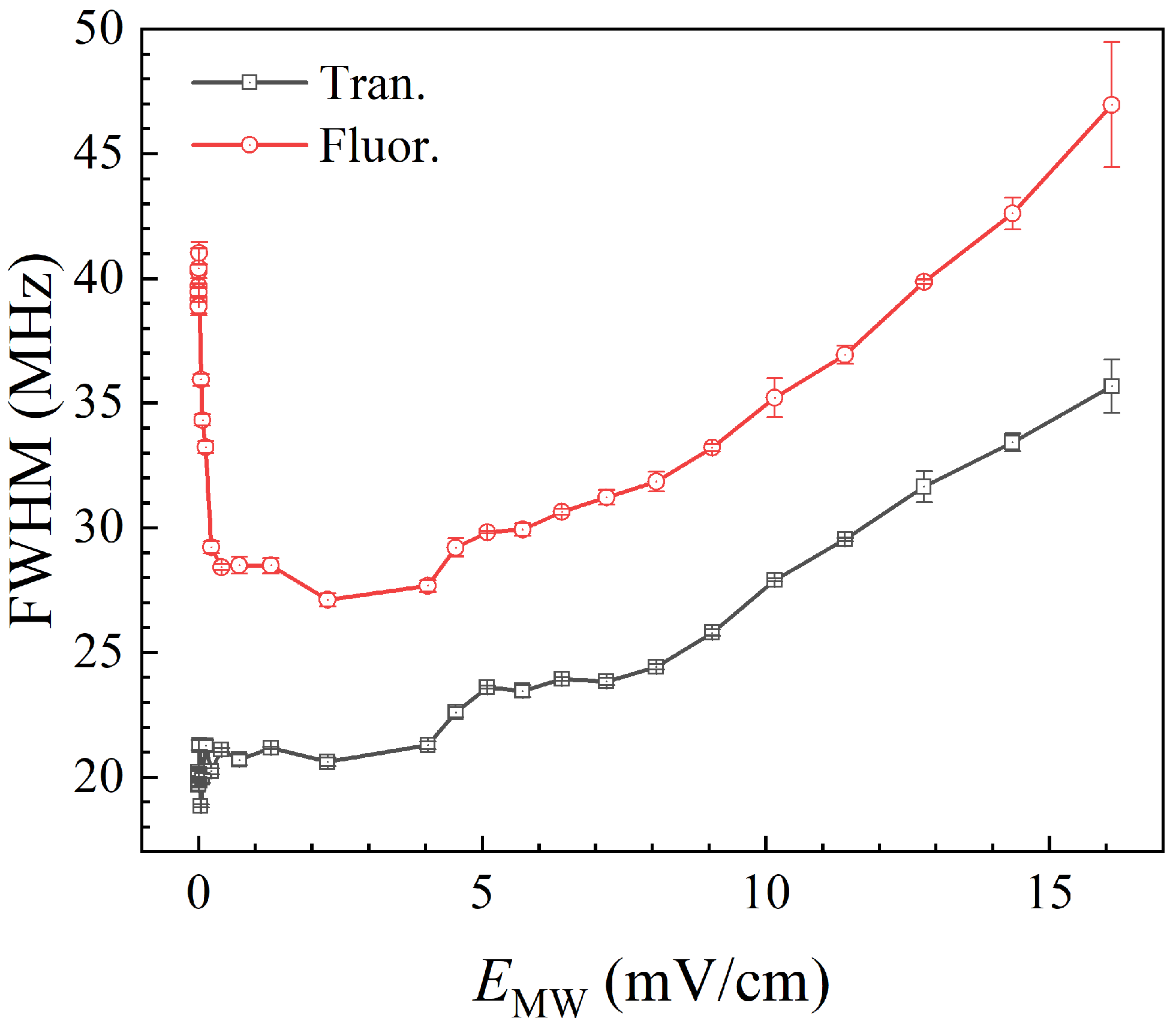
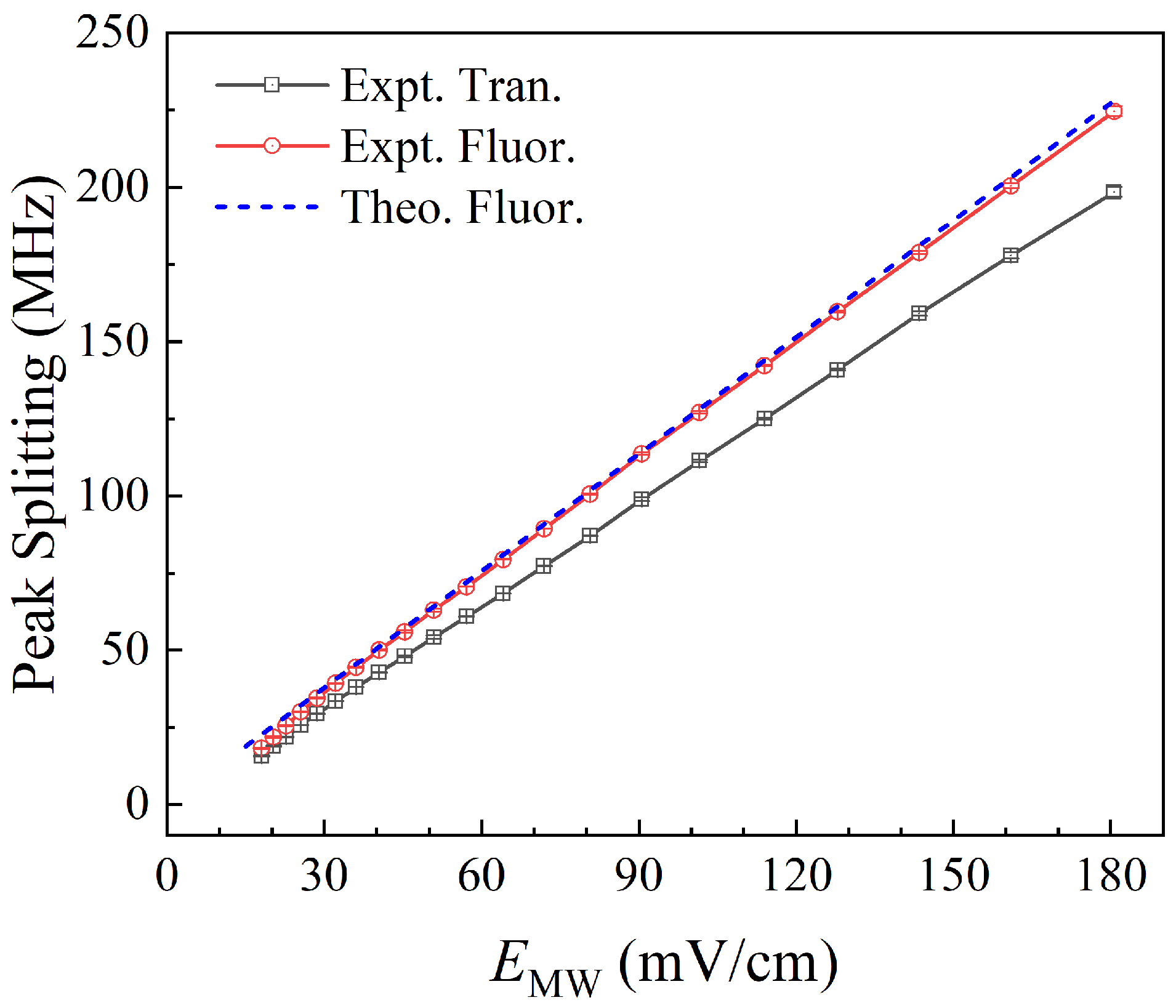
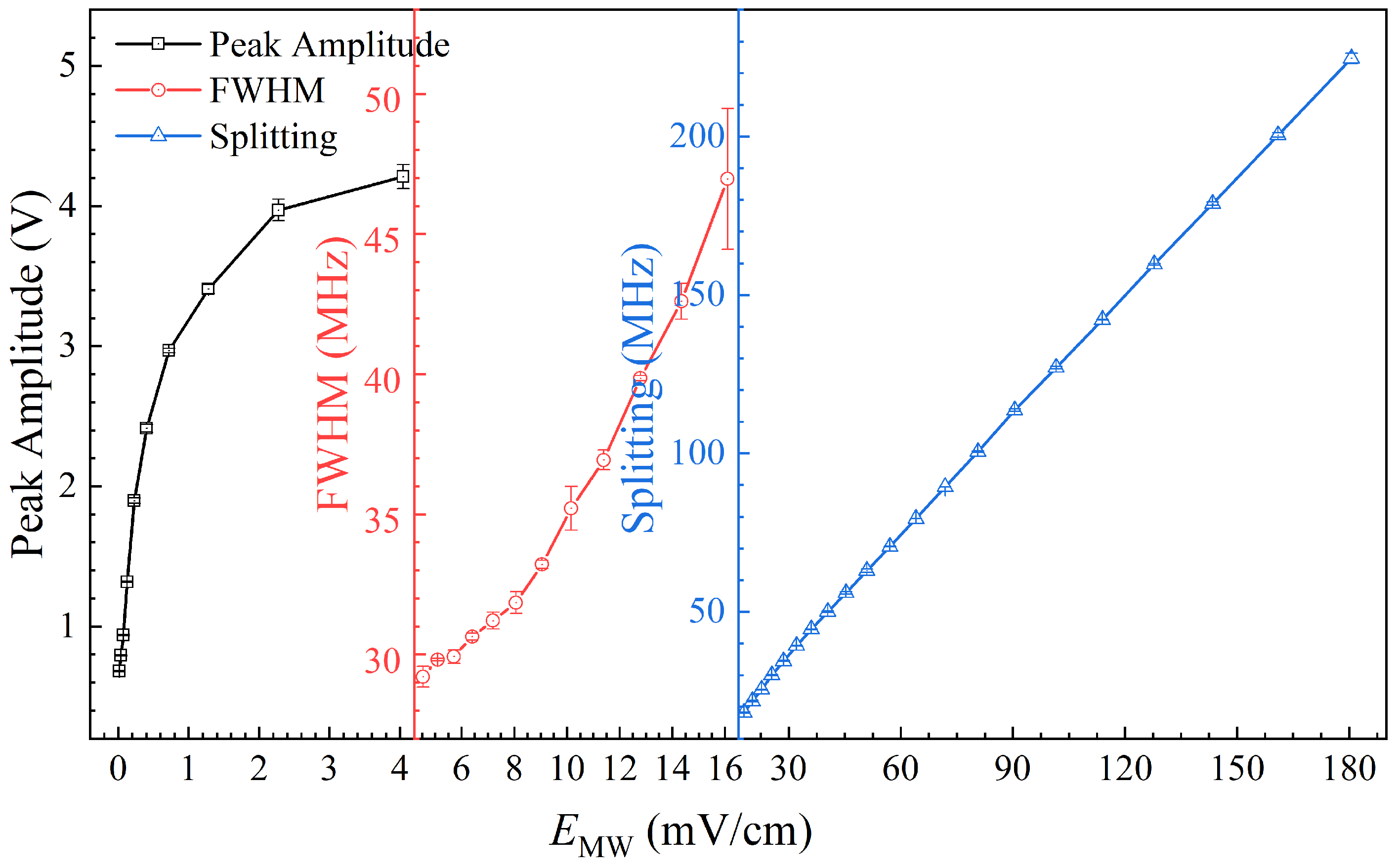
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RF | Radio frequency |
| SI | International System of Units |
| EIT | Electromagnetically induced transparency |
| Rb | Rubidium |
| AT | Autler–Townes |
| LIF | Laser-induced fluorescence |
| EIA | Electromagnetically induced absorption |
| PMT | Photomultiplier tube |
| MW | Microwave |
| AOM | Acousto-optic modulator |
| EOM | Electro-optic modulator |
| FWHM | Full width at half maximum |
| BBR | Blackbody radiation |
References
- Kobayashi, T.; Takamizawa, A.; Akamatsu, D.; Kawasaki, A.; Nishiyama, A.; Hosaka, K.; Hisai, Y.; Wada, M.; Inaba, H.; Tanabe, T.; et al. Search for Ultralight Dark Matter from Long-Term Frequency Comparisons of Optical and Microwave Atomic Clocks. Phys. Rev. Lett. 2022, 129, 241301. [Google Scholar] [CrossRef]
- Hanneke, D.; Fogwell, S.; Gabrielse, G. New Measurement of the Electron Magnetic Moment and the Fine Structure Constant. Phys. Rev. Lett. 2008, 100, 120801. [Google Scholar] [CrossRef]
- Bouchendira, R.; Cladé, P.; Guellati-Khélifa, S.; Nez, F.; Biraben, F. New Determination of the Fine Structure Constant and Test of the Quantum Electrodynamics. Phys. Rev. Lett. 2011, 106, 080801. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum Sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Ludlow, A.D. Optical Atomic Clocks. Rev. Mod. Phys. 2015, 87, 637–701. [Google Scholar] [CrossRef]
- Marti, G.E.; Hutson, R.B.; Goban, A.; Campbell, S.L.; Poli, N.; Ye, J. Imaging Optical Frequencies with 100 µHz Precision and 1.1 µm Resolution. Phys. Rev. Lett. 2018, 120, 103201. [Google Scholar] [CrossRef]
- Zhang, C.; Ooi, T.; Higgins, J.S.; Doyle, J.F.; von der Wense, L.; Beeks, K.; Leitner, A.; Kazakov, G.A.; Li, P.; Thirolf, P.G.; et al. Frequency Ratio of the 229mTh Nuclear Isomeric Transition and the 87Sr Atomic Clock. Nature 2024, 633, 63–70. [Google Scholar] [CrossRef]
- Müller, H.; Chiow, S.w.; Herrmann, S.; Chu, S.; Chung, K.Y. Atom-Interferometry Tests of the Isotropy of Post-Newtonian Gravity. Phys. Rev. Lett. 2008, 100, 031101. [Google Scholar] [CrossRef]
- Zhan, M.; Xie, X. Precision Measurement Physics: Physics That Precision Matters. Natl. Sci. Rev. 2020, 7, 1795. [Google Scholar] [CrossRef]
- Peters, A.; Chung, K.Y.; Chu, S. High-Precision Gravity Measurements Using Atom Interferometry. Metrologia 2001, 38, 25. [Google Scholar] [CrossRef]
- Saywell, J.C.; Carey, M.S.; Light, P.S.; Szigeti, S.S.; Milne, A.R.; Gill, K.S.; Goh, M.L.; Perunicic, V.S.; Wilson, N.M.; Macrae, C.D.; et al. Enhancing the Sensitivity of Atom-Interferometric Inertial Sensors Using Robust Control. Nat. Commun. 2023, 14, 7626. [Google Scholar] [CrossRef] [PubMed]
- Snadden, M.J.; McGuirk, J.M.; Bouyer, P.; Haritos, K.G.; Kasevich, M.A. Measurement of the Earth’s Gravity Gradient with an Atom Interferometer-Based Gravity Gradiometer. Phys. Rev. Lett. 1998, 81, 971–974. [Google Scholar] [CrossRef]
- Dang, H.B.; Maloof, A.C.; Romalis, M.V. Ultrahigh Sensitivity Magnetic Field and Magnetization Measurements with an Atomic Magnetometer. Appl. Phys. Lett. 2010, 97, 151110. [Google Scholar] [CrossRef]
- Merlet, S.; Bodart, Q.; Malossi, N.; Landragin, A.; Santos, F.P.D.; Gitlein, O.; Timmen, L. Comparison between Two Mobile Absolute Gravimeters: Optical versus Atomic Interferometers. Metrologia 2010, 47, L9. [Google Scholar] [CrossRef]
- Sedlacek, J.A.; Schwettmann, A.; Kübler, H.; Löw, R.; Pfau, T.; Shaffer, J.P. Microwave Electrometry with Rydberg Atoms in a Vapour Cell Using Bright Atomic Resonances. Nat. Phys. 2012, 8, 819–824. [Google Scholar] [CrossRef]
- Jing, M.; Hu, Y.; Ma, J.; Zhang, H.; Zhang, L.; Xiao, L.; Jia, S. Atomic Superheterodyne Receiver Based on Microwave-Dressed Rydberg Spectroscopy. Nat. Phys. 2020, 16, 911–915. [Google Scholar] [CrossRef]
- Ding, D.S.; Liu, Z.K.; Shi, B.S.; Guo, G.C.; Mølmer, K.; Adams, C.S. Enhanced Metrology at the Critical Point of a Many-Body Rydberg Atomic System. Nat. Phys. 2022, 18, 1447–1452. [Google Scholar] [CrossRef]
- Fan, H.; Kumar, S.; Sedlacek, J.; Kübler, H.; Karimkashi, S.; Shaffer, J.P. Atom Based RF Electric Field Sensing. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 202001. [Google Scholar] [CrossRef]
- Simons, M.T.; Gordon, J.A.; Holloway, C.L.; Anderson, D.A.; Miller, S.A.; Raithel, G. Using Frequency Detuning to Improve the Sensitivity of Electric Field Measurements via Electromagnetically Induced Transparency and Autler-Townes Splitting in Rydberg Atoms. Appl. Phys. Lett. 2016, 108, 174101. [Google Scholar] [CrossRef]
- Zhang, L.; Jia, Y.; Jing, M.; Guo, L.; Zhang, H.; Xiao, L.; Jia, S. Detuning Radio-Frequency Electrometry Using Rydberg Atoms in a Room-Temperature Vapor Cell. Laser Phys. 2019, 29, 035701. [Google Scholar] [CrossRef]
- Jia, F.; Yu, Y.; Liu, X.; Zhang, X.; Zhang, L.; Wang, F.; Mei, J.; Zhang, J.; Xie, F.; Zhong, Z. Dispersive Microwave Electrometry Using Zeeman Frequency Modulation Spectroscopy of Electromagnetically Induced Transparency in Rydberg Atoms. Appl. Opt. 2020, 59, 8253–8258. [Google Scholar] [CrossRef]
- Shi, Y.; Li, C.; Ouyang, K.; Ren, W.; Li, W.; Cao, M.; Xue, Z.; Shi, M. Tunable Frequency of a Microwave Mixed Receiver Based on Rydberg Atoms under the Zeeman Effect. Opt. Express 2023, 31, 36255–36262. [Google Scholar] [CrossRef]
- Li, X.; Cui, Y.; Hao, J.; Zhou, F.; Wang, Y.; Jia, F.; Zhang, J.; Xie, F.; Zhong, Z. Magnetic-Field-Induced Splitting of Rydberg Electromagnetically Induced Transparency and Autler-Townes Spectra in 87Rb Vapor Cell. Opt. Express 2023, 31, 38165–38178. [Google Scholar] [CrossRef] [PubMed]
- Schlossberger, N.; Rotunno, A.P.; Artusio-Glimpse, A.B.; Prajapati, N.; Berweger, S.; Shylla, D.; Simons, M.T.; Holloway, C.L. Zeeman-Resolved Autler-Townes Splitting in Rydberg Atoms with Tunable Resonances and a Single Transition Dipole Moment. Phys. Rev. A 2024, 109, L021702. [Google Scholar] [CrossRef]
- Jia, F.D.; Liu, X.B.; Mei, J.; Yu, Y.H.; Zhang, H.Y.; Lin, Z.Q.; Dong, H.Y.; Zhang, J.; Xie, F.; Zhong, Z.P. Span Shift and Extension of Quantum Microwave Electrometry with Rydberg Atoms Dressed by an Auxiliary Microwave Field. Phys. Rev. A 2021, 103, 063113. [Google Scholar] [CrossRef]
- Simons, M.T.; Artusio-Glimpse, A.B.; Holloway, C.L.; Imhof, E.; Jefferts, S.R.; Wyllie, R.; Sawyer, B.C.; Walker, T.G. Continuous Radio-Frequency Electric-Field Detection through Adjacent Rydberg Resonance Tuning. Phys. Rev. A 2021, 104, 032824. [Google Scholar] [CrossRef]
- Yuan, J.; Jin, T.; Wang, L.; Xiao, L.; Jia, S. Improvement of Microwave Electric Field Measurement Sensitivity via Dual-Microwave-Dressed Electromagnetically Induced Transparency in Rydberg Atoms. Laser Phys. Lett. 2022, 19, 125207. [Google Scholar] [CrossRef]
- Liu, X.H.; Liao, K.Y.; Zhang, Z.X.; Tu, H.T.; Bian, W.; Li, Z.Q.; Zheng, S.Y.; Li, H.H.; Huang, W.; Yan, H.; et al. Continuous-Frequency Microwave Heterodyne Detection in an Atomic Vapor Cell. Phys. Rev. Appl. 2022, 18, 054003. [Google Scholar] [CrossRef]
- Cui, Y.; Jia, F.D.; Hao, J.H.; Wang, Y.H.; Zhou, F.; Liu, X.B.; Yu, Y.H.; Mei, J.; Bai, J.H.; Bao, Y.Y.; et al. Extending Bandwidth Sensitivity of Rydberg-atom-based Microwave Electrometry Using an Auxiliary Microwave Field. Phys. Rev. A 2023, 107, 043102. [Google Scholar] [CrossRef]
- Liu, X.; Jia, F.; Zhang, H.; Mei, J.; Yu, Y.; Liang, W.; Zhang, J.; Xie, F.; Zhong, Z. Using Amplitude Modulation of the Microwave Field to Improve the Sensitivity of Rydberg-atom Based Microwave Electrometry. AIP Adv. 2021, 11, 085127. [Google Scholar] [CrossRef]
- Hao, J.H.; Jia, F.D.; Cui, Y.; Wang, Y.H.; Zhou, F.; Liu, X.B.; Zhang, J.; Xie, F.; Bai, J.H.; You, J.Q.; et al. Microwave Electrometry with Rydberg Atoms in a Vapor Cell Using Microwave Amplitude Modulation. Chin. Phys. B 2024, 33, 050702. [Google Scholar] [CrossRef]
- Gomes, N.D.; Pepino, V.M.; Borges, B.H.V.; Magalhães, D.V.; de Jesus Napolitano, R.; Torres, M.A.L.; Kondo, J.D.M.; Marcassa, L.G. Rydberg Atom-Based Microwave Electrometry Using Polarization Spectroscopy. J. Phys. B At. Mol. Opt. Phys. 2024, 57, 235502. [Google Scholar] [CrossRef]
- Liao, K.Y.; Tu, H.T.; Yang, S.Z.; Chen, C.J.; Liu, X.H.; Liang, J.; Zhang, X.D.; Yan, H.; Zhu, S.L. Microwave Electrometry via Electromagnetically Induced Absorption in Cold Rydberg Atoms. Phys. Rev. A 2020, 101, 053432. [Google Scholar] [CrossRef]
- Zhou, F.; Jia, F.; Liu, X.; Yu, Y.; Mei, J.; Zhang, J.; Xie, F.; Zhong, Z. Improving the Spectral Resolution and Measurement Range of Quantum Microwave Electrometry by Cold Rydberg Atoms. J. Phys. B At. Mol. Opt. Phys. 2023, 56, 025501. [Google Scholar] [CrossRef]
- Zhou, F.; Jia, F.D.; Liu, X.B.; Zhang, J.; Xie, F.; Zhong, Z.P. Measurement of Microwave Electric Field Based on Electromagnetically Induced Transparency by Using Cold Rydberg Atoms. Acta Phys. Sin. 2023, 72, 045204. [Google Scholar] [CrossRef]
- Kumar, S.; Fan, H.; Kübler, H.; Jahangiri, A.J.; Shaffer, J.P. Rydberg-Atom Based Radio-Frequency Electrometry Using Frequency Modulation Spectroscopy in Room Temperature Vapor Cells. Opt. Express 2017, 25, 8625–8637. [Google Scholar] [CrossRef] [PubMed]
- Gordon, J.A.; Simons, M.T.; Haddab, A.H.; Holloway, C.L. Weak Electric-Field Detection with Sub-1 Hz Resolution at Radio Frequencies Using a Rydberg Atom-Based Mixer. AIP Adv. 2019, 9, 045030. [Google Scholar] [CrossRef]
- Cai, M.; You, S.; Zhang, S.; Xu, Z.; Liu, H. Sensitivity Extension of Atom-Based Amplitude-Modulation Microwave Electrometry via High Rydberg States. Appl. Phys. Lett. 2023, 122, 161103. [Google Scholar] [CrossRef]
- Holloway, C.L.; Prajapati, N.; Artusio-Glimpse, A.B.; Berweger, S.; Simons, M.T.; Kasahara, Y.; Alù, A.; Ziolkowski, R.W. Rydberg Atom-Based Field Sensing Enhancement Using a Split-Ring Resonator. Appl. Phys. Lett. 2022, 120, 204001. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, L.H.; Wang, Q.F.; Ma, Y.; Han, T.Y.; Liu, Z.K.; Zhang, Z.Y.; Shao, S.Y.; Zhang, J.; Li, Q.; et al. Cavity-Enhanced Rydberg Atom Microwave Receiver. Chin. Phys. Lett. 2025, 42, 053201. [Google Scholar] [CrossRef]
- Wang, Q.; Liang, Y.; Wang, Z.; Guan, S.; Yang, P.; Zhang, P.; Li, G.; Zhang, T. High-Precision Measurement of Microwave Electric Field by Cavity-Enhanced Critical Behavior in a Many-Body Rydberg Atomic System. Sci. China Phys. Mech. Astron. 2025, 68, 264211. [Google Scholar] [CrossRef]
- Yang, W.; Jing, M.; Zhang, H.; Zhang, L.; Xiao, L.; Jia, S. Enhancing the Sensitivity of Atom-Based Microwave-Field Electrometry Using a Mach-Zehnder Interferometer. Phys. Rev. Appl. 2023, 19, 064021. [Google Scholar] [CrossRef]
- Holloway, C.L.; Gordon, J.A.; Schwarzkopf, A.; Anderson, D.A.; Miller, S.A.; Thaicharoen, N.; Raithel, G. Sub-Wavelength Imaging and Field Mapping via Electromagnetically Induced Transparency and Autler-Townes Splitting in Rydberg Atoms. Appl. Phys. Lett. 2014, 104, 244102. [Google Scholar] [CrossRef]
- Fan, H.Q.; Kumar, S.; Daschner, R.; Kübler, H.; Shaffer, J.P. Subwavelength Microwave Electric-Field Imaging Using Rydberg Atoms inside Atomic Vapor Cells. Opt. Lett. 2014, 39, 3030–3033. [Google Scholar] [CrossRef]
- Walker, D.A. A Fluorescence Technique for Measurement of Concentration in Mixing Liquids. J. Phys. E Sci. Instrum. 1987, 20, 217. [Google Scholar] [CrossRef]
- Prajapati, N.; Berweger, S.; Rotunno, A.P.; Artusio-Glimpse, A.B.; Schlossberger, N.; Shylla, D.; Watterson, W.J.; Simons, M.T.; LaMantia, D.; Norrgard, E.B.; et al. Investigation of Fluorescence versus Transmission Readout for Three-Photon Rydberg Excitation Used in Electrometry. AVS Quantum Sci. 2024, 6, 034401. [Google Scholar] [CrossRef]
- Holloway, C.L.; Simons, M.T.; Gordon, J.A.; Dienstfrey, A.; Anderson, D.A.; Raithel, G. Electric Field Metrology for SI Traceability: Systematic Measurement Uncertainties in Electromagnetically Induced Transparency in Atomic Vapor. J. Appl. Phys. 2017, 121. [Google Scholar] [CrossRef]
- Miller, B.N.; Meyer, D.H.; Virtanen, T.; O’Brien, C.M.; Cox, K.C. RydIQule: A Graph-Based Paradigm for Modeling Rydberg and Atomic Sensors. Comput. Phys. Commun. 2024, 294, 108952. [Google Scholar] [CrossRef]
- Šibalić, N.; Pritchard, J.D.; Adams, C.S.; Weatherill, K.J. ARC: An Open-Source Library for Calculating Properties of Alkali Rydberg Atoms. Comput. Phys. Commun. 2017, 220, 319–331. [Google Scholar] [CrossRef]
- Gordon, J.A.; Holloway, C.L.; Schwarzkopf, A.; Anderson, D.A.; Miller, S.; Thaicharoen, N.; Raithel, G. Millimeter Wave Detection via Autler-Townes Splitting in Rubidium Rydberg Atoms. Appl. Phys. Lett. 2014, 105, 024104. [Google Scholar] [CrossRef]
- Gordon, E.I. A Review of Acoustooptical Deflection and Modulation Devices. Appl. Opt. 1966, 5, 1629–1639. [Google Scholar] [CrossRef]
- van Wijngaarden, W.A.; Li, J. Calibration of Laser Frequency Scan with an Electro-Optic Modulator. Appl. Opt. 1997, 36, 5905–5907. [Google Scholar] [CrossRef]
- Kessler, T.; Hagemann, C.; Grebing, C.; Legero, T.; Sterr, U.; Riehle, F.; Martin, M.J.; Chen, L.; Ye, J. A Sub-40-mHz-linewidth Laser Based on a Silicon Single-Crystal Optical Cavity. Nat. Photon 2012, 6, 687–692. [Google Scholar] [CrossRef]
- Udem, T.; Holzwarth, R.; Hänsch, T.W. Optical Frequency Metrology. Nature 2002, 416, 233–237. [Google Scholar] [CrossRef] [PubMed]
- Rosenband, T.; Hume, D.B.; Schmidt, P.O.; Chou, C.W.; Brusch, A.; Lorini, L.; Oskay, W.H.; Drullinger, R.E.; Fortier, T.M.; Stalnaker, J.E.; et al. Frequency Ratio of Al+ and Hg+ Single-Ion Optical Clocks—Metrology at the 17th Decimal Place. Science 2008, 319, 1808–1812. [Google Scholar] [CrossRef]
- Morris, M.B.; McIlrath, T.J.; Snyder, J.J. Fizeau Wavemeter for Pulsed Laser Wavelength Measurement. Appl. Opt. 1984, 23, 3862–3868. [Google Scholar] [CrossRef] [PubMed]
- Robertson, E.J.; Šibalić, N.; Potvliege, R.M.; Jones, M.P.A. ARC 3.0: An Expanded Python Toolbox for Atomic Physics Calculations. Comput. Phys. Commun. 2021, 261, 107814. [Google Scholar] [CrossRef]
- Kaur, C.; Shen, P.; Booth, D.; Todd, A.; Shaffer, J.P. The Impact of Thermal Fields on Rydberg Atom Radio Frequency Sensors. arXiv 2025, arXiv:2508.17506. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Liu, Y.; Liu, Y.; Xu, Z.; Jia, F.; Wang, J.; Meng, F.; Wang, Q.; Zhang, J.; Zhong, Z. Advancing Three-Photon-Excited Rydberg RF Sensing: Fluorescence Readout for Wide-Dynamic-Range Characterization and Spatial Resolution Beyond Transmission. Sensors 2025, 25, 7185. https://doi.org/10.3390/s25237185
Zhang J, Liu Y, Liu Y, Xu Z, Jia F, Wang J, Meng F, Wang Q, Zhang J, Zhong Z. Advancing Three-Photon-Excited Rydberg RF Sensing: Fluorescence Readout for Wide-Dynamic-Range Characterization and Spatial Resolution Beyond Transmission. Sensors. 2025; 25(23):7185. https://doi.org/10.3390/s25237185
Chicago/Turabian StyleZhang, Jianan, Yuqing Liu, Yimin Liu, Zhenlu Xu, Fengdong Jia, Jinghui Wang, Fei Meng, Qiang Wang, Jianwei Zhang, and Zhiping Zhong. 2025. "Advancing Three-Photon-Excited Rydberg RF Sensing: Fluorescence Readout for Wide-Dynamic-Range Characterization and Spatial Resolution Beyond Transmission" Sensors 25, no. 23: 7185. https://doi.org/10.3390/s25237185
APA StyleZhang, J., Liu, Y., Liu, Y., Xu, Z., Jia, F., Wang, J., Meng, F., Wang, Q., Zhang, J., & Zhong, Z. (2025). Advancing Three-Photon-Excited Rydberg RF Sensing: Fluorescence Readout for Wide-Dynamic-Range Characterization and Spatial Resolution Beyond Transmission. Sensors, 25(23), 7185. https://doi.org/10.3390/s25237185





