Additively Manufactured Mechanically Tunable Cavity Resonator for Broadband Characterization of Liquid Permittivity
Abstract
1. Introduction
2. Design and Fabrication of Frequency Tunable Cavity Resonator
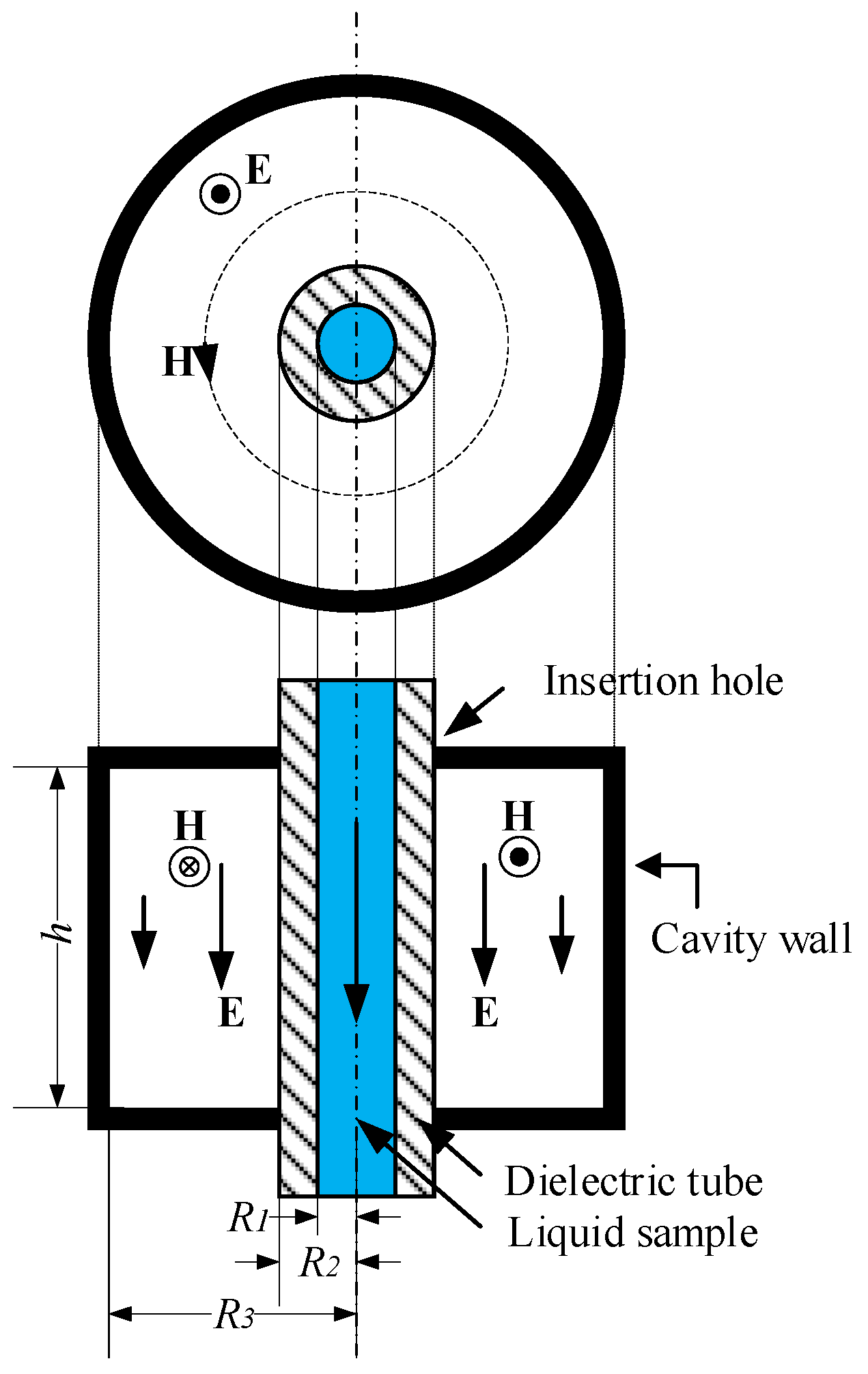
2.1. Working Principle
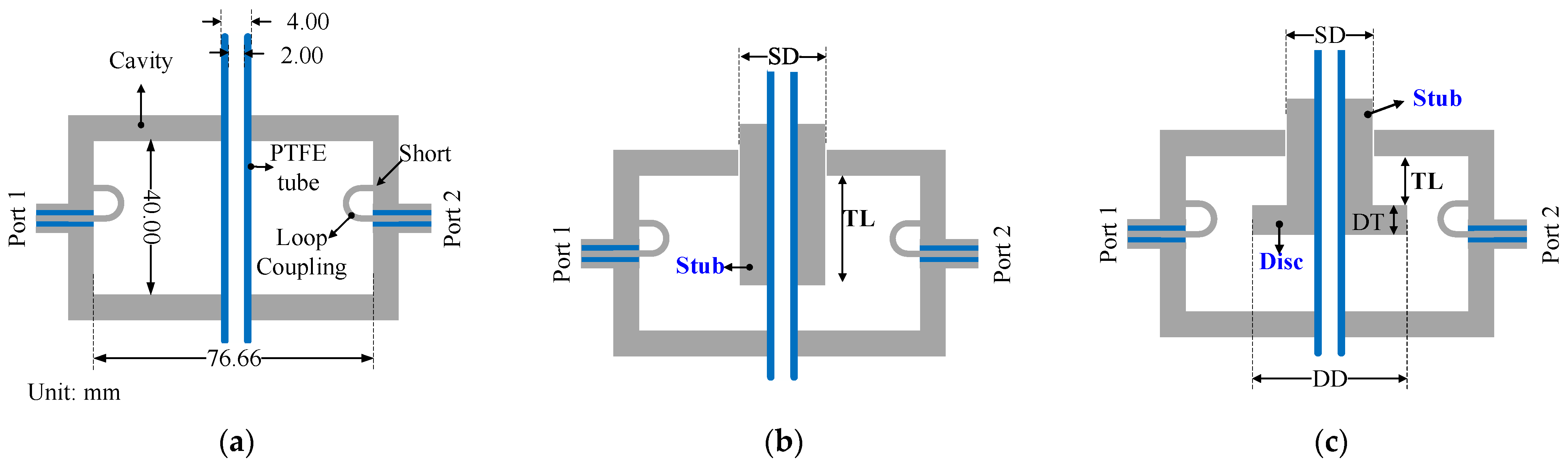
2.2. Design of Mechanically Tunable Cavity Resonator
2.3. Tunable Cavity Resonator Fabrication
3. Results and Discussion
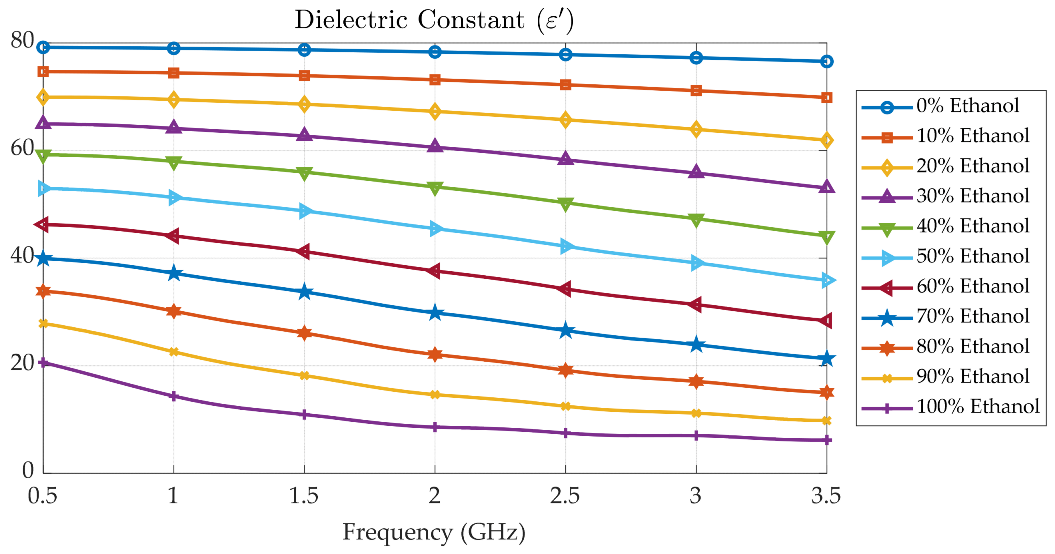
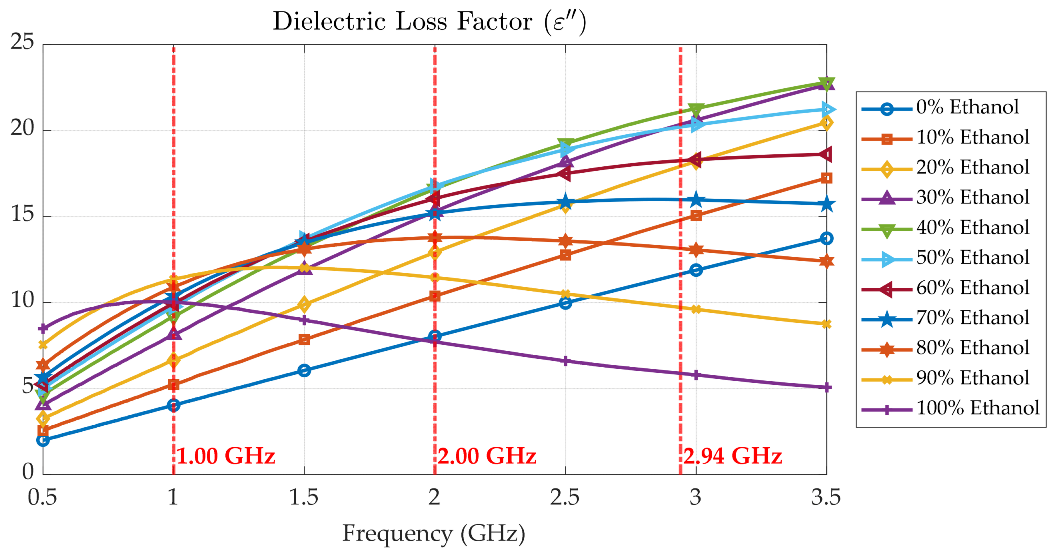
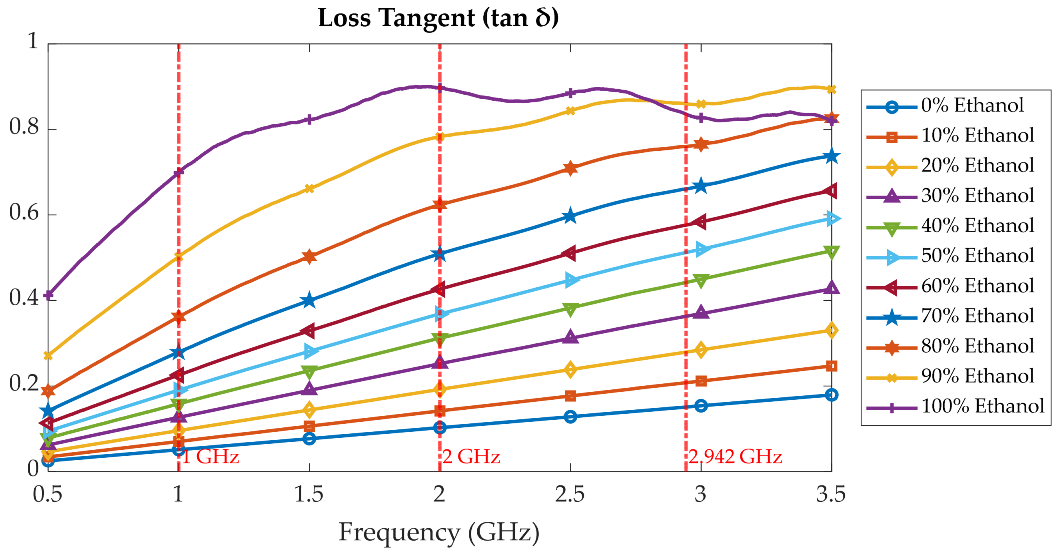
3.1. Measurement of Liquid Samples’ Dielectric Property Using Commercial Probe
- C1 is the concentration of pure ethanol (100%).
- V1 is the volume of pure ethanol.
- C2 is the desired ethanol concentration (Ec) (e.g., 90%, 80%, etc.).
- V2 is the final volume of the prepared mixture (fixed at 100 mL).
- Volume of distilled water = V2 − V1.
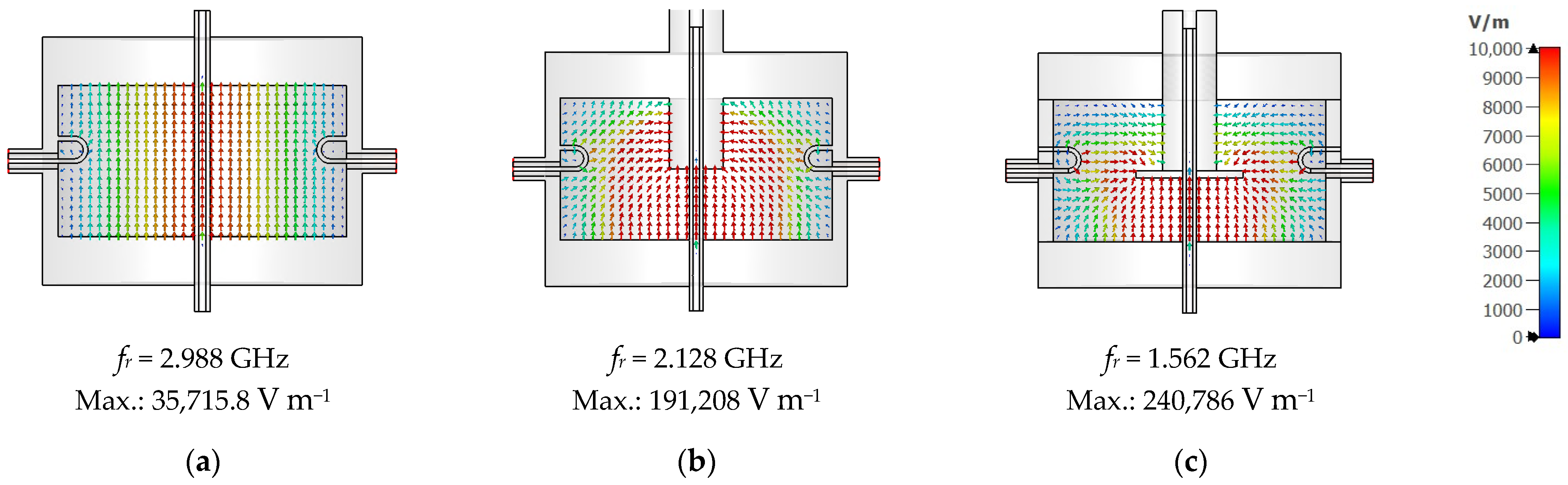
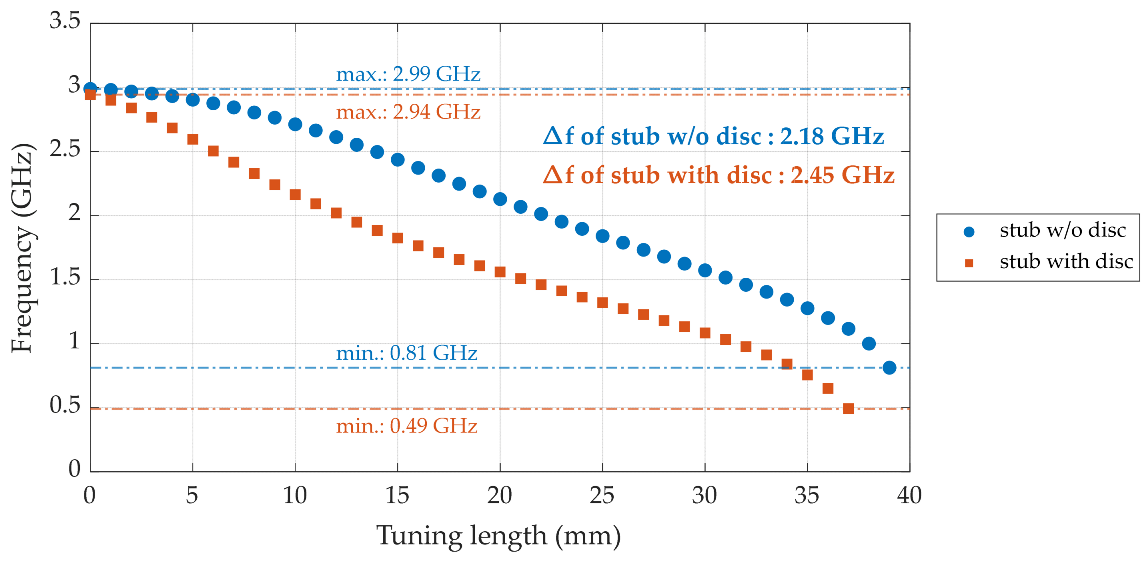
3.2. Cavity Measurement Setup and Initial Results
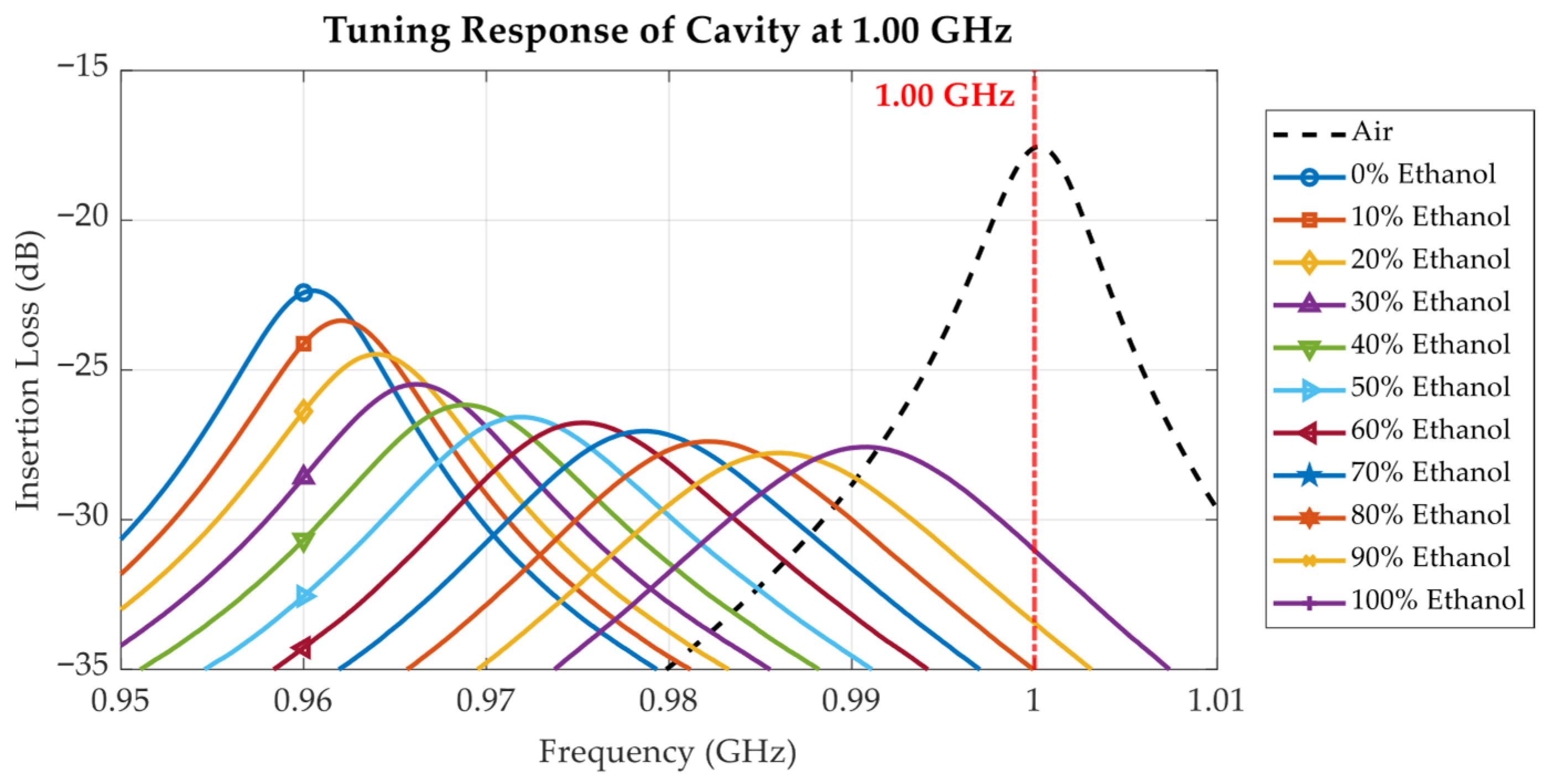
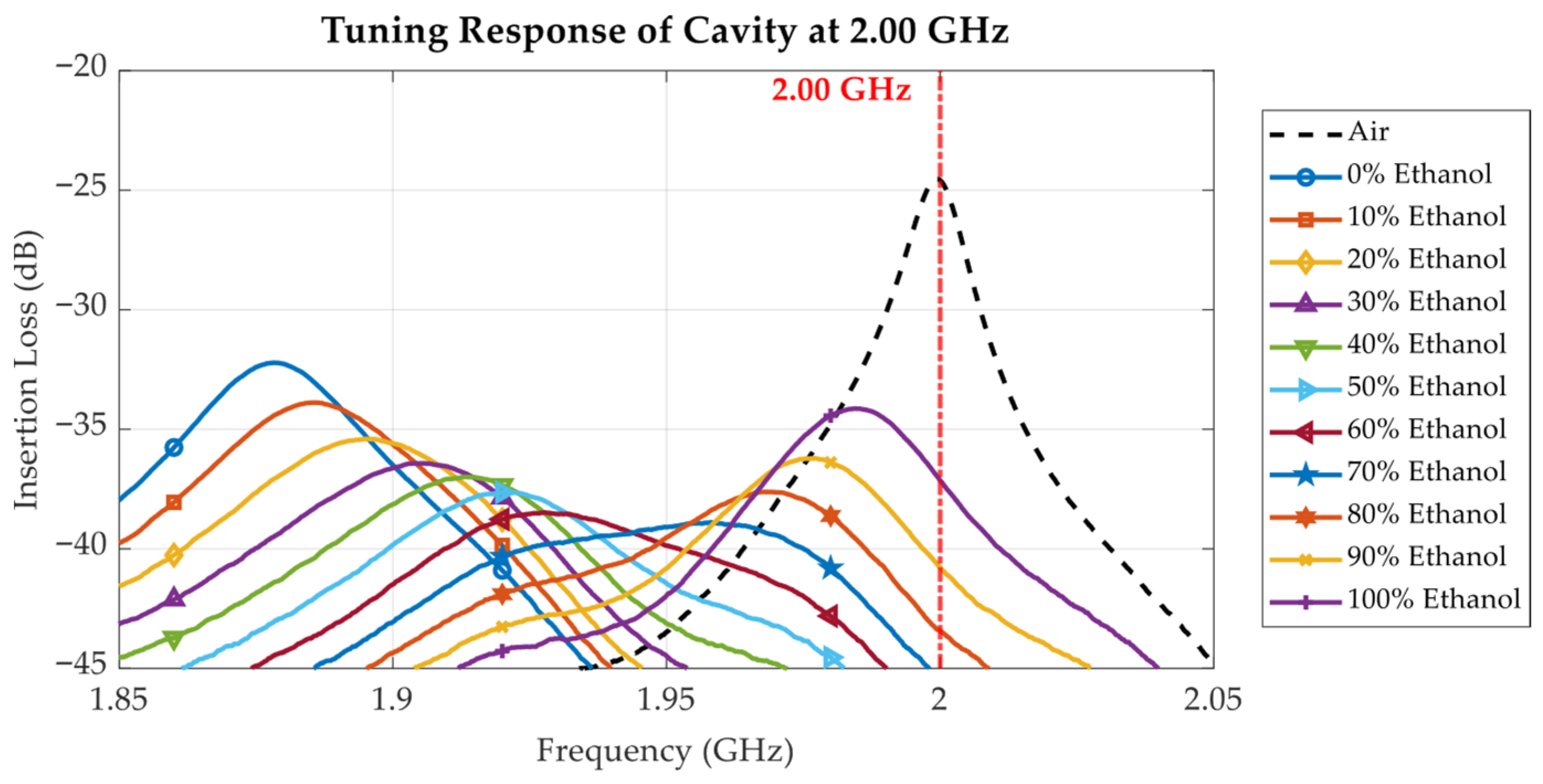
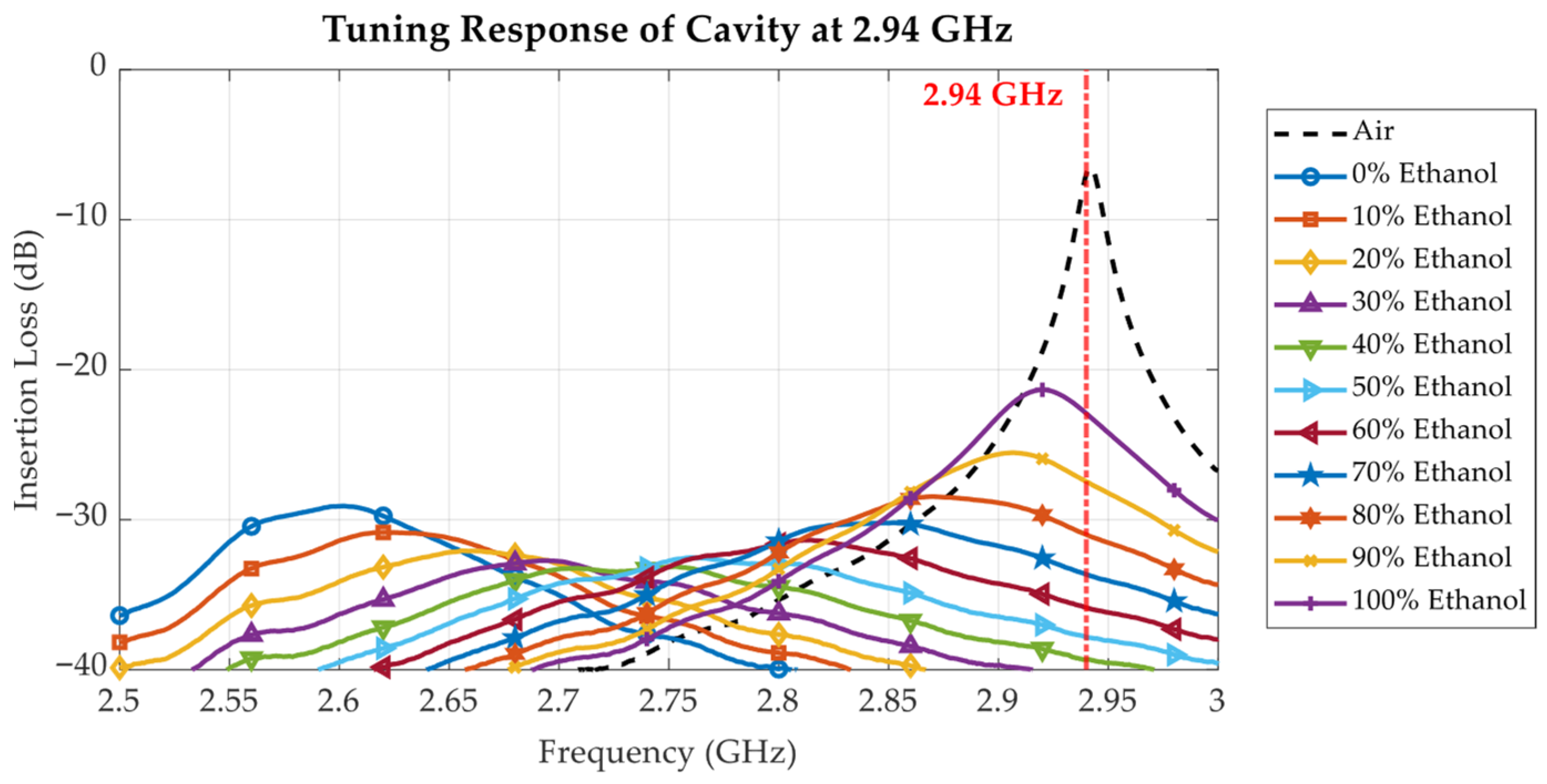
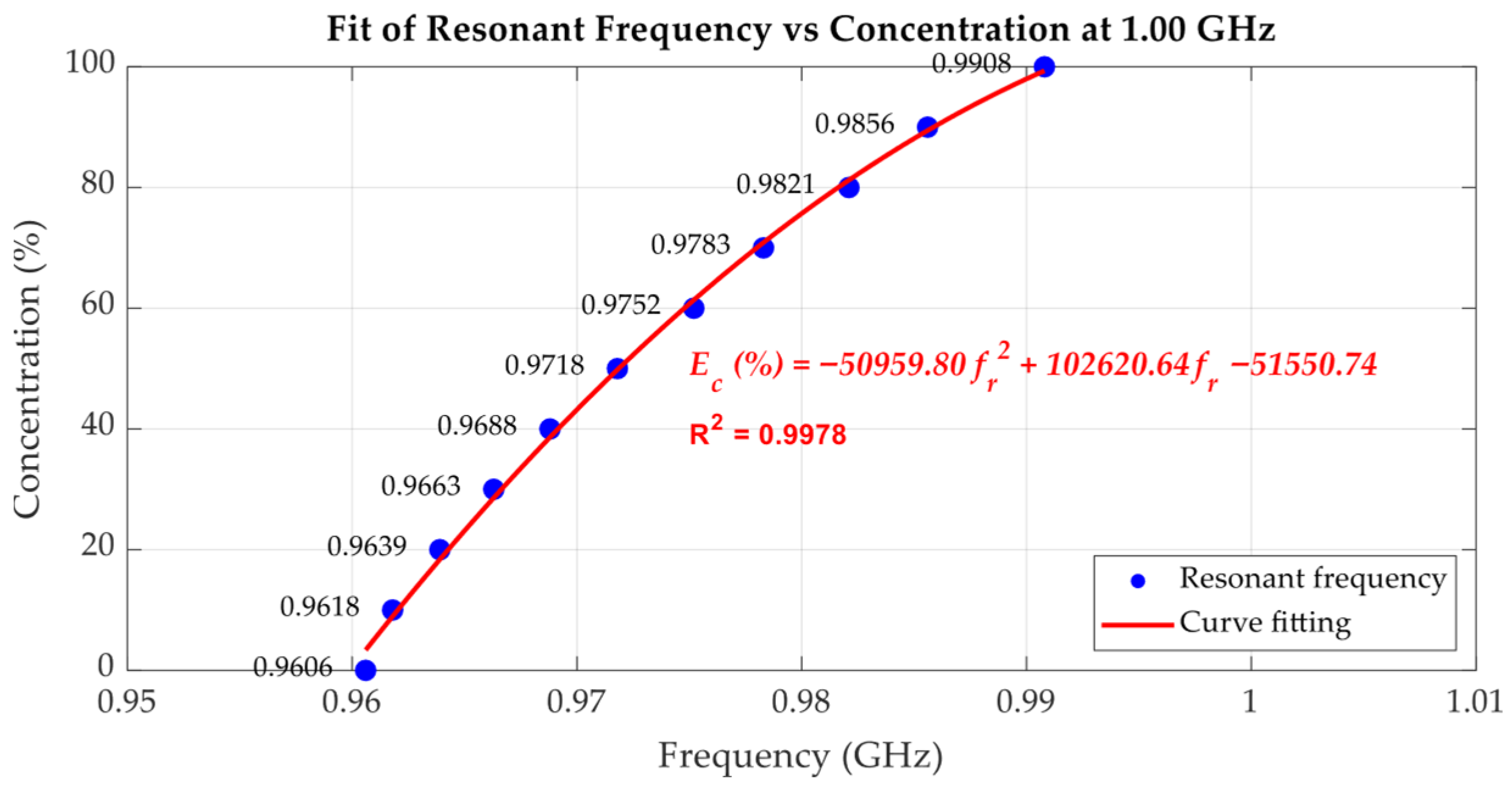
3.3. Ethanol Solution Characterization with Proposed Tunable Cavity Resonator
4. Further Application
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Z.; Meng, Z.; Haigh, A.; Wang, P.; Gibson, A. Characterisation of Water in Honey Using a Microwave Cylindrical Cavity Resonator Sensor. J. Food Eng. 2021, 292, 110373. [Google Scholar] [CrossRef]
- Li, Z.; Haigh, A.; Wang, P.; Soutis, C.; Gibson, A. Characterisation and Analysis of Alcohol in Baijiu with a Microwave Cavity Resonator. LWT 2021, 141, 110849. [Google Scholar] [CrossRef]
- Chudpooti, N.; Pechrkool, T.; Sangpet, P.; Akkaraekthalin, P.; Robertson, I.D.; Somjit, N. 5.58-GHz Modified Jerusalem Patch Sensor for 1%-Precision Ethanol and Methanol Discrimination in Disinfectant Solutions. IEEE Access 2024, 12, 112690–112701. [Google Scholar] [CrossRef]
- Li, Z.; Meng, Z.; Soutis, C.; Wang, P.; Gibson, A. Detection and Analysis of Metallic Contaminants in Dry Foods Using a Microwave Resonator Sensor. Food Control 2022, 133, 108634. [Google Scholar] [CrossRef]
- Li, Z.; Meng, Z.; Fei, F.; Gibson, A. Microwave Cylindrical Cavity Resonator Sensor for Detection and Characterization of Contaminants in Lubricating Oil. IEEE Sens. J. 2022, 22, 22600–22609. [Google Scholar] [CrossRef]
- Sharma, P.; Lao, L.; Falcone, G. A Microwave Cavity Resonator Sensor for Water-in-Oil Measurements. Sens. Actuators B Chem. 2018, 262, 200–210. [Google Scholar] [CrossRef]
- Asadi, R.; Li, C.; Mousavi, S.; Mousavi, S.M.; Vahdani, R.; Ye, X.; Kim, D.B. Design of the TM010 Mode Cylindrical Cavity Resonator for PCB Dielectric Characterization. In Proceedings of the IEEE EMCSIPI Symposium, Phoenix, AZ, USA, 5–9 August 2024. [Google Scholar] [CrossRef]
- Steiner, C.; Walter, S.; Malashchuk, V.; Hagen, G.; Kogut, I.; Fritze, H.; Moos, R. Determination of the Dielectric Properties of Storage Materials for Exhaust Gas Aftertreatment Using the Microwave Cavity Perturbation Method. Sensors 2020, 20, 6024. [Google Scholar] [CrossRef] [PubMed]
- Li, E.; Nie, Z.-P.; Guo, G.; Zhang, Q.; Li, Z.; He, F. Broadband measurements of dielectric properties of low-loss materials at high temperatures using circular cavity method. Prog. Electromagn. Res. 2009, 92, 103–120. [Google Scholar] [CrossRef]
- Gregory, A.P.; Clarke, R.N. A review of RF and microwave techniques for dielectric measurements on polar liquids. IEEE Trans. Dielectr. Electr. Insul. 2006, 13, 727–743. [Google Scholar] [CrossRef]
- Meng, B.; Booske, J.; Cooper, R. Extended cavity perturbation technique to determine the complex permittivity of dielectric materials. IEEE Trans. Microw. Theory Tech. 1995, 43, 2633–2636. [Google Scholar] [CrossRef]
- Sheen, J. Microwave measurements of dielectric properties using a closed cylindrical cavity dielectric resonator. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 1139–1144. [Google Scholar] [CrossRef]
- Kawabata, H.; Tanpo, H.; Kobayashi, Y. A Rigorous Analysis of a TM010 Mode Cylindrical Cavity to Measure Accurate Complex Permittivity of Liquid. In Proceedings of the 33rd European Microwave Conference, Munich, Germany, 2–10 October 2003. [Google Scholar] [CrossRef]
- Kawabata, H.; Kobayashi, Y. Accurate Measurements of Complex Permittivity of Liquid Based on a TM101 Mode Cylindrical Cavity Method. In Proceedings of the 2005 European Microwave Conference, Paris, France, 4–6 October 2005. [Google Scholar] [CrossRef]
- Barmatz, M.B.; Jackson, H.W.; Javeed, A.S.; Jamieson, C.S.; Steinfeld, D.E. An Accurate Radially Stratified Approach for Determining the Complex Permittivity of Liquids in a Cylindrical Microwave Cavity. IEEE Trans. Microw. Theory Tech. 2015, 63, 504–508. [Google Scholar] [CrossRef]
- Kanpan, P.; Khansalee, E.; Puangngernmak, N.; Chalermwisutkul, S. TM010 Mode Cylindrical Cavity for Complex Permittivity Measurement of Liquid Using Field Analysis Technique. In Proceedings of the 2012 9th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Phetchaburi, Thailand, 16–18 May 2012. [Google Scholar] [CrossRef]
- Sangdao, C. Feasibility Study of Dielectric Measurement Using a Concentric Cylindrical Cavity. In Proceedings of the 2019 7th International Electrical Engineering Congress (iEECON), Hua Hin, Thailand, 6–8 March 2019. [Google Scholar] [CrossRef]
- Zhang, Y.; Fan, Z.; Zhu, H.; Gao, C.; Yu, C.; Niu, X.; Li, E. Complex Permittivity Measurement of Materials with a Wide Loss Tangent Range Based on Multiholes Cylindrical Resonant Cavity. IEEE Microw. Wirel. Technol. Lett. 2025. Early Access. [Google Scholar] [CrossRef]
- Faz, U.; Siart, U.; Eibert, T.F. A Cylindrical Cavity Resonator for Material Measurements with Coupled Resonant Modes for Sensing and Position Offset Compensation of the Dielectric Specimen. In Proceedings of the 2015 German Microwave Conference (GeMiC), Nuremberg, Germany, 16–18 March 2015. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Metal, D. 316L v.2 Stainless Steel PureSinter Furnace; Desktop Metal, Inc.: Burlington, MA, USA, 2024. [Google Scholar]
- Metal, D. (Desktop Metal). Available online: https://www.desktopmetal.com/ (accessed on 29 July 2025).
- Yildiz, R.A.; Ozdogan, C.; Malekan, M. On the Surface Roughness of 316L Stainless Steel Fabricated Using L-PBF Additive Manufacturing. Tribologia–Finn. J. Tribol. 2024, 41, 54–56. [Google Scholar] [CrossRef]

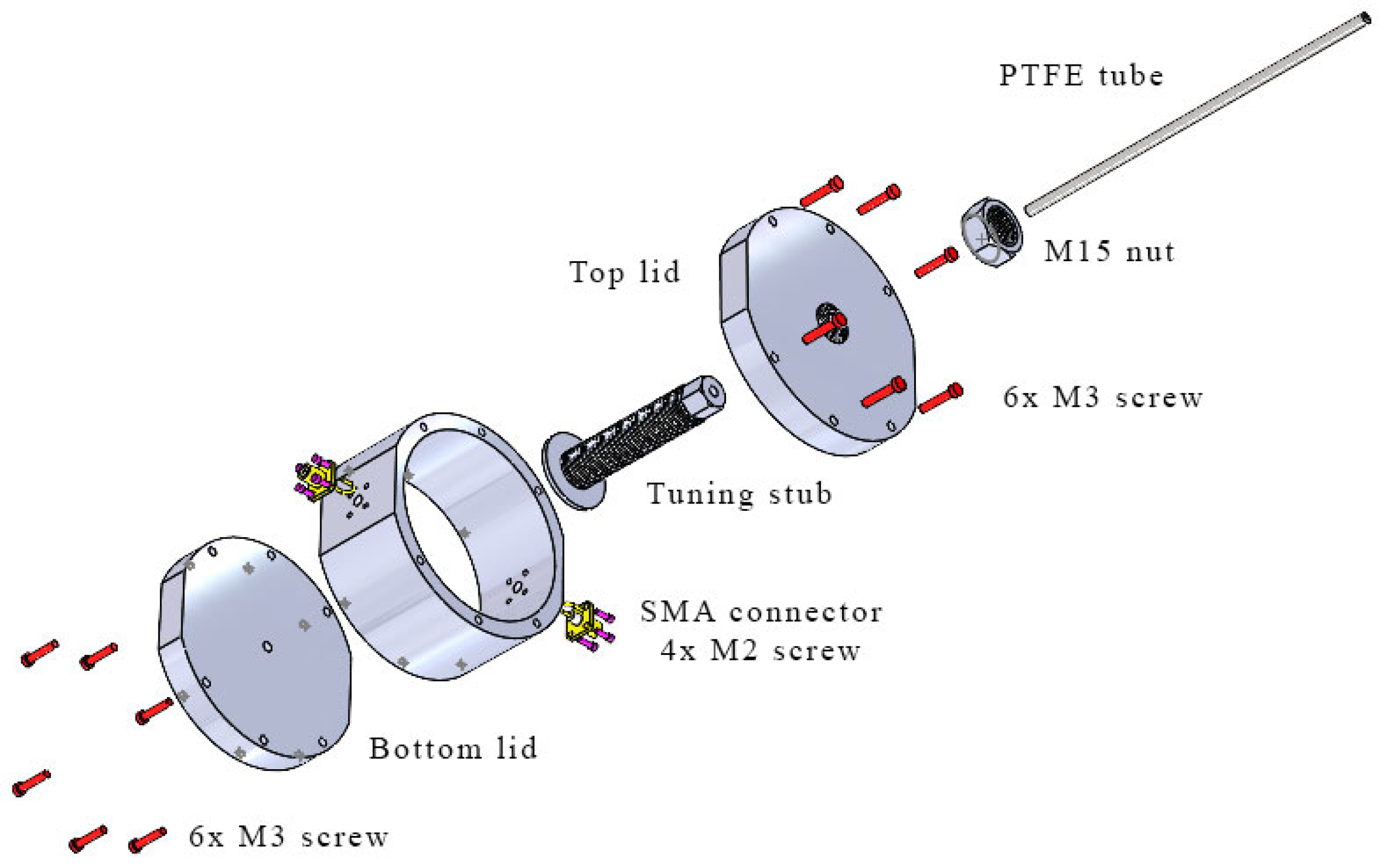
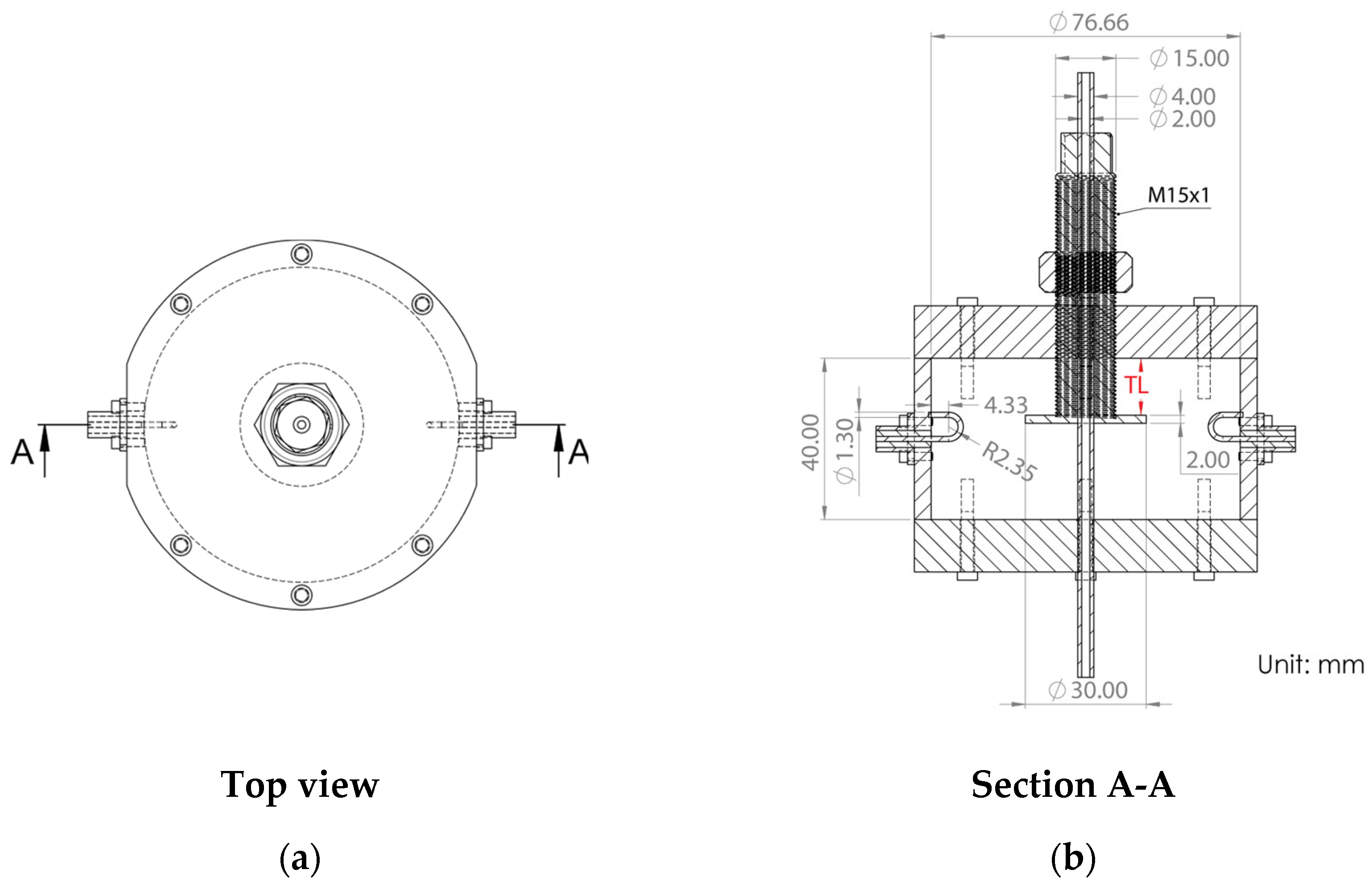
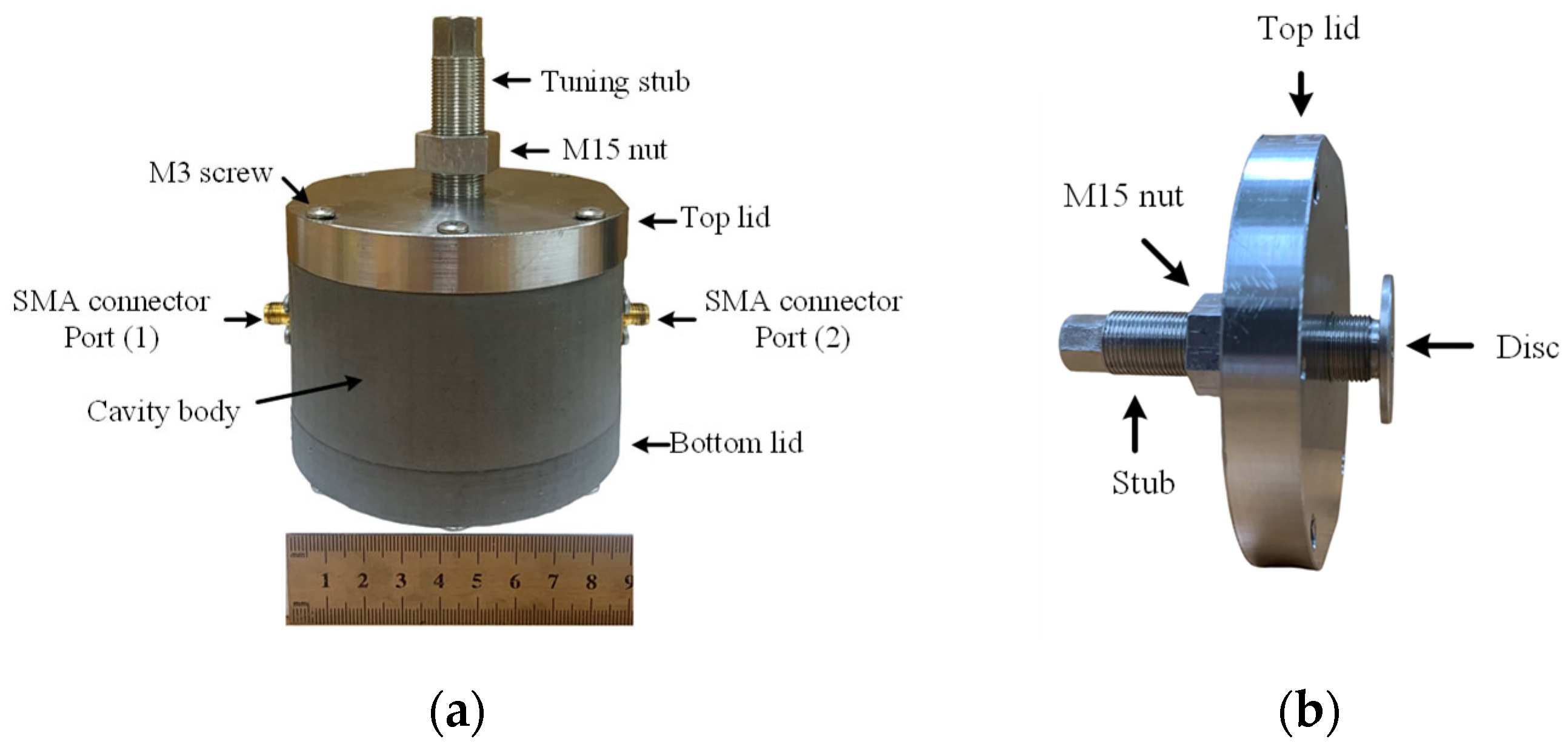


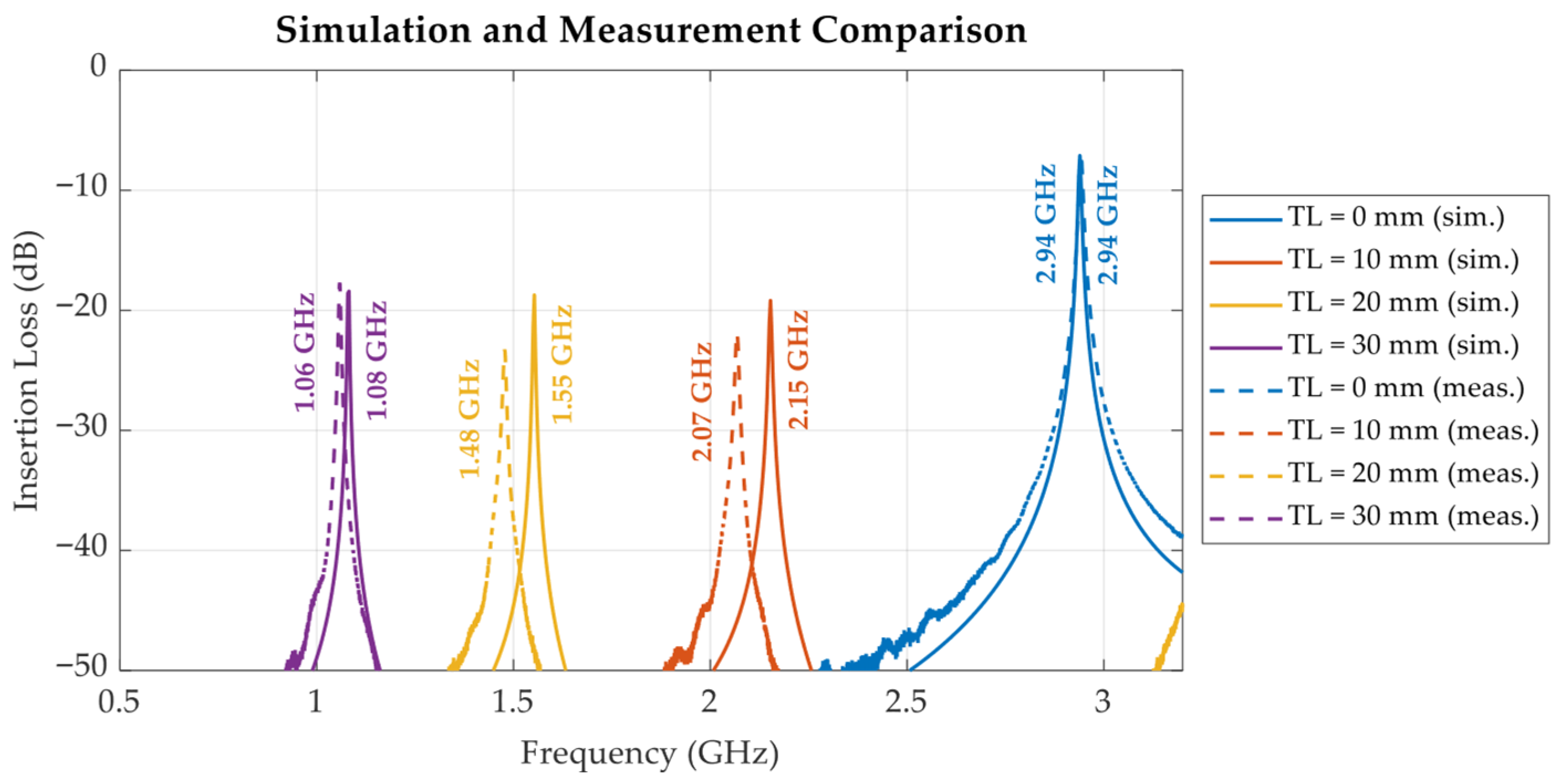
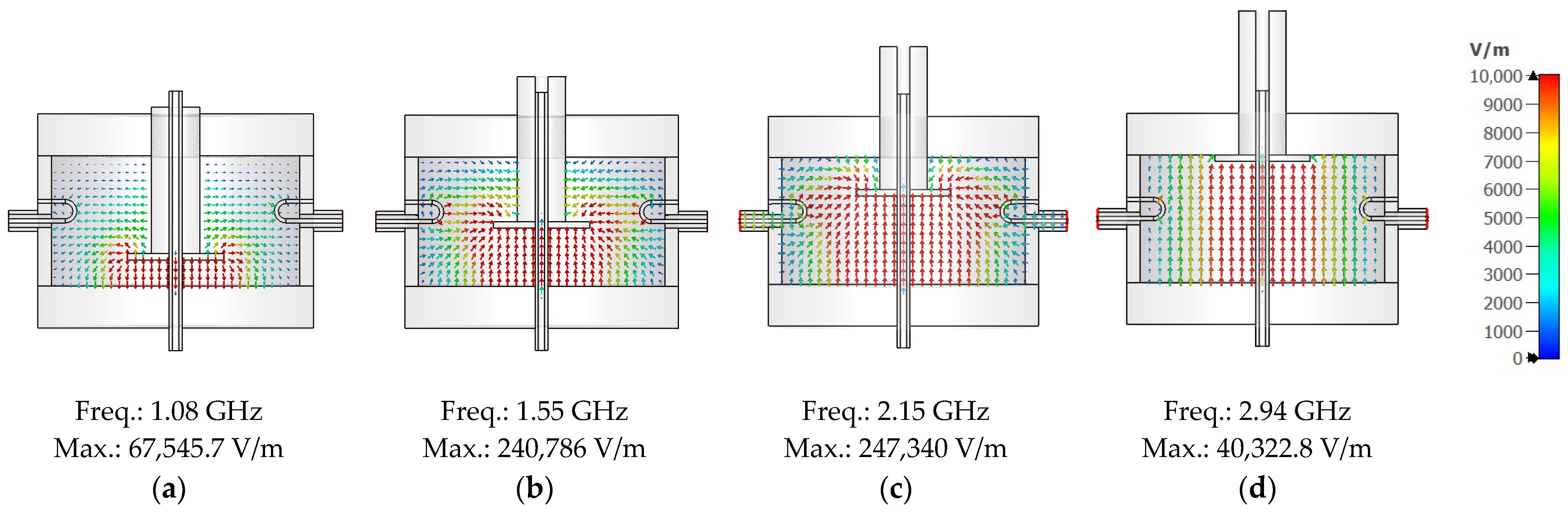
| Tuning Length | Freq. (Sim) | Q-Factor (Sim.) | Freq. (Meas.) | Q-Factor (Meas.) |
|---|---|---|---|---|
| 0 mm | 2.94 GHz | 489.83 | 2.94 GHz | 284.20 |
| 10 mm | 2.15 GHz | 303.24 | 2.06 GHz | 218.81 |
| 20 mm | 1.55 GHz | 304.51 | 1.33 GHz | 172.81 |
| 30 mm | 1.08 GHz | 189.82 | 1.06 GHz | 180.93 |
| Resonant Frequency (GHz) | Ethanol Concentration (%) | Ethanol Concentration (%) Extracted from (6) | Absolute Error (% of Ethanol Concentration) |
|---|---|---|---|
| 0.9606 | 0 | 3.37 | 3.37 |
| 0.9618 | 10 | 8.96 | 1.04 |
| 0.9639 | 20 | 18.38 | 1.62 |
| 0.9663 | 30 | 28.60 | 1.40 |
| 0.9688 | 40 | 38.62 | 1.38 |
| 0.9718 | 50 | 49.80 | 0.20 |
| 0.9752 | 60 | 61.37 | 1.37 |
| 0.9783 | 70 | 70.89 | 0.89 |
| 0.9821 | 80 | 81.22 | 1.22 |
| 0.9856 | 90 | 89.44 | 0.56 |
| 0.9908 | 100 | 99.34 | 0.66 |
| Resonant Frequency (GHz) | Ethanol Concentration (%) | Ethanol Concentration (%) Extracted from (7) | Absolute Error (% of Ethanol Concentration) |
|---|---|---|---|
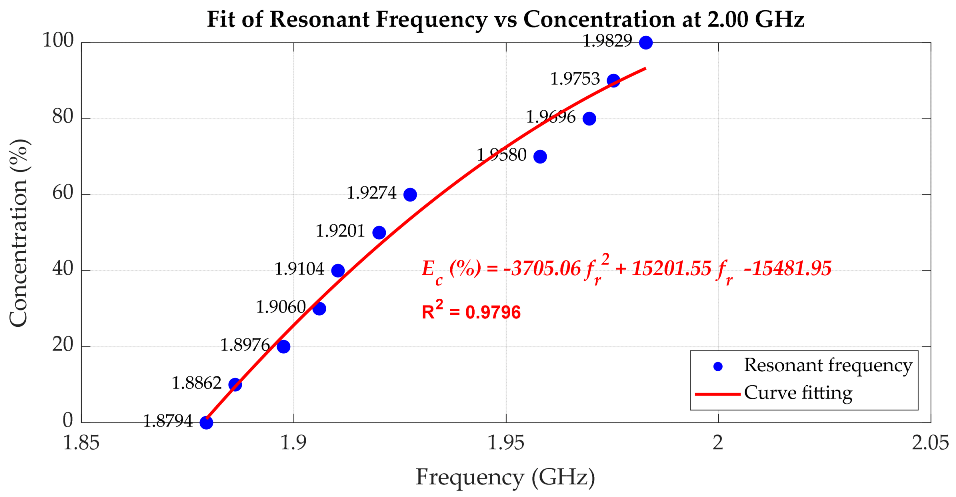
| 1.8794 | 0 | 1.04 | 1.04 |
| 1.8862 | 10 | 9.53 | 0.47 |
| 1.8976 | 20 | 23.01 | 3.01 |
| 1.9060 | 30 | 32.33 | 2.33 |
| 1.9104 | 40 | 37.00 | 3.00 |
| 1.9201 | 50 | 46.79 | 3.21 |
| 1.9274 | 60 | 53.70 | 6.30 |
| 1.9580 | 70 | 78.36 | 8.36 |
| 1.9696 | 80 | 85.89 | 5.89 |
| 1.9753 | 90 | 89.23 | 0.77 |
| 1.9829 | 100 | 93.31 | 6.69 |
| Resonant Frequency (GHz) | Ethanol Concentration (%) | Ethanol Concentration (%) Extracted from (8) | Absolute Error (% of Ethanol Concentration) |
|---|---|---|---|
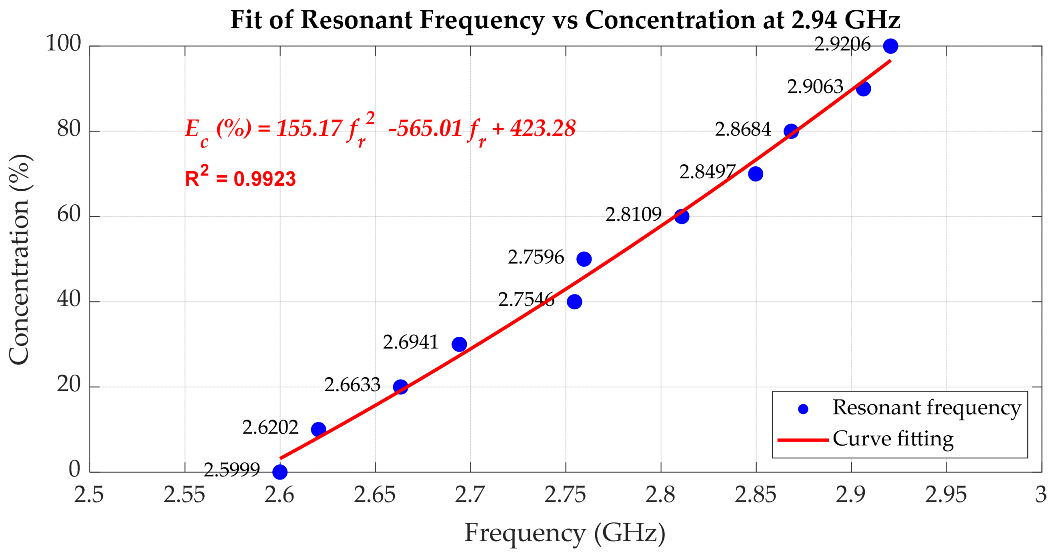
| 2.5999 | 0 | 3.18 | 3.18 |
| 2.6202 | 10 | 8.15 | 1.85 |
| 2.6633 | 20 | 19.14 | 0.86 |
| 2.6941 | 30 | 27.34 | 2.66 |
| 2.7546 | 40 | 44.31 | 4.31 |
| 2.7596 | 50 | 45.76 | 4.24 |
| 2.8109 | 60 | 61.12 | 1.12 |
| 2.8497 | 70 | 73.27 | 3.27 |
| 2.8684 | 80 | 79.30 | 0.70 |
| 2.9063 | 90 | 91.85 | 1.85 |
| 2.9206 | 100 | 96.70 | 3.30 |
| Resonant Frequency (GHz) | Dielectric Constant from Performance Probe | Dielectric Constant Extracted from (9) | Absolute Error Between Performance Probe and from (9) |
|---|---|---|---|
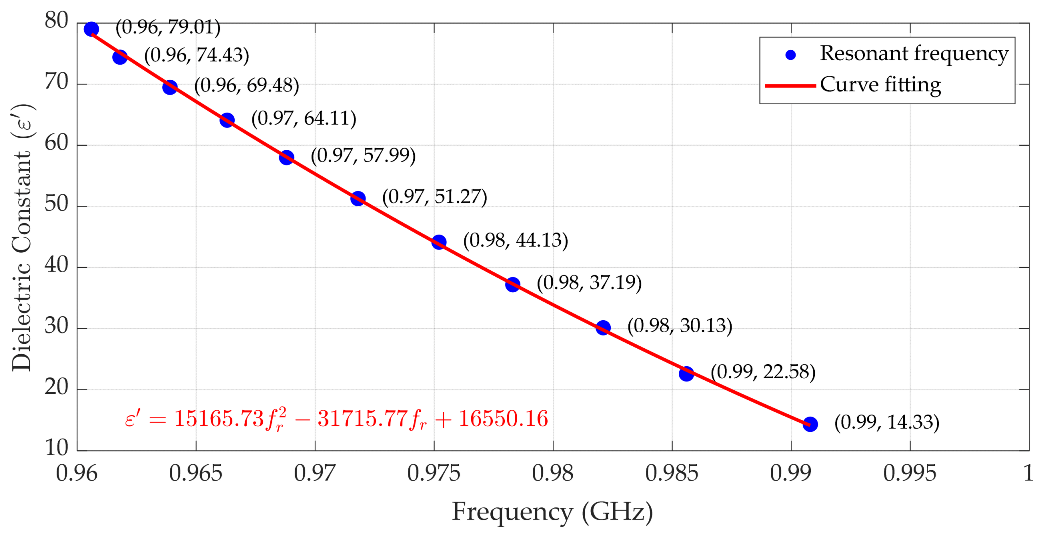
| 0.9606 | 79.01 | 78.20 | 0.81 |
| 0.9618 | 74.43 | 75.13 | 0.71 |
| 0.9639 | 69.48 | 69.86 | 0.37 |
| 0.9663 | 64.11 | 63.99 | 0.11 |
| 0.9688 | 57.99 | 58.07 | 0.08 |
| 0.9718 | 51.27 | 51.22 | 0.06 |
| 0.9752 | 44.13 | 43.78 | 0.35 |
| 0.9783 | 37.19 | 37.30 | 0.12 |
| 0.9821 | 30.13 | 29.76 | 0.37 |
| 0.9856 | 22.58 | 23.20 | 0.62 |
| 0.9606 | 14.33 | 14.14 | 0.19 |
| Ref. | Freq. (Air) (GHz) | Dimensions (mm) | Q-Factor (Air) | Q-Factor (Water) | Application |
|---|---|---|---|---|---|
| [13] | 1.991 | 15,890 | 430 | Liquid permittivity with perturbation theory | |
| [14] | 1.991 | 15,890 | 430 | Analytical validation of liquid permittivity | |
| [15] | 2.46 | 14,200 | - | Extraction of complex εusing multilayer field model | |
| [1] | 2.4917 | 2010.40 | 213.18 | Honey moisture analysis | |
| [18] | 0.997/2.289 (TM010, TM020) | 4198/5797 (TM010, TM020) | - | Wide-range loss tangent characterization with multi-hole cavity | |
| [16] | 3 | 445.58 | 23.912 | Detection of wear particle contaminants in oil | |
| [5] | 5.344 | 7517 | - | Detection of contaminants in lubricating oil | |
| [6] | 4.45 | - | 47 (Oil) | Measurement of water-in-oil concentration | |
| This work | 1.0–2.94 | 180–284 | 23–115 | Broadband dielectric characterization of liquids |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phakaew, T.; Oo, T.P.; Uzair, M.; Kowitwarangkul, P.; Chuchuay, P.; Yeetsorn, R.; Torrungrueng, D.; Chudpooti, N.; Chalermwisutkul, S. Additively Manufactured Mechanically Tunable Cavity Resonator for Broadband Characterization of Liquid Permittivity. Sensors 2025, 25, 7145. https://doi.org/10.3390/s25237145
Phakaew T, Oo TP, Uzair M, Kowitwarangkul P, Chuchuay P, Yeetsorn R, Torrungrueng D, Chudpooti N, Chalermwisutkul S. Additively Manufactured Mechanically Tunable Cavity Resonator for Broadband Characterization of Liquid Permittivity. Sensors. 2025; 25(23):7145. https://doi.org/10.3390/s25237145
Chicago/Turabian StylePhakaew, Thipamas, Thet Pai Oo, Muhammad Uzair, Pruet Kowitwarangkul, Piyapat Chuchuay, Rungsima Yeetsorn, Danai Torrungrueng, Nonchanutt Chudpooti, and Suramate Chalermwisutkul. 2025. "Additively Manufactured Mechanically Tunable Cavity Resonator for Broadband Characterization of Liquid Permittivity" Sensors 25, no. 23: 7145. https://doi.org/10.3390/s25237145
APA StylePhakaew, T., Oo, T. P., Uzair, M., Kowitwarangkul, P., Chuchuay, P., Yeetsorn, R., Torrungrueng, D., Chudpooti, N., & Chalermwisutkul, S. (2025). Additively Manufactured Mechanically Tunable Cavity Resonator for Broadband Characterization of Liquid Permittivity. Sensors, 25(23), 7145. https://doi.org/10.3390/s25237145








