Interpretable Ensemble Architectures with Theory-Informed Features for High-Fidelity Real-Time Congestion Forecasting on the Chalong Rat Expressway
Abstract
1. Introduction
- It proposes theory-guided feature engineering in which CTM, three-phase, and Helbing dynamics are combined with raw expressway data.
- It proposes the hybrid RF–XGBoost method with autoregressive embedding (“Hybrid-AR” and “Final Blend”), which outperforms the standard ML baselines.
- Robustness is tested with respect to peak/off-peak and congestion regimes, with statistical significance confirmed via bootstrap.
- Conformal prediction is applied for calibrated uncertainty intervals suitable for ITS deployment.
- It provides explainability using SHAP, and the results are consistent with traffic flow theory.
- It delivers a replicable end-to-end workflow from raw data preprocessing to real-time forecasting and visualization.
2. Related Work
2.1. Interpretable and Theory-Informed Models
2.2. Uncertainty-Aware Forecasting
2.3. Expressway and Bangkok Corridor Studies
2.4. Data Quality and ITS Reliability
3. Data and Methodology
3.1. Preprocessing and Time Alignment
3.2. Methodology Framework
3.3. Formalization of Predictive Modelling and Uncertainty Estimation
3.3.1. Temporal Backbone and Ensemble
3.3.2. Distributional Prediction and Calibrated Uncertainty
3.3.3. Statistical Significance, Interpretability, and Drift Diagnosis
3.4. Model Training, Validation, and Performance Evaluation
4. Results
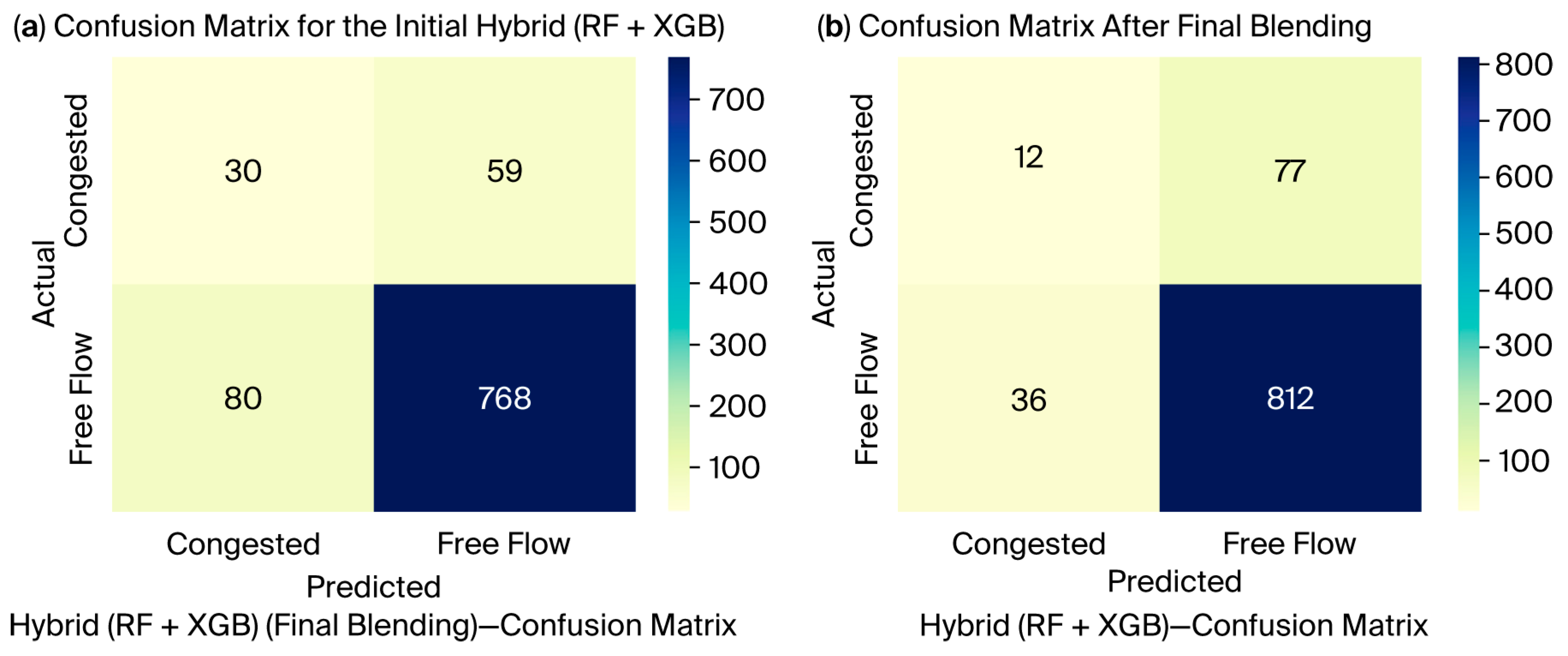
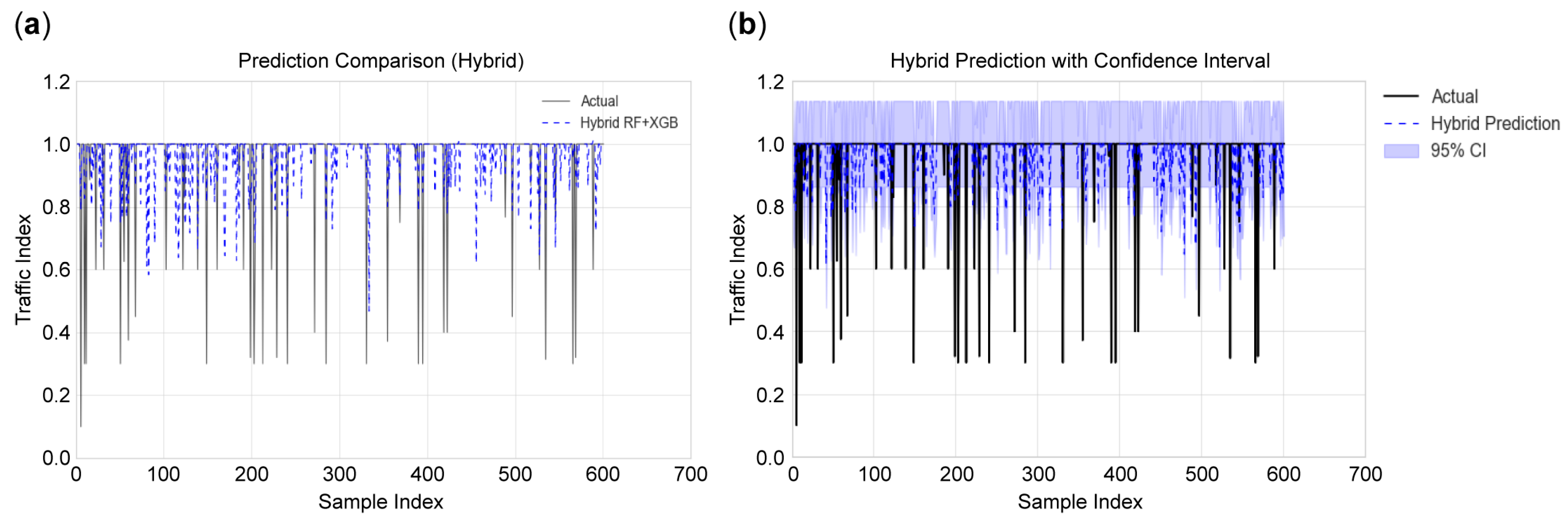
4.1. Overall Performance and Classification
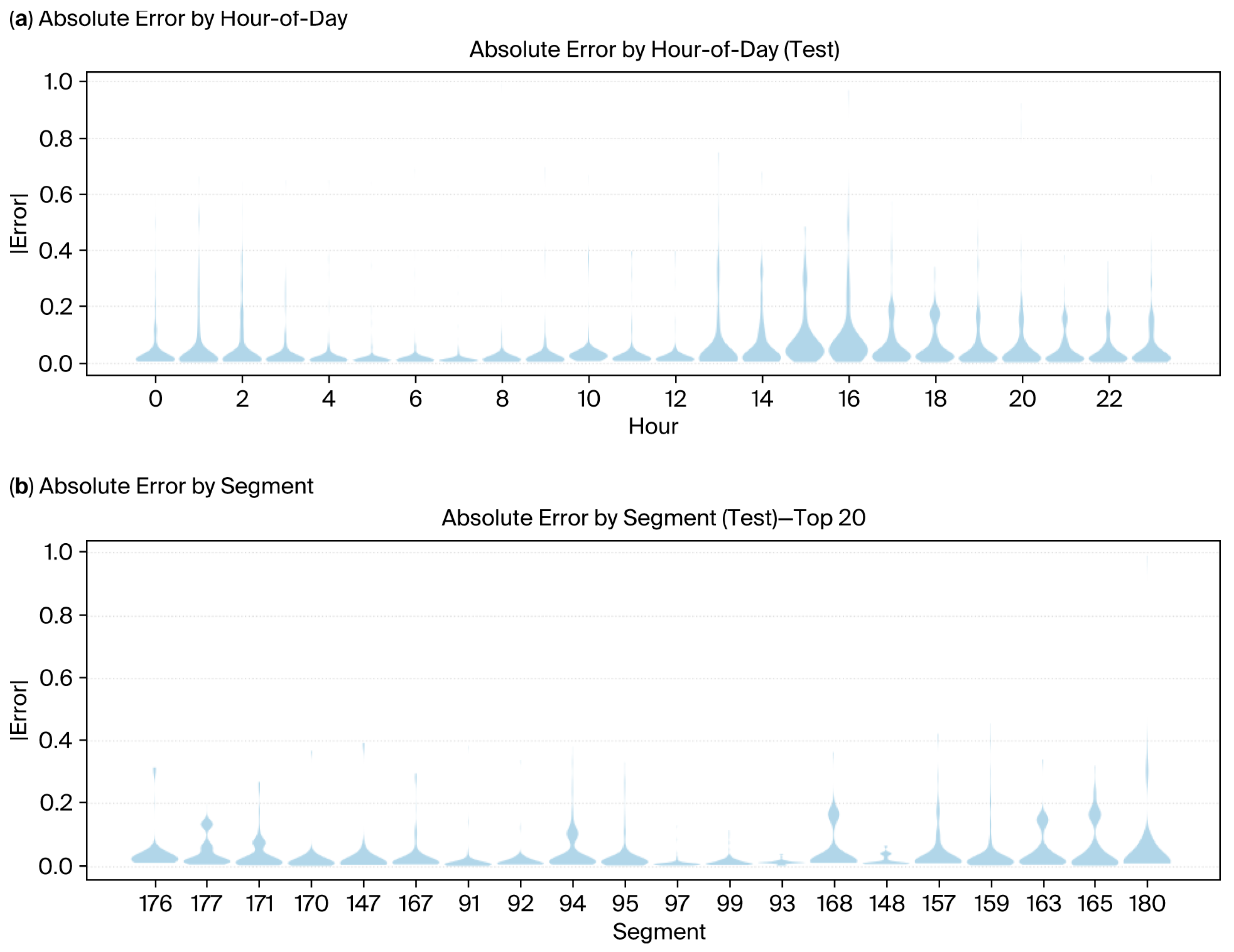
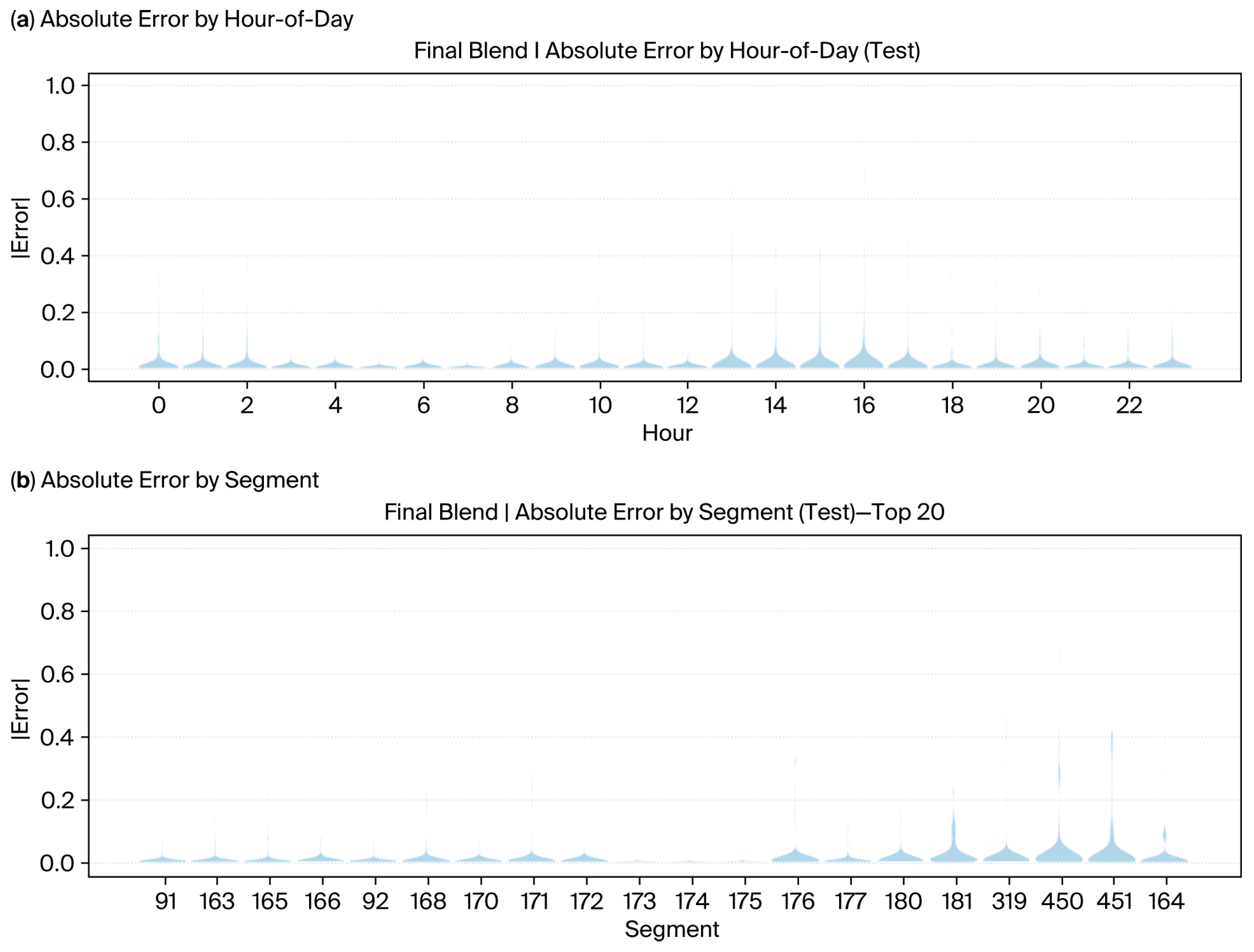
4.2. Robustness and Error Analysis
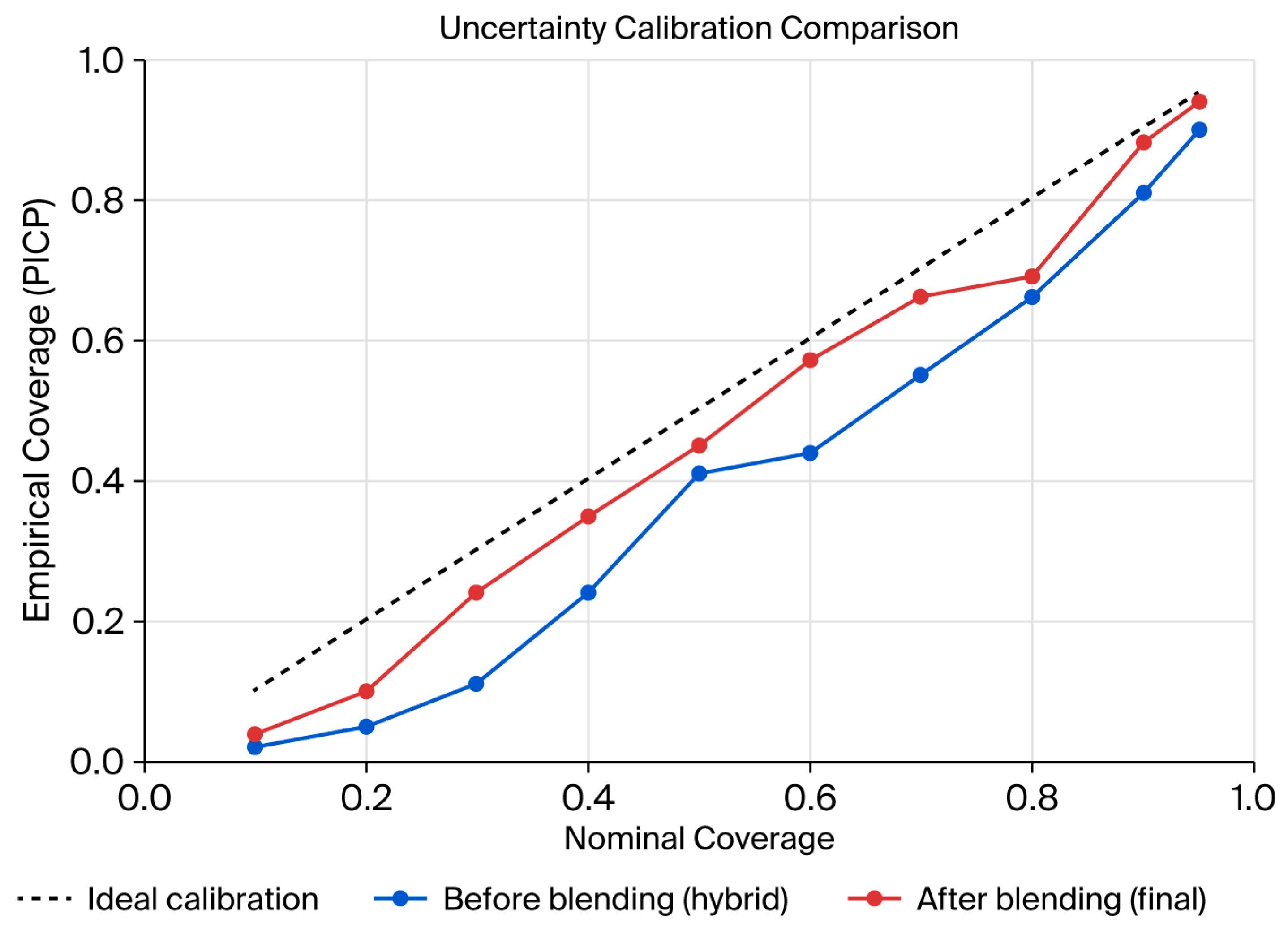
4.3. Uncertainty Quantification and Calibration
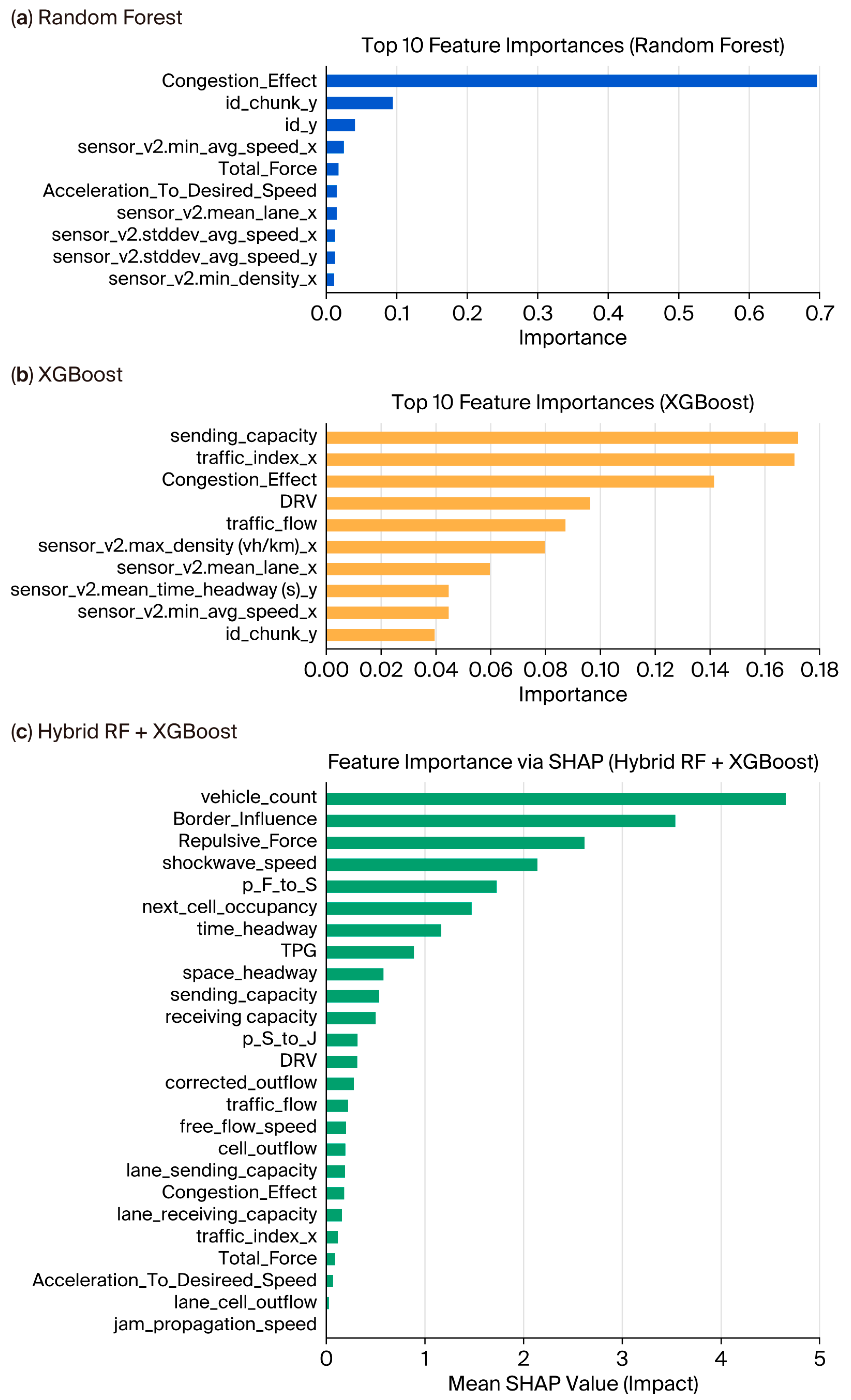
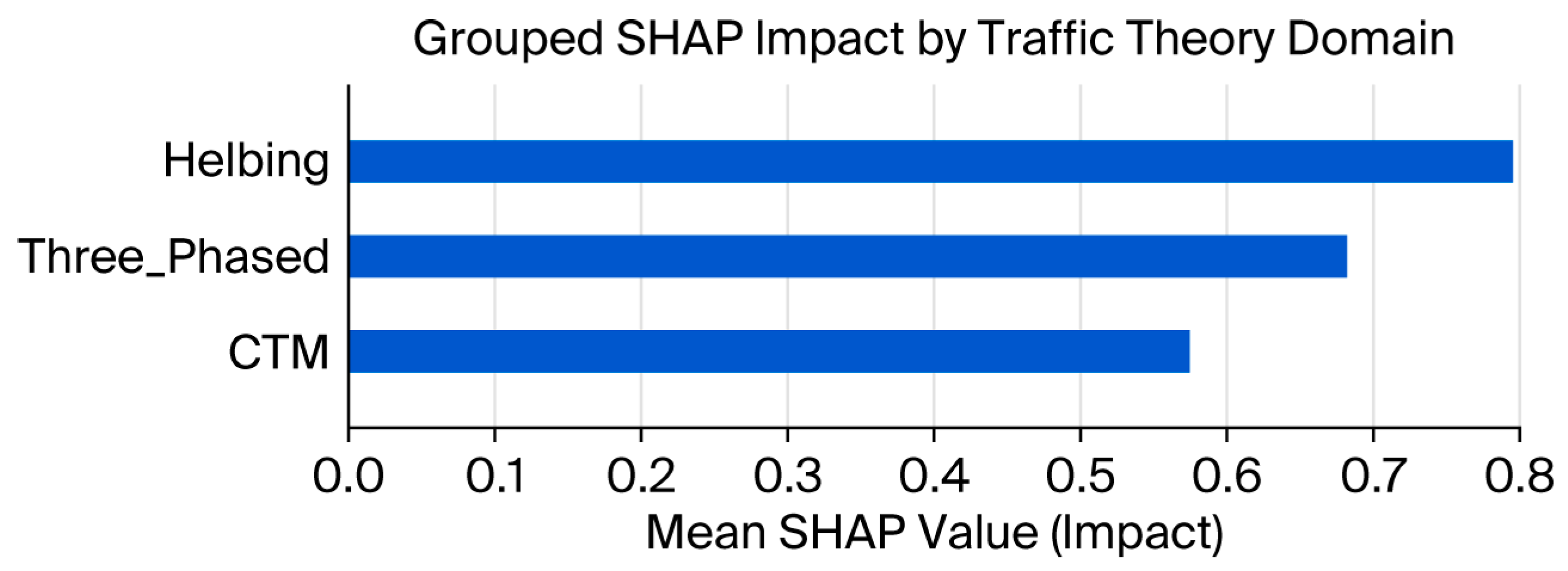
4.4. Interpretability and Feature Contributions
5. Discussion
5.1. Interpretation of Findings
5.2. Implications and Future Works
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ARX | AutoRegressive with eXogenous input |
| CQR | Conformalized quantile regression |
| IDM | Intelligent driver model |
| LWR | Lighthill–Whitham–Richards |
| TFD | Triangular fundamental diagram |
| EXAT | Expressway Authority of Thailand |
| ITS | Intelligent transportation system |
| CTM | Cell transmission model |
| SHAP | SHapley Additive exPlanations |
| RF | Random forest |
| XGB/XGBoost | Extreme gradient boosting |
| RMSE | Root mean square error |
| MAE | Mean absolute error |
| R2 | Coefficient of determination |
| PICP | Prediction interval coverage probability |
| MPIW | Mean prediction interval width |
Appendix A. Engineering Feature Models and Ensemble Formulas
Appendix A.1. Macroscopic Features and Short Derivation
Appendix A.2. Shockwave Speed and Three-Phase Kernel Surrogates
Appendix A.3. Microscopic Behavioural Features (Helbing)
Appendix B. Supplementary Statistical Analyses and Diagnostics
| Comparison | RMSE (Test) | 95% CI | p-Value | Block Length | w_xgb | α |
|---|---|---|---|---|---|---|
| Final Blend vs. persistence | 0.099 | [0.075, 0.125] | <0.001 | 2000 | 0.388 | 0.112 |
| Final Blend vs. hybrid (constrained) | 0.001 | [−0.001, 0.003] | 0.269 | 2000 | 0.388 | 0.112 |
| N | Mean Error | Std Error | MAE | RMSE | Durbin–Watson | Skewness | Kurtosis Excess |
|---|---|---|---|---|---|---|---|
| 2490 | 0.0020 | 0.1194 | 0.0671 | 0.1195 | 2.087 | −1.167 | 8.294 |
References
- Expressway Authority of Thailand (EXAT), Chalong Rat Expressway. Available online: https://www.exat.co.th/project/ทางพิเศษฉลองรัช/ (accessed on 24 September 2025).
- Lueanpech, P.; Kornkrai, T.; Panyachaiwatthanakool, S.; Ruttanapunyagorn, T. Evaluating the Impact of Proposed Speed Limit Policy on Urban Expressway. Appl. Sci. 2021, 11, 7420. [Google Scholar]
- Kongkhaensarn, T. Detecting Traffic Incident on Chalong Rat Expressway by Using Artificial Neural Network Based on Simulation Data. Master’s Thesis, Sirindhorn International Institute of Technology, Thammasat University, Pathum Thani, Thailand, 2021; pp. 30–38. [Google Scholar]
- Ou, J.; Li, J.; Wang, C.; Wang, Y.; Nie, Q. Building Trust for Traffic Flow Forecasting Components in ITS: An Interpretable Tree-Ensemble Approach. Digit. Transp. Syst. 2024, 2, 130–138. [Google Scholar]
- Chen, C.; Liu, J.; Li, Y.; Zhang, Y. Explainable Stacking-Based Learning Model for Traffic Forecasting. J. Transp. Eng. Part A Syst. 2024, 150, 04024057. [Google Scholar] [CrossRef]
- Cini, N.; Aydin, Z. A Deep Ensemble Approach for Long-Term Traffic Flow Prediction. Arab. J. Sci. Eng. 2024, 49, 12379–12385. [Google Scholar] [CrossRef]
- Wang, Z.; Chu, R.; Zhang, M.; Wang, X.; Luan, S. An Improved Hybrid Highway Traffic Flow Prediction Model Based on Random Forest and ARIMA. Sustainability 2020, 12, 8298. [Google Scholar] [CrossRef]
- Usama, M.; Hassanzadeh, H.R.; Dhillon, H.N. Uncertainty-Aware Traffic Prediction with Spatio-Temporal Graph Diffusion. IEEE Trans. Intell. Transp. Syst. 2024, 25, 1245–1249. [Google Scholar]
- Aimsun. Bangkok’s First Real-Time Traffic Simulation and Prediction System for EXAT. Available online: https://www.aimsun.com/latest/bangkoks-first-real-time-traffic-simulation-and-prediction-system/ (accessed on 25 September 2025).
- Lu, Z.; Xia, J.; Wang, M.; Nie, Q.; Ou, J. A Hybrid Short-Term Traffic Flow Forecasting Method Based on Temporal-Spatial Feature Extraction and Long Short-Term Memory Networks. Appl. Sci. 2020, 10, 356. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, Q.; Jiang, J.; Peng, M.; Zhu, M.; Yang, H.F. Short-Term Traffic Prediction Method Based on Advanced Graph Convolutional Network. Digit. Transp. 2024, 1, 100033. [Google Scholar]
- Qin, Y.; Wu, C.; Hu, Y. Traffic Flow Prediction by an Ensemble Framework with Data Denoising and Functional Principal Components Analysis. Transp. Res. Rec. 2024, 2678, 929–947. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, H.; Li, Z.; Bu, X.; Chen, Y.; Zhang, X.; Lv, Y.; Wang, F.-Y. STGSA: A Novel Spatial-Temporal Graph Synchronous Aggregation Model for Traffic Prediction. IEEE/CAA J. Autom. Sin. 2023, 10, 226–238. [Google Scholar] [CrossRef]
- Qian, Y.; Zhang, J.; Feng, Z.; Li, X.; Liu, Z.; Wang, H. Multi-task iTransformer: A Saturation-based Model for Short-term Highway Traffic Congestion Prediction Considering Event-induced Capacity Variability. IEEE Trans. Veh. Technol. 2025; early access. [Google Scholar] [CrossRef]
- Liu, X.; Qin, X.; Zhou, M.; Sun, H.; Han, S. Community-Based Dandelion Algorithm-Enabled Feature Selection and Broad Learning System for Traffic Flow Prediction. IEEE Trans. Intell. Transp. Syst. 2024, 25, 2508–2519. [Google Scholar] [CrossRef]
- Li, G.; Knoop, V.L.; van Lint, H. How Predictable Are Macroscopic Traffic States? A Perspective of Uncertainty Quantification. Transp. B Transp. Dyn. 2024, 12, 2314766. [Google Scholar] [CrossRef]
- Mallick, T.; Macfarlane, J.; Balaprakash, P. Uncertainty Quantification for Traffic Forecasting Using Deep-Ensemble-Based Spatiotemporal Graph Neural Networks. IEEE Trans. Intell. Transp. Syst. 2023, 24, 9143–9147. [Google Scholar] [CrossRef]
- Wu, Y.; Ye, Y.; Zeb, A.; Yu, J.J.; Wang, Z. Adaptive Modeling of Uncertainties for Traffic Forecasting. IEEE Trans. Intell. Transp. Syst. 2023, 24, 4430–4433. [Google Scholar] [CrossRef]
- Patil, M.; Ahmed, Q.; Midlam-Mohler, S. Benchmarking Uncertainty Quantification in Traffic Forecasting Models. arXiv 2024, arXiv:2509.12043. [Google Scholar]
- Cini, A.; Jenkins, A.; Mandic, D.; Alippi, C.; Bianchi, F.M. Benchmarking Uncertainty Quantification for Traffic Forecasting. arXiv 2024, arXiv:2502.09443. [Google Scholar]
- Klakhaeng, N.; Yaothanee, J.; Sinthupinyo, S.; Pattara-Atikom, W. Traffic Prediction Models for Bangkok Traffic Data. In Proceedings of the 8th ECTI Conference on Electrical Engineering/Electronics, Computer, Telecommunications, and Information Technology (ECTI-CON), Khon Kaen, Thailand, 17–19 May 2011; pp. 484–486. [Google Scholar]
- Ninsawat, K. Road Traffic Congestion Estimation System Using Fuzzy Logic Based on Data from Social Media and Floating Cars. Master’s Thesis, Sirindhorn International Institute of Technology, Thammasat University, Pathum Thani, Thailand, 2015; pp. 18–28. [Google Scholar]
- Panichpapiboon, S. Time-Headway Distributions on an Expressway in Bangkok, Thailand. J. Transp. Eng. 2014, 141, 04014086. [Google Scholar]
- Mon, E.E.; Ochiai, H.; Komolkiti, P.; Aswakul, C. Real-World Sensor Dataset for City Inbound–Outbound Traffic Estimation and Short-Term Prediction. Sci. Data 2022, 9, 357. [Google Scholar] [CrossRef]
- Sor, C.; Piantanakulchai, M. Traffic Anomaly Detection on Chalerm Mahanakhon Expressway Using Web-Based Traffic State Data. Thammasat Int. J. Sci. Technol. 2016, 21, 84–87. [Google Scholar]
- Zefreh, M.M.; Torok, A. Single Loop Detector Data Validation and Imputation of Missing Data. Measurement 2018, 116, 195. [Google Scholar] [CrossRef]
- Sun, T.; Zhu, S.; Hao, R.; Sun, B.; Xie, J. Short-Term Traffic Flow Prediction Based on Spatial–Temporal Attention Mechanism with Multi-Source Data. Mathematics 2022, 10, 2544. [Google Scholar] [CrossRef]
- Ljung, L. System Identification: Theory for the User, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Clemen, R.T.; Winkler, R.L. The Combination of Forecasts. J. R. Stat. Soc. Ser. A 1983, 146, 150–157. [Google Scholar]
- Koenker, R.; Bassett, G. Regression Quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Romano, Y.; Patterson, E.; Candès, E.J. Conformalized Quantile Regression. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Künsch, H.R. The Jackknife and the Bootstrap for General Stationary Observations. Ann. Stat. 1993, 21, 121–145, 6–33. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st Conference on Neural Information Processing Systems (NeurIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Cerqueira, V.; Torgo, L.; Mozetič, I. Evaluating Time Series Forecasting Models: An Empirical Study on Performance Estimation Methods. arXiv 2019, arXiv:1905.11744. [Google Scholar] [CrossRef]
- Bergmeir, C.; Hyndman, R.J.; Koo, B. A Note on the Validity of Cross-Validation for Evaluating Autoregressive Time Series Prediction. Comput. Stat. Data Anal. 2018, 120, 70–83. [Google Scholar] [CrossRef]
- Songkran 2023 Wraps up with Fierce Splashing in Khao San, Silom. The Nation. 16 April 2023. Available online: https://www.nationthailand.com/thailand/general/40026686 (accessed on 27 September 2025).
- Elliott, G. Averaging and the Optimal Combination of Forecasts; Working Paper; University of California: San Diego, CA, USA, 2011. [Google Scholar]
- Wang, Y.; Politis, D.N. Model-Free Bootstrap and Conformal Prediction in Regression: Conditionality, Conjecture Testing, and Pertinent Prediction Intervals. arXiv 2025, arXiv:2109.12156v3. [Google Scholar]
- Tamuly, P.; Nava, V. Machine Learning Based Conformal Predictors for Uncertainty-Aware Compressive Strength Estimation of Concrete. Constr. Build. Mater. 2025, 487, 141844. [Google Scholar] [CrossRef]
- Cheruiyot, E.K. A Model for Predicting Traffic Congestion Using Deep Learning Algorithm: Case of Nairobi Metropolitan. Master’s Thesis, KCA University, Nairobi, Kenya, 2023. [Google Scholar]
- Asad, M.; Yasir, R.M.; Nower, N.; Shoyaib, M. Traffic Congestion Prediction Using Machine Learning Techniques. arXiv 2022, arXiv:2206.10983. [Google Scholar] [CrossRef]
- Cervero, R.; Kockelman, K. Travel demand and the 3Ds: Density, diversity, and design. Transp. Res. Part D Transp. Environ. 1997, 2, 199–219. [Google Scholar] [CrossRef]
- Ewing, R.; Cervero, R. Travel and the built environment: A meta-analysis. J. Am. Plan. Assoc. 2010, 76, 265–294. [Google Scholar] [CrossRef]
- Li, F.; Zhou, T. Effects of urban form on air quality in China: An analysis based on the spatial autoregressive model. Cities 2019, 89, 130–140. [Google Scholar] [CrossRef]
- Lighthill, M.J.; Whitham, G.B. On Kinematic Waves. II. A Theory of Traffic Flow on Long Crowded Roads. Proc. R. Soc. Lond. A Math. Phys. Sci. 1955, 229, 317–345. [Google Scholar]
- Richards, P.I. Shock Waves on the Highway. Oper. Res. 1956, 4, 42–51. [Google Scholar] [CrossRef]
- Daganzo, C.F. The Cell Transmission Model: A Dynamic Representation of Highway Traffic Consistent with the Hydrodynamic Theory. Transp. Res. Part B Methodol. 1994, 28, 269–287. [Google Scholar] [CrossRef]
- Daganzo, C.F. The Cell Transmission Model, Part II: Network Traffic. Transp. Res. Part B Methodol. 1995, 29, 81–91. [Google Scholar] [CrossRef]
- Kerner, B.S. Basis of Three-Phase Traffic Theory. In The Physics of Traffic; Springer: Berlin, Germany, 2004; pp. 87–103. [Google Scholar]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested Traffic States in Empirical Observations and Microscopic Simulations. Phys. Rev. E 2000, 62, 5–9. [Google Scholar] [CrossRef]
- Helbing, D.; Molnár, P. Social Force Model for Pedestrian Dynamics. Phys. Rev. E 1995, 51, 4–7. [Google Scholar] [CrossRef] [PubMed]
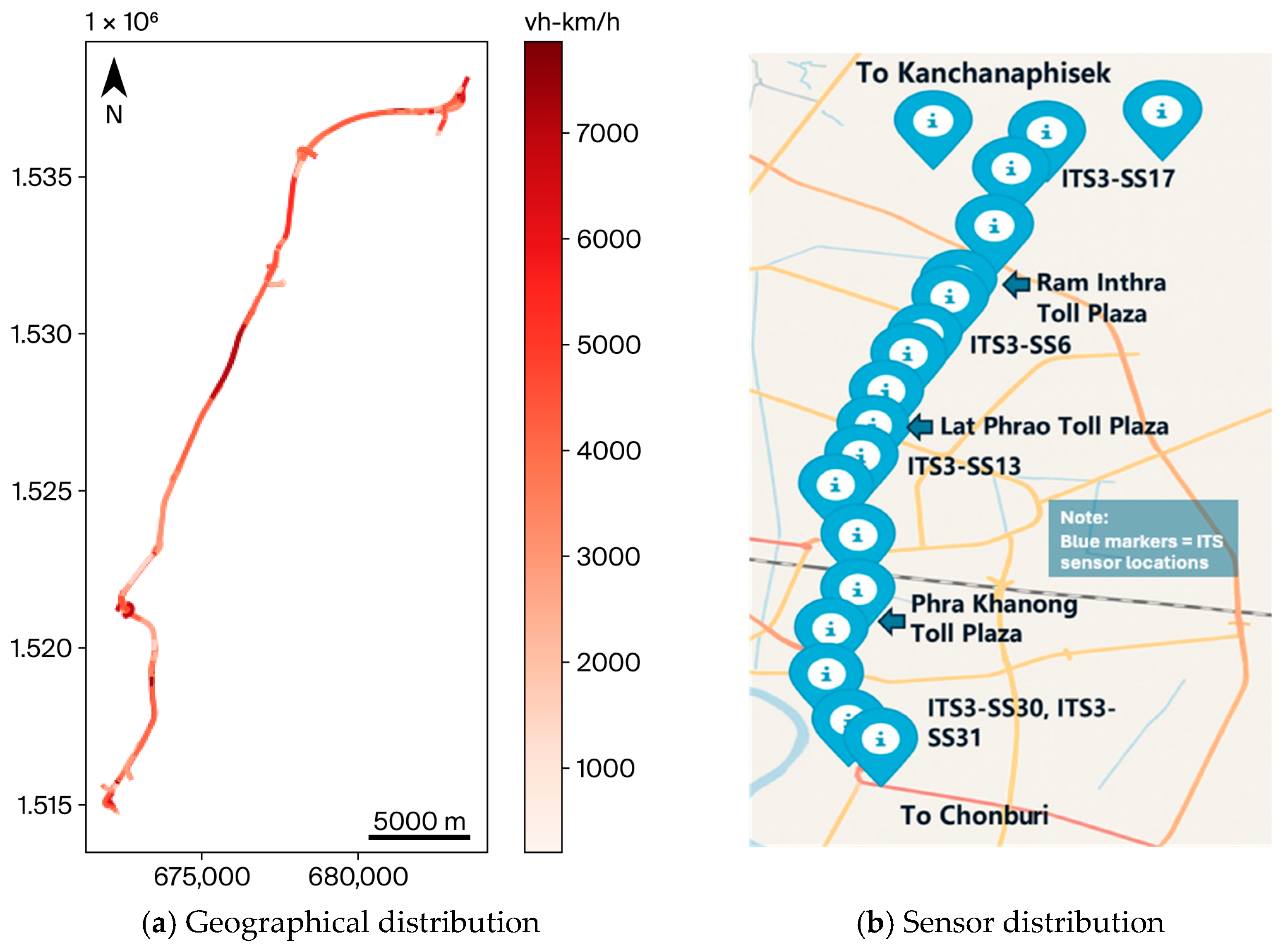
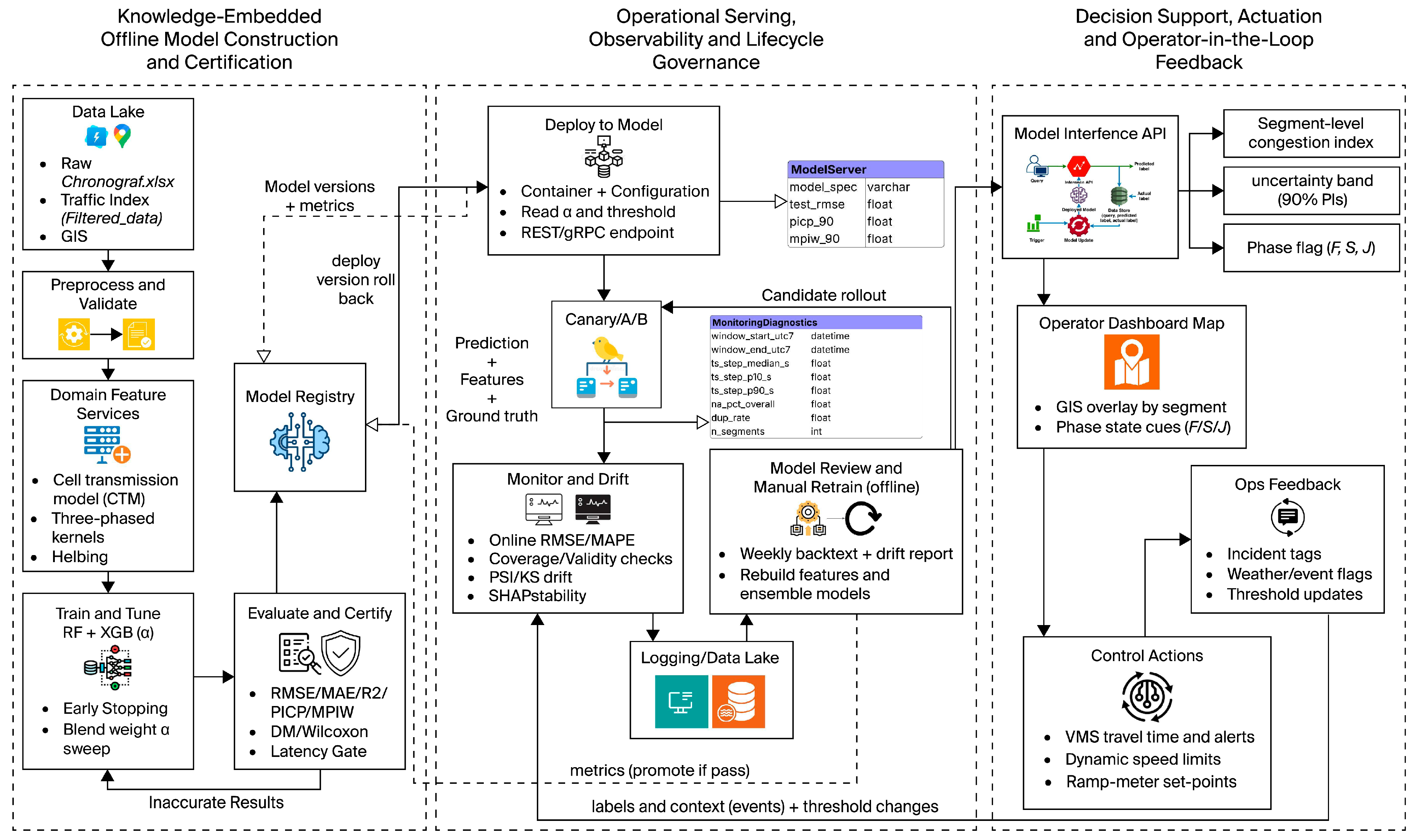
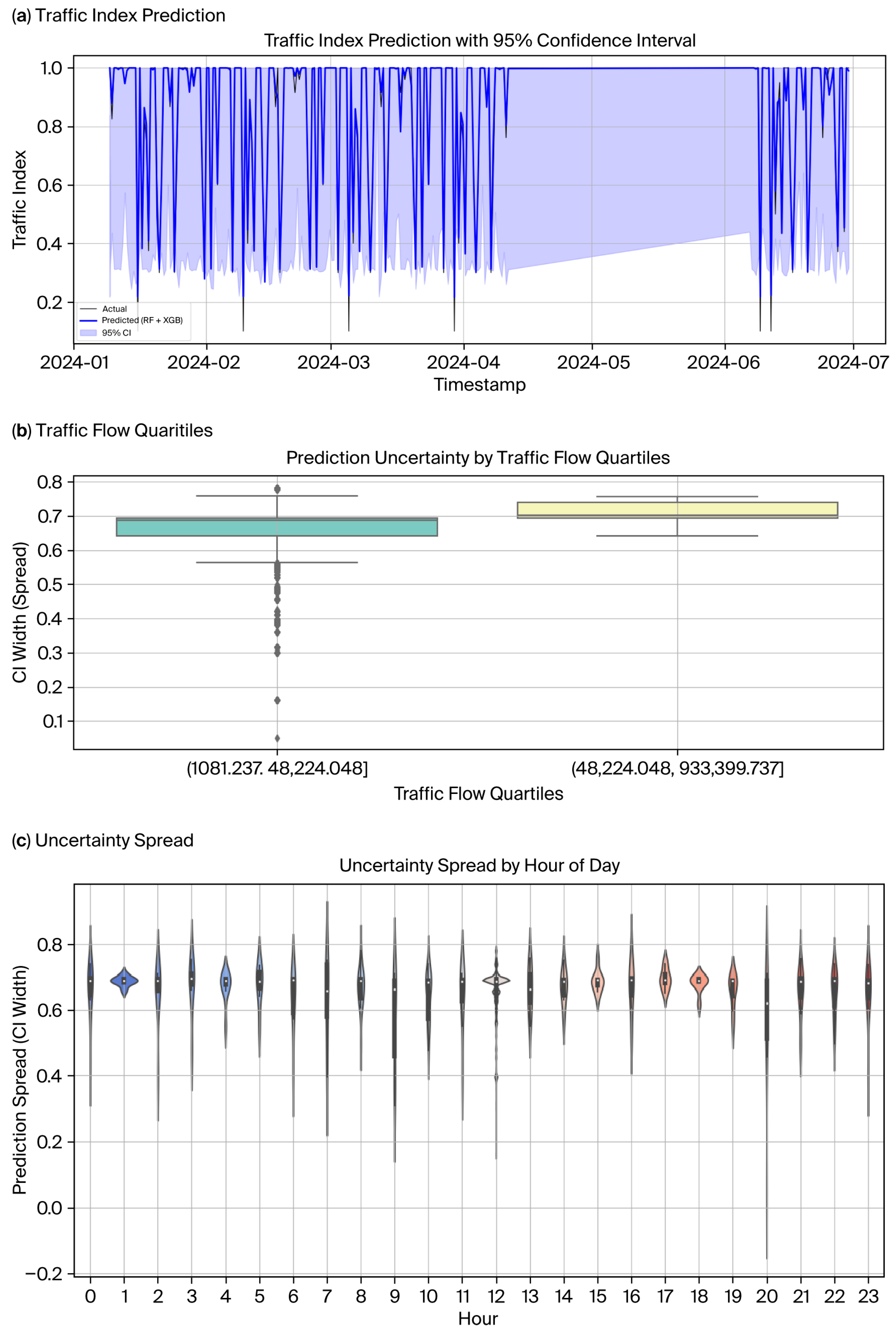
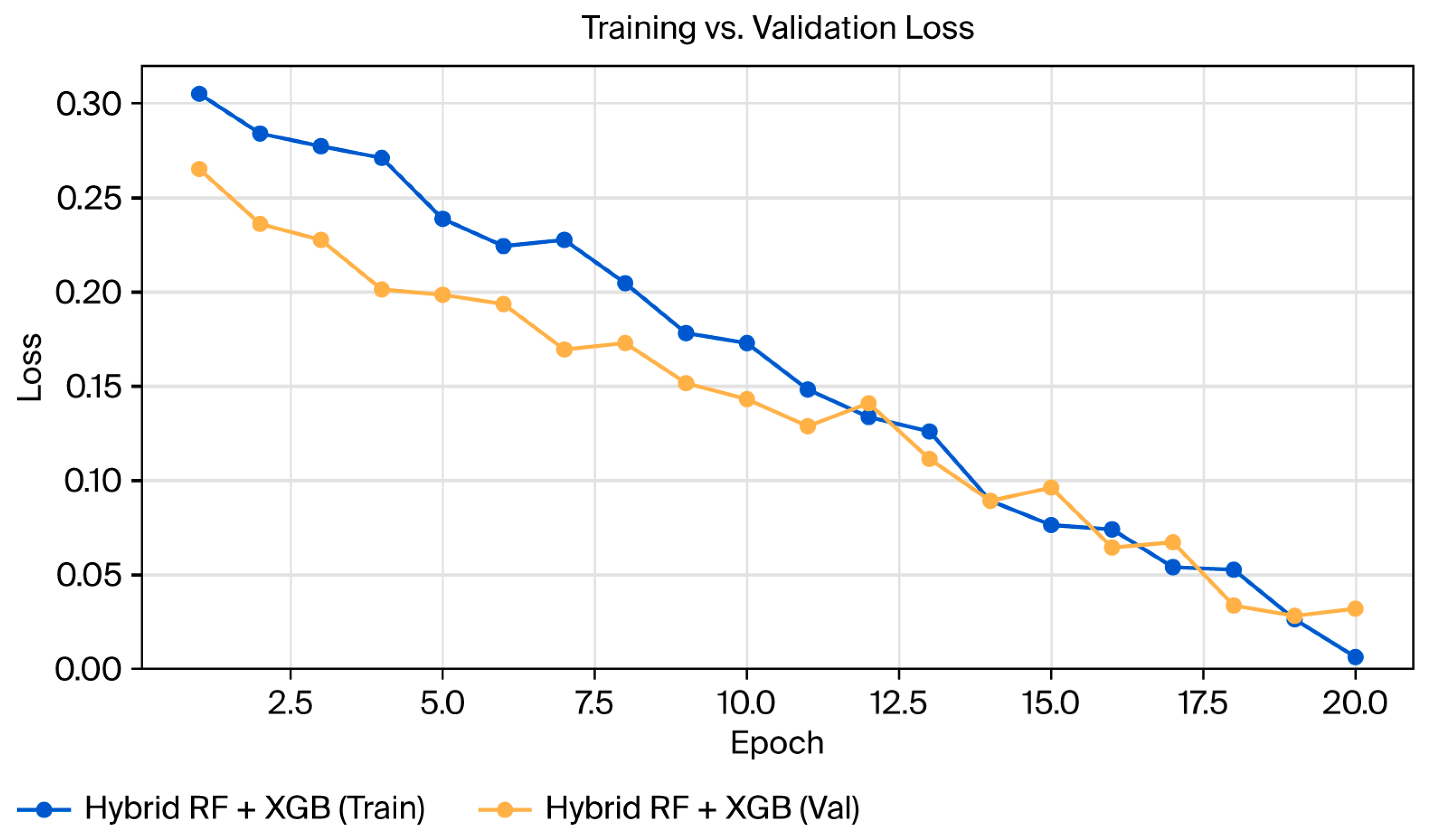
| Source | Variable | Unit | Description |
|---|---|---|---|
| Filtered_data | id | - | Unique ID for each data record |
| id_chunk | - | ID of road segment on the expressway | |
| traffic_index | - | Congestion level indicator | |
| Chronograf.xlsx | time (+7 UTC) | date time | Timestamp in Indochina time |
| sensor_v2.max_avg_speed | km/h | Maximum average vehicle speed | |
| sensor_v2.max_density | vh/km | Maximum vehicle density per lane | |
| sensor_v2.mean_avg_speed | km/h | Average vehicle speed | |
| sensor_v2.mean_density | vh/km | Average vehicle density per lane | |
| sensor_v2.mean_flow (vh/h) | vh/h | Vehicle flow per hour | |
| sensor_v2.mean_lane | - | Average lane index used | |
| sensor_v2.mean_occupancy | % | Average percentage of lane occupancy | |
| sensor_v2.mean_space_headway | Metre | Mean spacing between vehicles | |
| sensor_v2.mean_time_headway | Second | Mean time gap between vehicles | |
| sensor_v2.min_avg_speed | km/h | Minimum average speed | |
| sensor_v2.min_density | vh/km | Minimum vehicle density | |
| sensor_v2.stddev_avg_speed | km/h | Speed variability (standard deviation) | |
| sensor_v2.stddev_density | vh/km | Density variability (standard deviation) | |
| sensor_v2.sum_count_class1 | count | Count of motorbikes (2-wheel vehicles) | |
| sensor_v2.sum_count_class2 | count | Count of passenger cars | |
| sensor_v2.sum_count_class3 | count | Count of small trucks (e.g., 6 wheels) | |
| sensor_v2.sum_count_class4 | count | Count of large trucks (10 wheels and above) | |
| Derived (CTM) | vehicle_count | count | Total number of vehicles detected |
| sending_capacity | vh/h | Maximum vehicle outflow from a cell | |
| receiving_capacity | vh/h | Maximum vehicle inflow to a cell | |
| cell_outflow | vh/h | Actual vehicle outflow from a cell | |
| lane_sending_capacity | vh/h | Maximum outflow per lane | |
| lane_receiving_capacity | vh/h | Max inflow per lane | |
| lane_cell_outflow | vh/h | Vehicles leaving a specific cell lane segment | |
| free_flow_speed | km/h | Speed in ideal (uncongested) conditions | |
| corrected_outflow | vh/h | Adjusted outflow after capacity constraints | |
| Derived (Kernel) | shockwave_speed | km/h | Speed of traffic shockwave propagation |
| jam_propagation_speed | km/h | Speed of jam moving upstream | |
| p_F_to_S | Probability | Probability of free flow → synchronized transition | |
| p_S_to_J | Probability | Probability of synchronized flow → jam transition | |
| Derived (Helbing) | Acceleration_To_Desired_Speed | km/h | Driver’s acceleration toward desired speed |
| Repulsive_Force | N (Proxy) | Force maintaining safe distance from leading vehicle | |
| TPG | - | Traffic phase group indicator | |
| DRV | - | Driver behaviour variable used in modelling | |
| Border_Influence | - | Influence of road edges on vehicle movement | |
| Total_Force | N (Proxy) | Combined force from all dynamic effects | |
| Congestion_Effect | - | Impact of traffic congestion on driver dynamics |
| Dataset | Period Covered | Median (s) | Train | Validation | Test | Sampling Frequency (Hz) |
|---|---|---|---|---|---|---|
| Filtered_data.xlsx | February 2023–April 2024 | 300.0 | 113,876 | 24,353 | 24,393 | 0.0033 |
| Chronograf.xlsx | January 2023–June 2024 | 65,400 | 505 | 108 | 108 | 0.000015 |
| Model | Key Parameters | Value |
|---|---|---|
| Random forest | n_estimators | 800 |
| max_depth | 16 | |
| Min_samples_leaf | 5 | |
| max_features | Sqrt | |
| bootstrap | True | |
| XG Boost | objective | reg:squarederror |
| tree_method | hist | |
| max_depth | 6 | |
| eta | 0.05 | |
| subsample | 0.85 | |
| colsample_bytree | 0.85 | |
| reg_alpha | 0.5 | |
| reg_lampda | 4.0 | |
| best_iteration | 156 | |
| early_stopping_rounds | 100 |
| Set | Model | MAE | RMSE | R2 |
|---|---|---|---|---|
| Validation | Final Blend (Pers + (1-) Hybrid-AR) | 0.007263 | 0.034152 | 0.910922 |
| Hybrid—AR (safe) | 0.007602 | 0.034188 | 0.910739 | |
| Persistence | 0.003873 | 0.037508 | 0.892557 | |
| Hybrid (exogenous-only) | 0.060445 | 0.156530 | 0.871206 | |
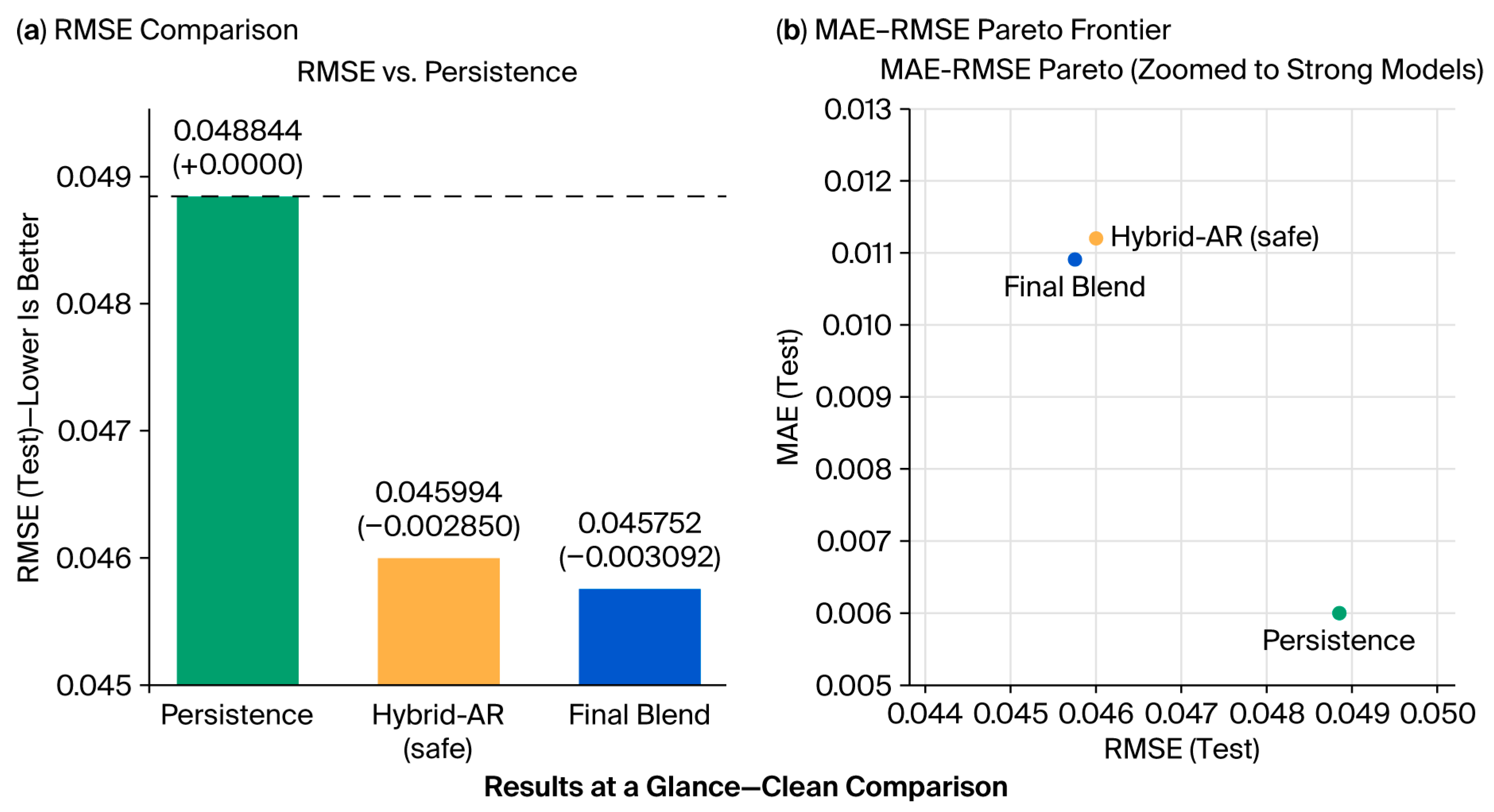
| Test | Final Blend (Pers + (1-) Hybrid-AR) | 0.010860 | 0.045752 | 0.889421 |
| Hybrid—AR (safe) | 0.011351 | 0.045994 | 0.888252 | |
| Persistence | 0.005969 | 0.048844 | 0.873973 | |
| Hybrid (exogenous-only) | 0.085516 | 0.184808 | 0.804216 |
| Model | Segment | n | MAE | RMSE | R2 | RMSE vs. Persistence |
|---|---|---|---|---|---|---|
| Final Blend | Peak | 660 | 0.059194 | 0.103935 | 0.879136 | 0.155673 |
| Final Blend | Off-peak | 1830 | 0.069895 | 0.124574 | 0.757467 | 0.077583 |
| Hybrid (constrained) | Peak | 660 | 0.054744 | 0.102139 | 0.884857 | 0.157469 |
| Hybrid (constrained) | Off-peak | 1830 | 0.069752 | 0.126372 | 0.757344 | 0.075785 |
| Segment | Model | n | MAE | RMSE | R2 | RMSE vs. Persistence |
|---|---|---|---|---|---|---|
| High | Final Blend | 1697 | 0.044695 | 0.084842 | 0.293755 | 0.050306 |
| High | Hybrid (constrained) | 1697 | 0.047384 | 0.092128 | 0.300862 | 0.043020 |
| Low | Final Blend | 793 | 0.114916 | 0.171463 | 0.750287 | 0.162178 |
| Low | Hybrid (constrained) | 793 | 0.105126 | 0.165449 | 0.756323 | 0.168191 |
| Alpha | Segment | N | PICP | MPIW |
|---|---|---|---|---|
| 0.05 | All | 24,393 | 0.926085 | 0.155303 |
| 0.05 | Peak | 6468 | 0.934601 | 0.155303 |
| 0.05 | Off-peak | 17,925 | 0.923013 | 0.155303 |
| 0.10 | All | 24,393 | 0.926085 | 0.155303 |
| 0.10 | Peak | 6468 | 0.934601 | 0.155303 |
| 0.10 | Off-peak | 17,925 | 0.923013 | 0.155303 |
| 0.20 | All | 24,393 | 0.926085 | 0.155303 |
| 0.20 | Peak | 6468 | 0.934601 | 0.155303 |
| 0.20 | Off-peak | 17,925 | 0.923013 | 0.155303 |
| Alpha | Nominal | Segment | n | PICP | MPIW |
|---|---|---|---|---|---|
| 0.05 | 0.95 | All | 2490 | 0.929719 | 0.435646 |
| 0.05 | 0.95 | Off-peak | 1830 | 0.920219 | 0.435646 |
| 0.05 | 0.95 | Peak | 660 | 0.956061 | 0.435646 |
| 0.10 | 0.90 | All | 2490 | 0.875904 | 0.276992 |
| 0.10 | 0.90 | Off-peak | 1830 | 0.857923 | 0.276992 |
| 0.10 | 0.90 | Peak | 660 | 0.925758 | 0.276992 |
| 0.20 | 0.80 | All | 2490 | 0.785141 | 0.165285 |
| 0.20 | 0.80 | Off-peak | 1830 | 0.781967 | 0.165285 |
| 0.20 | 0.80 | Peak | 660 | 0.793939 | 0.165285 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puttima, P.; Zhou, T.; Chen, Z. Interpretable Ensemble Architectures with Theory-Informed Features for High-Fidelity Real-Time Congestion Forecasting on the Chalong Rat Expressway. Sensors 2025, 25, 7090. https://doi.org/10.3390/s25227090
Puttima P, Zhou T, Chen Z. Interpretable Ensemble Architectures with Theory-Informed Features for High-Fidelity Real-Time Congestion Forecasting on the Chalong Rat Expressway. Sensors. 2025; 25(22):7090. https://doi.org/10.3390/s25227090
Chicago/Turabian StylePuttima, Pongphatana, Tongtong Zhou, and Zhihua Chen. 2025. "Interpretable Ensemble Architectures with Theory-Informed Features for High-Fidelity Real-Time Congestion Forecasting on the Chalong Rat Expressway" Sensors 25, no. 22: 7090. https://doi.org/10.3390/s25227090
APA StylePuttima, P., Zhou, T., & Chen, Z. (2025). Interpretable Ensemble Architectures with Theory-Informed Features for High-Fidelity Real-Time Congestion Forecasting on the Chalong Rat Expressway. Sensors, 25(22), 7090. https://doi.org/10.3390/s25227090






