OFDR Distributed Demodulation Optimization Algorithm Using Discrete-Time Analytic Signal Backscattered Rayleigh Spectrum
Abstract
1. Introduction
2. Principles and Methods
2.1. Principle of OFDR
2.2. Principle of Discrete-Time Analytic Signal
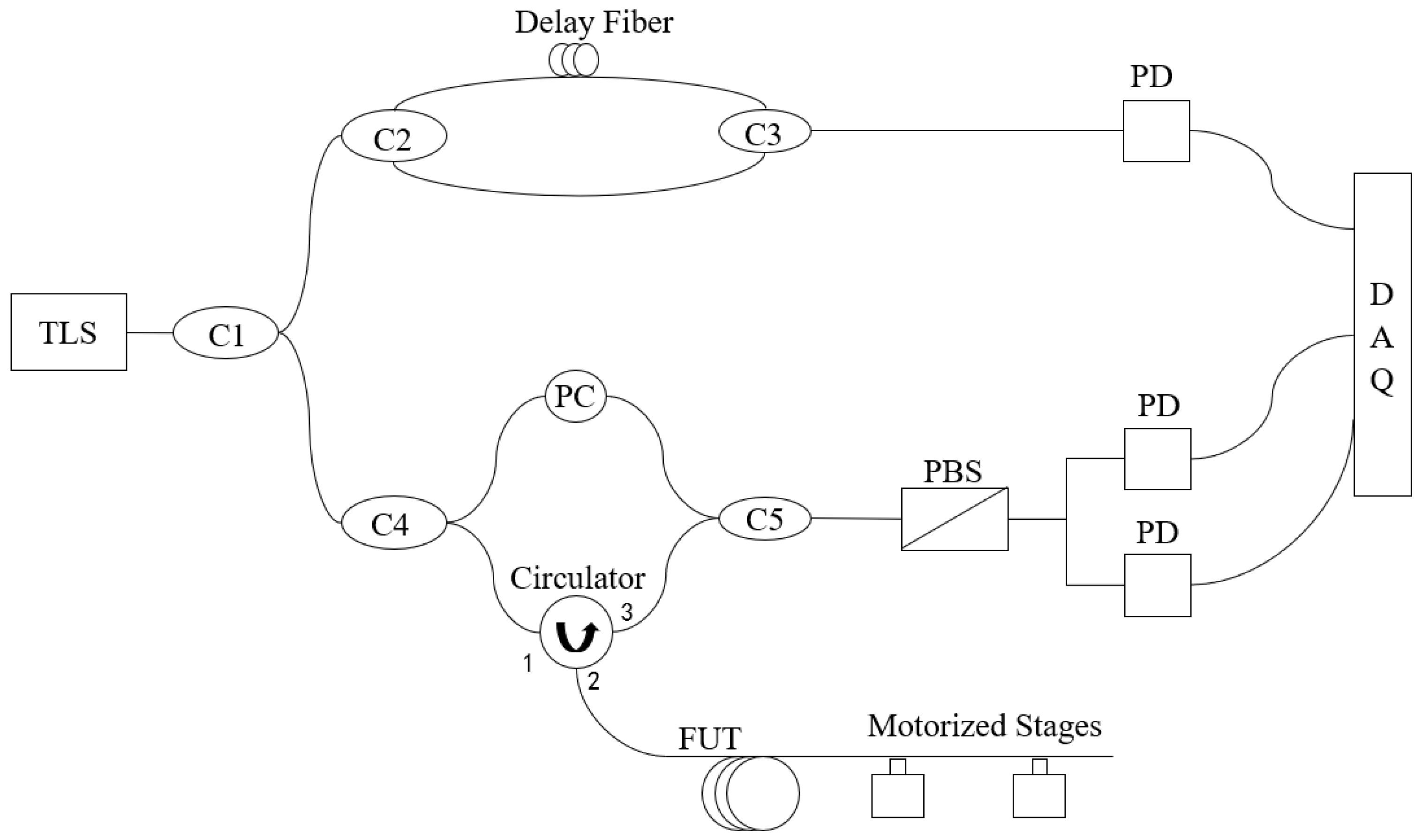
3. Experiments and Results Analysis
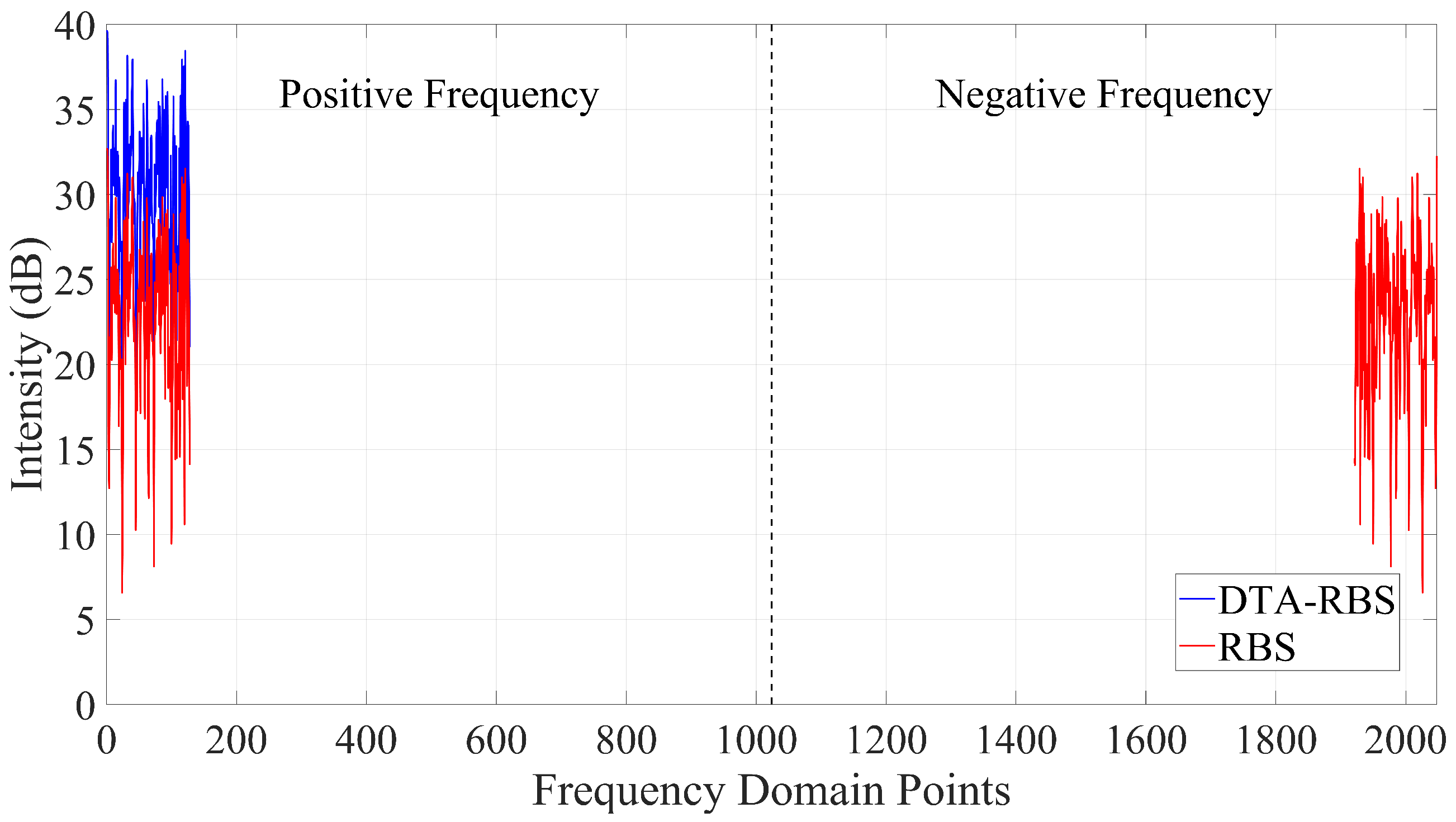
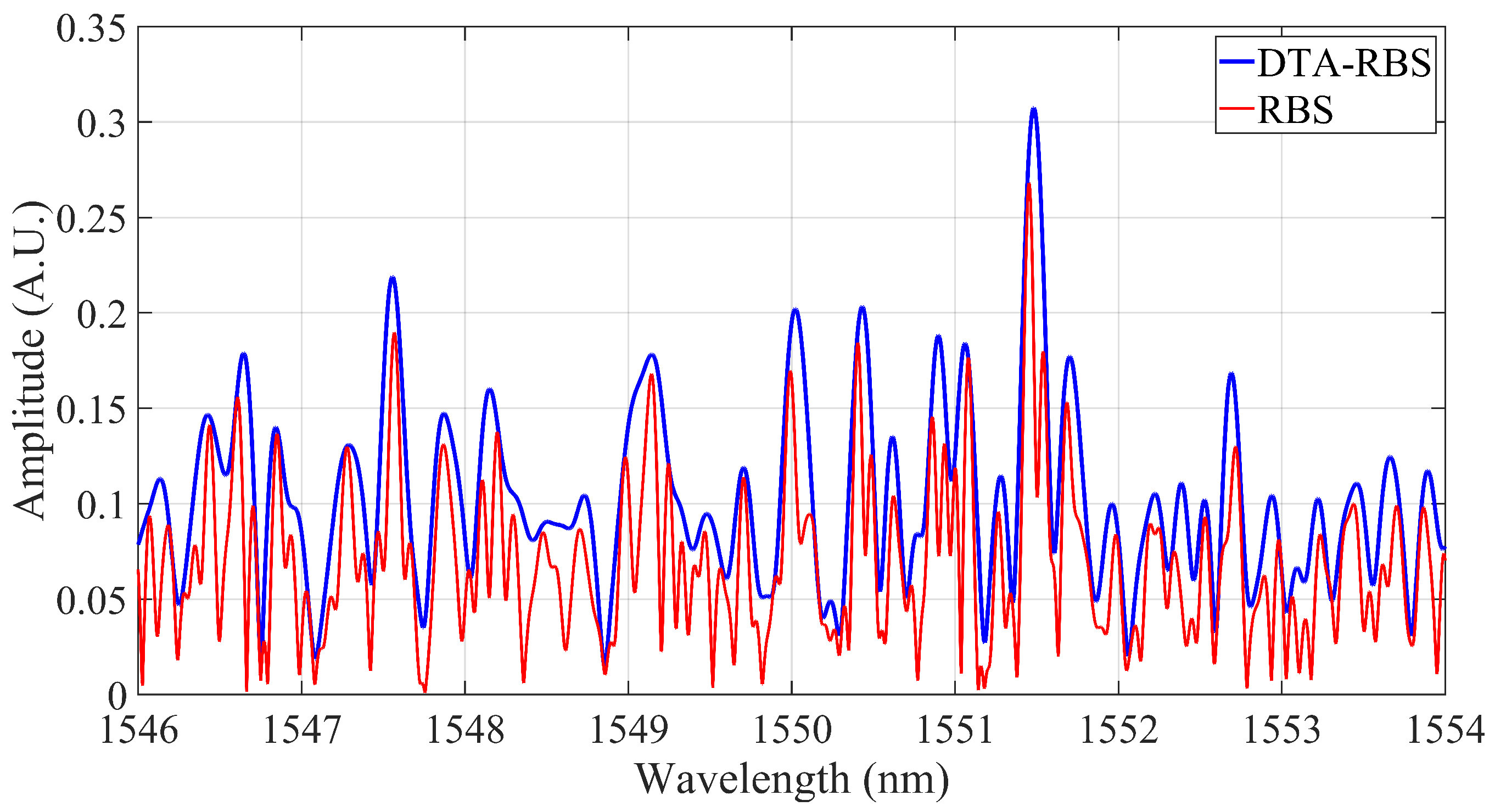
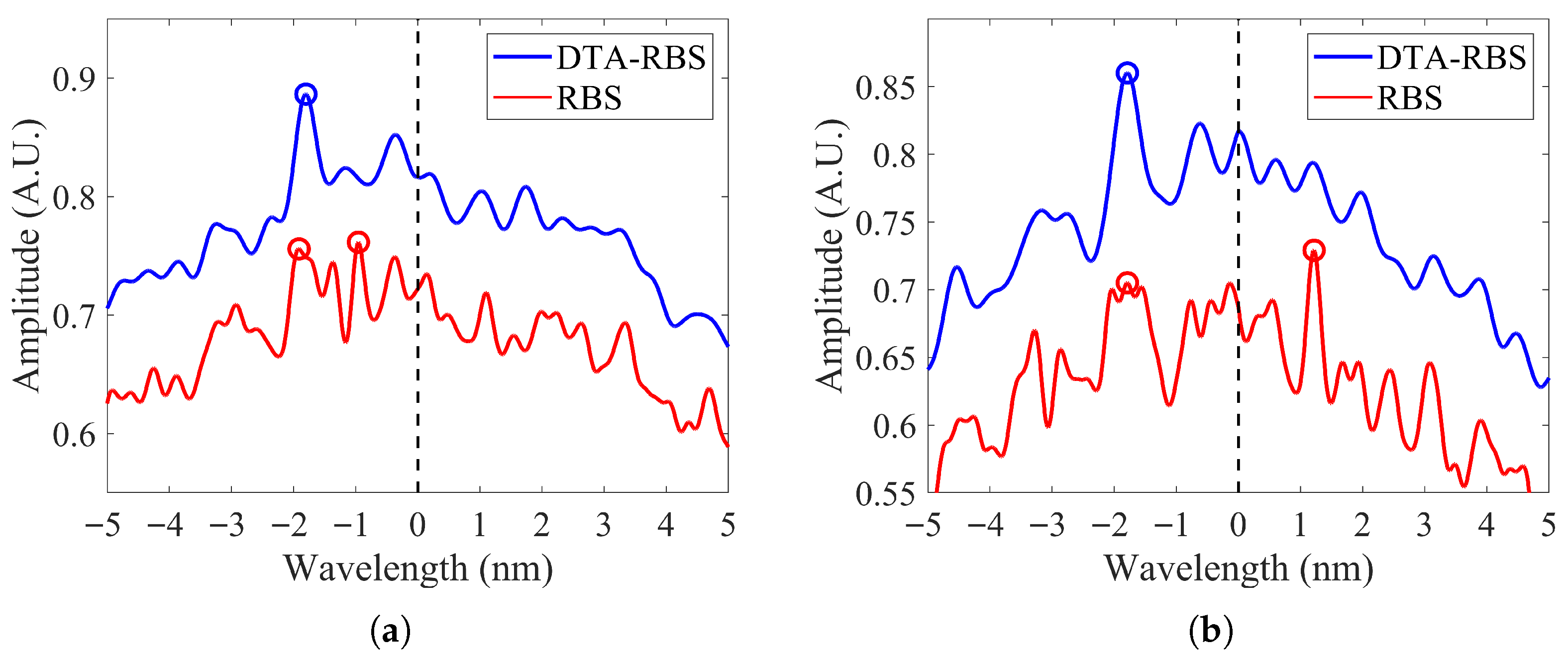
3.1. Reconstruction of RBS and DTA-RBS
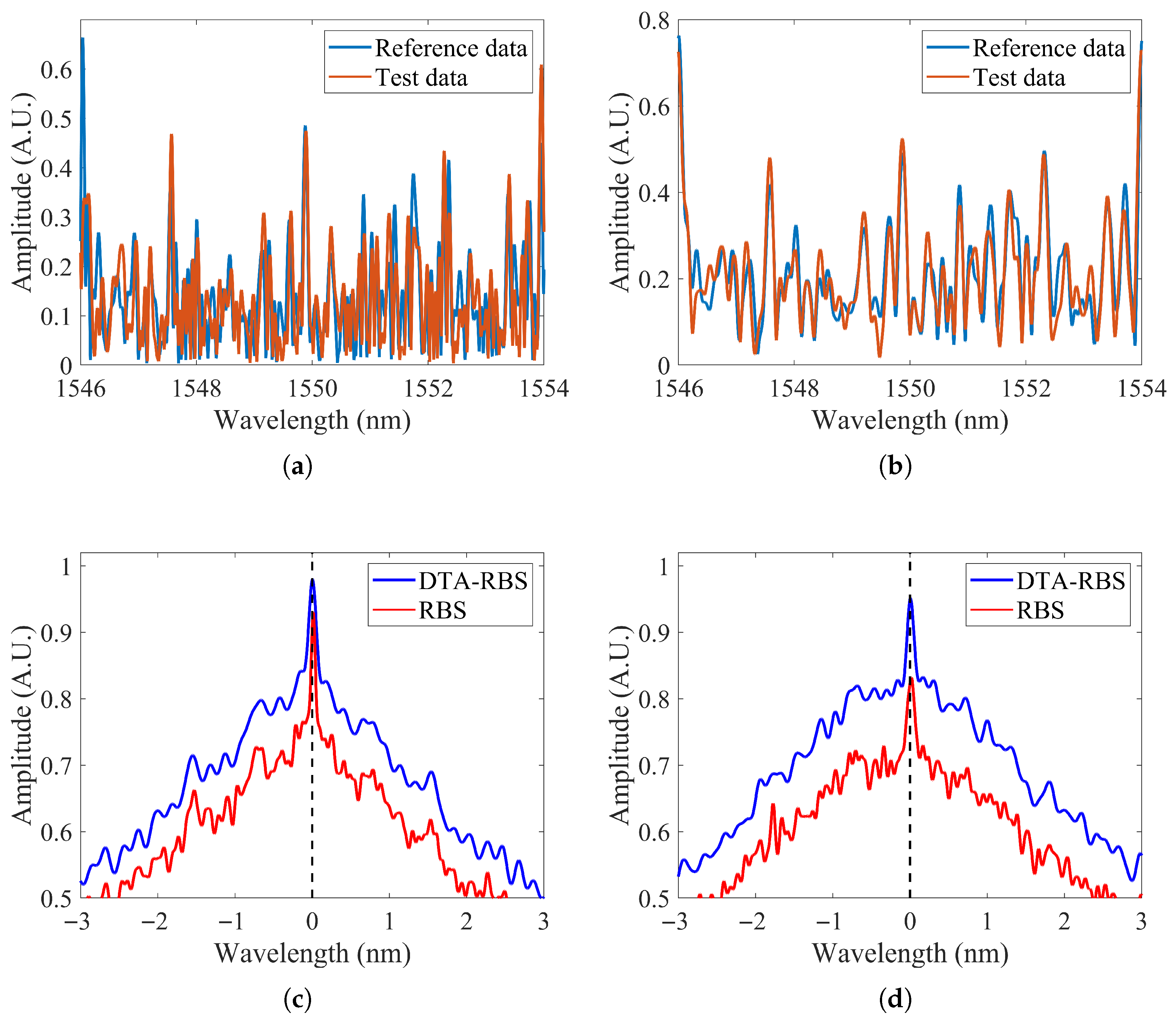
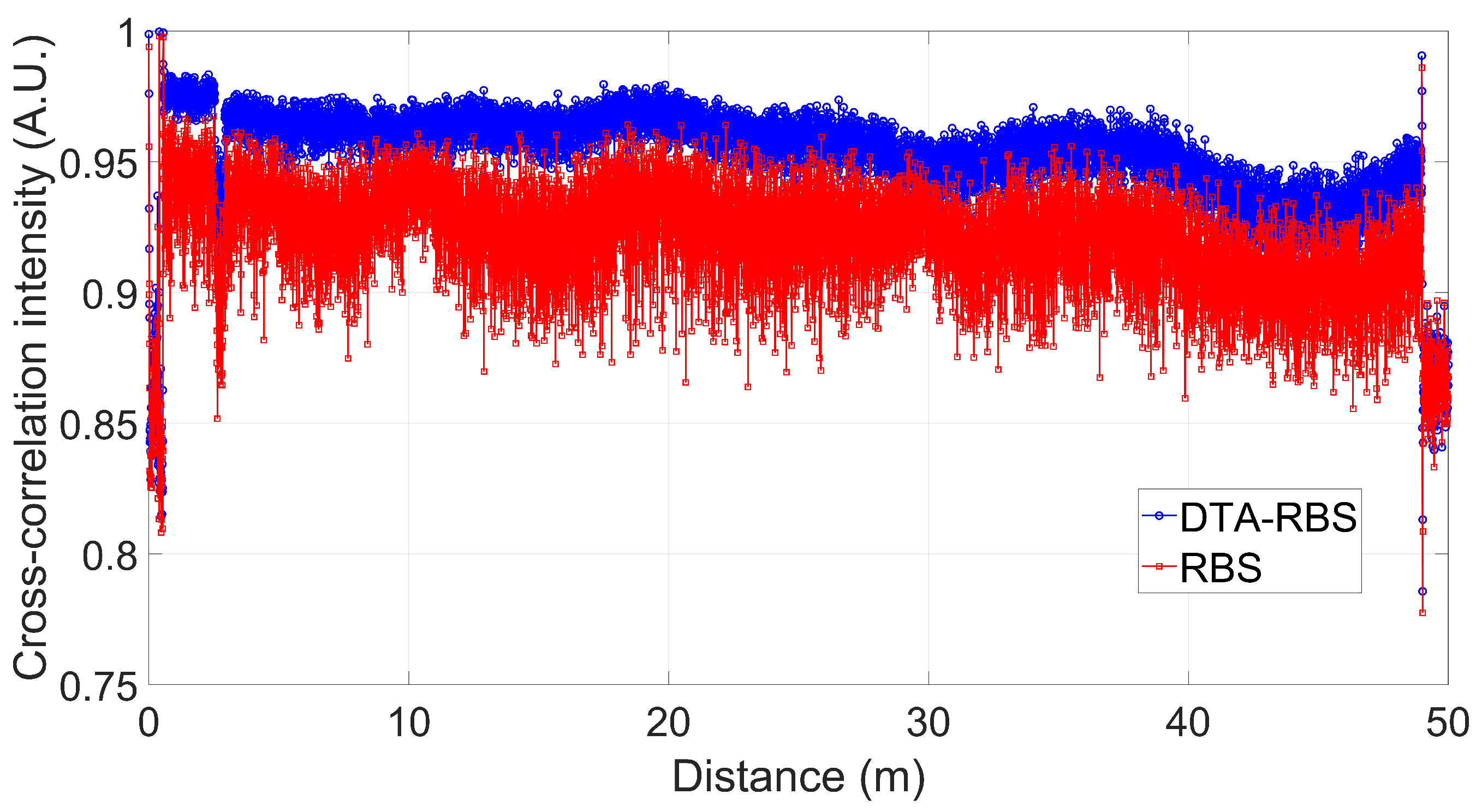
3.2. Cross-Correlation Intensity Experiments of RBS and DTA-RBS
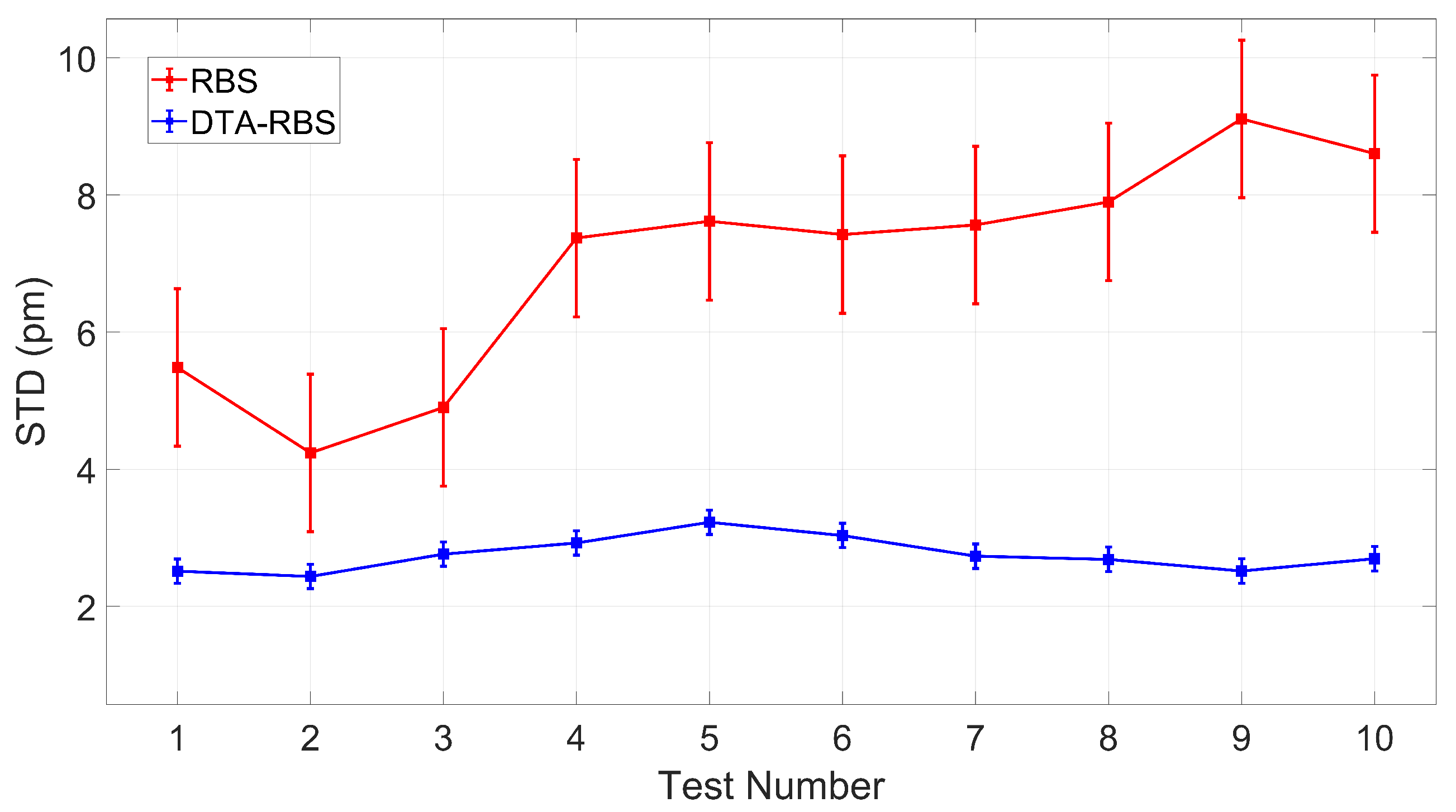
3.3. STD Performance Experiments of RBS and DTA-RBS
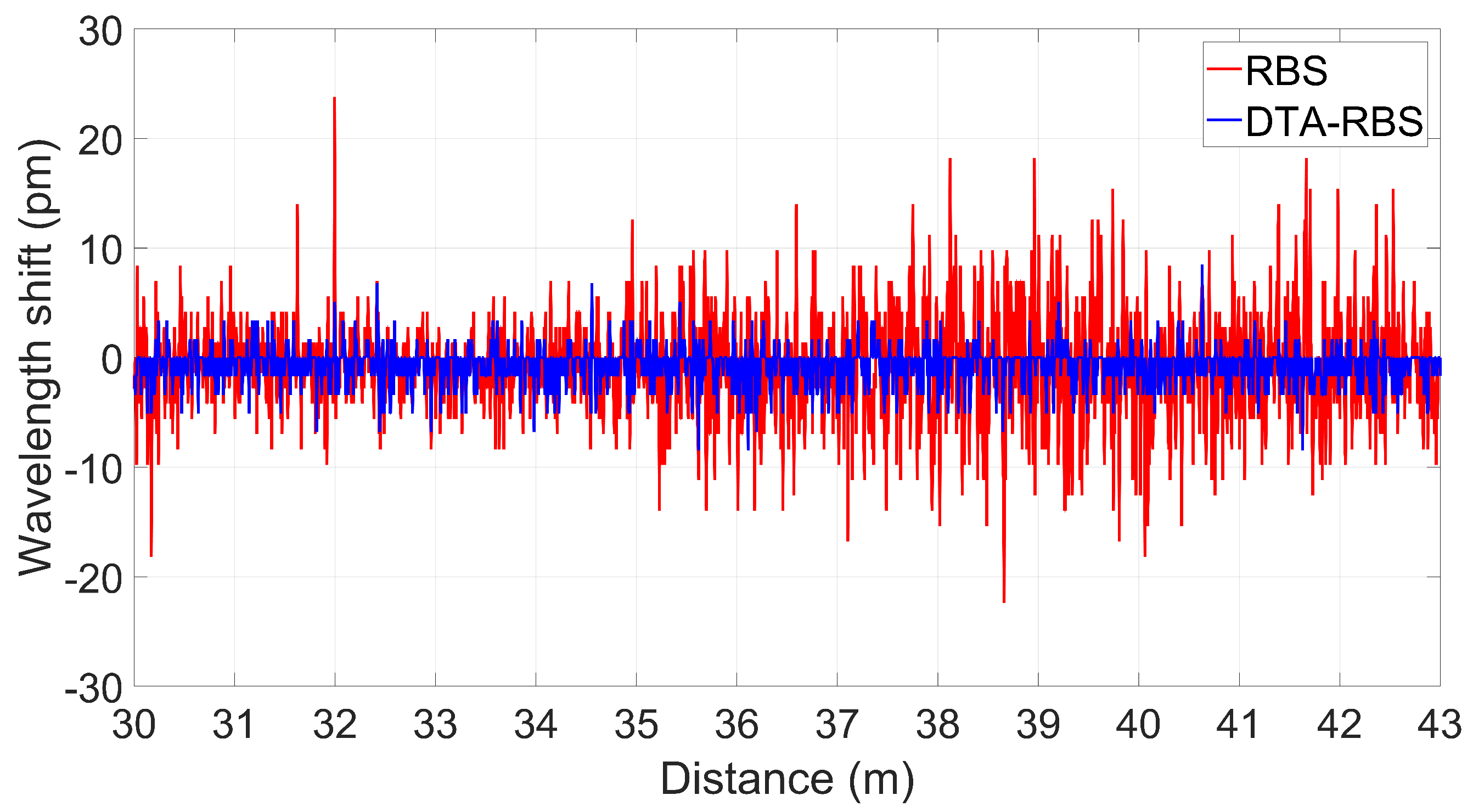
3.4. Distributed Strain Demodulation Experiments of RBS and DTA-RBS
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liang, C.; Wang, Y.; Gao, Y.; Zhang, H.; Jin, B.; Bai, Q. Spatial Resolution Enhancement in OFDR Using a Modified Cohen’s Class Analysis. J. Light. Technol. 2025, 43, 5915–5922. [Google Scholar] [CrossRef]
- Yang, K.; Ke, C.; Xv, Z.; Wang, Z.; Liu, D. High accuracy calibration method for 3D curve reconstruction based on a twisted multicore fiber. Opt. Lett. 2025, 50, 2113–2116. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Wang, Y.; Zhang, Z.; Zhang, W.; Cong, R.; Wu, S.; Liu, X. Accurate 3D Deformation Detection Approach for Microstrip Array Antenna Using Optical Frequency Domain Reflectometer. In Proceedings of the 2022 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Guangzhou, China, 27–29 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–3. [Google Scholar]
- Wang, H.; Zhang, Z.; Wang, Y.; Zhou, R.; Zhai, T.; Liu, Y.; Li, G.; Wei, Y. Research on real-time distributed temperature sensing with optical frequency domain reflectometry for high-voltage switchgear temperature monitoring applications. In Proceedings of the First Conference on Distributed Optical Fiber Sensing Technology and Applications (DOFS 2024), Nanjing, China, 22–24 November 2024; SPIE: Bellingham, WA, USA, 2025; Volume 13654, pp. 19–24. [Google Scholar]
- Badar, M.; Lu, P.; Wang, Q.; Boyer, T.; Chen, K.P.; Ohodnicki, P.R. Real-time optical fiber-based distributed temperature monitoring of insulation oil-immersed commercial distribution power transformer. IEEE Sens. J. 2020, 21, 3013–3019. [Google Scholar] [CrossRef]
- Zhao, S.; Cui, J.; Suo, L.; Wu, Z.; Zhou, D.P.; Tan, J. Performance investigation of OFDR sensing system with a wide strain measurement range. J. Light. Technol. 2019, 37, 3721–3727. [Google Scholar] [CrossRef]
- Zhao, S.; Cui, J.; Wu, Z.; Tan, J. Accuracy improvement in OFDR-based distributed sensing system by image processing. Opt. Lasers Eng. 2020, 124, 105824. [Google Scholar] [CrossRef]
- Liang, C.; Bai, Q.; Zhou, X.; Wang, Y.; Gao, Y.; Zhang, H.; Jin, B. Measurement Error Compensation at Strain Area Edge in OFDR Using Local Spectrum Division Method. J. Light. Technol. 2024, 42, 7368–7377. [Google Scholar] [CrossRef]
- Wang, Y.; Gu, X.; Wang, H.; Liu, Y.; Zhou, R.; Zhang, W.; Peng, X.; Zhang, Z. Fast demodulation algorithm implementation in OFDR with wavelength selection matching and local cross-correlation. Opt. Express 2024, 32, 45884–45903. [Google Scholar] [CrossRef]
- Silva, M.; Oliveira, R.; Rocha, F. Enhancing Time–Frequency Signal Analysis: Integrating Windowing with the Fractional Fourier Transform for Modern Applications. Circuits Syst. Signal Process. 2025, 44, 4988–5009. [Google Scholar] [CrossRef]
- Falaggis, K.; Kozacki, T.; Kujawinska, M. Computation of highly off-axis diffracted fields using the band-limited angular spectrum method with suppressed Gibbs related artifacts. Appl. Opt. 2013, 52, 3288–3297. [Google Scholar] [CrossRef] [PubMed]
- Helms, H.D.; Thomas, J.B. Truncation error of sampling-theorem expansions. Proc. IRE 2007, 50, 179–184. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, N.; Luo, Z.; Ren, G. Theoretical Exploration of Fourier Frequency Domain Filtering in High-Frequency Noise Control and Risk Measurement in the Financial Market. Financ. Econ. Res. 2025, 2, 69–77. [Google Scholar] [CrossRef]
- Cui, J.; Zhao, S.; Yang, D.; Ding, Z. Investigation of the interpolation method to improve the distributed strain measurement accuracy in optical frequency domain reflectometry systems. Appl. Opt. 2018, 57, 1424–1431. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhai, T.; Wang, Y.; Liu, Y.; Zhou, R.; Peng, X.; Zhang, Z. Real-time sensing approach for optical frequency domain reflectometry using an FPGA-based high-speed demodulation algorithm. Opt. Express 2024, 32, 33247–33261. [Google Scholar] [CrossRef] [PubMed]
- Yu, G.; HuanRan, C.; HaoTian, J.; GuoDong, L.; BingGuo, L.; FengDong, C.; BingHui, L. Research on the OFDR strain measurement method based on similarity features of dual-segment RSS. Opt. Express 2024, 32, 26640–26652. [Google Scholar] [CrossRef] [PubMed]
- Liang, C.; Bai, Q.; Yan, M.; Wang, Y.; Zhang, H.; Jin, B. A comprehensive study of optical frequency domain reflectometry. IEEE Access 2021, 9, 41647–41668. [Google Scholar] [CrossRef]
- Yang, J.; Zou, C.; Lin, C.; Zhu, Y.; Zhu, Y.; Dang, F.; Yuan, Y.; Yu, Z.; Wang, Y.; Qin, Y. Noise compensation methods for optical fiber frequency sweeping interferometry: A review. J. Light. Technol. 2022, 41, 4035–4050. [Google Scholar] [CrossRef]
- Wang, F.; Sun, Y.; Chen, Q.; Xing, J.; Xia, Y.; Zhang, Y.; Zhang, X. Enhancing the effect of nonlinear frequency sweep correction in OFDR with improved reference frequency. J. Light. Technol. 2022, 40, 269–276. [Google Scholar] [CrossRef]
- Džafić, D.; Džafić, I. Computation of Discrete-Time Analytic Signals. In Proceedings of the 2023 XXIX International Conference on Information, Communication and Automation Technologies (ICAT), Sarajevo, Bosnia and Herzegovina, 11–14 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Elfataoui, M.; Mirchandani, G. A frequency-domain method for generation of discrete-time analytic signals. IEEE Trans. Signal Process. 2006, 54, 3343–3352. [Google Scholar] [CrossRef]
- O’Toole, J.M.; Mesbah, M.; Boashash, B. A new discrete-time analytic signal for reducing aliasing in discrete time-frequency distributions. In Proceedings of the 2007 15th European Signal Processing Conference, Poznan, Poland, 3–7 September 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 591–595. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Wang, H.; Zhang, Z.; Wang, Y.; Huang, H. OFDR Distributed Demodulation Optimization Algorithm Using Discrete-Time Analytic Signal Backscattered Rayleigh Spectrum. Sensors 2025, 25, 7044. https://doi.org/10.3390/s25227044
Wang S, Wang H, Zhang Z, Wang Y, Huang H. OFDR Distributed Demodulation Optimization Algorithm Using Discrete-Time Analytic Signal Backscattered Rayleigh Spectrum. Sensors. 2025; 25(22):7044. https://doi.org/10.3390/s25227044
Chicago/Turabian StyleWang, Shuaipeng, Haomao Wang, Zhiguo Zhang, Yifan Wang, and Haichao Huang. 2025. "OFDR Distributed Demodulation Optimization Algorithm Using Discrete-Time Analytic Signal Backscattered Rayleigh Spectrum" Sensors 25, no. 22: 7044. https://doi.org/10.3390/s25227044
APA StyleWang, S., Wang, H., Zhang, Z., Wang, Y., & Huang, H. (2025). OFDR Distributed Demodulation Optimization Algorithm Using Discrete-Time Analytic Signal Backscattered Rayleigh Spectrum. Sensors, 25(22), 7044. https://doi.org/10.3390/s25227044





