Identification of Pipe Damage by Line-Structured Light and Regional Resonance Pairs
Abstract
1. Introduction
2. Methodology
2.1. Overview
2.2. Damage Database
2.3. Damage Indices
2.4. Damage Identification Process
3. Application of Proposed Method
3.1. Database Development
3.2. Establishment of Localization Bands
3.3. Evaluation of Damage Identification Accuracy
4. Experimental Verification and Discussion
4.1. Test Specimen
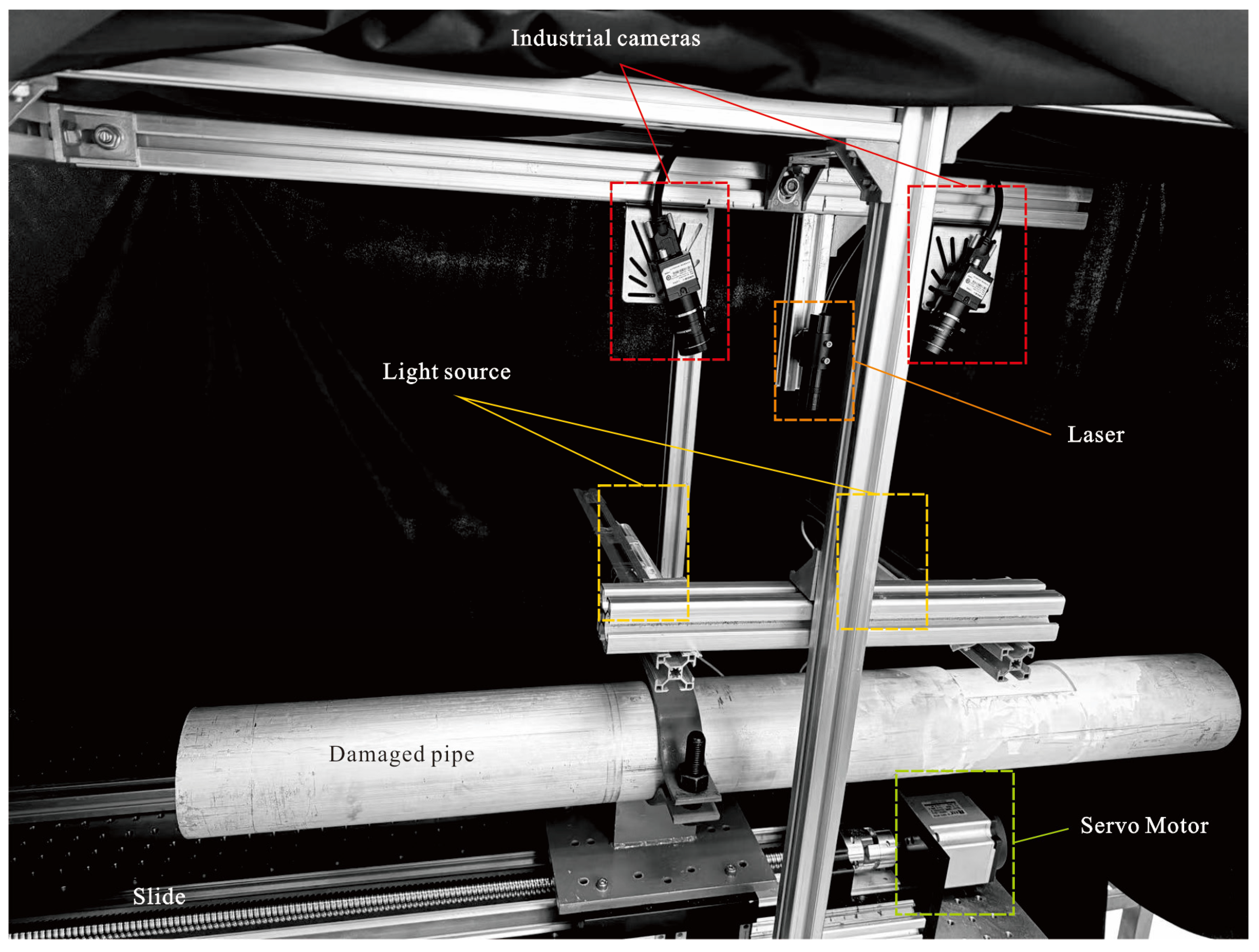
4.2. Experimental Setup and Procedure
4.3. Experimental Damage Identification Results
5. Conclusions
- 1.
- A novel baseline-free damage-identification method is developed. This method successfully combines RRP with the LSL method to systematically detect, locate, and quantify damage in tubular structures.
- 2.
- The key relationship between RRP and damage is established based on the proposed damage indices. The study demonstrates that the presence of RRP is a distinct characteristic of damage, and the damage location could be determined by sorting the RRP frequency ratios.
- 3.
- The reliability of the method is validated through large-scale simulations. Across 800 test cases, the proposed method achieved a 100% success rate in damage detection, a 97.17% accuracy rate in locating the damage centroid, and an 86.55% accuracy rate for damage quantification.
- 4.
- The effectiveness of the method is confirmed by experimental verification. The results from artificially pre-damaged pipes show the method successfully detected, located, and quantified the damage, achieving a quantification accuracy of 90.73%.
- 5.
- The practical advantages of the combined method are demonstrated. By using RRP to guide the LSL scan, the approach enables rapid damage localization, significantly improving the efficiency and robustness of pipe damage identification.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| D0 | Outside diameter of pipe |
| V | Damage indices: volume |
| V0 | Volume of undamaged pipe |
| Vd | Volume of damage |
| Vactual | Actual volume of damaged pipes |
| Vpredicted | Predicted volume of damaged pipes |
| A | Damage indices: Cross-sectional area |
| A0 | Cross-sectional area of undamaged pipe |
| Ad | Cross-sectional area of damage |
| S | Damage indices: Surface area |
| S0 | Surface area of undamaged pipe |
| Sd | Surface area of damage |
| Md | Axial distance from damage centroid to end of pipe |
| Xd | Offset of damage centroid from centroid of undamaged pipe in X axis |
| Zd | Offset of damage centroid from centroid of undamaged pipe in Z axis |
| P1, P2, P3 | Accuracy of Level 1, 2 and 3 damage identification prediction |
| αd | Angle subtended by damage |
| ε | Error in Level 3 damage identification prediction |
| j | Level 3 damage identification test case index |
| N1, N2 | Number of cases in which Level 1 and 2 damage identification is correctly predicted |
| N | Total number of test cases in set (or sub-set) |
| δx | Damage indices: cross-sectional symmetry |
| δz | Damage indices: axial symmetry |
| Mx, My, Mz | Shift in centroidal axis of pipe in X, Y and Z axes |
References
- Vanaei, H.; Eslami, A.; Egbewande, A. A review on pipeline corrosion, in-line inspection (ILI), and corrosion growth rate models. Int. J. Press. Vessel. Pip. 2017, 149, 43–54. [Google Scholar] [CrossRef]
- Amaya-Gómez, R.; Riascos-Ochoa, J.; Muñoz, F.; Bastidas-Arteaga, E.; Schoefs, F.; Sánchez-Silva, M. Modeling of pipeline corrosion degradation mechanism with a Lévy Process based on ILI (In-Line) inspections. Int. J. Press. Vessel. Pip. 2019, 172, 261–271. [Google Scholar] [CrossRef]
- Pandey, A.; Biswas, M.; Samman, M. Damage detection from changes in curvature mode shapes. J. Sound Vib. 1991, 145, 321–332. [Google Scholar] [CrossRef]
- Cawley, P.; Adams, R.D. The location of defects in structures from measurements of natural frequencies. J. Strain Anal. Eng. Des. 1979, 14, 49–57. [Google Scholar] [CrossRef]
- Cawley, P.; Lowe, M.; Alleyne, D.; Pavlakovic, B.; Wilcox, P. Practical long range guided wave inspection-applications to pipes and rail. Mater. Eval. 2003, 61, 66–74. [Google Scholar]
- Maeck, J.; De Roeck, G. Damage detection on a prestressed concrete bridge and RC beams using dynamic system identification. Key Eng. Mater. 1999, 167, 320–327. [Google Scholar] [CrossRef]
- Carrasco, C.J.; Osegueda, R.A.; Ferregut, C.M.; Grygier, M. Localization and quantification of damage in a space truss model using modal strain energy. Smart Structures and Materials 1997: Smart Systems for Bridges, Structures, and Highways. Proc. SPIE 1997, 3043, 181–192. [Google Scholar]
- Conejo, V.; Hernández, L.; Carreón, H. Non-destructive evaluation of aging in welded pipeline X60 and X65 by thermoelectric power means. Int. J. Press. Vessel. Pip. 2024, 207, 105103. [Google Scholar] [CrossRef]
- Kashfi, S.; Rouzegar, J.; Tavakolpour-Saleh, A. Piping structural health monitoring: ANN methods for internal semi-elliptical crack detection. Int. J. Press. Vessel. Pip. 2025, 214, 105417. [Google Scholar] [CrossRef]
- Gu, Y.; Liao, Z.; Gu, M.; Li, Z.; Jia, J.; Tu, S.-T. A novel coupling method for ultrasonic transducer based on pressureless sintering of nano-Ag. J. Mater. Res. Technol. 2024, 28, 2478–2487. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. An introduction to structural health monitoring. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 2007, 365, 303–315. [Google Scholar] [CrossRef]
- Ramesh Babu, J.; Karve, P.M.; Mahadevan, S. Probabilistic prediction of external corrosion fatigue life in buried steel pipes. Int. J. Press. Vessel. Pip. 2025, 214, 105415. [Google Scholar] [CrossRef]
- Pozo, F.; Arruga, I.; Mujica, L.E.; Ruiz, M.; Podivilova, E. Detection of structural changes through principal component analysis and multivariate statistical inference. Struct. Health Monit. 2016, 15, 127–142. [Google Scholar] [CrossRef]
- Banjara, N.K.; Sasmal, S.; Kapuria, S. Fatigue and leakage-type damage detection in metallic plates and pipelines using piezoelectric patch acoustic sensors. Int. J. Press. Vessel. Pip. 2024, 209, 105162. [Google Scholar] [CrossRef]
- Liang, H.; Wu, J.; Zhang, W.; Zheng, M.; Ma, H. Guided wave localization of small defects based on stochastic resonance characteristics of Duffing systems. Int. J. Press. Vessel. Pip. 2024, 209, 105215. [Google Scholar] [CrossRef]
- Zhai, S.; Zhou, S.; Chen, S. Researches on defect localization based on discrete ellipse imaging algorithm for curved plates. Int. J. Press. Vessel. Pip. 2019, 175, 103872. [Google Scholar] [CrossRef]
- Ozevin, D.; Harding, J. Novel leak localization in pressurized pipeline networks using acoustic emission and geometric connectivity. Int. J. Press. Vessel. Pip. 2012, 92, 63–69. [Google Scholar] [CrossRef]
- Entezami, A.; Shariatmadar, H. An unsupervised learning approach by novel damage indices in structural health monitoring for damage localization and quantification. Struct. Health Monit. 2018, 17, 325–345. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, M.; Wang, Y.e.; Jia, J.; Tu, S.-T. Influence of spread gap height on piezoelectric transducer coupled via pressureless sintering of nano-Ag. IEEE Sens. J. 2025, 25, 33473–33487. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, M.; Hou, Z.; Jia, J.; Tu, S.-T. Effect of the paste spreadability on ultrasonic transducer fabricated by pressureless sintering of nano-Ag. Measurement 2024, 236, 115110. [Google Scholar] [CrossRef]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B. A summary review of vibration-based damage identification methods. Shock Vib. Dig. 1998, 30, 91–105. [Google Scholar] [CrossRef]
- Zang, X.; Xu, Z.-D.; Lu, H.; Zhu, C.; Zhang, Z. Ultrasonic guided wave techniques and applications in pipeline defect detection: A review. Int. J. Press. Vessel. Pip. 2023, 206, 105033. [Google Scholar] [CrossRef]
- Song, J.; Guo, D.; Jia, J.; Tu, S. A new on-line ultrasonic thickness monitoring system for high temperature pipes. Int. J. Press. Vessel. Pip. 2022, 199, 104691. [Google Scholar] [CrossRef]
- Wu, J.; Yang, F.; Jing, L.; Liu, Z.; Lin, Y.; Ma, H. Defect detection in pipes using Van der Pol systems based on ultrasonic guided wave. Int. J. Press. Vessel. Pip. 2022, 195, 104577. [Google Scholar] [CrossRef]
- Jin, L.; Li, S.; Qin, G.; Xu, K. Outer surface defect detection of steel pipes with 3D vision based on multi-line structured lights. Meas. Sci. Technol. 2024, 35, 065203. [Google Scholar] [CrossRef]
- Gunatilake, A.; Piyathilaka, L.; Tran, A.; Vishwanathan, V.K.; Thiyagarajan, K.; Kodagoda, S. Stereo Vision Combined with Laser Profiling for Mapping of Pipeline Internal Defects. IEEE Sens. J. 2021, 21, 11926–11934. [Google Scholar] [CrossRef]
- Li, T.; Xie, P.; Liu, S. Collapse of pipes with non-uniform corrosion defects under external pressure: A reverse inversion modeling method. Eng. Fail. Anal. 2023, 153, 107594. [Google Scholar] [CrossRef]
- Ho, M.; El-Borgi, S.; Patil, D.; Song, G. Inspection and monitoring systems subsea pipelines: A review paper. Struct. Health Monit. 2020, 19, 606–645. [Google Scholar] [CrossRef]
- El-Gebeily, M.; Khulief, Y. Identification of wall-thinning and cracks in pipes utilizing vibration modes and wavelets. Appl. Math. Model. 2016, 40, 5335–5348. [Google Scholar] [CrossRef]
- Zhang, Y.; Lie, S.T.; Xiang, Z.; Lu, Q. A frequency shift curve based damage detection method for cylindrical shell structures. J. Sound Vib. 2014, 333, 1671–1683. [Google Scholar] [CrossRef]
- Yang, Z.; Oterkus, E. Corrosion detection in pipelines based on measurement of natural frequencies. Ann. Limnol. Oceanogr. 2017, 2, 001–003. [Google Scholar] [CrossRef]
- Farrar, C.R.; Lieven, N.A. Damage prognosis: The future of structural health monitoring. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 2007, 365, 623–632. [Google Scholar] [CrossRef]
- Flynn, E.B.; Todd, M.D. A Bayesian approach to optimal sensor placement for structural health monitoring with application to active sensing. Mech. Syst. Signal Process. 2010, 24, 891–903. [Google Scholar] [CrossRef]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Continuous symmetry measures. J. Am. Chem. Soc. 1992, 114, 7843–7851. [Google Scholar] [CrossRef]
- Chen, J.G.; Büyüköztürk, O. A symmetry measure for damage detection with mode shapes. J. Sound Vib. 2017, 408, 123–137. [Google Scholar] [CrossRef]
- Falahatpisheh, A.; Kheradvar, A. A measure of axisymmetry for vortex rings. Eur. J. Mech. B/Fluids 2015, 49, 264–271. [Google Scholar] [CrossRef]
- Wang, M.; Gu, Y.; Fu, Y.; Zhu, Y.; Jia, J.; Tu, S.-T. Baseline-free damage identification in clamped-clamped pipes based on regional resonance pairs. Int. J. Press. Vessel. Pip. 2025, 214, 105416. [Google Scholar] [CrossRef]

















| Material | Elasticity Modulus (Mpa) | Density (kg m−3) | Poisso’s Ratio - | Effective Length (mm) | Outside Diameter (mm) | Wall Thickness (mm) | Unit Mass (kg m−1) |
|---|---|---|---|---|---|---|---|
| AL 6063 T5 | 68,900 | 2700 | 0.33 | 900 | 103 | 6.5 | 5.32 |
| A0 (mm2) | S0 (mm2) | V0 (mm3) | Mx(max) (mm) | Mz(max) (mm) | f1A = f1P (Hz) | f2A = f2P (Hz) | f3A = f3P (Hz) |
|---|---|---|---|---|---|---|---|
| 1970.56 | 291,225.64 | 1,773,507.59 | 30.72 | 225 | 542.63 | 1318.60 | 2283.10 |
| Md (mm) | αd (°) | Td (mm) | Ld (mm) |
|---|---|---|---|
| 90 | 22.5 | 0.65 | 45 |
| 135 | 45 | 1.30 | 90 |
| 180 | 67.5 | 1.95 | 135 |
| 225 | 90 | 2.60 | - |
| 270 | - | - | - |
| 315 | - | - | - |
| 360 | - | - | - |
| 405 | - | - | - |
| 450 | - | - | - |
| Boundary | Md [mm (×L0)] | αd (°) | Td [mm (×T0)] | Ld [mm (×L0)] |
|---|---|---|---|---|
| Min | 90 (0.10) | 22.5 | 0.65 (0.10) | 45 (0.05) |
| Max | 450 (0.50) | 90 | 2.60 (0.40) | 135 (0.15) |
| Localization Band | Localization Bandwidth | RRP Frequency Ratio Ranking | Quantification Graph |
|---|---|---|---|
| 1 | 0.100L0 ≤ Md ≤ 0.175L0 | f3A/f3P > f1A/f1P > f2A/f2P | Figure 9a |
| Figure 9b | |||
| 2 | 0.175L0 < Md ≤ 0.225L0 | f2A/f2P > f1A/f1P > f3A/f3P | Figure 9c |
| 3 | 0.225L0 < Md ≤ 0.375L0 | f1A/f1P > f3A/f3P > f2A/f2P | Figure 9d |
| Figure 9e | |||
| Figure 9f | |||
| 4 | 0.375L0 < Md ≤ 0.425L0 | f3A/f3P > f2A/f2P > f1A/f1P | Figure 9g |
| 5 | 0.425L0 < Md ≤ 0.500L0 | f2A/f2P > f3A/f3P > f1A/f1P | Figure 9h |
| Figure 9i |
| Localization Band | RRP Frequency Ratio Ranking | Quantification Relation, Vibration Mode, i = 1 | Quantification Relation, Vibration Mode, i = 2 | Quantification Relation, Vibration Mode, i = 3 |
|---|---|---|---|---|
| 1 | f3A/f3P > f1A/f1P > f2A/f2P | y = 0.005x + 0.49995 | y = 0.0063x + 0.36923 | y = 0.0042x + 0.57967 |
| y = 0.00407x+ 0.59312 | y = 0.00711x + 0.28882 | y = 0.0034x + 0.65961 | ||
| 2 | f2A/f2P > f1A/f1P > f3A/f3P | y = 0.00211x + 0.78838 | y = 0.00188x + 0.81217 | y = 0.00185x + 0.81323 |
| 3 | f1A/f1P > f3A/f3P > f2A/f2P | y = 0.00175x + 0.82498 | y = 0.00705x + 0.29453 | y = 0.00333x + 0.66671 |
| y = 0.00063x + 0.93748 | y = 0.009x + 0.09943 | y = 0.00142x + 0.85808 | ||
| y = 0.00021x + 0.97854 | y = 0.00369x + 0.63025 | y = 0.00106x + 0.89359 | ||
| 4 | f3A/f3P > f2A/f2P > f1A/f1P | y = 0.00748x + 0.25129 | y = 0.00282x + 0.71745 | y = 0.00015x + 0.98494 |
| 5 | f2A/f2P > f3A/f3P > f1A/f1P | y = 0.00996x + 0.00402 | y = 0.00131x + 0.86907 | y = 0.00617x + 0.38288 |
| y = 0.01086x − 0.08609 | y = 0.00298x + 0.70152 | y = 0.00932x + 0.06758 |
| Band | Set 1 (%) | Set 2 (%) | Set 3 (%) | Set 4 (%) | Aggregate (%) |
|---|---|---|---|---|---|
| 1 | 97.67 | 96.97 | 97.67 | 97.30 | 97.35 |
| 2 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 3 | 96.55 | 97.53 | 97.59 | 97.37 | 97.50 |
| 4 | 88.00 | 88.00 | 89.29 | 96.15 | 91.14 |
| 5 | 97.67 | 100.00 | 100.00 | 97.44 | 98.95 |
| Aggregate | 96.50 | 97.00 | 97.00 | 97.50 | 97.17 |
| Localization Band | Optimum Quantification Relation | Source |
|---|---|---|
| 1 | y = 0.00671x + 0.32903 | Average of i = 2 |
| 2 | y = 0.00188x + 0.81217 | i = 2 |
| 3 | y = 0.00658x + 0.3414 | Average of i = 2 |
| 4 | y = 0.00748x + 0.25129 | i = 1 |
| 5 | y = 0.01041x − 0.04104 | Average of i = 1 |
| Band | Set 1 (%) | Set 2 (%) | Set 3 (%) | Set 4 (%) | Aggregate (%) |
|---|---|---|---|---|---|
| 1 | 90.16 | 88.50 | 87.46 | 91.78 | 89.25 |
| 2 | 75.19 | 63.39 | 68.42 | 70.79 | 67.53 |
| 3 | 87.53 | 89.76 | 89.35 | 86.42 | 88.51 |
| 4 | 93.22 | 93.22 | 92.93 | 92.31 | 92.82 |
| 5 | 95.94 | 93.68 | 96.06 | 94.24 | 94.66 |
| Aggregate | 88.41 | 85.71 | 86.84 | 87.11 | 86.55 |
| Pipe | D0 (mm) | T0 (mm) | L0 (mm) | Md (mm) | αd (°) | Td (mm) | Ld (mm) |
|---|---|---|---|---|---|---|---|
| Undamaged | 103 | 6.5 | 900 | - | - | - | - |
| Damaged | 103 | 6.5 | 900 | 225 | 90 | 4 | 125 |
| Pipe | Modal Frequencies (Hz) | RRP Frequency Ratios | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f1A | f1 | f1P | f2A | f2 | f2P | f3A | f3 | f3P | f1A/f1P | f2A/f2P | f3A/f3P | |
| Undamaged | - | 355 | - | - | 1164 | - | - | 2180 | - | 1.0000 | 1.0000 | 1.0000 |
| Damaged | 348 | - | 436 | 1131 | - | 1224 | 2153 | - | 2260 | 0.7982 | 0.9240 | 0.9527 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Gu, Y.; Wu, Y.; Jia, J.; Tu, S.-T. Identification of Pipe Damage by Line-Structured Light and Regional Resonance Pairs. Sensors 2025, 25, 7020. https://doi.org/10.3390/s25227020
Wang M, Gu Y, Wu Y, Jia J, Tu S-T. Identification of Pipe Damage by Line-Structured Light and Regional Resonance Pairs. Sensors. 2025; 25(22):7020. https://doi.org/10.3390/s25227020
Chicago/Turabian StyleWang, Mingyuan, Yiqing Gu, Yuhua Wu, Jiuhong Jia, and Shan-Tung Tu. 2025. "Identification of Pipe Damage by Line-Structured Light and Regional Resonance Pairs" Sensors 25, no. 22: 7020. https://doi.org/10.3390/s25227020
APA StyleWang, M., Gu, Y., Wu, Y., Jia, J., & Tu, S.-T. (2025). Identification of Pipe Damage by Line-Structured Light and Regional Resonance Pairs. Sensors, 25(22), 7020. https://doi.org/10.3390/s25227020





