Near-Infrared Spectroscopy for Oedema Quantification: An Ex Vivo Porcine Skin Model
Highlights
- NIRS proved to be a promising technique for oedema assessment, as it was sensitive to changes in water content within the tissue. This study establishes proof-of-concept for the use of NIRS in non-invasive oedema quantification.
- The ex vivo porcine skin model was shown to be a suitable and reproducible platform for inducing and studying oedema.
- These findings highlight the potential of NIRS for future in vivo applications. Ongoing work aims to validate this technique in a clinical study involving neonates with oedema, which could enable earlier diagnosis, improved treatment evaluation, and better patient management in conditions related to abnormal fluid accumulation.
- The porcine ex vivo model serves as a valuable intermediate step between controlled laboratory investigations and in vivo clinical validation.
Abstract
1. Introduction
2. Materials and Methods
3. Results
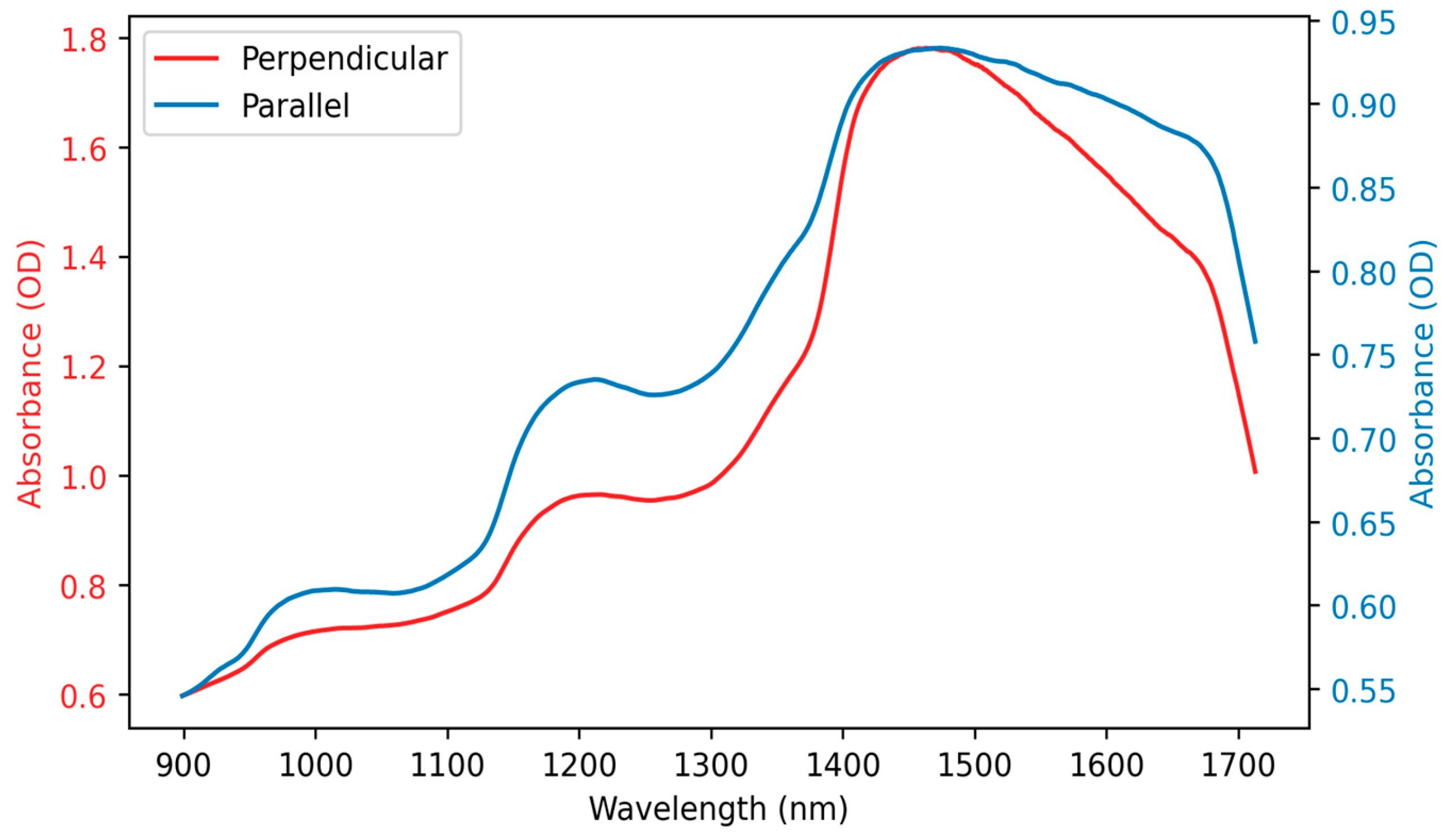
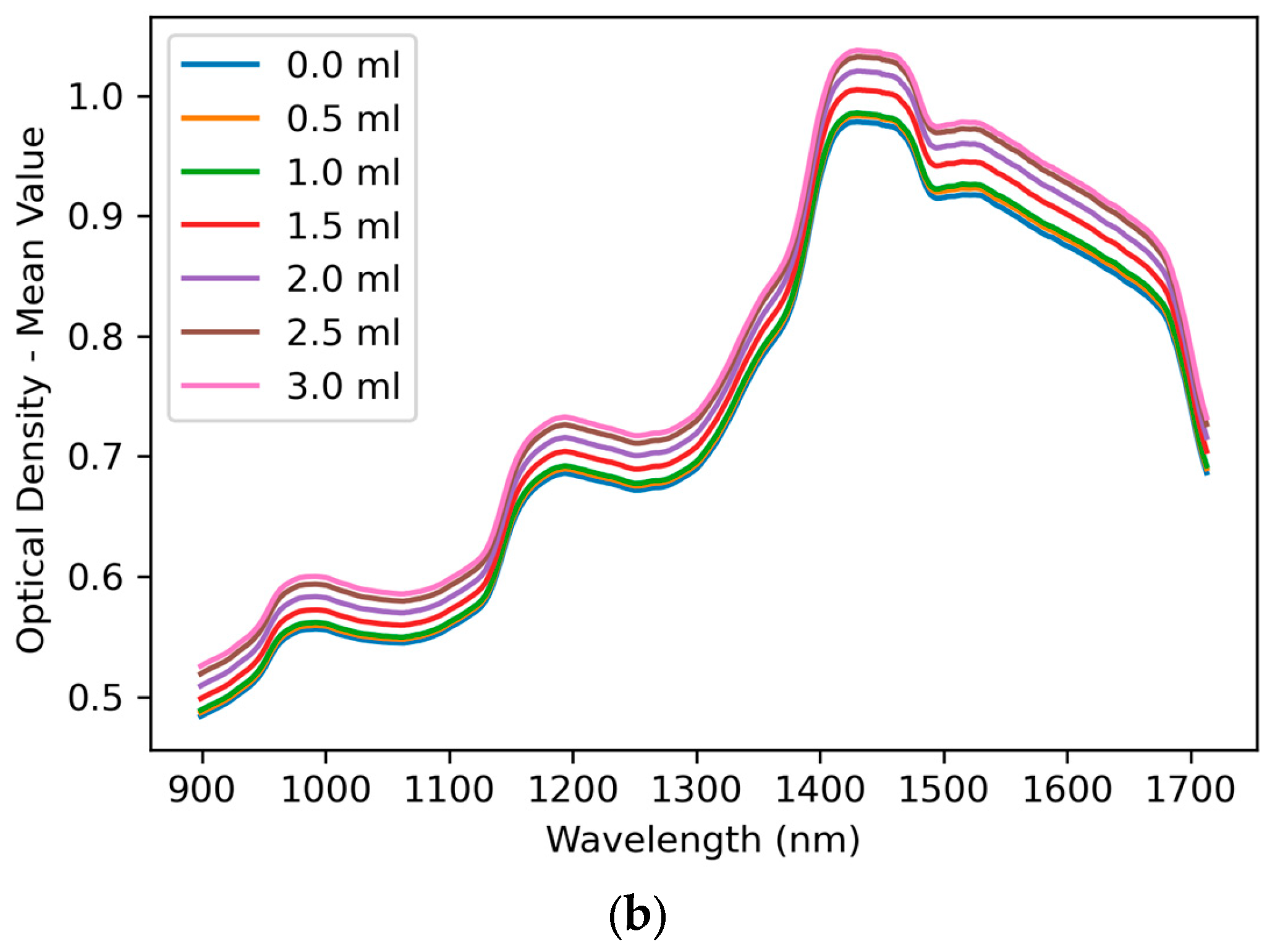
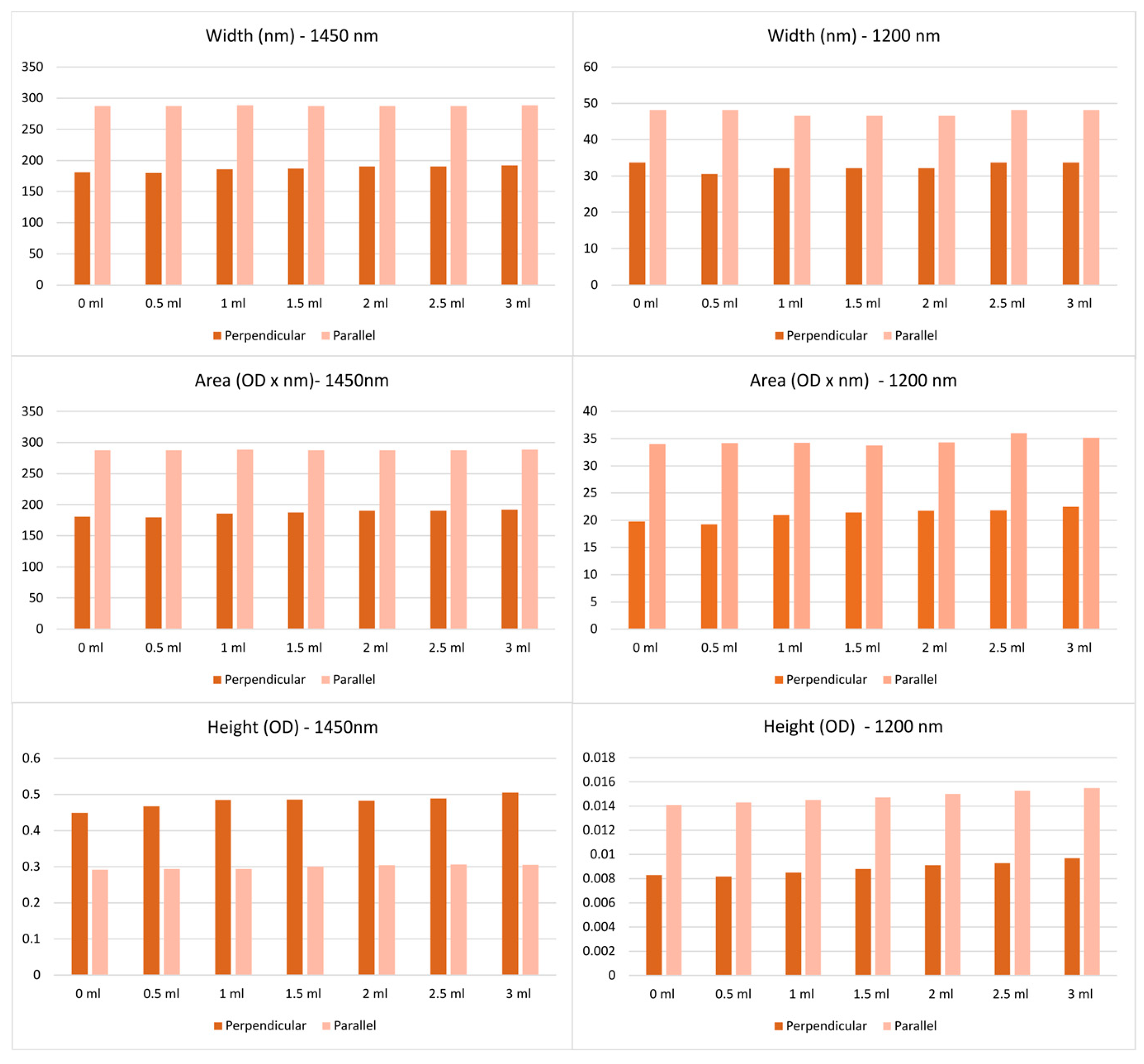
3.1. Spectral Features
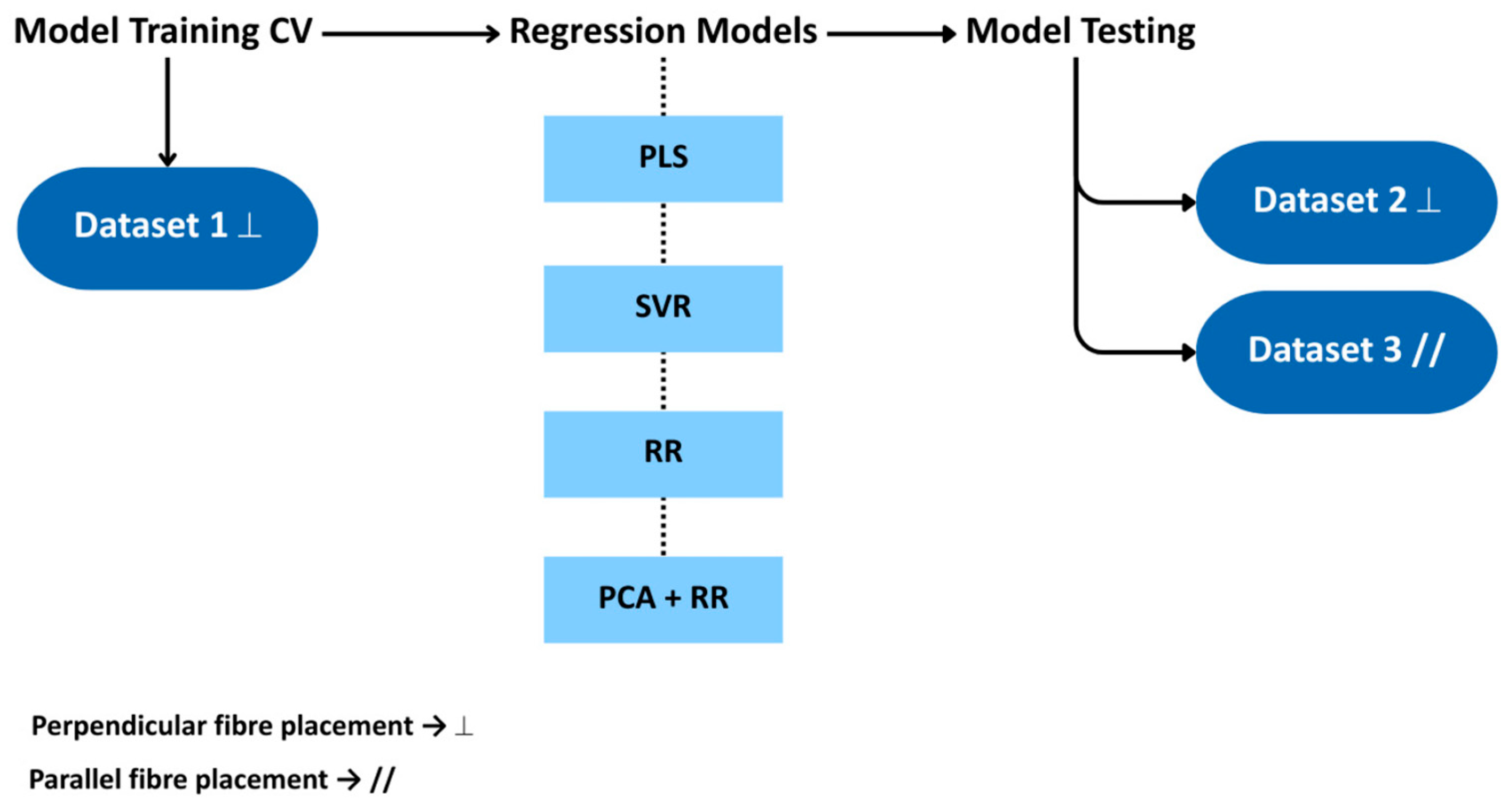
3.2. Regression Models
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lucking, S.E.; Maffei, F.A.; Tamburro, R.F.; Zaritsky, A. (Eds.) Pediatric Critical Care; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Shah, P.J. Perioperative Fluid Management and Blood Transfusion in Newborns and Neonates. In Clinical Anesthesia for the Newborn and the Neonate; Springer: Singapore, 2023; pp. 439–455. [Google Scholar] [CrossRef]
- Méio, M.D.B.B.; Moreira, M.E.L. Total Body Water in Newborns. In Handbook of Anthropometry: Physical Measures of Human Form in Health and Disease; Springer: New York, NY, USA, 2012; pp. 1121–1135. [Google Scholar] [CrossRef]
- Chen, C.; Lee, J.; Johnson, A.E.; Mark, R.G.; Celi, L.A.; Danziger, J. Right Ventricular Function, Peripheral Edema, and Acute Kidney Injury in Critical Illness. Kidney Int. Rep. 2017, 2, 1059–1065. [Google Scholar] [CrossRef]
- Clark, A.L.; Cleland, J.G.F. Causes and treatment of oedema in patients with heart failure. Nat. Rev. Cardiol. 2013, 10, 156–170. [Google Scholar] [CrossRef] [PubMed]
- Barrett, K.E.; Boitano, S.; Barman, S.M.; Brooks, H.L. Ganong’s Review of Medical Physiology, 23rd ed.; McGraw Hill: San Francisco, CA, USA, 1995. [Google Scholar]
- Watson, F.; Austin, P. Physiology of human fluid balance. Anaesth. Intensiv. Care Med. 2024, 25, 576–583. [Google Scholar] [CrossRef]
- Leung, A.K.C.; Robson, W.L.M. Oedema in childhood. Perspect. Public Health 2000, 120, 212–219. [Google Scholar] [CrossRef] [PubMed]
- Wound Essentials 4: Chronic Oedema—The Importance of Skin Care—Wounds UK. Available online: https://wounds-uk.com/wound-essentials/wound-essentials-4-chronic-oedema-the-importance-of-skin-care/ (accessed on 17 October 2024).
- Cartlidge, P.H.T.; Rutter, N. Serum albumin concentrations and oedema in the newborn. Arch. Dis. Child. 1986, 61, 657–660. [Google Scholar] [CrossRef]
- Schwartz, G.J.; Rashid, M. Overview, Structure, and Function of the Nephron. In Pediatric Critical Care; Springer: London, UK, 2021; pp. 863–909. [Google Scholar] [CrossRef]
- Goyal, A.; Singh, B.; Afzal, M. Peripheral Edema. In StatPearls; StatPearls Publishing: Treasure Island, FL, USA, 2025. Available online: https://www.ncbi.nlm.nih.gov/books/NBK554452/ (accessed on 6 August 2025).
- Gordon, L.; Grossmann, K.R.; Guillet, R.; Steflik, H.; Harer, M.W.; Askenazi, D.J.; Menon, S.; Selewski, D.T.; Starr, M.C. Approaches to evaluation of fluid balance and management of fluid overload in neonates among neonatologists: A Neonatal Kidney Collaborative survey. J. Perinatol. 2023, 43, 1314–1315. [Google Scholar] [CrossRef]
- Weaver, L.J.; Travers, C.P.; Ambalavanan, N.; Askenazi, D. Neonatal fluid overload—Ignorance is no longer bliss. Pediatr. Nephrol. 2023, 38, 47. [Google Scholar] [CrossRef]
- Sanderson, J.; Tuttle, N.; Box, R.; Reul-Hirche, H.M.; Laakso, E.L. The Pitting Test: An Investigation of an Unstandardized Assessment of Lymphedema. Lymphology 2015, 48, 175–183. [Google Scholar]
- Sanderson, J.; Tuttle, N.; Box, R.; Reul-Hirche, H.; Laakso, E.-L. Pitting Is Not Only a Measure of Oedema Presence: Using High-Frequency Ultrasound to Guide Pitting Test Standardisation for Assessment of Lymphoedema. Diagnostics 2024, 14, 1645. [Google Scholar] [CrossRef]
- Creber, R.M.; Chen, J.; Mao, T.; Qiu, Y.; Zhou, D.; Kostic, Z. Camera-based peripheral edema measurement using machine learning. In Proceedings of the 2018 IEEE International Conference on Healthcare Informatics (ICHI), New York, NY, USA, 4–7 June 2018; pp. 115–122. [Google Scholar] [CrossRef]
- Sanderson, J.K. A Detailed Investigation into the Pitting Test: Using High-Frequency Ultrasound to Evaluate the Effect of Applying Sustained Thumb Pressure to Lymphoedema Tissue. Ph.D. Thesis, School of Health Sciences and Social Work, Griffith University, Gold Coast, QL, Australia, 2023. [Google Scholar] [CrossRef]
- Welsh, J.R.; Arzouman, J.M.R.; Holm, K. Nurses’ Assessment and Documentation of Peripheral Edema. Clin. Nurse Spec. 1996, 10, 7–10. [Google Scholar] [CrossRef]
- Kushner, R.F.; Schoeller, D.A. Estimation of total body water by bioelectrical impedance analysis. Am. J. Clin. Nutr. 1986, 44, 417–424. [Google Scholar] [CrossRef] [PubMed]
- Ruste, M.; Chabanol, C.; Fellahi, J.L.; Jacquet-Lagrèze, M. Bioelectrical impedance analysis during deresuscitation: Correlation and agreement with cumulative fluid balance in ICU patients. J. Clin. Monit. Comput. 2023, 37, 679–687. [Google Scholar] [CrossRef] [PubMed]
- Van Loan, M.D. Bioelectrical Impedance Analysis to Determine Fat-Free Mass, Total Body Water and Body Fat. Sports Med. 1990, 10, 205–217. [Google Scholar] [CrossRef] [PubMed]
- Kotler, D.P.; Burastero, S.; Wang, J.; Pierson, R.N. Prediction of body cell mass, fat-free mass, and total body water with bioelectrical impedance analysis: Effects of race, sex, and disease. Am. J. Clin. Nutr. 1996, 64, 489S–497S. [Google Scholar] [CrossRef]
- Jaffrin, M.Y.; Morel, H. Body fluid volumes measurements by impedance: A review of bioimpedance spectroscopy (BIS) and bioimpedance analysis (BIA) methods. Med. Eng. Phys. 2008, 30, 1257–1269. [Google Scholar] [CrossRef]
- Madsen, J.M.; Wichmann, S.; Bestle, M.H.; Itenov, T.S. Bioimpedance as a measure of fluid status in critically ill patients: A systematic review. Acta Anaesthesiol. Scand. 2021, 65, 1155–1167. [Google Scholar] [CrossRef]
- Madsen, J.M.; Itenov, T.S.; Koch, E.B.; Bestle, M.H. Bioimpedance as a measure of fluids in patients with septic shock. A prospective observational study. Acta Anaesthesiol. Scand. 2023, 67, 319–328. [Google Scholar] [CrossRef]
- Topchyan, A.; Tatarinov, A.; Sarvazyan, N.; Sarvazyan, A. Ultrasound velocity in human muscle in vivo: Perspective for edema studies. Ultrasonics 2006, 44, 259–264. [Google Scholar] [CrossRef]
- Srinivasan, S.; Cornell, T.T. Bedside ultrasound in pediatric critical care: A review. Pediatr. Crit. Care Med. 2011, 12, 667–674. [Google Scholar] [CrossRef]
- Allinovi, M.; Saleem, M.; Romagnani, P.; Nazerian, P.; Hayes, W. Lung ultrasound: A novel technique for detecting fluid overload in children on dialysis. Nephrol. Dial. Transplant. 2017, 32, 541–547. [Google Scholar] [CrossRef]
- Budylin, G.S.; Davydov, D.A.; Zlobina, N.V.; Baev, A.V.; Artyushenko, V.G.; Yakimov, B.P.; Shirshin, E.A. In vivo sensing of cutaneous edema: A comparative study of diffuse reflectance, Raman spectroscopy and multispectral imaging. J. Biophotonics 2022, 15, e202100268. [Google Scholar] [CrossRef]
- Davydov, D.A.; Budylin, G.S.; Baev, A.V.; Vaypan, D.V.; Seredenina, E.M.; Matskeplishvili, S.T.; Evlashin, S.A.; Kamalov, A.A.; Shirshin, E.A. Monitoring the skin structure during edema in vivo with spatially resolved diffuse reflectance spectroscopy. J. Biomed. Opt. 2023, 28, 57002–57003. [Google Scholar] [CrossRef]
- Stamatas, G.N.; Southall, M.; Kollias, N. In Vivo Monitoring of Cutaneous Edema using Spectral Imaging in the Visible and Near Infrared. J. Investig. Dermatol. 2006, 126, 1753–1760. [Google Scholar] [CrossRef]
- Heymsfield, S.; Bell, J.D.; Heber, D. Phenotyping, Body Composition, and Precision Nutrition. In Precision Nutrition: The Science and Promise of Personalized Nutrition and Health; Academic Press: New York, NY, USA, 2024; pp. 143–152. [Google Scholar] [CrossRef]
- Laskey, M.A. Dual-energy X-ray absorptiometry and body composition. Nutrition 1996, 12, 45–51. [Google Scholar] [CrossRef] [PubMed]
- Krakauer, N.Y.; Krakauer, J.C. Association of X-ray Absorptiometry Body Composition Measurements with Basic Anthropometrics and Mortality Hazard. Int. J. Environ. Res. Public Health 2021, 18, 7927. [Google Scholar] [CrossRef] [PubMed]
- Bosy-Westphal, A.; Danielzik, S.; Becker, C.; Geisler, C.; Onur, S.; Korth, O.; Buhrens, F.; Muller, M.J. Need for Optimal Body Composition Data Analysis Using Air-Displacement Plethysmography in Children and Adolescents. J. Nutr. 2005, 135, 2257–2262. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.; Ridout, D.; Modi, N. Assessment of total body water using bioelectrical impedance analysis in neonates receiving intensive care. Arch. Dis. Child. Fetal Neonatal Ed. 1997, 77, F123. [Google Scholar] [CrossRef]
- Ferreira, D.M.; Souza, M.N. Bioelectrical impedance spectroscopy for the assessment of body fluid volumes of term neonates. Braz. J. Med. Biol. Res. 2004, 37, 1595–1606. [Google Scholar] [CrossRef]
- Klaus, S.; Eichler, W.; Heringlake, M.; Schmucker, P.; Bahlmann, L. Assessment of fluid balance by measurement of skin tissue thickness during clinical anaesthesia. Clin. Physiol. Funct. Imaging 2002, 22, 197–201. [Google Scholar] [CrossRef]
- Farr, B.J.; Bechard, L.J.; Rice-Townsend, S.E.; Mehta, N.M. Bio-impedance spectroscopy for total body water assessment in pediatric surgical patients: A single center pilot cohort study. J. Pediatr. Surg. 2022, 57, 962–966. [Google Scholar] [CrossRef]
- Lingwood, B.E. Bioelectrical impedance analysis for assessment of fluid status and body composition in neonates—The good, the bad and the unknown. Eur. J. Clin. Nutr. 2013, 67, S28–S33. [Google Scholar] [CrossRef]
- Mamouei, M.; Chatterjee, S.; Razban, M.; Qassem, M.; Kyriacou, P.A. Design and Analysis of a Continuous and Non-Invasive Multi-Wavelength Optical Sensor for Measurement of Dermal Water Content. Sensors 2021, 21, 2162. [Google Scholar] [CrossRef]
- Bashkatov, A.N.; Genina, E.A.; Kochubey, V.I.; Tuchin, V.V. Optical properties of human skin, subcutaneous and mucous tissues in the wavelength range from 400 to 2000 nm. J. Phys. D Appl. Phys. 2005, 38, 2543. [Google Scholar] [CrossRef]
- Qassem, M.; Kyriacou, P.A. Comparing the rates of absorption and weight loss during a desorption test using near infrared spectroscopy. Ski. Res. Technol. 2013, 19, 137–144. [Google Scholar] [CrossRef]
- Gidado, I.; Al-Halawani, R.; Qassem, M.; Kyriacou, P. Development and Analysis of a Multi-Wavelength Near-Infrared Sensor for Monitoring Skin Hydration and Validation Using Monte Carlo Simulation. Photonic Sens. 2024, 14, 240306. [Google Scholar] [CrossRef]
- Brunetti, G.; Patton, D.; Moore, Z.; Palomeque-Chavez, J.C.; O’Brien, F.J.; Boyle, C.J. Validation of a sub-epidermal moisture scanner for early detection of pressure ulcers in an ex vivo porcine model of localized oedema. J. Tissue Viability 2023, 32, 508–515. [Google Scholar] [CrossRef] [PubMed]
- Plevris, V.; Solorzano, G.; Bakas, N.P.; Seghier, M.E.A.B. Investigation of performance metrics in regression analysis and machine learning-based prediction models. In Proceedings of the ECCOMAS Congress 2022—8th European Congress on Computational Methods in Applied Sciences and Engineering, Oslo, Norway, 5–9 June 2022. [Google Scholar] [CrossRef]
- Jensen, H. Bridging the Gap: Analyzing Ridge Regression vs. PLS Regression. Top Acad. J. Eng. Math. 2021, 6, 1–23. [Google Scholar]
- Tange, R.I.; Rasmussen, M.A.; Taira, E.; Bro, R. Benchmarking support vector regression against partial least squares regression and artificial neural network: Effect of sample size on model performance. J. Near Infrared Spectrosc. 2017, 25, 381–390. [Google Scholar] [CrossRef]
- Ezenarro, J.; Schorn-García, D. How Are Chemometric Models Validated? A Systematic Review of Linear Regression Models for NIRS Data in Food Analysis. J. Chemom. 2025, 39, e70036. [Google Scholar] [CrossRef]
- Zhang, W.; Kasun, L.C.; Wang, Q.J.; Zheng, Y.; Lin, Z. A Review of Machine Learning for Near-Infrared Spectroscopy. Sensors 2022, 22, 9764. [Google Scholar] [CrossRef]
- Liu, B.; Wang, J.; Li, C. Application of PLS–NN model based on mid-infrared spectroscopy in the origin identification of Cornus officinalis. RSC Adv. 2024, 14, 15209–15219. [Google Scholar] [CrossRef]


| Model | Parameters for Optimisation |
|---|---|
| PLS | ‘LV’: range from 1 to 20. |
| SVR | ‘kernel’: [‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’], ‘gamma’: [‘scale’, ‘auto’, 0.01, 0.1, 1], ‘C’: [0.1, 1] |
| RR | ‘alpha’: [1, 10, 100], ‘solver’: [‘svd’, ‘cholesky’, ‘lsqr’, ‘sparse_cg’, ‘sag’, ‘saga’] |
| Groups | Range | Split 1 | Split 2 | Split 3 | Split 4 |
|---|---|---|---|---|---|
| 0 | 0 ml | ||||
| 1 | 0 mL to 0.5 mL | ||||
| 2 | 0.5 mL to 1 mL | ||||
| 3 | 1 mL to 1.5 mL | ||||
| 4 | 1.5 mL to 2 mL | ||||
| 5 | 2 mL to 2.5 mL | ||||
| 6 | 2.5 mL to 3 mL |
| CV Results (Mean ± sd) | Testing Results | |||||||
|---|---|---|---|---|---|---|---|---|
| Model | Splits | Optimal Parameters | R2 | MSE | R2 | MSE | RMSE | MAE |
| PLS | 1 | 5 LV | 0.9851 ± 0.0015 | 0.0164 ± 0.0015 | 0.9503 | 0.0135 | 0.1160 | 0.0986 |
| 2 | 5 LV | 0.9857 ± 0.0027 | 0.0166 ± 0.0030 | 0.8929 | 0.0290 | 0.1703 | 0.1341 | |
| 3 | 5 LV | 0.9858 ± 0.0024 | 0.0091 ± 0.0019 | 0.8937 | 0.0514 | 0.2268 | 0.1971 | |
| 4 | 6 LV | 0.9861 ± 0.0024 | 0.0072 ± 0.0013 | 0.9551 | 0.0803 | 0.2834 | 0.2601 | |
| SVR | 1 | C: 1, gamma: 0.1, kernel: ‘poly’ | 0.9907 ± 0.0016 | 0.0102 ± 0.0019 | 0.9334 | 0.0180 | 0.1343 | 0.1103 |
| 2 | C: 1, gamma: 0.1, kernel: ‘poly’ | 0.9914 ± 0.0022 | 0.0101 ± 0.0027 | 0.9160 | 0.0227 | 0.1508 | 0.1321 | |
| 3 | C: 1, gamma: 0.1, kernel: ‘poly’ | 0.9869 ± 0.0027 | 0.0084 ± 0.0018 | 0.7891 | 0.0615 | 0.2480 | 0.1933 | |
| 4 | C: 1, gamma: 0.1, kernel: ‘poly’ | 0.9819 ± 0.0050 | 0.0095 ± 0.0029 | 0.9512 | 0.0871 | 0.2952 | 0.2373 | |
| RR | 1 | alpha’: 1, ‘solver’: ‘cholesky’ | 0.8564 ± 0.0061 | 0.1587 ± 0.0098 | 0.2604 | 0.2003 | 0.4475 | 0.3805 |
| 2 | alpha’: 1, ‘solver’: ‘sag’ | 0.8292 ± 0.0223 | 0.1995 ± 0.0297 | 0.5928 | 0.1103 | 0.3321 | 0.2709 | |
| 3 | alpha’: 1, ‘solver’: ‘cholesky’ | 0.7082 ± 0.0278 | 0.1858 ± 0.0171 | 0.3748 | 0.1824 | 0.4271 | 0.3422 | |
| 4 | alpha’: 1, ‘solver’: ‘sag’ | 0.7795 ± 0.0339 | 0.1150 ± 0.0216 | 0.6767 | 0.5778 | 0.7601 | 0.6792 | |
| PCA + RR | 1 | alpha’: 1, ‘solver’: ‘svd’ | 0.9891 ± 0.0008 | 0.0120 ± 0.0010 | 0.9292 | 0.0192 | 0.1384 | 0.1195 |
| 2 | alpha’: 1, ‘solver’: ‘svd’ | 0.9913 ± 0.0008 | 0.0101 ± 0.0010 | 0.9026 | 0.0264 | 0.1624 | 0.1420 | |
| 3 | alpha’: 1, ‘solver’: ‘cholesky’ | 0.9828 ± 0.0027 | 0.0110 ± 0.0021 | 0.8245 | 0.0512 | 0.2263 | 0.1925 | |
| 4 | alpha’: 1, ‘solver’: ‘svd’ | 0.9824 ± 0.0032 | 0.0092 ± 0.0019 | 0.9608 | 0.0701 | 0.2648 | 0.2405 | |
| CV Results (Mean ± sd) | Testing Results | |||||||
|---|---|---|---|---|---|---|---|---|
| Model | Splits | Optimal Parameters | R2 | MSE | R2 | MSE | RMSE | MAE |
| PLS | 1 | 5 LV | 0.9971 ± 0.0005 | 0.0030 ± 0.0005 | 0.9780 | 0.0060 | 0.0772 | 0.0648 |
| 2 | 5 LV | 0.9974 ± 0.0003 | 0.0029 ± 0.0003 | 0.9693 | 0.0083 | 0.0912 | 0.0739 | |
| 3 | 5 LV | 0.9964 ± 0.0004 | 0.0023 ± 0.0002 | 0.9402 | 0.0162 | 0.1272 | 0.0965 | |
| 4 | 5 LV | 0.9960 ± 0.0002 | 0.0021 ± 0.0002 | 0.9913 | 0.0157 | 0.1253 | 0.1013 | |
| SVR | 1 | C: 1, gamma: ‘scale’, kernel: ‘poly’ | 0.9963 ± 0.0005 | 0.0038 ± 0.0005 | 0.9707 | 0.0079 | 0.0891 | 0.0733 |
| 2 | C: 1, gamma: ‘scale’, kernel: ‘poly’ | 0.9966 ± 0.0005 | 0.0038 ± 0.0005 | 0.9665 | 0.0091 | 0.0953 | 0.0772 | |
| 3 | C: 1, gamma: ‘scale’, kernel: ‘poly’ | 0.9949 ± 0.0008 | 0.0032 ± 0.0004 | 0.9162 | 0.0227 | 0.1505 | 0.1150 | |
| 4 | C: 1, gamma: ‘scale’, kernel: ‘poly’ | 0.9940 ± 0.0002 | 0.0031 ± 0.0001 | 0.9841 | 0.0287 | 0.1693 | 0.1369 | |
| RR | 1 | alpha’: 1, ‘solver’: ‘saga’ | 0.9741 ± 0.0017 | 0.0267 ± 0.0012 | 0.9202 | 0.0216 | 0.1471 | 0.1279 |
| 2 | alpha’: 1, ‘solver’: ‘lsqr’ | 0.9865 ± 0.0022 | 0.0151 ± 0.0021 | 0.7518 | 0.0672 | 0.2592 | 0.1951 | |
| 3 | alpha’: 1, ‘solver’: ‘saga’ | 0.9540 ± 0.0032 | 0.0293 ± 0.0006 | 0.9041 | 0.0259 | 0.1610 | 0.1140 | |
| 4 | alpha’: 1, ‘solver’: ‘sag’ | 0.9591 ± 0.0026 | 0.0213 ± 0.0016 | 0.9631 | 0.0664 | 0.2577 | 0.2449 | |
| PCA + RR | 1 | alpha’: 1, ‘solver’: ‘cholesky’ | 0.9951 ± 0.0011 | 0.0050 ± 0.0012 | 0.9678 | 0.0087 | 0.0934 | 0.0784 |
| 2 | alpha’: 1, ‘solver’: ‘svd’ | 0.9953 ± 0.0010 | 0.0053 ± 0.0011 | 0.9685 | 0.0085 | 0.0924 | 0.0751 | |
| 3 | alpha’: 1, ‘solver’: ‘svd’ | 0.9937 ± 0.0012 | 0.0040 ± 0.0007 | 0.8940 | 0.0287 | 0.1693 | 0.1340 | |
| 4 | alpha’: 1, ‘solver’: ‘svd’ | 0.9930 ± 0.0004 | 0.0037 ± 0.0001 | 0.9828 | 0.0310 | 0.1761 | 0.1433 | |
| CV Results (Mean ± sd) | Testing Results | |||||||
|---|---|---|---|---|---|---|---|---|
| Model | Optimal Parameters | R2 | MSE | Dataset Used for Testing | R2 | MSE | RMSE | MAE |
| PLS | 5 LV | 0.9800 ± 0.0044 | 0.0182 ± 0.0041 | Perpendicular | 0.9273 | 0.0635 | 0.2520 | 0.2084 |
| Parallel | 0.9742 | 0.0225 | 0.1499 | 0.1217 | ||||
| SVR | C: 1, gamma: 0.1, kernel: ‘linear’ | 0.9915 ± 0.0010 | 0.0077 ± 0.0011 | Perpendicular | 0.9156 | 0.0737 | 0.2714 | 0.2194 |
| Parallel | 0.9565 | 0.0379 | 0.1946 | 0.1590 | ||||
| RR | alpha’: 1, ‘solver’: ‘svd’ | 0.9904 ± 0.0013 | 0.0087 ± 0.0014 | Perpendicular | 0.9192 | 0.0706 | 0.2657 | 0.2156 |
| Parallel | 0.9645 | 0.0309 | 0.1758 | 0.1437 | ||||
| RR + PCA | alpha’: 1, ‘solver’: ‘svd’ | 0.9871 ± 0.0020 | 0.0118 ± 0.0021 | Perpendicular | 0.8892 | 0.0967 | 0.3110 | 0.2170 |
| Parallel | −2.8180 | 3.3211 | 1.8224 | 1.6103 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castro-Montano, M.; Qassem, M.; Kyriacou, P.A. Near-Infrared Spectroscopy for Oedema Quantification: An Ex Vivo Porcine Skin Model. Sensors 2025, 25, 6971. https://doi.org/10.3390/s25226971
Castro-Montano M, Qassem M, Kyriacou PA. Near-Infrared Spectroscopy for Oedema Quantification: An Ex Vivo Porcine Skin Model. Sensors. 2025; 25(22):6971. https://doi.org/10.3390/s25226971
Chicago/Turabian StyleCastro-Montano, Mariana, Meha Qassem, and Panayiotis A. Kyriacou. 2025. "Near-Infrared Spectroscopy for Oedema Quantification: An Ex Vivo Porcine Skin Model" Sensors 25, no. 22: 6971. https://doi.org/10.3390/s25226971
APA StyleCastro-Montano, M., Qassem, M., & Kyriacou, P. A. (2025). Near-Infrared Spectroscopy for Oedema Quantification: An Ex Vivo Porcine Skin Model. Sensors, 25(22), 6971. https://doi.org/10.3390/s25226971






