Improving EFDD with Neural Networks in Damping Identification for Structural Health Monitoring
Abstract
1. Introduction
- Excitation conditions differ across studies. The physical relation between the damping coefficient and damage remains insufficiently clear owing to the complexity of damping mechanisms. In practice, viscous damping, hysteretic damping, and frictional damping may act simultaneously. When identification is performed under the assumption of viscous damping, the resulting estimates can be interpreted as equivalent viscous damping, which indicates the energy dissipation rate during vibration. Different types of damage may lead to contrasting trends in damping variation, and the mechanisms involved under forced vibration are generally more complex than those under free decay.
- Measurement noise exerts a significant influence. When damping values are small, the immaturity of estimation techniques and operational errors can strongly affect the accuracy of damage detection. Achieving reliable damping identification under forced vibration conditions remains a pressing problem to be addressed [24,25].
2. Bias of EFDD and Neural Network Integration
- The selection of Welch parameters for power spectral density estimation, which introduces a trade-off between variance and leakage.
- The choice of frequency bands for modal isolation may result in either mode contamination or information loss.
- The truncation and regression of the log-envelope, which are highly sensitive to noise and gating heuristics.
2.1. Welch Parameters
2.2. Band Selection
2.3. Time Gating and Robust Regression
3. NN-Embedding Framework
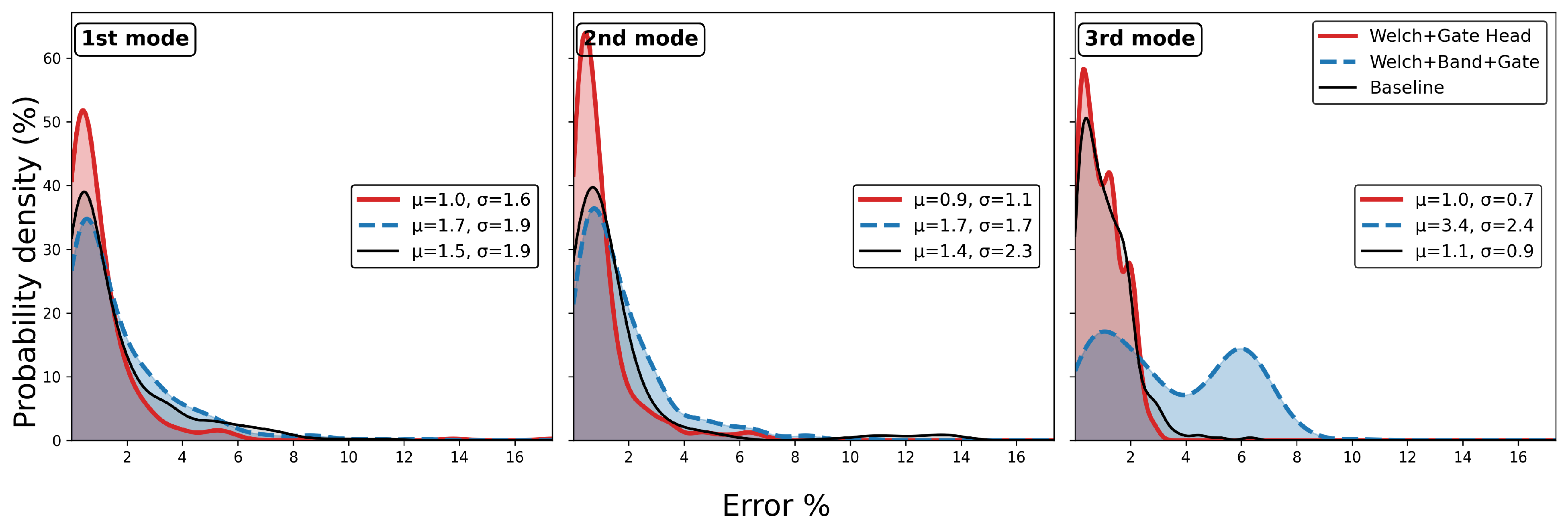
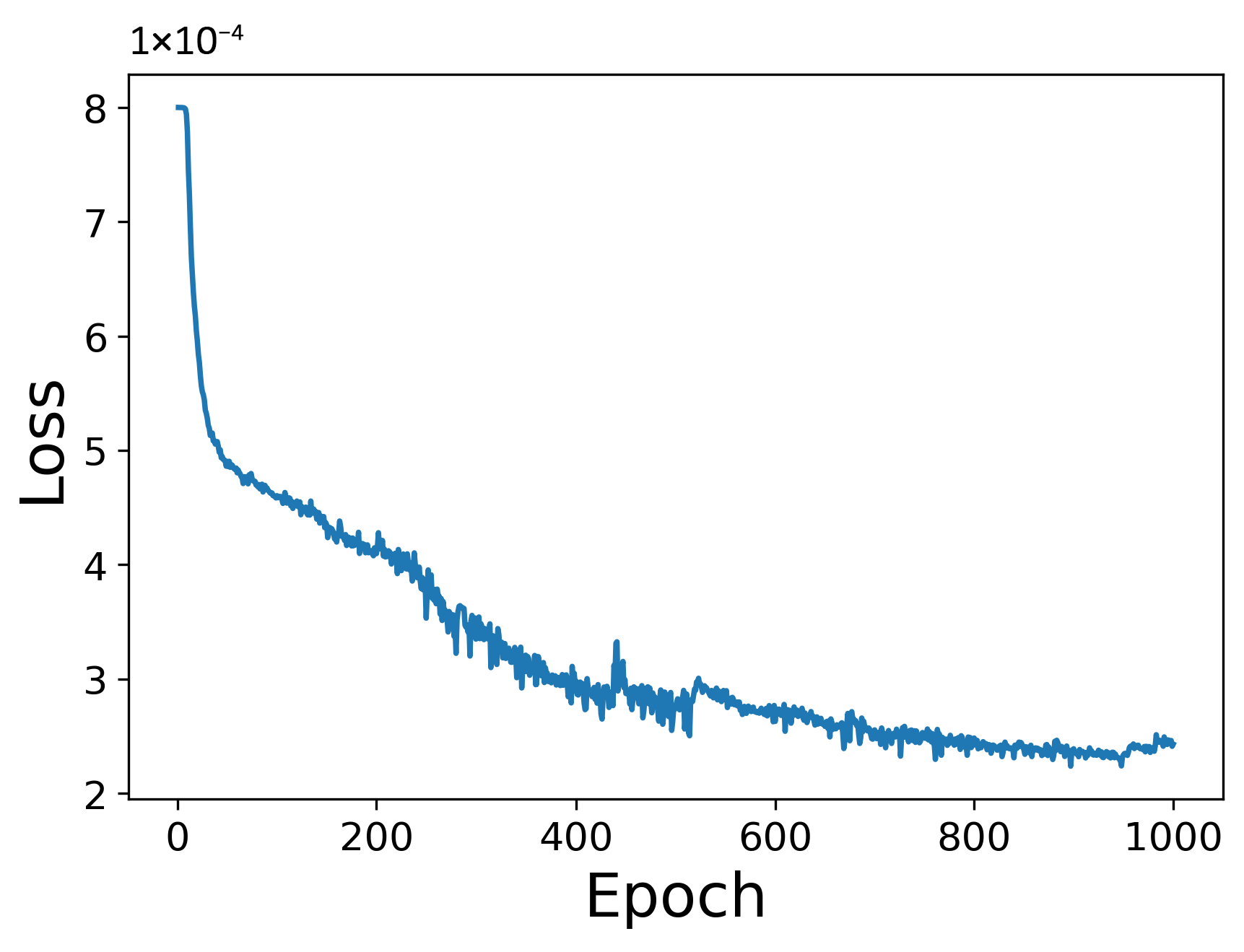
4. Numerical Verification
4.1. Step-Wise
4.2. Grid-Weight
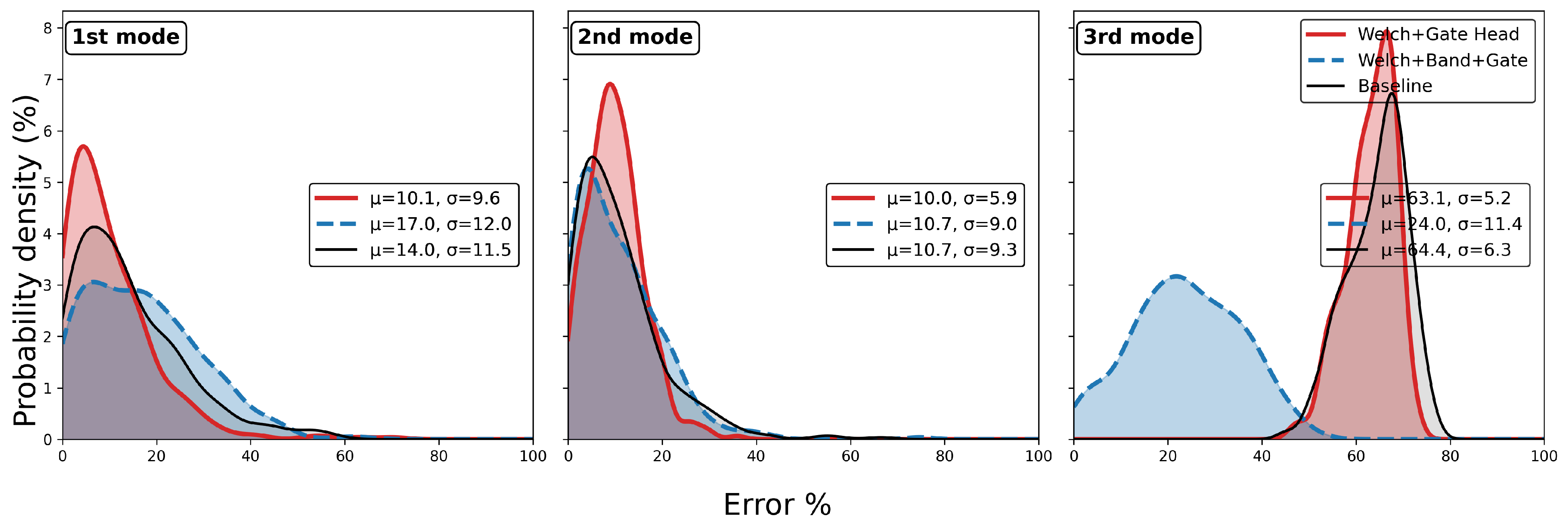
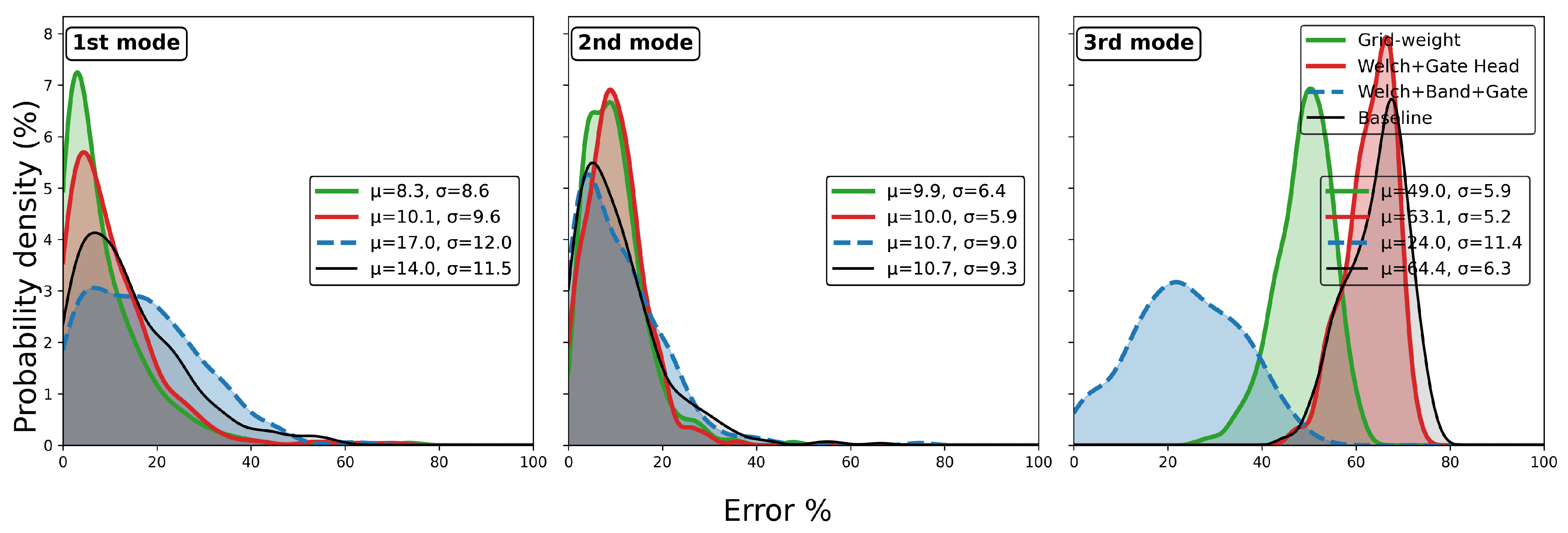
5. Experiments Application
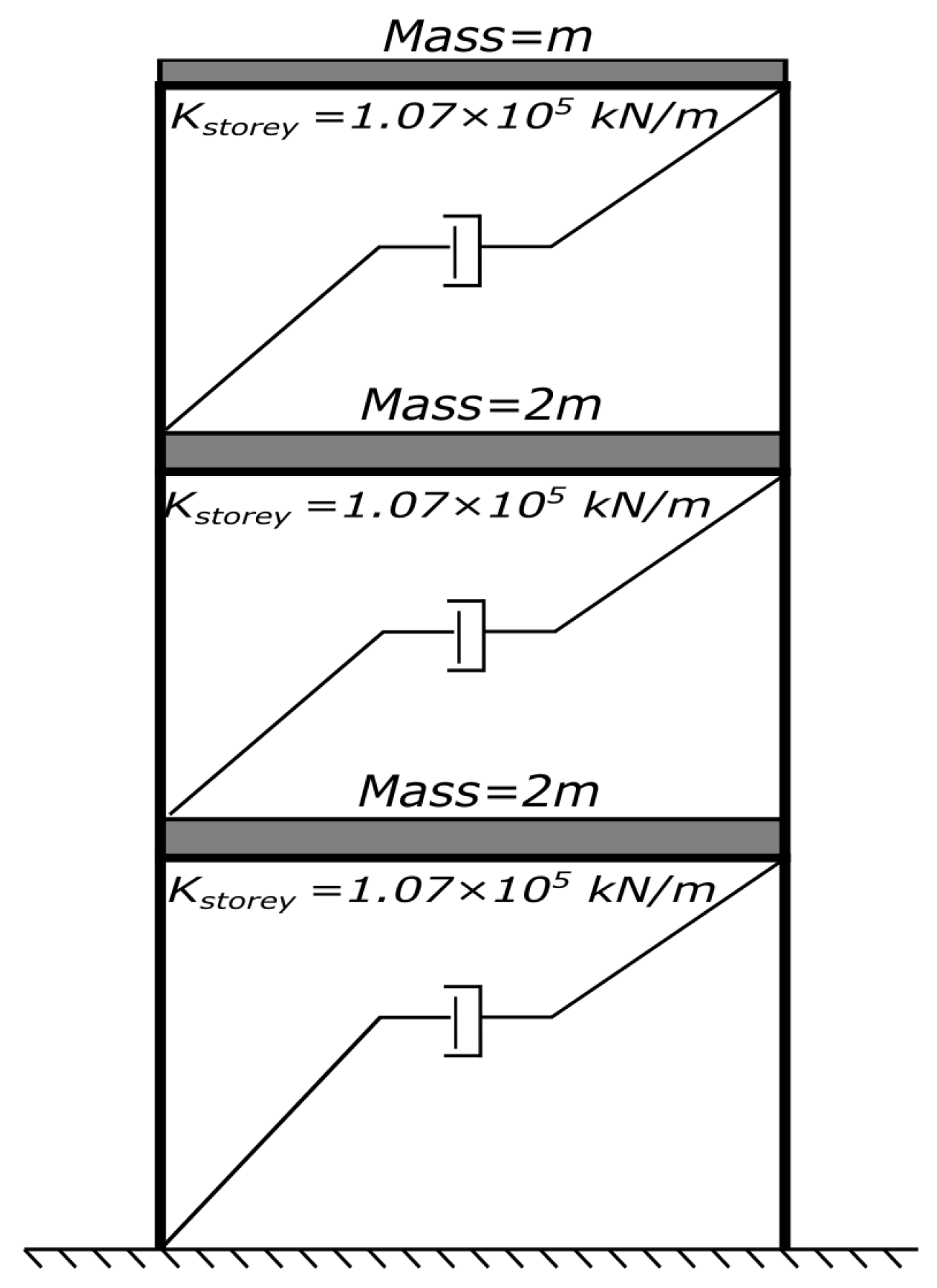
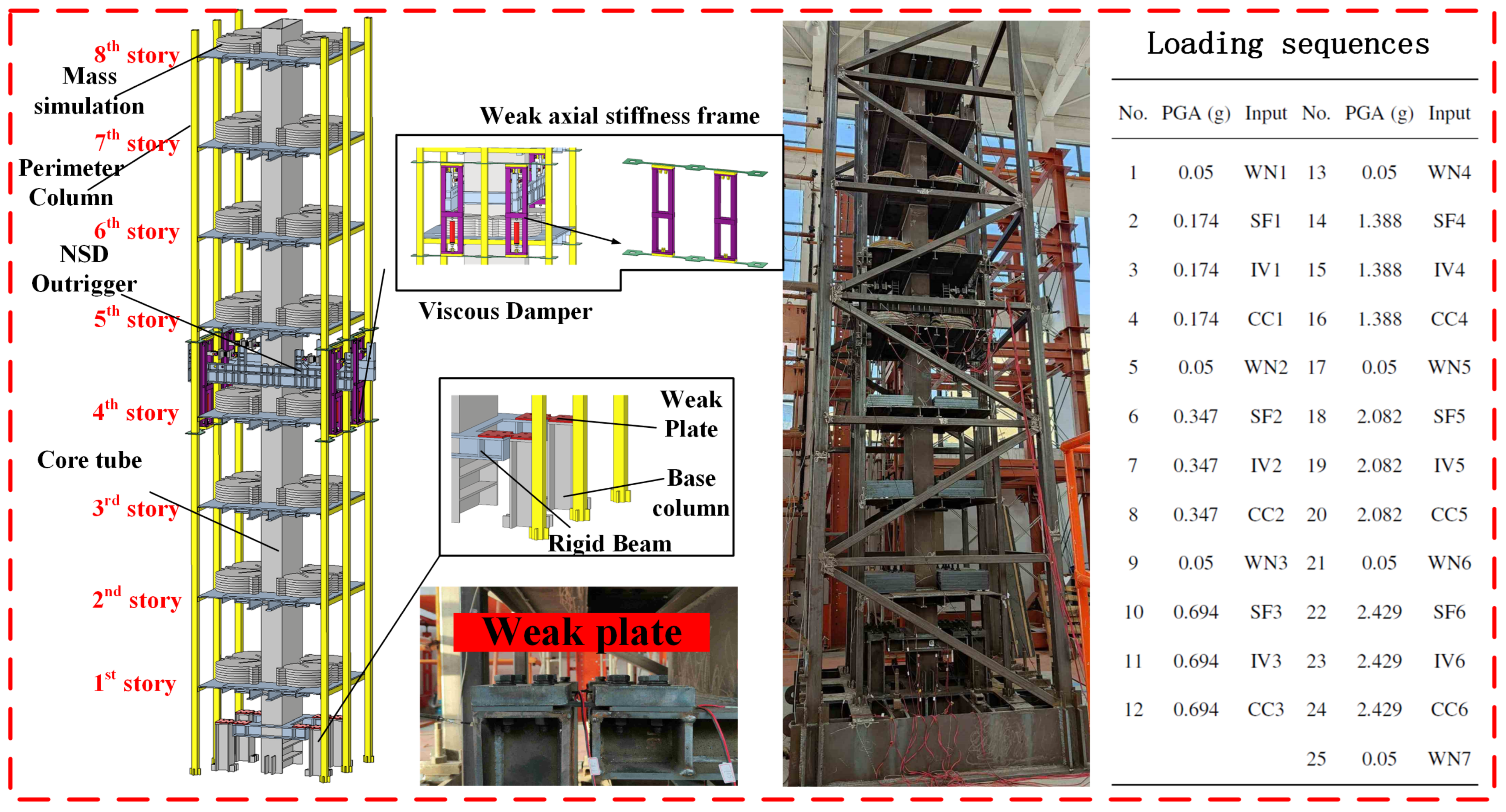
5.1. Eight-Storey Steel Structure
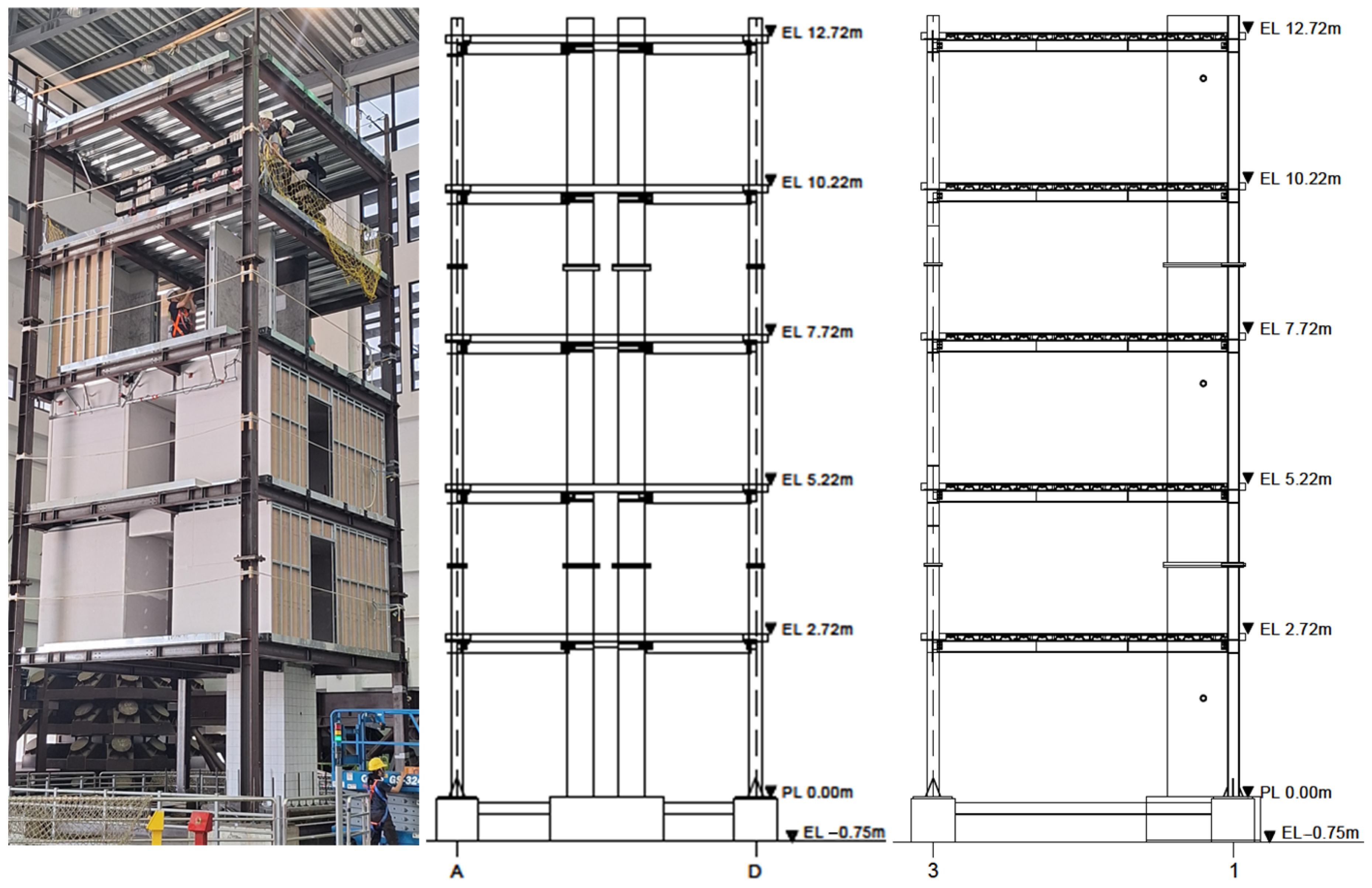
5.2. Five-Storey Steel–Concrete Hybrid Structure
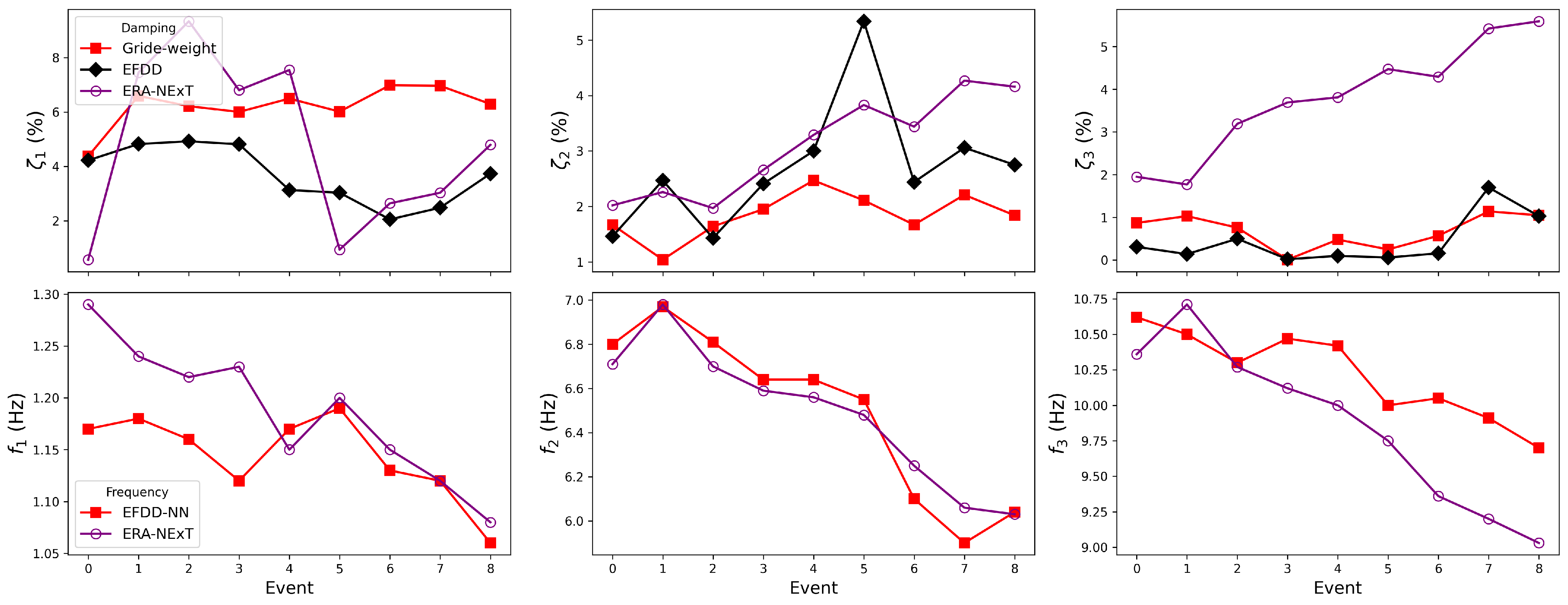
5.3. Discussion of Damage Detection
5.4. Practical Implications for Simulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Method | Mode | WN1 | WN2 | WN3 | WN4 | WN5 | WN6 | WN7 |
|---|---|---|---|---|---|---|---|---|
| Grid-weight | 1 | 1.18 | 1.12 | 1.14 | 1.24 | 1.51 | 1.41 | 1.38 |
| 2 | 0.81 | 0.81 | 0.81 | 0.80 | 0.70 | 0.67 | 0.66 | |
| 3 | 0.97 | 1.10 | 1.22 | 1.40 | 1.22 | 1.23 | 1.26 | |
| Step-wise | 1 | 1.19 | 1.13 | 1.13 | 1.24 | 1.49 | 1.41 | 1.39 |
| 2 | 0.76 | 0.76 | 0.75 | 0.80 | 0.67 | 0.65 | 0.64 | |
| 3 | 0.87 | 1.04 | 1.26 | 1.40 | 1.27 | 1.17 | 1.18 | |
| EFDD | 1 | 1.15 | 1.09 | 1.08 | 1.20 | 1.45 | 1.37 | 1.34 |
| 2 | 0.70 | 0.70 | 0.67 | 0.71 | 0.63 | 0.61 | 0.60 | |
| 3 | 0.59 | 0.88 | 0.84 | 0.95 | 0.79 | 0.73 | 0.69 | |
| ERA-NExT | 1 | 1.21 | 1.14 | 1.12 | 1.16 | 1.45 | 1.44 | 1.43 |
| 2 | 1.02 | 1.05 | 1.05 | 1.09 | 1.07 | 1.04 | 1.02 | |
| 3 | 1.12 | 1.26 | 1.34 | 1.40 | 1.42 | 1.37 | 1.33 |
| Method | Mode | WN1 | WN2 | WN3 | WN4 | WN5 | WN6 | WN7 |
|---|---|---|---|---|---|---|---|---|
| EFDD-NN | 1 | 3.29 | 3.28 | 3.28 | 3.28 | 3.22 | 3.19 | 3.18 |
| 2 | 13.41 | 13.40 | 13.39 | 13.36 | 13.21 | 13.16 | 13.14 | |
| 3 | 31.33 | 31.33 | 31.33 | 31.22 | 30.95 | 30.85 | 30.85 | |
| ERA-NExT | 1 | 3.29 | 3.29 | 3.28 | 3.27 | 3.22 | 3.19 | 3.19 |
| 2 | 13.41 | 13.40 | 13.39 | 13.36 | 13.19 | 13.15 | 13.12 | |
| 3 | 31.33 | 31.30 | 31.25 | 31.12 | 30.80 | 30.70 | 30.66 |
| Direction | Method | Mode | Events | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| X (NS) | Grid-weight | 1 | 2.29 | 2.66 | 2.98 | 2.79 | 3.07 | 4.98 | 4.55 | 4.77 | 4.93 |
| 2 | 2.01 | 2.06 | 2.32 | 1.99 | 1.93 | 2.26 | 1.91 | 2.71 | 1.41 | ||
| 3 | 1.34 | 1.37 | 0.97 | 1.35 | 1.30 | 1.40 | 1.35 | 0.03 | 0.06 | ||
| EFDD | 1 | 4.19 | 1.49 | 6.43 | 5.42 | 2.25 | 3.24 | 8.49 | 4.07 | 3.74 | |
| 2 | 1.26 | 0.81 | 2.96 | 3.00 | 4.00 | 3.70 | 4.08 | 4.49 | 5.50 | ||
| 3 | 0.73 | 0.31 | 2.17 | 1.97 | 2.35 | 0.26 | 1.98 | 2.63 | 2.60 | ||
| ERA-NExT | 1 | 6.67 | 1.86 | 7.98 | 4.05 | 8.15 | 4.43 | 4.42 | 4.98 | 1.91 | |
| 2 | 3.08 | 3.86 | 3.32 | 2.96 | 3.84 | 4.03 | 2.97 | 3.87 | 3.42 | ||
| 3 | 1.69 | 1.36 | 1.69 | 2.15 | 1.74 | 2.57 | 2.56 | 2.16 | 4.00 | ||
| Y (EW) | Grid-weight | 1 | 4.37 | 6.59 | 6.21 | 6.00 | 6.49 | 6.01 | 6.98 | 6.96 | 6.29 |
| 2 | 1.67 | 1.04 | 1.64 | 1.95 | 2.47 | 2.11 | 1.67 | 2.21 | 1.84 | ||
| 3 | 0.87 | 1.03 | 0.76 | 0.01 | 0.48 | 0.25 | 0.57 | 1.14 | 1.05 | ||
| EFDD | 1 | 4.22 | 4.82 | 4.92 | 4.81 | 3.13 | 3.03 | 2.05 | 2.48 | 3.73 | |
| 2 | 1.46 | 2.47 | 1.43 | 2.41 | 3.00 | 5.34 | 2.44 | 3.06 | 2.75 | ||
| 3 | 0.31 | 0.14 | 0.50 | 0.02 | 0.10 | 0.06 | 0.16 | 1.70 | 1.03 | ||
| ERA-NExT | 1 | 0.57 | 7.45 | 9.33 | 6.80 | 7.54 | 0.94 | 2.64 | 3.03 | 4.79 | |
| 2 | 2.02 | 2.26 | 1.97 | 2.66 | 3.29 | 3.83 | 3.44 | 4.27 | 4.16 | ||
| 3 | 1.95 | 1.77 | 3.19 | 3.69 | 3.81 | 4.47 | 4.29 | 5.42 | 5.59 | ||
| Direction | Method | Mode | Events | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| X (NS) | EFDD-NN | 1 | 2.08 | 2.02 | 1.89 | 1.92 | 1.89 | 1.20 | 1.15 | 1.09 | 1.05 |
| 2 | 11.88 | 11.61 | 11.67 | 11.68 | 11.62 | 11.47 | 10.34 | 10.09 | 9.87 | ||
| 3 | 30.84 | 30.92 | 30.18 | 28.62 | 28.91 | 28.54 | 27.58 | 26.67 | 26.91 | ||
| ERA-NExT | 1 | 2.04 | 1.99 | 1.86 | 1.88 | 1.79 | 1.18 | 1.16 | 1.17 | 1.18 | |
| 2 | 11.67 | 11.87 | 11.63 | 11.56 | 11.64 | 11.32 | 11.50 | 10.01 | 10.06 | ||
| 3 | 31.05 | 30.67 | 29.22 | 29.20 | 28.69 | 28.82 | 27.61 | 26.55 | 26.40 | ||
| Y (EW) | EFDD-NN | 1 | 1.17 | 1.18 | 1.16 | 1.12 | 1.17 | 1.17 | 1.19 | 1.13 | 1.06 |
| 2 | 6.80 | 6.97 | 6.81 | 6.64 | 6.64 | 6.64 | 6.55 | 6.10 | 6.04 | ||
| 3 | 10.62 | 10.50 | 10.30 | 10.47 | 10.42 | 10.00 | 10.05 | 9.91 | 9.70 | ||
| ERA-NExT | 1 | 1.29 | 1.24 | 1.22 | 1.23 | 1.15 | 1.20 | 1.15 | 1.12 | 1.08 | |
| 2 | 6.71 | 6.98 | 6.70 | 6.59 | 6.56 | 6.48 | 6.25 | 6.06 | 6.03 | ||
| 3 | 10.36 | 10.71 | 10.27 | 10.12 | 10.00 | 9.75 | 9.36 | 9.20 | 9.03 | ||
References
- Hou, R.; Xia, Y. Review on the new development of vibration-based damage identification for civil engineering structures: 2010–2019. J. Sound Vib. 2021, 491, 115741. [Google Scholar] [CrossRef]
- Cao, M.S.; Sha, G.G.; Gao, Y.F.; Ostachowicz, W. Structural damage identification using damping: A compendium of uses and features. Smart Mater. Struct. 2017, 26, 043001. [Google Scholar] [CrossRef]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B.; Shevitz, D.W. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: A Literature Review; Technical Report LA–13070-MS; Los Alamos National Lab.: Los Alamos, NM, USA, 1996. [Google Scholar] [CrossRef]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B. A Summary Review of Vibration-Based Damage Identification Methods. Shock Vib. Dig. 1998, 30, 91–105. [Google Scholar] [CrossRef]
- Yoon, M.K.; Heider, D.; Gillespie, J.W.; Ratcliffe, C.P.; Crane, R.M. Local damage detection using the two-dimensional gapped smoothing method. J. Sound Vib. 2005, 279, 119–139. [Google Scholar] [CrossRef]
- Bayissa, W.L.; Haritos, N.; Thelandersson, S. Vibration-based structural damage identification using wavelet transform. Mech. Syst. Signal Process. 2008, 22, 1194–1215. [Google Scholar] [CrossRef]
- Hearn, G.; Testa, R.B. Modal Analysis for Damage Detection in Structures. J. Struct. Eng. 1991, 117, 3042–3063. [Google Scholar] [CrossRef]
- Sun, X.; Ilanko, S.; Mochida, Y.; Tighe, R.C. A Review on Vibration-Based Damage Detection Methods for Civil Structures. Vibration 2023, 6, 843–875. [Google Scholar] [CrossRef]
- Salawu, O.S. Detection of structural damage through changes in frequency: A review. Eng. Struct. 1997, 19, 718–723. [Google Scholar] [CrossRef]
- Zou, Y.; Tong, L.; Steven, G.P. Vibration-Based Model-Dependent Damage (Delamination) Identification and Health Monitoring for Composite Structures—A Review. J. Sound Vib. 2000, 230, 357–378. [Google Scholar] [CrossRef]
- Farrar, C.R.; Jauregui, D.A. Comparative study of damage identification algorithms applied to a bridge: I. Experiment. Smart Mater. Struct. 1998, 7, 704. [Google Scholar] [CrossRef]
- Curadelli, R.O.; Riera, J.D.; Ambrosini, D.; Amani, M.G. Damage detection by means of structural damping identification. Eng. Struct. 2008, 30, 3497–3504. [Google Scholar] [CrossRef]
- Consuegra, F.; Irfanoglu, A. Variation of Small Amplitude Vibration Dynamic Properties with Displacement in Reinforced Concrete Structures. Exp. Mech. 2012, 52, 817–828. [Google Scholar] [CrossRef]
- Daneshjoo, F.; Gharighoran, A. Experimental and theoretical dynamic system identification of damaged RC beams. Electron. J. Struct. Eng. 2008, 8, 29–39. [Google Scholar] [CrossRef]
- Shahzad, S.; Yamaguchi, H.; Takanami, R.; Asamoto, S. Detection of Corrosion-Induced Damage in Reinforced Concrete Beams Based on Structural Damping Identification. In Proceedings of the Thirteenth East Asia-Pacific Conference on Structural Engineering and Construction (EASEC-13), Sapporo, Japan, 11–13 September 2013. [Google Scholar]
- Razak, H.A.; Choi, F.C. The effect of corrosion on the natural frequency and modal damping of reinforced concrete beams. Eng. Struct. 2001, 23, 1126–1133. [Google Scholar] [CrossRef]
- Wei, Z.; Yam, L.H.; Cheng, L. Detection of internal delamination in multi-layer composites using wavelet packets combined with modal parameter analysis. Compos. Struct. 2004, 64, 377–387. [Google Scholar] [CrossRef]
- Frizzarin, M.; Feng, M.Q.; Franchetti, P.; Soyoz, S.; Modena, C. Damage detection based on damping analysis of ambient vibration data. Struct. Control Health Monit. 2010, 17, 368–385. [Google Scholar] [CrossRef]
- Montalvão, D.; Karanatsis, D.; Ribeiro, A.M.; Arina, J.; Baxter, R. An experimental study on the evolution of modal damping with damage in carbon fiber laminates. J. Compos. Mater. 2015, 49, 2403–2413. [Google Scholar] [CrossRef]
- Panteliou, S.D.; Chondros, T.G.; Argyrakis, V.C.; Dimarogonas, A.D. Damping Factor as an Indicator of Crack Severity. J. Sound Vib. 2001, 241, 235–245. [Google Scholar] [CrossRef]
- Salawu, O.S.; Williams, C. Bridge Assessment Using Forced-Vibration Testing. J. Struct. Eng. 1995, 121, 161–173. [Google Scholar] [CrossRef]
- Kato, M.; Shimada, S. Vibration of PC Bridge during Failure Process. J. Struct. Eng. 1986, 112, 1692–1703. [Google Scholar] [CrossRef]
- Alampalli, S. Effects of Testing, Analysis, Damage, and Environment on Modal Parameters. Mech. Syst. Signal Process. 2000, 14, 63–74. [Google Scholar] [CrossRef]
- Zheng, Y.; Lee, C.L.; Shen, R.; Guo, J. Revisiting damping identification: Limitations and comparative evaluation under impulse, white noise, and seismic excitations. Front. Built Environ. 2025, 11, 1671758. [Google Scholar] [CrossRef]
- Zheng, Y.; Lee, C.L.; Shen, R. Comparison of Damping Ratio Identification Methods for Buildings Using Seismic Responses. In Proceedings of the 26th Australasian Conference on the Mechanics of Structures and Materials; Chouw, N., Zhang, C., Eds.; Springer: Singapore, 2024; pp. 491–499. [Google Scholar] [CrossRef]
- Brincker, R.; Ventura, C.E.; Andersen, P. Damping Estimation by Frequency Domain Decomposition: The International Modal Analysis Conference. In Proceedings of IMAC 19; Society for Experimental Mechanics: Bethel, CT, USA, 2001; pp. 698–703. [Google Scholar]
- Magalhães, F.; Cunha, Á.; Caetano, E.; Brincker, R. Damping estimation using free decays and ambient vibration tests. Mech. Syst. Signal Process. 2010, 24, 1274–1290. [Google Scholar] [CrossRef]
- Jokinen, H.; Ollila, J.; Aumala, O. On windowing effects in estimating averaged periodograms of noisy signals. Measurement 2000, 28, 197–207. [Google Scholar] [CrossRef]
- Antoni, J.; Schoukens, J. A comprehensive study of the bias and variance of frequency-response-function measurements: Optimal window selection and overlapping strategies. Automatica 2007, 43, 1723–1736. [Google Scholar] [CrossRef]
- Astfalck, L.C.; Sykulski, A.M.; Cripps, E.J. Debiasing Welch’s method for spectral density estimation. Biometrika 2024, 111, 1313–1329. [Google Scholar] [CrossRef]
- Jacobsen, N.J.; Andersen, P.; Brincker, R. Using Enhanced Frequency Domain Decomposition as a Robust Technique to Harmonic Excitation in Operational Modal Analysis: International Conference on Noise & Vibration Engineering. In Proceedings of ISMA2006; Katholieke Universiteit: Leuven, Belgium, 2006. [Google Scholar]
- Koukoura, C.; Natarajan, A.; Vesth, A. Identification of support structure damping of a full scale offshore wind turbine in normal operation. Renew. Energy 2015, 81, 882–895. [Google Scholar] [CrossRef]
- Zheng, Y.; Lee, C.L.; Shen, R. Insight on Damping Ratio Identification Techniques of the Enhanced Frequency Domain Decomposition. In Proceedings of the 18th World Conference on Earthquake Engineering, Milan, Italy, 30 June–5 July 2024. [Google Scholar]
- Yun, D.Y.; Oh, B.K.; Park, K.; Park, H.S. LSTM-Based Approach for Stable Identification of Modal Damping Ratio in Building Structures. Struct. Control Health Monit. 2024, 2024, 6645626. [Google Scholar] [CrossRef]
- Qin, M.; Chen, H.; Zheng, R.; He, X.; Ren, S. An Adaptive Operational Modal Analysis under Non-White Noise Excitation Using Hybrid Neural Networks. Appl. Sci. 2022, 12, 2471. [Google Scholar] [CrossRef]
- Jian, X.; Xia, Y.; Duthé, G.; Bacsa, K.; Liu, W.; Chatzi, E. Using graph neural networks and frequency domain data for automated operational modal analysis of populations of structures. Data-Centric Eng. 2025, 6, e45. [Google Scholar] [CrossRef]
- Zahid, F.B.; Ong, Z.C.; Khoo, S.Y. A review of operational modal analysis techniques for in-service modal identification. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 398. [Google Scholar] [CrossRef]
- Bin Abu Hasan, M.D.; Ahmad, Z.; Leong, M.; Hee, L. Enhanced frequency domain decomposition algorithm: A review of a recent development for unbiased damping ratio estimates. J. Vibroeng. 2018, 20, 1919–1936. [Google Scholar] [CrossRef]
- Tamura, Y.; Zhang, L.; Yoshida, A.; Nakata, S.; Itoh, T. Ambient vibration tests and modal identification of structures by FDD and 2DOF-RD technique. Proc. Symp. Motion Vib. Control 2002, 2003, 601–604. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition, reprinted ed.; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Pandey, P.C.; Barai, S.V. Multilayer perceptron in damage detection of bridge structures. Comput. Struct. 1995, 54, 597–608. [Google Scholar] [CrossRef]
- Fang, X.; Luo, H.; Tang, J. Structural damage detection using neural network with learning rate improvement. Comput. Struct. 2005, 83, 2150–2161. [Google Scholar] [CrossRef]
- Chang, C.C.; Chang, T.Y.P.; Xu, Y.G.; Wang, M.L. Structural Damage Detection Using an Iterative Neural Network. J. Intell. Mater. Syst. Struct. 2000, 11, 32–42. [Google Scholar] [CrossRef]
- Azimi, M.; Pekcan, G. Structural health monitoring using extremely compressed data through deep learning. Comput.-Aided Civ. Infrastruct. Eng. 2020, 35, 597–614. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Kiranyaz, S.; Gabbouj, M.; Inman, D.J. Real-time vibration-based structural damage detection using one-dimensional convolutional neural networks. J. Sound Vib. 2017, 388, 154–170. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Abdeljaber, O.; Avci, O.; Gabbouj, M. 1-D Convolutional Neural Networks for Signal Processing Applications. In Proceedings of the ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 8360–8364. [Google Scholar] [CrossRef]
- Zhao, B.; Cheng, C.; Peng, Z.; Dong, X.; Meng, G. Detecting the Early Damages in Structures with Nonlinear Output Frequency Response Functions and the CNN-LSTM Model. IEEE Trans. Instrum. Meas. 2020, 69, 9557–9567. [Google Scholar] [CrossRef]
- Yun, D.Y.; Park, H.S. Modal identification of building structures under unknown input conditions using extended Kalman filter and long-short term memory. Integr. Comput.-Aided Eng. 2023, 30, 185–201. [Google Scholar] [CrossRef]
- Guo, J.; Enokida, R.; Li, D.; Ikago, K. Combination of physics-based and data-driven modeling for nonlinear structural seismic response prediction through deep residual learning. Earthq. Eng. Struct. Dyn. 2023, 52, 2429–2451. [Google Scholar] [CrossRef]
- Solomon, O.M., Jr. PSD Computations Using Welch’s Method; Technical Report; Sandia National Laboratories: lbuquerque, NM, USA, 1991. [Google Scholar] [CrossRef]
- Rainieri, C.; Fabbrocino, G. Operational Modal Analysis of Civil Engineering Structures: An Introduction and Guide for Applications; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Harris, F. On the use of windows for harmonic analysis with the discrete Fourier transform. Proc. IEEE 1978, 66, 51–83. [Google Scholar] [CrossRef]
- Verboven, P.; Guillaume, P.; Cauberghe, B.; Vanlanduit, S.; Parloo, E. Modal parameter estimation from input–output Fourier data using frequency-domain maximum likelihood identification. J. Sound Vib. 2004, 276, 957–979. [Google Scholar] [CrossRef]
- Lee, C.L. Proportional viscous damping model for matching damping ratios. Eng. Struct. 2020, 207, 110178. [Google Scholar] [CrossRef]
- Lee, C.L.; Chang, T.L.; Carr, A.J. Consistent assembly method for elemental damping. Comput. Struct. 2023, 289, 107152. [Google Scholar] [CrossRef]
- Lee, C.L. Type 4 bell-shaped proportional damping model and energy dissipation for structures with inelastic and softening response. Comput. Struct. 2022, 258, 106663. [Google Scholar] [CrossRef]
- Lee, C.L. Sparse proportional viscous damping model for structures with large number of degrees of freedom. J. Sound Vib. 2020, 478, 115312. [Google Scholar] [CrossRef]
- Magalhães, F.; Cunha, A.; Caetano, E. Vibration based structural health monitoring of an arch bridge: From automated OMA to damage detection. Mech. Syst. Signal Process. 2012, 28, 212–228. [Google Scholar] [CrossRef]
- Brincker, R.; Ventura, C. Introduction to Operational Modal Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Pasca, D.P.; Aloisio, A.; Rosso, M.M.; Sotiropoulos, S. PyOMA and PyOMA_GUI: A Python module and software for Operational Modal Analysis. SoftwareX 2022, 20, 101216. [Google Scholar] [CrossRef]
- Yang, J.Q.; Sun, F.F.; Lee, C.L.; Liu, Y.; Zheng, Y.Q. Shaking table test and control effect analysis of structure with negative stiffness damped outrigger. Eng. Struct. 2025, 322, 119083. [Google Scholar] [CrossRef]
- Zitto, M.E.; Piotrkowski, R.; Gallego, A.; Sagasta, F.; Benavent-Climent, A. Damage assessed by wavelet scale bands and b-value in dynamical tests of a reinforced concrete slab monitored with acoustic emission. Mech. Syst. Signal Process. 2015, 60–61, 75–89. [Google Scholar] [CrossRef]
- Lee, C.L. Bell-shaped proportional viscous damping models with adjustable frequency bandwidth. Comput. Struct. 2021, 244, 106423. [Google Scholar] [CrossRef]


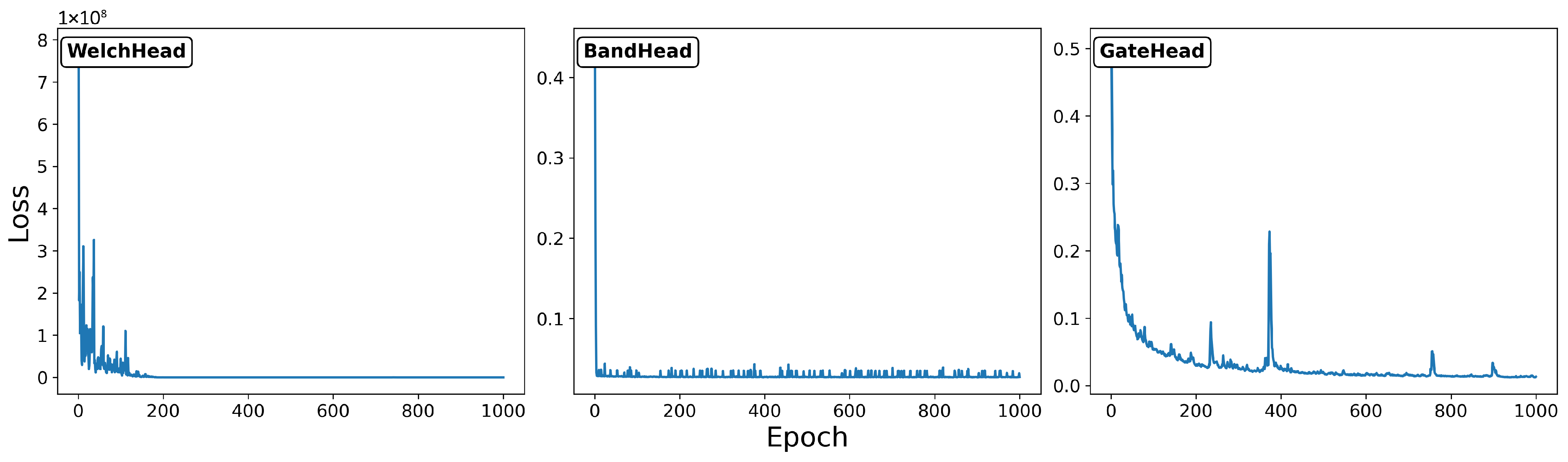




| Module | Input | Output | Theoretical Objective | Training Strategy |
|---|---|---|---|---|
| WelchHead | Global spectral statistics | Welch parameters | Maximise modal separation and minimise variance and spectral leakage | Pseudo-label imitation based on peak prominence and spectral smoothness scoring. |
| BandHead | Local spectral features | Band boundaries | Balance linearity, monotonicity, bandwidth, contamination, and asymmetry | Pseudo-label imitation using envelope and spectral quality evaluation. |
| GateHead | Envelope features | Time-gating weights | Robust regression minimisation of Equation (16) | Pseudo-label imitation using offline optimisation of . |
| No. | Earthquake | Magnitude | Station | Year | PGA |
|---|---|---|---|---|---|
| 1 | San Fernando (SF) | 6.61 | Isabella Dam | 1971 | 0.23 g |
| 2 | Imperial Valley (IV) | 6.53 | El Centro | 1979 | 0.45 g |
| 3 | Chi-Chi (CC) | 7.62 | TCU084 | 1999 | 0.32 g |
| Event | Intensity | Direction | G. Motion |
|---|---|---|---|
| 1 | 0.01 | - | White Noise |
| 0.25 | EW | El Centro (1940) × 1.32 | |
| 0.01 | - | White Noise | |
| 2 | 0.25 | NS | El Centro (1940) × 1.32 |
| 0.01 | - | White Noise | |
| 3 | 0.25 | EW + NS | El Centro (1940) × 1.32 |
| 0.01 | - | White Noise | |
| 4 | 0.25 | EW + NS + UD | El Centro (1940) × 1.32 |
| 0.01 | - | White Noise | |
| 5 | 0.50 | EW | El Centro (1940) × 1.32 |
| 0.01 | - | White Noise | |
| 6 | 0.50 | NS | El Centro (1940) × 1.32 |
| 0.01 | - | White Noise | |
| 7 | 0.50 | EW + NS | El Centro (1940) × 1.32 |
| 0.01 | - | White Noise | |
| 8 | 0.50 | EW + NS + UD | El Centro (1940) × 1.32 |
| 0.01 | - | White Noise |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Lee, C.-L.; Guo, J.; Shen, R.; Sun, F.; Yang, J.; Calad, A.S. Improving EFDD with Neural Networks in Damping Identification for Structural Health Monitoring. Sensors 2025, 25, 6929. https://doi.org/10.3390/s25226929
Zheng Y, Lee C-L, Guo J, Shen R, Sun F, Yang J, Calad AS. Improving EFDD with Neural Networks in Damping Identification for Structural Health Monitoring. Sensors. 2025; 25(22):6929. https://doi.org/10.3390/s25226929
Chicago/Turabian StyleZheng, Yuanqi, Chin-Long Lee, Jia Guo, Renjie Shen, Feifei Sun, Jiaqi Yang, and Alejandro Saenz Calad. 2025. "Improving EFDD with Neural Networks in Damping Identification for Structural Health Monitoring" Sensors 25, no. 22: 6929. https://doi.org/10.3390/s25226929
APA StyleZheng, Y., Lee, C.-L., Guo, J., Shen, R., Sun, F., Yang, J., & Calad, A. S. (2025). Improving EFDD with Neural Networks in Damping Identification for Structural Health Monitoring. Sensors, 25(22), 6929. https://doi.org/10.3390/s25226929






