A Comprehensive Review of Optical Metrology and Perception Technologies
Abstract
1. Introduction
2. Interferometry-Based Metrology
2.1. Laser Interferometry
2.1.1. Homodyne Systems
2.1.2. Heterodyne Interferometry
2.1.3. Superheterodyne Interferometry
2.1.4. Specialty Modalities
2.2. Grating Interferometry
2.2.1. Single-DOF and Planar Systems
2.2.2. Three-DOF and Six-DOF Systems
2.2.3. Multi-Optical-Head Architectures
2.3. Optical Frequency Comb-Based Interferometry
2.3.1. Absolute Distance Measurement
2.3.2. Dynamic Measurement and High-Speed Profiling
2.4. CCD-Based Optical Interferometry
2.4.1. Fizeau Interferometry
2.4.2. Digital Holographic Interferometry
2.5. Summary
3. Optical Imaging-Based Metrology
3.1. Geometric Optical Imaging
3.1.1. Laser Triangulation
3.1.2. Time-of-Flight Imaging
3.1.3. Stereo Vision
3.1.4. Structured Light 3D Reconstruction
3.2. Computational Optical Imaging
3.2.1. Compressed Imaging
3.2.2. Light Field Imaging
3.3. Super-Resolution Imaging
3.3.1. Near-Field Super-Resolution Imaging
3.3.2. Pupil-Filtering Confocal Super-Resolution Imaging
3.3.3. Structured Illumination Microscopy
3.3.4. Micro-Object-Based SR Imaging
3.4. Summary
4. Spectroscopy-Based Metrology
4.1. Confocal Optical Metrology
4.1.1. Chromatic Confocal Technology
4.1.2. Confocal Laser Scanning Microscopy
4.2. Optical Scatterometry
4.2.1. Mueller Matrix Ellipsometer
4.2.2. Imaging Ellipsometer
4.3. Summary
5. Hybrid & Frontier Metrology
5.1. Hyperspectral Imaging Metrology
5.2. Optical Vortex-Based Metrology
5.3. AI-Assisted Optical Metrology
6. Conclusions and Perspective
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zolfaghari, A.; Chen, T.; Allen, Y.Y. Additive manufacturing of precision optics at micro and nanoscale. Int. J. Extrem. Manuf. 2019, 1, 012005. [Google Scholar] [CrossRef]
- Qin, X.; Zhong, B.; Xu, H.; Jackman, J.A.; Xu, K.; Cho, N.J.; Lou, Z.; Wang, L. Manufacturing high-performance flexible sensors via advanced patterning techniques. Int. J. Extrem. Manuf. 2025, 7, 032003. [Google Scholar] [CrossRef]
- Xue, B.; Yan, H.; Liu, Z.; Yan, Y.; Geng, Y. Achieving tip-based down-milling forming of nanograting structures with variable heights through precise control of nano revolving trajectories. Int. J. Extrem. Manuf. 2025, 7, 055101. [Google Scholar] [CrossRef]
- Liu, X.; Huang, R.; Yu, Z.; Peng, K.; Pu, H. A high-accuracy capacitive absolute time-grating linear displacement sensor based on a multi-stage composite method. IEEE Sens. J. 2021, 21, 8969–8978. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhou, S.; Hong, C.; Xiao, Z.; Zhang, Z.; Chen, X.; Zeng, L.; Wu, J.; Wang, Y.; Li, X. Piezo-actuated smart mechatronic systems for extreme scenarios. Int. J. Extrem. Manuf. 2024, 7, 022003. [Google Scholar] [CrossRef]
- Yoshizawa, T. Handbook of Optical Metrology: Principles and Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Gao, W.; Kim, S.; Bosse, H.; Minoshima, K. Dimensional metrology based on ultrashort pulse laser and optical frequency comb. CIRP Ann. 2025, 74, 993–1018. [Google Scholar] [CrossRef]
- Xia, H.; Fei, Y.; Wang, Z. Research on the planar nanoscale displacement measurement system of 2-D grating. J. Hefei Univ. Technol. (Nat. Sci. Ed.) 2007, 30, 529–532. [Google Scholar]
- Zhang, S.; Yan, L.; Chen, B.; Xu, Z.; Xie, J. Real-time phase delay compensation of PGC demodulation in sinusoidal phase-modulation interferometer for nanometer displacement measurement. Opt. Express 2017, 25, 472–485. [Google Scholar] [CrossRef]
- Renishaw plc. XL-80 Laser Interferometer System. Available online: https://www.renishaw.com/en/xl-80-laser-system–8268 (accessed on 11 August 2025).
- Automated Precision Inc. XD Laser 5 D Laser Interferometer System. Available online: https://www.apimetrology.com/xd-laser-2020/ (accessed on 11 August 2025).
- Keem, T.; Gonda, S.; Misumi, I.; Huang, Q.; Kurosawa, T. Simple, real-time method for removing the cyclic error of a homodyne interferometer with a quadrature detector system. Appl. Opt. 2005, 44, 3492–3498. [Google Scholar] [CrossRef]
- Joo, K.N.; Ellis, J.D.; Spronck, J.W.; van Kan, P.J.; Schmidt, R.H.M. Simple heterodyne laser interferometer with subnanometer periodic errors. Opt. Lett. 2009, 34, 386–388. [Google Scholar] [CrossRef]
- Joo, K.N.; Ellis, J.D.; Buice, E.S.; Spronck, J.W.; Schmidt, R.H.M. High resolution heterodyne interferometer without detectable periodic nonlinearity. Opt. Express 2010, 18, 1159–1165. [Google Scholar] [CrossRef] [PubMed]
- Leirset, E.; Engan, H.E.; Aksnes, A. Heterodyne interferometer for absolute amplitude vibration measurements with femtometer sensitivity. Opt. Express 2013, 21, 19900–19921. [Google Scholar] [CrossRef]
- Yan, H.; Duan, H.Z.; Li, L.T.; Liang, Y.R.; Luo, J.; Yeh, H.C. A dual-heterodyne laser interferometer for simultaneous measurement of linear and angular displacements. Rev. Sci. Instrum. 2015, 86, 123102. [Google Scholar] [CrossRef] [PubMed]
- Dong Nguyen, T.; Higuchi, M.; Tung Vu, T.; Wei, D.; Aketagawa, M. 10-pm-order mechanical displacement measurements using heterodyne interferometry. Appl. Opt. 2020, 59, 8478–8485. [Google Scholar] [CrossRef]
- Le Floch, S.; Salvadé, Y.; Droz, N.; Mitouassiwou, R.; Favre, P. Superheterodyne configuration for two-wavelength interferometry applied to absolute distance measurement. Appl. Opt. 2010, 49, 714–717. [Google Scholar] [CrossRef]
- Yin, Z.; Li, F.; Sun, Y.; Zou, Y.; Wang, Y.; Yang, H.; Hu, P.; Fu, H.; Tan, J. High synchronization absolute distance measurement using a heterodyne and superheterodyne combined interferometer. Chin. Opt. Lett. 2024, 22, 011204. [Google Scholar] [CrossRef]
- Liu, Y.; Qu, S. Optical fiber Fabry–Perot interferometer cavity fabricated by femtosecond laser-induced water breakdown for refractive index sensing. Appl. Opt. 2014, 53, 469–474. [Google Scholar] [CrossRef]
- Xu, B.; Liu, Y.; Wang, D.; Li, J. Fiber Fabry–Pérot interferometer for measurement of gas pressure and temperature. J. Light. Technol. 2016, 34, 4920–4925. [Google Scholar] [CrossRef]
- Albert, A.; Donati, S.; Lee, S.L. Self-mixing interferometry on long distance: Theory and experimental validation. IEEE Trans. Instrum. Meas. 2024, 73, 1009808. [Google Scholar] [CrossRef]
- Zhang, M.; Li, J.; Xie, Z.; Xia, W.; Guo, D.; Wang, M. Laser self-mixing interferometry for dynamic displacement sensing of multiple targets. Opt. Eng. 2024, 63, 016105. [Google Scholar] [CrossRef]
- Herman, D.I.; Walsh, M.; Genest, J. Mode-resolved optical frequency comb fixed point localization via dual-comb interferometry. Opt. Lett. 2024, 49, 7098–7101. [Google Scholar] [CrossRef]
- Deng, Z.; Liu, Y.; Zhu, Z.; Luo, D.; Gu, C.; Zuo, Z.; Xie, G.; Li, W. Achieving precise spectral analysis and imaging simultaneously with a mode-resolved dual-comb interferometer. Sensors 2021, 21, 3166. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Jin, H.; Zhang, L.; Yan, L. Absolute distance measurement using frequency sweeping interferometry with large swept range and target drift compensation. Meas. Sci. Technol. 2023, 34, 085014. [Google Scholar] [CrossRef]
- Coggrave, C.; Ruiz, P.; Huntley, J.; Nolan, C.; Gribble, A.; Du, H.; Banakar, M.; Yan, X.; Tran, D.; Littlejohns, C. Adaptive delay lines implemented on a photonics chip for extended-range, high-speed absolute distance measurement. In Proceedings of the Emerging Applications in Silicon Photonics III, Birmingham, UK, 6–9 December 2022; SPIE: Bellingham, WA, USA, 2023; Volume 12334, pp. 22–27. [Google Scholar]
- Lawall, J. Interferometry for accurate displacement metrology. Opt. Photonics News 2004, 15, 40–45. [Google Scholar] [CrossRef]
- Zeng, Z.; Qu, X.; Tan, Y.; Tan, R.; Zhang, S. High-accuracy self-mixing interferometer based on single high-order orthogonally polarized feedback effects. Opt. Express 2015, 23, 16977–16983. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Chen, X.; Liu, C.; Cai, G.; Wang, W. A survey on the grating based optical position encoder. Opt. Laser Technol. 2021, 143, 107352. [Google Scholar] [CrossRef]
- Li, X.; Shi, Y.; Wang, P.; Ni, K.; Zhou, Q.; Wang, X. A Compact Design of Optical Scheme for a Two-Probe Absolute Surface Encoders. In Proceedings of the Tenth International Symposium on Precision Engineering Measurements and Instrumentation, Kunming, China, 8–10 August 2018; p. 155. [Google Scholar] [CrossRef]
- Li, X.; Xiao, X.; Lu, H.; Ni, K.; Zhou, Q.; Wang, X. Design and Testing of a Compact Optical Prism Module for Multi-Degree-of Freedom Grating Interferometry Application. In Proceedings of the Tenth International Symposium on Precision Engineering Measurements and Instrumentation, Kunming, China, 8–10 August 2018; p. 165. [Google Scholar] [CrossRef]
- Liao, B.; Wang, S.; Lin, J.; Dou, Y.; Wang, X.; Li, X. A Research on Compact Short-Distance Grating Interferometer Based on Ridge Prism. In Proceedings of the 2021 International Conference on Optical Instruments and Technology: Optoelectronic Measurement Technology and Systems, Online Only, China, 8–10 April 2022; p. 95. [Google Scholar] [CrossRef]
- Luo, L.; Gao, L.; Wang, S.; Deng, F.; Wu, Y.; Li, X. An Ultra-Precision Error Estimation for a Multi-Axes Grating Encoder Using Quadrant Photodetectors. In Proceedings of the Optical Metrology and Inspection for Industrial Applications IX, Online Only, China, 5–11 December 2022; p. 12. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, G.; Xue, G.; Zhou, Q.; Li, X. Heterodyne Three-Degree-of-Freedom Grating Interferometer for Ultra-Precision Positioning of Lithography Machine. In Proceedings of the 2021 International Conference on Optical Instruments and Technology: Optoelectronic Measurement Technology and Systems, Online Only, China, 8–10 April 2022; p. 113. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, S.; Li, X. Ultraprecision Grating Positioning Technology for Wafer Stage of Lithography Machine. Laser Optoelectron. Prog. 2022, 59, 0922019. (In Chinese) [Google Scholar]
- Li, Y.; Yang, L.; Wang, X.; Shan, S.; Deng, F.; He, Z.; Liu, Z.; Li, X. Overlay Metrology for Lithography Machine. Laser Optoelectron. Prog. 2022, 59, 0922023. (In Chinese) [Google Scholar]
- Zhong, Z.; Li, J.; Lu, T.; Li, X. High dynamic wavefront stability control for high-uniformity periodic microstructure fabrication. Precis. Eng. 2025, 93, 216–223. [Google Scholar] [CrossRef]
- Shao, C.; Li, X. Technologies for Fabricating Large-Size Diffraction Gratings. Sensors 2025, 25, 1990. [Google Scholar] [CrossRef]
- Gao, X.; Li, J.; Zhong, Z.; Li, X. Global alignment reference strategy for laser interference lithography pattern arrays. Microsyst. Nanoeng. 2025, 11, 41. [Google Scholar] [CrossRef] [PubMed]
- Cui, C.; Li, X.; Wang, X. Grating interferometer: The dominant positioning strategy in atomic and close-to-atomic scale manufacturing. J. Manuf. Syst. 2025, 82, 1227–1251. [Google Scholar]
- Huang, G.; Cui, C.; Lei, X.; Li, Q.; Yan, S.; Li, X.; Wang, G. A Review of Optical Interferometry for High-Precision Length Measurement. Micromachines 2024, 16, 6. [Google Scholar] [CrossRef] [PubMed]
- Luo, L.; Shan, S.; Li, X. A review: Laser interference lithography for diffraction gratings and their applications in encoders and spectrometers. Sensors 2024, 24, 6617. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Yuan, Y.; Luo, L.; Li, X. A Review: Absolute Linear Encoder Measurement Technology. Sensors 2025, 25, 5997. [Google Scholar] [CrossRef]
- Luo, L.; Zhao, M.; Li, X. A Review: Grating Encoder Technologies for Multi-Degree-of-Freedom Spatial Measurement. Sensors 2025, 25, 6071. [Google Scholar]
- Shi, Y.; Zhou, Q.; Li, X.; Ni, K.; Wang, X. Design and Testing of a Linear Encoder Capable of Measuring Absolute Distance. Sens. Actuators A Phys. 2020, 308, 111935. [Google Scholar] [CrossRef]
- Li, X.; Xiao, X.; Ni, K.; Zhou, Q.; Wang, H.; Wang, X. A Precise Reference Position Detection Method for Linear Encoders by Using a Coherence Function Algorithm. In Proceedings of the SPIE/COS Photonics Asia, Beijing, China, 14–16 October 2023; p. 100231D. [Google Scholar] [CrossRef]
- Lin, J.; Guan, J.; Wen, F.; Tan, J. High-resolution and wide range displacement measurement based on planar grating. Opt. Commun. 2017, 404, 132–138. [Google Scholar] [CrossRef]
- Ye, G.; Liu, H.; Wang, Y.; Lei, B.; Shi, Y.; Yin, L.; Lu, B. Ratiometric-linearization-based high-precision electronic interpolator for sinusoidal optical encoders. IEEE Trans. Ind. Electron. 2018, 65, 8224–8231. [Google Scholar] [CrossRef]
- Hsieh, H.; Lee, J.; Wu, W.; Chen, J.; Deturche, R.; Lerondel, G. Quasi-common-optical-path heterodyne grating interferometer for displacement measurement. Meas. Sci. Technol. 2010, 21, 115304. [Google Scholar] [CrossRef]
- Wu, C.C.; Hsu, C.C.; Lee, J.Y.; Chen, Y.Z. Heterodyne common-path grating interferometer with Littrow configuration. Opt. Express 2013, 21, 13322–13332. [Google Scholar] [CrossRef]
- Kimura, A.; Gao, W.; Arai, Y.; Lijiang, Z. Design and construction of a two-degree-of-freedom linear encoder for nanometric measurement of stage position and straightness. Precis. Eng. 2010, 34, 145–155. [Google Scholar] [CrossRef]
- Kimura, A.; Gao, W.; Lijiang, Z. Position and out-of-straightness measurement of a precision linear air-bearing stage by using a two-degree-of-freedom linear encoder. Meas. Sci. Technol. 2010, 21, 054005. [Google Scholar] [CrossRef]
- Kimura, A.; Hosono, K.; Kim, W.; Shimizu, Y.; Gao, W.; Zeng, L. A two-degree-of-freedom linear encoder with a mosaic scale grating. Int. J. Nanomanuf. 2011, 7, 73–91. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, Z.; Jiang, S.; Wang, W.; Yu, H.; Jiri, G.; Hao, Q.; Li, W. High-precision 2D grating displacement measurement system based on double-spatial heterodyne optical path interleaving. Opt. Lasers Eng. 2022, 158, 107167. [Google Scholar] [CrossRef]
- Yang, H.; Yin, Z.; Yang, R.; Hu, P.; Li, J.; Tan, J. Design for a highly stable laser source based on the error model of high-speed high-resolution heterodyne interferometers. Sensors 2020, 20, 1083. [Google Scholar] [CrossRef]
- Li, X.; Gao, W.; Muto, H.; Shimizu, Y.; Ito, S.; Dian, S. A Six-Degree-of-Freedom Surface Encoder for Precision Positioning of a Planar Motion Stage. Precis. Eng. 2013, 37, 771–781. [Google Scholar] [CrossRef]
- Gao, Z.; Hu, J.; Zhu, Y.; Duan, G. A new 6-degree-of-freedom measurement method of X-Y stages based on additional information. Precis. Eng. 2013, 37, 606–620. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, Y.; Zhang, Y.; Wu, P.; Xiong, X.; Du, H. A rotational angle detection method for reflective gratings based on interferometry. Laser Optoelectron. Prog. 2019, 56, 110501. (In Chinese) [Google Scholar] [CrossRef]
- Wang, S.; Zhu, J.; Shi, N.; Luo, L.; Wen, Y.; Li, X. Modeling and Test of an Absolute Four-Degree-of-Freedom (DOF) Grating Encoder. In Proceedings of the Optical Metrology and Inspection for Industrial Applications IX, Online Only, China, 5–11 December 2022; p. 15. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, G.; Wang, S.; Li, X. A Reflective-Type Heterodyne Grating Interferometer for Three-Degree-of-Freedom Subnanometer Measurement. IEEE Trans. Instrum. Meas. 2022, 71, 7007509. [Google Scholar] [CrossRef]
- Wang, S.; Liao, B.; Shi, N.; Li, X. A Compact and High-Precision Three-Degree-of-Freedom Grating Encoder Based on a Quadrangular Frustum Pyramid Prism. Sensors 2023, 23, 4022. [Google Scholar] [CrossRef]
- Hsieh, H.L.; Pan, S.W. Development of a grating-based interferometer for six-degree-of-freedom displacement and angle measurements. Opt. Express 2015, 23, 2451–2465. [Google Scholar] [CrossRef]
- Cui, C.; Gao, L.; Zhao, P.; Yang, M.; Liu, L.; Ma, Y.; Huang, G.; Wang, S.; Luo, L.; Li, X. Towards multi-dimensional atomic-level measurement: Integrated heterodyne grating interferometer with zero dead-zone. Light Adv. Manuf. 2025, 6, 40. [Google Scholar]
- Wang, S.; Luo, L.; Li, X. Design and parameter optimization of zero position code considering diffraction based on deep learning generative adversarial networks. Nanomanuf. Metrol. 2024, 7, 2. [Google Scholar] [CrossRef]
- Yu, K.; Zhu, J.; Yuan, W.; Zhou, Q.; Xue, G.; Wu, G.; Wang, X.; Li, X. Two-Channel Six Degrees of Freedom Grating-Encoder for Precision-Positioning of Sub-Components in Synthetic-Aperture Optics. Opt. Express 2021, 29, 21113. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Gao, L.; Huang, G.; Lei, X.; Cui, C.; Wang, S.; Yang, M.; Zhu, J.; Yan, S.; Li, X. A Wavelength-Stabilized and Quasi-Common-Path Heterodyne Grating Interferometer With Sub-Nanometer Precision. IEEE Trans. Instrum. Meas. 2024, 73, 7002509. [Google Scholar] [CrossRef]
- Ni, K.; Wang, H.; Li, X.; Wang, X.; Xiao, X.; Zhou, Q. Measurement Uncertainty Evaluation of the Three Degree of Freedom Surface Encoder. In Proceedings of the SPIE/COS Photonics Asia, Beijing, China, 12–14 October 2016; p. 100230Z. [Google Scholar] [CrossRef]
- Ye, W.; Zhang, M.; Zhu, Y.; Wang, L.; Hu, J.; Li, X.; Hu, C. Ultraprecision real-time displacements calculation algorithm for the grating interferometer system. Sensors 2019, 19, 2409. [Google Scholar] [CrossRef]
- Kang, H.J.; Chun, B.J.; Jang, Y.S.; Kim, Y.J.; Kim, S.W. Real-time compensation of the refractive index of air in distance measurement. Opt. Express 2015, 23, 26377–26385. [Google Scholar] [CrossRef]
- Liu, H.; Xiang, H.; Chen, J.; Yang, R. Measurement and compensation of machine tool geometry error based on Abbe principle. Int. J. Adv. Manuf. Technol. 2018, 98, 2769–2774. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, L.; Wang, X.; Wang, C.; Xiang, H.; Tong, G.; Zhao, D. Modeling method of CNC tooling volumetric error under consideration of Abbé error. Int. J. Adv. Manuf. Technol. 2022, 119, 7875–7887. [Google Scholar] [CrossRef]
- Li, X.; Su, X.; Zhou, Q.; Ni, K.; Wang, X. A Real-Time Distance Measurement Data Processing Platform for Multi-Axis Grating Interferometry Type Optical Encoders. In Proceedings of the Tenth International Symposium on Precision Engineering Measurements and Instrumentation, Kunming, China, 8–10 August 2018; p. 170. [Google Scholar] [CrossRef]
- Shimizu, Y.; Ito, T.; Li, X.; Kim, W.; Gao, W. Design and Testing of a Four-Probe Optical Sensor Head for Three-Axis Surface Encoder with a Mosaic Scale Grating. Meas. Sci. Technol. 2014, 25, 094002. [Google Scholar] [CrossRef]
- Han, Y.; Ni, K.; Li, X.; Wu, G.; Yu, K.; Zhou, Q.; Wang, X. An fpga platform for next-generation grating encoders. Sensors 2020, 20, 2266. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Shimizu, Y.; Ito, T.; Cai, Y.; Ito, S.; Gao, W. Measurement of Six-Degree-of-Freedom Planar Motions by Using a Multiprobe Surface Encoder. Opt. Eng. 2014, 53, 122405. [Google Scholar] [CrossRef]
- Shimizu, Y.; Chen, L.C.; Kim, D.W.; Chen, X.; Li, X.; Matsukuma, H. An Insight on Optical Metrology in Manufacturing. Meas. Sci. Technol. 2020, 32, 042003. [Google Scholar] [CrossRef]
- Wang, S.; Luo, L.; Zhu, J.; Shi, N.; Li, X. An Ultra-Precision Absolute-Type Multi-Degree-of-Freedom Grating Encoder. Sensors 2022, 22, 9047. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, H.; Ni, K.; Zhou, Q.; Mao, X.; Zeng, L.; Wang, X.; Xiao, X. Two-Probe Optical Encoder for Absolute Positioning of Precision Stages by Using an Improved Scale Grating. Opt. Express 2016, 24, 21378. [Google Scholar] [CrossRef]
- Li, X.; Shi, Y.; Xiao, X.; Zhou, Q.; Wu, G.; Lu, H.; Ni, K. Design and Testing of a Compact Optical Prism Module for Multi-Degree-of-Freedom Grating Interferometry Application. Appl. Sci. 2018, 8, 2495. [Google Scholar] [CrossRef]
- Matsukuma, H.; Ishizuka, R.; Furuta, M.; Li, X.; Shimizu, Y.; Gao, W. Reduction in Cross-Talk Errors in a Six-Degree-of-Freedom Surface Encoder. Nanomanuf. Metrol. 2019, 2, 111–123. [Google Scholar] [CrossRef]
- Shi, Y.; Ni, K.; Li, X.; Zhou, Q.; Wang, X. Highly Accurate, Absolute Optical Encoder Using a Hybrid-Positioning Method. Opt. Lett. 2019, 44, 5258. [Google Scholar] [CrossRef]
- Wang, S.; Luo, L.; Gao, L.; Ma, R.; Wang, X.; Li, X. Long Binary Coding Design for Absolute Positioning Using Genetic Algorithm. In Proceedings of the Optical Metrology and Inspection for Industrial Applications X, Beijing, China, 15–16 October 2023; p. 4. [Google Scholar] [CrossRef]
- Zhu, J.; Yu, K.; Xue, G.; Zhou, Q.; Wang, X.; Li, X. An Improved Signal Filtering Strategy Based on EMD Algorithm for Ultrahigh Precision Grating Encoder. In Proceedings of the Real-Time Photonic Measurements, Data Management, and Processing VI, Nantong, China, 10–12 October 2021; p. 51. [Google Scholar] [CrossRef]
- Zhu, J.; Yu, K.; Xue, G.; Shi, N.; Zhou, Q.; Wang, X.; Li, X. A Simplified Two-Phase Differential Decoding Algorithm for High Precision Grating Encoder. In Proceedings of the Optical Metrology and Inspection for Industrial Applications VIII, Nantong, China, 10–19 October 2021; p. 14. [Google Scholar] [CrossRef]
- Li, J.; Wang, S.; Li, X. Cross-scale structures fabrication via hybrid lithography for nanolevel positioning. Microsyst. Nanoeng. 2025, 11, 163. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Q.; Zhu, X.; Lu, H.; Yang, L.; Ma, D.; Sun, J.; Ni, K.; Wang, X. Holographic Fabrication of an Arrayed One-Axis Scale Grating for a Two-Probe Optical Linear Encoder. Opt. Express 2017, 25, 16028. [Google Scholar] [CrossRef]
- Xue, G.; Lu, H.; Li, X.; Zhou, Q.; Wu, G.; Wang, X.; Zhai, Q.; Ni, K. Patterning Nanoscale Crossed Grating with High Uniformity by Using Two-Axis Lloyd’s Mirrors Based Interference Lithography. Opt. Express 2020, 28, 2179. [Google Scholar] [CrossRef]
- Li, X. A Two-Axis Lloyd’s Mirror Interferometer for Fabrication of Two-Dimensional Diffraction Gratings. CIRP Ann. 2014, 63, 461–464. [Google Scholar] [CrossRef]
- Li, X.; Lu, H.; Zhou, Q.; Wu, G.; Ni, K.; Wang, X. An Orthogonal Type Two-Axis Lloyd’s Mirror for Holographic Fabrication of Two-Dimensional Planar Scale Gratings with Large Area. Appl. Sci. 2018, 8, 2283. [Google Scholar] [CrossRef]
- Xue, G.; Zhai, Q.; Lu, H.; Zhou, Q.; Ni, K.; Lin, L.; Wang, X.; Li, X. Polarized holographic lithography system for high-uniformity microscale patterning with periodic tunability. Microsyst. Nanoeng. 2021, 7, 31. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, C.; Sun, J.; Peng, X.; Tian, H.; Li, X.; Chen, X.; Chen, X.; Shao, J. Electric-driven flexible-roller nanoimprint lithography on the stress-sensitive warped wafer. Int. J. Extrem. Manuf. 2023, 5, 035101. [Google Scholar]
- Wang, Y.; Zhao, F.; Luo, L.; Li, X. A Review on Recent Advances in Signal Processing in Interferometry. Sensors 2025, 25, 5013. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Wang, X.; Bayanheshig; Liu, Z.; Wang, W.; Jiang, S.; Li, Y.; Li, S.; Zhang, W.; Jiang, Y.; et al. Controlling the wavefront aberration of a large-aperture and high-precision holographic diffraction grating. Light Sci. Appl. 2025, 14, 112. [Google Scholar] [CrossRef]
- Chang, D.; Sun, Y.; Wang, J.; Yin, Z.; Hu, P.; Tan, J. Multiple-beam grating interferometry and its general Airy formulae. Opt. Lasers Eng. 2023, 164, 107534. [Google Scholar] [CrossRef]
- Li, M.; Xiang, X.; Zhou, C.; Wei, C.; Jia, W.; Xiang, C.; Lu, Y.; Zhu, S. Two-dimensional grating fabrication based on ultra-precision laser direct writing system. Acta Opt. Sin. 2019, 39, 0905001. [Google Scholar]
- Chai, Y.; Li, F.; Wang, J.; Karvinen, P.; Kuittinen, M.; Kang, G. Enhanced sensing performance from trapezoidal metallic gratings fabricated by laser interference lithography. Opt. Lett. 2022, 47, 1009–1012. [Google Scholar] [CrossRef]
- Cunbao, L.; Shuhua, Y.; Fusheng, Y.; Zhiguang, D. Synthetical modeling and experimental study of fabrication and assembly errors of two-dimensional gratings. Infrared Laser Eng. 2016, 45, 1217005. [Google Scholar] [CrossRef]
- Deng, X.; Li, T.; Cheng, X. Self-traceable grating reference material and application. Opt. Precis. Eng. 2022, 30, 2608–2625. [Google Scholar] [CrossRef]
- Maksymov, I.S.; Huy Nguyen, B.Q.; Pototsky, A.; Suslov, S. Acoustic, phononic, Brillouin light scattering and Faraday wave-based frequency combs: Physical foundations and applications. Sensors 2022, 22, 3921. [Google Scholar] [CrossRef]
- Wang, G.; Tan, L.; Yan, S. Real-time and meter-scale absolute distance measurement by frequency-comb-referenced multi-wavelength interferometry. Sensors 2018, 18, 500. [Google Scholar] [CrossRef] [PubMed]
- Coluccelli, N.; Cassinerio, M.; Redding, B.; Cao, H.; Laporta, P.; Galzerano, G. The optical frequency comb fibre spectrometer. Nat. Commun. 2016, 7, 12995. [Google Scholar] [CrossRef]
- Fortier, T.; Baumann, E. 20 years of developments in optical frequency comb technology and applications. Commun. Phys. 2019, 2, 153. [Google Scholar] [CrossRef]
- Yu, H.; Ni, K.; Zhou, Q.; Li, X.; Wang, X.; Wu, G. Digital Error Correction of Dual-Comb Interferometer without External Optical Referencing Information. Opt. Express 2019, 27, 29425. [Google Scholar] [CrossRef] [PubMed]
- Matsukuma, H.; Sato, R.; Shimizu, Y.; Gao, W. Measurement range expansion of chromatic confocal probe with supercontinuum light source. Int. J. Autom. Technol. 2021, 15, 529–536. [Google Scholar] [CrossRef]
- Coddington, I.; Swann, W.C.; Newbury, N.R. Coherent multiheterodyne spectroscopy using stabilized optical frequency combs. Phys. Rev. Lett. 2008, 100, 013902. [Google Scholar] [CrossRef]
- Kubota, T.; Nara, M.; Yoshino, T. Interferometer for measuring displacement and distance. Opt. Lett. 1987, 12, 310–312. [Google Scholar] [CrossRef]
- Jang, Y.S.; Kim, S.W. Compensation of the refractive index of air in laser interferometer for distance measurement: A review. Int. J. Precis. Eng. Manuf. 2017, 18, 1881–1890. [Google Scholar] [CrossRef]
- Kajima, M.; Minoshima, K. Optical zooming interferometer for subnanometer positioning using an optical frequency comb. Appl. Opt. 2010, 49, 5844–5850. [Google Scholar] [CrossRef]
- Hofer, M.; Ober, M.; Haberl, F.; Fermann, M. Characterization of ultrashort pulse formation in passively mode-locked fiber lasers. IEEE J. Quantum Electron. 2002, 28, 720–728. [Google Scholar] [CrossRef]
- Fizeau, M. Sur les hypothèses relatives à l’éther lumineux, et sur une expérience qui parait démontrer que le mouvement des corps change la vitesse avec laquelle la lumière se propage dans leur intérieur. SPIE Milest. Ser. 1991, 28, 445–449. [Google Scholar]
- Schober, C.; Beisswanger, R.; Gronle, A.; Pruss, C.; Osten, W. Tilted Wave Fizeau Interferometer for flexible and robust asphere and freeform testing. Light Adv. Manuf. 2022, 3, 687–698. [Google Scholar] [CrossRef]
- Sommargren, G.E. Interferometric Wavefront Measurement. U.S. Patent 4,594,003, 10 June 1986. [Google Scholar]
- Aikens, D.M.; Roussel, A.; Bray, M. Derivation of preliminary specifications for transmitted wavefront and surface roughness for large optics used in inertial confinement fusion. In Proceedings of the Solid State Lasers for Application to Inertial Confinement Fusion (ICF), Monterey, CA, USA, 30 May–2 June 1995; SPIE: Bellingham, WA, USA, 1995; Volume 2633, pp. 350–360. [Google Scholar]
- Deck, L.L.; Soobitsky, J.A. Phase-shifting via wavelength tuning in very large aperture interferometers. In Proceedings of the Optical Manufacturing and Testing III, Denver, CO, USA, 20–23 July 1999; SPIE: Bellingham, WA, USA, 1999; Volume 3782, pp. 432–442. [Google Scholar]
- Xu, T.; Wang, Z.; Jia, Z.; Chen, J.; Feng, Z. A dual-stage correction approach for high-precision phase-shifter in Fizeau interferometers. Opt. Lasers Eng. 2024, 178, 108205. [Google Scholar] [CrossRef]
- Morrow, K.; da Silva, M.B.; Alcock, S. Correcting retrace and system imaging errors to achieve nanometer accuracy in full aperture, single-shot Fizeau interferometry. Opt. Express 2023, 31, 27654–27666. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Peng, S.; Xu, Z.; Bai, J.; Wu, L.; Shen, Y.; Liu, D. Breaking the mid-spatial-frequency noise floor to sub-nanometer in Fizeau interferometry via anisotropic spatial-coherence engineering. Opt. Lett. 2025, 50, 4410–4413. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Huang, X.; Guo, C.; Xu, J.; Xu, J.; Hao, H.; Zhao, H.; Tang, W.; Wang, P.; Li, H. Orbital-angular-momentum beams-based Fizeau interferometer using the advanced azimuthal-phase-demodulation method. Appl. Phys. Lett. 2022, 121, 241102. [Google Scholar] [CrossRef]
- Lu, H.; Guo, C.; Huang, X.; Zhao, H.; Tang, W. Orbital angular momentum-based Fizeau interferometer measurement system. In Proceedings of the Optical Design and Testing XII, Online. 5–11 December 2022; SPIE: Bellingham, WA, USA, 2022; Volume 12315, pp. 342–346. [Google Scholar]
- Kühnel, M.; Langlotz, E.; Rahneberg, I.; Dontsov, D.; Probst, J.; Krist, T.; Braig, C.; Erko, A. Interferometrical profilometer for high precision 3D measurements of free-form optics topography with large local slopes. In Proceedings of the Eighth European Seminar on Precision Optics Manufacturing, Teisnach, Germany, 13–14 April 2021; SPIE: Bellingham, WA, USA, 2021; Volume 11853, pp. 51–58. [Google Scholar]
- Da Silva, M.B.; Alcock, S.G.; Nistea, I.T.; Sawhney, K. A Fizeau interferometry stitching system to characterize X-ray mirrors with sub-nanometre errors. Opt. Lasers Eng. 2023, 161, 107192. [Google Scholar] [CrossRef]
- Zygo Corporation. MST Series Optical Profilers; Zygo Corporation, 2023. Product Brochure. Available online: https://www.zygo.com/products/metrology-systems/laser-interferometers/verifire-mst (accessed on 11 August 2025).
- Taylor Hobson Ltd. Talysurf PGI Optics Surface Profiling System; Taylor Hobson Ltd., 2023. Product Datasheet. Available online: https://www.taylor-hobson.com/products/surface-analysis/talysurf-pgi-optics (accessed on 11 August 2025).
- Kreis, T. Handbook of Holographic Interferometry: Optical and Digital Methods; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Stetson, K.A. The discovery of holographic interferometry, its development and applications. Light Adv. Manuf. 2022, 3, 349–357. [Google Scholar] [CrossRef]
- Osten, W.; Faridian, A.; Gao, P.; Körner, K.; Naik, D.; Pedrini, G.; Singh, A.K.; Takeda, M.; Wilke, M. Recent advances in digital holography. Appl. Opt. 2014, 53, G44–G63. [Google Scholar] [CrossRef]
- Gao, Y.; Cao, L. Generalized optimization framework for pixel super-resolution imaging in digital holography. Opt. Express 2021, 29, 28805–28823. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.; Khare, K. Single-shot full resolution region-of-interest (ROI) reconstruction in image plane digital holographic microscopy. J. Mod. Opt. 2018, 65, 1127–1134. [Google Scholar] [CrossRef]
- Min, J.; Yao, B.; Gao, P.; Guo, R.; Ma, B.; Zheng, J.; Lei, M.; Yan, S.; Dan, D.; Duan, T.; et al. Dual-wavelength slightly off-axis digital holographic microscopy. Appl. Opt. 2012, 51, 191–196. [Google Scholar] [CrossRef]
- Di, J.; Song, Y.; Xi, T.; Zhang, J.; Li, Y.; Ma, C.; Wang, K.; Zhao, J. Dual-wavelength common-path digital holographic microscopy for quantitative phase imaging of biological cells. Opt. Eng. 2017, 56, 111712. [Google Scholar] [CrossRef]
- Morimoto, Y.; Matui, T.; Fujigaki, M.; Kawagishi, N. Subnanometer displacement measurement by averaging of phase difference in windowed digital holographic interferometry. Opt. Eng. 2007, 46, 025603. [Google Scholar] [CrossRef]
- Everett, S.; Yanny, B.; Kuropatkin, N. Application of holographic interferometry for plasma diagnostics. Usp. Fiz. Nauk. 1986, 149, 105–138. [Google Scholar]
- Martínez-León, L.; Clemente, P.; Mori, Y.; Climent, V.; Lancis, J.; Tajahuerce, E. Single-pixel digital holography with phase-encoded illumination. Opt. Express 2017, 25, 4975–4984. [Google Scholar] [CrossRef]
- Asundi, A.; Singh, V.R. Amplitude and phase analysis in digital dynamic holography. Opt. Lett. 2006, 31, 2420–2422. [Google Scholar] [CrossRef] [PubMed]
- Shimobaba, T.; Takahashi, T.; Yamamoto, Y.; Endo, Y.; Shiraki, A.; Nishitsuji, T.; Hoshikawa, N.; Kakue, T.; Ito, T. Digital holographic particle volume reconstruction using a deep neural network. Appl. Opt. 2019, 58, 1900–1906. [Google Scholar] [CrossRef]
- Ren, Z.; Xu, Z.; Lam, E.Y. End-to-end deep learning framework for digital holographic reconstruction. Adv. Photonics 2019, 1, 016004. [Google Scholar] [CrossRef]
- Schretter, C.; Blinder, D.; Bettens, S.; Ottevaere, H.; Schelkens, P. Regularized non-convex image reconstruction in digital holographic microscopy. Opt. Express 2017, 25, 16491–16508. [Google Scholar] [CrossRef]
- Bettens, S.; Yan, H.; Blinder, D.; Ottevaere, H.; Schretter, C.; Schelkens, P. Studies on the sparsifying operator in compressive digital holography. Opt. Express 2017, 25, 18656–18676. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Depeursinge, C.; Popescu, G. Quantitative phase imaging in biomedicine. Nat. Photonics 2018, 12, 578–589. [Google Scholar] [CrossRef]
- Lee, A.J.; Hugonnet, H.; Park, W.; Park, Y. Three-dimensional label-free imaging and quantification of migrating cells during wound healing. Biomed. Opt. Express 2020, 11, 6812–6824. [Google Scholar] [CrossRef]
- Sun, B.; Ahmed, A.; Atkinson, C.; Soria, J. A novel 4D digital holographic PIV/PTV (4D-DHPIV/PTV) methodology using iterative predictive inverse reconstruction. Meas. Sci. Technol. 2020, 31, 104002. [Google Scholar] [CrossRef]
- Li, J.; Zhou, Q.; Li, X.; Chen, R.; Ni, K. An Improved Low-Noise Processing Methodology Combined with PCL for Industry Inspection Based on Laser Line Scanner. Sensors 2019, 19, 3398. [Google Scholar] [CrossRef]
- Ding, D.; Zhao, Z.; Zhang, X.; Fu, Y.; Xu, J. Evaluation and compensation of laser-based on-machine measurement for inclined and curved profiles. Measurement 2020, 151, 107236. [Google Scholar] [CrossRef]
- Ibaraki, S.; Kitagawa, Y.; Kimura, Y.; Nishikawa, S. On the limitation of dual-view triangulation in reducing the measurement error induced by the speckle noise in scanning operations. Int. J. Adv. Manuf. Technol. 2017, 88, 731–737. [Google Scholar] [CrossRef]
- Chen, R.; Li, Y.; Xue, G.; Tao, Y.; Li, X. Laser Triangulation Measurement System with Scheimpflug Calibration Based on the Monte Carlo Optimization Strategy. Opt. Express 2022, 30, 25290. [Google Scholar] [CrossRef] [PubMed]
- Hao, C.; Jigui, Z.; Bin, X. Impact of rough surface scattering characteristics to measurement accuracy of laser displacement sensor based on position sensitive detector. Chin. J. Lasers 2013, 40, 0808003. [Google Scholar] [CrossRef]
- Wang, L.; Feng, Q.; Li, J. Tilt error analysis for laser triangulation sensor based on ZEMAX. In Proceedings of the Optical Sensing and Imaging Technologies and Applications, Beijing, China, 22–24 May 2018; SPIE: Bellingham, WA, USA, 2018; Volume 10846, pp. 161–168. [Google Scholar]
- Li, S.; Yang, Y.; Jia, X.; Chen, M. The impact and compensation of tilt factors upon the surface measurement error. Optik 2016, 127, 7367–7373. [Google Scholar] [CrossRef]
- Yu, P. The Analysis of Error and Study on Improvement Measures in the Detection of Displacement by Laser Triangulation; Changchun University of Technology: Changchun, China, 2013. [Google Scholar]
- Wei, J.; He, Y.; Wang, F.; He, Y.; Rong, X.; Chen, M.; Wang, Y.; Yue, H.; Liu, J. Convolutional neural network assisted infrared imaging technology: An enhanced online processing state monitoring method for laser powder bed fusion. Infrared Phys. Technol. 2023, 131, 104661. [Google Scholar] [CrossRef]
- Tsagaris, A.; Mansour, G. Path planning optimization for mechatronic systems with the use of genetic algorithm and ant colony. IOP Conf. Ser. Mater. Sci. Eng. 2019, 564, 012051. [Google Scholar] [CrossRef]
- Xie, G.; Du, X.; Li, S.; Yang, J.; Hei, X.; Wen, T. An efficient and global interactive optimization methodology for path planning with multiple routing constraints. ISA Trans. 2022, 121, 206–216. [Google Scholar] [CrossRef]
- Hui, D.; Li, D.; Wang, B.; Li, Y.; Ding, J.; Zhang, L.; Qiao, D. A MEMS grating modulator with a tunable sinusoidal grating for large-scale extendable apertures. Microsyst. Nanoeng. 2025, 11, 39. [Google Scholar] [CrossRef]
- Piron, F.; Morrison, D.; Yuce, M.R.; Redouté, J.M. A review of single-photon avalanche diode time-of-flight imaging sensor arrays. IEEE Sens. J. 2020, 21, 12654–12666. [Google Scholar] [CrossRef]
- Hsu, T.H.; Liu, C.H.; Lin, T.C.; Sang, T.H.; Tsai, C.M.; Lin, G.; Lin, S.D. High-precision pulsed laser ranging using CMOS single-photon avalanche diodes. Opt. Laser Technol. 2024, 176, 110921. [Google Scholar] [CrossRef]
- Zou, C.; Ou, Y.; Zhu, Y.; Martins, R.P.; Chan, C.H.; Zhang, M. A 256 × 192-Pixel Direct Time-of-Flight LiDAR Receiver With a Current-Integrating-Based AFE Supporting 240-m-Range Imaging. IEEE J. Solid-State Circuits 2024, 59, 3525–3537. [Google Scholar] [CrossRef]
- Dabidian, S.; Jami, S.T.; Kavehvash, Z.; Fotowat-Ahmady, A. Direct time-of-flight (d-ToF) pulsed LiDAR sensor with simultaneous noise and interference suppression. IEEE Sens. J. 2024, 24, 27578–27586. [Google Scholar] [CrossRef]
- Li, D.; Li, P.; Hu, J.; Wang, X.; Ma, R.; Zhu, Z. A SPAD-Based Hybrid Time-of-Flight Image Sensor With PWM and Non-Linear Spatiotemporal Coincidence. IEEE Trans. Circuits Syst. I Regul. Pap. 2025, 72, 5610–5619. [Google Scholar] [CrossRef]
- Piron, F.; Pierre, H.; Redouté, J.M. An 8-Windows Continuous-Wave Indirect Time-of-Flight Method for High-Frequency SPAD-Based 3-D Imagers in 0.18 μm CMOS. IEEE Sens. J. 2024, 24, 20495–20503. [Google Scholar] [CrossRef]
- Lee, S.H.; Kwon, W.H.; Lim, Y.S.; Park, Y.H. Highly precise AMCW time-of-flight scanning sensor based on parallel-phase demodulation. Measurement 2022, 203, 111860. [Google Scholar] [CrossRef]
- Lee, S.H.; Lim, Y.S.; Kwon, W.H.; Park, Y.H. Multipath Interference Suppression of Amplitude-Modulated Continuous Wave Coaxial-Scanning LiDAR Using Model-Based Synthetic Data Learning. IEEE Sens. J. 2023, 23, 23822–23835. [Google Scholar] [CrossRef]
- Lee, S.H.; Kwon, W.H.; Lim, Y.S.; Park, Y.H. Distance measurement error compensation using machine learning for laser scanning AMCW time-of-flight sensor. In Proceedings of the MOEMS and Miniaturized Systems XXI, San Francisco, CA, USA, 28 January–2 February 2017; SPIE: Bellingham, WA, USA, 2022; Volume 12013, pp. 9–14. [Google Scholar]
- Li, X.; Li, W.; Yin, X.; Ma, X.; Yuan, X.; Zhao, J. Camera-mirror binocular vision-based method for evaluating the performance of industrial robots. IEEE Trans. Instrum. Meas. 2021, 70, 5019214. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Z.; Zhao, C. Vehicle High Beam Light Detection Based on Zoom Binocular Camera and Light Sensor Array. In Proceedings of the 2021 6th International Conference on Control, Robotics and Cybernetics (CRC), Shanghai, China, 9–11 October 2021; pp. 176–180. [Google Scholar]
- Zhang, Z.; Wang, H.; Li, Y.; Li, Z.; Gui, W.; Wang, X.; Zhang, C.; Liang, X.; Li, X. Fringe-Based Structured-Light 3D Reconstruction: Principles, Projection Technologies, and Deep Learning Integration. Sensors 2025, 25, 6296. [Google Scholar] [CrossRef] [PubMed]
- Han, M.; Lei, F.; Shi, W.; Lu, S.; Li, X. Uniaxial MEMS-Based 3D Reconstruction Using Pixel Refinement. Opt. Express 2023, 31, 536. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Zhang, C.; Han, M.; Lei, F.; Liang, X.; Wang, X.; Gui, W.; Li, X. Deep Learning-Driven One-Shot Dual-View 3-D Reconstruction for Dual-Projector System. IEEE Trans. Instrum. Meas. 2024, 73, 5021314. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Liang, X.; Huang, H.; Qian, X.; Feng, F.; Zhang, C.; Wang, X.; Gui, W.; Li, X. Global Phase Accuracy Enhancement of Structured Light System Calibration and 3D Reconstruction by Overcoming Inevitable Unsatisfactory Intensity Modulation. Measurement 2024, 236, 114952. [Google Scholar] [CrossRef]
- Zhou, Q.; Qiao, X.; Ni, K.; Li, X.; Wang, X. Depth Detection in Interactive Projection System Based on One-Shot Black-and-White Stripe Pattern. Opt. Express 2017, 25, 5341. [Google Scholar] [CrossRef]
- Han, M.; Xing, Y.; Wang, X.; Li, X. Projection Superimposition for the Generation of High-Resolution Digital Grating. Optics Lett. 2024, 49, 4473. [Google Scholar] [CrossRef] [PubMed]
- Zheng, T.X.; Huang, S.; Li, Y.F.; Feng, M. Key techniques for vision based 3D reconstruction: A review. Acta Autom. Sin. 2020, 46, 631–652. [Google Scholar]
- Li, Y.; Chen, W.; Li, Z.; Zhang, C.; Wang, X.; Gui, W.; Gao, W.; Liang, X.; Li, X. SL3D-BF: A Real-World Structured Light 3D Dataset with Background-to-Foreground Enhancement. IEEE Trans. Circuits Syst. Video Technol. 2025, 35, 9850–9864. [Google Scholar] [CrossRef]
- Geng, J. Structured-light 3D surface imaging: A tutorial. Adv. Opt. Photonics 2011, 3, 128–160. [Google Scholar] [CrossRef]
- Zong, Y.; Duan, M.; Yu, C.; Li, J. Robust phase unwrapping algorithm for noisy and segmented phase measurements. Opt. Express 2021, 29, 24466–24485. [Google Scholar] [CrossRef]
- Zhu, Z.; Li, M.; Xie, Y.; Zhou, F.; Liu, Y.; Wang, W. The optimal projection intensities determination strategy for robust strip-edge detection in adaptive fringe pattern measurement. Optik 2022, 257, 168771. [Google Scholar] [CrossRef]
- Wang, H.; Lu, Z.; Huang, Z.; Li, Y.; Zhang, C.; Qian, X.; Wang, X.; Gui, W.; Liang, X.; Li, X. A High-Accuracy and Reliable End-to-End Phase Calculation Network and Its Demonstration in High Dynamic Range 3D Reconstruction. Nanomanuf. Metrol. 2025, 8, 5. [Google Scholar] [CrossRef]
- Han, M.; Shi, W.; Lu, S.; Lei, F.; Li, Y.; Wang, X.; Li, X. Internal–External Layered Phase Shifting for Phase Retrieval. IEEE Trans. Instrum. Meas. 2024, 73, 4501013. [Google Scholar] [CrossRef]
- Han, M.; Jiang, H.; Lei, F.; Xing, Y.; Wang, X.; Li, X. Modeling window smoothing effect hidden in fringe projection profilometry. Measurement 2025, 242, 115852. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.; Liu, C.; Lu, S.; Qian, X.; Wang, X.; Zou, Y.; Li, X. An efficient exposure fusion method for 3D measurement with high-reflective objects. In Proceedings of the Optoelectronic Imaging and Multimedia Technology XI, Nantong, China, 13–15 October 2024; SPIE: Bellingham, WA, USA, 2024; Volume 13239, pp. 348–356. [Google Scholar]
- Ri, S.; Takimoto, T.; Xia, P.; Wang, Q.; Tsuda, H.; Ogihara, S. Accurate phase analysis of interferometric fringes by the spatiotemporal phase-shifting method. J. Opt. 2020, 22, 105703. [Google Scholar] [CrossRef]
- Zhang, S.; Yau, S.T. High-resolution, real-time 3D absolute coordinate measurement based on a phase-shifting method. Opt. Express 2006, 14, 2644–2649. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.S.; Su, X.Y. A direct mapping algorithm for phase-measuring profilometry. J. Mod. Opt. 1994, 41, 89–94. [Google Scholar] [CrossRef]
- Huang, L.; Chua, P.S.; Asundi, A. Least-squares calibration method for fringe projection profilometry considering camera lens distortion. Appl. Opt. 2010, 49, 1539–1548. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, H.; Zhang, S.; Guo, T.; Towers, C.E.; Towers, D.P. Simple calibration of a phase-based 3D imaging system based on uneven fringe projection. Opt. Lett. 2011, 36, 627–629. [Google Scholar] [CrossRef]
- Hu, X.; Wang, G.; Zhang, Y.; Yang, H.; Zhang, S. Large depth-of-field 3D shape measurement using an electrically tunable lens. Opt. Express 2019, 27, 29697–29709. [Google Scholar] [CrossRef]
- Cheng, N.J.; Su, W.H. Phase-shifting projected fringe profilometry using binary-encoded patterns. Photonics 2021, 8, 362. [Google Scholar] [CrossRef]
- Xie, X.; Tian, X.; Shou, Z.; Zeng, Q.; Wang, G.; Huang, Q.; Qin, M.; Gao, X. Deep learning phase-unwrapping method based on adaptive noise evaluation. Appl. Opt. 2022, 61, 6861–6870. [Google Scholar] [CrossRef]
- Yu, J.; Da, F. Absolute phase unwrapping for objects with large depth range. IEEE Trans. Instrum. Meas. 2023, 72, 5013310. [Google Scholar] [CrossRef]
- Yue, M.; Wang, J.; Zhang, J.; Zhang, Y.; Tang, Y.; Feng, X. Color crosstalk correction for synchronous measurement of full-field temperature and deformation. Opt. Lasers Eng. 2022, 150, 106878. [Google Scholar] [CrossRef]
- Li, Z.; Gao, N.; Meng, Z.; Zhang, Z.; Gao, F.; Jiang, X. Aided imaging phase measuring deflectometry based on concave focusing mirror. Photonics 2023, 10, 519. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Zhang, Z.; Gao, F.; Jiang, X. 3D measurement of structured specular surfaces using stereo direct phase measurement deflectometry. Machines 2021, 9, 170. [Google Scholar] [CrossRef]
- Lei, F.; Ma, R.; Li, X. Use of Phase-Angle Model for Full-Field 3D Reconstruction under Efficient Local Calibration. Sensors 2024, 24, 2581. [Google Scholar] [CrossRef]
- Lei, F.; Han, M.; Jiang, H.; Wang, X.; Li, X. A Phase-Angle Inspired Calibration Strategy Based on MEMS Projector for 3D Reconstruction with Markedly Reduced Calibration Images and Parameters. Opt. Lasers Eng. 2024, 176, 108078. [Google Scholar] [CrossRef]
- Srinivasan, V.; Liu, H.C.; Halioua, M. Automated phase-measuring profilometry of 3-D diffuse objects. Appl. Opt. 1984, 23, 3105–3108. [Google Scholar] [CrossRef]
- Zhong, J.; Weng, J. Phase retrieval of optical fringe patterns from the ridge of a wavelet transform. Opt. Lett. 2005, 30, 2560–2562. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Chen, W. Fourier transform profilometry: A review. Opt. Lasers Eng. 2001, 35, 263–284. [Google Scholar] [CrossRef]
- Saldner, H.O.; Huntley, J.M. Temporal phase unwrapping: Application to surface profiling of discontinuous objects. Appl. Opt. 1997, 36, 2770–2775. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J.; Zhang, Y. Absolute phase-measurement technique based on number theory in multifrequency grating projection profilometry. Appl. Opt. 2001, 40, 492–500. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, C.; Liang, X.; Han, Z.; Li, Y.; Yang, C.; Gui, W.; Gao, W.; Wang, X.; Li, X. Attention Mono-depth: Attention-enhanced transformer for monocular depth estimation of volatile kiln burden surface. IEEE Trans. Circuits Syst. Video Technol. 2024, 35, 1686–1699. [Google Scholar] [CrossRef]
- Han, M.; Zhang, C.; Zhang, Z.; Li, X. Review of MEMS vibration-mirror-based 3D reconstruction of structured light. Opt. Precis. Eng 2025, 33, 1065–1090. [Google Scholar] [CrossRef]
- Sato, R.; Li, X.; Fischer, A.; Chen, L.C.; Chen, C.; Shimomura, R.; Gao, W. Signal processing and artificial intelligence for dual-detection confocal probes. Int. J. Precis. Eng. Manuf. 2024, 25, 199–223. [Google Scholar] [CrossRef]
- Li, C.; Yan, H.; Qian, X.; Zhu, S.; Zhu, P.; Liao, C.; Tian, H.; Li, X.; Wang, X.; Li, X. A domain adaptation YOLOv5 model for industrial defect inspection. Measurement 2023, 213, 112725. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Z.; Ma, R.; Zhang, C.; Liang, X.; Li, X. Correction of grating patterns for high dynamic range 3D measurement based on deep learning. In Proceedings of the Optoelectronic Imaging and Multimedia Technology XI, Nantong, China, 13–15 October 2024; SPIE: Bellingham, WA, USA, 2024; Volume 13239, pp. 317–325. [Google Scholar]
- Li, K.; Zhang, Z.; Lin, J.; Sato, R.; Matsukuma, H.; Gao, W. Angle measurement based on second harmonic generation using artificial neural network. Nanomanuf. Metrol. 2023, 6, 28. [Google Scholar] [CrossRef]
- Yin, W.; Che, Y.; Li, X.; Li, M.; Hu, Y.; Feng, S.; Lam, E.Y.; Chen, Q.; Zuo, C. Physics-informed deep learning for fringe pattern analysis. Opto-Electron. Adv. 2024, 7, 230034. [Google Scholar] [CrossRef]
- Han, M.; Kan, J.; Yang, G.; Li, X. Robust Ellipsoid Fitting Using Combination of Axial and Sampson Distances. IEEE Trans. Instrum. Meas. 2023, 72, 2526714. [Google Scholar] [CrossRef]
- Li, C.; Pan, X.; Zhu, P.; Zhu, S.; Liao, C.; Tian, H.; Qian, X.; Li, X.; Wang, X.; Li, X. Style Adaptation module: Enhancing detector robustness to inter-manufacturer variability in surface defect detection. Comput. Ind. 2024, 157, 104084. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, C.; Qian, X.; Wang, X.; Gui, W.; Gao, W.; Liang, X.; Li, X. HDRSL Net for Accurate High Dynamic Range Imaging-based Structured Light 3D Reconstruction. IEEE Trans. Image Process. 2025, 34, 5486–5499. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; He, X.; Zhang, C.; Liang, X.; Zhu, P.; Wang, X.; Gui, W.; Li, X.; Qian, X. Accelerating surface defect detection using normal data with an attention-guided feature distillation reconstruction network. Measurement 2025, 246, 116702. [Google Scholar] [CrossRef]
- Duarte, M.F.; Davenport, M.A.; Takhar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R.G. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef]
- Haldar, J.P.; Hernando, D.; Liang, Z.P. Compressed-sensing MRI with random encoding. IEEE Trans. Med. Imaging 2010, 30, 893–903. [Google Scholar] [CrossRef] [PubMed]
- Studer, V.; Bobin, J.; Chahid, M.; Mousavi, H.S.; Candes, E.; Dahan, M. Compressive fluorescence microscopy for biological and hyperspectral imaging. Proc. Natl. Acad. Sci. USA 2012, 109, E1679–E1687. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.K.; Liu, X.F.; Yao, X.R.; Wang, C.; Zhai, Y.; Zhai, G.J. Complementary compressive imaging for the telescopic system. Sci. Rep. 2014, 4, 5834. [Google Scholar] [CrossRef] [PubMed]
- Gong, W.; Zhao, C.; Yu, H.; Chen, M.; Xu, W.; Han, S. Three-dimensional ghost imaging lidar via sparsity constraint. Sci. Rep. 2016, 6, 26133. [Google Scholar] [CrossRef]
- Candès, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Yao, H.; Dai, F.; Zhang, S.; Zhang, Y.; Tian, Q.; Xu, C. Dr2-net: Deep residual reconstruction network for image compressive sensing. Neurocomputing 2019, 359, 483–493. [Google Scholar] [CrossRef]
- Cheng, Z.; Lu, R.; Wang, Z.; Zhang, H.; Chen, B.; Meng, Z.; Yuan, X. BIRNAT: Bidirectional recurrent neural networks with adversarial training for video snapshot compressive imaging. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 258–275. [Google Scholar]
- Hahn, J.; Debes, C.; Leigsnering, M.; Zoubir, A.M. Compressive sensing and adaptive direct sampling in hyperspectral imaging. Digit. Signal Process. 2014, 26, 113–126. [Google Scholar] [CrossRef]
- Clemente, P.; Durán, V.; Tajahuerce, E.; Andrés, P.; Climent, V.; Lancis, J. Compressive holography with a single-pixel detector. Opt. Lett. 2013, 38, 2524–2527. [Google Scholar] [CrossRef]
- Durán, V.; Clemente, P.; Fernández-Alonso, M.; Tajahuerce, E.; Lancis, J. Single-pixel polarimetric imaging. Opt. Lett. 2012, 37, 824–826. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, S.; Peng, J.; Yao, M.; Zheng, G.; Zhong, J. Simultaneous spatial, spectral, and 3D compressive imaging via efficient Fourier single-pixel measurements. Optica 2018, 5, 315–319. [Google Scholar] [CrossRef]
- Ng, R.; Levoy, M.; Brédif, M.; Duval, G.; Horowitz, M.; Hanrahan, P. Light Field Photography with a Hand-Held Plenoptic Camera. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2005. [Google Scholar]
- Dansereau, D.G.; Pizarro, O.; Williams, S.B. Decoding, calibration and rectification for lenselet-based plenoptic cameras. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1027–1034. [Google Scholar]
- Broxton, M.; Grosenick, L.; Yang, S.; Cohen, N.; Andalman, A.; Deisseroth, K.; Levoy, M. Wave optics theory and 3-D deconvolution for the light field microscope. Opt. Express 2013, 21, 25418–25439. [Google Scholar] [CrossRef]
- Prevedel, R.; Yoon, Y.G.; Hoffmann, M.; Pak, N.; Wetzstein, G.; Kato, S.; Schrödel, T.; Raskar, R.; Zimmer, M.; Boyden, E.S.; et al. Simultaneous whole-animal 3D imaging of neuronal activity using light-field microscopy. Nat. Methods 2014, 11, 727–730. [Google Scholar] [CrossRef] [PubMed]
- Gortler, S.J.; Grzeszczuk, R.; Szeliski, R.; Cohen, M.F. The lumigraph. In Seminal Graphics Papers: Pushing the Boundaries, Volume 2; Association for Computing Machinery: New York, NY, USA, 2023; pp. 453–464. [Google Scholar]
- Wilburn, B.; Joshi, N.; Vaish, V.; Talvala, E.V.; Antunez, E.; Barth, A.; Adams, A.; Horowitz, M.; Levoy, M. High performance imaging using large camera arrays. ACM Trans. Graph. (TOG) 2005, 24, 765–776. [Google Scholar] [CrossRef]
- Wang, T.C.; Zhu, J.Y.; Kalantari, N.K.; Efros, A.A.; Ramamoorthi, R. Light field video capture using a learning-based hybrid imaging system. ACM Trans. Graph. (TOG) 2017, 36, 133. [Google Scholar] [CrossRef]
- Veeraraghavan, A.; Raskar, R.; Agrawal, A.; Mohan, A.; Tumblin, J. Dappled photography: Mask enhanced cameras for heterodyned light fields and coded aperture refocusing. ACM Trans. Graph. 2007, 26, 69. [Google Scholar] [CrossRef]
- Marwah, K.; Wetzstein, G.; Bando, Y.; Raskar, R. Compressive light field photography using overcomplete dictionaries and optimized projections. ACM Trans. Graph. (TOG) 2013, 32, 46. [Google Scholar] [CrossRef]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. Nerf: Representing scenes as neural radiance fields for view synthesis. Commun. ACM 2021, 65, 99–106. [Google Scholar] [CrossRef]
- Yoon, Y.; Jeon, H.G.; Yoo, D.; Lee, J.Y.; Kweon, I.S. Light-field image super-resolution using convolutional neural network. IEEE Signal Process. Lett. 2017, 24, 848–852. [Google Scholar] [CrossRef]
- Xiao, Z.; Shi, J.; Jiang, X.; Guillemot, C. Axial refocusing precision model with light fields. Signal Process. Image Commun. 2022, 106, 116721. [Google Scholar] [CrossRef]
- Wanner, S.; Goldluecke, B. Variational light field analysis for disparity estimation and super-resolution. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 606–619. [Google Scholar] [CrossRef]
- Si, L.; Zhu, H.; Wang, Q. Epipolar Plane Image Rectification and Flat Surface Detection in Light Field. J. Electr. Comput. Eng. 2017, 2017, 6142795. [Google Scholar] [CrossRef]
- Ng, R. Digital Light Field Photography; Stanford University: Stanford, CA, USA, 2006. [Google Scholar]
- Ihrke, I.; Restrepo, J.; Mignard-Debise, L. Principles of light field imaging: Briefly revisiting 25 years of research. IEEE Signal Process. Mag. 2016, 33, 59–69. [Google Scholar] [CrossRef]
- Hu, X.; Li, Z.; Miao, L.; Fang, F.; Jiang, Z.; Zhang, X. Measurement technologies of light field camera: An overview. Sensors 2023, 23, 6812. [Google Scholar] [CrossRef]
- Shi, S.; New, T. Development and Application of Light-Field Cameras in Fluid Measurements; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Zhang, H.; Zhou, W.; Lin, L.; Lumsdaine, A. Cascade residual learning based adaptive feature aggregation for light field super-resolution. Pattern Recognit. 2025, 165, 111616. [Google Scholar] [CrossRef]
- Sakai, K.; Takahashi, K.; Fujii, T.; Nagahara, H. Acquiring dynamic light fields through coded aperture camera. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 368–385. [Google Scholar]
- Yang, F.; Yan, W.; Tian, P.; Li, F.; Peng, F. Dynamic three-dimensional shape measurement based on light field imaging. In Proceedings of the 9th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Meta-Surface-Wave and Planar Optics, Chengdu, China, 26–29 June 2018; SPIE: Bellingham, WA, USA, 2019; Volume 10841, pp. 90–96. [Google Scholar]
- Ma, H.; Qian, Z.; Mu, T.; Shi, S. Fast and accurate 3D measurement based on light-field camera and deep learning. Sensors 2019, 19, 4399. [Google Scholar] [CrossRef]
- Chen, X.; Xie, W.; Ma, H.; Chu, J.; Qi, B.; Ren, G.; Sun, X.; Chen, F. Wavefront measurement method based on improved light field camera. Results Phys. 2020, 17, 103007. [Google Scholar] [CrossRef]
- Zhou, P.; Zhang, Y.; Yu, Y.; Cai, W.; Zhou, G. 3D shape measurement based on structured light field imaging. Math. Biosci. Eng. 2020, 17, 654–668. [Google Scholar] [CrossRef] [PubMed]
- Vogt, N. Volumetric imaging with confocal light field microscopy. Nat. Methods 2020, 17, 956. [Google Scholar] [CrossRef]
- Kim, Y.; Jeong, J.; Jang, J.; Kim, M.W.; Park, Y. Polarization holographic microscopy for extracting spatio-temporally resolved Jones matrix. Opt. Express 2012, 20, 9948–9955. [Google Scholar] [CrossRef]
- Huang, B.; Bates, M.; Zhuang, X. Super-resolution fluorescence microscopy. Annu. Rev. Biochem. 2009, 78, 993–1016. [Google Scholar] [CrossRef]
- Schermelleh, L.; Ferrand, A.; Huser, T.; Eggeling, C.; Sauer, M.; Biehlmaier, O.; Drummen, G.P. Super-resolution microscopy demystified. Nat. Cell Biol. 2019, 21, 72–84. [Google Scholar] [CrossRef]
- Huszka, G.; Gijs, M.A. Super-resolution optical imaging: A comparison. Micro Nano Eng. 2019, 2, 7–28. [Google Scholar] [CrossRef]
- Harootunian, A.; Betzig, E.; Isaacson, M.; Lewis, A. Super-resolution fluorescence near-field scanning optical microscopy. Appl. Phys. Lett. 1986, 49, 674–676. [Google Scholar] [CrossRef]
- Betzig, E.; Isaacson, M.; Lewis, A. Collection mode near-field scanning optical microscopy. Appl. Phys. Lett. 1987, 51, 2088–2090. [Google Scholar] [CrossRef]
- Hecht, B.; Sick, B.; Wild, U.P.; Deckert, V.; Zenobi, R.; Martin, O.J.; Pohl, D.W. Scanning near-field optical microscopy with aperture probes: Fundamentals and applications. J. Chem. Phys. 2000, 112, 7761–7774. [Google Scholar] [CrossRef]
- Gleyzes, P.; Boccara, A.; Bachelot, R. Near field optical microscopy using a metallic vibrating tip. Ultramicroscopy 1995, 57, 318–322. [Google Scholar] [CrossRef]
- Reddick, R.; Warmack, R.; Ferrell, T. New form of scanning optical microscopy. Phys. Rev. B 1989, 39, 767. [Google Scholar] [CrossRef] [PubMed]
- Heinzelmann, H.; Hecht, B.; Novotny, L.; Pohl, D. Forbidden light scanning near-field optical microscopy. J. Microsc. 1995, 177, 115–118. [Google Scholar] [CrossRef]
- Zenhausern, F.; Martin, Y.; Wickramasinghe, H. Scanning interferometric apertureless microscopy: Optical imaging at 10 angstrom resolution. Science 1995, 269, 1083–1085. [Google Scholar] [CrossRef]
- Fischer, U.C.; Koglin, J.; Fuchs, H. The tetrahedral tip as a probe for scanning near-field optical microscopy at 30 nm resolution. J. Microsc. 1994, 176, 231–237. [Google Scholar] [CrossRef]
- Takahashi, S.; Ikeda, Y.; Takamasu, K. Study on nano thickness inspection for residual layer of nanoimprint lithography using near-field optical enhancement of metal tip. CIRP Ann. 2013, 62, 527–530. [Google Scholar] [CrossRef]
- Ohtsu, M. Progress of high-resolution photon scanning tunneling microscopy due to a nanometric fiber probe. J. Light. Technol. 1995, 13, 1200–1221. [Google Scholar] [CrossRef]
- Quantum Design GmbH. neaSNOM Scattering-Type Scanning Near-Field Optical Microscope. 2021. Available online: https://www.qd-china.com/zh/pro/detail/3/1912091147703?bing-pc-719-151amp;msclkid=aa7a5d9e593b177526543492148d8d7e (accessed on 8 August 2025).
- Di Francia, G.T. Super-gain antennas and optical resolving power. Il Nuovo C. 1952, 9, 426–438. [Google Scholar] [CrossRef]
- Okazaki, S. High resolution optical lithography or high throughput electron beam lithography: The technical struggle from the micro to the nano-fabrication evolution. Microelectron. Eng. 2015, 133, 23–35. [Google Scholar] [CrossRef]
- Tang, F.; Wang, Y.; Qiu, L.; Zhao, W.; Sun, Y. Super-resolution radially polarized-light pupil-filtering confocal sensing technology. Appl. Opt. 2014, 53, 7407–7414. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Tan, J.; Qiu, L. Bipolar absolute differential confocal approach to higher spatial resolution. Opt. Express 2004, 12, 5013–5021. [Google Scholar] [CrossRef]
- Li, Z.; Herrmann, K.; Pohlenz, F. Lateral scanning confocal microscopy for the determination of in-plane displacements of microelectromechanical systems devices. Opt. Lett. 2007, 32, 1743–1745. [Google Scholar] [CrossRef]
- Aguilar, J.F.; Lera, M.; Sheppard, C.J. Imaging of spheres and surface profiling by confocal microscopy. Appl. Opt. 2000, 39, 4621–4628. [Google Scholar] [CrossRef]
- Arrasmith, C.L.; Dickensheets, D.L.; Mahadevan-Jansen, A. MEMS-based handheld confocal microscope for in-vivo skin imaging. Opt. Express 2010, 18, 3805–3819. [Google Scholar] [CrossRef]
- Sun, C.C.; Liu, C.K. Ultrasmall focusing spot with a long depth of focus based on polarization and phase modulation. Opt. Lett. 2003, 28, 99–101. [Google Scholar] [CrossRef]
- Heintzmann, R.; Huser, T. Super-resolution structured illumination microscopy. Chem. Rev. 2017, 117, 13890–13908. [Google Scholar] [CrossRef]
- Wu, Y.; Shroff, H. Faster, sharper, and deeper: Structured illumination microscopy for biological imaging. Nat. Methods 2018, 15, 1011–1019. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, S.; Kudo, R.; Usuki, S.; Takamasu, K. Super resolution optical measurements of nanodefects on Si wafer surface using infrared standing evanescent wave. CIRP Ann. 2011, 60, 523–526. [Google Scholar] [CrossRef]
- Gustafsson, M.G. Nonlinear structured-illumination microscopy: Wide-field fluorescence imaging with theoretically unlimited resolution. Proc. Natl. Acad. Sci. USA 2005, 102, 13081–13086. [Google Scholar] [CrossRef] [PubMed]
- Habuchi, S. Super-resolution molecular and functional imaging of nanoscale architectures in life and materials science. Front. Bioeng. Biotechnol. 2014, 2, 20. [Google Scholar] [CrossRef]
- Chen, Z.; Taflove, A.; Backman, V. Photonic nanojet enhancement of backscattering of light by nanoparticles: A potential novel visible-light ultramicroscopy technique. Opt. Express 2004, 12, 1214–1220. [Google Scholar] [CrossRef]
- Li, X.; Chen, Z.; Taflove, A.; Backman, V. Optical analysis of nanoparticles via enhanced backscattering facilitated by 3-D photonic nanojets. Opt. Express 2005, 13, 526–533. [Google Scholar] [CrossRef]
- Itagi, A.; Challener, W. Optics of photonic nanojets. J. Opt. Soc. Am. A 2005, 22, 2847–2858. [Google Scholar] [CrossRef]
- Ferrand, P.; Wenger, J.; Devilez, A.; Pianta, M.; Stout, B.; Bonod, N.; Popov, E.; Rigneault, H. Direct imaging of photonic nanojets. Opt. Express 2008, 16, 6930–6940. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Guo, W.; Li, L.; Luk’Yanchuk, B.; Khan, A.; Liu, Z.; Chen, Z.; Hong, M. Optical virtual imaging at 50 nm lateral resolution with a white-light nanoscope. Nat. Commun. 2011, 2, 218. [Google Scholar] [CrossRef]
- Lee, J.Y.; Hong, B.H.; Kim, W.Y.; Min, S.K.; Kim, Y.; Jouravlev, M.V.; Bose, R.; Kim, K.S.; Hwang, I.C.; Kaufman, L.J.; et al. Near-field focusing and magnification through self-assembled nanoscale spherical lenses. Nature 2009, 460, 498–501. [Google Scholar] [CrossRef]
- Berera, R.; van Grondelle, R.; Kennis, J.T. Ultrafast transient absorption spectroscopy: Principles and application to photosynthetic systems. Photosynth. Res. 2009, 101, 105–118. [Google Scholar] [CrossRef]
- Zacharioudaki, D.E.; Fitilis, I.; Kotti, M. Review of fluorescence spectroscopy in environmental quality applications. Molecules 2022, 27, 4801. [Google Scholar] [CrossRef]
- Yi, J.; You, E.M.; Hu, R.; Wu, D.Y.; Liu, G.K.; Yang, Z.L.; Zhang, H.; Gu, Y.; Wang, Y.H.; Wang, X.; et al. Surface-enhanced Raman spectroscopy: A half-century historical perspective. Chem. Soc. Rev. 2025, 54, 1453–1551. [Google Scholar] [CrossRef] [PubMed]
- Fathy, A.; Sabry, Y.M.; Nazeer, S.; Bourouina, T.; Khalil, D.A. On-chip parallel Fourier transform spectrometer for broadband selective infrared spectral sensing. Microsystems Nanoeng. 2020, 6, 10. [Google Scholar] [CrossRef]
- Bamji, C.; Godbaz, J.; Oh, M.; Mehta, S.; Payne, A.; Ortiz, S.; Nagaraja, S.; Perry, T.; Thompson, B. A review of indirect time-of-flight technologies. IEEE Trans. Electron Devices 2022, 69, 2779–2793. [Google Scholar] [CrossRef]
- Restelli, F.; Pollo, B.; Vetrano, I.G.; Cabras, S.; Broggi, M.; Schiariti, M.; Falco, J.; de Laurentis, C.; Raccuia, G.; Ferroli, P.; et al. Confocal laser microscopy in neurosurgery: State of the art of actual clinical applications. J. Clin. Med. 2021, 10, 2035. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Yu, Q.; Shang, W.; Wang, C.; Liu, T.; Wang, Y.; Cheng, F. Chromatic confocal measurement system and its experimental study based on inclined illumination. Chin. Opt. 2022, 15, 514–524. [Google Scholar] [CrossRef]
- Wang, J.; Chen, F.; Liu, B.; Gan, Y.; Liu, G. White LED-based spectrum confocal displacement sensor. China Meas. Test 2017, 43, 69–73. [Google Scholar]
- Mullan, F.; Bartlett, D.; Austin, R.S. Measurement uncertainty associated with chromatic confocal profilometry for 3D surface texture characterization of natural human enamel. Dent. Mater. 2017, 33, e273–e281. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ma, R.; Bai, J. High-precision chromatic confocal technologies: A review. Micromachines 2024, 15, 1224. [Google Scholar] [CrossRef]
- Wu, J.; Yao, J.; Ren, A.; Ju, Z.; Lin, R.; Wang, Z.; Zhu, W.; Ju, B.; Tsai, D.P. Meta-Dispersive 3D Chromatic Confocal Measurement. Adv. Sci. 2025, 12, e08774. [Google Scholar] [CrossRef]
- Zhou, R.; Shen, D.; Huang, P.; Kong, L.; Zhu, Z. Chromatic confocal sensor-based sub-aperture scanning and stitching for the measurement of microstructured optical surfaces. Opt. Express 2021, 29, 33512–33526. [Google Scholar] [CrossRef]
- Nadim, E.H.; Hichem, N.; Nabil, A.; Mohamed, D.; Olivier, G. Comparison of tactile and chromatic confocal measurements of aspherical lenses for form metrology. Int. J. Precis. Eng. Manuf. 2014, 15, 821–829. [Google Scholar] [CrossRef]
- Rishikesan, V.; Samuel, G. Evaluation of surface profile parameters of a machined surface using confocal displacement sensor. Procedia Mater. Sci. 2014, 5, 1385–1391. [Google Scholar] [CrossRef]
- Nouira, H.; El-Hayek, N.; Yuan, X.; Anwer, N. Characterization of the main error sources of chromatic confocal probes for dimensional measurement. Meas. Sci. Technol. 2014, 25, 044011. [Google Scholar] [CrossRef]
- Bai, J.; Wang, Y.; Wang, X.; Zhou, Q.; Ni, K.; Li, X. Three-probe error separation with chromatic confocal sensors for roundness measurement. Nanomanuf. Metrol. 2021, 4, 247–255. [Google Scholar] [CrossRef]
- Lan, H.; Lei, D.; Qian, L.; Xia, H.; Sun, S. A non contact system for measurement of rotating error based on confocal chromatic displacement sensor. Manuf. Technol. Mach. Tool 2017, 2017, 141–145. [Google Scholar]
- Zakrzewski, A.; Koruba, P.; Ćwikła, M.; Reiner, J. The determination of the measurement beam source in a chromatic confocal displacement sensor integrated with an optical laser head. Opt. Laser Technol. 2022, 153, 108268. [Google Scholar] [CrossRef]
- Bi, C.; Li, D.; Fang, J.; Zhang, B. Application of chromatic confocal displacement sensor in measurement of tip clearance. In Proceedings of the Optical Measurement Technology and Instrumentation, Beijing, China, 9–11 May 2016; SPIE: Bellingham, WA, USA, 2016; Volume 10155, pp. 455–462. [Google Scholar]
- Ueda, S.i.; Michihata, M.; Hayashi, T.; Takaya, Y. Wide-range axial position measurement for jumping behavior of optically trapped microsphere near surface using chromatic confocal sensor. Int. J. Optomechatronics 2015, 9, 131–140. [Google Scholar] [CrossRef]
- Agoyan, M.; Fourneau, G.; Cheymol, G.; Ladaci, A.; Maskrot, H.; Destouches, C.; Fourmentel, D.; Girard, S.; Boukenter, A. Toward confocal chromatic sensing in nuclear reactors: In situ optical refractive index measurements of bulk glass. IEEE Trans. Nucl. Sci. 2022, 69, 722–730. [Google Scholar] [CrossRef]
- Dai, W.; Liu, Y.; Su, F.; Wang, W. Chromatic confocal imaging based mechanical test platform for micro porous membrane. In Proceedings of the 2016 13th IEEE International Conference on Solid-State and Integrated Circuit Technology (ICSICT), Hangzhou, China, 25–28 October 2016; pp. 266–268. [Google Scholar]
- Berkovic, G.; Zilberman, S.; Shafir, E.; Cohen-Sabban, J. Vibrometry using a chromatic confocal sensor. In Proceedings of the 11th International Conference on Vibration Measurements by Laser and Noncontact Techniques-Aivela 2014: Advances and Applications, Ancona, Italy, 25–27 June 2014; Volume 1600, pp. 439–444. [Google Scholar]
- Yang, W.; Liu, X.; Lu, W.; Guo, X. Influence of probe dynamic characteristics on the scanning speed for white light interference based AFM. Precis. Eng. 2018, 51, 348–352. [Google Scholar] [CrossRef]
- Wang, J.; Liu, T.; Tang, X.; Hu, J.; Wang, X.; Li, G.; He, T.; Yang, S. Fiber-coupled chromatic confocal 3D measurement system and comparative study of spectral data processing algorithms. Acta Photonica Sin. 2021, 50, 1112001. [Google Scholar]
- Zhang, N.; Xu, X.; Wu, J.; Liu, Y.; Li, L. Study on Thickness Measurement System of Transparent Materials Based on Chromatic Confocal. J. Chang. Univ. Sci. Technol. (Nat. Sci. Ed.) 2013, 36, 1–6. (In Chinese) [Google Scholar]
- Yu, Q.; Zhang, K.; Cui, C.; Zhou, R.; Cheng, F.; Ye, R.; Zhang, Y. Method of thickness measurement for transparent specimens with chromatic confocal microscopy. Appl. Opt. 2018, 57, 9722–9728. [Google Scholar] [CrossRef]
- Chen, Y.C.; Dong, S.P.; Wang, C.C.; Kuo, S.H.; Wang, W.C.; Tai, H.M. Using chromatic confocal apparatus for in situ rolling thickness measurement in hot embossing process. In Proceedings of the Instrumentation, Metrology, and Standards for Nanomanufacturing IV, San Diego, CA, USA, 2–4 August 2010; SPIE: Bellingham, WA, USA, 2010; Volume 7767, pp. 128–134. [Google Scholar]
- Niese, S.; Quodbach, J. Application of a chromatic confocal measurement system as new approach for in-line wet film thickness determination in continuous oral film manufacturing processes. Int. J. Pharm. 2018, 551, 203–211. [Google Scholar] [CrossRef] [PubMed]
- Bai, J.; Li, J.; Wang, X.; Zhou, Q.; Ni, K.; Li, X. A new method to measure spectral reflectance and film thickness using a modified chromatic confocal sensor. Opt. Lasers Eng. 2022, 154, 107019. [Google Scholar] [CrossRef]
- Li, S.; Song, B.; Peterson, T.; Hsu, J.; Liang, R. MicroLED chromatic confocal microscope. Opt. Lett. 2021, 46, 2722–2725. [Google Scholar] [CrossRef]
- Bai, J.; Li, X.; Wang, X.; Zhou, Q.; Ni, K. Chromatic confocal displacement sensor with optimized dispersion probe and modified centroid peak extraction algorithm. Sensors 2019, 19, 3592. [Google Scholar] [CrossRef]
- Shi, K.; Li, P.; Yin, S.; Liu, Z. Chromatic confocal microscopy using supercontinuum light. Opt. Express 2004, 12, 2096–2101. [Google Scholar] [CrossRef]
- Minoni, U.; Manili, G.; Bettoni, S.; Varrenti, E.; Modotto, D.; De Angelis, C. Chromatic confocal setup for displacement measurement using a supercontinuum light source. Opt. Laser Technol. 2013, 49, 91–94. [Google Scholar] [CrossRef]
- Liu, H.; Wang, B.; Wang, R.; Wang, M.; Yu, D.; Wang, W. Photopolymer-based coaxial holographic lens for spectral confocal displacement and morphology measurement. Opt. Lett. 2019, 44, 3554–3557. [Google Scholar] [CrossRef]
- Reyes, J.G.; Meneses, J.; Plata, A.; Tribillon, G.M.; Gharbi, T. Axial resolution of a chromatic dispersion confocal microscopy. In Proceedings of the 5th Iberoamerican Meeting on Optics and 8th Latin American Meeting on Optics, Lasers, and Their Applications, Porlamar, Venezuela, 3–8 October 2004; SPIE: Bellingham, WA, USA, 2004; Volume 5622, pp. 766–771. [Google Scholar]
- Chen, X.; Nakamura, T.; Shimizu, Y.; Chen, C.; Chen, Y.L.; Matsukuma, H.; Gao, W. A chromatic confocal probe with a mode-locked femtosecond laser source. Opt. Laser Technol. 2018, 103, 359–366. [Google Scholar] [CrossRef]
- Molesini, G.; Pedrini, G.; Poggi, P.; Quercioli, F. Focus-wavelength encoded optical profilometer. Opt. Commun. 1984, 49, 229–233. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, Q.; Shang, W.; Wang, C.; Liu, T.; Wang, Y.; Cheng, F. Design and Experimental Study of an Oblique-Illumination Color Confocal Measurement System. Chin. Opt. 2022, 15, 514–524. (In Chinese) [Google Scholar]
- Li, Y.; Fan Sr, J.; Wang, J.; Wang, C.; Fan, H. Design research of chromatic lens in chromatic confocal point sensors. In Proceedings of the Sixth International Conference on Optical and Photonic Engineering (icOPEN 2018), Shanghai, China, 8–11 May 2018; SPIE: Bellingham, WA, USA, 2018; Volume 10827, pp. 73–76. [Google Scholar]
- Niu, C.; Li, X.; Lang, X. Design and Performance Optimization of Spectral Confocal Lens Assembly. J. Beijing Inf. Sci. Technol. Univ. 2013, 28, 42–45. (In Chinese) [Google Scholar]
- Liu, Q.; Yang, W.; Yuan, D.; Wang, Y. Design of Linearly Dispersive Objective for Spectral Confocal Microscopy. Opt. Precis. Eng. 2013, 21, 2473–2479. (In Chinese) [Google Scholar]
- Liu, Q.; Wang, Y.; Yang, W.; Yuan, D. Spectral Confocal Measurement Technique with Linear Dispersion Design. High Power Laser Part. Beams 2014, 26, 58–63. (In Chinese) [Google Scholar]
- Shao, T.; Guo, W.; Xi, Y.; Liu, Z.; Yang, K.; Xia, M. Design and Performance Evaluation of a Large-Range Spectral Confocal Displacement Sensor. Chin. J. Lasers 2022, 49, 1804002. (In Chinese) [Google Scholar]
- Wang, A.s.; Xie, B.; Liu, Z.w. Design of measurement system of 3D surface profile based on chromatic confocal technology. In Proceedings of the 2017 International Conference on Optical Instruments and Technology: Optical Systems and Modern Optoelectronic Instruments, Beijing, China, 28–30 October 2017; SPIE: Bellingham, WA, USA, 2018; Volume 10616, pp. 342–347. [Google Scholar]
- Yang, R.; Yun, Y.; Xie, B.; Wang, A.; Liu, Z.; Liu, C. Design of a Super-Dispersive Linear Objective Lens for Spectral Confocal 3D Profilometer. High Power Laser Part. Beams 2018, 30, 9–13. (In Chinese) [Google Scholar]
- Dobson, S.L.; Sun, P.c.; Fainman, Y. Diffractive lenses for chromatic confocal imaging. Appl. Opt. 1997, 36, 4744–4748. [Google Scholar] [CrossRef] [PubMed]
- Garzón, J.; Duque, D.; Alean, A.; Toledo, M.; Meneses, J.; Gharbi, T. Diffractive elements performance in chromatic confocal microscopy. J. Phys. Conf. Ser. 2011, 274, 012069. [Google Scholar] [CrossRef]
- Rayer, M.; Mansfield, D. Chromatic confocal microscopy using staircase diffractive surface. Appl. Opt. 2014, 53, 5123–5130. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Wang, J.; Liu, Q.; Hu, J.; Wang, Z.; Wan, C.; Yang, S. Chromatic confocal measurement method using a phase Fresnel zone plate. Opt. Express 2022, 30, 2390–2401. [Google Scholar] [CrossRef]
- Hillenbrand, M.; Lorenz, L.; Kleindienst, R.; Grewe, A.; Sinzinger, S. Spectrally multiplexed chromatic confocal multipoint sensing. Opt. Lett. 2013, 38, 4694–4697. [Google Scholar] [CrossRef]
- Hillenbrand, M.; Mitschunas, B.; Wenzel, C.; Grewe, A.; Ma, X.; Feßer, P.; Bichra, M.; Sinzinger, S. Hybrid hyperchromats for chromatic confocal sensor systems. Adv. Opt. Technol. 2012, 1, 187–194. [Google Scholar] [CrossRef]
- Jin, B.; Deng, W.; Niu, C.; Li, X. Design of dispersive lens group for chromatic confocal measuring system. Opt. Tech. 2012, 38, 660–664. [Google Scholar]
- Pruss, C.; Ruprecht, A.; Korner, K.; Osten, W.; Lucke, P. Diffractive elements for chromatic confocal sensors. DGaO Proc. 2005, 2–3. Available online: https://www.dgao-proceedings.de/download/106/106_a1.pdf (accessed on 11 August 2025).
- Fleischle, D.; Lyda, W.; Schaal, F.; Osten, W. Chromatic confocal sensor for in-process measurement during lathing. In Proceedings of the 10th International Symposium of Measurement Technology and Intelligent Instruments, Daejeon, Republic of Korea, 29 June–2 July 2011; Volume 29. [Google Scholar]
- Ruprecht, A.K.; Pruss, C.; Tiziani, H.J.; Osten, W.; Lucke, P.; Last, A.; Mohr, J.; Lehmann, P. Confocal micro-optical distance sensor: Principle and design. In Proceedings of the Optical Measurement Systems for Industrial Inspection IV, Munich, Germany, 13–17 June 2005; SPIE: Bellingham, WA, USA, 2005; Volume 5856, pp. 128–135. [Google Scholar]
- Park, H.M.; Kwon, U.; Joo, K.N. Vision chromatic confocal sensor based on a geometrical phase lens. Appl. Opt. 2021, 60, 2898–2901. [Google Scholar] [CrossRef] [PubMed]
- Luecke, P.; Last, A.; Mohr, J.; Ruprecht, A.; Osten, W.; Tiziani, H.J.; Lehmann, P. Confocal micro-optical distance sensor for precision metrology. In Proceedings of the Optical Sensing, Strasbourg, France, 26–30 April 2004; SPIE: Bellingham, WA, USA, 2004; Volume 5459, pp. 180–184. [Google Scholar]
- Ruprecht, A.; Wiesendanger, T.; Tiziani, H. Chromatic confocal microscopy with a finite pinhole size. Opt. Lett. 2004, 29, 2130–2132. [Google Scholar] [CrossRef]
- Tiziani, H.; Achi, R.; Krämer, R. Chromatic confocal microscopy with microlenses. J. Mod. Opt. 1996, 43, 155–163. [Google Scholar] [CrossRef]
- Tiziani, H.J.; Uhde, H.M. Three-dimensional image sensing by chromatic confocal microscopy. Appl. Opt. 1994, 33, 1838–1843. [Google Scholar] [CrossRef]
- Ang, K.T.; Fang, Z.P.; Tay, A. Note: Development of high speed confocal 3D profilometer. Rev. Sci. Instruments 2014, 85, 116103. [Google Scholar] [CrossRef]
- Hwang, J.; Kim, S.; Heo, J.; Lee, D.; Ryu, S.; Joo, C. Frequency-and spectrally-encoded confocal microscopy. Opt. Express 2015, 23, 5809–5821. [Google Scholar] [CrossRef]
- Hillenbrand, M.; Weiss, R.; Endrödy, C.; Grewe, A.; Hoffmann, M.; Sinzinger, S. Chromatic confocal matrix sensor with actuated pinhole arrays. Appl. Opt. 2015, 54, 4927–4936. [Google Scholar] [CrossRef]
- Chanbai, S.; Wiora, G.; Weber, M.; Roth, H. A novel confocal line scanning sensor. In Proceedings of the Scanning Microscopy 2009, Monterey, CA, USA, 4–7 May 2009; SPIE: Bellingham, WA, USA, 2009; Volume 7378, pp. 351–358. [Google Scholar]
- Hu, H.; Mei, S.; Fan, L.; Wang, H. A line-scanning chromatic confocal sensor for three-dimensional profile measurement on highly reflective materials. Rev. Sci. Instruments 2021, 92, 053707. [Google Scholar] [CrossRef]
- Cui, Q.; Liang, R. Chromatic confocal microscopy using liquid crystal display panels. Appl. Opt. 2019, 58, 2085–2090. [Google Scholar] [CrossRef] [PubMed]
- Luo, D.; Kuang, C.; Liu, X. Fiber-based chromatic confocal microscope with Gaussian fitting method. Opt. Laser Technol. 2012, 44, 788–793. [Google Scholar] [CrossRef]
- Chen, C.; Yang, W.; Wang, J.; Lu, W.; Liu, X.; Jiang, X. Accurate and efficient height extraction in chromatic confocal microscopy using corrected fitting of the differential signal. Precis. Eng. 2019, 56, 447–454. [Google Scholar] [CrossRef]
- Shi, K.; Li, P.; Yin, S.; Liu, Z. Surface profile measurement using chromatic confocal microscopy. In Proceedings of the Two-and Three-Dimensional Vision Systems for Inspection, Control, and Metrology II, Philadelphia, PA, USA, 26–27 October 2004; SPIE: Bellingham, WA, USA, 2004; Volume 5606, pp. 124–131. [Google Scholar]
- Ruprecht, A.K.; Koerner, K.; Wiesendanger, T.F.; Tiziani, H.J.; Osten, W. Chromatic confocal detection for high-speed microtopography measurements. In Proceedings of the Three-Dimensional Image Capture and Applications VI, San Jose, CA, USA, 19–20 January 2004; SPIE: Bellingham, WA, USA, 2004; Volume 5302, pp. 53–60. [Google Scholar]
- Taphanel, M.; Hovestreydt, B.; Beyerer, J. Speed-up chromatic sensors by optimized optical filters. In Proceedings of the Optical Measurement Systems for Industrial Inspection VIII, Munich, Germany, 13–17 May 2013; SPIE: Bellingham, WA, USA, 2013; Volume 8788, pp. 190–199. [Google Scholar]
- Kim, T.; Kim, S.H.; Do, D.; Yoo, H.; Gweon, D. Chromatic confocal microscopy with a novel wavelength detection method using transmittance. Opt. Express 2013, 21, 6286–6294. [Google Scholar] [CrossRef]
- Chen, L.C.; Nguyen, D.T.; Chang, Y.W. Precise optical surface profilometry using innovative chromatic differential confocal microscopy. Opt. Lett. 2016, 41, 5660–5663. [Google Scholar] [CrossRef]
- Yu, Q.; Zhang, K.; Zhou, R.; Cui, C.; Cheng, F.; Fu, S.; Ye, R. Calibration of a chromatic confocal microscope for measuring a colored specimen. IEEE Photonics J. 2018, 10, 6901109. [Google Scholar] [CrossRef]
- Bai, J.; Li, X.; Wang, X.; Wang, J.; Ni, K.; Zhou, Q. Self-reference dispersion correction for chromatic confocal displacement measurement. Opt. Lasers Eng. 2021, 140, 106540. [Google Scholar] [CrossRef]
- Tan, J.; Liu, C.; Liu, J.; Wang, H. Sinc2 fitting for height extraction in confocal scanning. Meas. Sci. Technol. 2015, 27, 025006. [Google Scholar] [CrossRef]
- Ruprecht, A.; Wiesendanger, T.; Tiziani, H. Signal evaluation for high-speed confocal measurements. Appl. Opt. 2002, 41, 7410–7415. [Google Scholar] [CrossRef] [PubMed]
- Deng, W.; Niu, C.; Lv, N.; Gao, X. Research on chromatic confocal technology for displacement measurement. In Proceedings of the Fourth International Seminar on Modern Cutting and Measurement Engineering, Beijing, China, 10–12 December 2010; SPIE: Bellingham, WA, USA, 2011; Volume 7997, pp. 457–462. [Google Scholar]
- Niu, C.H.; Lv, Y. Chromatic confocal displacement measurment based on correlation algorithm. Appl. Mech. Mater. 2014, 446, 909–914. [Google Scholar] [CrossRef]
- Lu, W.; Chen, C.; Zhu, H.; Wang, J.; Leach, R.; Liu, X.; Wang, J.; Jiang, X. Fast and accurate mean-shift vector based wavelength extraction for chromatic confocal microscopy. Meas. Sci. Technol. 2019, 30, 115104. [Google Scholar] [CrossRef]
- Rey-Barroso, L.; Peña-Gutiérrez, S.; Yáñez, C.; Burgos-Fernández, F.J.; Vilaseca, M.; Royo, S. Optical technologies for the improvement of skin cancer diagnosis: A review. Sensors 2021, 21, 252. [Google Scholar] [CrossRef]
- Nishiyabu, R.; Shimizu, A. Boronic acid as an efficient anchor group for surface modification of solid polyvinyl alcohol. Chem. Commun. 2016, 52, 9765–9768. [Google Scholar] [CrossRef] [PubMed]
- Forbes, A.; Haverkamp, R.G.; Robertson, T.; Bryant, J.; Bearsley, S. Studies of the microstructure of polymer-modified bitumen emulsions using confocal laser scanning microscopy. J. Microsc. 2001, 204, 252–257. [Google Scholar] [CrossRef]
- Werner, J.G.; Deveney, B.T.; Nawar, S.; Weitz, D.A. Dynamic microcapsules with rapid and reversible permeability switching. Adv. Funct. Mater. 2018, 28, 1803385. [Google Scholar] [CrossRef]
- Chen, X.; Zeng, Z.; Wang, H.; Xi, P. Three-dimensional multimodal sub-diffraction imaging with spinning-disk confocal microscopy using blinking/fluctuating probes. Nano Res. 2015, 8, 2251–2260. [Google Scholar] [CrossRef]
- Teodori, L.; Crupi, A.; Costa, A.; Diaspro, A.; Melzer, S.; Tarnok, A. Three-dimensional imaging technologies: A priority for the advancement of tissue engineering and a challenge for the imaging community. J. Biophotonics 2017, 10, 24–45. [Google Scholar] [CrossRef]
- Mou, C.L.; Wang, W.; Li, Z.L.; Ju, X.J.; Xie, R.; Deng, N.N.; Wei, J.; Liu, Z.; Chu, L.Y. Trojan-horse-like stimuli-responsive microcapsules. Adv. Sci. 2018, 5, 1700960. [Google Scholar] [CrossRef]
- Yang, P.; Li, Q.; Wang, S.; Zhuang, W.; Zhou, J.; Zhu, S.; Wu, J.; Ying, H. Application of a humidity-mediated method to remove residual solvent from crystal lattice. Food Chem. 2019, 294, 123–129. [Google Scholar] [CrossRef] [PubMed]
- Alali, S.; Vitkin, A. Polarized light imaging in biomedicine: Emerging Mueller matrix methodologies for bulk tissue assessment. J. Biomed. Opt. 2015, 20, 061104. [Google Scholar] [CrossRef] [PubMed]
- Zaffar, M.; Pradhan, A. Assessment of anisotropy of collagen structures through spatial frequencies of Mueller matrix images for cervical pre-cancer detection. Appl. Opt. 2020, 59, 1237–1248. [Google Scholar] [CrossRef]
- Novikova, T.; Pierangelo, A.; Manhas, S.; Benali, A.; Validire, P.; Gayet, B.; De Martino, A. The origins of polarimetric image contrast between healthy and cancerous human colon tissue. Appl. Phys. Lett. 2013, 102, 241103. [Google Scholar] [CrossRef]
- Zhao, W.; Tang, L.; Yang, S.; Qiu, L. Research on high-precision large-aperture laser differential confocal-interferometric optical element multi-parameter measurement method. Light Adv. Manuf. 2025, 5, 553–566. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, T.; Yang, Y.; Mi, X.; Wang, J. Differential Confocal Optical Probes with Optimized Detection Efficiency and Pearson Correlation Coefficient Strategy Based on the Peak-Clustering Algorithm. Micromachines 2023, 14, 1163. [Google Scholar] [CrossRef]
- Wang, F.; Tan, J.; Zhao, W. Optical probe using differential confocal technique for surface profile. In Proceedings of the Process Control and Inspection for Industry, Beijing, China, 8–10 November 2000; SPIE: Bellingham, WA, USA, 2000; Volume 4222, pp. 194–197. [Google Scholar]
- Sun, Y.; Zhao, W.; Qiu, L.; Li, R.; Wang, Y. Axial high-resolution differential confocal microscopy. Meas. Sci. Technol. 2019, 30, 125402. [Google Scholar] [CrossRef]
- Si, K.; Gong, W.; Sheppard, C.J. Three-dimensional coherent transfer function for a confocal microscope with two D-shaped pupils. Appl. Opt. 2009, 48, 810–817. [Google Scholar] [CrossRef]
- Wang, Y.; Qiu, L.; Zhao, X.; Zhao, W. Divided-aperture differential confocal fast-imaging microscopy. Meas. Sci. Technol. 2017, 28, 035401. [Google Scholar] [CrossRef]
- Zou, L.M.; Li, X.; Zhang, H.J.; Ding, X.M. Improvement of lateral resolution property of differential confocal system using radial birefringent pupil filter. In Proceedings of the Fifth International Symposium on Instrumentation Science and Technology, Shenyang, China, 15–18 September 2008; SPIE: Bellingham, WA, USA, 2009; Volume 7133, pp. 941–951. [Google Scholar]
- Wang, Y.; Qiu, L.; Zhao, W. High precision radially-polarized-light pupil-filtering differential confocal measurement. Opt. Laser Technol. 2016, 82, 87–93. [Google Scholar] [CrossRef]
- Wu, G.W.; Chen, L.C. Precise 3-D microscopic profilometry using diffractive image microscopy and artificial neural network in single-exposure manner. Opt. Lasers Eng. 2021, 147, 106732. [Google Scholar] [CrossRef]
- Sheng, Z.; Wang, Y.; Zhao, W.; Qiu, L.; Sun, Y. Laser differential fitting confocal microscopy with high imaging efficiency. Appl. Opt. 2016, 55, 6903–6909. [Google Scholar] [CrossRef]
- Zhao, W.; Jiang, Q.; Qiu, L.; Liu, D. Dual-axes differential confocal microscopy with high axial resolution and long working distance. Opt. Commun. 2011, 284, 15–19. [Google Scholar] [CrossRef]
- Mauch, F.; Lyda, W.; Gronle, M.; Osten, W. Improved signal model for confocal sensors accounting for object depending artifacts. Opt. Express 2012, 20, 19936–19945. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, T.; Yang, Y.; Yang, Y.; Mi, X.; Wang, J. Precise Two-Dimensional Tilt Measurement Sensor with Double-Cylindrical Mirror Structure and Modified Mean-Shift Algorithm for a Confocal Microscopy System. Sensors 2022, 22, 6794. [Google Scholar] [CrossRef]
- Cacace, L. An Optical Distance Sensor: Tilt Robust Differential Confocal Measurement with mm Range and nm Uncertainty; Technische Universiteit Eindhoven: Eindhoven, The Netherlands, 2009. [Google Scholar]
- Moharam, M.; Gaylord, T.K. Rigorous coupled-wave analysis of planar-grating diffraction. J. Opt. Soc. Am. 1981, 71, 811–818. [Google Scholar] [CrossRef]
- Weidner, P.; Kasic, A.; Hingst, T.; Ehlers, C.; Philipp, S.; Marschner, T.; Moert, M. Model-free and model-based methods for dimensional metrology during the lifetime of a product. In Proceedings of the Ninth International Symposium on Laser Metrology, Singapore, 30 June–2 July 2008; SPIE: Bellingham, WA, USA, 2008; Volume 7155, pp. 319–326. [Google Scholar]
- Azzam, R.M.; Bashara, N.M.; Ballard, S.S. Ellipsometry and polarized light. Opt. Acta Int. J. Opt. 1978, 25, 270–271. [Google Scholar] [CrossRef]
- Fujiwara, H. Spectroscopic Ellipsometry: Principles and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Minhas, B.K.; Coulombe, S.A.; Naqvi, S.S.H.; McNeil, J.R. Ellipsometric scatterometry for the metrology of sub-0.1-μm-linewidth structures. Appl. Opt. 1998, 37, 5112–5115. [Google Scholar] [CrossRef] [PubMed]
- Coulombe, S.A.; Minhas, B.K.; Raymond, C.J.; Sohail, H. Naqvi, S.; McNeil, J.R. Scatterometry measurement of sub-0.1 μm linewidth gratings. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 1998, 16, 80–87. [Google Scholar]
- Huang, H.T.; Kong, W.; Terry Jr, F.L. Normal-incidence spectroscopic ellipsometry for critical dimension monitoring. Appl. Phys. Lett. 2001, 78, 3983–3985. [Google Scholar] [CrossRef]
- Niu, X.; Jakatdar, N.; Bao, J.; Spanos, C.J. Specular spectroscopic scatterometry. IEEE Trans. Semicond. Manuf. 2001, 14, 97–111. [Google Scholar] [CrossRef]
- Tompkins, H.G.; McGahan, W.A. Spectroscopic Ellipsometry and Reflectometry: A User’s Guide; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Losurdo, M.; Bergmair, M.; Bruno, G.; Cattelan, D.; Cobet, C.; De Martino, A.; Fleischer, K.; Dohcevic-Mitrovic, Z.; Esser, N.; Galliet, M.; et al. Spectroscopic ellipsometry and polarimetry for materials and systems analysis at the nanometer scale: State-of-the-art, potential, and perspectives. J. Nanopart. Res. 2009, 11, 1521–1554. [Google Scholar] [CrossRef]
- Novikova, T.; Martino, A.D.; Bulkin, P.; Nguyen, Q.; Drévillon, B.; Popov, V.; Chumakov, A. Metrology of replicated diffractive optics with Mueller polarimetry in conical diffraction. Opt. Express 2007, 15, 2033–2046. [Google Scholar] [CrossRef]
- Novikova, T.; De Martino, A.; Ossikovski, R.; Drevillon, B. Metrological applications of Mueller polarimetry in conical diffraction for overlay characterization in microelectronics. Eur. Phys. J. Appl. Phys. 2005, 31, 63–69. [Google Scholar] [CrossRef]
- Novikova, T.; De Martino, A.; Hatit, S.B.; Drévillon, B. Application of Mueller polarimetry in conical diffraction for critical dimension measurements in microelectronics. Appl. Opt. 2006, 45, 3688–3697. [Google Scholar] [CrossRef]
- Schuster, T.; Rafler, S.; Osten, W.; Reinig, P.; Hingst, T. Scatterometry from crossed grating structures in different configurations. In Proceedings of the Modeling Aspects in Optical Metrology, Munich, Germany, 17–21 June 2007; SPIE: Bellingham, WA, USA, 2007; Volume 6617, pp. 343–351. [Google Scholar]
- Kim, Y.N.; Paek, J.S.; Rabello, S.; Lee, S.; Hu, J.; Liu, Z.; Hao, Y.; McGahan, W. Device based in-chip critical dimension and overlay metrology. Opt. Express 2009, 17, 21336–21343. [Google Scholar] [CrossRef] [PubMed]
- Collins, R.; Koh, J. Dual rotating-compensator multichannel ellipsometer: Instrument design for real-time Mueller matrix spectroscopy of surfaces and films. J. Opt. Soc. Am. A 1999, 16, 1997–2006. [Google Scholar] [CrossRef]
- Liu, S.; Chen, X.; Zhang, C. Development of a broadband Mueller matrix ellipsometer as a powerful tool for nanostructure metrology. Thin Solid Films 2015, 584, 176–185. [Google Scholar] [CrossRef]
- Garcia-Caurel, E.; De Martino, A.; Gaston, J.P.; Yan, L. Application of spectroscopic ellipsometry and Mueller ellipsometry to optical characterization. Appl. Spectrosc. 2013, 67, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Du, W.; Yuan, K.; Chen, J.; Jiang, H.; Zhang, C.; Liu, S. Development of a spectroscopic Mueller matrix imaging ellipsometer for nanostructure metrology. Rev. Sci. Instrum. 2016, 87, 053707. [Google Scholar] [CrossRef]
- Chen, X.-G.; Yuan, K.; Du, W.-C.; Chen, J.; Jing, H.; Zhang, C.-W.; Liu, S.-Y. Large-scale nanostructure metrology using Mueller matrix imaging ellipsometry. Acta Phys. Sin. 2016, 65, 070703. [Google Scholar] [CrossRef]
- Park, S.; Kim, E.; Kim, J.; An, I. Comparison null imaging ellipsometry using polarization rotator. Jpn. J. Appl. Phys. 2018, 57, 052501. [Google Scholar] [CrossRef]
- Torres, J.F.; Komiya, A.; Shoji, E.; Okajima, J.; Maruyama, S. Development of phase-shifting interferometry for measurement of isothermal diffusion coefficients in binary solutions. Opt. Lasers Eng. 2012, 50, 1287–1296. [Google Scholar] [CrossRef]
- Shoji, E.; Komiya, A.; Okajima, J.; Kubo, M.; Tsukada, T. Three-step phase-shifting imaging ellipsometry to measure nanofilm thickness profiles. Opt. Lasers Eng. 2019, 112, 145–150. [Google Scholar] [CrossRef]
- Chen, X.; Yuan, K.; Du, W.; Chen, J.; Jiang, H.; Zhang, C.; Liu, S. Large-Area Measurement of Geometrical Parameters of Nanostructures Using Mueller Matrix Imaging Ellipsometry. Acta Phys. Sin. 2016, 65, 070703. (In Chinese) [Google Scholar] [CrossRef]
- Kim, D.H.; Yun, Y.H.; Joo, K.N. LASIE: Large area spectroscopic imaging ellipsometry for characterizing multi-layered film structures. Int. J. Precis. Eng. Manuf. 2018, 19, 1125–1132. [Google Scholar] [CrossRef]
- Seo, Y.B.; Yun, Y.H.; Joo, K.N. 3D multi-layered film thickness profile measurements based on photometric type imaging ellipsometry. Int. J. Precis. Eng. Manuf. 2016, 17, 989–993. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, Y.; Hu, P.; Wu, Y. A review of the application of hyperspectral imaging technology in agricultural crop economics. Coatings 2024, 14, 1285. [Google Scholar] [CrossRef]
- Meng, H.; Gao, Y.; Wang, X.; Li, X.; Wang, L.; Zhao, X.; Sun, B. Quantum dot-enabled infrared hyperspectral imaging with single-pixel detection. Light Sci. Appl. 2024, 13, 121. [Google Scholar] [CrossRef]
- Yang, Z.; Albrow-Owen, T.; Cui, H.; Alexander-Webber, J.; Gu, F.; Wang, X.; Wu, T.C.; Zhuge, M.; Williams, C.; Wang, P.; et al. Single-nanowire spectrometers. Science 2019, 365, 1017–1020. [Google Scholar] [CrossRef] [PubMed]
- Wen, J.; Gao, H.; Shi, W.; Feng, S.; Hao, L.; Liu, Y.; Xu, L.; Shao, Y.; Zhang, Y.; Shen, W.; et al. On-chip Real-time Hyperspectral Imager with Full CMOS Resolution Enabled by Massively Parallel Neural Network. arXiv 2024, arXiv:2404.09500. [Google Scholar]
- Specim, Spectral Imaging Ltd. Specim IQ Portable VNIR Hyperspectral Imaging Camera. Product Page, Specim Website. 2025. Spectral Range 400–1000 nm, Resolution Approximately 7 nm, 512 × 512 Pixels; Portable Handheld Device. Available online: https://www.specim.com/iq/tech-specs/ (accessed on 5 August 2025).
- Han, X.H.; Wang, J.; Jiang, H. Recent Advancements in Hyperspectral Image Reconstruction from a Compressive Measurement. Sensors 2025, 25, 3286. [Google Scholar] [CrossRef]
- Zhang, G.; Zhao, S.; Li, W.; Du, Q.; Ran, Q.; Tao, R. HTD-Net: A deep convolutional neural network for target detection in hyperspectral imagery. Remote Sens. 2020, 12, 1489. [Google Scholar] [CrossRef]
- Li, Y.; Hu, J.; Zhao, X.; Xie, W.; Li, J. Hyperspectral image super-resolution using deep convolutional neural network. Neurocomputing 2017, 266, 29–41. [Google Scholar] [CrossRef]
- Cheng, M.F.; Mukundan, A.; Karmakar, R.; Valappil, M.A.E.; Jouhar, J.; Wang, H.C. Modern Trends and Recent Applications of Hyperspectral Imaging: A Review. Technologies 2025, 13, 170. [Google Scholar] [CrossRef]
- Yan, Y.; Ren, J.; Zhao, H.; Windmill, J.F.; Ijomah, W.; De Wit, J.; Von Freeden, J. Non-destructive testing of composite fiber materials with hyperspectral imaging—Evaluative studies in the EU H2020 FibreEUse project. IEEE Trans. Instrum. Meas. 2022, 71, 6002213. [Google Scholar] [CrossRef]
- Fabelo, H.; Ortega, S.; Szolna, A.; Bulters, D.; Piñeiro, J.F.; Kabwama, S.; JO’Shanahan, A.; Bulstrode, H.; Bisshopp, S.; Kiran, B.R.; et al. In-vivo hyperspectral human brain image database for brain cancer detection. IEEE Access 2019, 7, 39098–39116. [Google Scholar] [CrossRef]
- Chabrillat, S.; Foerster, S.; Segl, K.; Beamish, A.; Brell, M.; Asadzadeh, S.; Milewski, R.; Ward, K.J.; Brosinsky, A.; Koch, K.; et al. The EnMAP spaceborne imaging spectroscopy mission: Initial scientific results two years after launch. Remote Sens. Environ. 2024, 315, 114379. [Google Scholar] [CrossRef]
- EO Portal. Pixxel Satellite Mission. Available online: https://www.eoportal.org/satellite-missions/pixxel (accessed on 5 August 2025).
- Bhargava, A.; Sachdeva, A.; Sharma, K.; Alsharif, M.H.; Uthansakul, P.; Uthansakul, M. Hyperspectral imaging and its applications: A review. Heliyon 2024, 10, e33208. [Google Scholar] [CrossRef] [PubMed]
- Díaz, M.; Guerra, R.; Horstrand, P.; Martel, E.; López, S.; López, J.F.; Sarmiento, R. Real-time hyperspectral image compression onto embedded GPUs. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 2, 2792–2809. [Google Scholar] [CrossRef]
- Eckstein, B.A.; Arlen, R. IEEE PROJECT 4001–Standards for Characterization and Calibration of Hyperspectral Imaging Devices. Proc. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, XLIV-M-3-2021, 43–47. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.; Woerdman, J. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef]
- Lavery, M.P.; Speirits, F.C.; Barnett, S.M.; Padgett, M.J. Detection of a spinning object using light’s orbital angular momentum. Science 2013, 341, 537–540. [Google Scholar] [CrossRef] [PubMed]
- Luo, Z.; Liu, R.; Wu, L.; Ran, J.; Wang, Y.; Qin, S.; Lv, C.; Bai, Z.; Xu, X.; Wang, Y.; et al. Fiber angular displacement sensor utilizing orbital angular momentum beam interference. Opt. Lett. 2025, 50, 2759–2762. [Google Scholar] [CrossRef]
- Jeffries, G.D.; Edgar, J.S.; Zhao, Y.; Shelby, J.P.; Fong, C.; Chiu, D.T. Using polarization-shaped optical vortex traps for single-cell nanosurgery. Nano Lett. 2007, 7, 415–420. [Google Scholar] [CrossRef]
- Pan, Y.; Ou, J.; Chi, H. High-dimensional signal encoding and decoding method based on multi-ring perfect vortex beam. Opt. Express 2024, 32, 30800–30812. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Li, X.; Tai, Y.; Li, H.; Wang, J.; Tang, M.; Tang, J.; Wang, Y.; Nie, Z. Generation of circular optical vortex array. Ann. Der Phys. 2017, 529, 1700285. [Google Scholar] [CrossRef]
- Chen, Y.; Xia, K.Y.; Shen, W.G.; Gao, J.; Yan, Z.Q.; Jiao, Z.Q.; Dou, J.P.; Tang, H.; Lu, Y.Q.; Jin, X.M. Vector vortex beam emitter embedded in a photonic chip. Phys. Rev. Lett. 2020, 124, 153601. [Google Scholar] [CrossRef]
- Du, J.; Quan, Z.; Li, K.; Wang, J. Optical vortex array: Generation and applications. Chin. Opt. Lett. 2024, 22, 020011. [Google Scholar] [CrossRef]
- Su, R.; Leach, R. Physics-based virtual coherence scanning interferometer for surface measurement. Light Adv. Manuf. 2021, 2, 120–135. [Google Scholar] [CrossRef]
- Giordani, T.; Suprano, A.; Polino, E.; Acanfora, F.; Innocenti, L.; Ferraro, A.; Paternostro, M.; Spagnolo, N.; Sciarrino, F. Machine learning-based classification of vector vortex beams. Phys. Rev. Lett. 2020, 124, 160401. [Google Scholar] [CrossRef]
- Panthong, P.; Srisuphaphon, S.; Pattanaporkratana, A.; Chiangga, S.; Deachapunya, S. A study of optical vortices inside the Talbot interferometer. arXiv 2015, arXiv:1510.00272. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, P.; Liao, J.; Dai, M.; Zhou, J.; Xiao, W.; Chen, H. Vortex decomposition and reconfiguration via transformation optics. Phys. Rev. Appl. 2024, 21, 054006. [Google Scholar] [CrossRef]
- Gao, H.; Yang, D.; Hu, X.; He, W.; Yang, Z.; Liu, Z. High-precision micro-displacement measurement in a modified reversal shearing interferometer using vortex beams. Opt. Commun. 2023, 537, 129454. [Google Scholar] [CrossRef]
- Serrano-Trujillo, A.; Anderson, M.E. Surface profilometry using vortex beams generated with a spatial light modulator. Opt. Commun. 2018, 427, 557–562. [Google Scholar] [CrossRef]
- Passos, M.; Lemos, M.; Almeida, S.; Balthazar, W.; Da Silva, L.; Huguenin, J. Speckle patterns produced by an optical vortex and its application to surface roughness measurements. Appl. Opt. 2017, 56, 330–335. [Google Scholar] [CrossRef]
- Yang, Y.; Ren, Y.X.; Rosales-Guzmán, C. Optical Vortices: Fundamentals and Applications; IOP Publishing: Bristol, UK, 2024. [Google Scholar]
- Zuo, C.; Qian, J.; Feng, S.; Yin, W.; Li, Y.; Fan, P.; Han, J.; Qian, K.; Chen, Q. Deep learning in optical metrology: A review. Light Sci. Appl. 2022, 11, 39. [Google Scholar] [CrossRef]
- Wang, K.; Song, L.; Wang, C.; Ren, Z.; Zhao, G.; Dou, J.; Di, J.; Barbastathis, G.; Zhou, R.; Zhao, J.; et al. On the use of deep learning for phase recovery. Light Sci. Appl. 2024, 13, 4. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Yan, N.; Shao, B.; Yuan, S.; Zhang, X. Deep learning in fringe projection: A review. Neurocomputing 2024, 581, 127493. [Google Scholar] [CrossRef]
- Wang, H.; Hu, J.; Wei, S.; Qu, Y. One-shot TSOM with a multi-task learning model for simultaneous dimension measurement and defect inspection. Opt. Lasers Eng. 2024, 181, 108345. [Google Scholar] [CrossRef]
- Houben, T.; Huisman, T.; Pisarenco, M.; Van Der Sommen, F.; de With, P. Training procedure for scanning electron microscope 3D surface reconstruction using unsupervised domain adaptation with simulated data. J. Micro/Nanopatterning Mater. Metrol. 2023, 22, 031208. [Google Scholar] [CrossRef]
- Liu, M. Scattering approaches. In Advances in Optical Surface Texture Metrology; IOP Publishing: Bristol, UK, 2020; pp. 1–6. [Google Scholar]
- Saba, A.; Gigli, C.; Ayoub, A.B.; Psaltis, D. Physics-informed neural networks for diffraction tomography. Adv. Photonics 2022, 4, 066001. [Google Scholar] [CrossRef]
- Gigli, C.; Saba, A.; Ayoub, A.B.; Psaltis, D. Predicting nonlinear optical scattering with physics-driven neural networks. Apl Photonics 2023, 8, 026105. [Google Scholar] [CrossRef]
- Medvedev, V.; Erdmann, A.; Rosskopf, A. Physics-informed deep learning for 3D modeling of light diffraction from optical metasurfaces. Opt. Express 2025, 33, 1371–1384. [Google Scholar] [CrossRef]
- Park, S.; Kim, Y.; Moon, I. Automated phase unwrapping in digital holography with deep learning. Biomed. Opt. Express 2021, 12, 7064–7081. [Google Scholar] [CrossRef]
- Fang, L.; Monroe, F.; Novak, S.W.; Kirk, L.; Schiavon, C.R.; Yu, S.B.; Zhang, T.; Wu, M.; Kastner, K.; Latif, A.A.; et al. Deep learning-based point-scanning super-resolution imaging. Nat. Methods 2021, 18, 406–416. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Tang, X.; Zhao, Y.; Shen, Z.; Zhang, M.; Shen, Y.; Li, T.; Chung, C.H.Y.; Zhang, L.; Wang, J.; et al. Single-frame deep-learning super-resolution microscopy for intracellular dynamics imaging. Nat. Commun. 2023, 14, 2854. [Google Scholar] [CrossRef] [PubMed]
- White, J.; Wang, S.; Eschen, W.; Rothhardt, J. Real-time phase-retrieval and wavefront sensing enabled by an artificial neural network. Opt. Express 2021, 29, 9283–9293. [Google Scholar] [CrossRef]
- Fang, Q.; Xia, H.; Song, Q.; Zhang, M.; Guo, R.; Montresor, S.; Picart, P. Speckle denoising based on deep learning via a conditional generative adversarial network in digital holographic interferometry. Opt. Express 2022, 30, 20666–20683. [Google Scholar] [CrossRef]
- Yu, H.; Fang, Q.; Song, Q.; Montresor, S.; Picart, P.; Xia, H. Unsupervised speckle denoising in digital holographic interferometry based on 4-f optical simulation integrated cycle-consistent generative adversarial network. Appl. Opt. 2024, 63, 3557–3569. [Google Scholar] [CrossRef]
- Durech, E.; Newberry, W.; Franke, J.; Sarunic, M.V. Wavefront sensor-less adaptive optics using deep reinforcement learning. Biomed. Opt. Express 2021, 12, 5423–5438. [Google Scholar] [CrossRef]
- Landman, R.; Haffert, S.Y.; Radhakrishnan, V.M.; Keller, C.U. Self-optimizing adaptive optics control with reinforcement learning for high-contrast imaging. J. Astron. Telesc. Instruments Syst. 2021, 7, 039002. [Google Scholar] [CrossRef]
- Roos-Hoefgeest, S.; Roos-Hoefgeest, M.; Álvarez, I.; González, R.C. Reinforcement Learning Approach to Optimizing Profilometric Sensor Trajectories for Surface Inspection. Sensors 2025, 25, 2271. [Google Scholar] [CrossRef]
- Wong, J.C.; Chiu, P.H.; Ooi, C.C.; Da, M.H. Robustness of physics-informed neural networks to noise in sensor data. arXiv 2022, arXiv:2211.12042. [Google Scholar] [CrossRef]
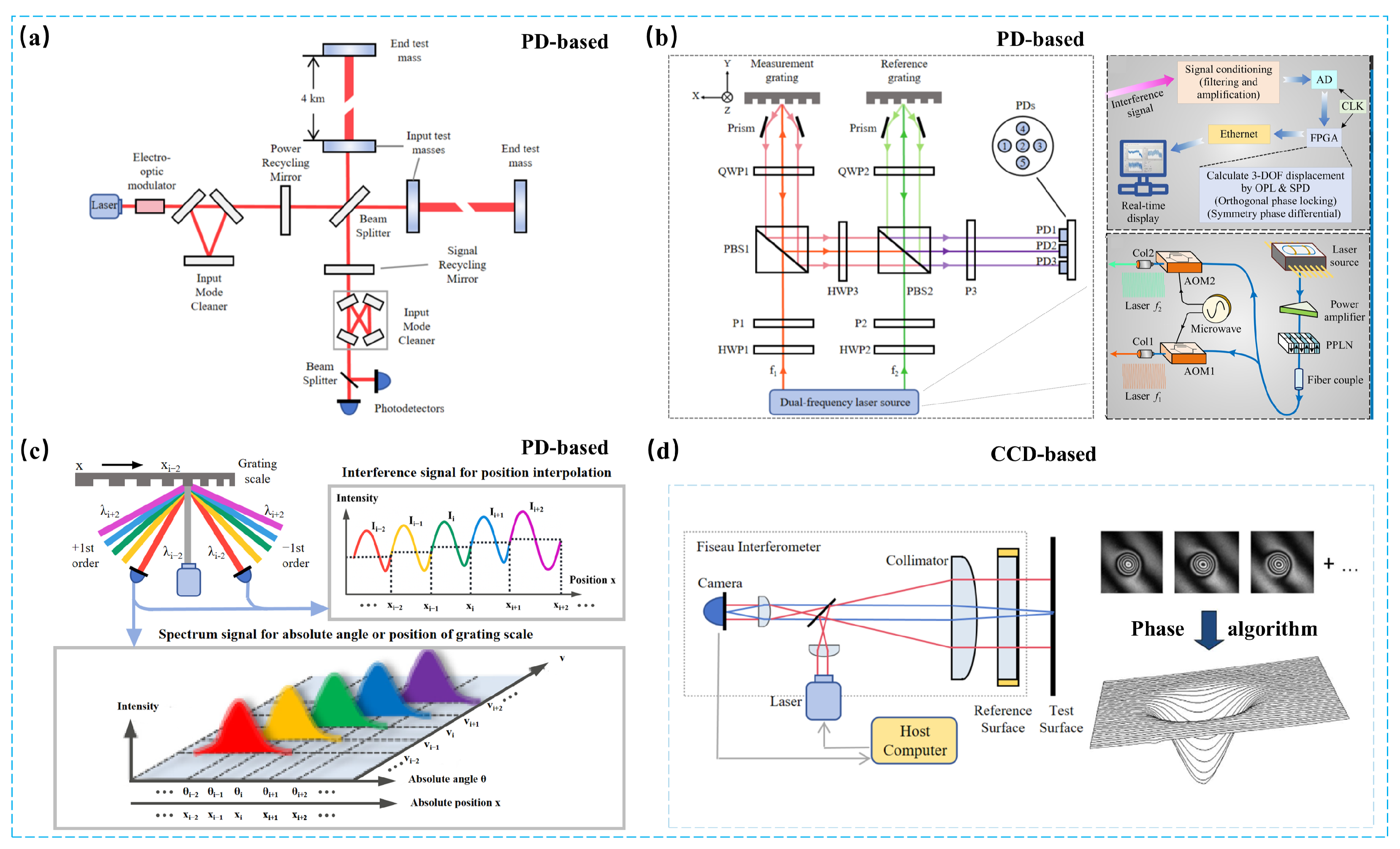
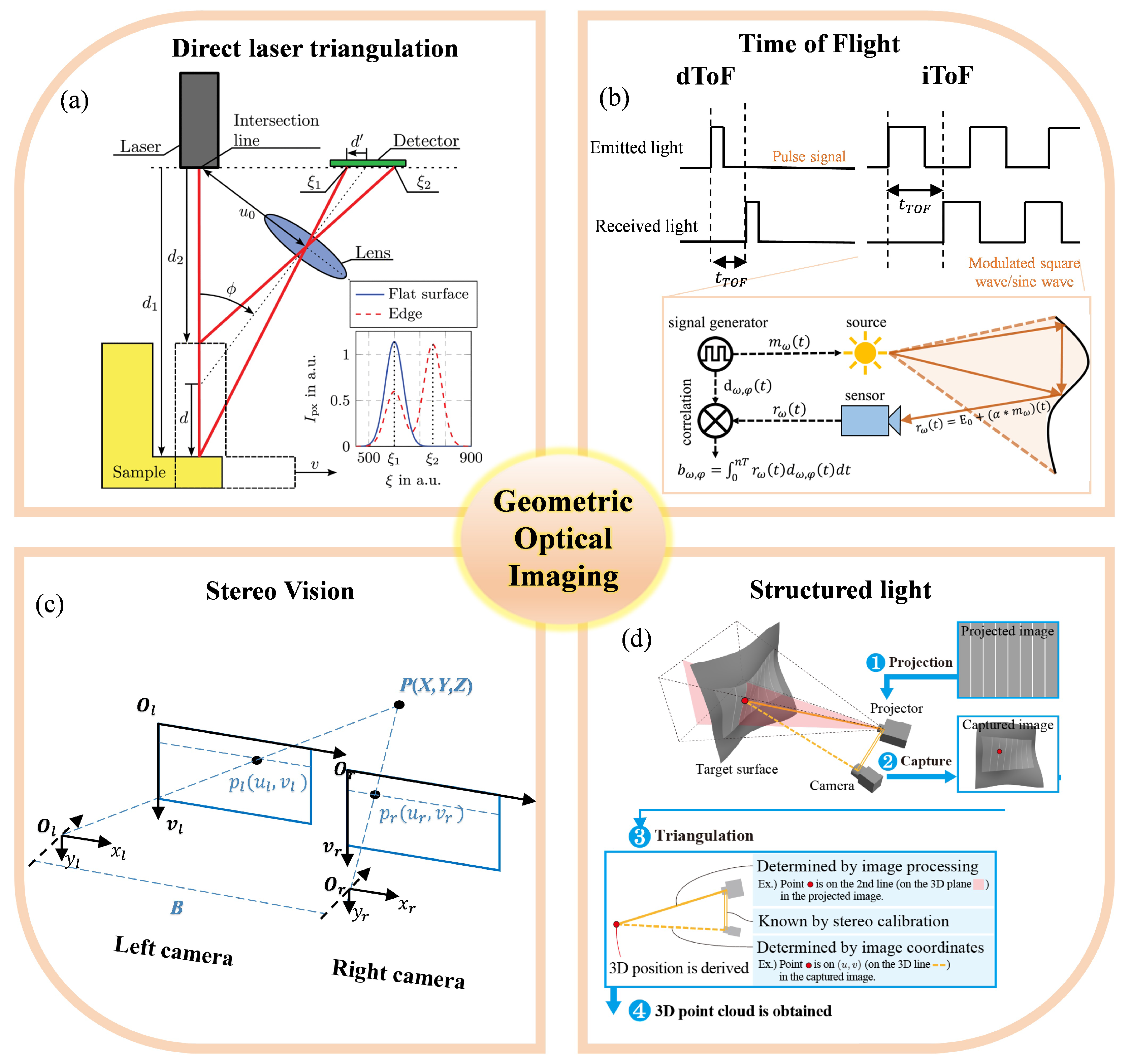

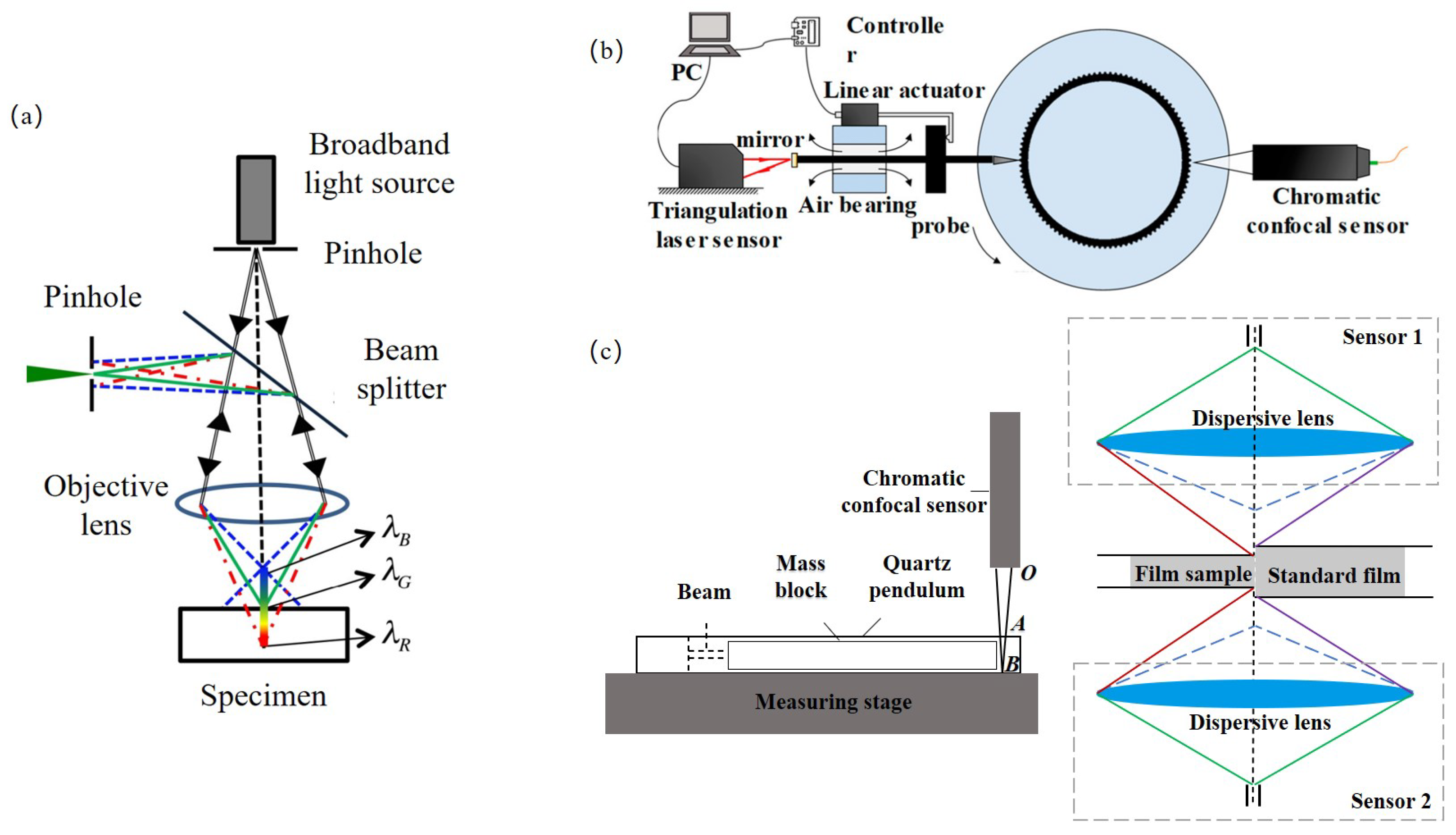
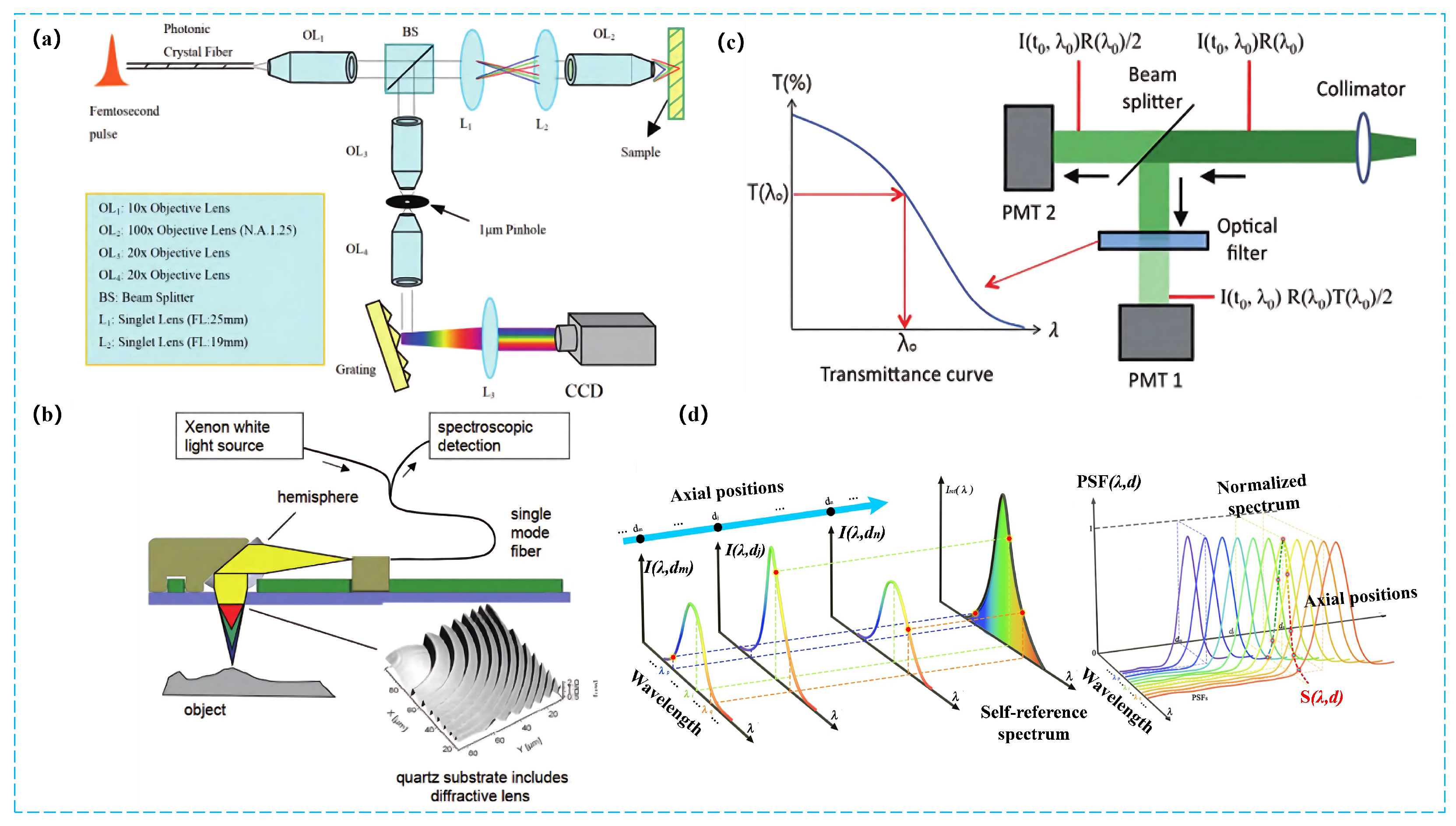


| Scale | Accuracy | Measurement Range | Technique | Typical Application |
|---|---|---|---|---|
| Nanometer | nm | 0.1–1 mm | White-light interferometry | Wafer surface topography inspection |
| Nanometer | nm | 0.01–0.5 mm | Fizeau interferometry | Optical component surface metrology |
| Micrometer | 0.2 μm | 0.1–5 mm | Laser confocal microscopy | Reverse engineering of precision parts |
| Micrometer | 0.1 μm | 1–10 mm | Spectral confocal microscopy | Thickness measurement of transparent materials |
| Micrometer | μm | 0.05–2 mm | Structured light (sinusoidal fringe) | High-reflectivity surface inspection |
| Millimeter | μm | 50–500 mm | Structured light (speckle encoding) | 3D reconstruction of automotive bodies |
| Millimeter | mm | 3–7 cm | Laser triangulation | Dimensional inspection of industrial parts |
| Centimeter | mm | 0.1–300 m | LiDAR (dToF) | Large-scale 3D industrial mapping |
| Centimeter | cm | 1–10 m | Stereo vision | Kinect motion capture |
| Decimeter | cm | 1–50 m | iToF phase ranging | VR gesture interaction |
| Meter | 1–100 m | FMCW coherent ranging | Autonomous driving obstacle detection | |
| Cross-scale | Pixel level | 0.1–100 m | Computational imaging | Imaging through scattering media |
| Cross-scale | Photon level | 1–1000 m | Quantum imaging | Single-photon night vision systems |
| Special scale | nm | 1–100 μm | Microscopic imaging | 3D reconstruction of biological cells |
| Category | Typical Methods | Measurement Principle | Characteristics and Limitations |
|---|---|---|---|
| Absorption/ Transmission | UV–Vis, NIR spectroscopy | Measures light absorption or transmission at specific wavelengths | Offers fast data acquisition and simple setup; however, spatial resolution is limited for material composition analysis. |
| Reflection Spectroscopy | White-light reflectance, RIFS | Analyzes wavelength-dependent surface reflection properties | Provides surface sensitivity but limited morphological discrimination; requires careful calibration for quantitative use. |
| Raman Spectroscopy | Raman microscopy, confocal imaging | Detects inelastic scattering frequency shifts induced by molecular vibrations | Enables chemical mapping with high specificity, but the inherently weak Raman signals demand long acquisition times. |
| Fluorescence Spectroscopy | Time-resolved micro-fluorescence | Detects excitation–emission spectra from fluorescent markers | Achieves high sensitivity and selectivity; however, fluorophore tagging is often required and may alter sample properties. |
| Dispersive Focus Profiling | Chromatic confocal technology (CCT) | Encodes depth information via wavelength-dependent focal shifts | Provides non-contact, tilt-tolerant 3D profiling for complex or transparent surfaces. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, S.; Zhao, F.; Li, Z.; Luo, L.; Li, X. A Comprehensive Review of Optical Metrology and Perception Technologies. Sensors 2025, 25, 6811. https://doi.org/10.3390/s25226811
Shan S, Zhao F, Li Z, Luo L, Li X. A Comprehensive Review of Optical Metrology and Perception Technologies. Sensors. 2025; 25(22):6811. https://doi.org/10.3390/s25226811
Chicago/Turabian StyleShan, Shuonan, Fangyuan Zhao, Zinan Li, Linbin Luo, and Xinghui Li. 2025. "A Comprehensive Review of Optical Metrology and Perception Technologies" Sensors 25, no. 22: 6811. https://doi.org/10.3390/s25226811
APA StyleShan, S., Zhao, F., Li, Z., Luo, L., & Li, X. (2025). A Comprehensive Review of Optical Metrology and Perception Technologies. Sensors, 25(22), 6811. https://doi.org/10.3390/s25226811




