Motion Artifacts Removal from Measured Arterial Pulse Signals at Rest: A Generalized SDOF-Model-Based Time–Frequency Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Arterial Pulse Signal Measurement Using a Tactile Sensor and a PPG Sensor
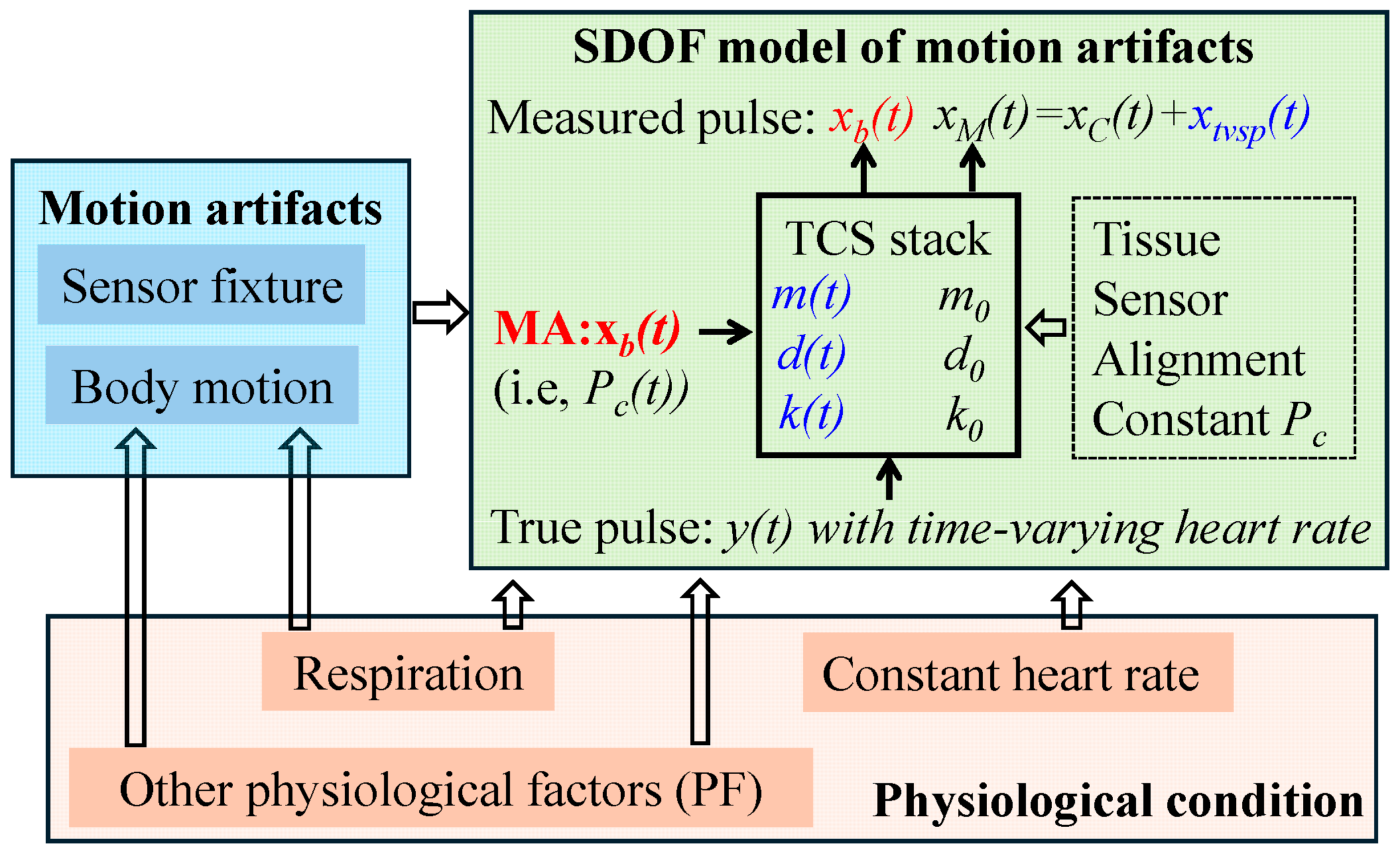
2.2. An SDOF Model of MA in a Measured Pulse Signal
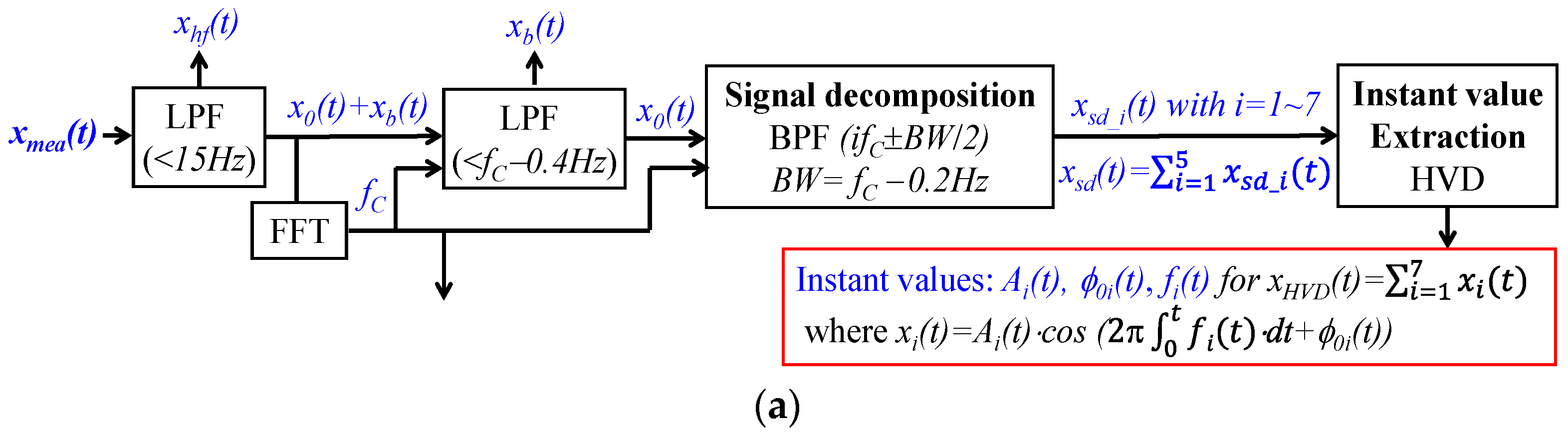
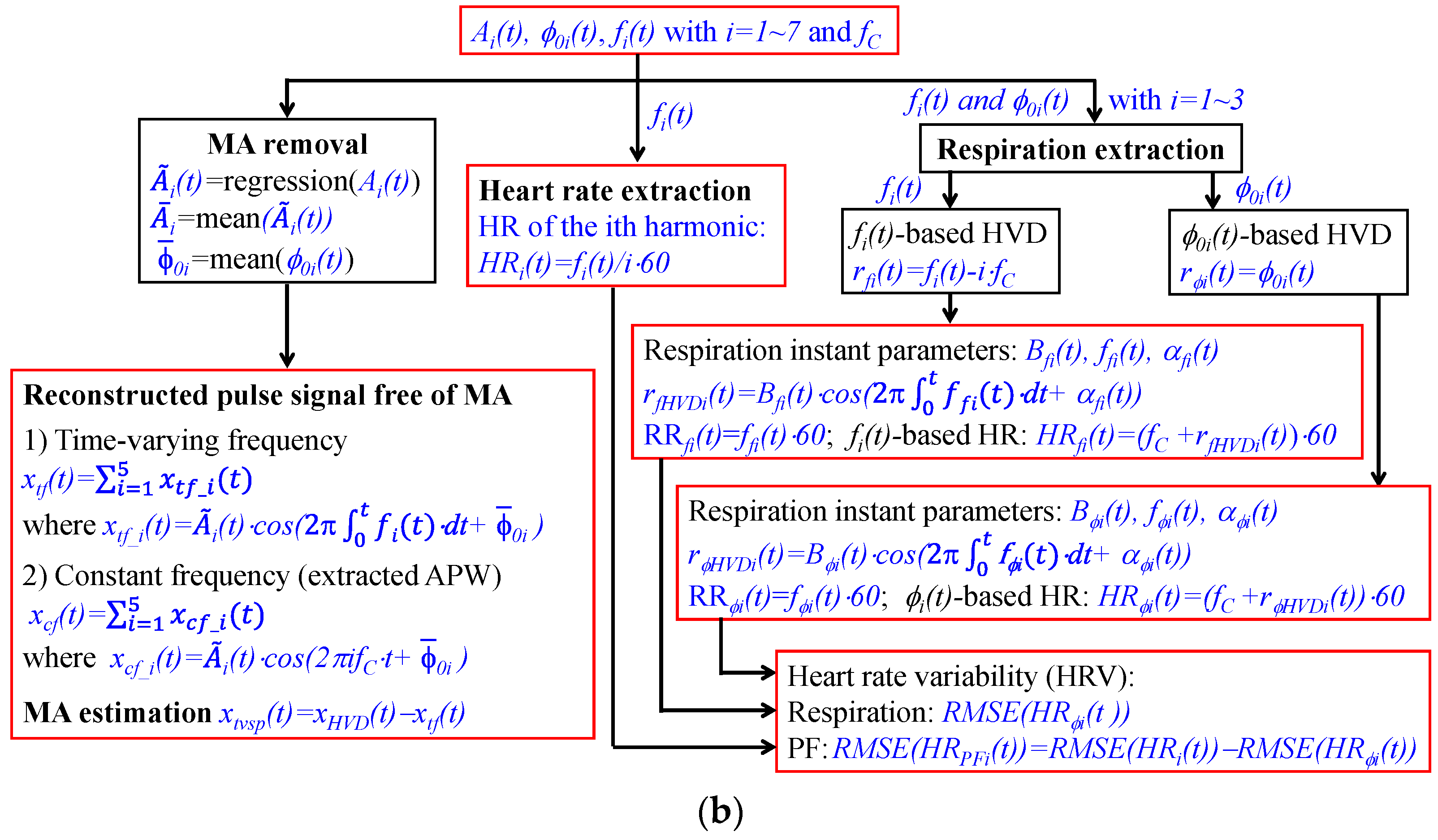
2.3. A Generalized SDOF-Model-Based Time–Frequency (SDOF-TF) Method
2.3.1. Nature of an Arterial Pulse Signal
2.3.2. A Generalized SDOF-TF Method
2.4. Calculation
2.4.1. The Effects of MA and Respiration on a Measured Pulse Signal
2.4.2. Application of the Generalized SDOF-TF Method to Measured Pulse Signals
3. Results
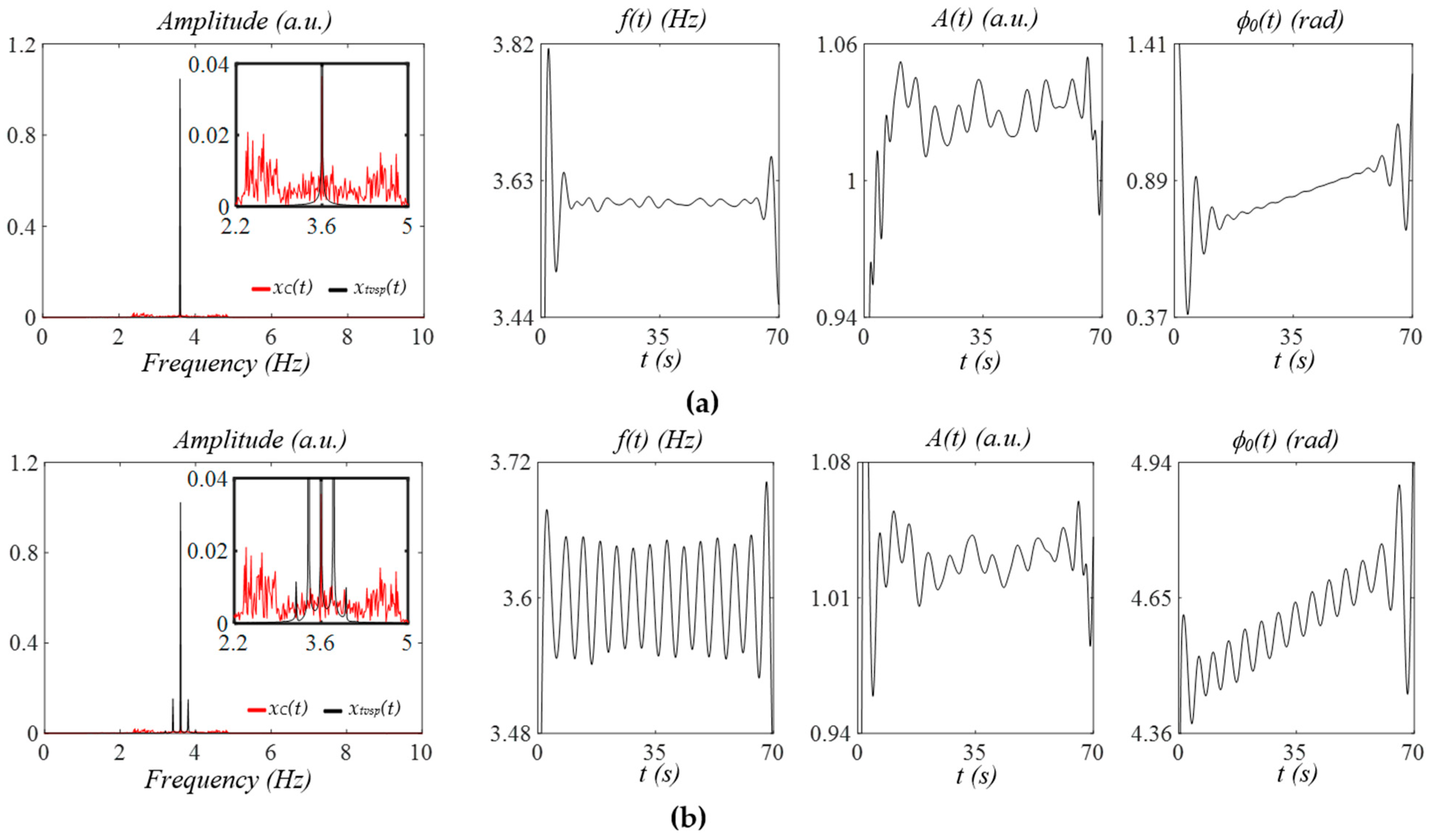
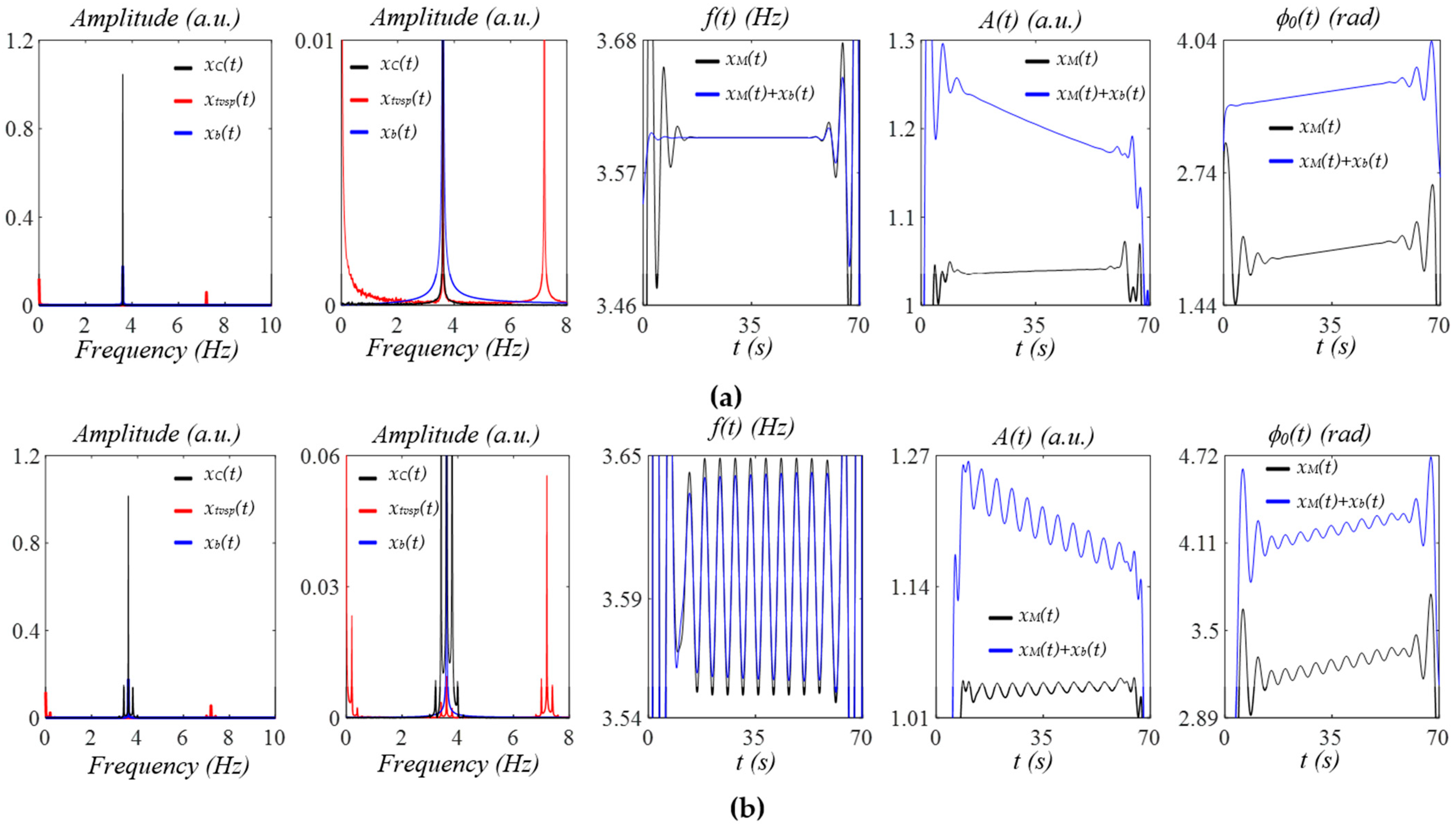
3.1. The Effects of MA and Respiration on a Measured Pulse Signal from the SDOF Model of MA
- The MA at rest greatly affects instant amplitude, affects instant frequency to a very limited extent, and has almost no effect on instant initial phase.
- The MA during activities generates multiple signals at different frequencies. These multiple signals will affect those harmonics in a measured pulse signal whose frequencies are close to theirs.
- Instant frequency captures HRV (from constant HR or fC) due to respiration and PF, and instant initial phase captures HRV due to respiration only.
- Regardless of MA at rest or during activities, instant frequency and instant initial phase carry the respiration signal in HR. The respiration signal in the instant initial phase is almost immune to MA compared to its counterpart in the instant frequency.
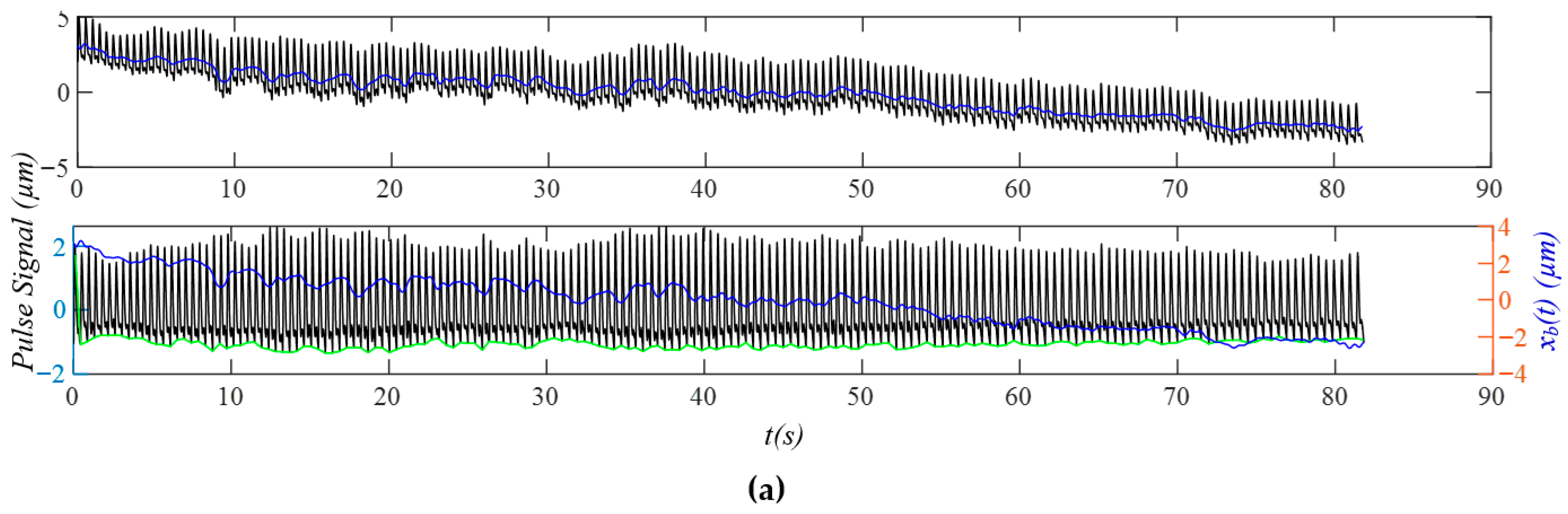
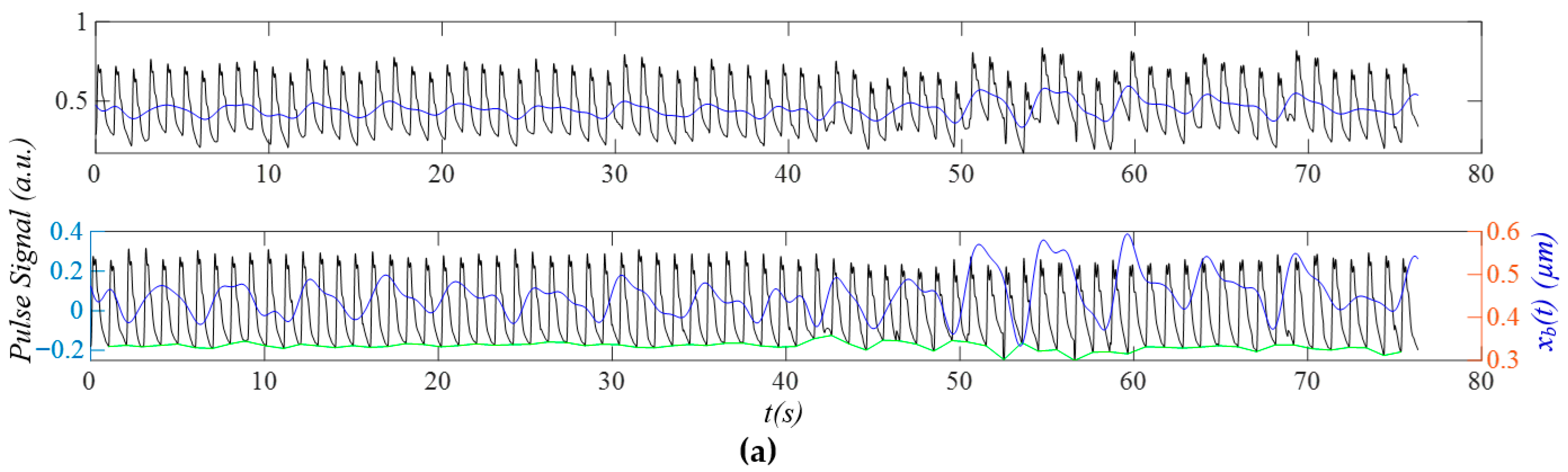
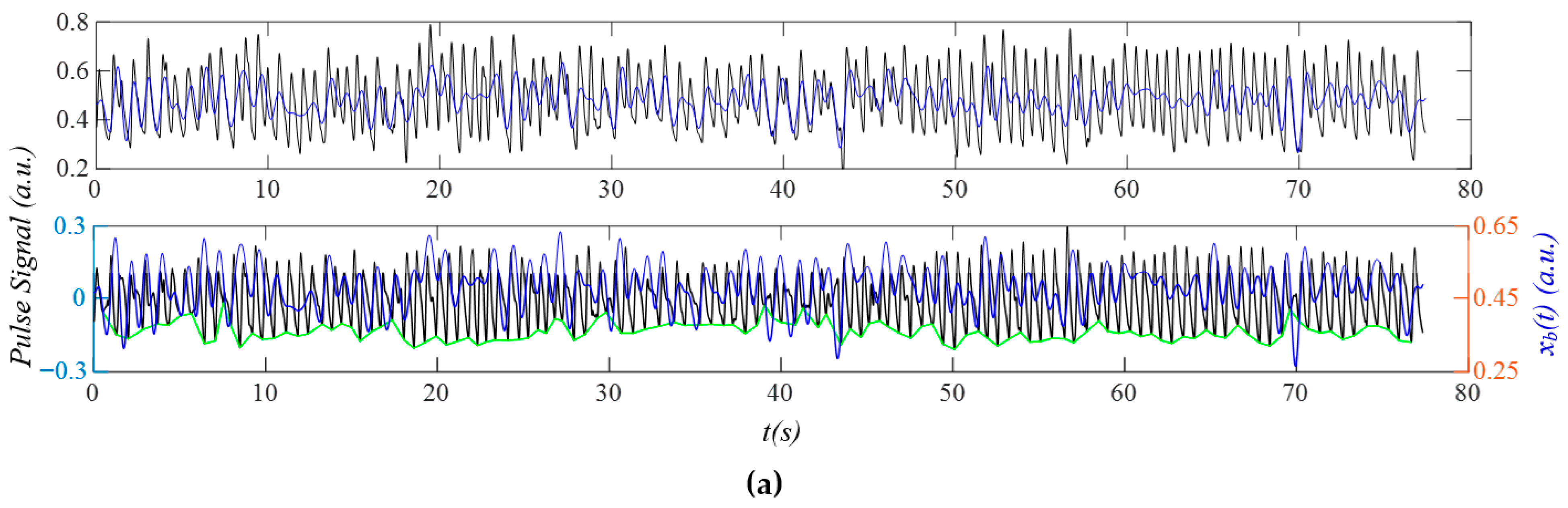
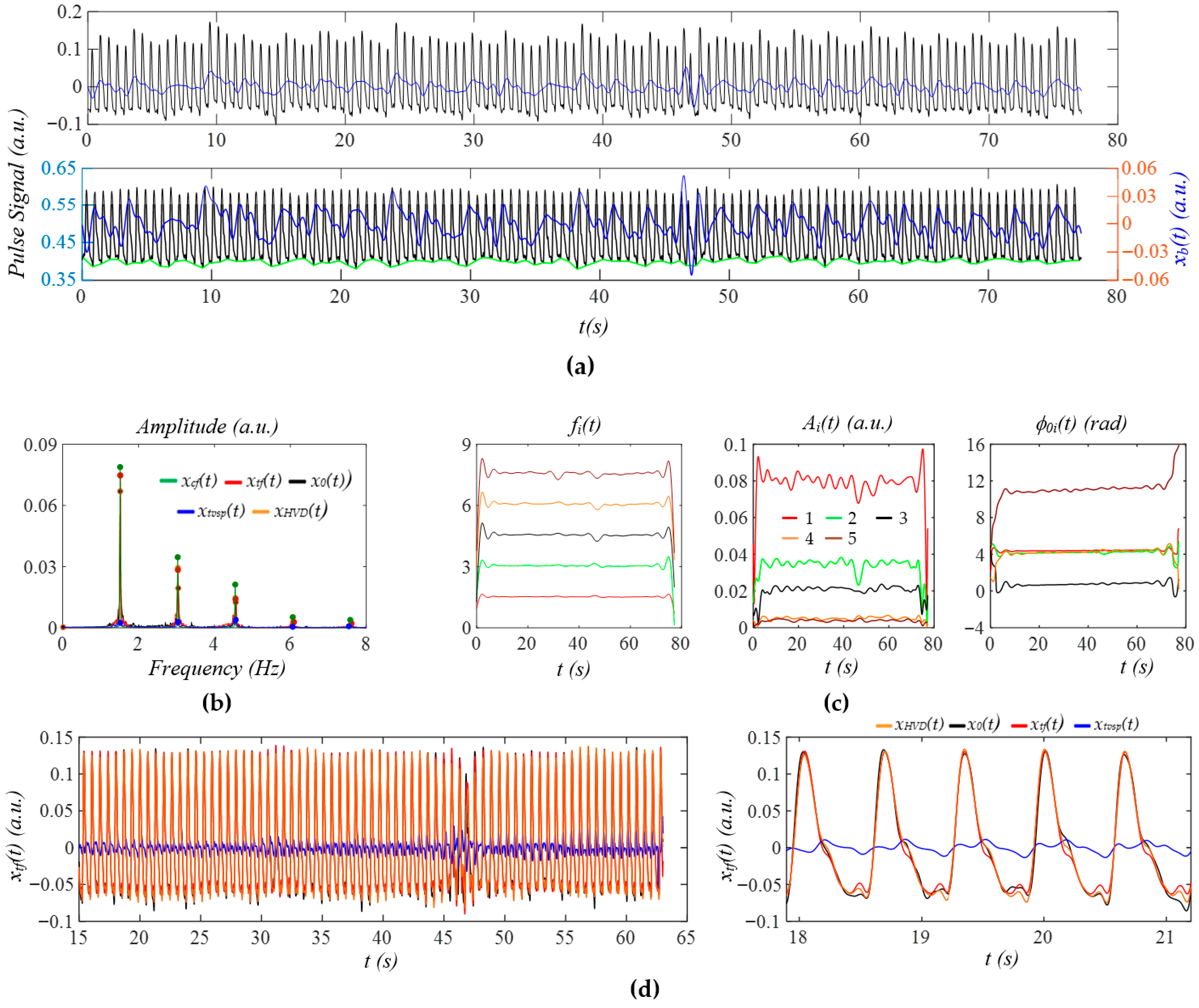
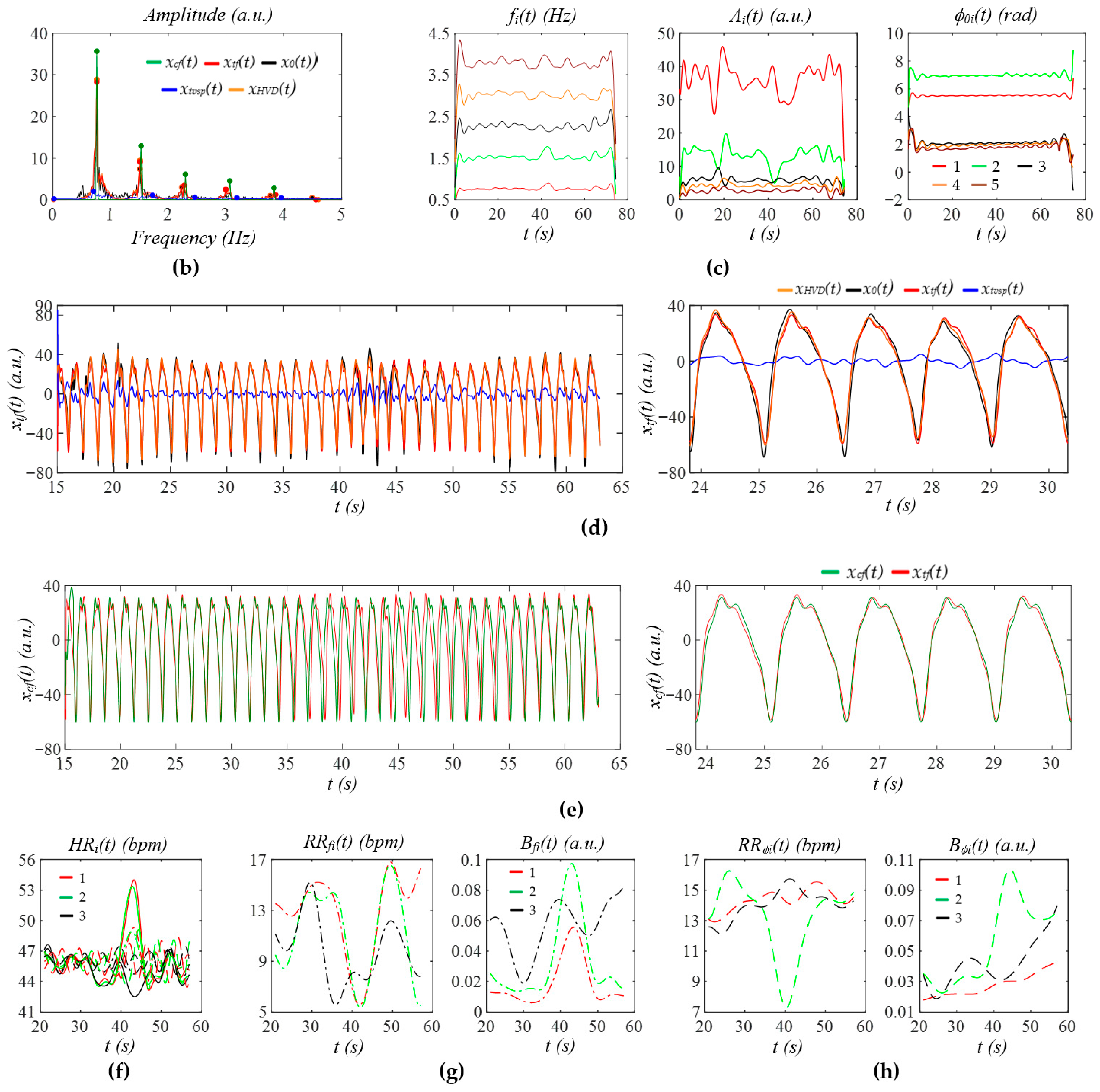
3.2. Measured Pulse Signals Using a Tactile Sensor
3.3. PPG Signals
3.4. Comparison of Measured Pulse Signals Under Different Physiological Conditions
3.5. Comparison of Measured Pulse Signals Between at Rest and During Activities
4. Discussion
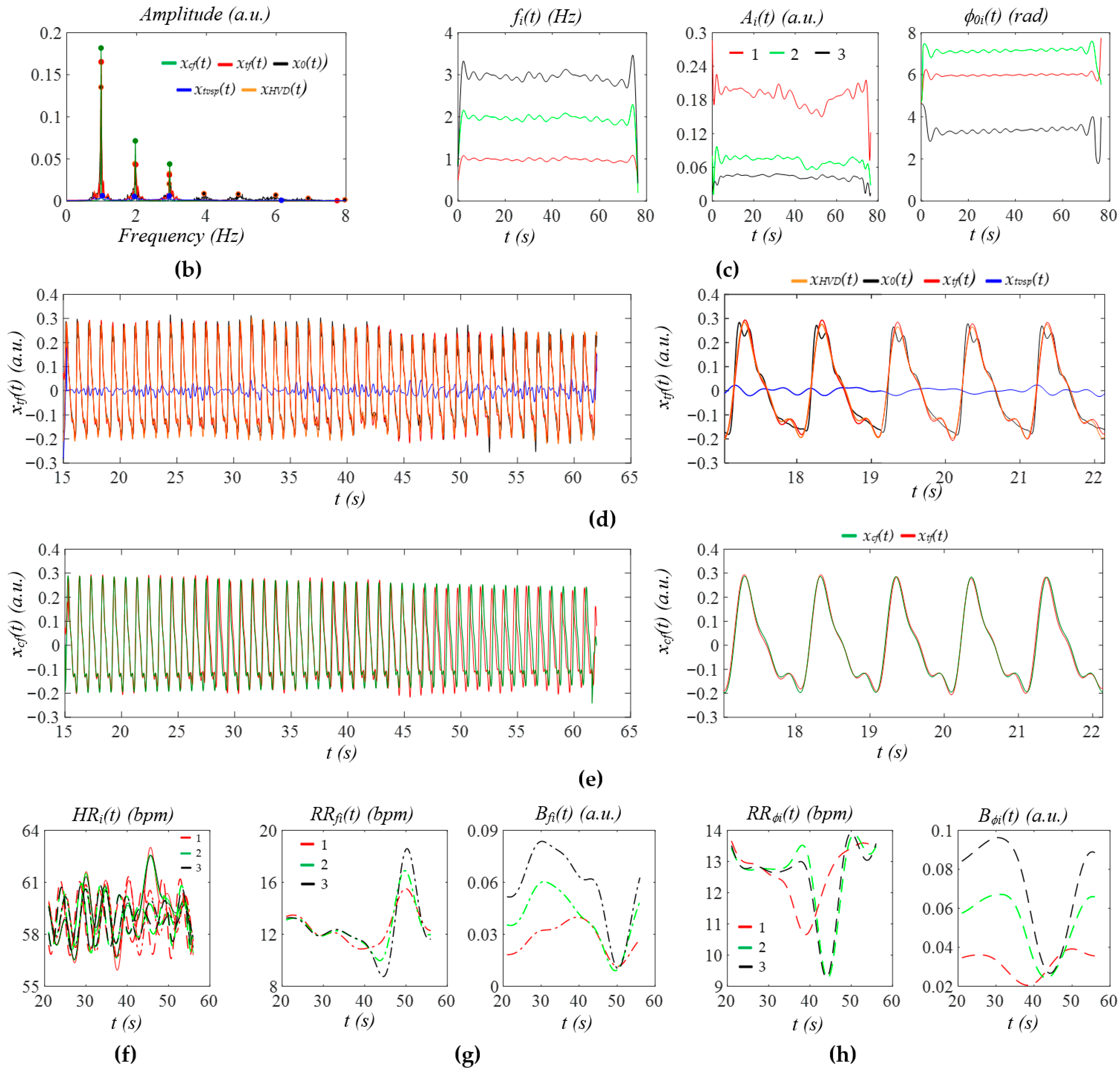
4.1. Qualitative Validation of the Generalized SDOF-TF Method
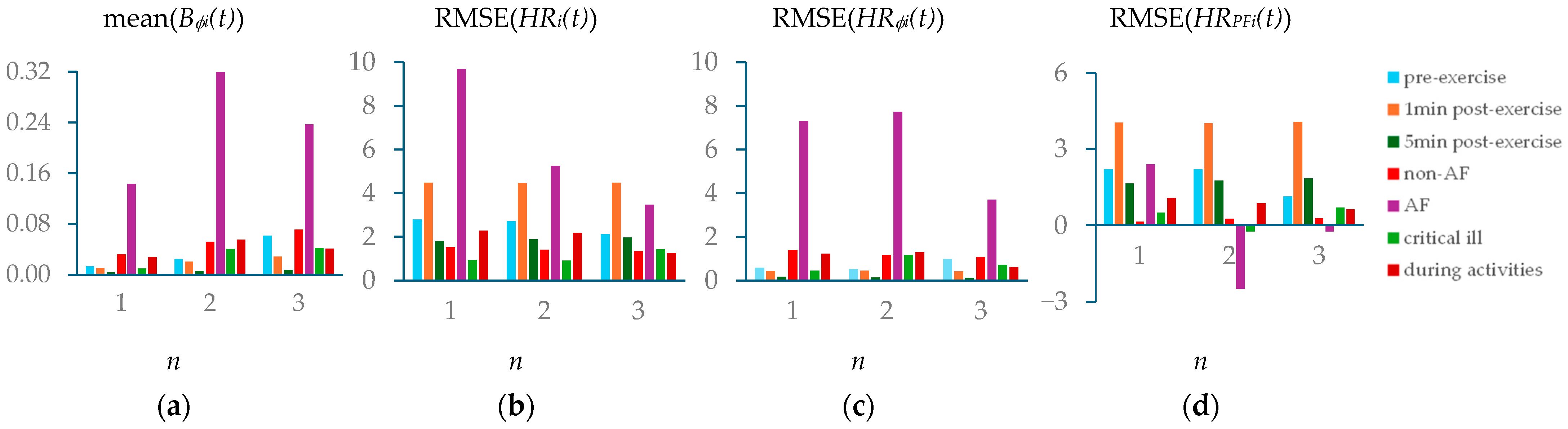
4.2. The Effect of MA and HRV on Extracted APW, HR, and Respiration Parameters
4.3. Comparison with the Related Studies
- The effects of MA at rest and respiration on a measured pulse signal are different: (1) the MA affects a measured pulse signal via its effect on the TCS stack (or xtvsp(t)), and (2) respiration affects a measured pulse signal via its effect on HR. Their effects on the instant parameters of each harmonic in a measured pulse signal are different.
- The effect of MA at rest on a measured pulse signal can be removed via the regression line of instant amplitude and the mean of instant initial phase.
- As compared to instant frequency, instant initial phase is almost immune to MA and nonlinearity, provides the extraction of respiration parameters and HRV due to respiration with better accuracy, and better distinguishes the HRV due to respiration from the HRV due to PF.
- A large HRV (or a large time-varying frequency) affects the APW (amplitude and initial phase of each harmonic) to a great extent. The reconstructed pulse signal with constant HR serves better as the extracted APW to derive the amplitude and initial phase of each harmonic for comparison between physiological conditions.
- A large HRV translates to large multiple sidebands of MA (or xtvsp(t)) and, by extension, large broadband noise, given the same sensor.
- Due to the unpredictability of MA during activities, in terms of its frequency, MA in a measured pulse signal during activities is difficult to detect and remove.
4.4. Study Limitation
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| APW | Arterial pulse waveform |
| MA | Motion artifacts |
| TVSP | Time-varying system parameters |
| SDOF | Single degree of freedom |
| SDOF-TF | Single degree of freedom time–frequency |
| HVD | Hilbert vibration decomposition |
| HR | Heart rate |
| HRV | Heart rate variability (in terms of RMSE) |
| RR | Respiration rate |
| PF | Physiological factors excluding respiration on heart rate regulation |
References
- Elgendi, M. On the Analysis of Fingertip Photoplethysmogram Signals. Curr. Cardiol. Rev. 2012, 8, 14–25. [Google Scholar] [CrossRef]
- Wang, H.; Wang, L.; Sun, N.; Yao, Y.; Hao, L.; Xu, L.; Greenwald, S.E. Quantitative Comparison of the Performance of Piezoresistive, Piezoelectric, Acceleration, and Optical Pulse Wave Sensors. Front. Physiol. 2020, 10, 1563. [Google Scholar] [CrossRef]
- Wang, D.; Reynolds, L.; Alberts, T.; Vahala, L.; Hao, Z. Model-based analysis of arterial pulse signals for tracking changes in arterial wall parameters: A pilot study. Biomech. Model. Mechanobiol. 2019, 18, 1629–1638. [Google Scholar] [CrossRef]
- Xu, L.; Zhou, S.; Wang, L.; Yao, Y.; Hao, L.; Qi, L.; Yao, Y.; Han, H.; Mukkamala, R.; Greenwald, S.E. Improving the accuracy and robustness of carotid-femoral pulse wave velocity measurement using a simplified tube-load model. Sci. Rep. 2022, 12, 5147. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.; Yan, B.P.; Zhang, Y.-T.; Liu, J.; Zhao, N.; Tsang, H.K. Pulse Transit Time Based Continuous Cuffless Blood Pressure Estimation: A New Extension and A Comprehensive Evaluation. Sci. Rep. 2017, 7, 11554. [Google Scholar] [CrossRef] [PubMed]
- Hao, Z. A 2-DOF Model of the Artery-Sensor System for Interpreting Variability in Measured Arterial Pulse Waveform. IEEE Sens. J. 2023, 23, 22668–22678. [Google Scholar] [CrossRef]
- Rahman, M.M.; Toraskar, S.; Hasan, M.; Hao, Z. An Analytical Model of Motion Artifacts in a Measured Arterial Pulse Signal—Part I: Accelerometers and PPG Sensors. Sensors 2025, 25, 5710. [Google Scholar] [CrossRef]
- Rahman, M.M.; Toraskar, S.; Hasan, M.; Hao, Z. An Analytical Model of Motion Artifacts in a Measured Arterial Pulse Signal—Part II: Tactile Sensors. Sensors 2025, 25, 5700. [Google Scholar] [CrossRef] [PubMed]
- Charlton, P.H.; Kotzen, K.; Mejía-Mejía; Aston, P.J.; Budidha, K.; Mant, J.; Pettit, C.; Behar, J.A.; Kyriacou, P.A. Detecting beats in the photoplethysmogram: Benchmarking open-source algorithms. Physiol. Meas. 2022, 43, 085007. [Google Scholar] [CrossRef]
- Bashar, S.K.; Han, D.; Hajeb-Mohammadalipour, S.; Ding, E.; Whitcomb, C.; McManus, D.D.; Chon, K.H. Atrial Fibrillation Detection from Wrist Photoplethysmography Signals Using Smartwatches. Sci. Rep. 2019, 9, 15054. [Google Scholar] [CrossRef]
- Hoog Antink, C.; Mai, Y.; Peltokangas, M.; Leonhardt, S.; Oksala, N.; Vehkaoja, A. Accuracy of heart rate variability estimated with reflective wrist-PPG in elderly vascular patients. Sci. Rep. 2021, 11, 8123. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Zhang, D.; Wang, K.; Li, N.; Wang, X. Baseline wander correction in pulse waveforms using wavelet-based cascaded adaptive filter. Comput. Biol. Med. 2007, 37, 716–731. [Google Scholar] [CrossRef] [PubMed]
- Kan, L.; Jianqing, L.; Jianfeng, W.; Gaozhi, X. A cascade filter for pulse wave baseline drift elimination. In Proceedings of the 2012 5th International Congress on Image and Signal Processing, Chongqing, China, 16–18 October 2012; pp. 1495–1499. [Google Scholar] [CrossRef]
- Hao, Z. Harmonics of Pulsatile Pressure at Different Ages and Its Effect on Other Pulsatile Parameters and Waveform-Based Clinical Indices. J. Eng. Sci. Med. Diagn. Ther. 2024, 7, 011001. [Google Scholar] [CrossRef]
- Hao, Z. Relations of Radial Vibration of the Arterial Wall to Pulsatile Parameters in Blood Flow for Extraction of Arterial Indices. J. Eng. Sci. Med. Diagn. Ther. 2023, 6, 011002. [Google Scholar] [CrossRef]
- Chon, K.H.; Dash, S.; Ju, K. Estimation of respiratory rate from photoplethysmogram data using time-frequency spectral estimation. IEEE Trans. Biomed. Eng. 2009, 56, 2054–2063. [Google Scholar] [CrossRef]
- Chen, Z.; Brown, E.N.; Barbieri, R. Assessment of autonomic control and respiratory sinus arrhythmia using point process models of human heart beat dynamics. IEEE Trans. Biomed. Eng. 2009, 56, 1791–1802. [Google Scholar] [CrossRef]
- Liu, H.; Chen, F.; Hartmann, V.; Khalid, S.G.; Hughes, S.; Zheng, D. Comparison of different modulations of photoplethysmography in extracting respiratory rate: From a physiological perspective. Physiol. Meas. 2020, 41, 094001. [Google Scholar] [CrossRef]
- Afandizadeh Zargari, A.H.; Aqajari, S.A.H.; Khodabandeh, H.; Rahmani, A.; Kurdahi, F. An accurate non-accelerometer-based PPG motion artifact removal technique using CycleGAN. ACM Trans. Comput. Healthc. 2023, 4, 20. [Google Scholar] [CrossRef]
- Pollreisz, D.; Taherinejad, N. Detection and Removal of Motion Artifacts in PPG Signals. Mob. Netw. Appl. 2022, 27, 728–738. [Google Scholar] [CrossRef]
- Rahman, M.M.; Hasan, M.; Hao, Z. Motion Artifacts (MA) At-Rest in Measured Arterial Pulse Signals: Time-Varying Amplitude in Each Harmonic and Non-Flat Harmonic-MA-Coupled Baseline. Biosensors 2025, 15, 578. [Google Scholar] [CrossRef] [PubMed]
- Yin, Z.; Liu, C.; Xie, C.; Nie, Z.; Wei, J.; Zhang, W.; Liang, H. Identification of Atrial Fibrillation Using Heart Rate Variability: A Meta-Analysis. Front. Cardiovasc. Med. 2025, 12, 1581683. [Google Scholar] [CrossRef] [PubMed]
- Bashar, S.K.; Hossain, M.B.; Ding, E.; Walkey, A.J.; McManus, D.D.; Chon, K.H. Atrial Fibrillation Detection During Sepsis: Study on MIMIC III ICU Data. IEEE J. Biomed. Health Inform. 2020, 24, 3124–3135. [Google Scholar] [CrossRef]
- Mathivani, H.; Niranjana, V.; Vaishali, B.; Jayanthi, T. AI-Based Atrial Fibrillation Detection Using Pulse Rate Variability from PPG: A Comparative Study with HRV. In Proceedings of the 2025 International Conference on Artificial Intelligence and Data Engineering (AIDE), Nitte, India, 6–7 February 2025; pp. 262–266. [Google Scholar] [CrossRef]
- Charlton, P.H. MIMIC PERform Datasets (1.01) [Data Set]. Zenodo. 2022. Available online: https://zenodo.org/records/6807403 (accessed on 4 June 2025).
- Pachori, D.; Tripathy, R.K.; Jain, T.K. Detection of Atrial Fibrillation from PPG Sensor Data Using Variational Mode Decomposition. IEEE Sens. Lett. 2024, 8, 6001904. [Google Scholar] [CrossRef]
- Pedrosa-Rodriguez, A.; Camara, C.; Peris-Lopez, P. Leveraging IoT Devices for Atrial Fibrillation Detection: A Comprehensive Study of AI Techniques. Appl. Sci. 2024, 14, 8945. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, S.; Kim, S.K.; Yon, D.K.; Nam, Y.; Lee, J. Cooperative PPG/ECG Wearable System for Atrial Fibrillation Diagnosis. IEEE Sens. J. 2025, 25, 7331–7344. [Google Scholar] [CrossRef]
- Aldughayfiq, B.; Ashfaq, F.; Jhanjhi, N.Z.; Humayun, M. A Deep Learning Approach for Atrial Fibrillation Classification Using Multi-Feature Time Series Data from ECG and PPG. Diagnostics 2023, 13, 2442. [Google Scholar] [CrossRef]
- Park, J.; Seok, H.S.; Kim, S.S.; Shin, H. Photoplethysmogram Analysis and Applications: An Integrative Review. Front. Physiol. 2022, 12, 808451. [Google Scholar] [CrossRef]
- Zhang, Z.; Pi, Z.; Liu, B. TROIKA: A General Framework for Heart Rate Monitoring Using Wrist-Type Photoplethysmographic Signals During Intensive Physical Exercise. IEEE Trans. Biomed. Eng. 2015, 62, 522–531. [Google Scholar] [CrossRef]
- Obi, A.I. An Overview of Wearable Photoplethysmographic Sensors and Various Algorithms for Tracking of Heart Rates. Eng. Proc. 2021, 10, 77. [Google Scholar] [CrossRef]
- Ismail, S.; Akram, U.; Siddiqi, I. Heart rate tracking in photoplethysmography signals affected by motion artifacts: A review. EURASIP J. Adv. Signal Process. 2021, 5, 2021. [Google Scholar] [CrossRef]
- Lee, S.; Park, Y.; Choi, H. Motion Artifact Removal Techniques for Wearable EEG and PPG Sensor Systems. Front. Electron. 2021, 2, 685513. [Google Scholar] [CrossRef]
- Chen, J.; Sun, K.; Zheng, R.; Sun, Y.; Yang, H.; Zhong, Y.; Li, X. Three-Dimensional Arterial Pulse Signal Acquisition in Time Domain Using Flexible Pressure-Sensor Dense Arrays. Micromachines 2021, 12, 569. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, N.; Xu, J.; Liu, Z.; Zhou, Y.; Yang, Y.; Li, S.; Huang, Y.; Jiang, S. Flexible Electronics for Cardiovascular Healthcare Monitoring. Innovation 2023, 4, 100485. [Google Scholar] [CrossRef]
- Kumar, N.J.; Johnson, A.; Cobden, R.; Valsamakis, G.; Gristock, J.; Pouryazdan, A.; Roggen, D.; Münzenrieder, N. A Flexible Inductive Sensor for Non-Invasive Arterial Pulse Measurement. In Proceedings of the 2023 IEEE SENSORS, Vienna, Austria, 29 October–1 November 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Chew, J.W.; Gan, S.X.; Cui, J.; Chan, W.D.; Chu, S.T.; Tam, H.-Y. Recent Advancements in Optical Fiber Sensors for Non-Invasive Arterial Pulse Waveform Monitoring Applications: A Review. Photonics 2025, 12, 662. [Google Scholar] [CrossRef]
- Pang, C.; Zhang, Y.; Wang, Y.; Lee, G.-Y.; Kim, T.-I.; Kim, S.M.; Kim, H.N.; Ahn, S.-H.; Suh, K.-Y. A Flexible and Highly Sensitive Strain-Gauge Sensor Using Reversible Interlocking of Nanofibres. Nat. Mater. 2012, 11, 795–801. [Google Scholar] [CrossRef]
- Zang, Y.; Zhang, F.; Di, C.-A.; Zhu, D. Advances of Flexible Pressure Sensors Toward Artificial Intelligence and Health Care Applications. Mater. Horiz. 2015, 2, 140–156. [Google Scholar] [CrossRef]
- Dagdeviren, C.; Yang, H.; Le, C.; Joe, P.; Yona, R.; Liu, Y.; Kim, Y.-S.; Huang, Y.; Damadoran, A.R.; Xia, J.; et al. Conformable Amplified Lead Zirconate Titanate Sensors with Enhanced Piezoelectric Response for Cutaneous Pressure Monitoring. Nat. Commun. 2014, 5, 4496. [Google Scholar] [CrossRef]
- Pang, C.; Zhang, Y.; Chen, W.; Koo, J.H.; Nguyen, A.; Caves, J.M.; Kim, M.-G.; Chortos, A.; Kim, K.; Wang, P.J.; et al. Highly Skin-Conformal Microhairy Sensor for Pulse Signal Amplification. Adv. Mater. 2015, 27, 634–640. [Google Scholar] [CrossRef] [PubMed]
- Drotlef, D.M.; Amjadi, M.; Yunusa, M.; Sitti, M. Bioinspired Composite Microfibers for Skin Adhesion and Signal Amplification of Wearable Sensors. Adv. Mater. 2017, 29, 1701353. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Lee, K.; Kim, J.; Shim, J.; Jeong, S.; Yi, G.-R.; Chae, H.; Bae, J.W.; Kim, S.O.; Pang, C. Microtopography-Guided Conductive Patterns of Liquid-Driven Graphene Nanoplatelet Networks for Stretchable and Skin-Conformal Sensor Array. Adv. Mater. 2017, 29, 1606453. [Google Scholar] [CrossRef]
- Pandey, R.K.; Chao, P.C.P. A Dual-Channel PPG Readout System with Motion-Tolerant Adaptability for OLED-OPD Sensors. IEEE Trans. Biomed. Circuits Syst. 2022, 16, 36–51. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.-J.; Ma, H.-P. A physiological information extraction method based on wearable PPG sensors with motion artifact removal. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 23–27 May 2016; pp. 1–6. [Google Scholar]
- Michael, S.; Graham, K.S.; Davis, G.M. Cardiac Autonomic Responses during Exercise and Post-exercise Recovery Using Heart Rate Variability and Systolic Time Intervals-A Review. Front. Physiol. 2017, 8, 301. [Google Scholar] [CrossRef] [PubMed]
- Holmes, C.J.; MacDonald, H.V.; Esco, M.R.; Fedewa, M.V.; Wind, S.A.; Winchester, L.J. Comparison of Heart Rate Variability Responses to Varying Resistance Exercise Volume-Loads. Res. Q. Exerc. Sport 2022, 93, 391–400. [Google Scholar] [CrossRef]
- Aschbacher, K.; Yilmaz, D.; Kerem, Y.; Crawford, S.; Benaron, D.; Liu, J.; Eaton, M.; Tison, G.H.; Olgin, J.E.; Li, Y.; et al. Atrial fibrillation detection from raw photoplethysmography waveforms: A deep learning application. Heart Rhythm O2 2020, 1, 3–9. [Google Scholar] [CrossRef] [PubMed]
- Kraft, D.; Rumm, P. Atrial Fibrillation and Atrial Flutter Detection Using Deep Learning. Sensors 2025, 25, 4109. [Google Scholar] [CrossRef]
- Neha; Sardana, H.K.; Kanawade, R.; Dogra, N. Photoplethysmograph-Based Arrhythmia Detection Using Morphological Features. Biomed. Signal Process. Control 2023, 81, 104422. [Google Scholar] [CrossRef]
- Pereira, T.; Tran, N.; Gadhoumi, K.; Pelter, M.M.; Do, D.H.; Lee, R.J.; Colorado, R.; Meisel, K.; Hu, X. Photoplethysmography-Based Atrial Fibrillation Detection: A Review. npj Digit. Med. 2020, 3, 3. [Google Scholar] [CrossRef]
- Chen, W.; Yi, Z.; Lim, L.J.R.; Lim, R.Q.R.; Zhang, A.; Qian, Z.; Huang, J.; He, J.; Liu, B. Deep Learning and Remote Photoplethysmography Powered Advancements in Contactless Physiological Measurement. Front. Bioeng. Biotechnol. 2024, 12, 1420100. [Google Scholar] [CrossRef]











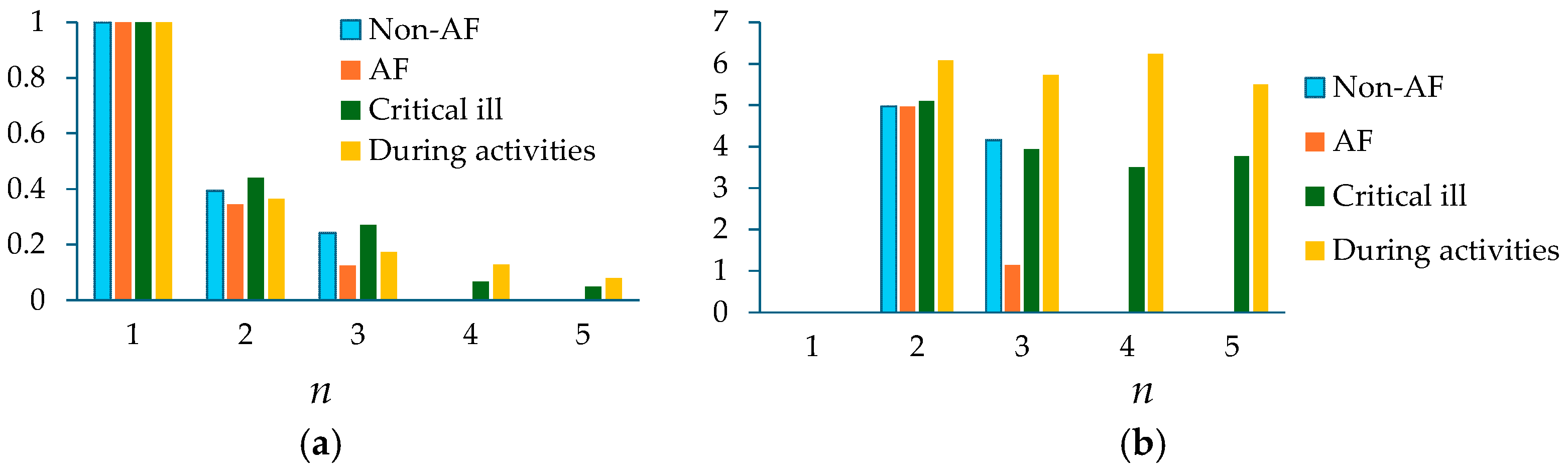
| n | 1 | Ax0i/Ax01 | Atf_i/Atf_1 | Acf_i/Acf_1 | 0i − 01 | |
|---|---|---|---|---|---|---|
| pre-exercise | 1 | 1 | 1 | 1 | 1 | 0 |
| 2 | 0.457 | 0.324 | 0.332 | 0.457 | 5.781 | |
| 3 | 0.407 | 0.209 | 0.219 | 0.407 | 5.420 | |
| 4 | 0.231 | 0.128 | 0.114 | 0.231 | 4.460 | |
| 5 | 0.146 | 0.085 | 0.071 | 0.146 | 3.864 | |
| 6 | 0.115 | 0.067 | 0.070 | 0.115 | 3.716 | |
| 7 | 0.066 | 0.033 | 0.036 | 0.065 | 2.854 | |
| 1 min post-exercise | 1 | 1 | 1 | 1 | 1 | 0 |
| 2 | 0.698 | 0.571 | 0.515 | 0.698 | 4.954 | |
| 3 | 0.261 | 0.147 | 0.151 | 0.261 | 4.335 | |
| 4 | 0.156 | 0.088 | 0.088 | 0.155 | 3.380 | |
| 5 | 0.074 | 0.040 | 0.032 | 0.073 | 2.501 | |
| 6 | 0.032 | 0.015 | 0.014 | 0.032 | 2.005 | |
| 7 | 0.016 | 0.008 | 0.006 | 0.016 | 3.004 | |
| 5 min post-exercise | 1 | 1 | 1 | 1 | 1 | 0 |
| 2 | 0.612 | 0.524 | 0.541 | 0.611 | 5.082 | |
| 3 | 0.237 | 0.151 | 0.154 | 0.236 | 4.060 | |
| 4 | 0.127 | 0.072 | 0.070 | 0.126 | 3.408 | |
| 5 | 0.043 | 0.023 | 0.028 | 0.042 | 3.011 | |
| 6 | 0.010 | 0.008 | 0.007 | 0.010 | 3.003 | |
| 7 | 0.010 | 0.007 | 0.001 | 0.010 | 3.104 |
| Pre-Exercise | 1 min Post-Exercise | 5 min Post-Exercise | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Harmonics (n) | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| mean(HRi(t)) | 61.88 | 61.88 | 61.48 | 127.18 | 127.20 | 127.19 | 102.12 | 102.12 | 102.11 |
| RSME(HRi(t)) | 2.78 | 2.72 | 2.12 | 4.48 | 4.47 | 4.48 | 1.81 | 1.89 | 1.97 |
| mean(RRfi(t)) | 10.14 | 10.01 | 7.02 | 7.27 | 7.29 | 7.21 | 6.29 | 6.32 | 6.30 |
| mean(Bfi(t)) | 0.029 | 0.055 | 0.092 | 0.032 | 0.063 | 0.092 | 0.027 | 0.061 | 0.099 |
| mean(HRfi(t)) | 60.65 | 60.74 | 60.85 | 127.76 | 127.76 | 127.75 | 102.10 | 102.14 | 102.12 |
| mean(RRϕi(t)) | 14.92 | 14.74 | 13.44 | 13.43 | 13.39 | 13.35 | 12.58 | 12.36 | 12.40 |
| mean(Bϕi(t)) | 0.013 | 0.024 | 0.062 | 0.010 | 0.020 | 0.028 | 0.004 | 0.006 | 0.007 |
| mean(HRϕi(t)) | 60.72 | 60.71 | 60.73 | 127.73 | 127.73 | 127.73 | 102.15 | 102.14 | 102.14 |
| RMSE(HRϕi(t)) | 0.58 | 0.53 | 0.97 | 0.43 | 0.45 | 0.42 | 0.16 | 0.13 | 0.12 |
| RMSE(HRPFi(t)) | 2.20 | 2.19 | 1.14 | 4.04 | 4.02 | 4.06 | 1.65 | 1.76 | 1.85 |
| Non-AF | AF | Critically Ill | During Activities | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 |
| i/i | 1 | 0.393 | 0.241 | 1 | 0.345 | 0.123 | 1 | 0.440 | 0.270 | 0.066 | 0.049 | 1 | 0.363 | 0.172 | 0.128 | 0.080 |
| Ax0i/Ax01 | 1 | 0.470 | 0.203 | 1 | 0.287 | 0.075 | 1 | 0.290 | 0.186 | 0.045 | 0.029 | 1 | 0.255 | 0.104 | 0.083 | 0.035 |
| Atf_i/Atf_1 | 1 | 0.260 | 0.186 | 1 | 0.280 | 0.048 | 1 | 0.379 | 0.187 | 0.036 | 0.028 | 1 | 0.321 | 0.122 | 0.089 | 0.044 |
| Acf_i/Acf_1 | 1 | 0.393 | 0.241 | 1 | 0.344 | 0.124 | 1 | 0.439 | 0.269 | 0.066 | 0.049 | 1 | 0.363 | 0.172 | 0.127 | 0.080 |
| 0i − 01 | 0 | 4.972 | 4.156 | 0 | 4.973 | 1.140 | 0 | 5.099 | 3.940 | 3.497 | 3.766 | 0 | 6.080 | 5.725 | 6.239 | 5.503 |
| Non-AF | AF | Critically Ill | During Activities | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| mean(HRi(t)) | 59.09 | 59.11 | 59.12 | 97.97 | 94.08 | 90.98 | 91.11 | 91.10 | 90.69 | 45.86 | 45.87 | 45.04 |
| RMSE(HRi(t)) | 1.52 | 1.40 | 1.35 | 9.69 | 5.25 | 3.47 | 0.94 | 0.91 | 1.41 | 2.28 | 2.17 | 1.26 |
| mean(RRfi(t)) | 12.56 | 12.59 | 12.58 | 9.38 | 10.55 | 10.36 | 10.76 | 12.19 | 10.54 | 12.71 | 11.31 | 9.83 |
| mean(Bfi(t)) | 0.027 | 0.039 | 0.057 | 0.143 | 0.186 | 0.109 | 0.014 | 0.023 | 0.050 | 0.019 | 0.034 | 0.055 |
| mean(HRfi(t)) | 58.95 | 58.94 | 58.94 | 94.63 | 95.57 | 95.43 | 90.97 | 90.95 | 90.94 | 46.13 | 46.11 | 45.90 |
| mean(RRϕi(t)) | 12.58 | 12.54 | 12.47 | 10.63 | 12.46 | 11.05 | 12.82 | 11.58 | 12.98 | 14.35 | 13.16 | 14.06 |
| mean(Bϕi(t)) | 0.032 | 0.052 | 0.071 | 0.143 | 0.319 | 0.237 | 0.010 | 0.040 | 0.042 | 0.028 | 0.055 | 0.041 |
| mean(HRϕi(t)) | 58.89 | 58.89 | 58.91 | 95.66 | 95.14 | 95.30 | 90.97 | 90.96 | 90.97 | 45.94 | 45.94 | 46.04 |
| RSME(HRϕi(t)) | 1.38 | 1.16 | 1.07 | 7.30 | 7.74 | 3.71 | 0.44 | 1.15 | 0.71 | 1.21 | 1.29 | 0.61 |
| RMSE(HRPFi(t)) | 0.13 | 0.25 | 0.27 | 2.39 | −2.49 | −0.24 | 0.50 | −0.24 | 0.70 | 1.07 | 0.88 | 0.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, Z. Motion Artifacts Removal from Measured Arterial Pulse Signals at Rest: A Generalized SDOF-Model-Based Time–Frequency Method. Sensors 2025, 25, 6808. https://doi.org/10.3390/s25216808
Hao Z. Motion Artifacts Removal from Measured Arterial Pulse Signals at Rest: A Generalized SDOF-Model-Based Time–Frequency Method. Sensors. 2025; 25(21):6808. https://doi.org/10.3390/s25216808
Chicago/Turabian StyleHao, Zhili. 2025. "Motion Artifacts Removal from Measured Arterial Pulse Signals at Rest: A Generalized SDOF-Model-Based Time–Frequency Method" Sensors 25, no. 21: 6808. https://doi.org/10.3390/s25216808
APA StyleHao, Z. (2025). Motion Artifacts Removal from Measured Arterial Pulse Signals at Rest: A Generalized SDOF-Model-Based Time–Frequency Method. Sensors, 25(21), 6808. https://doi.org/10.3390/s25216808






