Feasibility of Initial Bias Estimation in Real Maritime IMU Data Including X- and Y-Axis Accelerometers
Abstract
1. Introduction
1.1. Background and Motivation
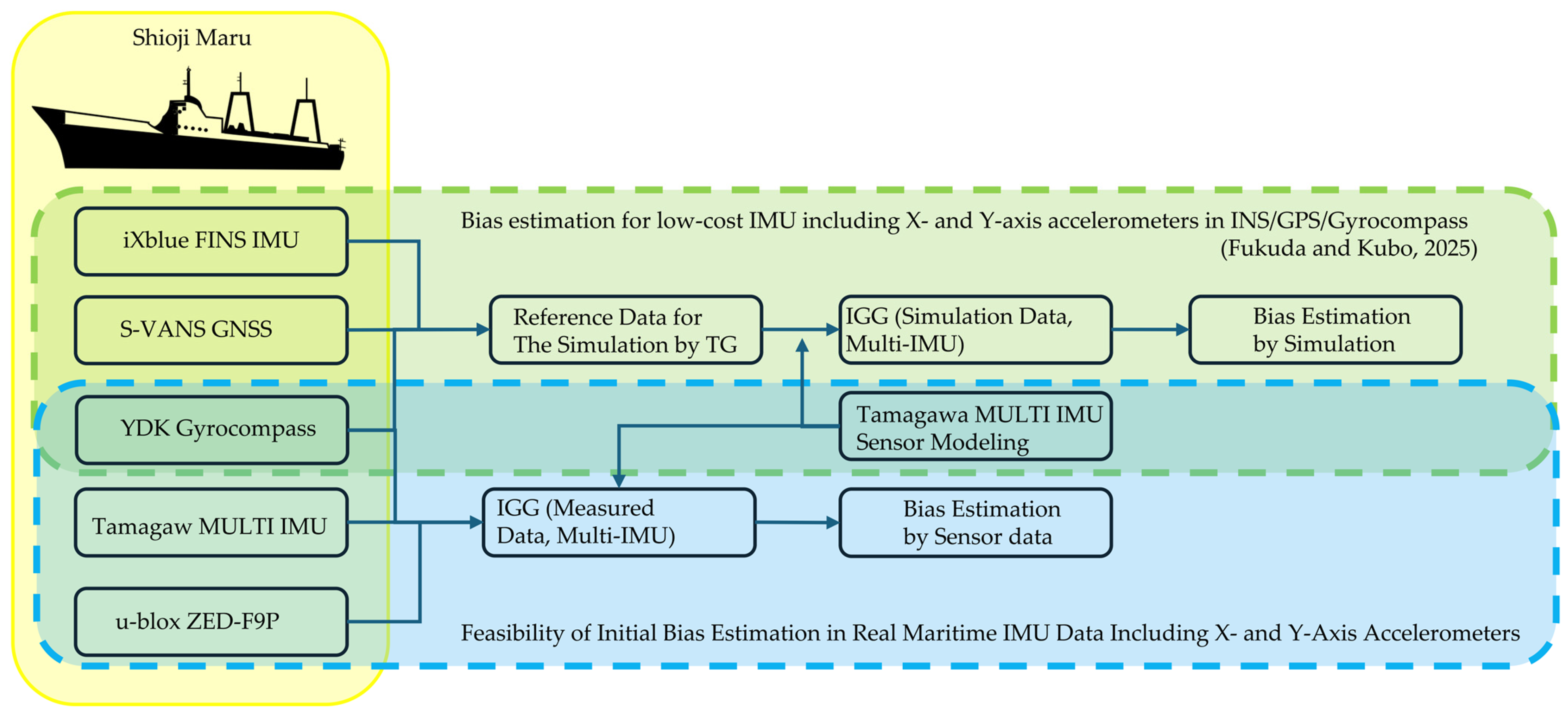
1.2. Method Inheritance and Innovation
2. Materials and Methods
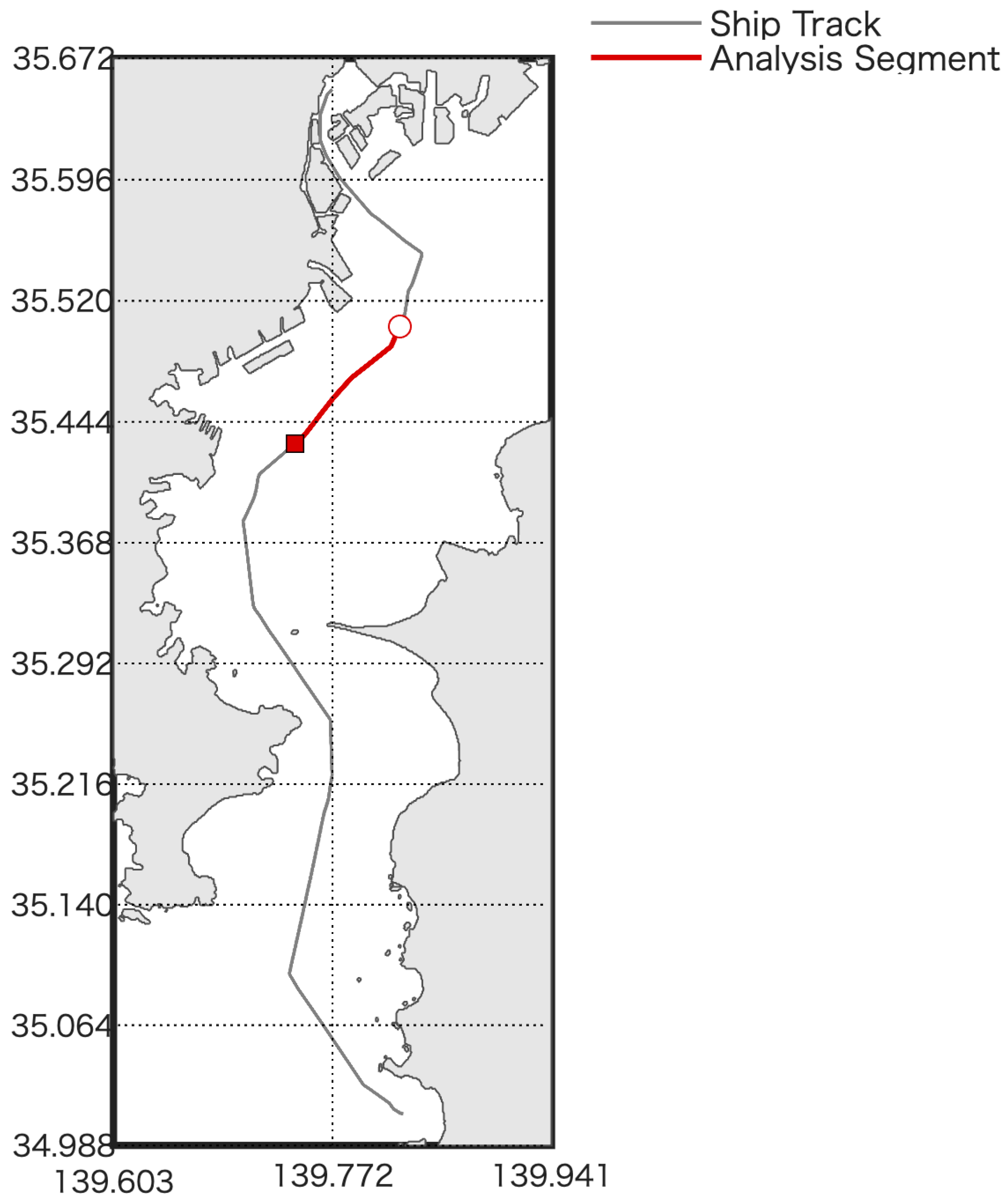
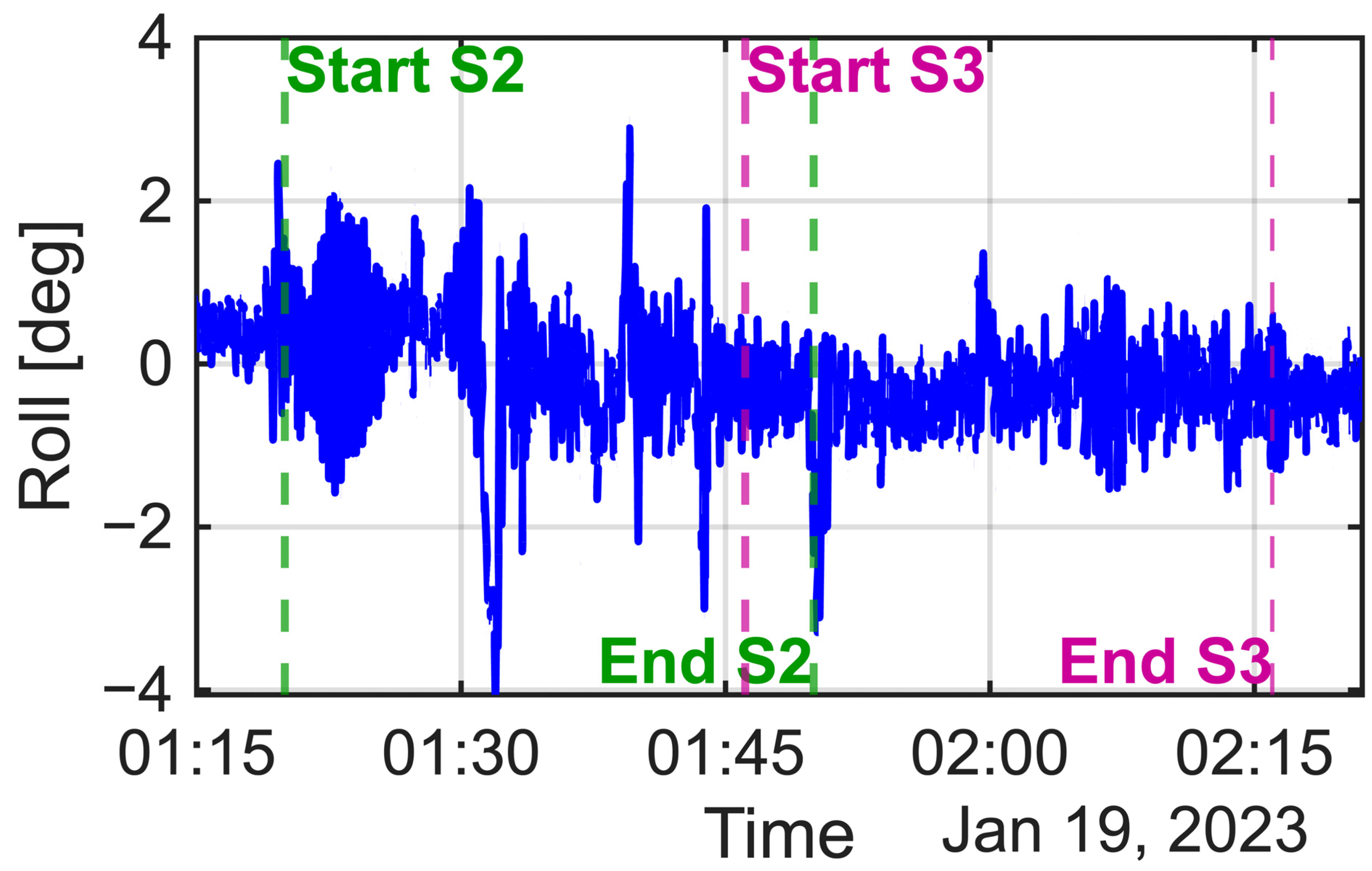
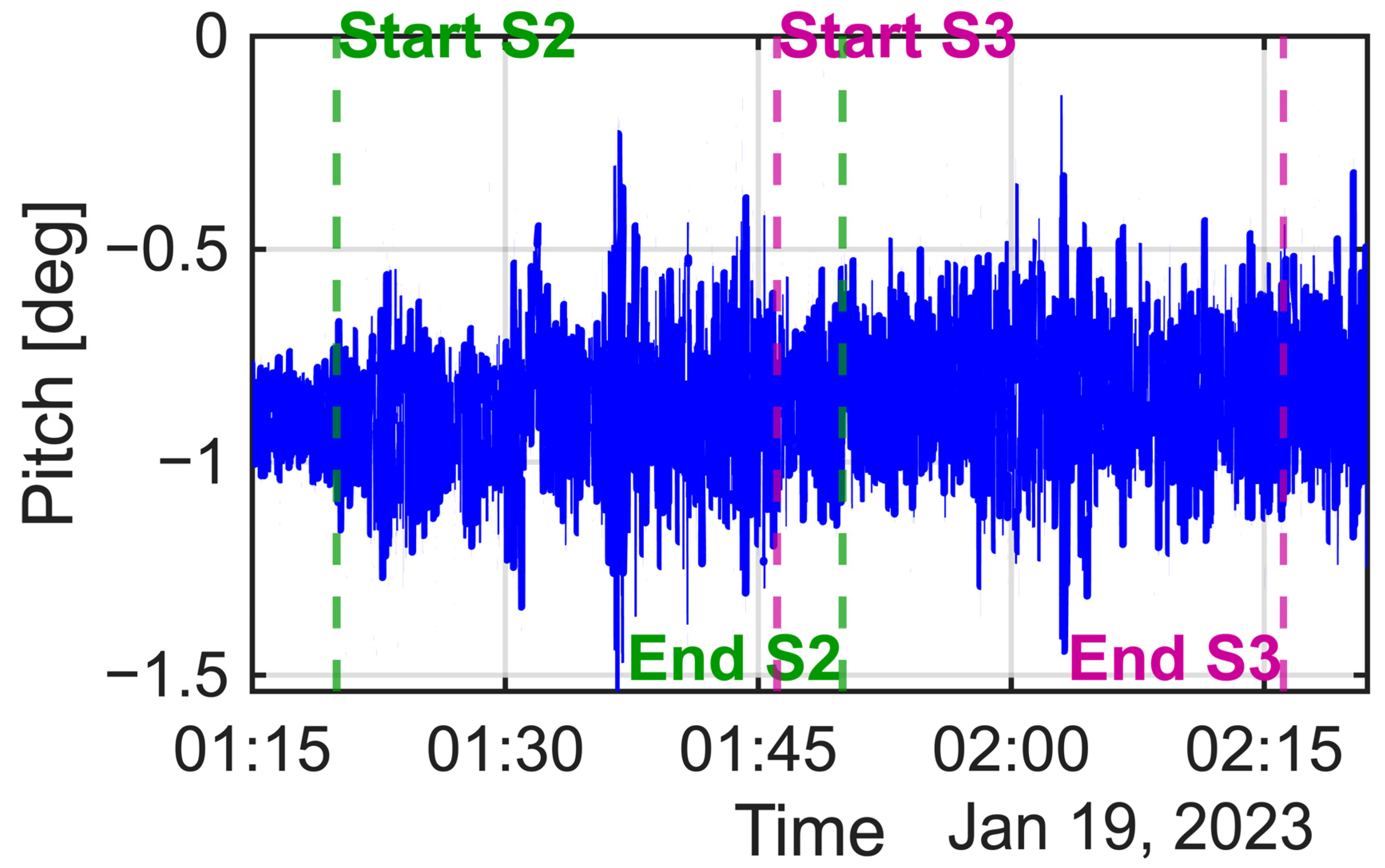
2.1. Experimental Setup and Sensors
2.2. Bias-Estimation Method
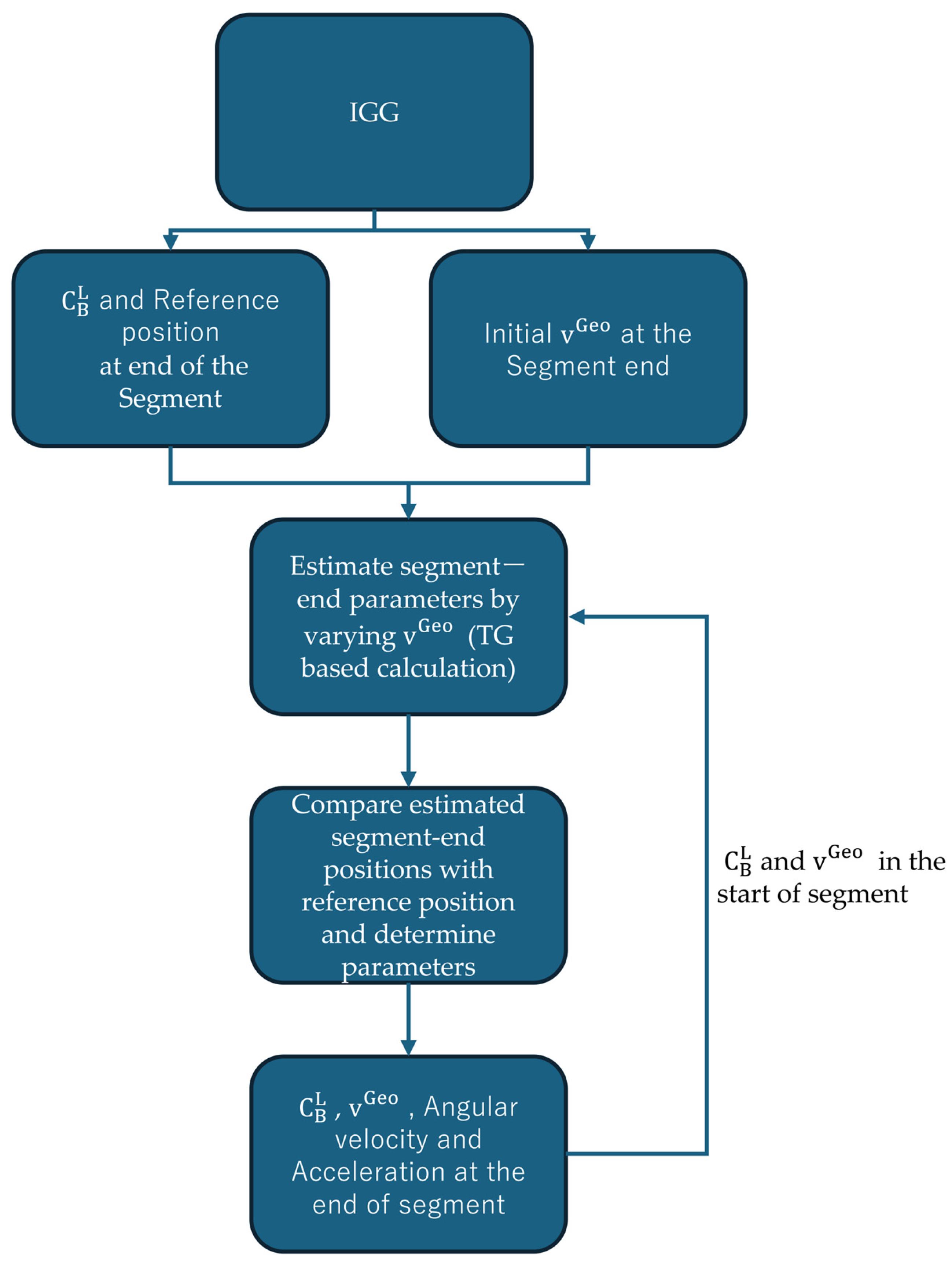
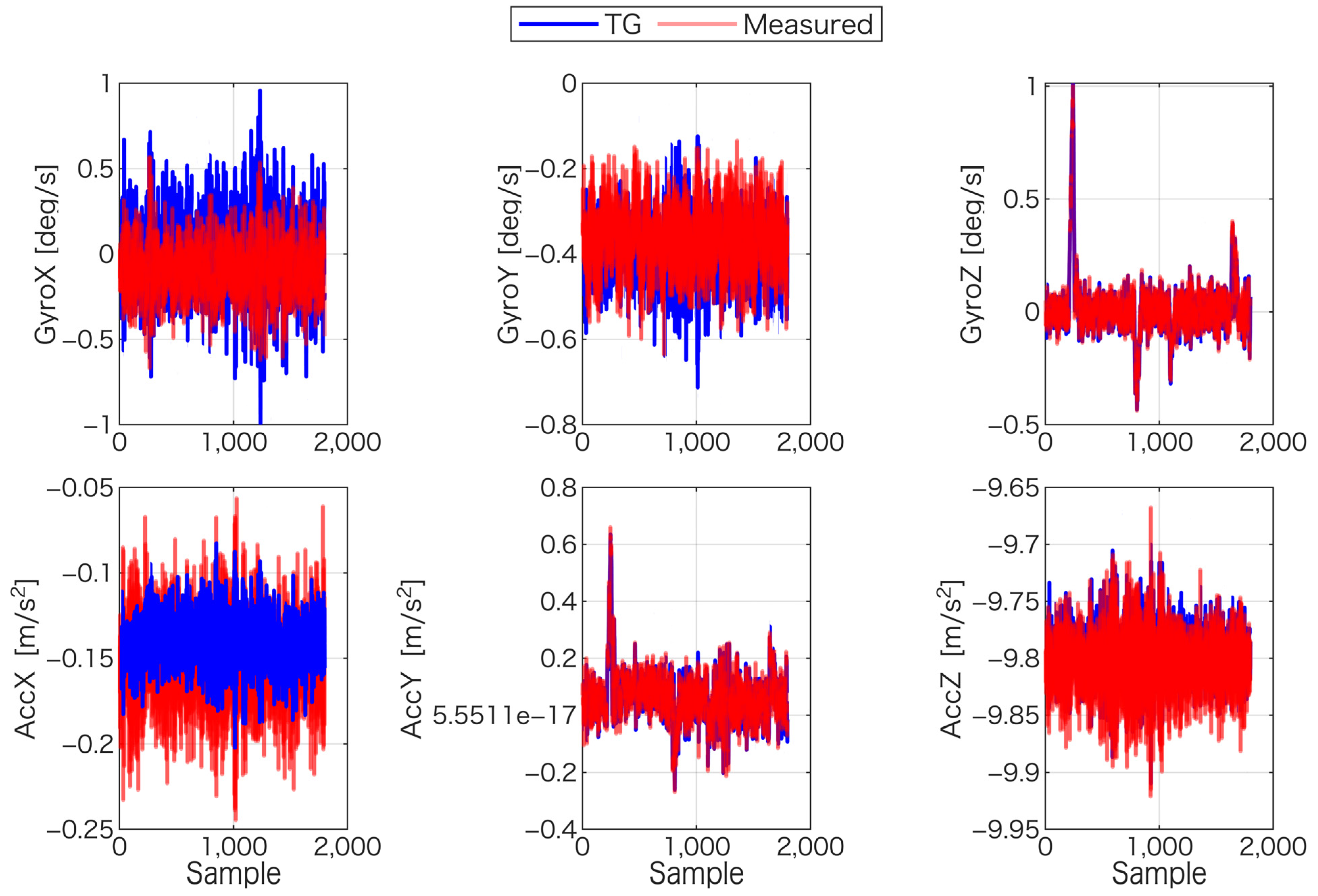
2.2.1. Acceleration and Angular Velocity Estimation Using a TG-Based Estimation
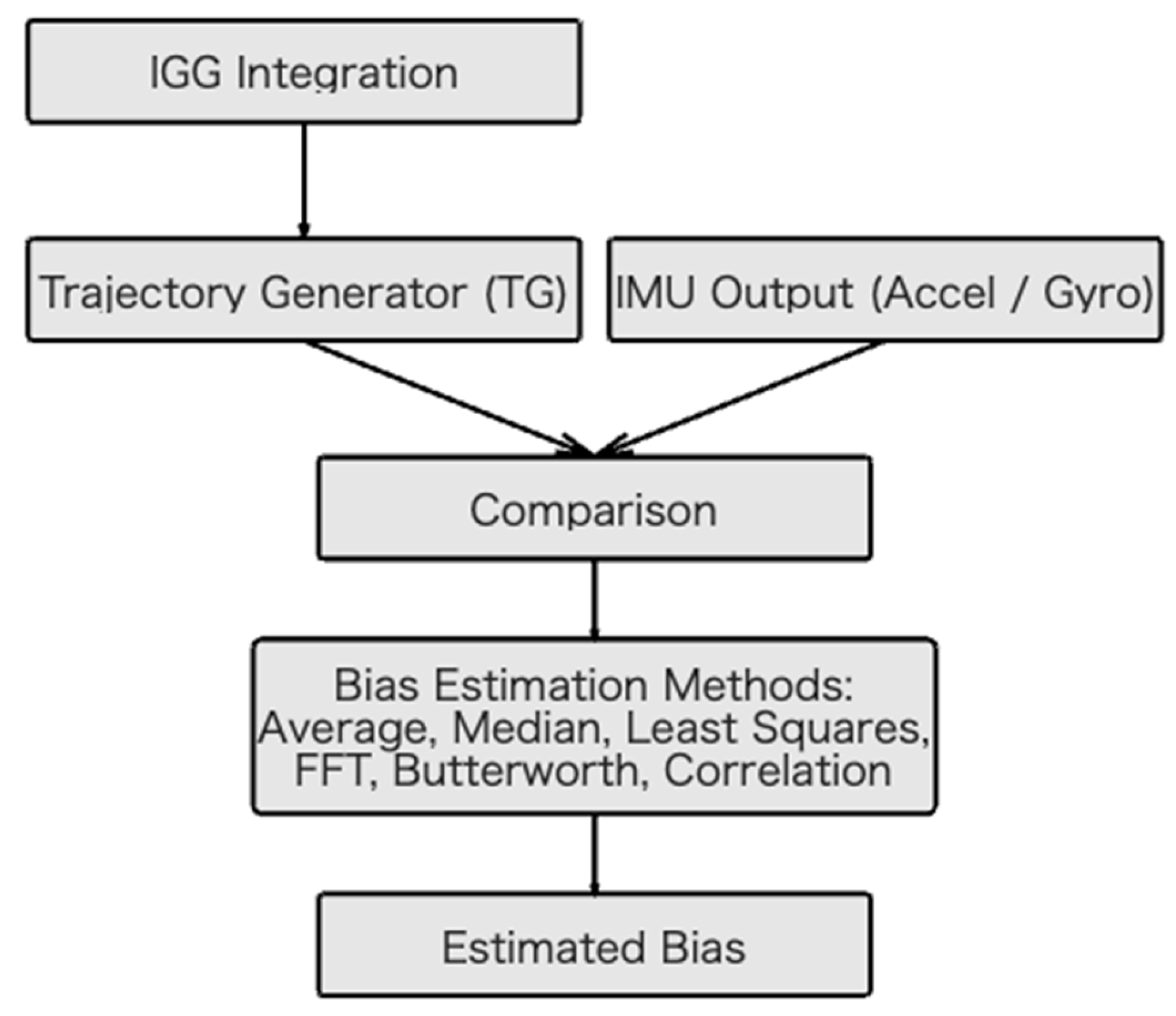
2.2.2. Bias Estimation
- Mean Difference Method: The bias is the mean of the difference between the IMU measurement and TG output.
- Median Difference Method: The bias is the median of the differences, providing robustness against outliers.
- Normalized Cross-Correlation Method: The bias is the offset that maximizes the correlation between the IMU measurements and the TG outputs.
- Least-Squares Approximation: The bias is estimated by minimizing the sum of squared errors between the bias-corrected measurement and TG output.
- Frequency-Domain Analysis (Fast Fourier Transform (FFT)): The bias is considered the DC component of the difference signal.
- Butterworth Filter Method: A low-pass Butterworth filter (cutoff 0.1–0.5 Hz) is applied to the difference signal, and the steady-state component is considered as the bias.
2.2.3. Estimation of X/Y-Axis Accelerometer Biases Using Altitude Differences
- Fix the bias of one horizontal axis and vary the other within a predefined range.
- Select the bias value that minimizes the altitude difference.
- Swap the axes and repeat the procedure.
2.3. Data Processing
2.4. Evaluation Metrics
2.4.1. Bias-Estimation Accuracy
2.4.2. Verification in a Simulation Environment
2.4.3. Evaluation of Estimated X- and Y-Axis Accelerometer Biases
3. Results
3.1. Bias-Estimation Accuracy Results
3.2. Validation in a Simulation Environment
3.3. Estimated X- and Y-Axis Accelerometer Biases
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| INS | Inertial Navigation System |
| EKF | Extended Kalman filter |
| TG | Trajectory generator |
| FFT | Fast Fourier transform |
| RMS | Root-mean-squared |
| GNSS | Global Navigation Satellite Systems |
| RTK | Real-time kinematics |
| PPP | Precise point positioning |
| IMU | Inertial measurement unit |
| MEMS | Micro-electro-mechanical systems |
| MSE | Mean squared error |
| FOG | Fiber-optic gyroscope |
| IGG | INS/GNSS/gyrocompass |
References
- Androjna, A.; Perkovič, M. Impact of spoofing of navigation systems on maritime situational awareness. Trans. Marit. Sci. 2021, 10, 361–373. [Google Scholar] [CrossRef]
- Smith, A. UN Agencies Warn of Satellite Navigation Jamming and Spoofing. International Telecommunication Union 2025. Available online: https://www.itu.int/hub/2025/03/un-agencies-warn-of-satellite-navigation-jamming-and-spoofing/ (accessed on 9 September 2025).
- Norse, E. GNSS Under Attack: Recognizing and Mitigating Jamming and Spoofing Threats. GPS World 2025. Available online: https://www.gpsworld.com/gnss-under-attack-recognizing-and-mitigating-jamming-and-spoofing-threats/ (accessed on 9 September 2025).
- Milner, G. How Vulnerable is G.P.S? The New Yorker 2020. Available online: https://www.newyorker.com/tech/annals-of-technology/how-vulnerable-is-gps (accessed on 9 September 2025).
- Kauranen, A. Finland Detects Satellite Navigation Jamming and Spoofing in Baltic Sea. Reuters 2024. Available online: https://www.reuters.com/world/europe/finland-detects-satellite-navigation-jamming-spoofing-baltic-sea-2024-10-31/ (accessed on 9 September 2025).
- The Maritime Executive. Multiple Vessels Report GPS Disruption in Strait of Hormuz. 2025. Available online: https://maritime-executive.com/article/multiple-vessels-report-gps-disruption-in-strait-of-hormuz (accessed on 3 October 2025).
- Becker, S. MSC Box Ship Grounds in Apparent GPS Jamming Incident. World Ports 2025. Available online: https://www.worldports.org/msc-box-ship-grounds-in-apparent-gps-jamming-incident/ (accessed on 9 September 2025).
- Park, K.-D.; Yoon, W.-J.; Lee, J.-S. Reduction of multipath effect in GNSS positioning by applying pseudorange acceleration as weight. Sensors 2024, 24, 6880. [Google Scholar] [CrossRef] [PubMed]
- Skone, S.; Knudsen, K.; de Jong, M. Limitations in GPS receiver tracking performance under ionospheric scintillation conditions. Phys. Chem. Earth Part Solid Earth Geod. 2001, 26, 613–621. [Google Scholar] [CrossRef]
- Jacobsen, K.S.; Sokolova, N.; Ouassou, M.; Solberg, A.M. Study of time- and distance-dependent degradations of network RTK performance at high latitudes in Norway. SN Appl. Sci. 2023, 5, 126. [Google Scholar] [CrossRef]
- Jin, Y.; Oksavik, K. GPS scintillations and losses of signal lock at high latitudes during the 2015 St. Patrick’s Day storm. J. Geophys. Res. Space Phys. 2018, 123, 7943–7957. [Google Scholar] [CrossRef]
- Skone, S.; Yousuf, R. Performance of satellite-based navigation for marine users during ionospheric disturbances. Space Weather 2007, 5, SW000246. [Google Scholar] [CrossRef]
- Fukuda, G.; Kubo, N. Bias estimation for low-cost IMU including X- and Y-axis accelerometers in INS/GPS/gyrocompass. Sensors 2025, 25, 1315. [Google Scholar] [CrossRef] [PubMed]
- TAMAGAWA SEIKI Co. Ltd. MEMS-Based IMU. Available online: https://mems.tamagawa-seiki.com/en/ (accessed on 21 January 2025).
- Savage, P.G. Strapdown Analytics, 2nd ed.; Part 2; Strapdown Associates Inc.: Maple Plain, MN, USA, 2000. [Google Scholar]
- Fukuda, G.; Kubo, N. Application of initial bias estimation method for inertial navigation system (INS)/Doppler velocity log (DVL) and INS/DVL/gyrocompass using micro-electro-mechanical system sensors. Sensors 2022, 22, 5334. [Google Scholar] [CrossRef] [PubMed]

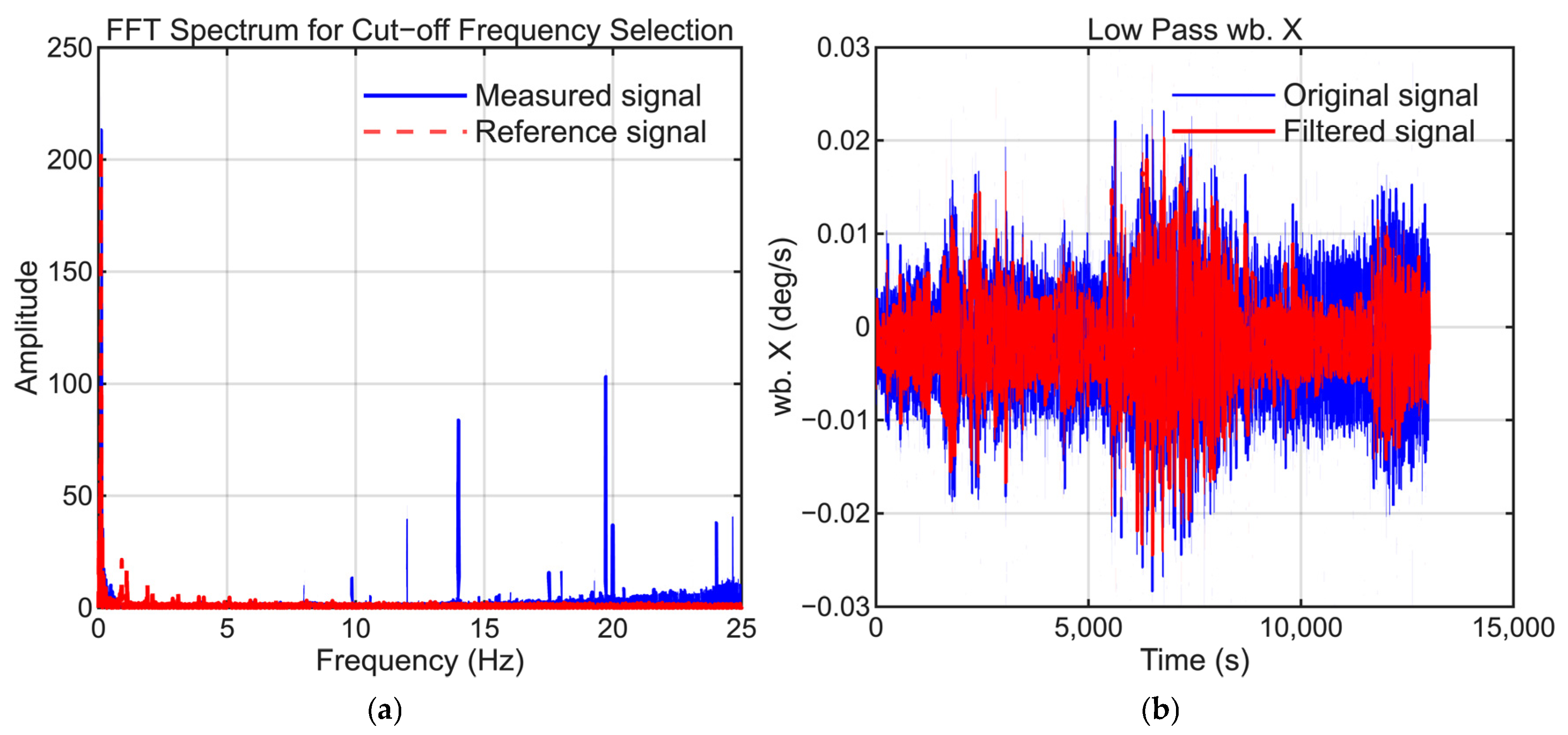
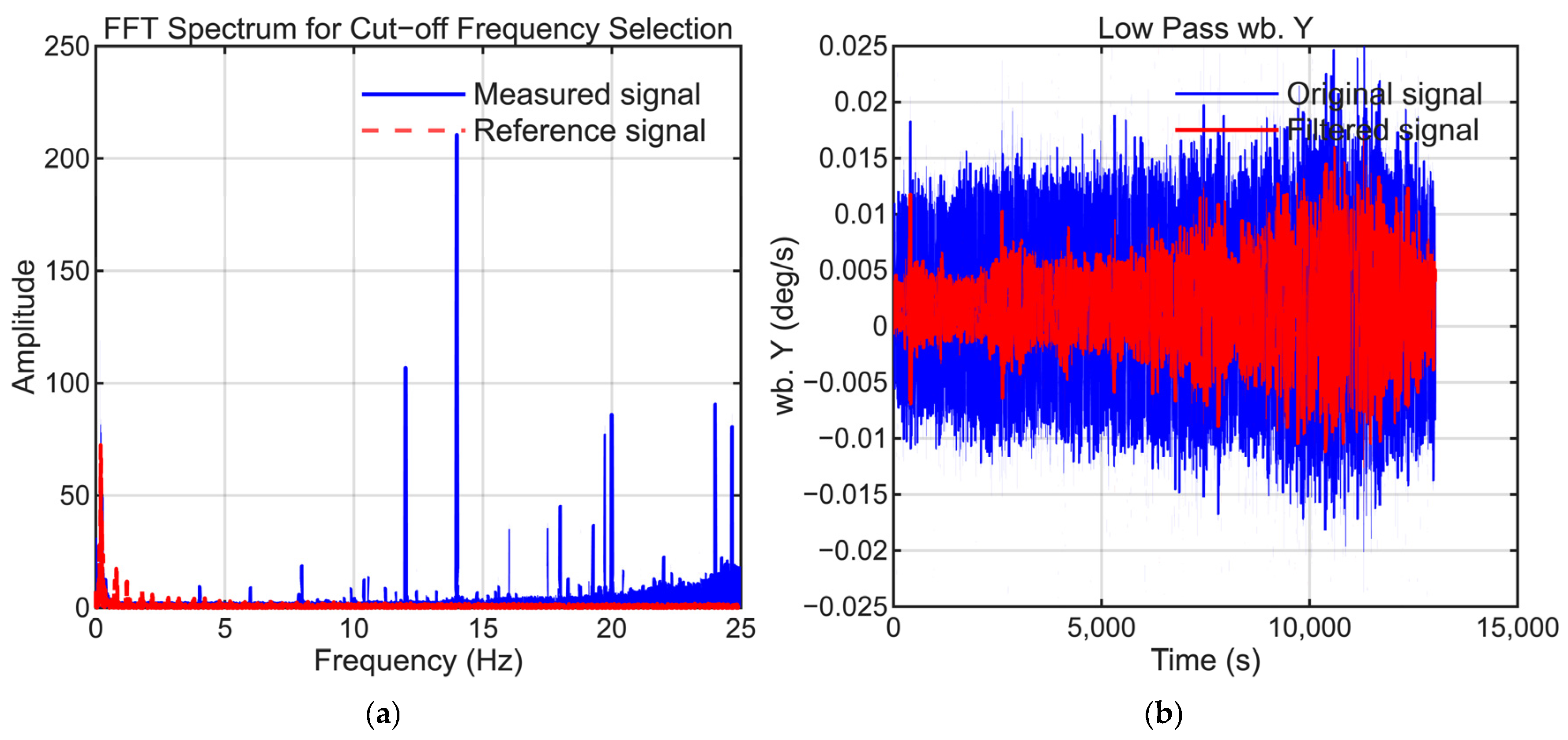

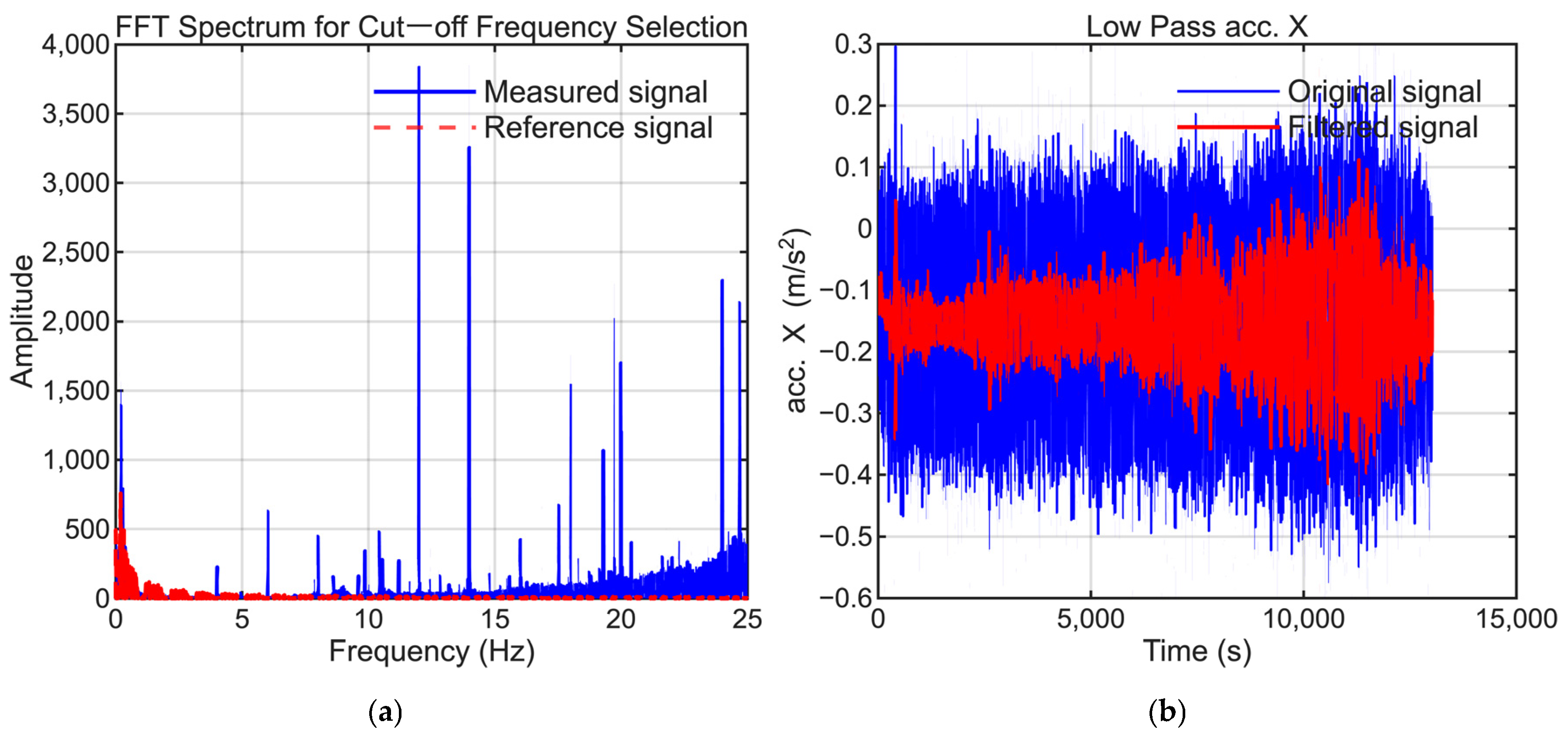
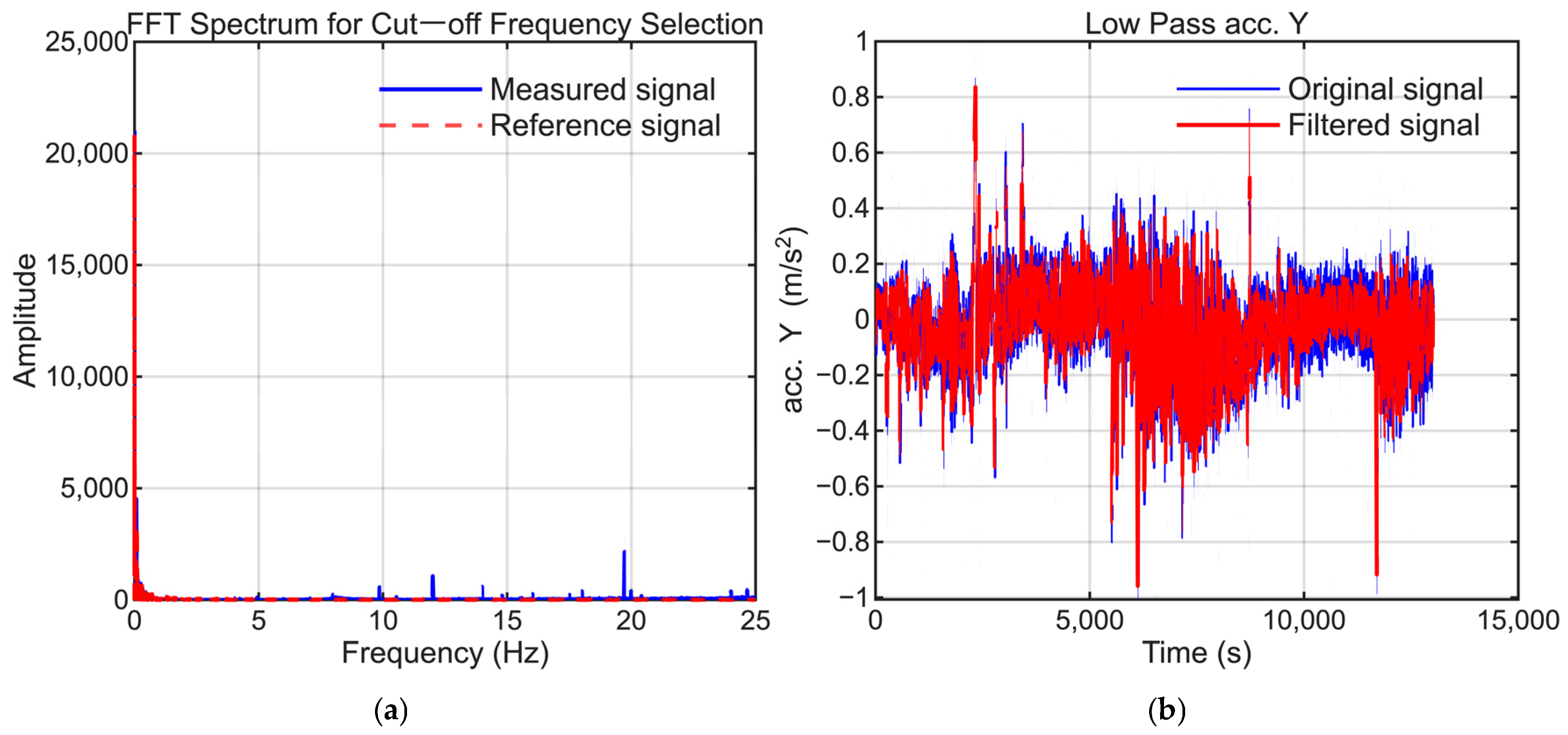

| STD (deg/s) (m/s2) | Random Walk (deg/s) (m/s2) | Bias Instability (deg/s) (m/s2) | |
|---|---|---|---|
| Gyro X | 4.485 × 10−2 | 6.423 × 10−3 | 5.334 × 10−3 |
| Gyro Y | 3.998 × 10−2 | 5.968 × 10−3 | 4.922 × 10−3 |
| Gyro Z | 1.371 × 10−3 | 1.882 × 10−4 | 2.191 × 10−5 |
| Acc X | 1.920 × 10−3 | 2.063 × 10−4 | 2.534 × 10−5 |
| Acc Y | 2.412 × 10−3 | 2.958 × 10−4 | 3.073 × 10−5 |
| Acc Z | 2.526 × 10−3 | 3.013 × 10−4 | 7.848 × 10−5 |
| Method | GyroX | GyroY | GyroZ | AccX | AccY | AccZ |
|---|---|---|---|---|---|---|
| deg/s | deg/s | deg/s | m/s2 | m/s2 | m/s2 | |
| Average | −0.0913 | 0.1020 | 0.003585 | −0.01033 | 0.00308 | −0.01033 |
| Normalized Correlation | −0.0900 | −0.3000 | 0.000500 | 0.20000 | −0.00492 | 0.20000 |
| Least Squares | −0.0913 | 0.1020 | 0.003585 | −0.01033 | 0.00308 | −0.01033 |
| FFT | −0.0913 | 0.1020 | 0.003585 | −0.01033 | 0.00308 | −0.01033 |
| Butterworth | −0.0915 | 0.1017 | 0.003550 | −0.01024 | 0.00308 | −0.01034 |
| Median | −0.0941 | 0.0998 | 0.004397 | −0.00928 | 0.00493 | −0.00956 |
| Sensor | Average | Corr | Least | FFT | Butter | Median |
|---|---|---|---|---|---|---|
| GyroX [deg/s] | 0 | −2.28 × 10−5 | 0 | 0 | 3.04 × 10−6 | 3.04 × 10−6 |
| GyroY [deg/s] | 0 | 7.02 × 10−3 | 0 | 0 | 5.89 × 10−6 | 3.89 × 10−5 |
| GyroZ [deg/s] | 0 | 5.38 × 10−5 | 0 | 0 | 6.12 × 10−7 | −1.42 × 10−5 |
| AccX [m/s2] | 0 | −2.10 × 10−1 | 0 | 0 | −8.50 × 10−5 | −1.05 × 10−3 |
| AccY [m/s2] | 0 | 8.00 × 10−3 | 0 | 0 | −5.94 × 10−6 | −1.85 × 10−3 |
| AccZ [m/s2] | 0 | −2.10 × 10−1 | 0 | 0 | 9.80 × 10−6 | −7.74 × 10−4 |
| Sensor | Average | Corr | Least | FFT | Butter | Median |
|---|---|---|---|---|---|---|
| GyroX [deg/s] | −4.93 × 10−5 | −7.21× 10−5 | −4.93 × 10−5 | −4.93 × 10−5 | −4.63 × 10−5 | −4.63 × 10−5 |
| GyroY [deg/s] | −3.89 × 10−5 | 6.98 × 10−3 | −3.89 × 10−5 | −3.89 × 10−5 | −3.30 × 10−5 | 0 |
| GyroZ [deg/s] | 1.42 × 10−5 | 6.80 × 10−5 | 1.42 × 10−5 | 1.42 × 10−5 | 1.48 × 10−5 | 0 |
| AccX [m/s2] | 1.05 × 10−3 | −2.09 × 10−1 | 1.05 × 10−3 | 1.05 × 10−3 | 9.61 × 10−4 | 0 |
| AccY [m/s2] | 1.85 × 10−3 | 9.85 × 10−3 | 1.85 × 10−3 | 1.85 × 10−3 | 1.85 × 10−3 | 0 |
| AccZ [m/s2] | 7.74 × 10−4 | −2.10 × 10−1 | 7.74 × 10−4 | 7.74 × 10−4 | 7.84 × 10−4 | 0 |
| Sensor | Average | Corr | Least | FFT | Butter | Median |
|---|---|---|---|---|---|---|
| GyroX [deg/s] | 3.28 × 10−3 | 3.28 × 10−3 | 3.28 × 10−3 | 3.28 × 10−3 | 3.28 × 10−3 | 3.28 × 10−3 |
| GyroY [deg/s] | 3.49 × 10−3 | 7.84 × 10−3 | 3.49 × 10−3 | 3.49 × 10−3 | 3.49 × 10−3 | 3.49 × 10−3 |
| GyroZ [deg/s] | 5.58 × 10−4 | 5.61 × 10−4 | 5.58 × 10−4 | 5.58 × 10−4 | 5.58 × 10−4 | 5.58 × 10−4 |
| AccX [m/s2] | 3.04 × 10−2 | 2.13 × 10−1 | 3.04 × 10−2 | 3.04 × 10−2 | 3.04 × 10−2 | 3.05 × 10−2 |
| AccY [m/s2] | 3.80 × 10−2 | 3.88 × 10−2 | 3.80 × 10−2 | 3.80 × 10−2 | 3.80 × 10−2 | 3.80 × 10−2 |
| AccZ [m/s2] | 2.30 × 10−2 | 2.12 × 10−1 | 2.30 × 10−2 | 2.30 × 10−2 | 2.30 × 10−2 | 2.30 × 10−2 |
| Sensor | Average | Corr | Least | FFT | Butter | Median |
|---|---|---|---|---|---|---|
| GyroX | 0.783 | 0.783 | 0.783 | 0.783 | 0.783 | 0.783 |
| GyroY | 0.638 | 0.126 | 0.638 | 0.638 | 0.638 | 0.637 |
| GyroZ | 0.971 | 0.971 | 0.971 | 0.971 | 0.971 | 0.971 |
| AccX | 0.986 | 0.995 | 0.986 | 0.986 | 0.986 | 0.986 |
| AccY | 0.953 | 0.954 | 0.953 | 0.953 | 0.953 | 0.952 |
| AccZ | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Method | X Gyro deg/s | Y Gyro deg/s | Z Gyro deg/s | |||
|---|---|---|---|---|---|---|
| −0.0913 | 0.102 | 0.003585 | ||||
| Est. | Error | Est. | Error | Est. | Error | |
| Average | −0.0914 | 0.0001 | 0.0995 | 0.0025 | 0.003580 | 0.000005 |
| Normalized correlation | −0.0900 | 0.0013 | 0.1000 | 0.0020 | 0.000500 | 0.003085 |
| Least squares | −0.0914 | 0.0001 | 0.0995 | 0.0025 | 0.003580 | 0.000005 |
| FFT | −0.0914 | 0.0001 | 0.0995 | 0.0025 | 0.003580 | 0.000005 |
| Butterworth | −0.0914 | 0.0001 | 0.0997 | 0.0023 | 0.003586 | 0.000001 |
| Median | −0.0925 | 0.0012 | 0.1013 | 0.0007 | 0.003671 | 0.000086 |
| Method | X Acc m/s2 | Y Acc m/s2 | Z Acc m/s2 | |||
|---|---|---|---|---|---|---|
| 0.03900 | 0.01600 | −0.01033 | ||||
| Est. | Error | Est. | Error | Est | Error | |
| Average | −5.8223 × 10−3 | 4.4822 × 10−2 | −2.4506 × 10−3 | 1.8451 × 10−2 | −1.0186 × 10−2 | 1.4413 × 10−4 |
| Normalized correlation | −4.4700 × 10−3 | 4.3470 × 10−2 | −2.5200 × 10−3 | 1.8520 × 10−2 | 1.0731 × 10−1 | 1.1764 × 10−1 |
| Least squares | −5.8223 × 10−3 | 4.4822 × 10−2 | −2.4506 × 10−3 | 1.8451 × 10−2 | −1.0186 × 10−2 | 1.4413 × 10−4 |
| FFT | −5.8223 × 10−3 | 4.4822 × 10−2 | −2.4506 × 10−3 | 1.8451 × 10−2 | −1.0186 × 10−2 | 1.4413 × 10−4 |
| Butterworth | −5.8532 × 10−3 | 4.4853 × 10−2 | −2.4028 × 10−3 | 1.8403 × 10−2 | −1.0183 × 10−2 | 1.4737 × 10−4 |
| Median | −6.0291 × 10−3 | 4.5029 × 10−2 | −2.4424 × 10−3 | 1.8442 × 10−2 | −1.0285 × 10−2 | 4.4625 × 10−5 |
| Method | X Gyro deg/s | Y Gyro deg/s | Z Gyro deg/s | |||
|---|---|---|---|---|---|---|
| −0.09413 | 0.0998 | 0.004397 | ||||
| Est. | Error | Est. | Error | Est. | Error | |
| Average | −0.0943 | 0.0001 | 0.0973 | 0.0025 | 0.004392 | 0.000005 |
| Normalized correlation | −0.0900 | 0.0041 | 0.1000 | 0.0002 | 0.000500 | 0.003897 |
| Least squares | −0.0943 | 0.0001 | 0.0973 | 0.0025 | 0.004392 | 0.000005 |
| FFT | −0.0943 | 0.0001 | 0.0973 | 0.0025 | 0.004392 | 0.000005 |
| Butterworth | −0.0943 | 0.0001 | 0.0975 | 0.0023 | 0.004397 | 0.000000 |
| Median | −0.0953 | 0.0012 | 0.0991 | 0.0007 | 0.004482 | 0.000085 |
| Method | X Acc m/s2 | Y Acc m/s2 | Z Acc m/s2 | |||
|---|---|---|---|---|---|---|
| 0.03900 | 0.01600 | −0.00956 | ||||
| Est. | Error | Est. | Error | Est | Error | |
| Average | −5.7525 × 10−3 | 4.4753 × 10−2 | −2.5897 × 10−3 | 1.8590 × 10−2 | −9.4128 × 10−3 | 1.4522 × 10−4 |
| Normalized correlation | −4.4100 × 10−3 | 4.3410 × 10−2 | −2.6600 × 10−3 | 1.8660 × 10−2 | 1.0799 × 10−1 | 1.1755 × 10−1 |
| Least squares | −5.7525 × 10−3 | 4.4753 × 10−2 | −2.5897 × 10−3 | 1.8590 × 10−2 | −9.4128 × 10−3 | 1.4522 × 10−4 |
| FFT | −5.7525 × 10−3 | 4.4753 × 10−2 | −2.5897 × 10−3 | 1.8590 × 10−2 | −9.4128 × 10−3 | 1.4522 × 10−4 |
| Butterworth | −5.7835 × 10−3 | 4.4783 × 10−2 | −2.5418 × 10−3 | 1.8542 × 10−2 | −9.4095 × 10−3 | 1.4846 × 10−4 |
| Median | −6.0573 × 10−3 | 4.5057 × 10−2 | −2.6254 × 10−3 | 1.8625 × 10−2 | −9.5176 × 10−3 | 4.0386 × 10−5 |
| For Loop | First | Second | Third | Fourth | ||||
|---|---|---|---|---|---|---|---|---|
| X-axis bias m/s2 | 0.05 | (0.05) | 0.04 | (0.04) | 0.04 | (0.04) | 0.04 | (0.04) |
| Y-axis bias m/s2 | 0.00 | 0.15 | (0.15) | 0.16 | (0.16) | 0.16 | (0.16) | 0.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fukuda, G.; Kubo, N. Feasibility of Initial Bias Estimation in Real Maritime IMU Data Including X- and Y-Axis Accelerometers. Sensors 2025, 25, 6804. https://doi.org/10.3390/s25216804
Fukuda G, Kubo N. Feasibility of Initial Bias Estimation in Real Maritime IMU Data Including X- and Y-Axis Accelerometers. Sensors. 2025; 25(21):6804. https://doi.org/10.3390/s25216804
Chicago/Turabian StyleFukuda, Gen, and Nobuaki Kubo. 2025. "Feasibility of Initial Bias Estimation in Real Maritime IMU Data Including X- and Y-Axis Accelerometers" Sensors 25, no. 21: 6804. https://doi.org/10.3390/s25216804
APA StyleFukuda, G., & Kubo, N. (2025). Feasibility of Initial Bias Estimation in Real Maritime IMU Data Including X- and Y-Axis Accelerometers. Sensors, 25(21), 6804. https://doi.org/10.3390/s25216804








