An Efficient Vision Mamba–Transformer Hybrid Architecture for Abdominal Multi-Organ Image Segmentation
Abstract
1. Introduction
- 1.
- We integrate an EViM module before Transformer layers to preserve local feature details while enhancing the aggregation of global information and channel-wise interactions.
- 2.
- We systematically compared three region-level loss functions—Dice, Jaccard, and Tversky. Jaccard loss yields the best convergence and segmentation performance.
- 3.
- Extensive experiments on Synapse and ACDC datasets demonstrate state-of-the-art accuracy and strong cross-modal generalization.
2. Related Work
2.1. Transformer
2.2. Mamba
2.3. Dual Attention (DA) Mechanism
3. Method
3.1. Overall Framework
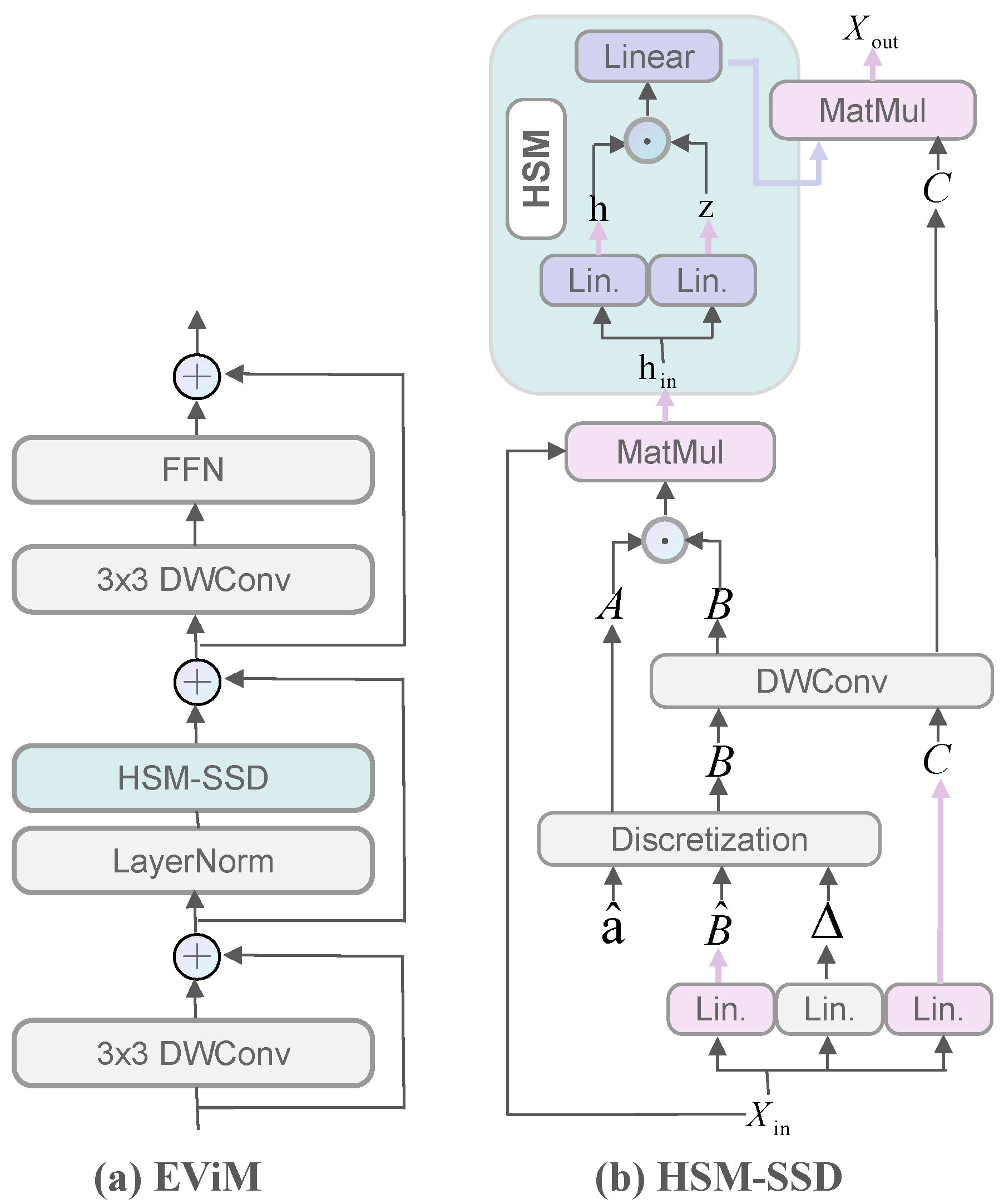
3.2. EViM Module
3.3. Loss Functions
4. Experiments
4.1. Datasets
4.2. Implementation Details and Evaluation
4.3. Comparisons with State-of-the-Arts (SOTA)
4.4. Ablation Studies
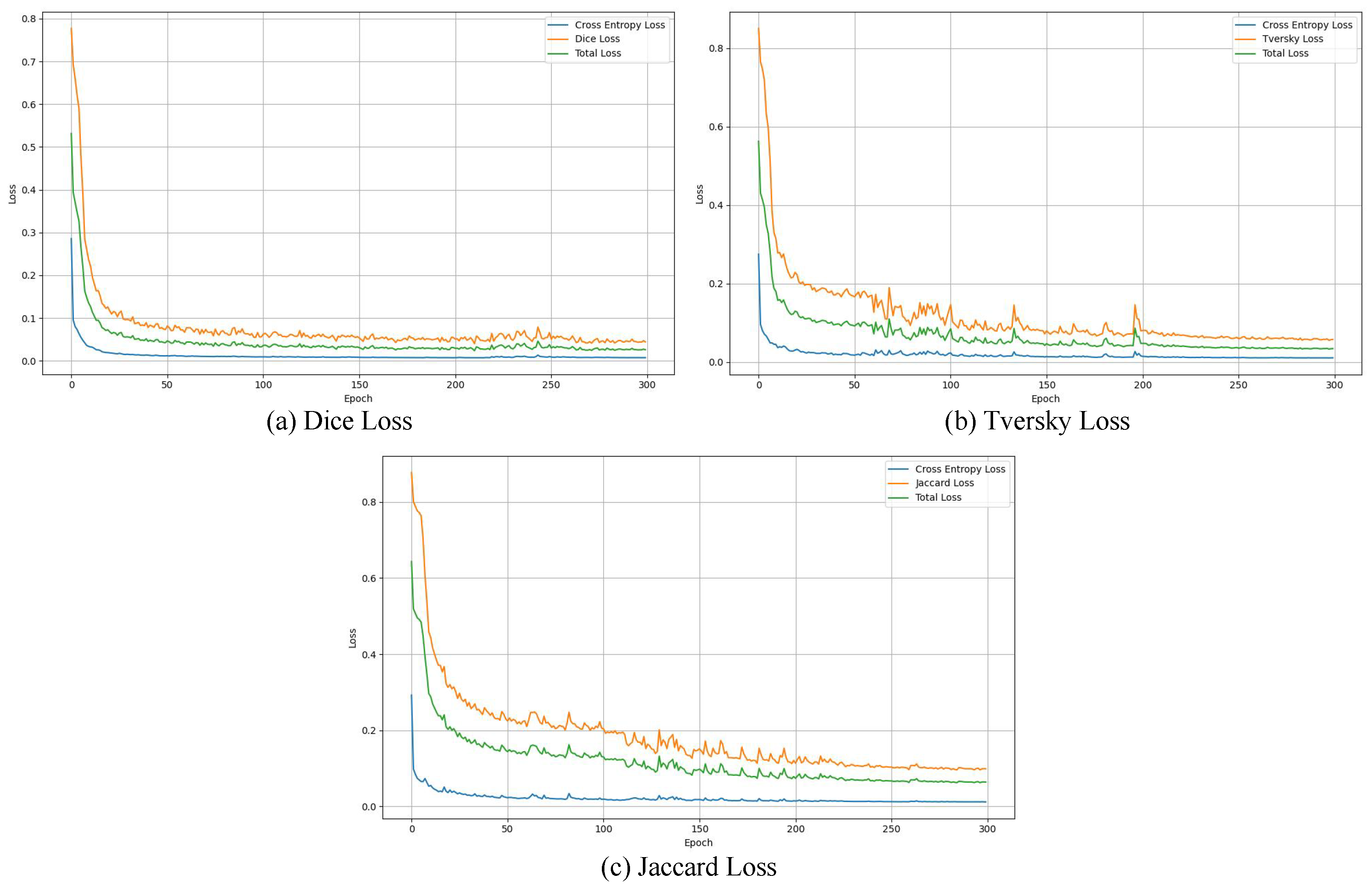
4.4.1. Regional Loss Selection
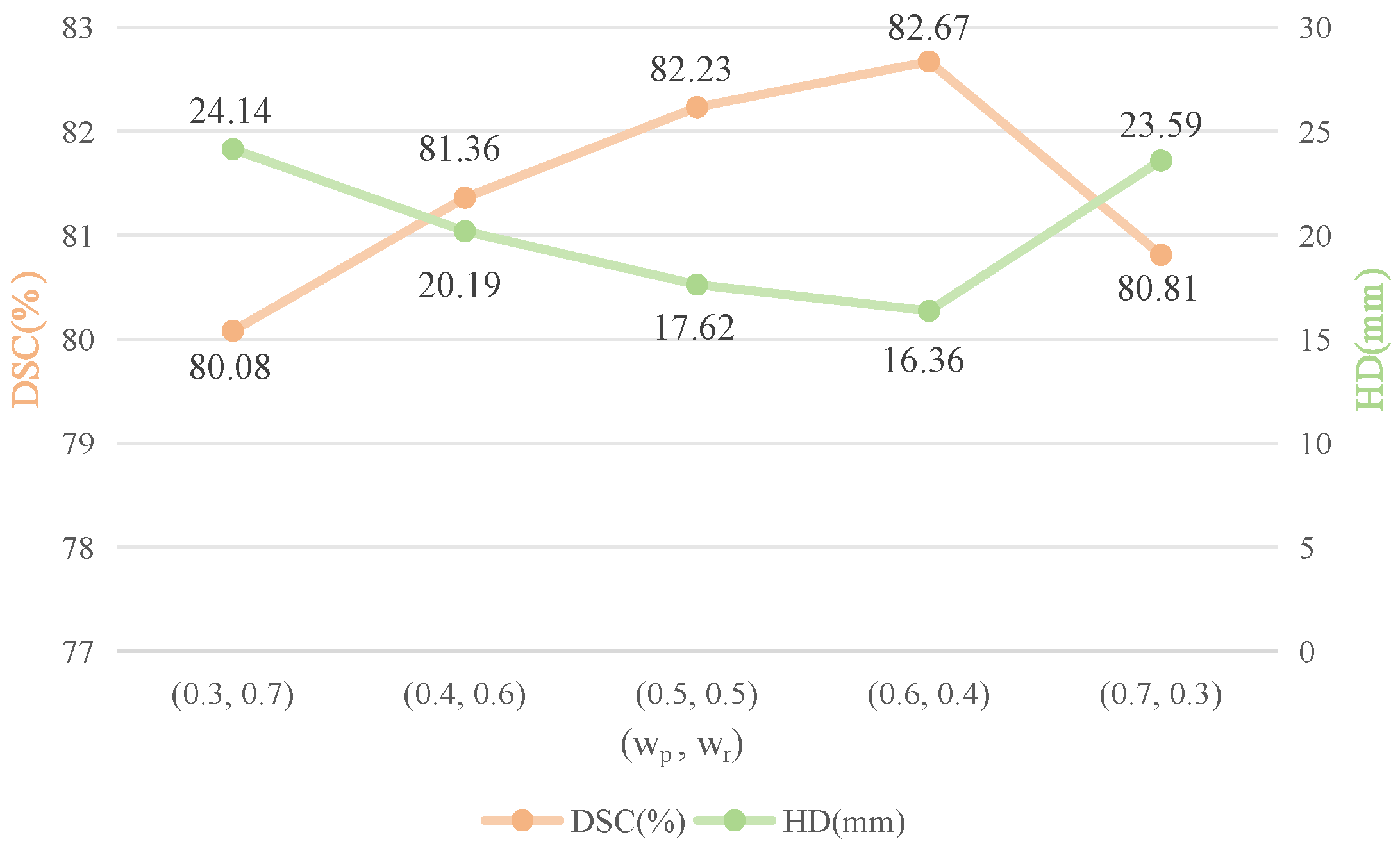
4.4.2. Weights Balancing Between Pixel and Regional Losses
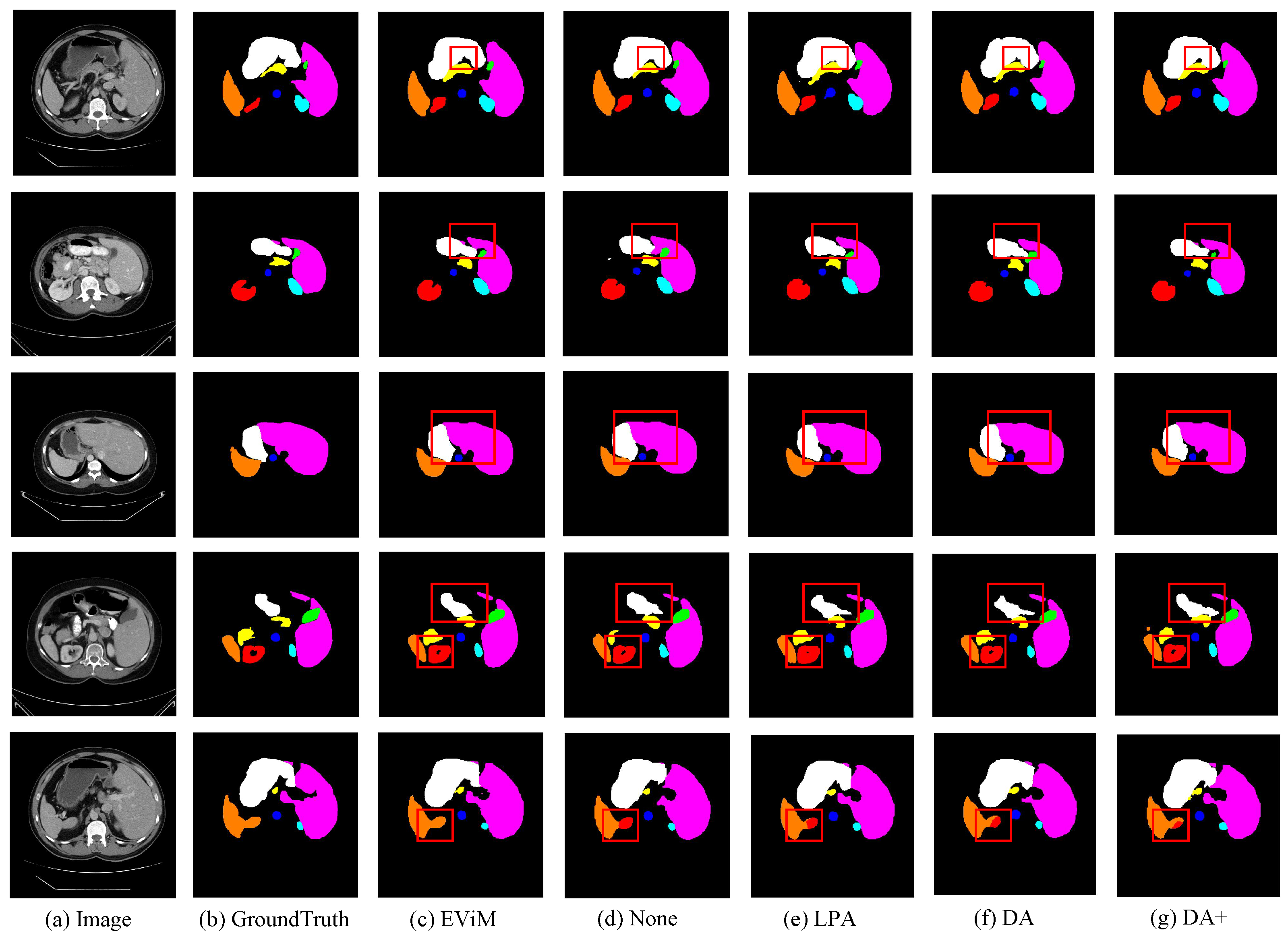
4.4.3. Ablation Study of EViM Module Contributions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rachmawati, E.; Sumarna, F.R.; Kartamihardja, A.H.S.; Achmad, A.; Shintawati, R. Bone scan image segmentation based on active shape model for cancer metastasis detection. In Proceedings of the 2020 8th International Conference on Information and Communication Technology (ICoICT), Yogyakarta, Indonesia, 24–26 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, MICCAI 2015, Munich, Germany, 5–9 October 2015; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Zhou, Z.; Siddiquee, M.M.R.; Tajbakhsh, N.; Liang, J. UNet++: Redesigning skip connections to exploit multiscale features in image segmentation. IEEE Trans. Med. Imaging. 2019, 39, 1856–1867. [Google Scholar] [CrossRef]
- Diakogiannis, F.I.; Waldner, F.; Caccetta, P.; Wu, C. ResUNet-a: A deep learning framework for semantic segmentation of remotely sensed data. ISPRS J. Photogramm. Remote Sens. 2020, 162, 94–114. [Google Scholar] [CrossRef]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention U-Net: Learning where to look for the pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar] [CrossRef]
- Zunair, H.; Hamza, A.B. Sharp U-Net: Depthwise convolutional network for biomedical image segmentation. Comput. Biol. Med. 2021, 136, 104699. [Google Scholar] [CrossRef] [PubMed]
- Ruan, J.; Xie, M.; Xiang, S.; Liu, T.; Fu, Y. MEW-UNet: Multi-axis representation learning in frequency domain for medical image segmentation. arXiv 2022, arXiv:2210.14007. [Google Scholar]
- Jha, A.; Kumar, A.; Pande, S.; Banerjee, B.; Chaudhuri, S. MT-UNet: A novel U-Net based multi-task architecture for visual scene understanding. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 25–28 October 2020; pp. 2191–2195. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16×16 words: Transformers for image recognition at scale. In Proceedings of the Ninth International Conference on Learning Representations, Online, 3–7 May 2021. [Google Scholar]
- Chen, J.; Lu, Y.; Yu, Q.; Luo, X.; Adeli, E.; Wang, Y.; Lu, L.; Yuille, A.L.; Zhou, Y. TransUNet: Transformers make strong encoders for medical image segmentation. arXiv 2021, arXiv:2102.04306. [Google Scholar] [CrossRef]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-Unet: Unet-like pure transformer for medical image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–27 October 2022; Springer Nature: Cham, Switzerland, 2022; pp. 205–218. [Google Scholar]
- Hatamizadeh, A.; Nath, V.; Tang, Y.; Yang, D.; Roth, H.R.; Xu, D. Swin UNETR: Swin transformers for semantic segmentation of brain tumors in MRI images. In Proceedings of the International MICCAI Brainlesion Workshop, Online, 27 September 2021; Springer: Cham, Switzerland, 2021; pp. 272–284. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Sun, G.; Pan, Y.; Kong, W.; Xu, Z.; Ma, J.; Racharak, T.; Nguyen, L.M.; Xin, J. DA-TransUNet: Integrating spatial and channel dual attention with transformer U-net for medical image segmentation. Front. Bioeng. Biotechnol. 2024, 12, 1398237. [Google Scholar] [CrossRef]
- Azad, R.; Al-Antary, M.T.; Heidari, M.; Merhof, D. TransNorm: Transformer provides a strong spatial normalization mechanism for a deep segmentation model. IEEE Access. 2022, 10, 108205–108215. [Google Scholar] [CrossRef]
- Lu, F.; Xu, J.; Sun, Q.; Lou, Q. FMD-TransUNet: Abdominal Multi-Organ Segmentation Based on Frequency Domain Multi-Axis Representation Learning and Dual Attention Mechanisms. arXiv 2025, arXiv:2509.16044. [Google Scholar]
- Du, H.; Wang, J.; Liu, M.; Wang, Y.; Meijering, E. SwinPA-Net: Swin transformer-based multiscale feature pyramid aggregation network for medical image segmentation. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 5355–5366. [Google Scholar] [CrossRef]
- Hamilton, J.D. State-space models. In Handbook of Econometrics; Elsevier: Amsterdam, The Netherlands, 1994; Volume 4, pp. 3039–3080. [Google Scholar]
- Gu, A.; Dao, T. Mamba: Linear-time sequence modeling with selective state spaces. In Proceedings of the First Conference on Language Modeling, Philadelphia, PA, USA, 7–9 October 2024. [Google Scholar]
- Gu, A.; Goel, K.; Ré, C. Efficiently modeling long sequences with structured state spaces. arXiv 2021, arXiv:2111.00396. [Google Scholar]
- Ruan, J.; Xiang, S. VM-UNet: Vision Mamba UNet for medical image segmentation. arXiv 2024, arXiv:2402.02491. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, Y.; Zhao, Y.; Yu, H.; Xie, L.; Wang, Y.; Ye, Q.; Jiao, J.; Liu, Y. Vmamba: Visual state space model. Adv. Neural Inf. Process. Syst. (NeurIPS) 2024, 37, 103031–103063. [Google Scholar]
- Ma, J.; Li, F.; Wang, B. U-Mamba: Enhancing long-range dependency for biomedical image segmentation. arXiv 2024, arXiv:2401.04722. [Google Scholar]
- Lee, S.; Choi, J.; Kim, H.J. EfficientViM: Efficient vision mamba with hidden state mixer based state space duality. In Proceedings of the IEEE/CVF Computer Vision and Pattern Recognition Conference (CVPR), Nashville, TN, USA, 11–15 June 2025; pp. 14923–14933. [Google Scholar]
- Xu, J.; Lan, Y.; Zhang, Y.; Zhang, C.; Stirenko, S.; Li, H. CDA-Mamba: Cross-directional attention Mamba for enhanced 3D medical image segmentation. Sci. Rep. 2025, 15, 21357. [Google Scholar] [CrossRef]
- Azad, R.; Heidari, M.; Shariatnia, M.; Aghdam, E.K.; Karimijafarbigloo, S.; Adeli, E.; Merhof, D. TransDeepLab: Convolution-free transformer-based DeepLab v3+ for medical image segmentation. In Proceedings of the International Workshop on Predictive Intelligence in Medicine, Singapore, 22 September 2022; Springer: Cham, Switzerland, 2022; pp. 91–102. [Google Scholar]
- Zhu, L.; Liao, B.; Zhang, Q.; Wang, X.; Liu, W.; Wang, X. Vision Mamba: Efficient visual representation learning with bidirectional state space model. arXiv 2024, arXiv:2401.09417. [Google Scholar] [CrossRef]
- Xing, Z.; Ye, T.; Yang, Y.; Liu, G.; Zhu, L. SegMamba: Long-range sequential modeling Mamba for 3D medical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention—MICCAI 2024, Marrakesh, Morocco, 6–10 October 2024; Springer: Cham, Switzerland, 2024; pp. 578–588. [Google Scholar]
- Liu, J.; Yang, H.; Zhou, H.Y.; Xi, Y.; Yu, L.; Li, C.; Liang, Y.; Shi, G.; Yu, Y.; Zhang, S.; et al. Swin-UMamba: Mamba-based UNet with ImageNet-based pretraining. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2024, Marrakesh, Morocco, 6–10 October 2024; Springer: Cham, Switzerland, 2024; pp. 615–625. [Google Scholar]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3146–3154. [Google Scholar]
- Xue, H.; Liu, C.; Wan, F.; Jiao, J.; Ji, X.; Ye, Q. DANet: Divergent activation for weakly supervised object localization. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6589–6598. [Google Scholar]
- Li, H.; Ding, J.; Shi, X.; Zhang, Q.; Yu, P.; Li, H. D-SAT: Dual semantic aggregation transformer with dual attention for medical image segmentation. Phys. Med. Biol. 2023, 69, 015013. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning (ICML 2015), Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Dao, T.; Gu, A. Transformers are SSMs: Generalized models and efficient algorithms through structured state space duality. In Proceedings of the 41st International Conference on Machine Learning (ICML), Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Azad, R.; Heidary, M.; Yilmaz, K.; Hüttemann, M.; Karimijafarbigloo, S.; Wu, Y.; Schmeink, A.; Merhof, D. Loss functions in the era of semantic segmentation: A survey and outlook. arXiv 2023, arXiv:2312.05391. [Google Scholar] [CrossRef]
- Landman, B.; Xu, Z.; Igelsias, J.; Styner, M.; Langerak, T.; Klein, A. MICCAI multi-atlas labeling beyond the cranial vault—Workshop and challenge. In Proceedings of the MICCAI Multi-Atlas Labeling Beyond Cranial Vault Challenge, Munich, Germany, 5–9 October 2015; Volume 5, p. 12. [Google Scholar]
- Bernard, O.; Lalande, A.; Zotti, C.; Cervenansky, F.; Yang, X.; Heng, P.A.; Cetin, I.; Lekadir, K.; Camara, O.; Ballester, M.A.G.; et al. Deep learning techniques for automatic MRI cardiac multi-structures segmentation and diagnosis: Is the problem solved? IEEE Trans. Med. Imaging. 2018, 37, 2514–2525. [Google Scholar] [PubMed]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Hatamizadeh, A.; Tang, Y.; Nath, V.; Yang, D.; Myronenko, A.; Landman, B.; Roth, H.R.; Xu, D. UNETR: Transformers for 3D medical image segmentation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA,, 3–8 January 2022; pp. 574–584. [Google Scholar]



| Type | Method | HD95↓ | DSC↑ | Aorta | Gallbladder | Kidney (L) | Kidney (R) | Liver | Pancreas | Spleen | Stomach |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CNN | UNet [4] | 39.70 | 76.85 | 89.07 | 69.72 | 77.77 | 68.60 | 93.43 | 53.98 | 86.67 | 75.58 |
| UNet++ [5] | 36.93 | 76.91 | 88.19 | 68.89 | 81.76 | 75.27 | 93.01 | 58.20 | 83.44 | 70.52 | |
| Residual UNet [6] | 38.44 | 76.95 | 87.06 | 66.05 | 83.43 | 76.83 | 93.99 | 51.86 | 85.25 | 70.13 | |
| Attention UNet [7] | 36.02 | 77.77 | 89.55 | 68.88 | 77.98 | 71.11 | 93.57 | 58.04 | 87.30 | 75.75 | |
| MEW-UNet [9] | 16.44 | 78.92 | 86.68 | 65.32 | 82.87 | 80.02 | 93.63 | 58.36 | 90.19 | 74.26 | |
| ViT | TransUNet [12] | 31.69 | 77.48 | 87.23 | 63.13 | 81.87 | 77.02 | 94.08 | 55.86 | 85.08 | 75.62 |
| TransNorm [17] | 30.25 | 78.40 | 86.23 | 65.10 | 82.18 | 78.63 | 94.22 | 55.34 | 89.50 | 76.01 | |
| Swin-UNet [13] | 21.55 | 79.13 | 85.47 | 66.53 | 83.28 | 79.61 | 94.29 | 56.58 | 90.66 | 76.60 | |
| MT-UNet [10] | 26.59 | 78.59 | 87.92 | 64.99 | 81.47 | 77.29 | 93.06 | 59.46 | 87.75 | 76.81 | |
| DA-TransUNet [16] | 23.48 | 79.80 | 86.54 | 65.27 | 81.70 | 80.45 | 94.57 | 61.62 | 88.53 | 79.73 | |
| TransDeepLab [28] | 21.25 | 80.16 | 86.04 | 69.16 | 84.08 | 79.88 | 93.53 | 61.19 | 89.00 | 78.40 | |
| FMD-TransUNet [18] | 16.35 | 81.32 | 88.76 | 65.23 | 85.12 | 82.12 | 94.19 | 66.31 | 89.73 | 79.13 | |
| Mamba | VM-UNet [23] | 19.21 | 81.08 | 86.40 | 69.41 | 86.16 | 82.76 | 94.17 | 58.80 | 89.51 | 81.40 |
| Ours | 16.36 | 82.67 | 88.26 | 69.90 | 84.49 | 83.26 | 95.18 | 65.76 | 90.52 | 83.96 |
| Type | Method | HD95↓ (mm) | DSC↑ (%) | RV | MYO | LV |
|---|---|---|---|---|---|---|
| CNN | R50-UNet [4] | - | 87.60 | 84.62 | 84.52 | 93.68 |
| R50 AttnUNet [7] | - | 86.90 | 83.27 | 84.33 | 93.53 | |
| UNet++ [5] | - | 89.58 | 87.23 | 87.13 | 94.37 | |
| DeepLabv3+ [42] | - | 88.25 | 85.41 | 85.44 | 93.90 | |
| ViT | ViT-CUP [11] | - | 83.41 | 80.93 | 78.12 | 91.17 |
| R50 ViT [11] | - | 86.19 | 82.51 | 83.01 | 93.05 | |
| R50-ViT-CUP [11] | - | 87.57 | 86.07 | 81.88 | 94.75 | |
| TransUNet [12] | - | 89.71 | 86.67 | 87.27 | 95.18 | |
| Swin-UNet [13] | - | 88.07 | 85.77 | 84.42 | 94.03 | |
| UNETR [43] | - | 86.61 | 85.29 | 86.52 | 94.02 | |
| MT-UNET [10] | 2.23 | 90.43 | 86.64 | 89.04 | 95.62 | |
| FMD-TransUNet [18] | 2.07 | 90.10 | 87.87 | 87.48 | 94.96 | |
| Ours | 1.15 | 90.53 | 88.76 | 87.60 | 95.22 |
| Loss Function | Model | DSC (%) | HD95 (mm) |
|---|---|---|---|
| Dice Loss | TransUNet | 77.48 | 31.69 |
| FMD-TransUNet | 79.09 | 28.87 | |
| Ours | 80.57 | 21.01 | |
| Tversky Loss | TransUNet | 79.09 | 28.87 |
| FMD-TransUNet | 80.23 | 23.59 | |
| Ours | 80.29 | 20.64 | |
| Jaccard Loss | TransUNet | 79.54 | 27.55 |
| FMD-TransUNet | 81.65 | 17.98 | |
| Ours | 82.23 | 17.62 |
| Module | DSC (%) | HD95 (mm) |
|---|---|---|
| - | 79.11 | 26.89 |
| DA | 79.82 | 23.06 |
| DA+ | 80.18 | 19.96 |
| LPA | 79.60 | 24.01 |
| EViM | 82.67 | 16.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, F.; Xu, J.; Sun, Q.; Lou, Q. An Efficient Vision Mamba–Transformer Hybrid Architecture for Abdominal Multi-Organ Image Segmentation. Sensors 2025, 25, 6785. https://doi.org/10.3390/s25216785
Lu F, Xu J, Sun Q, Lou Q. An Efficient Vision Mamba–Transformer Hybrid Architecture for Abdominal Multi-Organ Image Segmentation. Sensors. 2025; 25(21):6785. https://doi.org/10.3390/s25216785
Chicago/Turabian StyleLu, Fang, Jingyu Xu, Qinxiu Sun, and Qiong Lou. 2025. "An Efficient Vision Mamba–Transformer Hybrid Architecture for Abdominal Multi-Organ Image Segmentation" Sensors 25, no. 21: 6785. https://doi.org/10.3390/s25216785
APA StyleLu, F., Xu, J., Sun, Q., & Lou, Q. (2025). An Efficient Vision Mamba–Transformer Hybrid Architecture for Abdominal Multi-Organ Image Segmentation. Sensors, 25(21), 6785. https://doi.org/10.3390/s25216785




