Magnetoelectric Energy Harvesting for Industrial IoT Applications: Frequency-Tunable Converter with Enhanced Performance
Abstract
1. Introduction
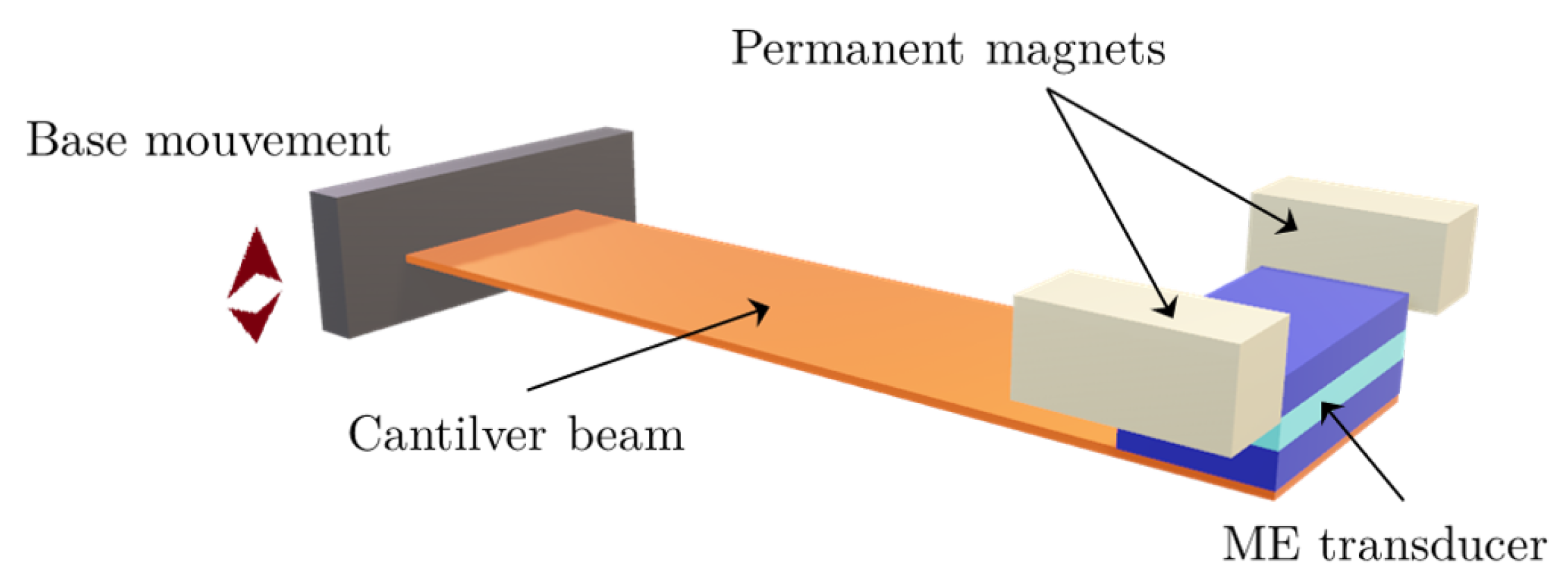
2. Harvester Design
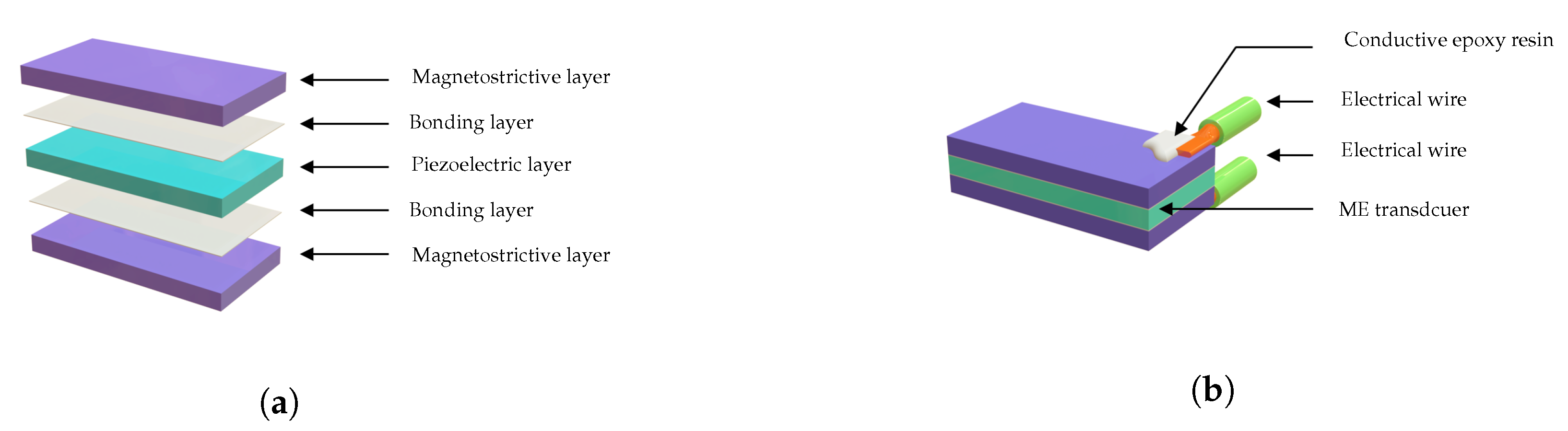
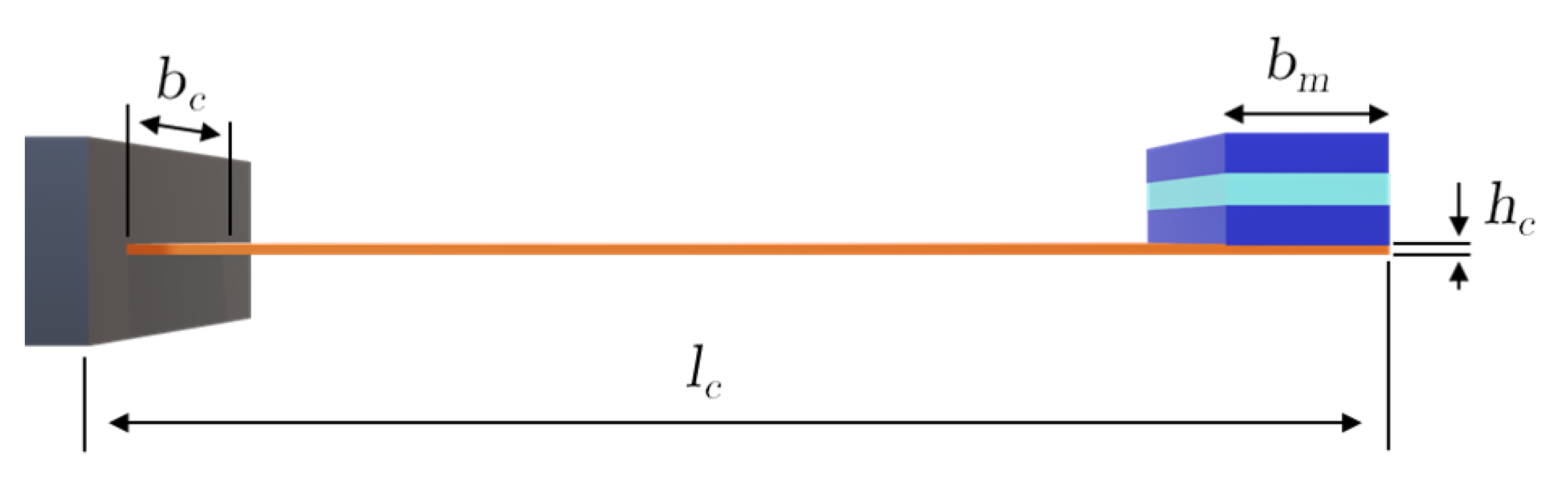
2.1. Magnetoelectric Converter Architecture
2.2. Bonding Layer
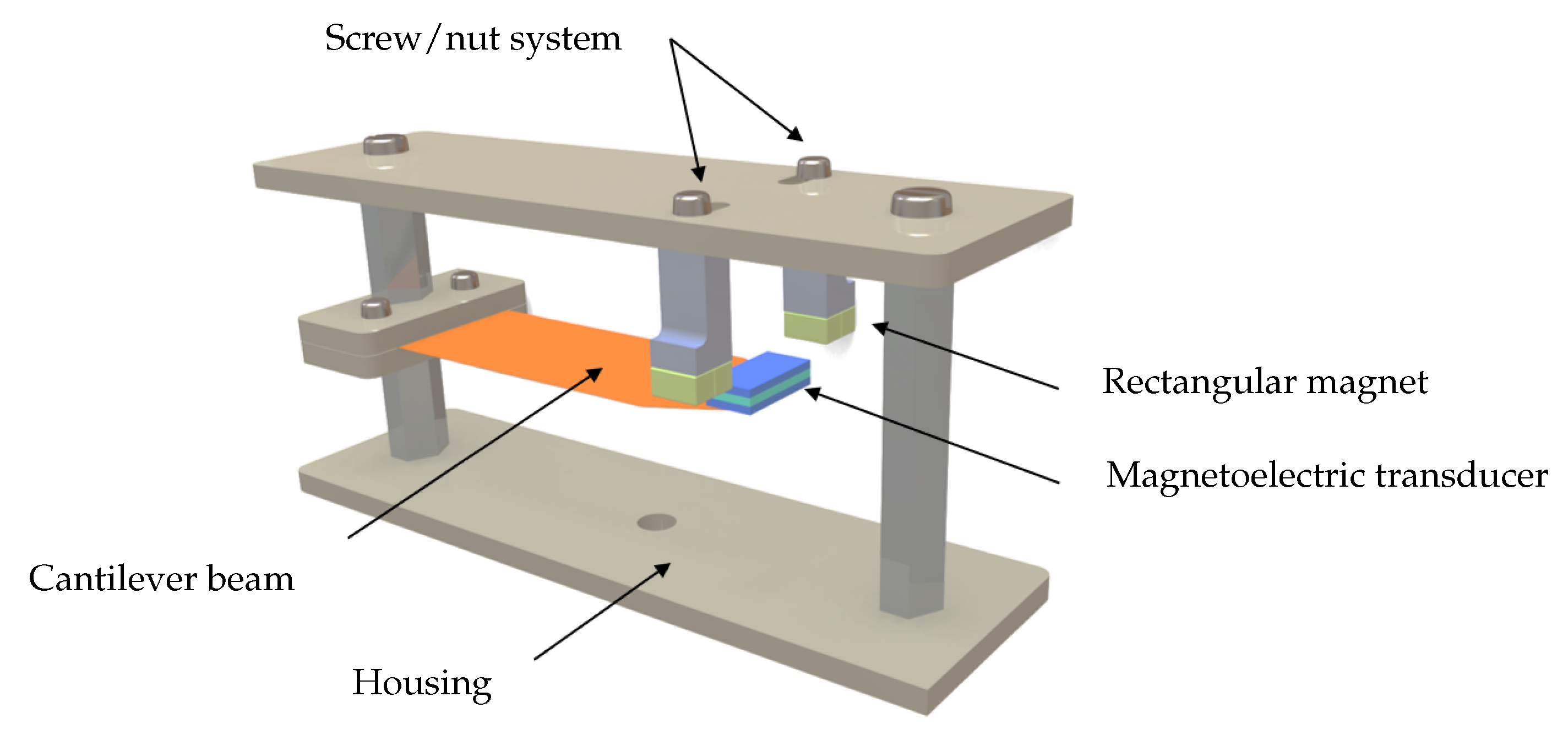
2.3. Prototype Fabrication
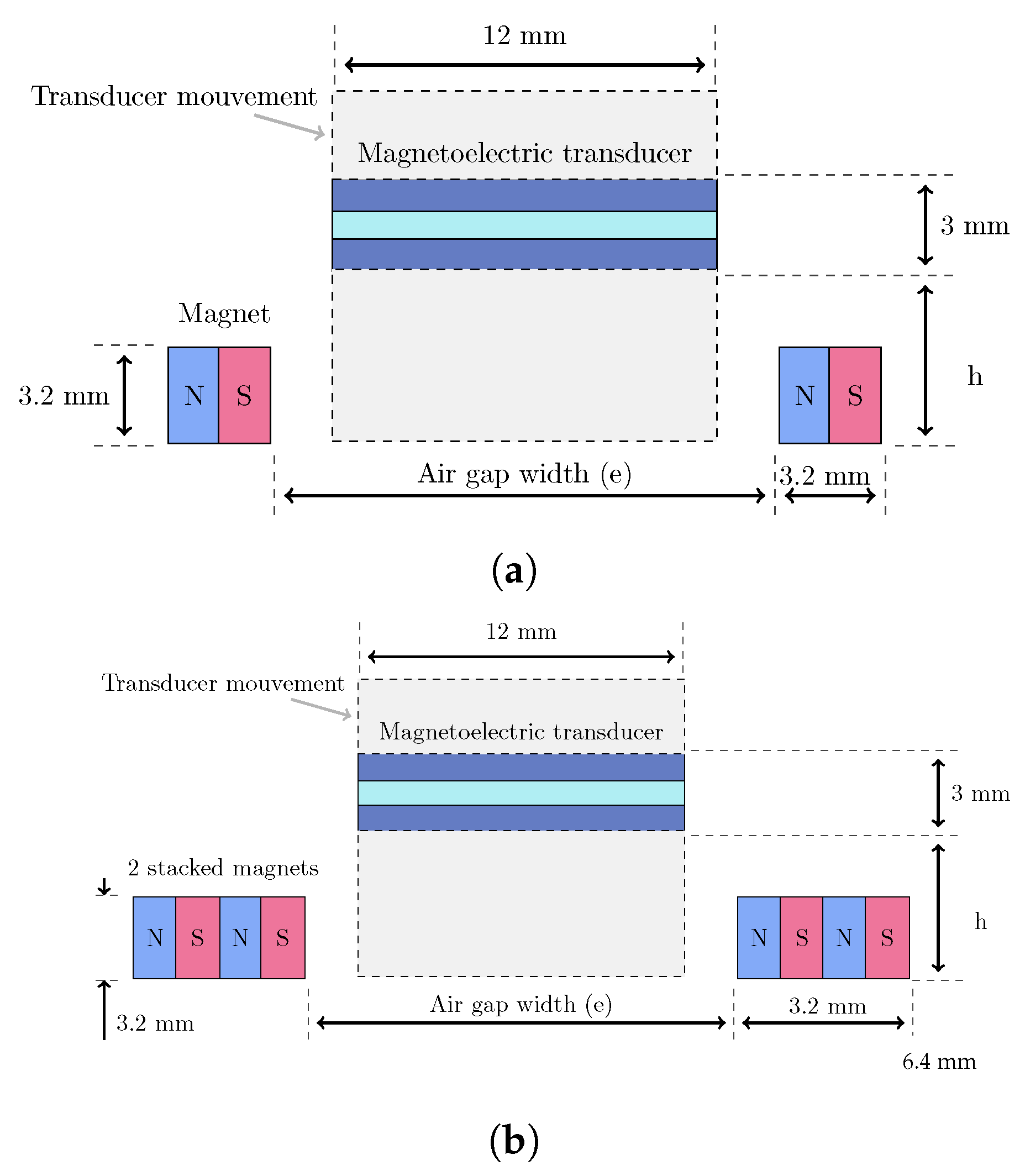
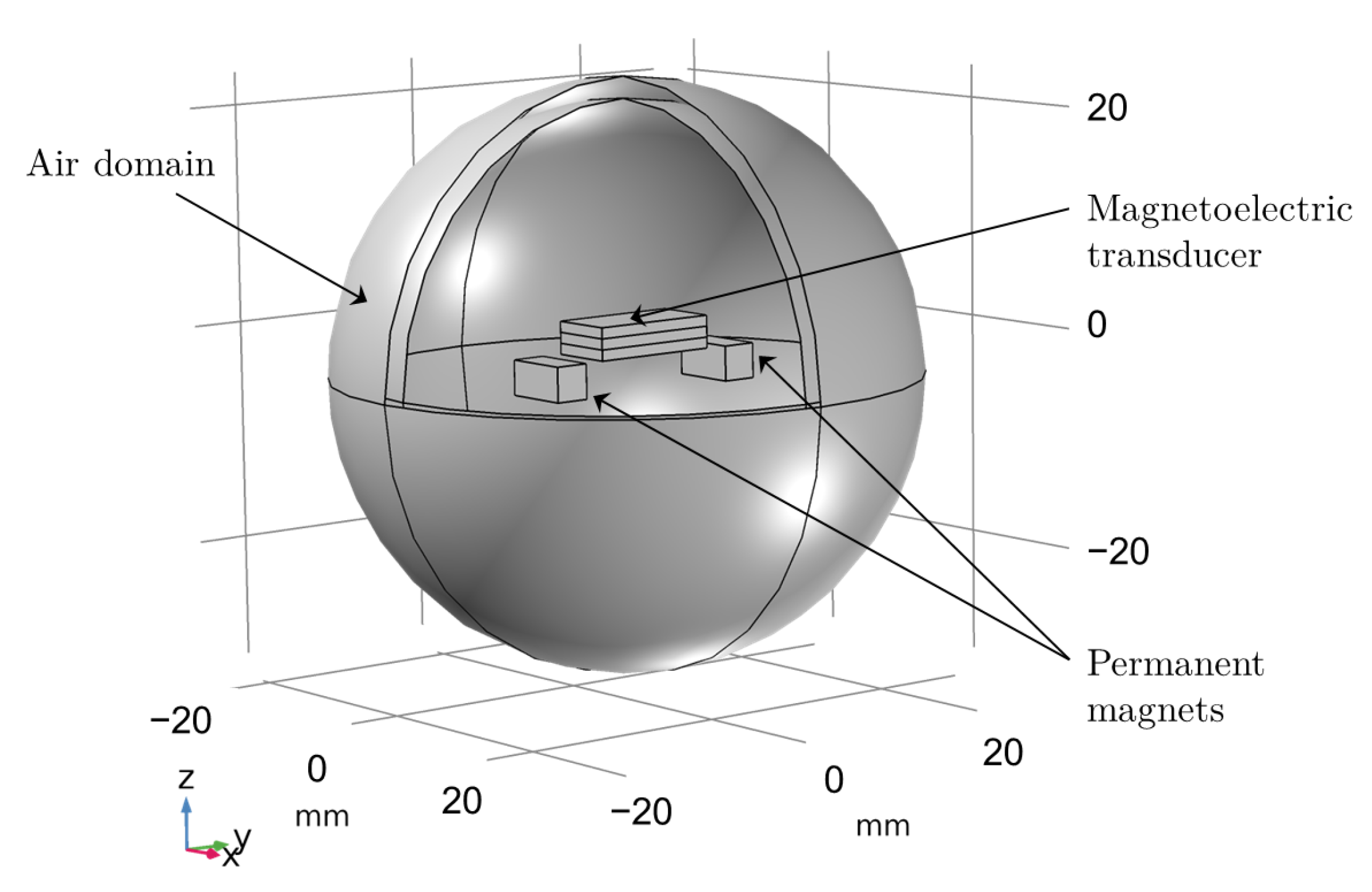
2.4. Magnetic Circuit Configuration
3. Theoretical Framework
3.1. Governing Equation
3.2. Position-Dependent Magnetic Force Analysis
3.3. Effective System Stiffness and Frequency Tuning
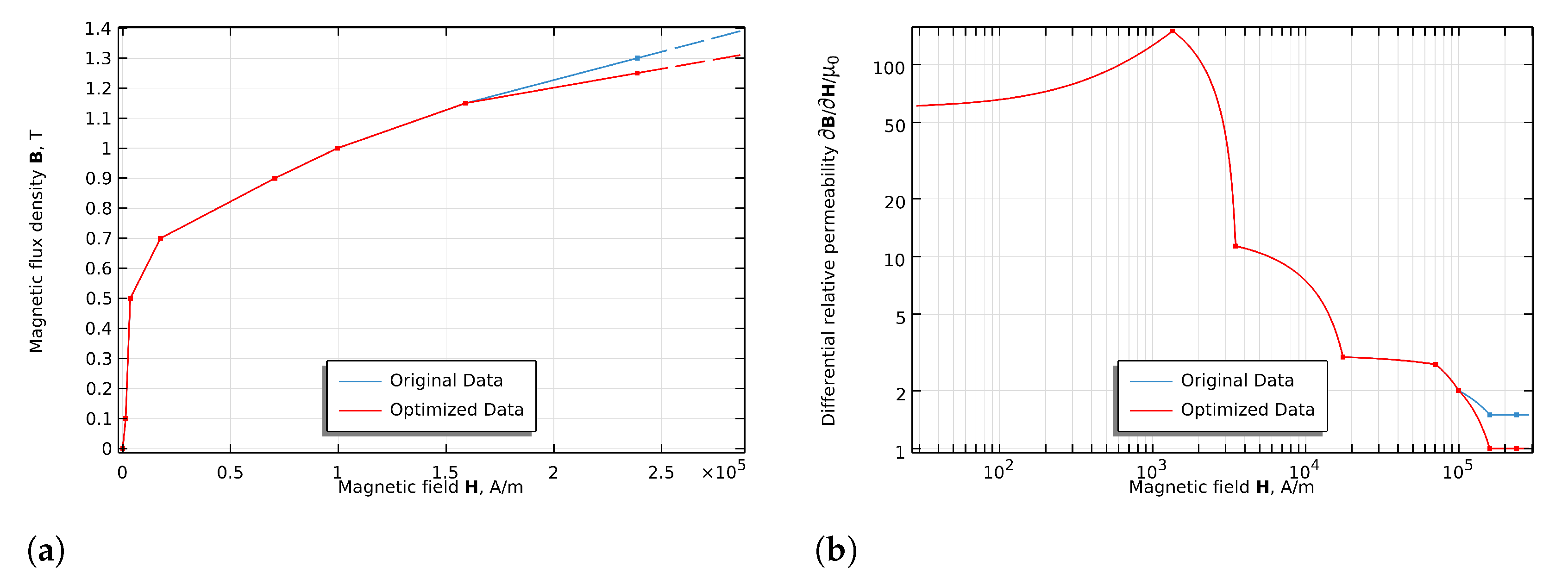
3.4. Field-Dependent Material Properties
4. Finite Element Analysis
4.1. Terfenol-D Magnetic Property Characterization
4.2. Finite Element Model and Configuration Design
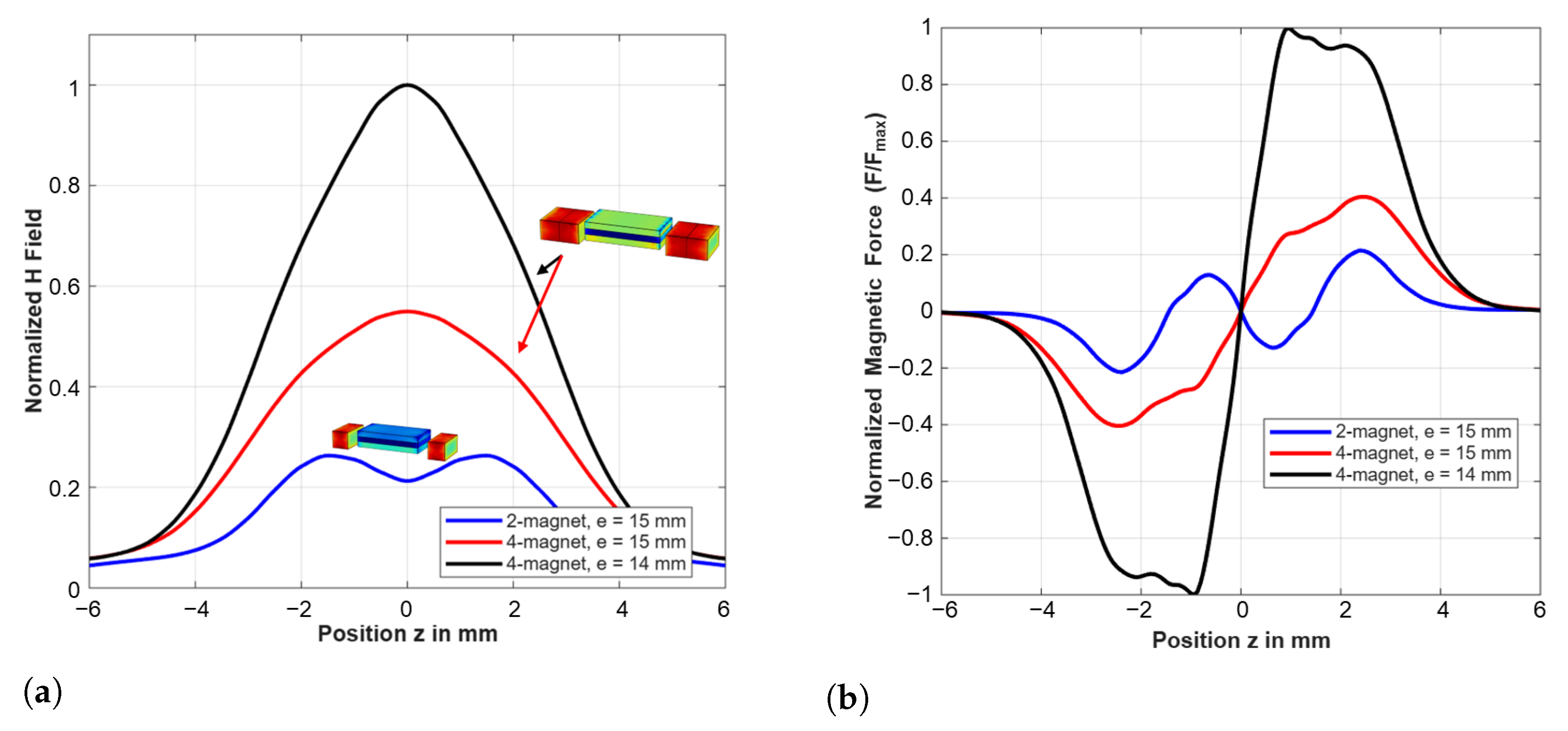
- Effect of magnet number: To study the influence of magnet quantity on system performance, two configurations with fixed air gap (e = 15 mm) were compared: two-magnet and four-magnet designs.
- Effect of air gap variation: To investigate air gap influence on magnetic forces, the four-magnet configuration was analyzed with reduced air gap from 15 mm to 14 mm.
4.3. Magnetic Field Distribution and Force Analysis
5. Experimental Characterization and Performance Evaluation
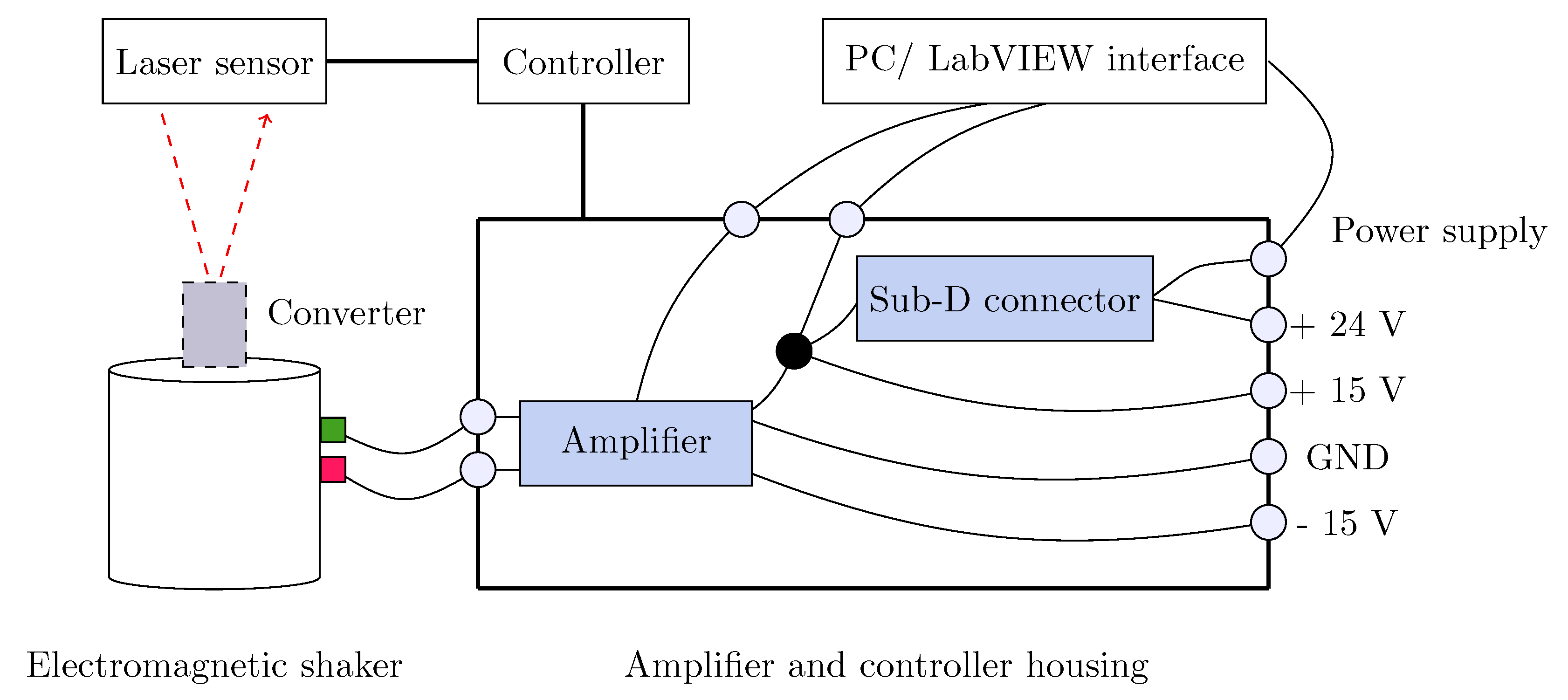
5.1. Experimental Setup
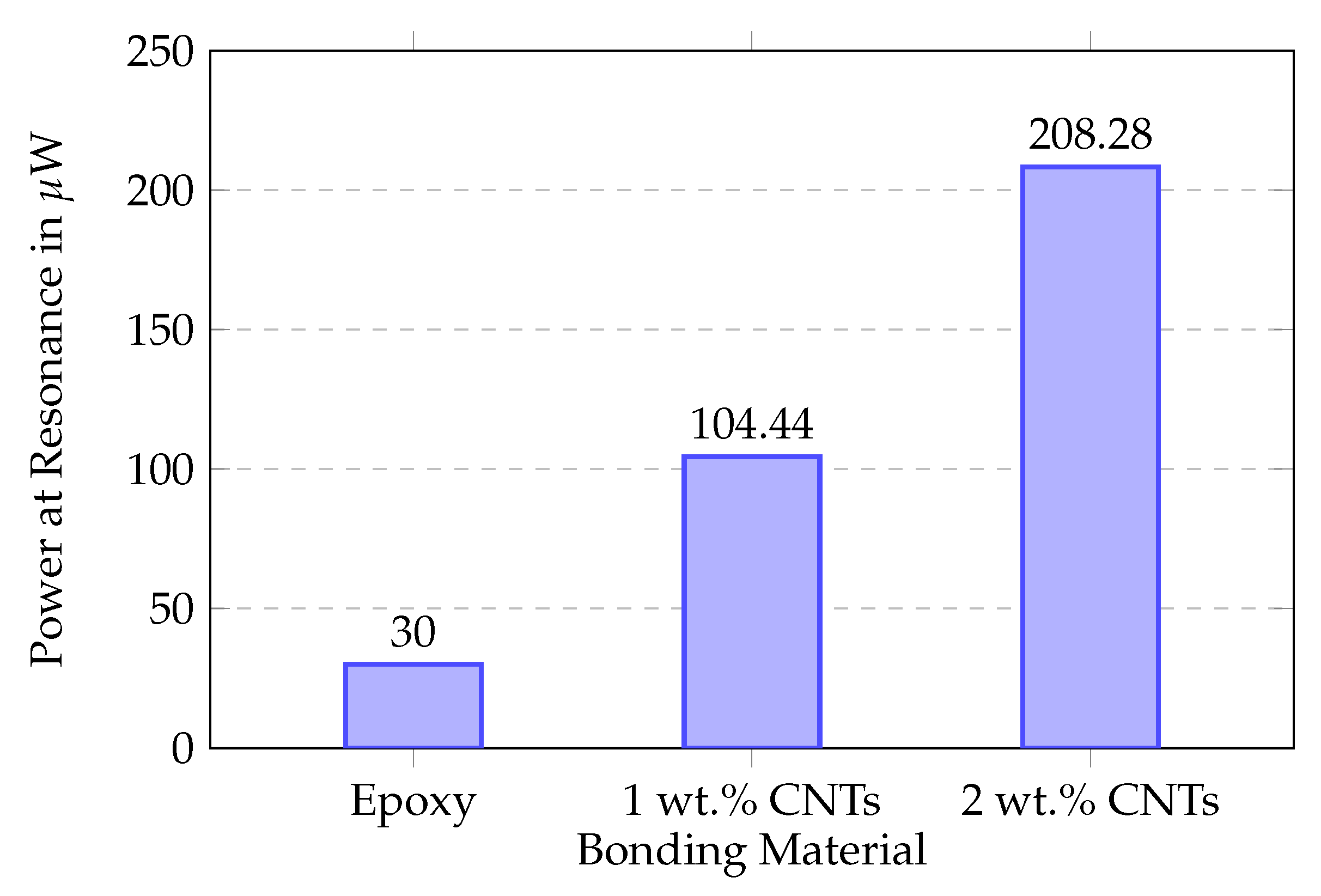
5.2. MWCNT-Enhanced Bonding Layer
5.3. Experimental Performance Validation
5.4. Theoretical Model Validation
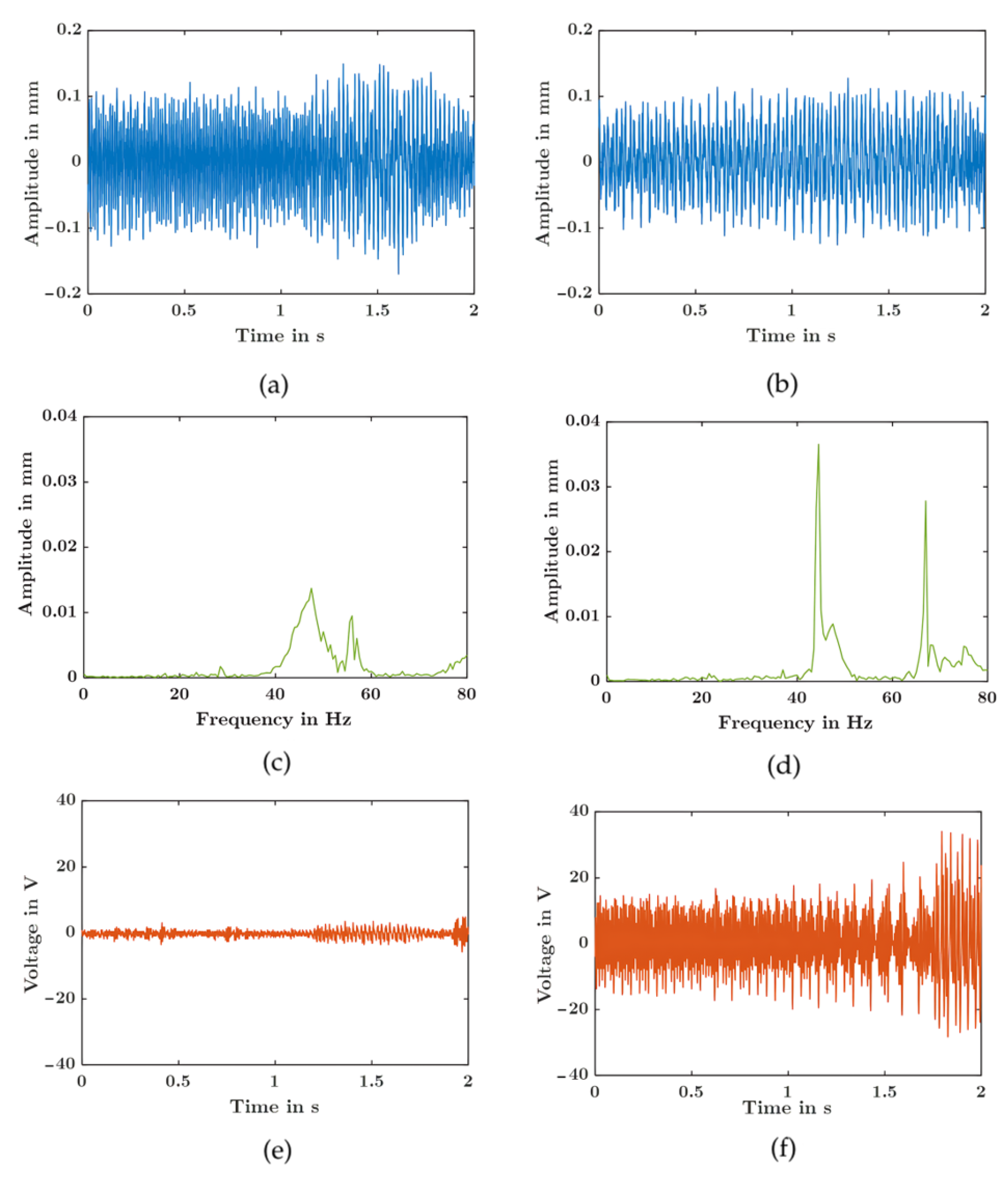
5.5. Response Under Real Vibration Profiles
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Naifar, S.; Grimmeisen, F.; Viehweger, C.; Hu, Z.; Bauer, A.; Hörschelmann, P.; Kanoun, O. Pendulum-Based River Current Energy Converter for Hydrometric Monitoring Systems. Sensors 2022, 22, 4246. [Google Scholar] [CrossRef]
- Shaikh, F.K.; Zeadally, S. Energy harvesting in wireless sensor networks: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 55, 1041–1054. [Google Scholar] [CrossRef]
- Motora, K.G.; Wu, C.M.; Jose, C.R.M.; Rani, G.M. Waste-to-energy: Development of a Highly Efficient Keratin Enhanced Chitosan Bio-waste-derived Triboelectric Nanogenerator for Energy Harvesting and Real Applications. Adv. Funct. Mater. 2024, 34, 2315069. [Google Scholar] [CrossRef]
- Wang, X.; Yin, G.; Sun, T.; Xu, X.; Rasool, G.; Abbas, K. Mechanical Vibration Energy Harvesting and Vibration Monitoring Based on Triboelectric Nanogenerators. Energy Technol. 2024, 12, 2300931. [Google Scholar] [CrossRef]
- Teng, J.; Cao, Z.; Ren, C.; Xu, J.; Guo, X.; Ye, X. Efficient Energy Harvesting from Broadband Low-frequency Vibrations via 3D-interdigital Electrostatic Generator. Appl. Energy 2025, 388, 125701. [Google Scholar] [CrossRef]
- Sabzpoushan, S.; Woias, P. Electret-based Energy Harvesters: A Review. Nano Energy 2024, 131, 110167. [Google Scholar] [CrossRef]
- Safaei, M.; Sodano, H.A.; Anton, S.R. A review of energy harvesting using piezoelectric materials: State-of-the-art a decade later (2008–2018). Smart Mater. Struct. 2019, 28, 113001. [Google Scholar] [CrossRef]
- Schott, L.; Bouattour, G.; Fromm, R.; Strakosch, F.; Kanoun, O.; Derbel, F. Analysis of piezoelectric harvester with multi-array configuration for ultra-low power sensor nodes. Results Eng. 2025, 27, 106728. [Google Scholar] [CrossRef]
- Bradai, S.; Naifar, S.; Viehweger, C.; Kanoun, O.; Litak, G. Nonlinear analysis of an electrodynamic broadband energy harvester. Eur. Phys. J. Spec. Top. 2015, 224, 2919–2927. [Google Scholar] [CrossRef]
- Beeby, S.P.; Tudor, M.J.; White, N.M. Energy harvesting vibration sources for microsystems applications. Meas. Sci. Technol. 2006, 17, R175–R195. [Google Scholar] [CrossRef]
- Yang, J.; Wen, Y.; Li, P. Magnetoelectric energy harvesting from vibrations of multiple frequencies. J. Intell. Mater. Syst. Struct. 2011, 22, 1631–1639. [Google Scholar] [CrossRef]
- Karadag, C.V.; Topaloglu, N. A self-sufficient and frequency tunable piezoelectric vibration energy harvester. J. Vib. Acoust. 2017, 139, 011004. [Google Scholar] [CrossRef]
- Eichhorn, C.; Goldschmidtboeing, F.; Woias, P. A frequency tunable piezoelectric energy converter based on a cantilever beam. Proc. PowerMEMS 2008, 2008, 309–312. [Google Scholar]
- Ferrari, M.; Ferrari, V.; Guizzetti, M.; Marioli, D.; Taroni, A. Piezoelectric multifrequency energy converter for power harvesting in autonomous microsystems. Sens. Actuators A Phys. 2008, 142, 329–335. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P. Demonstrator to show the effects of negative stiffness on the natural frequency of a simple oscillator. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2008, 222, 1189–1192. [Google Scholar] [CrossRef]
- Jiang, B.; Zhu, F.; Yang, Y.; Zhu, J.; Yang, Y.; Yuan, M. A hybrid piezoelectric and electromagnetic broadband harvester with double cantilever beams. Micromachines 2023, 14, 240. [Google Scholar] [CrossRef]
- Chen, L.; Li, C.; Fang, J. Design of a multi-direction piezoelectric and electromagnetic hybrid energy harvester used for ocean wave energy harvesting. Rev. Sci. Instruments 2023, 94, 125005. [Google Scholar] [CrossRef]
- Li, L.; Li, J.; Luo, D.; Zhang, Z.; Zeng, K.; Chen, S. A piezo-electromagnetic hybrid multi-directional vibration energy harvester in freight trains. Sustain. Mater. Technol. 2024, 41, e00989. [Google Scholar] [CrossRef]
- Challa, V.R.; Prasad, M.G.; Shi, Y.; Fisher, F.T. A vibration energy harvesting device with bidirectional resonance frequency tunability. Smart Mater. Struct. 2008, 17, 015035. [Google Scholar] [CrossRef]
- Lee, D.-G.; Kim, J.-H.; Cho, K.-H.; Song, H.-C. Autonomous Resonance-Tuning Mechanism for Environmental Adaptive Energy Harvesting. Adv. Sci. 2023, 10, 2205179. [Google Scholar] [CrossRef]
- Lin, Z.; Yang, J.; Zhao, J.; Zhao, N.; Liu, J.; Wen, Y.; Li, P. Enhanced broadband vibration energy harvesting using multimodal nonlinear magnetoelectric converter. J. Electron. Mater. 2016, 45, 3554–3561. [Google Scholar] [CrossRef]
- Yekta, H.B.; Fakhari, V. Nonlinear modeling and parametric study of magnetoelectric energy harvesters in large amplitude vibrations. J. Magn. Magn. Mater. 2021, 519, 167419. [Google Scholar] [CrossRef]
- Cryns, J.W.; Hatchell, B.K.; Santiago-Rojas, E.; Silvers, K.L. Experimental Analysis of a Piezoelectric Energy Harvesting System for Harmonic, Random, and Sine on Random Vibration. Adv. Acoust. Vib. 2013, 2013, 241025. [Google Scholar] [CrossRef]
- Waterbury, A.C.; Wright, P.K. Vibration energy harvesting to power condition monitoring sensors for industrial and manufacturing equipment. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2013, 227, 1187–1202. [Google Scholar] [CrossRef]
- Blyakhman, F.A.; Safronov, A.P.; Zubarev, A.Y.; Melnikov, G.Y.; Sokolov, S.Y.; Varga, A.L.; Kurlyandskaya, G.V. Mechanical Force Acting on Ferrogel in a Non-Uniform Magnetic Field: Measurements and Modeling. Micromachines 2022, 13, 1165. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Xia, S.; Peng, C.; Gao, Y.; Peng, S.; Zhang, Z.; Zhang, W.; Xing, X.; Liu, Y. A Highly Sensitive and High-Resolution Resonant MEMS Electrostatic Field Microsensor Based on Electrostatic Stiffness Perturbation. Micromachines 2023, 14, 1489. [Google Scholar] [CrossRef]
- Dapino, M.J. Nonlinear and hysteretic magnetomechanical model for magnetostrictive transducers. IEEE Trans. Magn. 2004, 40, 429–437. [Google Scholar]
- Rao, D.K.; Kuptsov, V. Effective Use of Magnetization Data in the Design of Electric Machines with Overfluxed Regions. IEEE Trans. Magn. 2015, 51, 1–9. [Google Scholar] [CrossRef]
- B-H Curve Checker. COMSOL Multiphysics Application Gallery. Available online: https://www.comsol.com/model/b-h-curve-checker-71651 (accessed on 9 June 2025).
- Xue, G.; Zhang, P.; Li, X.; He, Z.; Wang, H.; Li, Y.; Ce, R.; Zeng, W.; Li, B. A review of giant magnetostrictive injector (GMI). Sens. Actuators A Phys. 2018, 273, 159–181. [Google Scholar] [CrossRef]
- Nonlinear Magnetostrictive Transducer. Available online: https://www.comsol.com/model/nonlinear-magnetostrictive-transducer-6063 (accessed on 12 October 2023).
- Ferroelectric Relaxor-Based Piezoelectric PMNT Crytal. Available online: http://www.siccas.com/FerroelectricRelaxorbasedPiezoelectricPMNTCry.htm (accessed on 12 October 2023).
- Jia, Y.; Tian, X.; Si, J.; Huang, S.; Wu, Z.; Zhu, C. Modulation of strain, resistance, and capacitance of tantalum oxide film by converse piezoelectric effect. Appl. Phys. Lett. 2011, 99, 011905. [Google Scholar] [CrossRef]
- Ceylan, R.; Ozun, E.; Çoban, O.; Bora, M.Ö. The effect of hygrothermal aging on the adhesion performance of nanomaterial reinforced aluminium adhesive joints. Int. J. Adhes. Adhes. 2023, 121, 103304. [Google Scholar] [CrossRef]



| Material | Property | Value | Unit | References |
|---|---|---|---|---|
| Terfenol-D | Density | 9250 | kg/m3 | [30,31] |
| Young’s modulus | 30 | GPa | ||
| Poisson’s ratio | 0.5 | – | ||
| Magnetostriction coeff. | 1600 | ppm | ||
| Relative permittivity | 1 | – | ||
| PMNT | Density | 8100 | kg/m3 | [32,33] |
| Young’s modulus | 20 | GPa | ||
| Poisson’s ratio | 0.32 | – |
| Configuration | Air Gap | (Theory) | (Exp.) | Error | |
|---|---|---|---|---|---|
| (mm) | (mm) | (Hz) | (Hz) | (%) | |
| two-magnet | 15 | 2.38 | 52.21 | 55 | −5.1 |
| four-magnet | 15 | 2.44 | 62.41 | 64 | −2.5 |
| four-magnet | 14 | 0.93 | 41.31 | 40 | +3.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naifar, S.; Kanoun, O. Magnetoelectric Energy Harvesting for Industrial IoT Applications: Frequency-Tunable Converter with Enhanced Performance. Sensors 2025, 25, 6735. https://doi.org/10.3390/s25216735
Naifar S, Kanoun O. Magnetoelectric Energy Harvesting for Industrial IoT Applications: Frequency-Tunable Converter with Enhanced Performance. Sensors. 2025; 25(21):6735. https://doi.org/10.3390/s25216735
Chicago/Turabian StyleNaifar, Slim, and Olfa Kanoun. 2025. "Magnetoelectric Energy Harvesting for Industrial IoT Applications: Frequency-Tunable Converter with Enhanced Performance" Sensors 25, no. 21: 6735. https://doi.org/10.3390/s25216735
APA StyleNaifar, S., & Kanoun, O. (2025). Magnetoelectric Energy Harvesting for Industrial IoT Applications: Frequency-Tunable Converter with Enhanced Performance. Sensors, 25(21), 6735. https://doi.org/10.3390/s25216735







