An Anti-Interference Demultiplexing Method for Electromagnetic Bessel Beams Carrying Orbital Angular Momentum
Abstract
1. Introduction
2. Methods
2.1. Scalar and Vector Bessel Beam
2.2. Smoothed Dynamic Mode Decomposition
3. Results
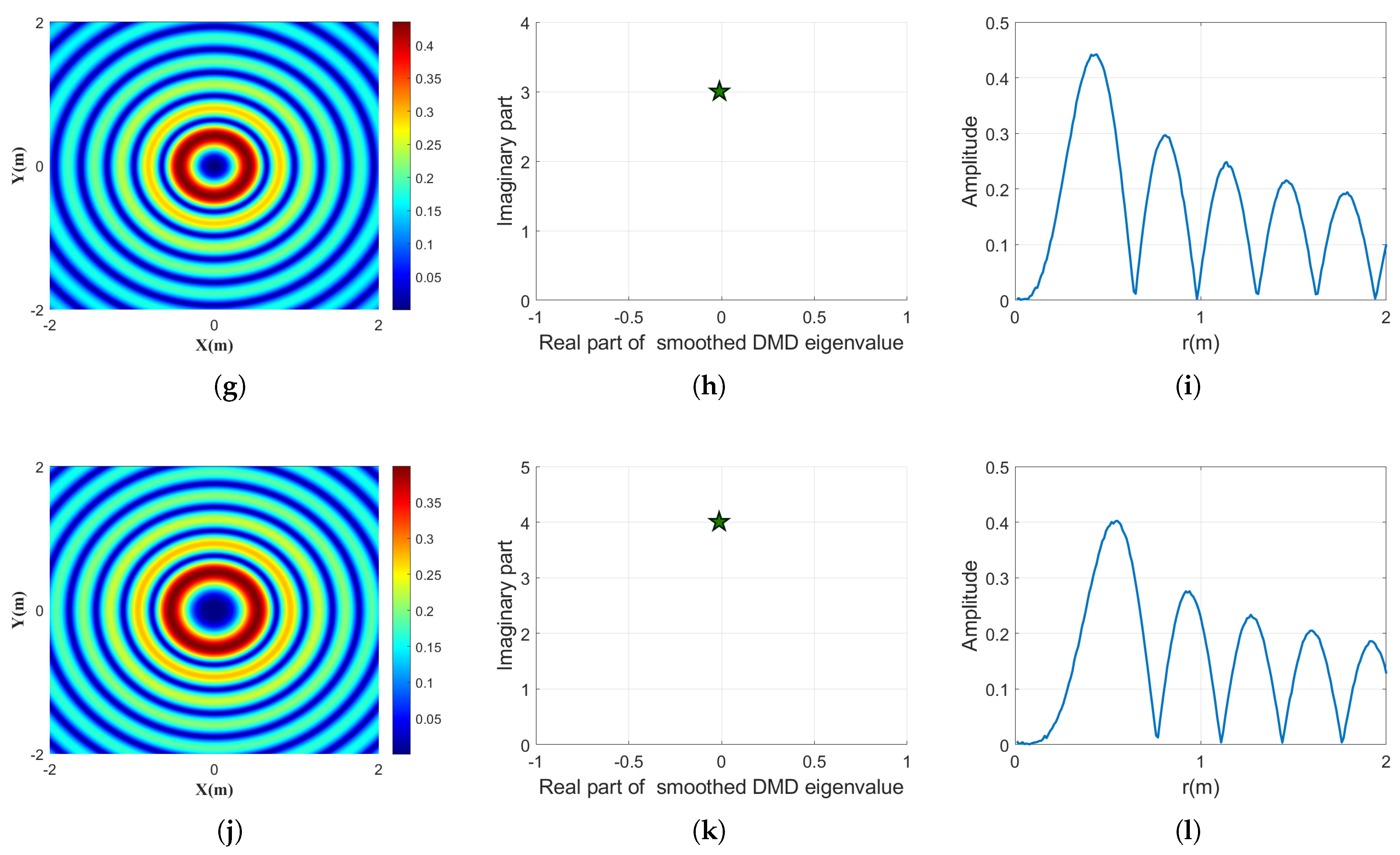
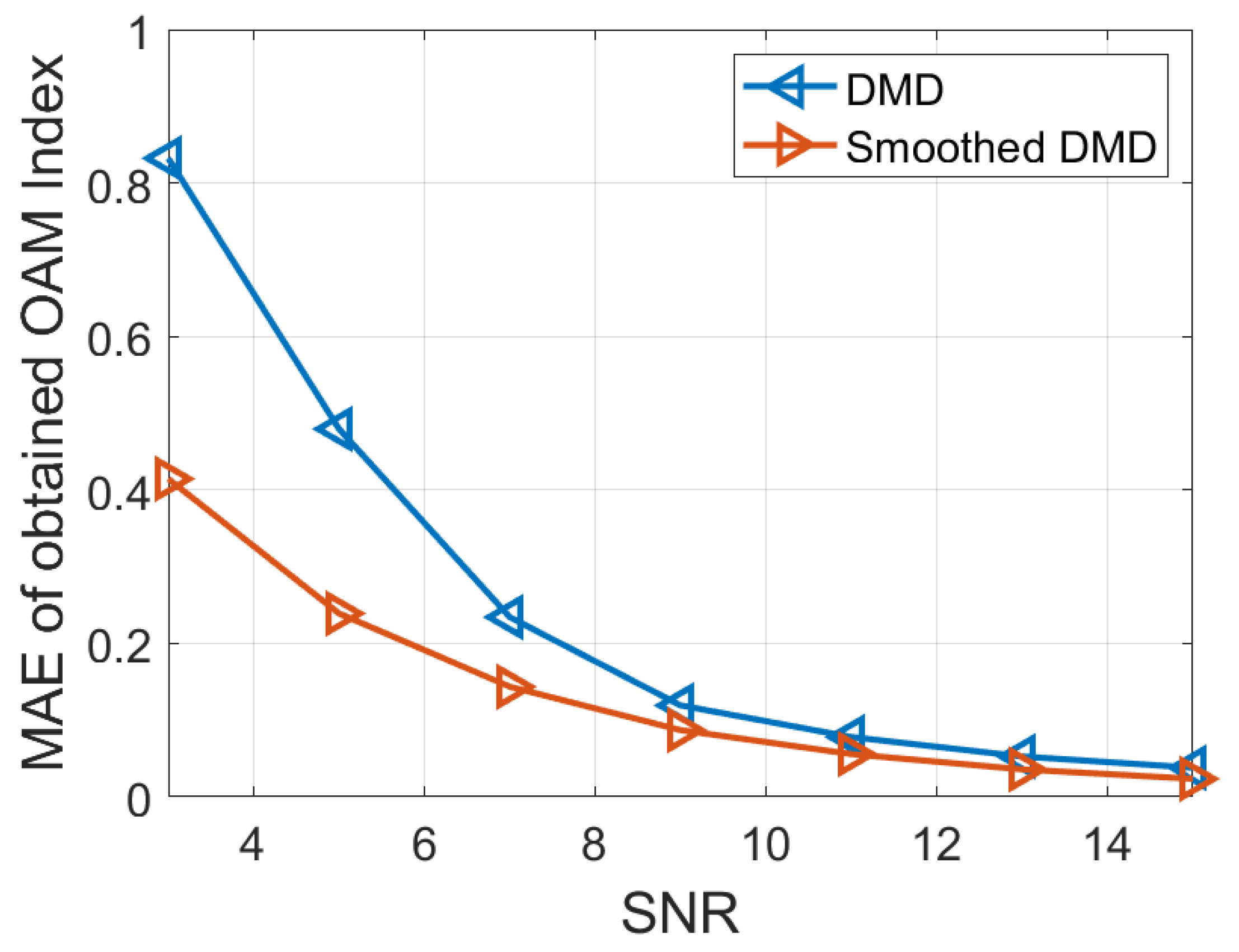
3.1. Single Bessel Beam
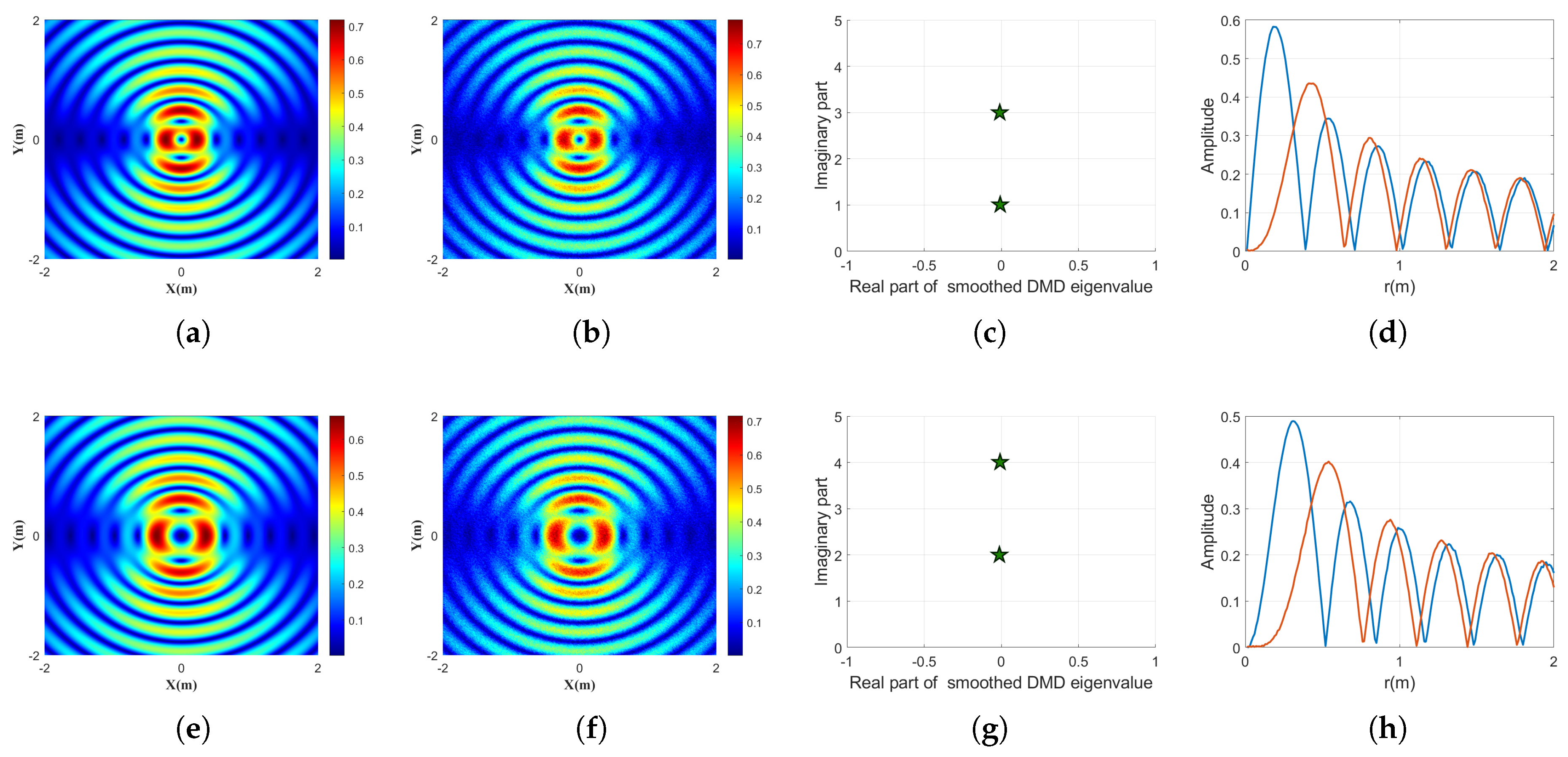
3.2. Mixed Bessel Beam
3.3. Partial Aperture Receiving Scheme
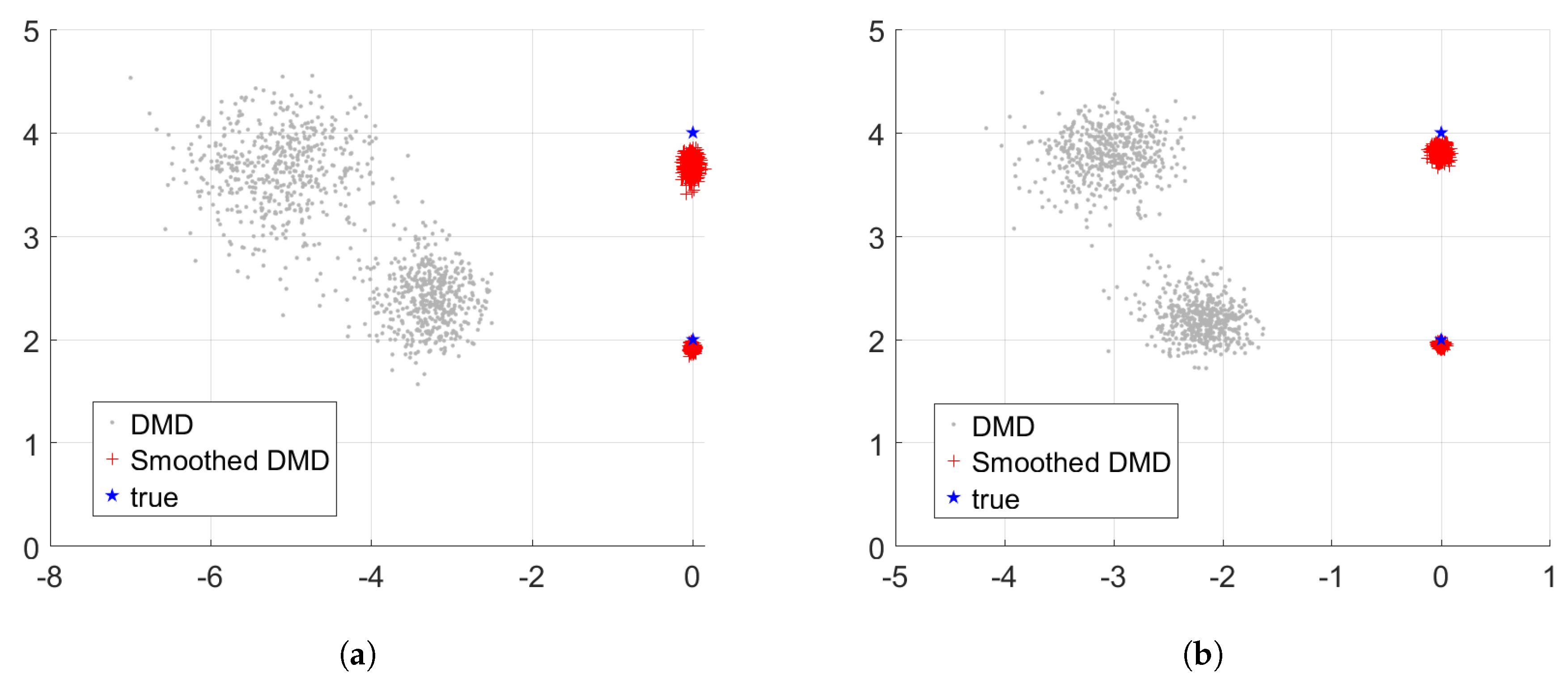
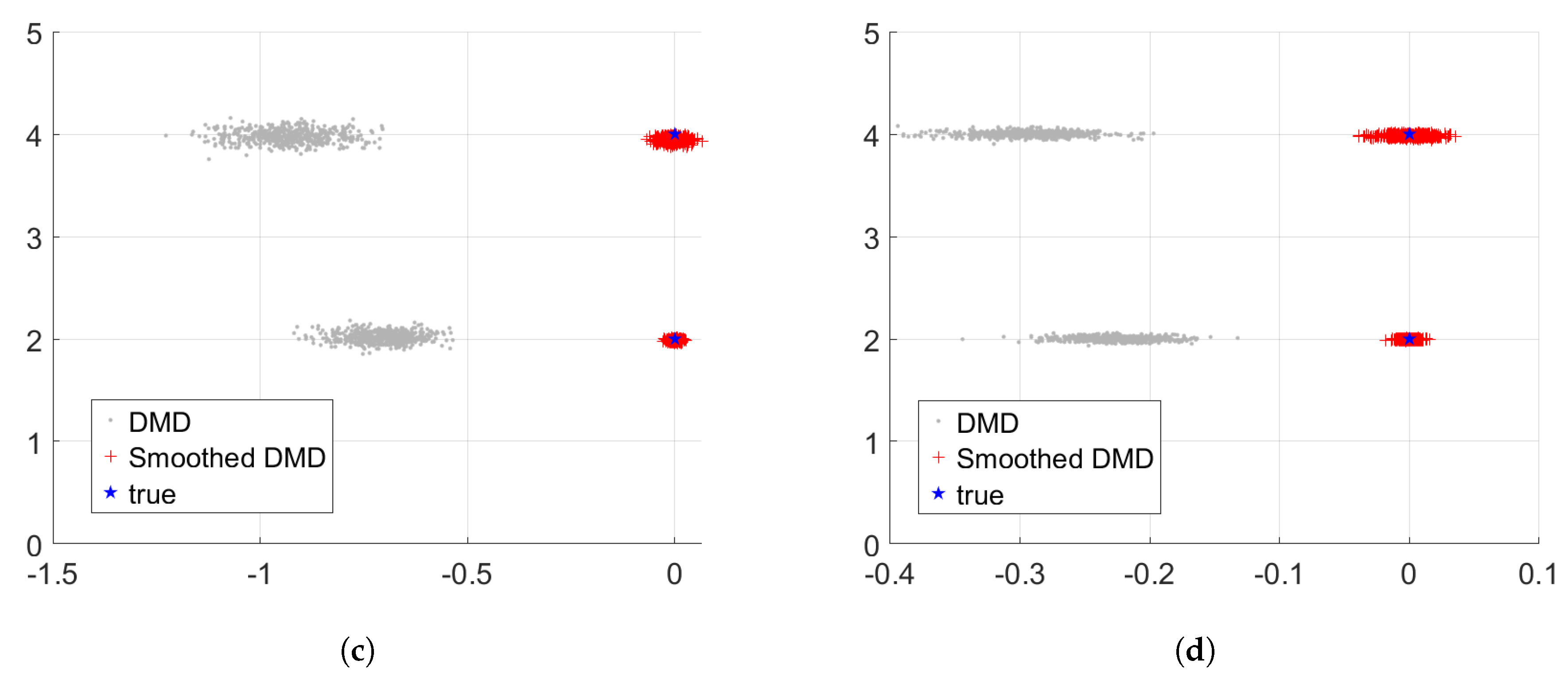
3.4. Robustness Performance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, M.L.N.; Jiang, L.J. Analysis of electromagnetic vortex beams using modified dynamic mode decomposition in spatial angular domain. Opt. Express 2019, 27, 27702–27711. [Google Scholar] [CrossRef]
- Osintseva, N.D.; Gerasimov, V.V.; Choporova, Y.Y.; Kukotenko, V.D.; Pavelyev, V.S.; Knyazev, B.A. Identification of the Hermite-Gaussian and Bessel modes of a terahertz beam with diffractive optical elements. J. Opt. Technol. 2024, 91, 215–221. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, L. A Novel Demultiplexing Scheme for Vortex Beams in Radio Communication Systems. IEEE Trans. Veh. Technol. 2021, 70, 7243–7248. [Google Scholar] [CrossRef]
- Chen, Z.; Long, W.X.; Chen, R.; Moretti, M. Low-Cost OAM Spatial Oversampling Receiver With 1-bit Quantized Comparators and DL-Based Detector. IEEE Commun. Lett. 2024, 28, 1407–1411. [Google Scholar] [CrossRef]
- Wang, S.; Wang, F.; Gao, R.; Guo, D.; Chang, H.; Li, Z.; Pan, X.; Zhou, S.; Zhang, Q.; Xin, X. SNR enhanced OAM mode division multiplexing with in-band noise modulation based on cascade delta-sigma modulation. Opt. Express 2025, 33, 1058–1068. [Google Scholar] [CrossRef] [PubMed]
- Edfors, O.; Johansson, A.J. Is Orbital Angular Momentum (OAM) Based Radio Communication an Unexploited Area? IEEE Trans. Antennas Propag. 2012, 60, 1126–1131. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, L. Suppressing White-Noise Interference for Orbital Angular Momentum Waves via the Forward–Backward Dynamic Mode Decomposition. IEEE Trans. Antennas Propag. 2023, 71, 2879–2884. [Google Scholar] [CrossRef]
- Rodenburg, B.; Lavery, M.P.J.; Malik, M.; O’Sullivan, M.N.; Mirhosseini, M.; Robertson, D.J.; Padgett, M.; Boyd, R.W. Influence of atmospheric turbulence on states of light carrying orbital angular momentum. Opt. Lett. 2012, 37, 3735–3737. [Google Scholar] [CrossRef]
- Xu, P.; Tong, X.; Zeng, Z.; Liu, S.; Zhao, D. High-Resolution Recognition of Orbital Angular Momentum Modes in Asymmetric Bessel Beams Assisted by Deep Learning. Chin. Phys. Lett. 2024, 41, 074201. [Google Scholar] [CrossRef]
- Lyu, R.; Cheng, W.; Wang, M.; Zhang, W. Fractal OAM generation and detection schemes. IEEE J. Sel. Areas Commun. 2024, 42, 1598–1612. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, M.L.N.; Jiang, L. Extraction of the characteristics of vortex beams with a partial receiving aperture at arbitrary locations. J. Opt. 2021, 23, 085601. [Google Scholar] [CrossRef]
- Mirhosseini, M.; Malik, M.; Shi, Z.; Boyd, R.W. Efficient separation of the orbital angular momentum eigenstates of light. Nat. Commun. 2013, 4, 2781. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Cheng, M.; Guo, L.; Yi, X.; Li, J.; Wang, J.; Forbes, A. Machine learning assisted speckle and OAM spectrum analysis for enhanced turbulence characterisation. arXiv 2025, arXiv:2505.21878. [Google Scholar] [CrossRef]
- Xu, Q.; Gao, R.; Wang, F.; Cheng, Z.; Cui, Y.; Li, Z.; Guo, D.; Chang, H.; Zhou, S.; Zhang, Q.; et al. End-to-end learning of joint noise shaping and probabilistic shaping for OAM mode division multiplexing transmission. Opt. Lett. 2024, 49, 5767–5770. [Google Scholar] [CrossRef]
- Wang, S.; Pan, X.; Gao, R.; Guo, D.; Chang, H.; Li, Z.; Zhou, S.; Du, C.; Yan, W.; Wang, F.; et al. High-SNR OAM mode division multiplexing based on delta-sigma modulation using a power domain layer. Opt. Lett. 2025, 50, 4150–4153. [Google Scholar] [CrossRef]
- Chang, H.; Xu, P.; Yao, H.; Li, J.; Xin, X.; Guizani, M. Nonprobe adaptive compensation for optical wireless communications based on orbital angular momentum. IEEE Trans. Wireless Commun. 2024, 23, 9033–9043. [Google Scholar] [CrossRef]
- Chen, R.; Yang, W.; Xu, H.; Li, J. A 2-D FFT-based transceiver architecture for OAM-OFDM systems with UCA antennas. IEEE Trans. Veh. Technol. 2018, 67, 5481–5485. [Google Scholar] [CrossRef]
- Karan, S.; Van Exter, M.P.; Jha, A.K. Broadband uniform-efficiency OAM-mode detector. Sci. Adv. 2025, 11, eadq7201. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition and its variants. Annu. Rev. Fluid Mech. 2022, 54, 225–254. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, L. A novel data-driven analysis method for electromagnetic radiations based on dynamic mode decomposition. IEEE Trans. Electromagn. Compat. 2020, 62, 1443–1450. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, P.; Jiang, L.; Gao, S. Time-Resolved Electromagnetic Near-Field Scanning: Dual Sparse Sampling in Time and Space. IEEE Trans. Electromagn. Compat. 2024, 66, 928–938. [Google Scholar] [CrossRef]
- Chew, W.C. Waves and Fields in Inhomogenous Media; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Stearns, S.D. Transverse and longitudinal structure of bessel vortex beam solutions to Maxwell’s equations. In Proceedings of the 2014 IEEE Antennas and Propagation Society International Symposium (APSURSI), Memphis, TN, USA, 6–11 July 2014; pp. 1218–1219. [Google Scholar]
- Céspedes Vicente, O.; Caloz, C. Bessel beams: A unified and extended perspective. Optica 2021, 8, 451–457. [Google Scholar] [CrossRef]
- Wang, W.C. Electromagnetic Wave Theory. 1986. Available online: https://depts.washington.edu/mictech/optics/me557/week2.pdf (accessed on 16 January 2025).
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, L.; Ewe, H.T. A Novel Data-Driven Modeling Method for the Spatial–Temporal Correlated Complex Sea Clutter. IEEE Geosci. Remote Sens. 2022, 60, 5104211. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mi, C.; Huang, X.; Qiao, W.; Zhang, Y. An Anti-Interference Demultiplexing Method for Electromagnetic Bessel Beams Carrying Orbital Angular Momentum. Sensors 2025, 25, 6706. https://doi.org/10.3390/s25216706
Mi C, Huang X, Qiao W, Zhang Y. An Anti-Interference Demultiplexing Method for Electromagnetic Bessel Beams Carrying Orbital Angular Momentum. Sensors. 2025; 25(21):6706. https://doi.org/10.3390/s25216706
Chicago/Turabian StyleMi, Congwei, Xiuqiong Huang, Wensheng Qiao, and Yanming Zhang. 2025. "An Anti-Interference Demultiplexing Method for Electromagnetic Bessel Beams Carrying Orbital Angular Momentum" Sensors 25, no. 21: 6706. https://doi.org/10.3390/s25216706
APA StyleMi, C., Huang, X., Qiao, W., & Zhang, Y. (2025). An Anti-Interference Demultiplexing Method for Electromagnetic Bessel Beams Carrying Orbital Angular Momentum. Sensors, 25(21), 6706. https://doi.org/10.3390/s25216706




