Estimation of Fugl–Meyer Assessment Upper-Extremity Sub-Scores Using a Mixup-Augmented LSTM Autoencoder and Wearable Sensor Data
Highlights
- A targeted 7-motion protocol enables rapid (10-minute) estimation of FMA-UE subdomain scores—hand, wrist, elbow-shoulder, and coordination—by capturing distinct joint synergies often missed by total-score estimators.
- The integration of mixup augmentation with an LSTM-based autoencoder attains high generalization (R2 > 0.82, Pearson’s correlation coefficient r > 0.90) through leave-one-subject-out validation.
- A comprehensive motion set is essential for precise estimation across all FMA-UE functional domains, as confirmed by reduced motion analysis.
- The proposed model offers a clinically viable, objective screening tool for stroke assessment and therapy triage, completable within 10 minutes.
Abstract
1. Introduction
2. Materials and Methods
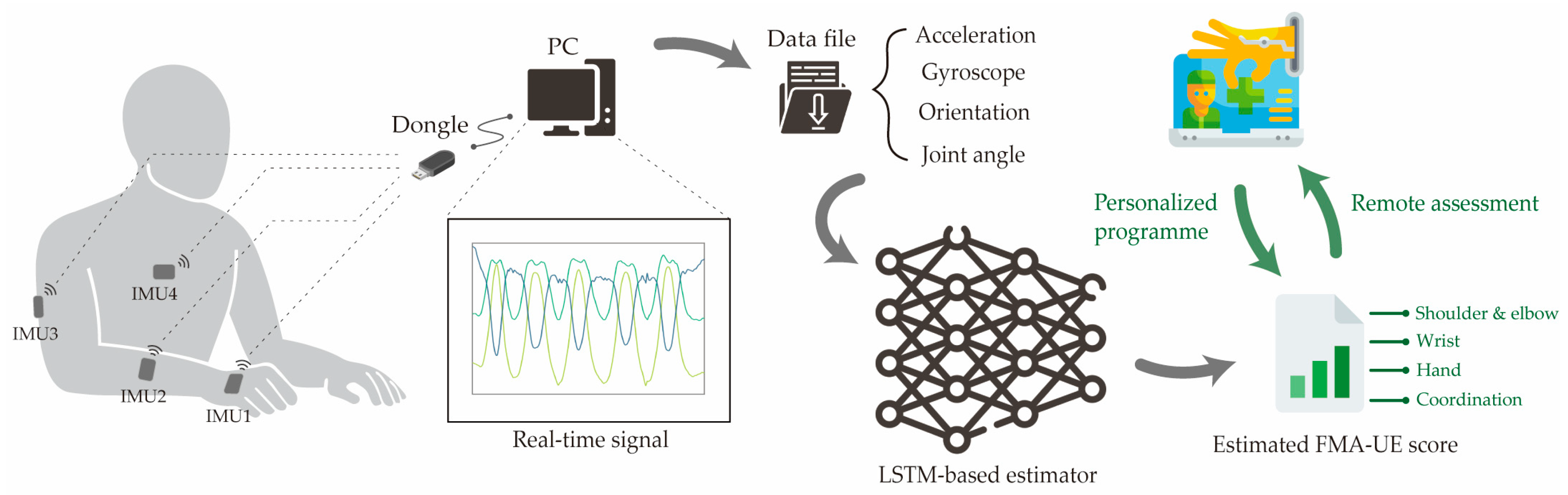
2.1. Data Collection Method
2.1.1. Participants
2.1.2. Experimental Procedures
2.1.3. Hardware and Software
2.1.4. Specialized Upper Limb Motions from FMA-UE
2.2. AI Model Training and Evaluation
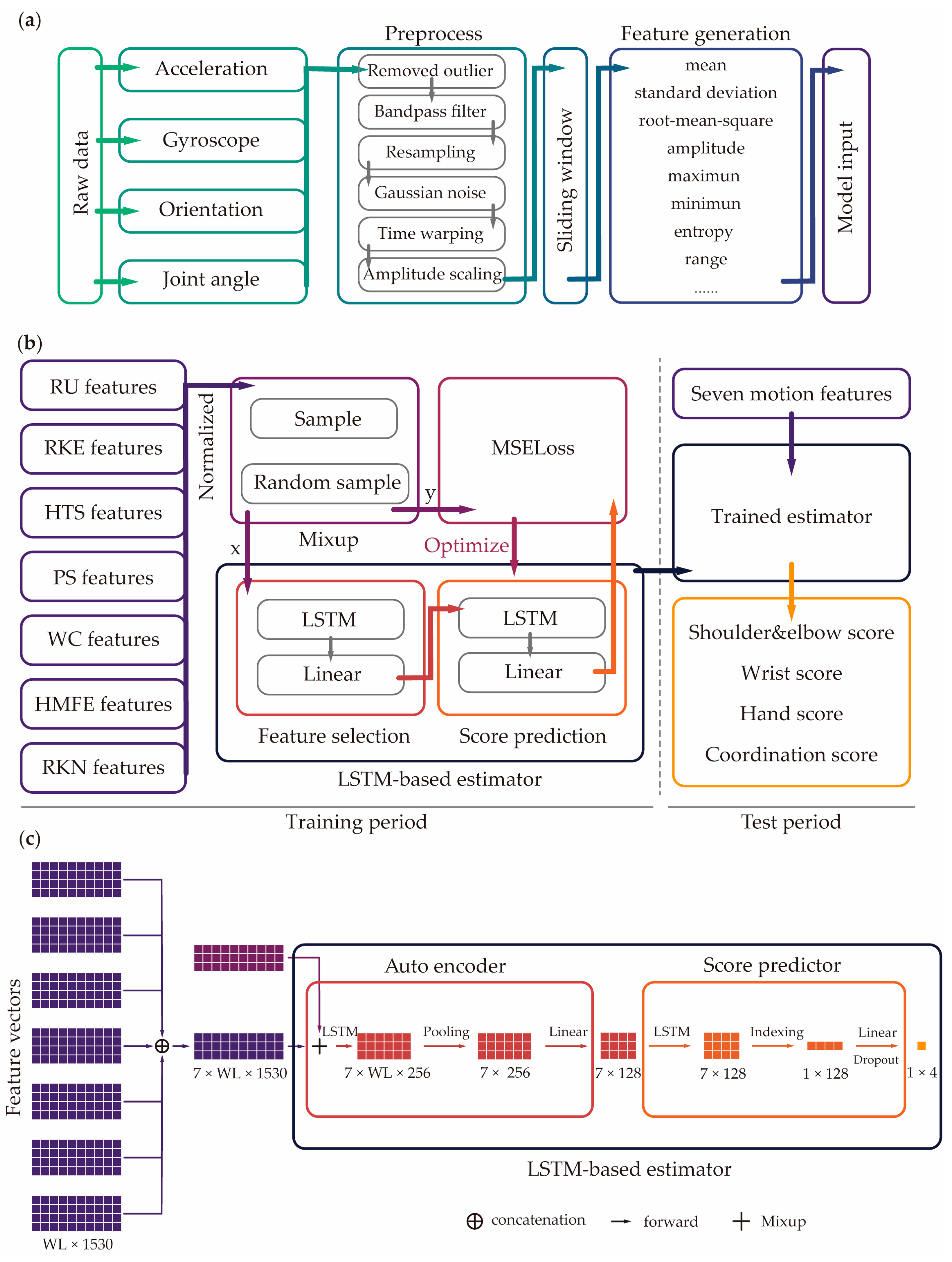
2.2.1. Data Processing
2.2.2. AI Model Design
2.2.3. Model Evaluation
3. Results
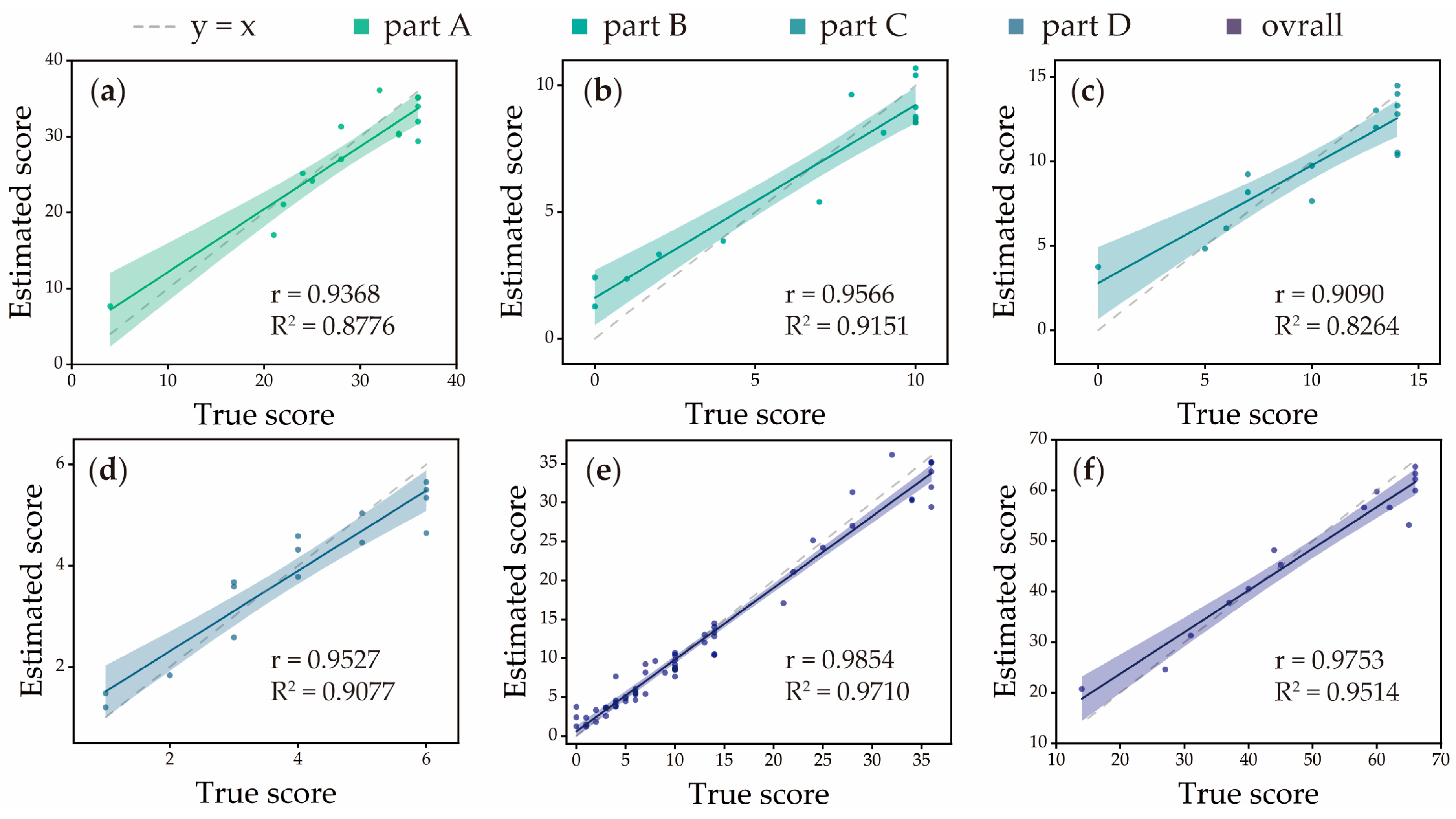
3.1. Accuracy of Estimator
3.2. Comparisons with Different Reduced Motion Set
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Katan, M.; Luft, A. Global burden of stroke. In Proceedings of the Seminars in Neurology; Thieme Medical Publishers: New York, NY, USA, 2018; pp. 208–211. [Google Scholar]
- Wu, S.; Wu, B.; Liu, M.; Chen, Z.; Wang, W.; Anderson, C.S.; Sandercock, P.; Wang, Y.; Huang, Y.; Cui, L. Stroke in China: Advances and challenges in epidemiology, prevention, and management. Lancet Neurol. 2019, 18, 394–405. [Google Scholar] [CrossRef]
- Wang, W.; Jiang, B.; Sun, H.; Ru, X.; Sun, D.; Wang, L.; Wang, L.; Jiang, Y.; Li, Y.; Wang, Y. Prevalence, incidence, and mortality of stroke in China: Results from a nationwide population-based survey of 480 687 adults. Circulation 2017, 135, 759–771. [Google Scholar] [CrossRef]
- Pulman, J.; Buckley, E. Assessing the efficacy of different upper limb hemiparesis interventions on improving health-related quality of life in stroke patients: A systematic review. Top. Stroke Rehabil. 2013, 20, 171–188. [Google Scholar] [CrossRef]
- Whitehead, S.; Baalbergen, E. Post-stroke rehabilitation. S. Afr. Med. J. 2019, 109, 81–83. [Google Scholar] [CrossRef]
- Richards, C.L.; Malouin, F.; Nadeau, S. Stroke rehabilitation: Clinical picture, assessment, and therapeutic challenge. Prog. Brain Res. 2015, 218, 253–280. [Google Scholar]
- Barnes, M.P. Principles of neurological rehabilitation. J. Neurol. Neurosurg. Psychiatry 2003, 74, iv3–iv7. [Google Scholar] [CrossRef] [PubMed]
- Winstein, C.J.; Stein, J.; Arena, R.; Bates, B.; Cherney, L.R.; Cramer, S.C.; Deruyter, F.; Eng, J.J.; Fisher, B.; Harvey, R.L. Guidelines for adult stroke rehabilitation and recovery: A guideline for healthcare professionals from the American Heart Association/American Stroke Association. Stroke 2016, 47, e98–e169. [Google Scholar] [CrossRef] [PubMed]
- Anderson, C.; Mhurchu, C.N.; Rubenach, S.; Clark, M.; Spencer, C.; Winsor, A. Home or hospital for stroke Rehabilitation? Results of a randomized controlled trial: II: Cost minimization analysis at 6 months. Stroke 2000, 31, 1032–1037. [Google Scholar] [CrossRef] [PubMed]
- Young, B.M.; Holman, E.A.; Cramer, S.C. Rehabilitation therapy doses are low after stroke and predicted by clinical factors. Stroke 2023, 54, 831–839. [Google Scholar] [CrossRef]
- Fugl-Meyer, A.R.; Jääskö, L.; Leyman, I.; Olsson, S.; Steglind, S. A method for evaluation of physical performance. Scand J. Rehabil Med. 1975, 7, 13–31. [Google Scholar] [CrossRef]
- Gor-García-Fogeda, M.D.; Molina-Rueda, F.; Cuesta-Gómez, A.; Carratalá-Tejada, M.; Alguacil-Diego, I.M.; Miangolarra-Page, J.C. Scales to assess gross motor function in stroke patients: A systematic review. Arch. Phys. Med. Rehabil. 2014, 95, 1174–1183. [Google Scholar] [CrossRef]
- Poole, J.L.; Whitney, S.L. Assessments of motor function post stroke: A review. Phys. Occup. Ther. Geriatr. 2001, 19, 1–22. [Google Scholar] [CrossRef]
- Gladstone, D.J.; Danells, C.J.; Black, S.E. The Fugl-Meyer assessment of motor recovery after stroke: A critical review of its measurement properties. Neurorehabilit. Neural Repair 2002, 16, 232–240. [Google Scholar] [CrossRef] [PubMed]
- Duncan, P.W.; Propst, M.; Nelson, S.G. Reliability of the Fugl-Meyer assessment of sensorimotor recovery following cerebrovascular accident. Phys. Ther. 1983, 63, 1606–1610. [Google Scholar] [CrossRef] [PubMed]
- Simbaña, E.D.O.; Baeza, P.S.-H.; Huete, A.J.; Balaguer, C.J. Review of automated systems for upper limbs functional assessment in neurorehabilitation. IEEE Access 2019, 7, 32352–32367. [Google Scholar] [CrossRef]
- Lee, H.H.; Kim, D.Y.; Sohn, M.K.; Shin, Y.-I.; Oh, G.-J.; Lee, Y.-S.; Joo, M.C.; Lee, S.Y.; Han, J.; Ahn, J. Revisiting the proportional recovery model in view of the ceiling effect of Fugl-Meyer assessment. Stroke 2021, 52, 3167–3175. [Google Scholar] [CrossRef]
- Lee, S.I.; Adans-Dester, C.P.; Grimaldi, M.; Dowling, A.V.; Horak, P.C.; Black-Schaffer, R.M.; Bonato, P.; Gwin, J.T. Enabling stroke rehabilitation in home and community settings: A wearable sensor-based approach for upper-limb motor training. IEEE J. Transl. Eng. Health Med. 2018, 6, 1–11. [Google Scholar] [CrossRef]
- Wang, Q.; Markopoulos, P.; Yu, B.; Chen, W.; Timmermans, A. Interactive wearable systems for upper body rehabilitation: A systematic review. J. Neuroeng. Rehabil. 2017, 14, 20. [Google Scholar] [CrossRef]
- Maceira-Elvira, P.; Popa, T.; Schmid, A.-C.; Hummel, F.C. Wearable technology in stroke rehabilitation: Towards improved diagnosis and treatment of upper-limb motor impairment. J. Neuroeng. Rehabil. 2019, 16, 142. [Google Scholar] [CrossRef]
- Toh, S.F.M.; Fong, K.N.; Gonzalez, P.C.; Tang, Y.M. Application of home-based wearable technologies in physical rehabilitation for stroke: A scoping review. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 1614–1623. [Google Scholar] [CrossRef]
- Filippeschi, A.; Schmitz, N.; Miezal, M.; Bleser, G.; Ruffaldi, E.; Stricker, D. Survey of motion tracking methods based on inertial sensors: A focus on upper limb human motion. Sensors 2017, 17, 1257. [Google Scholar] [CrossRef]
- Favata, A.; Gallart-Agut, R.; Pamies-Vila, R.; Torras, C.; Font-Llagunes, J.M. IMU-based systems for upper limb kinematic analysis in clinical applications: A systematic review. IEEE Sens. J. 2024, 24, 28576–28594. [Google Scholar] [CrossRef]
- Formstone, L.; Huo, W.; Wilson, S.; McGregor, A.; Bentley, P.; Vaidyanathan, R. Quantification of motor function post-stroke using novel combination of wearable inertial and mechanomyographic sensors. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 1158–1167. [Google Scholar] [CrossRef] [PubMed]
- Weizman, Y.; Tirosh, O.; Fuss, F.K.; Tan, A.M.; Rutz, E. Recent state of wearable IMU sensors use in people living with spasticity: A systematic review. Sensors 2022, 22, 1791. [Google Scholar] [CrossRef] [PubMed]
- Del Din, S.; Patel, S.; Cobelli, C.; Bonato, P. Estimating Fugl-Meyer clinical scores in stroke survivors using wearable sensors. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 5839–5842. [Google Scholar]
- Yu, L.; Xiong, D.; Guo, L.; Wang, J. A remote quantitative Fugl-Meyer assessment framework for stroke patients based on wearable sensor networks. Comput. Methods Programs Biomed. 2016, 128, 100–110. [Google Scholar] [CrossRef]
- Adans-Dester, C.; Hankov, N.; O’Brien, A.; Vergara-Diaz, G.; Black-Schaffer, R.; Zafonte, R.; Dy, J.; Lee, S.I.; Bonato, P. Enabling precision rehabilitation interventions using wearable sensors and machine learning to track motor recovery. npj Digit. Med. 2020, 3, 121. [Google Scholar] [CrossRef]
- Oubre, B.; Daneault, J.-F.; Jung, H.-T.; Whritenour, K.; Miranda, J.G.V.; Park, J.; Ryu, T.; Kim, Y.; Lee, S.I. Estimating upper-limb impairment level in stroke survivors using wearable inertial sensors and a minimally-burdensome motor task. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 601–611. [Google Scholar] [CrossRef]
- Zhou, Y.M.; Raman, N.; Proietti, T.; Arnold, J.; Pathak, P.; Pont-Esteban, D.; Nuckols, K.; Rishe, K.; Doshi-Velez, F.; Lin, D.; et al. Estimating Upper Extremity Fugl-Meyer Assessment Scores From Reaching Motions Using Wearable Sensors. IEEE J. Biomed. Health Inform. 2025, 29, 4134–4146. [Google Scholar] [CrossRef]
- Martino Cinnera, A.; Picerno, P.; Bisirri, A.; Koch, G.; Morone, G.; Vannozzi, G. Upper limb assessment with inertial measurement units according to the international classification of functioning in stroke: A systematic review and correlation meta-analysis. Top. Stroke Rehabil. 2024, 31, 66–85. [Google Scholar] [CrossRef]
- Schwarz, A.; Bhagubai, M.M.; Wolterink, G.; Held, J.P.; Luft, A.R.; Veltink, P.H. Assessment of upper limb movement impairments after stroke using wearable inertial sensing. Sensors 2020, 20, 4770. [Google Scholar] [CrossRef]
- Miao, S.; Shen, C.; Feng, X.; Zhu, Q.; Shorfuzzaman, M.; Lv, Z. Upper limb rehabilitation system for stroke survivors based on multi-modal sensors and machine learning. IEEE Access 2021, 9, 30283–30291. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.; Xie, S.Q.; Shi, C.; Li, J.; Zhang, Z.-Q. Quantitative upper limb impairment assessment for stroke rehabilitation: A review. IEEE Sens. J. 2024, 24, 7432–7447. [Google Scholar] [CrossRef]
- Tozlu, C.; Edwards, D.; Boes, A.; Labar, D.; Tsagaris, K.Z.; Silverstein, J.; Pepper Lane, H.; Sabuncu, M.R.; Liu, C.; Kuceyeski, A.; et al. Machine learning methods predict individual upper-limb motor impairment following therapy in chronic stroke. Neurorehabilit. Neural Repair 2020, 34, 428–439. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Yang, H.; Cheng, L.; Huang, F.; Zhao, S.; Li, D.; Yan, R. Quantitative assessment of hand motor function for post-stroke rehabilitation based on HAGCN and multimodality fusion. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 2032–2041. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Shi, Y.; Wang, Y.; Cheng, Y. Deep Learning-Based Image Automatic Assessment and Nursing of Upper Limb Motor Function in Stroke Patients. J. Healthc. Eng. 2021, 2021, 9059411. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.-J.; Wei, M.-Y.; Chen, Y.-J. Multiple inertial measurement unit combination and location for recognizing general, fatigue, and simulated-fatigue gait. Gait Posture 2022, 96, 330–337. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Shu, X.; Sheng, X.; Jia, J.; Zhu, X. A novel automated RGB-D sensor-based measurement of voluntary items of the Fugl-Meyer assessment for upper extremity: A feasibility study. Brain Sci. 2022, 12, 1380. [Google Scholar] [CrossRef]
- Julianjatsono, R.; Ferdiana, R.; Hartanto, R. High-resolution automated Fugl-Meyer Assessment using sensor data and regression model. In Proceedings of the 2017 3rd International Conference on Science and Technology-Computer (ICST), Yogyakarta, Indonesia, 11–12 July 2017; pp. 28–32. [Google Scholar]
- Song, X.; Chen, S.; Jia, J.; Shull, P.B. Cellphone-based automated Fugl-Meyer assessment to evaluate upper extremity motor function after stroke. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 2186–2195. [Google Scholar] [CrossRef]
- Lee, S.; Lee, Y.-S.; Kim, J. Automated evaluation of upper-limb motor function impairment using Fugl-Meyer assessment. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 26, 125–134. [Google Scholar] [CrossRef]
- Kim, W.-S.; Cho, S.; Baek, D.; Bang, H.; Paik, N.-J. Upper extremity functional evaluation by Fugl-Meyer assessment scoring using depth-sensing camera in hemiplegic stroke patients. PLoS ONE 2016, 11, e0158640. [Google Scholar] [CrossRef]
- Oubre, B.; Lee, S.I. Estimating post-stroke upper-limb impairment from four activities of daily living using a single wrist-worn inertial sensor. In Proceedings of the 2022 IEEE-EMBS International Conference on Biomedical and Health Informatics (BHI), Ioannina, Greece, 27–30 September 2022; pp. 01–04. [Google Scholar]
- Oubre, B.; Lee, S.I. Detection and assessment of point-to-point movements during functional activities using deep learning and kinematic analyses of the stroke-affected wrist. IEEE J. Biomed. Health Inform. 2023, 28, 1022–1030. [Google Scholar] [CrossRef] [PubMed]
- Roby-Brami, A.; Feydy, A.; Combeaud, M.; Biryukova, E.; Bussel, B.; Levin, M.F. Motor compensation and recovery for reaching in stroke patients. Acta Neurol. Scand. 2003, 107, 369–381. [Google Scholar] [CrossRef] [PubMed]
- Beravs, T.; Podobnik, J.; Munih, M. Three-axial accelerometer calibration using Kalman filter covariance matrix for online estimation of optimal sensor orientation. IEEE Trans. Instrum. Meas. 2012, 61, 2501–2511. [Google Scholar] [CrossRef]
- Repnik, E.; Puh, U.; Goljar, N.; Munih, M.; Mihelj, M. Using inertial measurement units and electromyography to quantify movement during action research arm test execution. Sensors 2018, 18, 2767. [Google Scholar] [CrossRef]
- Slade, P.; Habib, A.; Hicks, J.L.; Delp, S.L. An open-source and wearable system for measuring 3D human motion in real-time. IEEE Trans. Biomed. Eng. 2021, 69, 678–688. [Google Scholar] [CrossRef]
- Zhou, W.; Fu, D.; Duan, Z.; Wang, J.; Zhou, L.; Guo, L. Achieving precision assessment of functional clinical scores for upper extremity using IMU-Based wearable devices and deep learning methods. J. Neuroeng. Rehabil. 2025, 22, 84. [Google Scholar] [CrossRef]
- Dietterich, T.G. Machine learning for sequential data: A review. In Proceedings of the Joint IAPR International Workshops on Statistical Techniques in Pattern Recognition (SPR) and Structural and Syntactic Pattern Recognition (SSPR), Windsor, ON, Canada, 6–9 August 2002; pp. 15–30. [Google Scholar]
- Ramasubramanian, S.; Rangwani, H.; Takemori, S.; Samanta, K.; Umeda, Y.; Radhakrishnan, V.B. Selective Mixup Fine-Tuning for Optimizing Non-Decomposable Objectives. arXiv 2024, arXiv:2403.18301. [Google Scholar]
- Teney, D.; Wang, J.; Abbasnejad, E. Selective mixup helps with distribution shifts, but not (only) because of mixup. arXiv 2023, arXiv:2305.16817. [Google Scholar] [CrossRef]
- Zhang, H.; Cisse, M.; Dauphin, Y.N.; Lopez-Paz, D. mixup: Beyond empirical risk minimization. arXiv 2017, arXiv:1710.09412. [Google Scholar]
- Thulasidasan, S.; Chennupati, G.; Bilmes, J.A.; Bhattacharya, T.; Michalak, S. On mixup training: Improved calibration and predictive uncertainty for deep neural networks. Adv. Neural Inf. Process. Syst. 2019, 32. Available online: https://proceedings.neurips.cc/paper_files/paper/2019/file/36ad8b5f42db492827016448975cc22d-Paper.pdf (accessed on 23 October 2025).
- Yan, S.; Song, H.; Li, N.; Zou, L.; Ren, L. Improve unsupervised domain adaptation with mixup training. arXiv 2020, arXiv:2001.00677. [Google Scholar] [CrossRef]
- Chou, H.-P.; Chang, S.-C.; Pan, J.-Y.; Wei, W.; Juan, D.-C. Remix: Rebalanced mixup. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 95–110. [Google Scholar]
- Roy, A.; Shah, A.; Shah, K.; Dhar, P.; Cherian, A.; Chellappa, R. Felmi: Few shot learning with hard mixup. Adv. Neural Inf. Process. Syst. 2022, 35, 24474–24486. [Google Scholar]
- Zhu, R.; Yu, X.; Li, S. Progressive mix-up for few-shot supervised multi-source domain transfer. In Proceedings of the Eleventh International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- Darkwah Jnr, Y.; Kang, D.-K. Enhancing few-shot learning using targeted mixup. Appl. Intell. 2025, 55, 279. [Google Scholar] [CrossRef]
- Suk, H.-I.; Lee, S.-W.; Shen, D.; Alzheimer’s Disease Neuroimaging Initiative. Latent feature representation with stacked auto-encoder for AD/MCI diagnosis. Brain Struct. 2015, 220, 841–859. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Ji, Z.; Guo, J.; Zhang, Z. Zero-shot learning via latent space encoding. IEEE Trans. Cybern. 2018, 49, 3755–3766. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi Foumani, N.; Miller, L.; Tan, C.W.; Webb, G.I.; Forestier, G.; Salehi, M. Deep learning for time series classification and extrinsic regression: A current survey. ACM Comput. Surv. 2024, 56, 1–45. [Google Scholar] [CrossRef]
- Schambra, H.M.; Parnandi, A.; Pandit, N.G.; Uddin, J.; Wirtanen, A.; Nilsen, D.M. A taxonomy of functional upper extremity motion. Front. Neurol. 2019, 10, 857. [Google Scholar] [CrossRef]
- Raghavan, P. Upper limb motor impairment post stroke. Phys. Med. Rehabil. Clin. N. Am. 2015, 26, 599. [Google Scholar] [CrossRef]
- Shi, X.-Q.; Ti, C.-H.E.; Lu, H.-Y.; Hu, C.-P.; Xie, D.-S.; Yuan, K.; Heung, H.-L.; Leung, T.W.-H.; Li, Z.; Tong, R.K.-Y.; et al. Task-oriented training by a personalized electromyography-driven soft robotic hand in chronic stroke: A randomized controlled trial. Neurorehabilit. Neural Repair 2024, 38, 595–606. [Google Scholar] [CrossRef]


| Characteristics | Value | Mean ± Standard Deviation | Min–Max |
|---|---|---|---|
| Age | - | 50.93 ± 17.31 | 26–74 |
| Gender (male/female) | 7/8 | - | - |
| Tested side (left/right) | 4/11 | - | - |
| FMA-UE score | - | 49.80 ± 17.05 | 14–66 |
| Part A | - | 28.80 ± 8.80 | 4–24 |
| Part B | - | 6.73 ± 4.09 | 0–10 |
| Part C | - | 10.33 ± 4.40 | 0–14 |
| Part D | - | 3.93 ± 1.75 | 1–6 |
| Motion | Description | FMA-UE Motion Items | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Part A | Part B | Part C | Part D | |||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | ||
| Reaching upward (RU) | Paretic limb lifting up | √ | √ | √ | ||||||||||||||||||||
| Reaching knee to ear (RKE) | Hand from contralateral knee to ipsilateral ear, then from ipsilateral ear to contralateral knee | √ | √ | √ | √ | √ | ||||||||||||||||||
| Hand to lumbar spine (HTS) | Start with hand on lap | √ | √ | |||||||||||||||||||||
| Elbow pronation–supination (EPS) | Elbow at 90 degrees, shoulder at 0 degrees | √ | √ | |||||||||||||||||||||
| Wrist circumduction (WC) | Elbow at 90 degrees, forearm pronated, shoulder at 0 degrees | √ | √ | √ | √ | √ | √ | |||||||||||||||||
| Hand mass flexion and extension (HMFE) | Fully active extension and fully active flexion | √ | √ | √ | √ | √ | √ | √ | ||||||||||||||||
| Reaching knee to nose (RKN) | Closed eyes, five times | √ | √ | √ | √ | √ | √ | |||||||||||||||||
| Subdivision of FMA-UE [11] | R2 | r | MAE | NMAE | RMSE | NRMSE |
|---|---|---|---|---|---|---|
| Part A | 0.8776 | 0.9368 * | 2.7054 | 0.0751 | 3.1927 | 0.0998 |
| Part B | 0.9151 | 0.9566 * | 1.2023 | 0.1202 | 1.3160 | 0.1316 |
| Part C | 0.8264 | 0.9090 * | 1.3633 | 0.0974 | 1.9007 | 0.1358 |
| Part D | 0.9077 | 0.9527 * | 0.4722 | 0.0787 | 0.5597 | 0.1257 |
| Subdivision of FMA-UE [11] | R2 | r | NMAE | NRMSE |
|---|---|---|---|---|
| Part A | 0.8606 | 0.9330 * | 0.0786 | 0.1056 |
| Part B | 0.6474 | 0.8046 * | 0.1823 | 0.2419 |
| Part C | 0.7647 | 0.8745 * | 0.1102 | 0.1506 |
| Part D | 0.7988 | 0.8937 * | 0.1130 | 0.1913 |
| Motion Set | R2 | r | NMAE | NRMSE |
|---|---|---|---|---|
| A*B*C*D* | 0.9710 | 0.9854 * | 0.0929 | 0.1144 |
| __B*C*D* | 0.8767 | 0.9364 * | 0.1896 | 0.2330 |
| A*__C*D* | 0.9482 | 0.9737 * | 0.1326 | 0.1778 |
| A*B*__D* | 0.9112 | 0.9546 * | 0.1437 | 0.2011 |
| A*B*C*__ | 0.9150 | 0.9565 * | 0.1553 | 0.1988 |
| Authors | Sensor | Task Set | Model | FMA-UE Subdivision | Total FMA-UE | |||
|---|---|---|---|---|---|---|---|---|
| Part A | Part B | Part C | Part D | |||||
| Oubre et al. (2020) [29] | 1 IMUs | 1–2 min motions | Support vector regressor | - | - | - | - | R2 = 0.70 NRMSE = 0.182 |
| Adans-Dester et al. (2020) [28] | 5 accelerometers | 33 items | Modified balanced random forest | - | - | - | - | R2 = 0.86 |
| Oubre et al. (2022) [44] | 3 IMUs | 4 ADL motions | Random forest | - | - | - | - | R2 = 0.75 NRMSE = 0.170 |
| Zhou et al. (2025) [30] | 4 IMUs | 3 motions | Support vector regressor | - | - | - | - | R2 = 0.67 NRMSE = 0.069 |
| Present Study (2025) | 4 IMUs | 7 motions | LSTM | R2 = 0.87 | R2 = 0.91 | R2 = 0.82 | R2 = 0.90 | R2 = 0.95 NRMSE = 0.067 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Lu, H.-Y.; Tong, S.-F.; Liang, D.; Sun, H.; Xing, T.; Shi, X.; Yu, H.; Tong, R.K.-Y. Estimation of Fugl–Meyer Assessment Upper-Extremity Sub-Scores Using a Mixup-Augmented LSTM Autoencoder and Wearable Sensor Data. Sensors 2025, 25, 6663. https://doi.org/10.3390/s25216663
Liu M, Lu H-Y, Tong S-F, Liang D, Sun H, Xing T, Shi X, Yu H, Tong RK-Y. Estimation of Fugl–Meyer Assessment Upper-Extremity Sub-Scores Using a Mixup-Augmented LSTM Autoencoder and Wearable Sensor Data. Sensors. 2025; 25(21):6663. https://doi.org/10.3390/s25216663
Chicago/Turabian StyleLiu, Minghao, Hsuan-Yu Lu, Shuk-Fan Tong, Dezhi Liang, Haoyuan Sun, Tian Xing, Xiangqian Shi, Hongliu Yu, and Raymond Kai-Yu Tong. 2025. "Estimation of Fugl–Meyer Assessment Upper-Extremity Sub-Scores Using a Mixup-Augmented LSTM Autoencoder and Wearable Sensor Data" Sensors 25, no. 21: 6663. https://doi.org/10.3390/s25216663
APA StyleLiu, M., Lu, H.-Y., Tong, S.-F., Liang, D., Sun, H., Xing, T., Shi, X., Yu, H., & Tong, R. K.-Y. (2025). Estimation of Fugl–Meyer Assessment Upper-Extremity Sub-Scores Using a Mixup-Augmented LSTM Autoencoder and Wearable Sensor Data. Sensors, 25(21), 6663. https://doi.org/10.3390/s25216663








