Persistence-Weighted Performance Metric for PID Gain Optimization in Optical Tracking of Unknown Space Objects
Abstract
1. Introduction
2. Related Work
2.1. Optical Tracking and Identification for Space Objects
2.2. PID-Based Offset Control in Optical Tracking Systems
2.3. Metaheuristic Approaches to PID Gain Tuning
2.4. Performance Metrics in Optical Offset Tracking
3. Tracking Performance Metric and Optimization Framework
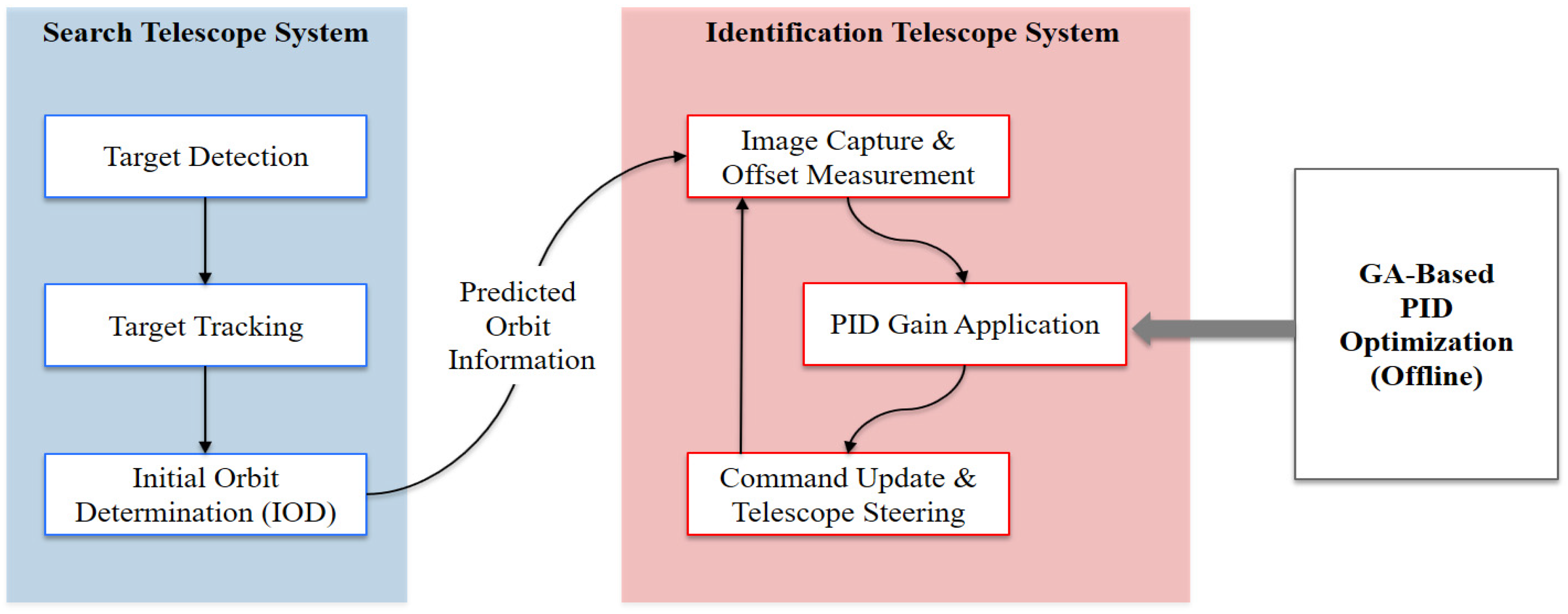
3.1. System Overview and Target Scenario
3.2. Revisiting Previously Used Metrics in the Context of Optical Identification
3.3. Definition of the Persistence-Weighted Tracking Index (PWTI)
3.4. Genetic Algorithm-Based PID Gain Optimization
3.4.1. Optimization Framework Overview
- 1.
- Initialization: An initial population of PID gain sets (Kp, Ki, Kd)) is randomly generated within predefined bounds.
- 2.
- Evaluation: Each individual (i.e., PID set) is evaluated via simulation using the selected performance index.
- 3.
- Selection: Individuals with superior performance are selected as parents.
- 4.
- Crossover and Mutation: Genetic operators are applied to generate new offspring, ensuring both exploitation and exploration.
- 5.
- Termination: The process iterates over generations until convergence or a maximum number of iterations is reached.
3.4.2. Parameter Settings and Simulation Setup
3.4.3. Metric-Specific Optimization Strategies
- RMS error: Measures the average magnitude of tracking error across the entire sequence.
- Persistence Time: Captures the longest continuous time span during which the tracking error remains below a predefined threshold (e.g., 10 arcsec).
- PWTI (Proposed): Integrates both the size and duration of tracking error into a unified score, giving higher weights to long-lasting small errors and penalizing large or intermittent deviations.
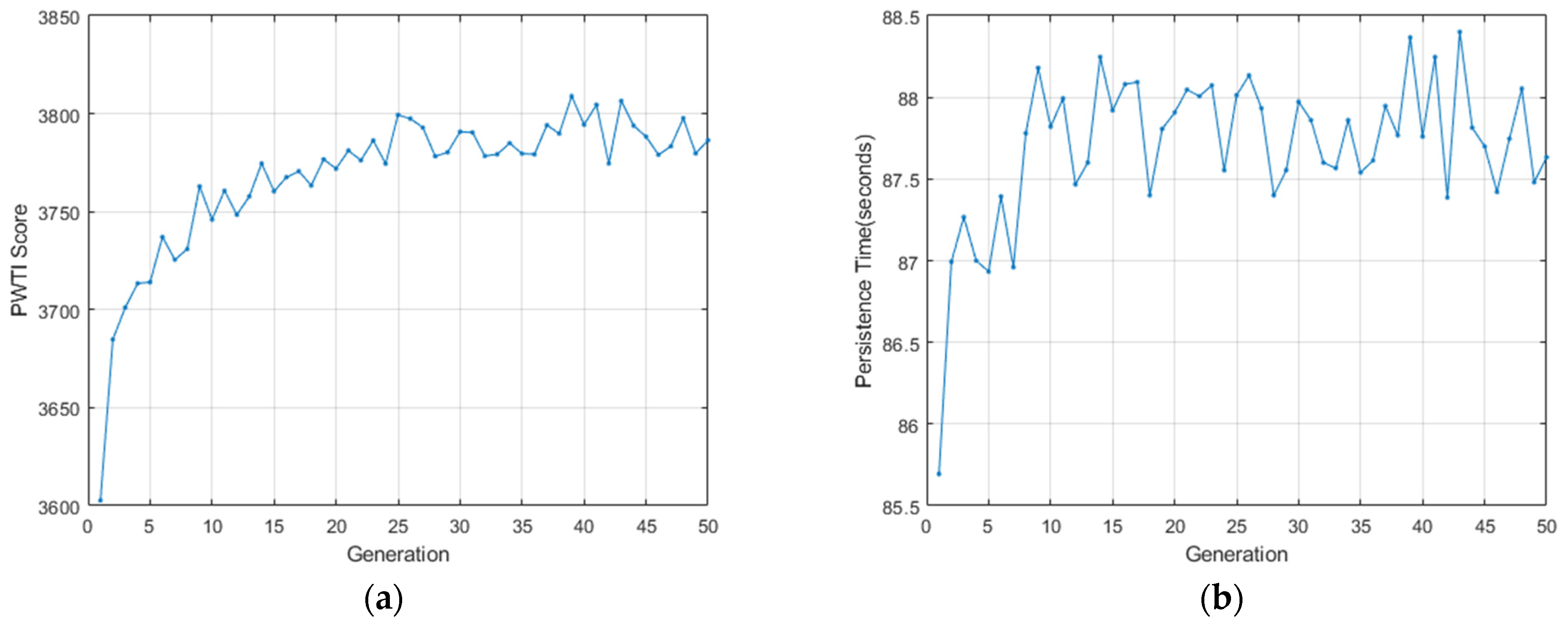
3.4.4. Genetic Optimization Results
4. Simulation and Evaluation Results
4.1. Simulation Setup and Scenario Design
- Grid-RMS: PID gains selected through grid search to minimize RMS error.
- GA-RMS: Genetic algorithm tuning using RMS error as the fitness function.
- GA-PT: Genetic algorithm tuning using persistence time as the objective.
- GA-PWTI: Genetic algorithm tuning using the proposed PWTI as the optimization metric.
4.2. Performance Comparison Across Metrics
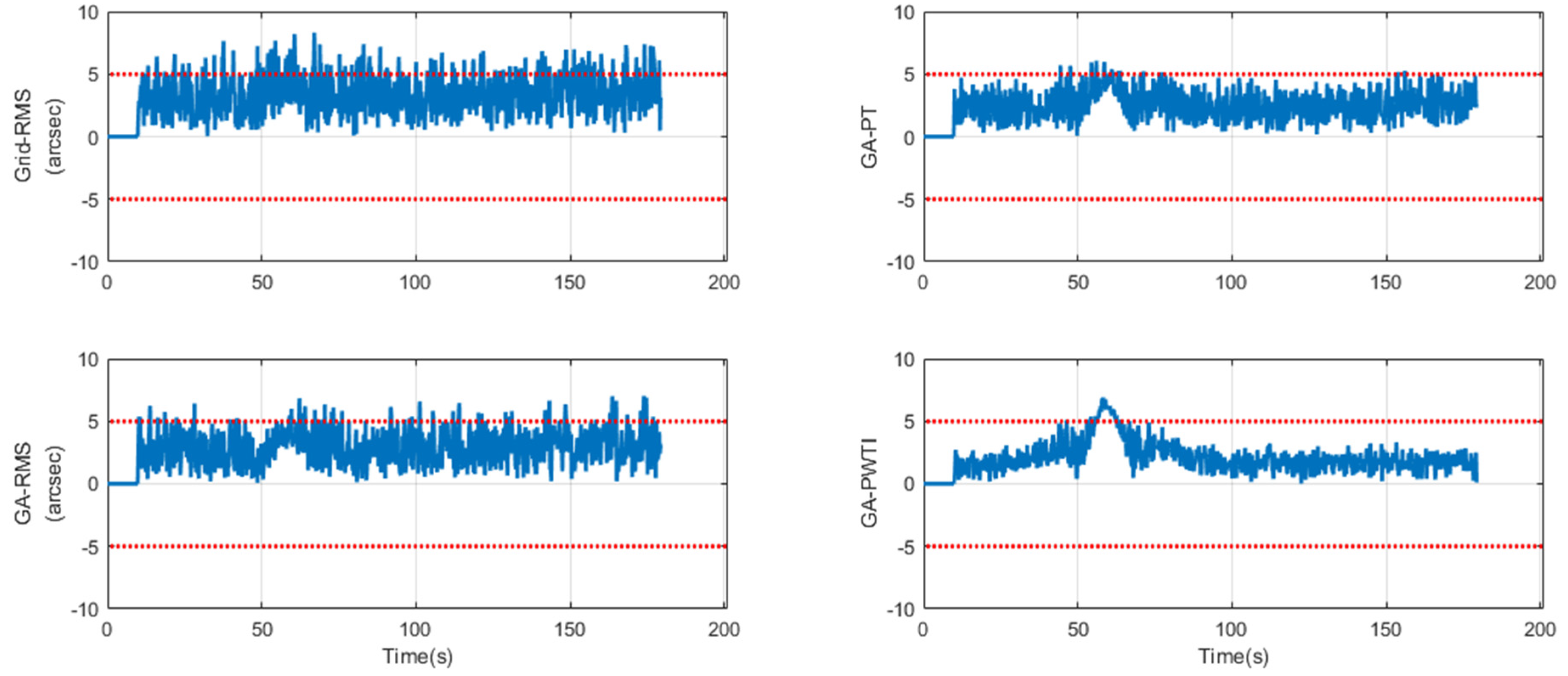
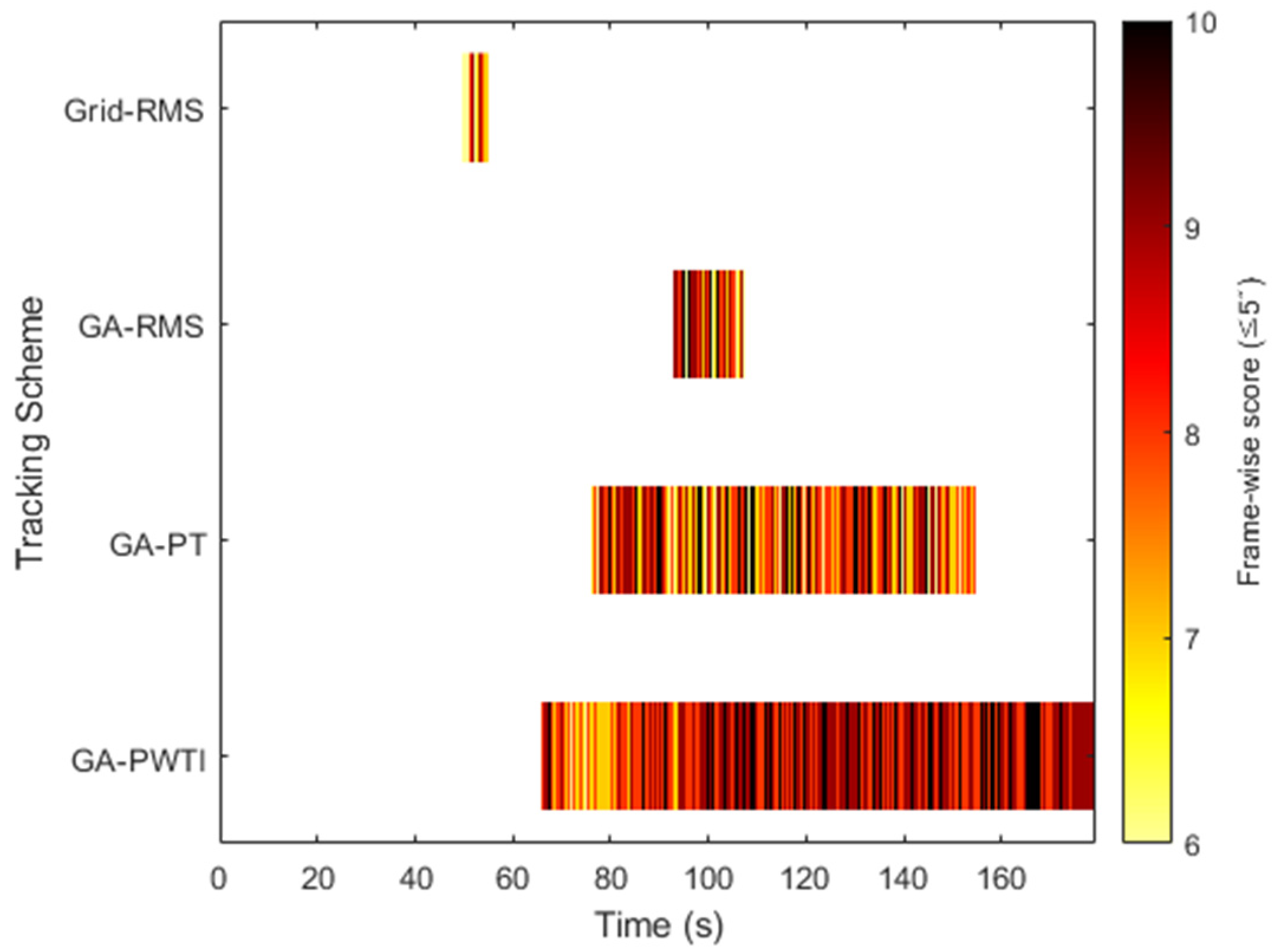
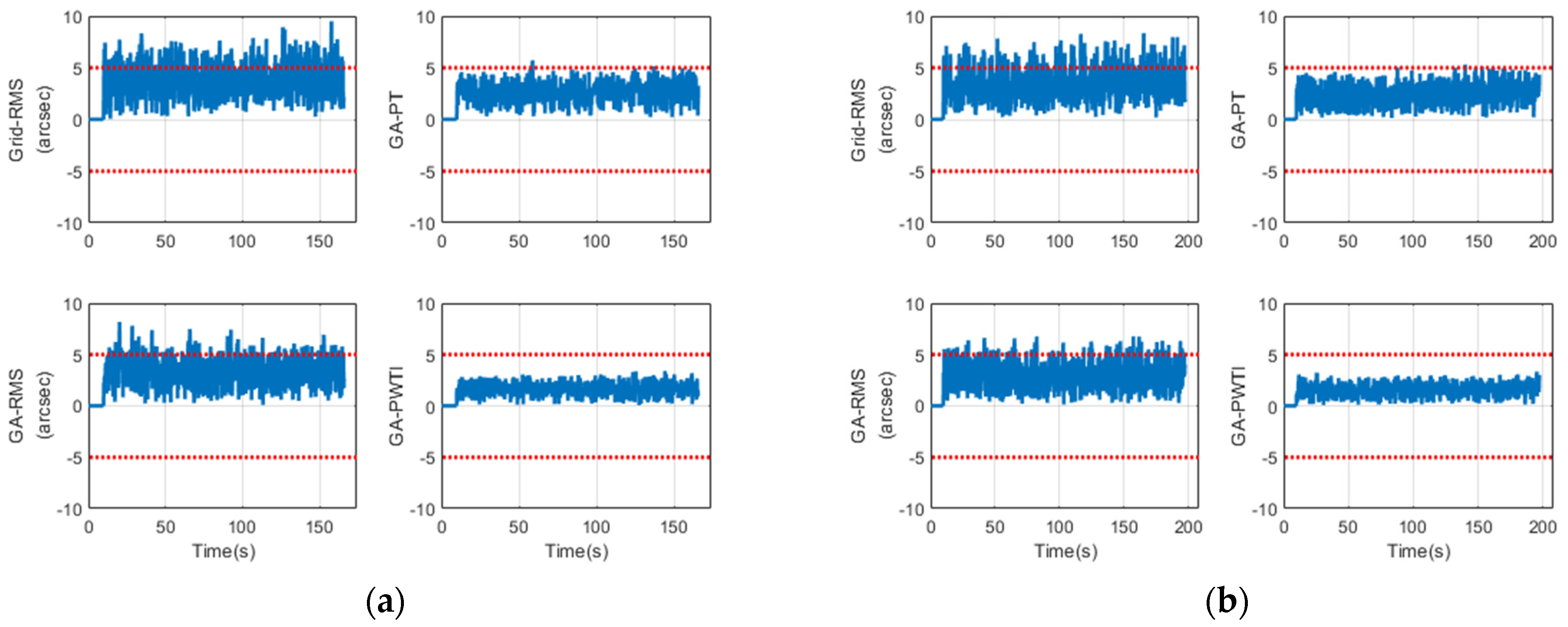
4.3. Visual Analysis of Tracking Behavior
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Az | Azimuth |
| El | Elevation |
| FOV | Field of view |
| GA | Genetic algorithm |
| GA-PT | Genetic-algorithm tuning using the PT objective |
| GA-PWTI | Genetic-algorithm tuning using the PWTI objective |
| GA-RMS | Genetic-algorithm tuning using the RMS objective |
| IOD | Initial orbit determination |
| LEO | Low Earth orbit |
| PID | Proportional–integral–derivative |
| PT | Persistence time |
| PWTI | Persistence-Weighted Tracking Index |
| RMS | Root-mean-square |
References
- Hyun, C.; Kim, D.; Kim, H.; Park, S. Improving Optical Tracking Performance for Space Objects Using PID-based Offset Compensation. J. Korean Inst. Inf. Commun. Eng. 2024, 28, 927–934. [Google Scholar] [CrossRef]
- Hyun, C.; Kim, D.; Kim, H.; Park, S. Genetic Algorithm-Based Proportional, Integral, Derivative (PID) Gain Optimization in an Offset-Compensated Optical Tracking System. J. Space Technol. Appl. 2025, 5, 102–113. [Google Scholar] [CrossRef]
- Hyun, C.; Kim, D.; Kim, H.; Park, S. PID Gain Optimization Using Genetic Algorithm Based on Tracking Persistence for Optical Tracking of Unknown Space Objects. J. Aerosp. Syst. Eng. 2025, 19, 92–98. [Google Scholar]
- Zhang, Z.; Zhang, G.; Cao, J.; Li, C.; Chen, W.; Ning, X.; Wang, Z. Overview on Space-Based Optical Orbit Determination Method Employed for Space Situational Awareness: From Theory to Application. Photonics 2024, 11, 610. [Google Scholar] [CrossRef]
- Kazemi, S.; Azad, N.L.; Scott, K.A.; Oqab, H.B.; Dietrich, G.B. Orbit determination for space situational awareness: A survey. Acta Astronaut. 2024, 222, 272–295. [Google Scholar] [CrossRef]
- Coder, R.D.; Holzinger, M.J. Multi-objective design of optical systems for space situational awareness. Acta Astronaut. 2016, 128, 669–684. [Google Scholar] [CrossRef]
- Zimmer, P.; McGraw, J.T.; Ackermann, M.R. Real-Time Optical Space Situational Awareness of Low-Earth Orbit with Small Telescopes. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference (AMOS), Maui, HI, USA, 11–14 September 2018; Available online: https://amostech.com/TechnicalPapers/2018/Poster/Zimmer.pdf (accessed on 20 October 2025).
- Shaddix, J.; Key, C.; Ferris, A.; Herring, J.; Singh, N.; Brost, T.; Aristoff, J. Daytime Optical Contributions Toward Timely Space Domain Awareness in Low Earth Orbit. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference (AMOS), Maui, HI, USA, 13–17 September 2021; Available online: https://amostech.com/TechnicalPapers/2021/SSA-SDA/Shaddix.pdf (accessed on 20 October 2025).
- Hickson, P. A fast algorithm for the detection of faint orbital debris tracks in optical images. Adv. Space Res. 2018, 62, 3078–3085. [Google Scholar] [CrossRef]
- Hampf, D.; Wagner, P.; Riede, W. Optical Technologies for Observation of Low Earth Orbit Objects. In Proceedings of the 65th International Astronautical Congress (IAC), Toronto, ON, Canada, 29 September–3 October 2014; Available online: https://www.researchgate.net/publication/271387832 (accessed on 7 August 2025).
- Bahcivan, H.; Brady, D. Space-Time Projection Optical Tomography: Search Space and Orbit Determination. arXiv 2022, arXiv:2211.13040. [Google Scholar] [CrossRef]
- Das, S.; Pan, I.; Das, S.; Gupta, A. Genetic Algorithm Based Improved Sub Optimal Model Reduction in Nyquist Plane for Optimal Tuning Rule Extraction of PID and PIλDμ Controllers via Genetic Programming. arXiv 2012, arXiv:1202.5686. [Google Scholar] [CrossRef]
- Mirzal, A.; Yoshii, S.; Furukawa, M. PID Parameters Optimization by Using Genetic Algorithm. arXiv 2012, arXiv:1204.0885. [Google Scholar] [CrossRef]
- Ortatepe, Z. Genetic Algorithm based PID Tuning Software Design and Implementation for a DC Motor Control System. Gazi Univ. J. Sci. Part A Eng. Innov. 2023, 10, 286–300. [Google Scholar] [CrossRef]
- Mahfoud, S.; Derouich, A.; EL Ouanjli, N.; EL Mahfoud, M.; Taoussi, M. A New Strategy-Based PID Controller Optimized by Genetic Algorithm for DTC of the Doubly Fed Induction Motor. Systems 2021, 9, 37. [Google Scholar] [CrossRef]
- Rodríguez-Abreo, O.; Garcia-Guendulain, J.M.; Hernández-Alvarado, R.; Rangel, A.F.; Fuentes-Silva, C. Genetic Algorithm-Based Tuning of Backstepping Controller for a Quadrotor-Type Unmanned Aerial Vehicle. Electronics 2020, 9, 1735. [Google Scholar] [CrossRef]
- Yao, J.; Luo, X.; Li, F.; Li, J.; Dou, J.; Luo, H. Research on hybrid strategy Particle Swarm Optimization algorithm and its applications. Sci. Rep. 2024, 14, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Parque, V.; Khalifa, A. PID Tuning Using Differential Evolution With Success-Based Particle Adaptations. IEEE Access 2023, 11, 136219–136268. [Google Scholar] [CrossRef]
- Guilmeau, T.; Chouzenoux, É.; Elvira, V. Simulated Annealing: A Review and a New Scheme. In Proceedings of the IEEE Statistical Signal Processing Workshop (SSP), Rio de Janeiro, Brazil, 12–14 July 2021; pp. 101–105. [Google Scholar] [CrossRef]
- Gong, C.; Yang, Y.; Yuan, L.; Wang, J. An improved ant colony algorithm for integrating global path planning and local obstacle avoidance for mobile robot in dynamic environment. Math. Biosci. Eng. 2022, 19, 12405–12426. [Google Scholar] [CrossRef] [PubMed]
- Van ’t Veld, R.; Van Kampen, E.-J.; Chu, Q.P. Stability and Robustness Analysis and Improvements for Incremental Nonlinear Dynamic Inversion Control. In Proceedings of the AIAA SciTech Forum 2018, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- González-García, J.; Narcizo-Nuci, N.A.; García-Valdovinos, L.G.; Salgado-Jiménez, T.; Gómez-Espinosa, A.; Cuan-Urquizo, E.; Cabello, J.A.E. Model-Free High Order Sliding Mode Control with Finite-Time Tracking for Unmanned Underwater Vehicles. Appl. Sci. 2021, 11, 1836. [Google Scholar] [CrossRef]
- Čehovin, L.; Leonardis, A.; Kristan, M. Visual Object Tracking Performance Measures Revisited. IEEE Trans. Image Process. 2016, 25, 1261–1274. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Zhu, F.; Zeng, Z.; Qiu, X.; Shen, Y.; Wu, J. SQE: A Self Quality Evaluation Metric for Parameters Optimization in Multi-Object Tracking. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 8303–8311. [Google Scholar]
- Bernardin, K.; Stiefelhagen, R. Evaluating Multiple Object Tracking Performance: The CLEAR MOT Metrics. EURASIP J. Image Video Process. 2008, 2008, 1–10. [Google Scholar] [CrossRef]
- Ristani, E.; Solera, F.; Zou, R.; Cucchiara, R.; Tomasi, C. Performance Measures and a Data Set for Multi-Target, Multi-Camera Tracking. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Amsterdam, The Netherlands, 8–10 October 2016; pp. 17–35. [Google Scholar] [CrossRef]
- Luiten, J.; Ošep, A.; Dendorfer, P.; Torr, P.; Geiger, A.; Leal-Taixé, L.; Leibe, B. HOTA: A Higher Order Metric for Evaluating Multi-object Tracking. Int. J. Comput. Vis. 2020, 129, 548–578. [Google Scholar] [CrossRef] [PubMed]



| Parameter | Value |
|---|---|
| Population size | 30 |
| Maximum generations | 50 |
| Crossover rate | 0.8 |
| Mutation rate | 0.1 |
| Evaluation method | Depends on PI (RMS/PT/PWTI) |
| Search range Kp | [0.9–2.0] |
| Search range Ki | [0.9–2.0] |
| Search range Kd | [0.00–0.06] |
| Case | Condition | RMS [arcsec] | |||
|---|---|---|---|---|---|
| Grid-RMS | GA-RMS | GA-PT | GA-PWTI | ||
| Traj-01 | Nominal | 4.2914 | 3.8987 | 3.0638 | 1.991 |
| Traj-02 | Nominal | 4.2936 | 3.8928 | 3.0746 | 1.9974 |
| Traj-03 | Nominal | 4.204 | 3.8279 | 3.007 | 1.9486 |
| Traj-04 | Nominal | 4.2758 | 3.9049 | 3.0596 | 1.9873 |
| Traj-05 | Nominal | 4.2929 | 3.9002 | 3.0604 | 1.9872 |
| Traj-06 | Nominal | 4.3211 | 3.9168 | 3.0811 | 2.0015 |
| Traj-07 | Nominal | 4.2901 | 3.8985 | 3.0522 | 1.9836 |
| Traj-08 | Nominal | 4.3109 | 3.9228 | 3.0807 | 2.0003 |
| Traj-09 | Harsh | 4.3198 | 3.9201 | 3.0882 | 2.0116 |
| Traj-10 | Harsh | 4.4087 | 4.0277 | 3.301 | 2.6353 |
| Traj-11 | Harsh * | 5.9122 | 5.8314 | 6.1831 | 8.1468 |
| Case | Condition | PT [s] | |||
|---|---|---|---|---|---|
| Grid-RMS | GA-RMS | GA-PT | GA-PWTI | ||
| Traj-01 | Nominal | 3.562 | 5.4 | 30.814 | 161.8 |
| Traj-02 | Nominal | 3.584 | 5.354 | 29.142 | 165.4 |
| Traj-03 | Nominal | 3.256 | 4.972 | 28.534 | 98.8 |
| Traj-04 | Nominal | 3.732 | 5.392 | 30.516 | 151.2 |
| Traj-05 | Nominal | 3.624 | 5.32 | 30.306 | 156 |
| Traj-06 | Nominal | 3.782 | 5.49 | 33.988 | 199.8 |
| Traj-07 | Nominal | 3.662 | 5.514 | 28.198 | 146.4 |
| Traj-08 | Nominal | 3.538 | 5.564 | 33.208 | 187.4 |
| Traj-09 | Harsh | 3.842 | 5.42 | 31.944 | 203.2 |
| Traj-10 | Harsh | 3.802 | 5.53 | 28.808 | 131.96 |
| Traj-11 | Harsh * | 3.394 | 4.78 | 23.478 | 86.44 |
| Case | Condition | PWTI | |||
|---|---|---|---|---|---|
| Grid-RMS | GA-RMS | GA-PT | GA-PWTI | ||
| Traj-01 | Nominal | 130.96 | 200.73 | 1175.01 | 6943.48 |
| Traj-02 | Nominal | 132.45 | 199.74 | 1109.55 | 7092.95 |
| Traj-03 | Nominal | 119.77 | 185.03 | 1086.37 | 4241.09 |
| Traj-04 | Nominal | 137.01 | 201.16 | 1162.18 | 6489.04 |
| Traj-05 | Nominal | 134 | 198.51 | 1151.45 | 6696.6 |
| Traj-06 | Nominal | 140.2 | 205.67 | 1293.43 | 8576.29 |
| Traj-07 | Nominal | 135.14 | 205.46 | 1074.02 | 6285.71 |
| Traj-08 | Nominal | 130.37 | 207.36 | 1263.11 | 8045.51 |
| Traj-09 | Harsh | 141.28 | 202.02 | 1214.53 | 8718.98 |
| Traj-10 | Harsh | 140.3 | 205.15 | 1098.08 | 5627.41 |
| Traj-11 | Harsh * | 125.72 | 177.74 | 893.73 | 3670.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hyun, C.; Kim, D.; Kim, H.; Park, S. Persistence-Weighted Performance Metric for PID Gain Optimization in Optical Tracking of Unknown Space Objects. Sensors 2025, 25, 6659. https://doi.org/10.3390/s25216659
Hyun C, Kim D, Kim H, Park S. Persistence-Weighted Performance Metric for PID Gain Optimization in Optical Tracking of Unknown Space Objects. Sensors. 2025; 25(21):6659. https://doi.org/10.3390/s25216659
Chicago/Turabian StyleHyun, Chul, Donggeon Kim, Hyunseung Kim, and Seungwook Park. 2025. "Persistence-Weighted Performance Metric for PID Gain Optimization in Optical Tracking of Unknown Space Objects" Sensors 25, no. 21: 6659. https://doi.org/10.3390/s25216659
APA StyleHyun, C., Kim, D., Kim, H., & Park, S. (2025). Persistence-Weighted Performance Metric for PID Gain Optimization in Optical Tracking of Unknown Space Objects. Sensors, 25(21), 6659. https://doi.org/10.3390/s25216659





