Bi-Directional Fabry–Perot Cavity Antenna Based on Polarization-Dependent Transmit–Reflect Metasurface
Abstract
1. Introduction
2. Design Principle
3. Bi-Directional PFC Metasurface Antenna Design
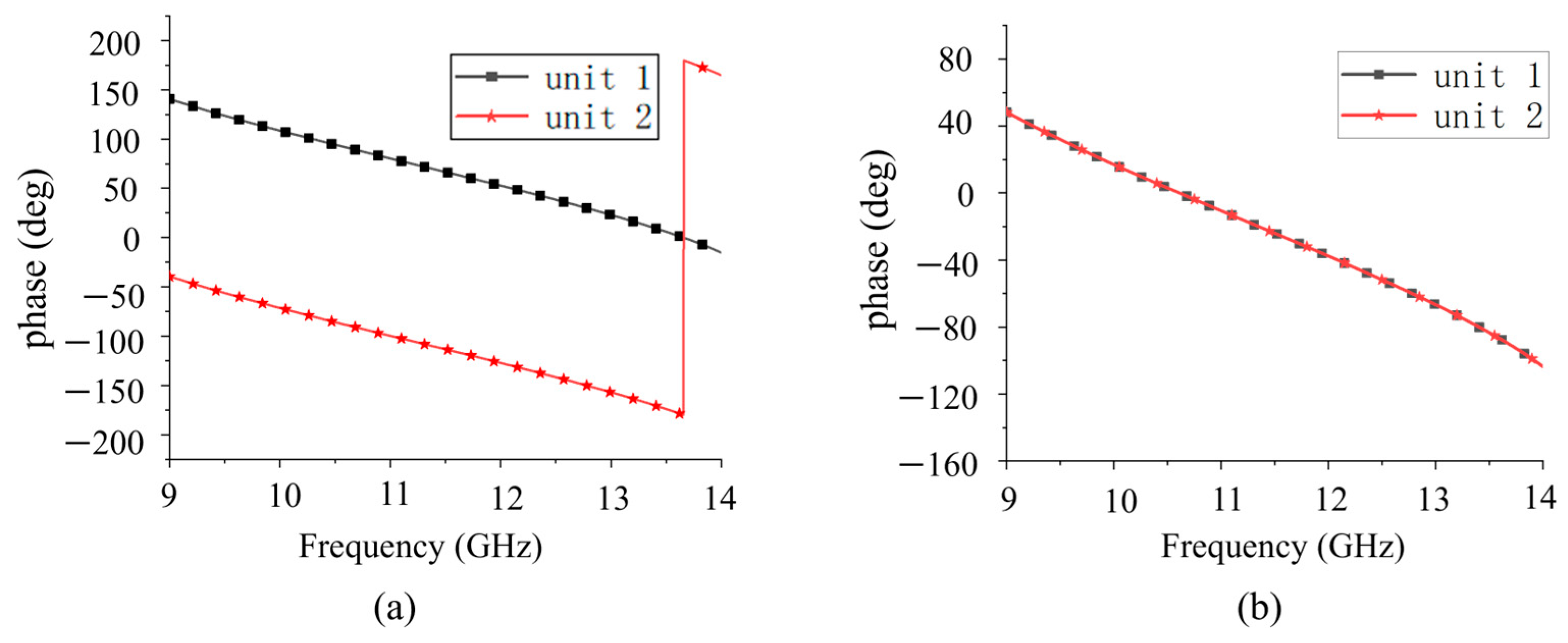
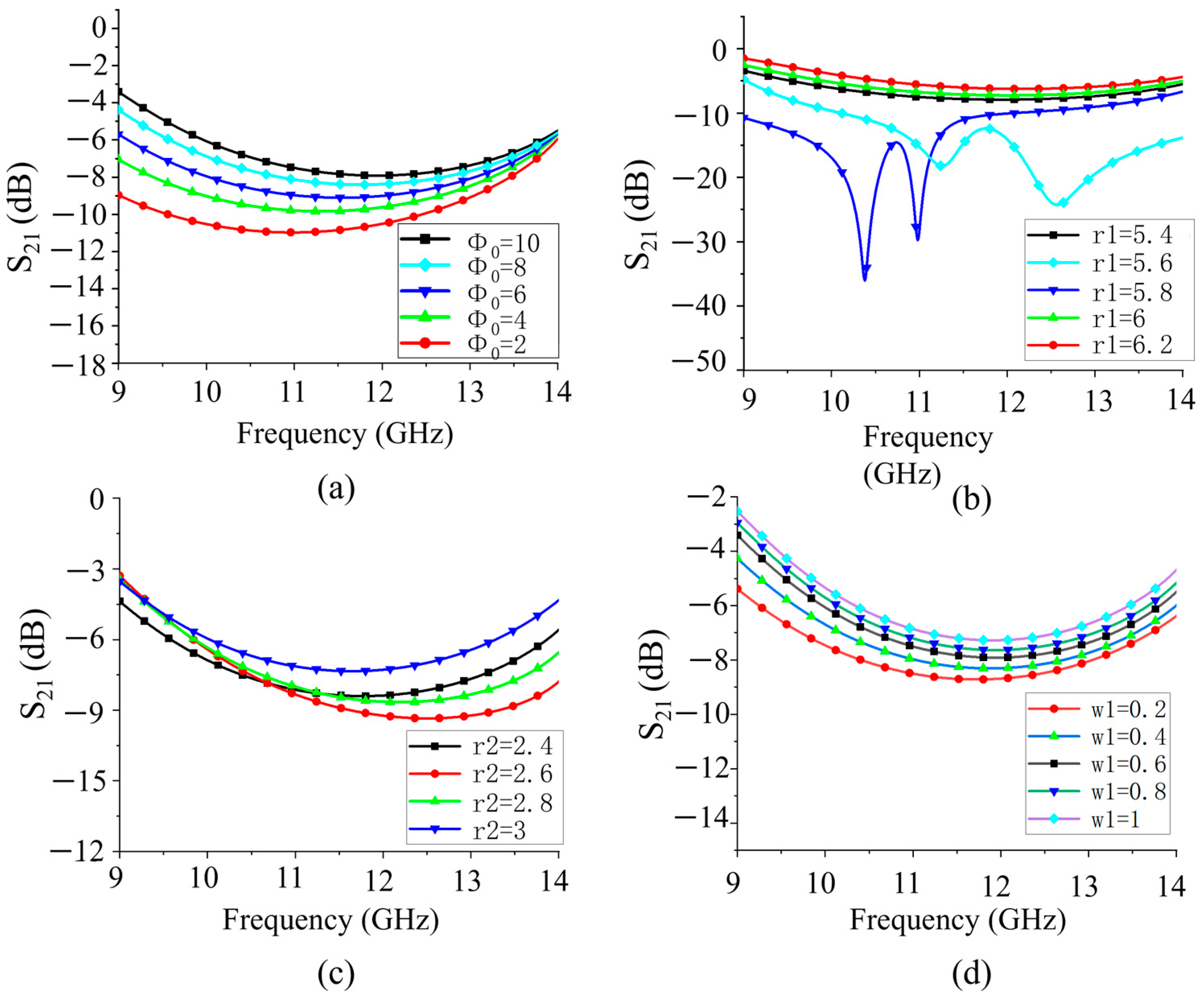
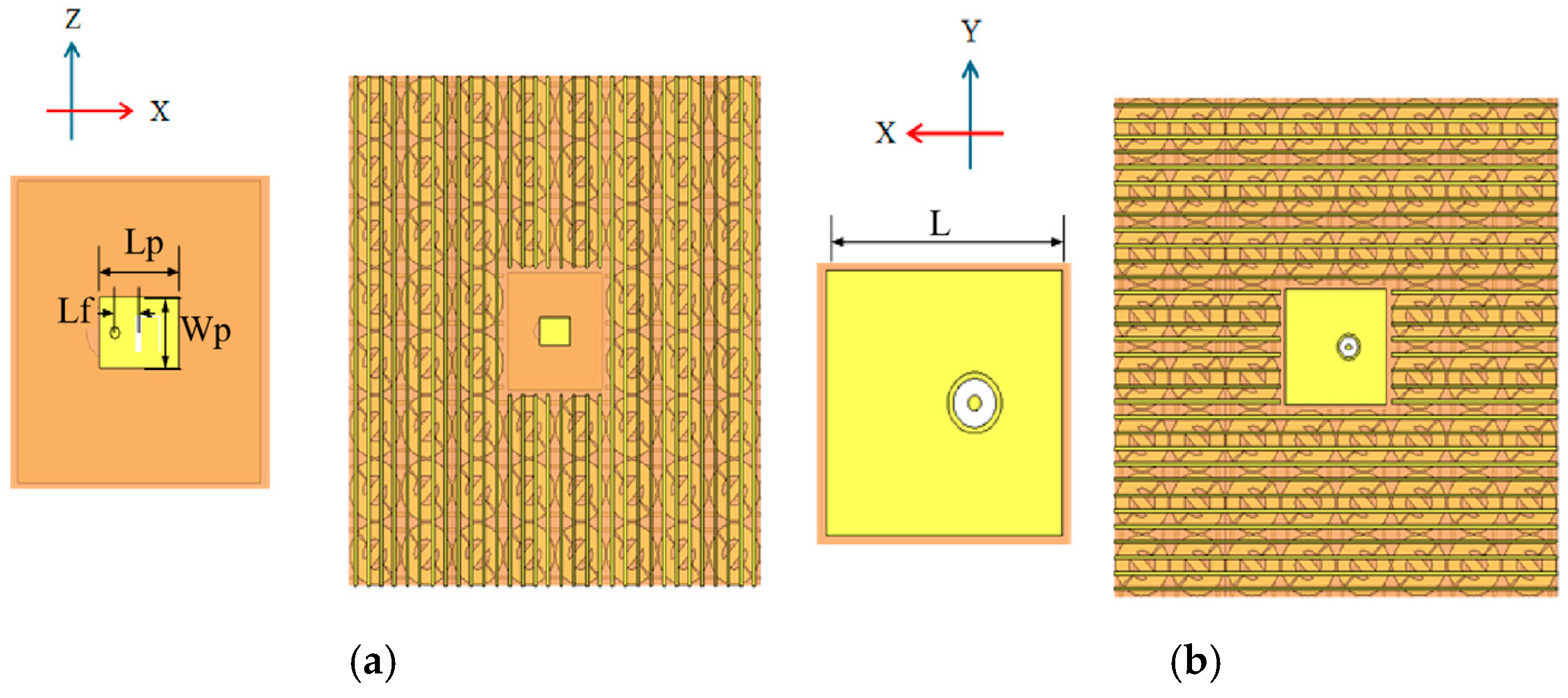
3.1. Unit Design
3.2. Feeding Antenna Design
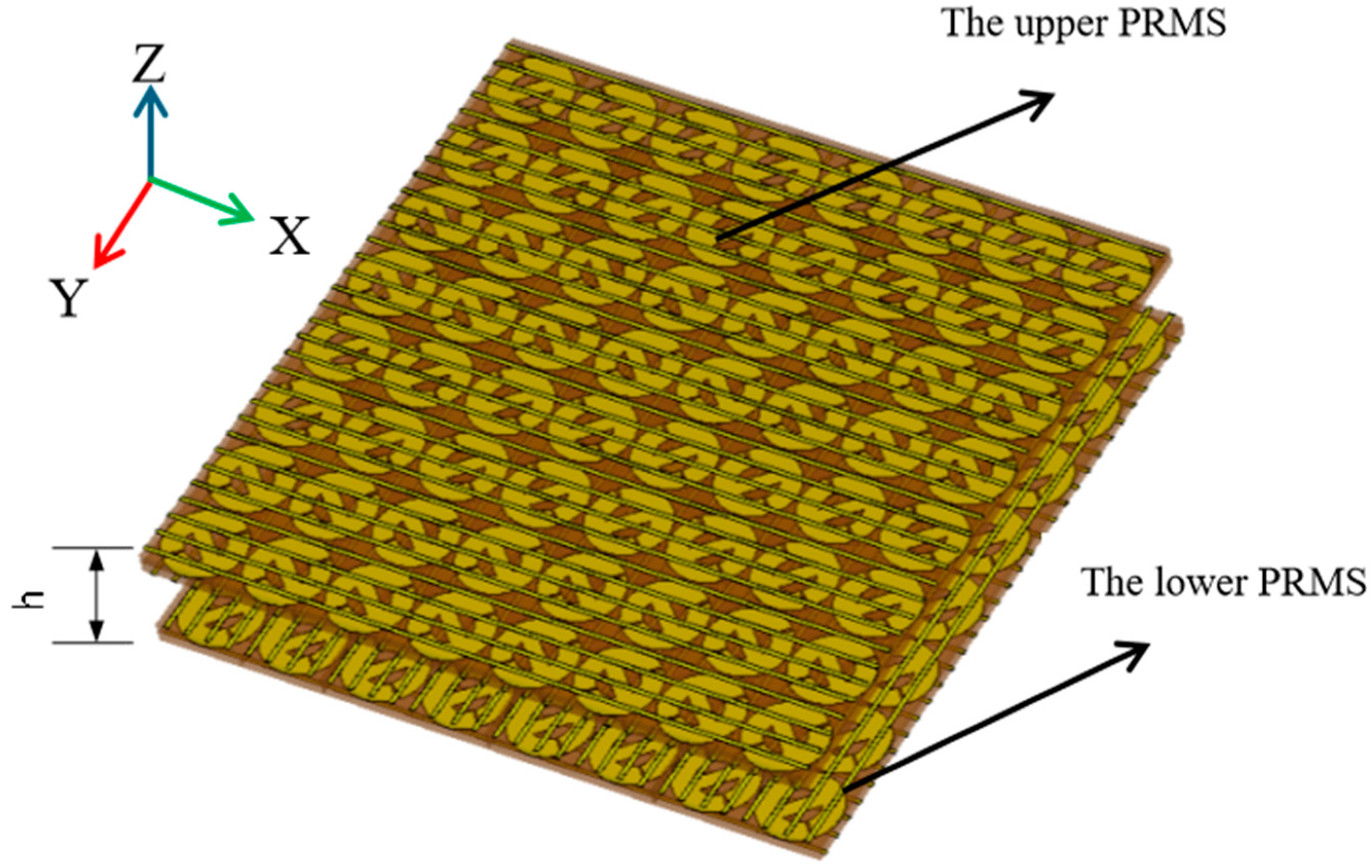
3.3. Design of the Bi-Directional FPC Metasurface Antenna
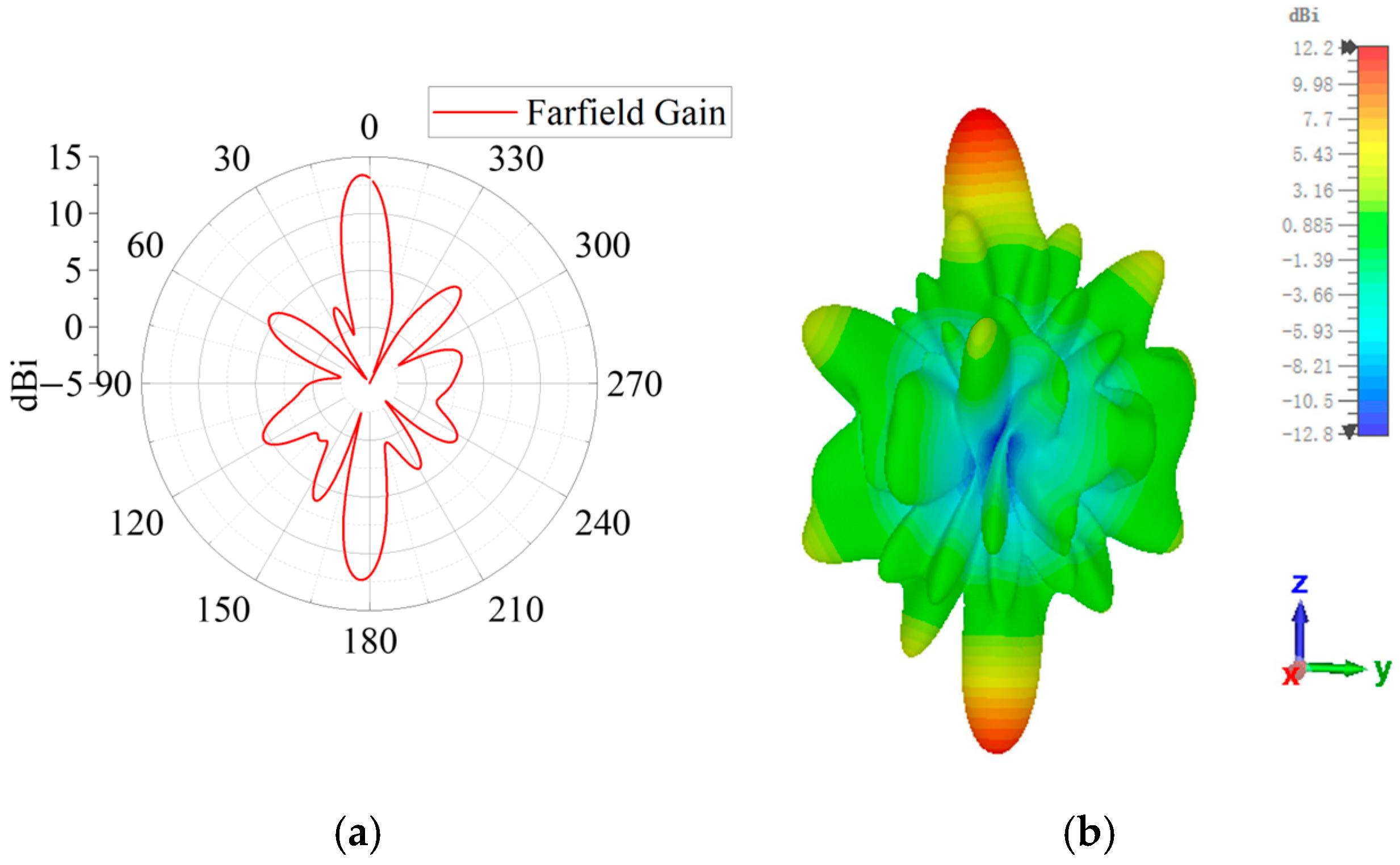
3.3.1. Antenna 1 with Dual-Beam Radiation
3.3.2. Antenna 2 with Tri-Beam Radiation
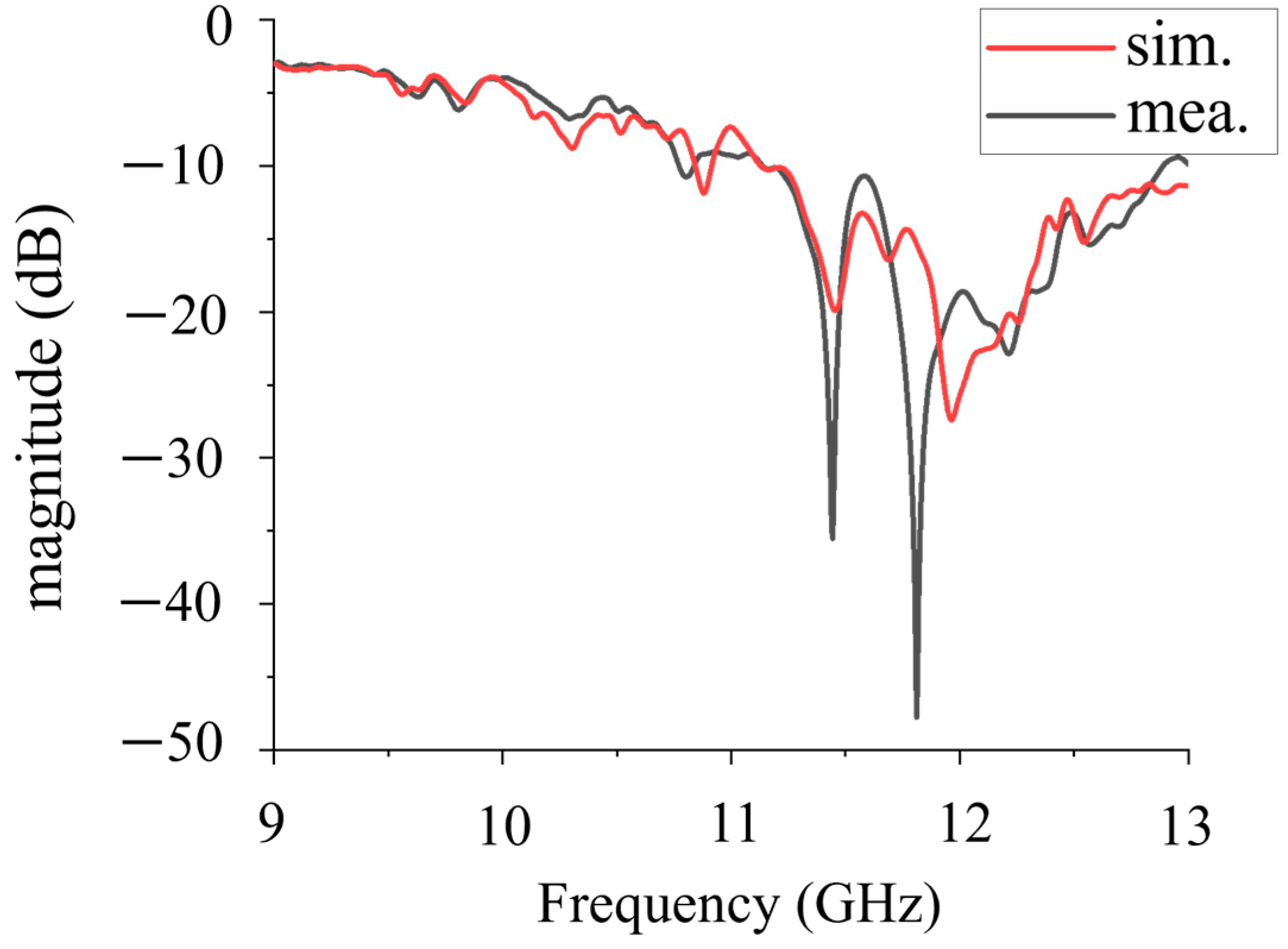
4. Fabrication and Measurement
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ghosh, A.; Thomas, T.A.; Cudak, M.C.; Ratasuk, R.; Moorut, P.; Vook, F.W.; Rappaport, T.S.; MacCartney, G.R.; Sun, S.; Nie, S. Millimeter-Wave Enhanced Local Area Systems: A High-Data-Rate Approach for Future Wireless Networks. IEEE J. Sel. Areas Commun. 2014, 32, 1152–1163. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Xing, Y.; MacCartney, G.R.; Molisch, A.F.; Mellios, E.; Zhang, J. Overview of Millimeter Wave Communications for Fifth-Generation (5G) Wireless Networks—With a Focus on Propagation Models. IEEE Trans. Antennas Propagat. 2017, 65, 6213–6230. [Google Scholar] [CrossRef]
- Li, L.; Liao, S.; Che, W.; Xue, Q. Integrated Antenna with Distributed Architecture Using the Same Basic Structure for Millimeter-Wave Applications. IEEE Trans. Antennas Propagat. 2023, 71, 9962–9967. [Google Scholar] [CrossRef]
- Guo, Q.-Y.; Wong, H. Wideband and High-Gain Fabry-Pérot Cavity Antenna with Switched Beams for Millimeter-Wave Applications. IEEE Trans. Antennas Propagat. 2019, 67, 4339–4347. [Google Scholar] [CrossRef]
- Guo, Q.-Y.; Lin, Q.W.; Wong, H. A High Gain Millimeter-Wave Circularly Polarized Fabry–Pérot Antenna Using PRS-Integrated Polarizer. IEEE Trans. Antennas Propagat. 2021, 69, 1179–1183. [Google Scholar] [CrossRef]
- Guo, Q.-Y.; Wong, H. 155 GHz Dual-Polarized Fabry-Perot Cavity Antenna Using LTCC-Based Feeding Source and Phase-Shifting Surface. IEEE Trans. Antennas Propagat. 2021, 69, 2347–2352. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, Z.; Tian, Z.; Feng, Z. A Bi-directional High-Gain Cascaded Ring Antenna for Communication in Coal Mine. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 761–764. [Google Scholar] [CrossRef]
- Wu, J.; Lian, R.; Wang, Z.; Yin, Y. Strip-Coupling Circularly Polarized Antenna and Its Same-Sense Bi-directional Array. J. Electromagn. Waves Appl. 2015, 29, 1859–1866. [Google Scholar] [CrossRef]
- Xu, H.-X.; Tang, S.; Wang, G.-M.; Cai, T.; Huang, W.; He, Q.; Sun, S.; Zhou, L. Multifunctional Microstrip Array Combining a Linear Polarizer and Focusing Metasurface. IEEE Trans. Antennas Propagat. 2016, 64, 3676–3682. [Google Scholar] [CrossRef]
- Rohani, B.; Takahashi, K.; Arai, H.; Kimura, Y.; Ihara, T. Improving Channel Capacity in Indoor 4\times 4 MIMO Base Station Utilizing Small Bi-directional Antenna. IEEE Trans. Antennas Propagat. 2018, 66, 393–400. [Google Scholar] [CrossRef]
- Jackson, B.R.; Boyes, S.J. Radiation Pattern-Agile Dual Planar Inverted-F Antenna. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2090–2093. [Google Scholar] [CrossRef]
- Rajender, R.; Choudhury, S.; Subhashini, K.R.; Ciarpi, G.; Genovesi, S.; Rossi, D. Design of Linear and Planar Arrays with Low Sidelobe Levels and High Directivity Using Two-Way Array Factor. IEEE Trans. Antennas Propagat. 2024, 72, 4150–4160. [Google Scholar] [CrossRef]
- Yi, X.; Su, T.; Li, X.; Wu, B.; Yang, L. A Double-Layer Wideband Transmitarray Antenna Using Two Degrees of Freedom Elements Around 20 GHz. IEEE Trans. Antennas Propagat. 2019, 67, 2798–2802. [Google Scholar] [CrossRef]
- Zhu, J.; Yang, Y.; Liao, S.; Xue, Q. Dual-Band Antenna Hybridizing Folded Transmitarray and Folded Reflectarray. IEEE Trans. Antennas Propagat. 2022, 70, 3070–3075. [Google Scholar] [CrossRef]
- Zhong, X.; Xu, H.-X.; Chen, L.; Li, W.; Wang, H.; Shi, X. An FSS-Backed Broadband Phase-Shifting Surface Array with Multimode Operation. IEEE Trans. Antennas Propagat. 2019, 67, 5974–5981. [Google Scholar] [CrossRef]
- Yang, S.; Yan, Z.; Zhang, T.; Cai, M.; Fan, F.; Li, X. Multifunctional Tri-Band Dual-Polarized Antenna Combining Transmitarray and Reflectarray. IEEE Trans. Antennas Propagat. 2021, 69, 6016–6021. [Google Scholar] [CrossRef]
- Yang, F.; Deng, R.; Xu, S.; Li, M. Design and Experiment of a Near-Zero-Thickness High-Gain Transmit-Reflect-Array Antenna Using Anisotropic Metasurface. IEEE Trans. Antennas Propagat. 2018, 66, 2853–2861. [Google Scholar] [CrossRef]
- Wang, M.; Xu, S.; Yang, F.; Li, M. A 1-Bit Bi-directional Reconfigurable Transmit-Reflect-Array Using a Single-Layer Slot Element with PIN Diodes. IEEE Trans. Antennas Propagat. 2019, 67, 6205–6210. [Google Scholar] [CrossRef]
- Ding, G.; Chen, K.; Jiang, T.; Sima, B.; Zhao, J.; Feng, Y. Full Control of Conical Beam Carrying Orbital Angular Momentum by Reflective Metasurface. Opt. Express 2018, 26, 20990–21002. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Chen, K.; Zhao, J.; Jiang, T.; Feng, Y. A Wideband High-Efficiency Transmit-Reflect-Array Antenna for Bi-directional Radiations with Distinct Circular Polarizations Based on a Metasurface. IEEE Trans. Antennas Propagat. 2023, 71, 3695–3700. [Google Scholar] [CrossRef]
- Yue, H.; Chen, L.; Yang, Y.; He, L.; Shi, X. Design and Implementation of a Dual Frequency and Bi-directional Phase Gradient Metasurface for Beam Convergence. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 54–58. [Google Scholar] [CrossRef]
- Wu, J.L.; Pan, Y.M.; Zheng, S.Y. Design of Single-Layer Polarization-Dependent Transmissive and Reflective Focusing Metasurface. IEEE Trans. Antennas Propagat. 2021, 69, 7637–7646. [Google Scholar] [CrossRef]
- Hussain, N.; Jeong, M.-J.; Park, J.; Kim, N. A Broadband Circularly Polarized Fabry-Perot Resonant Antenna Using A Single-Layered PRS for 5G MIMO Applications. IEEE Access 2019, 7, 42897–42907. [Google Scholar] [CrossRef]
- Chang, Z.; Luo, Z.; Cao, S.; Ouyang, K.; Ge, K.; Wan, Z. Narrow-Band Tunable Optical Filters Based on Cascaded Fabry-Perot Cavities. Opt. Express 2022, 30, 13864–13874. [Google Scholar] [CrossRef]
- Li, K.; Liu, Y.; Jia, Y.; Guo, Y.J. A Circularly Polarized High-Gain Antenna with Low RCS Over a Wideband Using Chessboard Polarization Conversion Metasurfaces. IEEE Trans. Antennas Propagat. 2017, 65, 4288–4292. [Google Scholar] [CrossRef]
- Xie, P.; Wang, G.; Li, H.; Gao, X. A Novel Methodology for Gain Enhancement of the Fabry-Pérot Antenna. IEEE Access 2019, 7, 176170–176176. [Google Scholar] [CrossRef]
- Guo, X.; Luo, Y.; Yan, N.; An, W.; Ma, K. Multibeam Transmit-Reflect-Array Antenna Using Alternating Transmission and Reflection Elements for Space–Air–Ground–Sea Integrated Network. IEEE Trans. Antennas Propag. 2023, 71, 8668–8676. [Google Scholar] [CrossRef]
- Sima, B.; Xu, Y.; Wang, X.; Li, H.; Cheng, G.; Wu, L.; Kang, W.; Wu, W. Design of a Low-Profile Bi-Directional Radiated Fabry-Perot Cavity Antenna with Independent Forward and Backward Radiation Based on Metasurface Technique. Opt. Express 2024, 32, 25818–25829. [Google Scholar] [CrossRef] [PubMed]
- Gao, R.; Yang, M.-Q.; Guo, Q.-Y.; He, W. A Low-Profile and High-Gain Antenna with Bi-directional Beams Enabled by Integrating Folded Transmitarray and Fabry–Perot Cavity. IEEE Trans. Antennas Propag. 2024, 72, 6209–6218. [Google Scholar] [CrossRef]








| Simulation | Measurement | |
|---|---|---|
| Forward radiation (right space) | −7.6 dB | −8.7 dB |
| Forward radiation (right space) | −8.3 dB | −9.7 dB |
| Backward radiation (right space) | −8.6 dB | −6.0 dB |
| Backward radiation (left space) | −6.5 dB | −5.8 dB |
| Ref. | Major Operating Frequency (GHz) | Profile Height (λ) | Peak Gain (dBi) | HPBW (°) | Beam Shape | Independent Control of Bi-Directional Radiation | Polarization State for Bi-Directional Radiation |
|---|---|---|---|---|---|---|---|
| [9] | 9.3 | >1.18 | 18.5 | 15 | Single beam | Yes | Orthogonal |
| [11] | 1.65–2.2 | 0.74 | 8 | / | Single beam | No | Same state |
| [14] | TA at 11; RA at 17 | 2.56 (11 GHz); 4 (17 GHz) | 21.3 (11 GHz); 23.8 (17 GHz) | 16.8 (11 GHz); 9.6 (17 GHz) | Single beam | Yes | Orthogonal |
| [27] | 30 | 4 | 17.9 | / | Multibeam | Yes | Same state |
| [28] | 10.4 | 0.81 | 8.6 | / | Multibeam | Yes | Same state |
| This work | 11.5 | 0.69 | 13.02 | 13.8 | Multibeam | Yes | Orthogonal |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Y.; Xi, Z.; Wang, T.; Liu, Q.; Zhang, S.; Sun, Z.; Sima, B.; Zeng, H. Bi-Directional Fabry–Perot Cavity Antenna Based on Polarization-Dependent Transmit–Reflect Metasurface. Sensors 2025, 25, 6642. https://doi.org/10.3390/s25216642
Ren Y, Xi Z, Wang T, Liu Q, Zhang S, Sun Z, Sima B, Zeng H. Bi-Directional Fabry–Perot Cavity Antenna Based on Polarization-Dependent Transmit–Reflect Metasurface. Sensors. 2025; 25(21):6642. https://doi.org/10.3390/s25216642
Chicago/Turabian StyleRen, Yanfei, Zhenghu Xi, Tao Wang, Qinqin Liu, Shunli Zhang, Zhiwei Sun, Boyu Sima, and Hao Zeng. 2025. "Bi-Directional Fabry–Perot Cavity Antenna Based on Polarization-Dependent Transmit–Reflect Metasurface" Sensors 25, no. 21: 6642. https://doi.org/10.3390/s25216642
APA StyleRen, Y., Xi, Z., Wang, T., Liu, Q., Zhang, S., Sun, Z., Sima, B., & Zeng, H. (2025). Bi-Directional Fabry–Perot Cavity Antenna Based on Polarization-Dependent Transmit–Reflect Metasurface. Sensors, 25(21), 6642. https://doi.org/10.3390/s25216642






