Microstructure Identification of Additive Manufactured Titanium Alloy by Using Lamb Wave-DenseNet Network
Abstract
1. Introduction
2. Principles
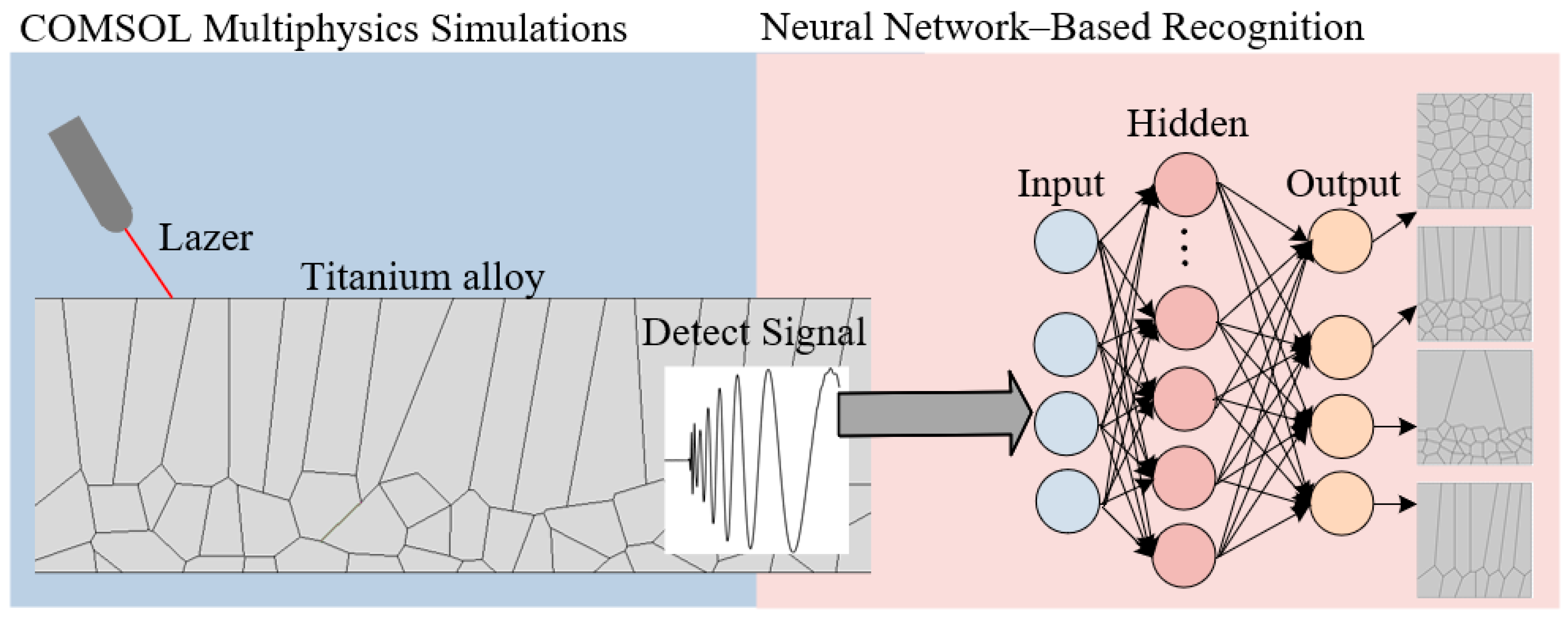
2.1. Principles of Simulation Model Establishment
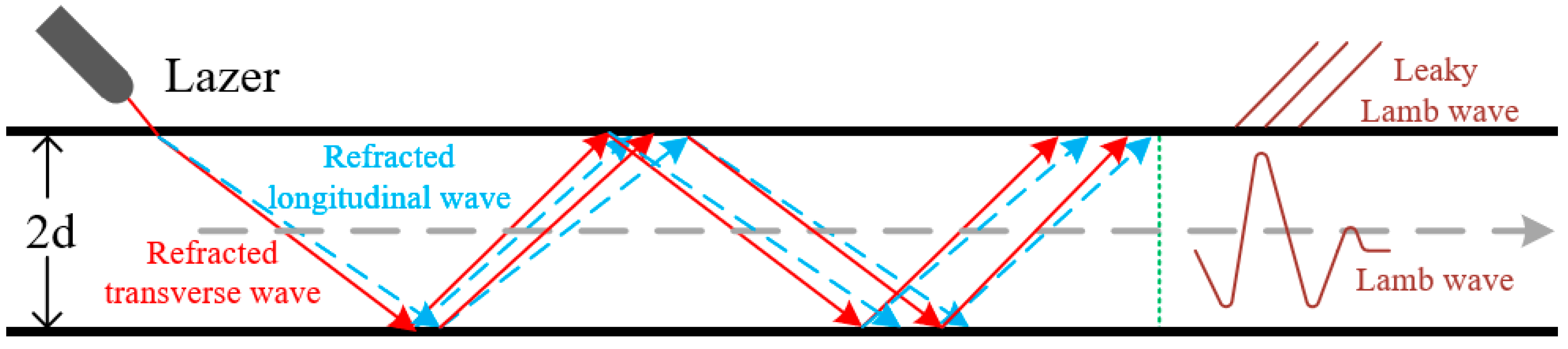
2.2. Principles of Laser-Induced Ultrasonic Lamb Waves Model
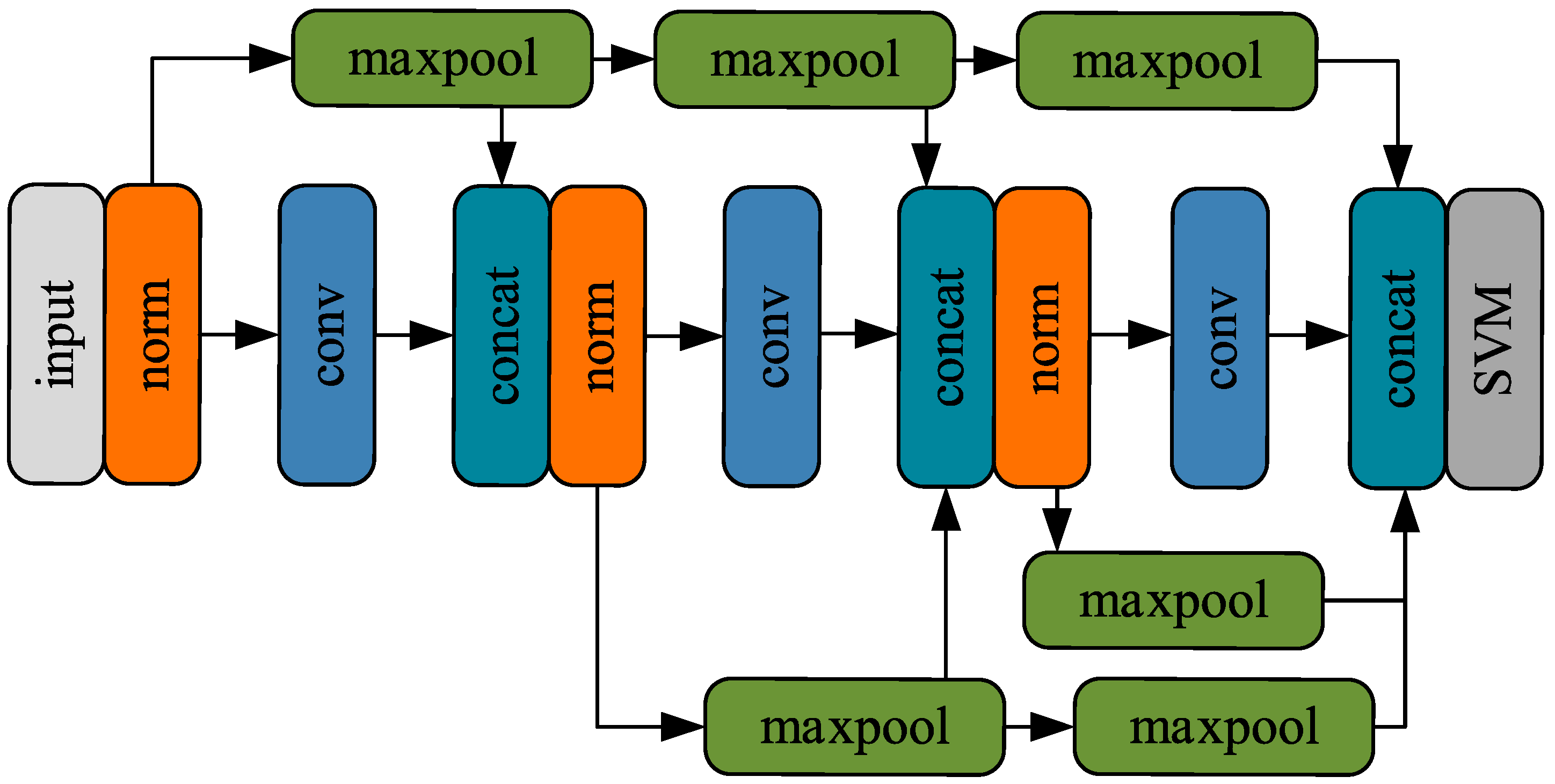
2.3. Neural Network Structure
3. Simulation Experimental System Setup
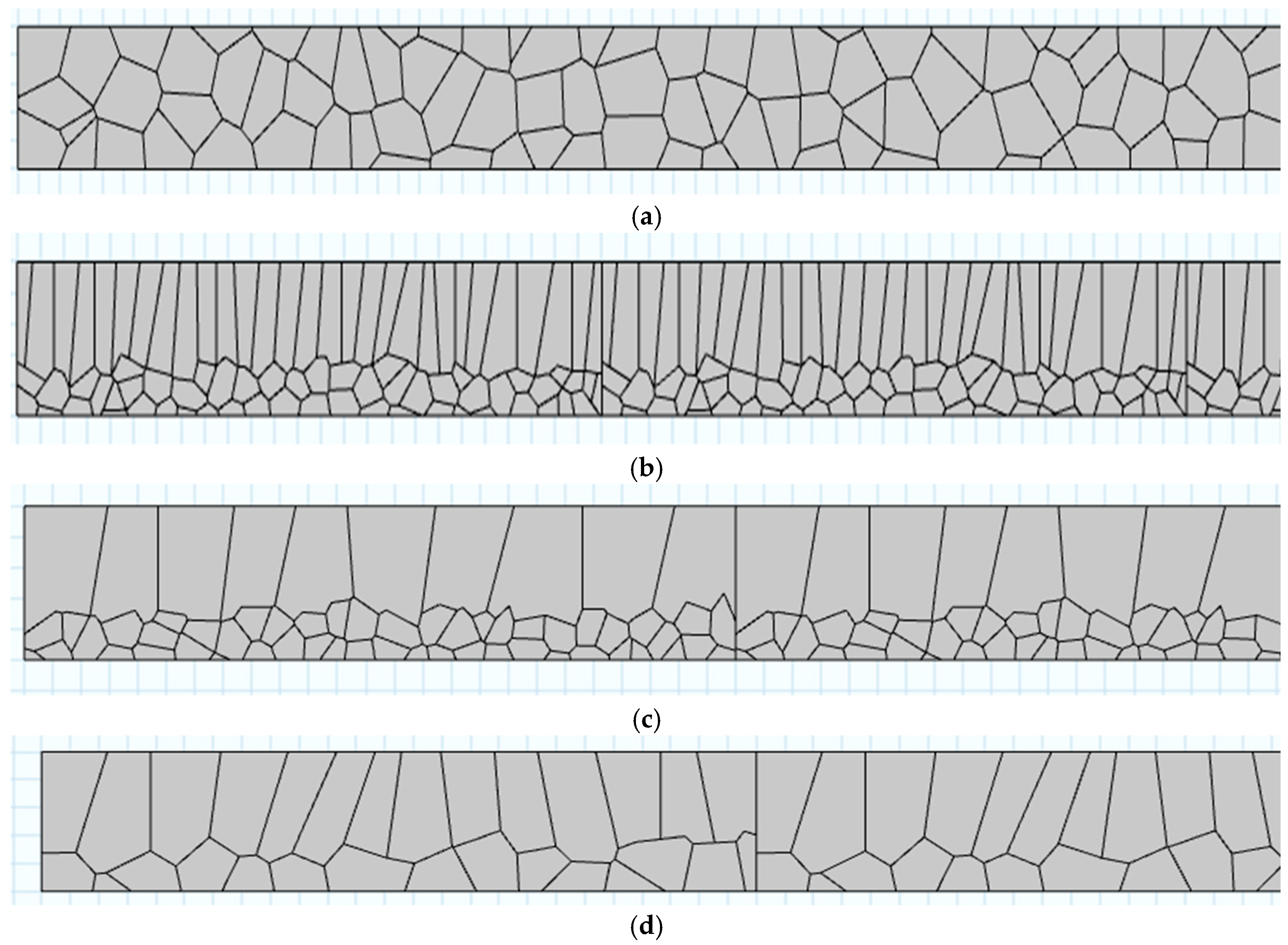
3.1. Establishment of the Ultrasonic Testing Simulation Model
3.2. Deep Learning Parameter Settings
4. Results and Analysis
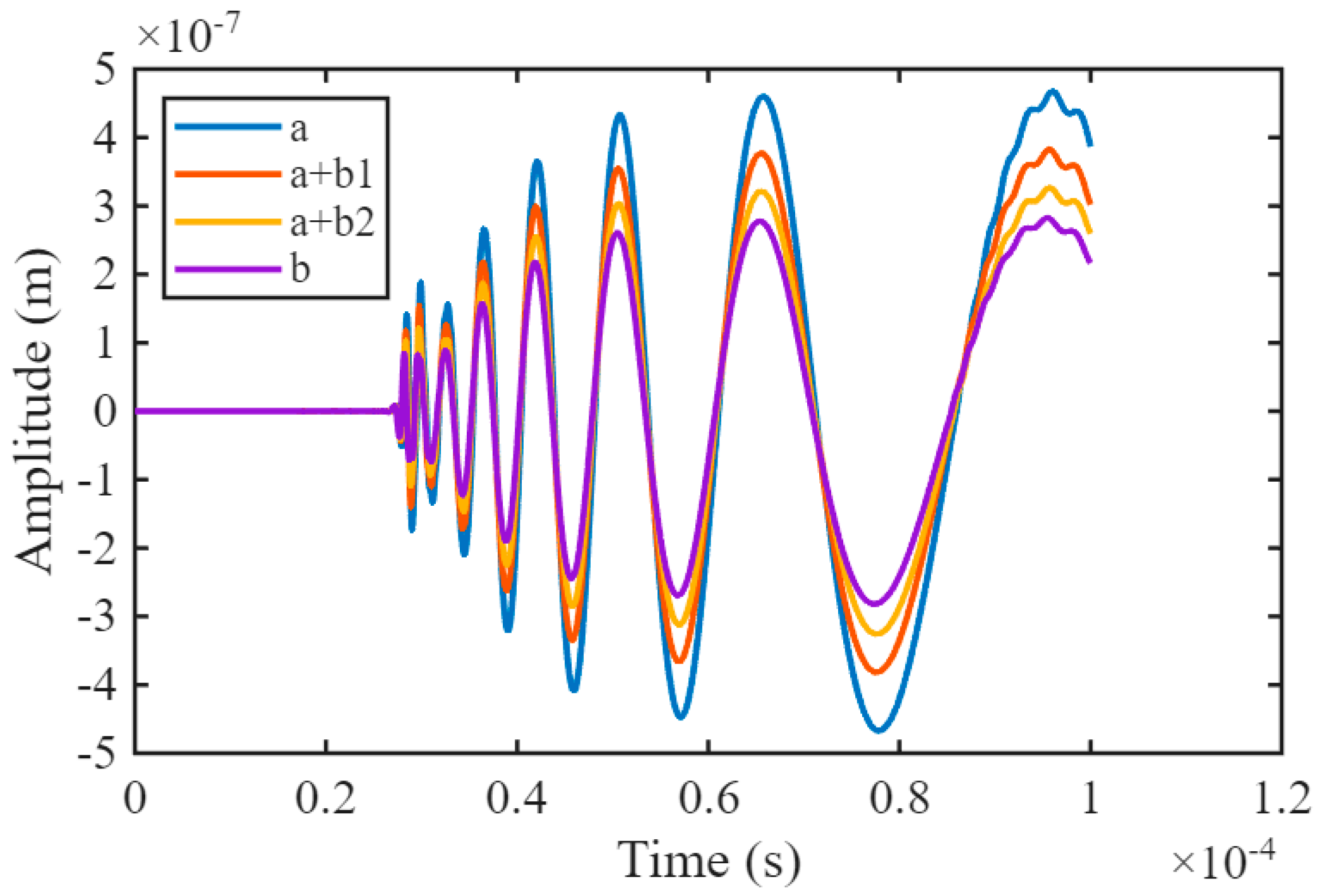
4.1. Analysis of Simulation Results of LIULW Detection
4.2. Analysis of Neural Network Classification Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AM | Additive manufacturing |
| CVT | Centroidal Voronoi Tessellations |
| LIULW | Laser-induced ultrasonic Lamb wave |
| NDT | Nondestructive testing |
| CNN | Convolutional Neural Network |
| SVM | Support Vector Machine |
| RBF | Radial Basis Function |
References
- Alexander, M.; Iosif, G.; Eugeniy, G.; Podrabinnik, P.; Kuznetsova, E.; Peretyagin, P.; Peretyagin, N. Properties of Journal Bearing Materials That Determine Their Wear Resistance on the Example of Aluminum-Based Alloys. Materials 2021, 14, 535. [Google Scholar] [CrossRef]
- Li, W.; Wang, S.; Yang, X.; Duan, H.; Wang, Y.; Yang, Z. Research Progress on Fatigue Damage and Surface Strengthening Technology of Titanium Alloys for Aerospace Applications. Metals 2025, 15, 192. [Google Scholar] [CrossRef]
- Wei, X.; Wang, Z.; Zhang, P.; Pang, M.; Liu, K.; Su, J. Environment-Friendly and Low Toxicity Polishing Solution Preparation and Performance Testing for Medical Titanium Alloy Materials. J. Mater. Eng. Perform. 2025, 34, 18997–19007. [Google Scholar] [CrossRef]
- Wang, S.; Wang, J.; Xu, Z.; Wang, J.; Li, R. Numerical Calculation of Overlapping Line Heating for Marine Titanium Alloy Curved Plate. Ocean Eng. 2024, 296, 117021. [Google Scholar] [CrossRef]
- Soltan Aboujaila, A.S.K.; Esen, İ.; Kara, S.A.; Ahlatçı, H. Examination of the Corrosion Behavior of Shape Memory NiTi Material for Biomedical Applications. Materials 2023, 16, 3951. [Google Scholar] [CrossRef]
- Nesterenkov, V.; Akhonin, S.; Klochkov, I.; Matviichuk, V.; Berezos, V.; Motrunich, S. High Cyclic Fatigue Behavior of 3D-Printed Titanium Alloy TA15. Weld World 2025, 69, 717–725. [Google Scholar] [CrossRef]
- Chong, Y.; Gholizadeh, R.; Tsuru, T.; Zhang, R.; Inoue, K.; Gao, W.; Godfrey, A.; Mitsuhara, M.; Morris, J.W., Jr.; Minor, A.M.; et al. Grain Refinement in Titanium Prevents Low Temperature Oxygen Embrittlement. Nat. Commun. 2023, 14, 404. [Google Scholar] [CrossRef]
- Fengal, M.; Mora, P.; Shokouhi, P.; Durand, O.; Dérobert, X.; Palma-Lopes, S.; Lehujeur, M.; Villain, G.; Gennesseaux, E.; Abraham, O. Coherent and Incoherent Rayleigh Wave Attenuation for Discriminating Microstructural Effects of Thermal Damage from Moisture Conditions in Concrete. NDT E Int. 2025, 156, 103473. [Google Scholar] [CrossRef]
- Xie, Y.; Li, J.; Tao, Y.; Wang, S.; Yin, W.; Xu, L. Edge Effect Analysis and Edge Defect Detection of Titanium Alloy Based on Eddy Current Testing. Appl. Sci. 2020, 10, 8796. [Google Scholar] [CrossRef]
- Ali, A.; Mohammed, S.; Essam, B.; Saleh, M.A.; Damoom, M.M.; Alhawsawi, A.M.; Al-Hada, N.M.; Alharbi, W.R.; Saeed, A. Radiographic Testing of 3D-Printed Thermoplastics Using Am-241 as a Gamma-Ray Source. Mater. Res. Express 2023, 10, 065302. [Google Scholar] [CrossRef]
- Vázquez, S.; Gosálbez, J.; Bosch, I.; Carrión, A.; Gallardo, C.; Payá, J. Comparative Study of Coupling Techniques in Lamb Wave Testing of Metallic and Cementitious Plates. Sensors 2019, 19, 4068. [Google Scholar] [CrossRef]
- Rieger, K.; Erni, D.; Rueter, D. Unidirectional Emission and Detection of Lamb Waves Based on a Powerful and Compact Coils-Only EMAT. NDT E Int. 2021, 122, 102492. [Google Scholar] [CrossRef]
- Zhou, Y.X. Research on Defect Detection Method of Aircraft Panel Based on Ultrasonic Lamb Waves. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2024. [Google Scholar] [CrossRef]
- Tan, D.G.; Zhou, J.X.; Wang, K.; Xu, D. Research on Nondestructive Testing Method for Defects in Additively Manufactured Plates Based on Secondary Waves. J. Dyn. Control 2022, 20, 68–77. [Google Scholar]
- Cantero-Chinchilla, S.; Wilcox, P.D.; Croxford, A.J. Deep Learning in Automated Ultrasonic NDE—Developments, Axioms and Opportunities. NDT E Int. 2022, 131, 102610. [Google Scholar] [CrossRef]
- Park, S.; Choi, S.; Jhang, K. Porosity Evaluation of Additively Manufactured Components Using Deep Learning-Based Ultrasonic Nondestructive Testing. Int. J. Precis. Eng. Manuf.-Green Technol. 2021, 9, 395–407. [Google Scholar] [CrossRef]
- Christian, Z.; Zhipeng, J.; Ryan, S.; Tian, Z.; Netchaev, A.; Dickerson, C.; Tian, W.; Bian, L. Deep Multi-Modal U-Net Fusion Methodology of Thermal and Ultrasonic Images for Porosity Detection in Additive Manufacturing. J. Manuf. Sci. Eng. 2023, 145, 061009. [Google Scholar]
- Yadav, A.; Prajapati, K.K.; Mitra, M. Deep Learning-Assisted Prediction of Mean Grain Size of Polycrystalline Materials from Ultrasonic Wave Response. Mech. Mater. 2025, 207, 105367. [Google Scholar] [CrossRef]
- Du, Q.; Gunzburger, M.; Ju, L.L. Advances in Studies and Applications of Centroidal Voronoi Tessellations. Numer. Math.-Theory Methods Appl. 2010, 3, 119–142. [Google Scholar]
- Liu, B.; Cheng, H.Q.; Liu, M.Y.; Cao, W.; Jiang, K. Adaptive Anisotropic Porous Structure Design and Modeling for 2.5D Mechanical Parts. Mater. Des. 2021, 206, 109786. [Google Scholar] [CrossRef]
- Mu, C.G.; Lü, X.H.; Bian, C.X.; Yuan, W. Research on Lamb Wave Phased Array Ultrasonic Testing Technology for Titanium Alloy Thin Plates. Technol. Innov. Appl. 2023, 13, 94–97. [Google Scholar]
- Huang, G.; Liu, Z.; Laurens, V.D.M.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar] [CrossRef]
- Oluchi, G.A.; Ifeanyi, C.N.; Jae-Min, L.; Kim, D.S. RBF-SVM Kernel-Based Model for Detecting DDoS Attacks in SDN Integrated Vehicular Network. Ad Hoc Netw. 2023, 140, 103–120. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Liu, C.; Tian, X.; Tang, H.; Wang, H.M. Microstructural Characterization of Laser Melting Deposited Ti–5Al-5Mo–5V–1Cr–1Fe Near β Titanium Alloy. J. Alloys Compd. 2013, 572, 17–24. [Google Scholar] [CrossRef]
- Ma, J.; Li, J.; Wang, Z.; Cui, D.; Wang, Z.; Wang, J. Microstructure and Mechanical Properties of the Bonding Zone in Forging-Additive Hybrid Manufactured Ti-6Al-4V Alloy. Acta Metall. Sin. 2021, 57, 1315–1324. [Google Scholar] [CrossRef]
- He, Y.; Xu, X.; Cao, H.; Pan, J.H.; Li, D.Y.; Fang, Z.J.; Li, Y.M. Correlation between Microstructural Evolution and Ultrasonic Propagation Behavior in Extra-Low-Interstitial-Grade Ti6Al4V Alloys. Rare Met. 2025, 44, 5781–5792. [Google Scholar] [CrossRef]




| Setting Options | Value |
|---|---|
| Laser rise time | 10 ns |
| Laser energy density | 5 × 1011 W/m2 |
| Laser spot radius | 0.2 mm |
| Material | Ti-6Al-4V |
| Elastic modulus | 110 GPa |
| Density | 4.43 g/cm3 |
| Coefficient of linear thermal expansion | 9.5 × 10−6/°C |
| Hardware | Disposition |
|---|---|
| CPU | Intel Xeon Silver 4210R (Intel, Santa Clara, CA, USA) |
| Number of CPU cores | 20 |
| GPU | Nvidia RTX A5000 (Nvidia, Santa Clara, CA, USA) |
| RAM | 24 G |
| Setting Options | Value |
|---|---|
| Epochs | 100 |
| Batch-size | 64 |
| Shuffle | every-epoch |
| InitialLearnRate | 0.01 |
| LearnRateSchedule | Piecewise |
| LearnRateDropPeriod | 10 |
| L2Regularization | 0.001 |
| Optimize Algorithms | adam |
| Network | Accuracy | Single Signal Recognition Duration |
|---|---|---|
| RNN | 90.72% | 1.57 ± 0.18 ms |
| LSTM | 91.16% | 4.31 ± 0.23 ms |
| CNN | 94.07% | 3.74 ± 0.21 ms |
| DenseNet | 96.21% | 5.21 ± 0.24 ms |
| Lamb wave-DenseNet | 97.93% | 8.15 ± 0.27 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Zhao, Y.; Zhao, G.; Yang, P. Microstructure Identification of Additive Manufactured Titanium Alloy by Using Lamb Wave-DenseNet Network. Sensors 2025, 25, 6630. https://doi.org/10.3390/s25216630
Huang Y, Zhao Y, Zhao G, Yang P. Microstructure Identification of Additive Manufactured Titanium Alloy by Using Lamb Wave-DenseNet Network. Sensors. 2025; 25(21):6630. https://doi.org/10.3390/s25216630
Chicago/Turabian StyleHuang, Yufeng, Yang Zhao, Gang Zhao, and Pinghua Yang. 2025. "Microstructure Identification of Additive Manufactured Titanium Alloy by Using Lamb Wave-DenseNet Network" Sensors 25, no. 21: 6630. https://doi.org/10.3390/s25216630
APA StyleHuang, Y., Zhao, Y., Zhao, G., & Yang, P. (2025). Microstructure Identification of Additive Manufactured Titanium Alloy by Using Lamb Wave-DenseNet Network. Sensors, 25(21), 6630. https://doi.org/10.3390/s25216630







