A Universal Tool Interaction Force Estimation Approach for Robotic Tool Manipulation
Abstract
1. Introduction
- A high-precision and rapid tool-end force estimation approach is proposed for robotic tool manipulation, especially when the robot changes tools or their grasping postures during a manipulation task.
- A two-stage wrist sensor compensation strategy is presented to achieve high accuracy in tool-end force estimation with a root-mean-square error below 0.5 N, through zero-drift error identification and creep error SNN-based compensation.
- The proposed tool-end interaction force estimation method is implemented in a robotic manipulation controller and verified to be precise and rapid in a robotic adhesive scraping manipulation task.
2. Methodology
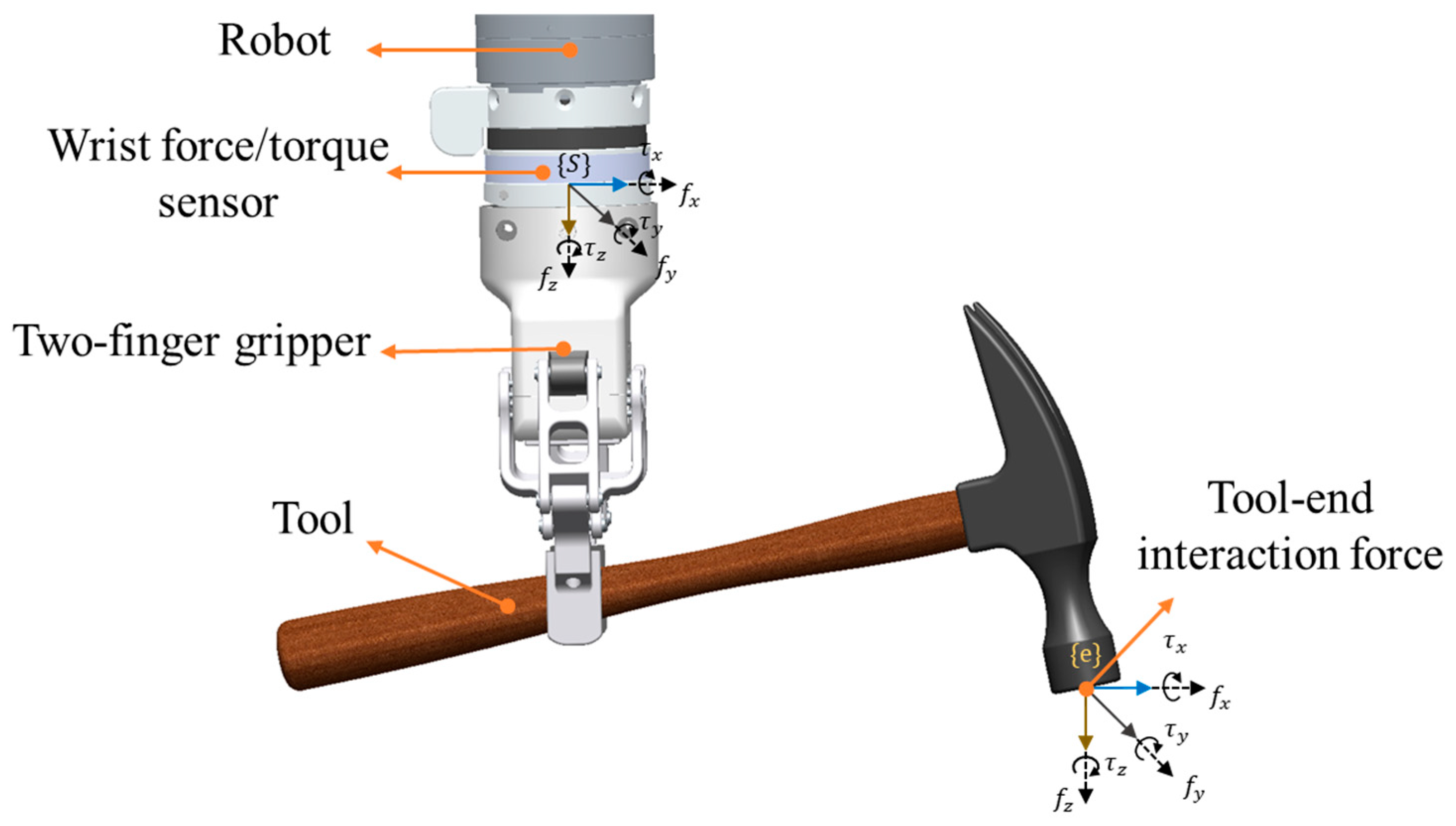
2.1. Force Decoupling
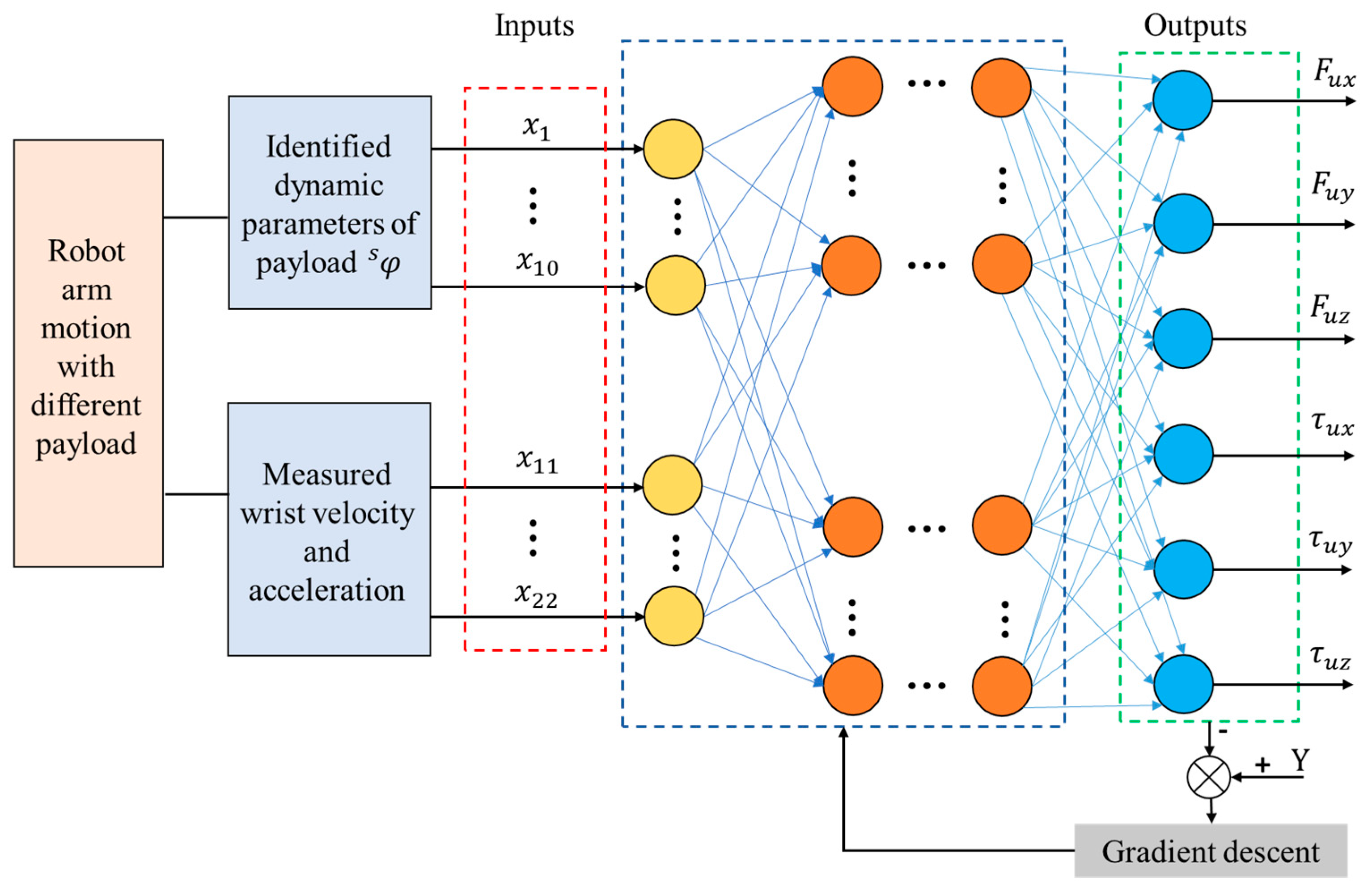
2.2. Gripper–Tool Dynamic Parameter Identification
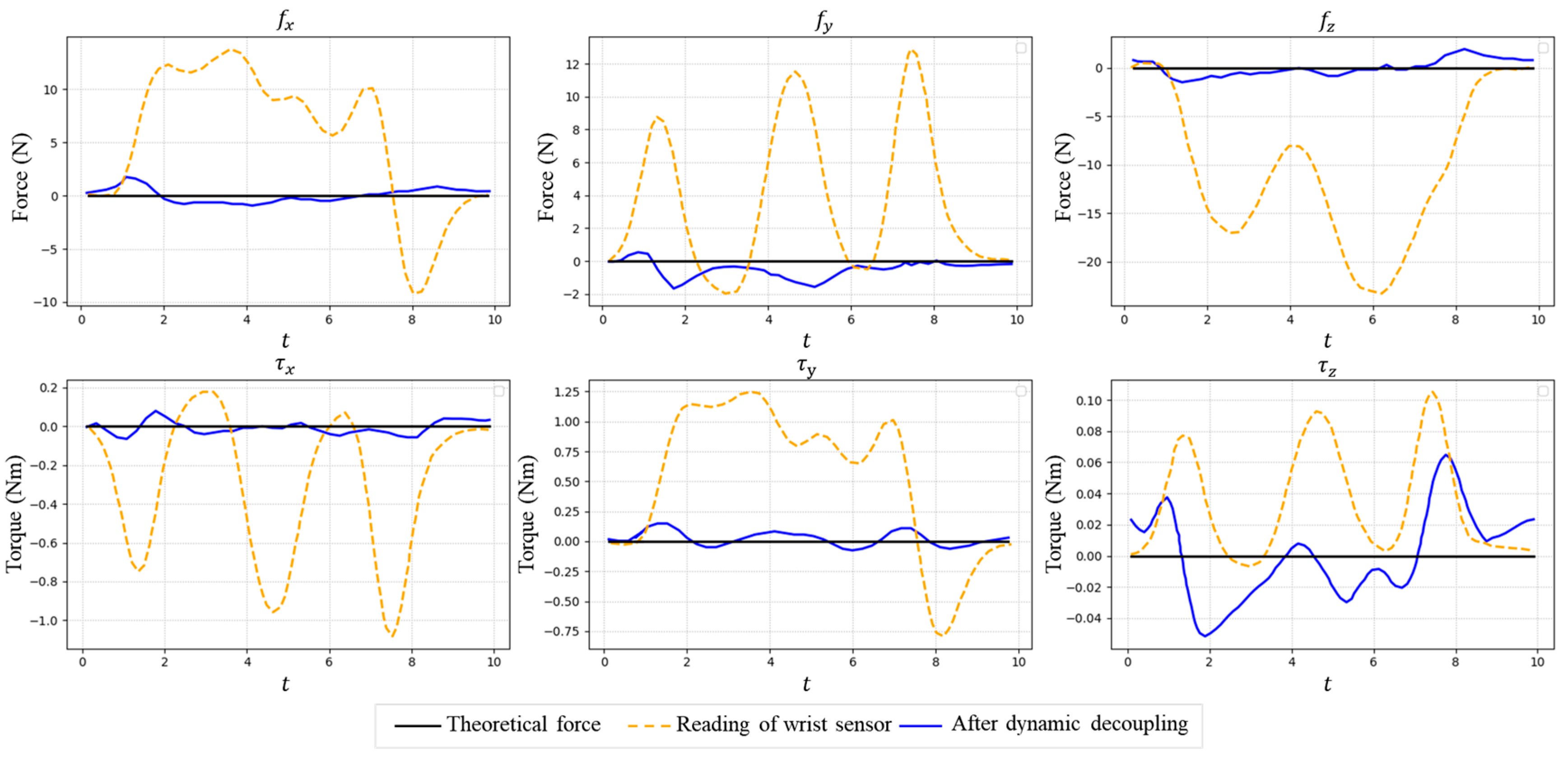
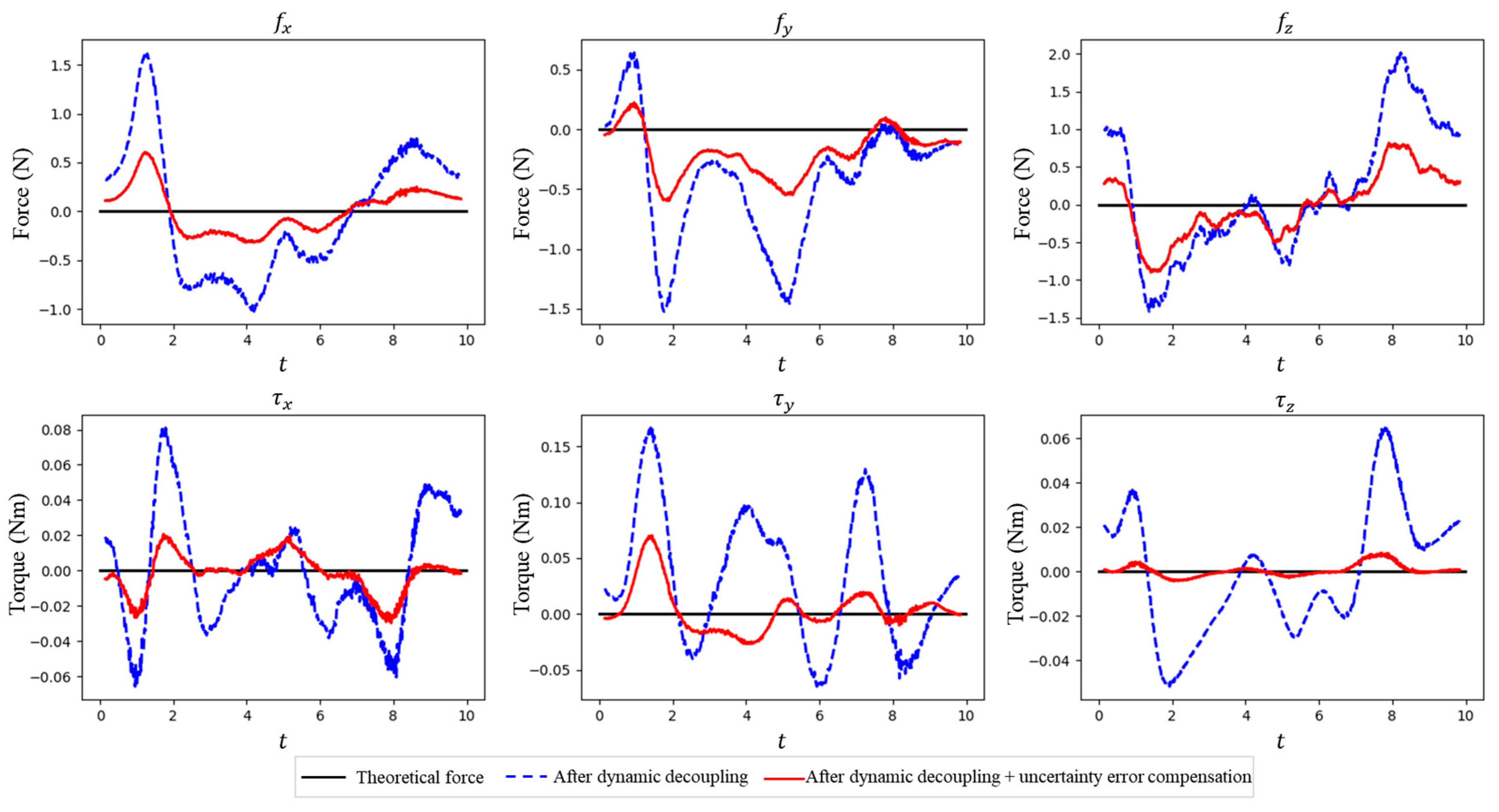
2.3. Sensor Uncertain Error Compensation
3. Experimental Verification
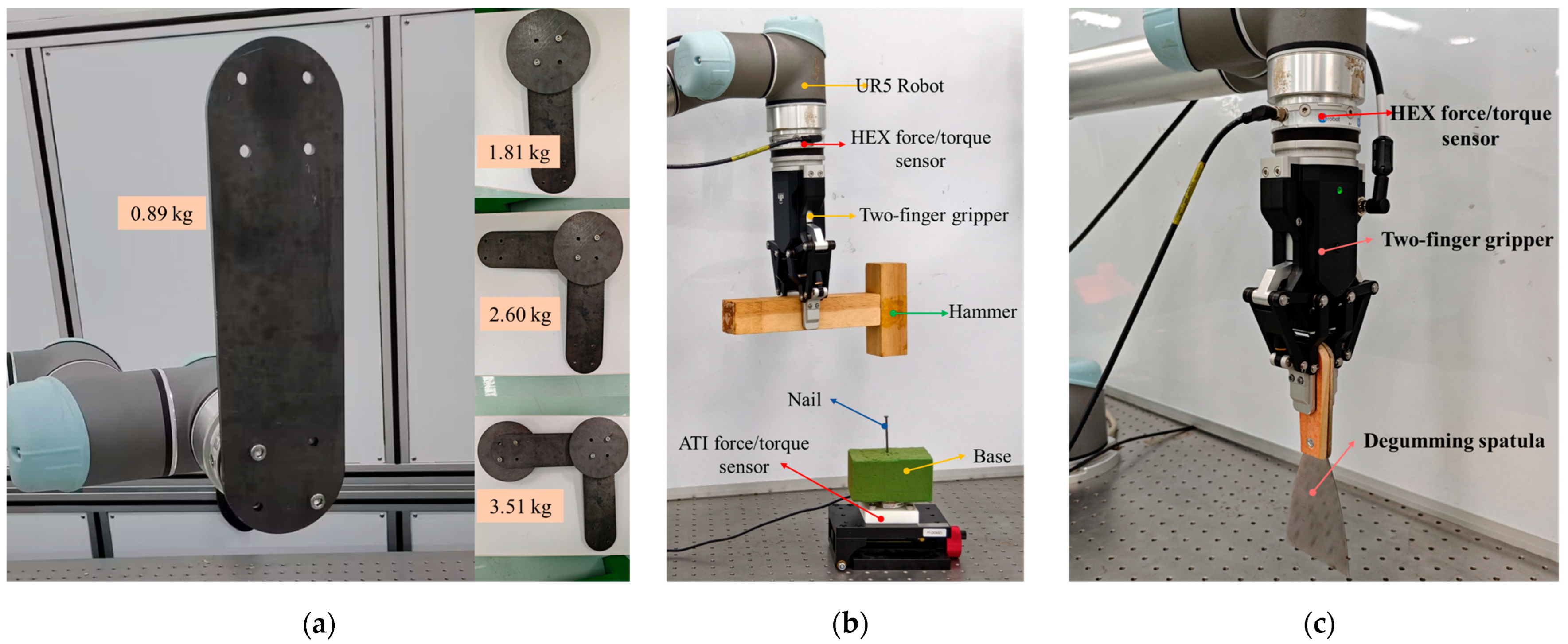
3.1. Experimental Setups
3.2. Identification of Tool Inertial Parameters
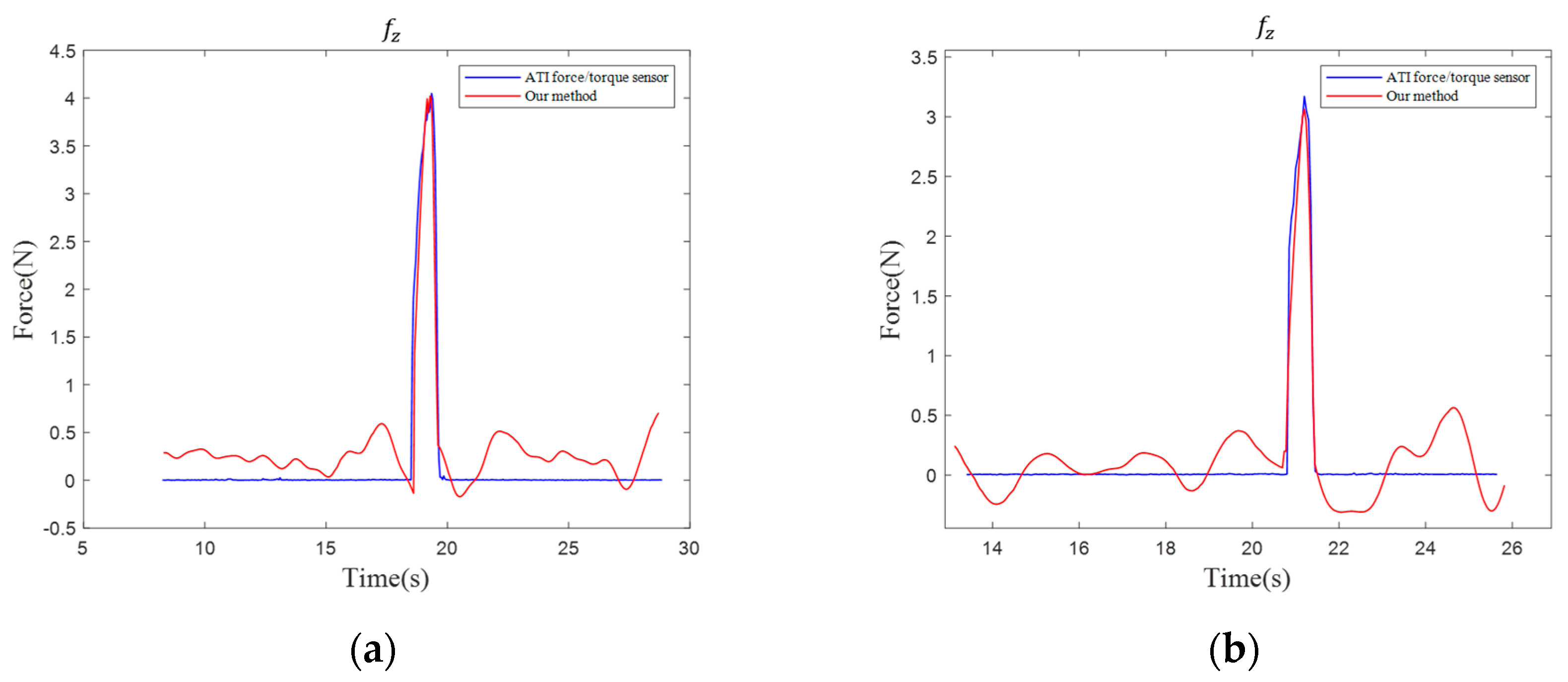
3.3. Tool-End Interaction Force Estimation
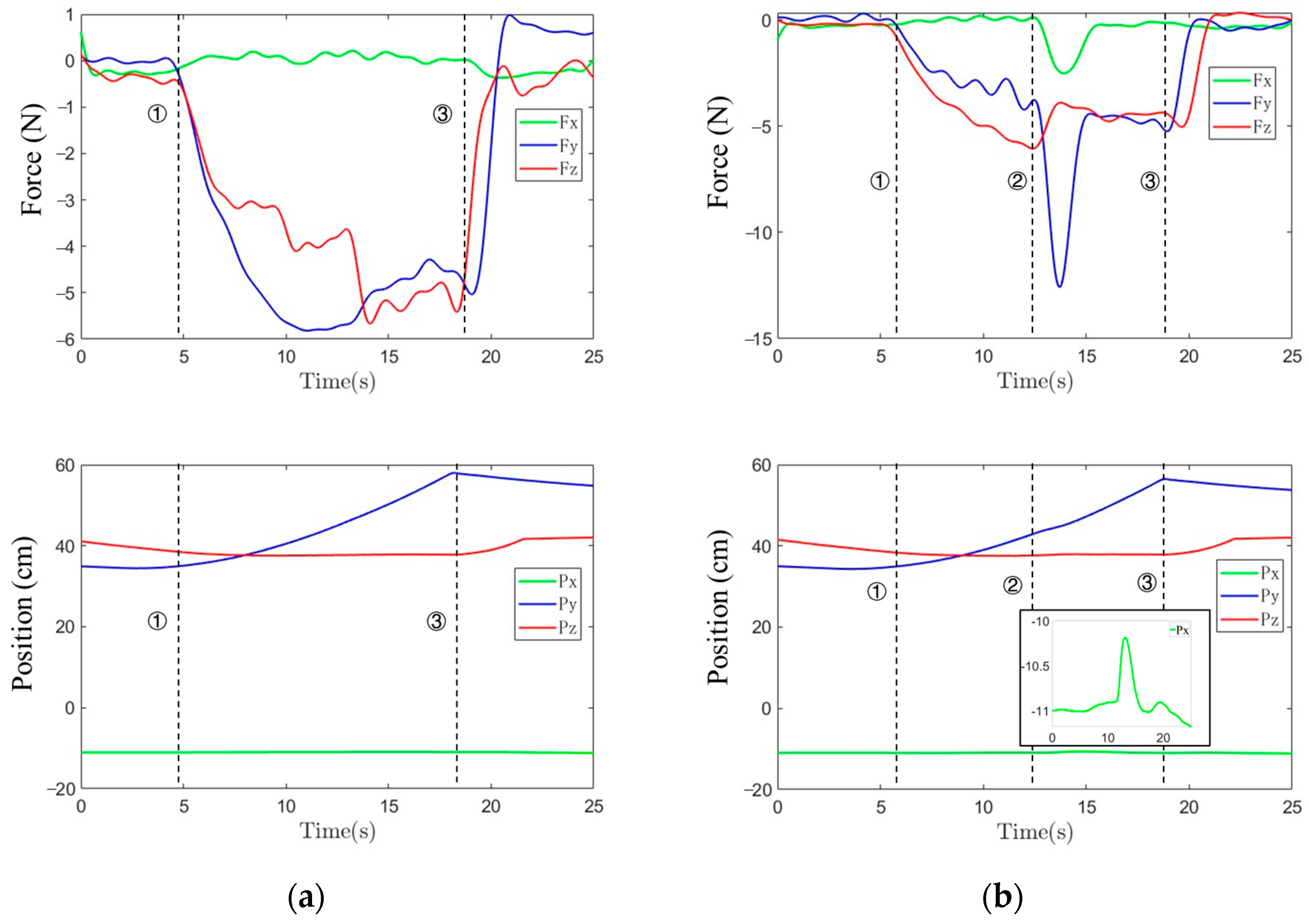
3.4. Tool-End Interaction Force for Manipulation Controller
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Billard, A.; Kragic, D. Trends and challenges in robot manipulation. Science 2019, 364, eaat8414. [Google Scholar] [CrossRef]
- Huan, Z.; Ma, W.; Wang, J.; Wu, F. Path planning and optimization for micro-robot in a vessel-mimic environment. Front. Neurorobot. 2022, 16, 923348. [Google Scholar] [CrossRef]
- Yang, C.; Xie, Y.; Liu, S.; Sun, D. Force Modeling, Identification, and Feedback Control of Robot-Assisted Needle Insertion: A Survey of the Literature. Sensors 2018, 18, 561. [Google Scholar] [CrossRef]
- Wang, R.; Xie, Y.; Liu, H.; Zhou, W. Center-of-Mass-Based object regrasping: A reinforcement learning approach and the effects of perception modality. IEEE/ASME Trans. Mechatron. 2024, 30, 1356–1365. [Google Scholar] [CrossRef]
- Tang, L.; Jia, Y.-B.; Xue, Y. Robotic manipulation of hand tools: The case of screwdriving. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–16 May 2024; pp. 13883–13890. [Google Scholar]
- Xia, Z.; Deng, Z.; Fang, B.; Yang, Y.; Sun, F. A review on sensory perception for dexterous robotic manipulation. Int. J. Adv. Robot. Syst. 2022, 19, 17298806221095974. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, F.; Ge, S.S.; Wu, Y.; Mei, X. End-effector force estimation for flexible-joint robots with global friction approximation using neural networks. IEEE Trans. Ind. Inform. 2018, 15, 1730–1741. [Google Scholar] [CrossRef]
- Le, D.P.; Choi, J.; Kang, S. External force estimation using joint torque sensors and its application to impedance control of a robot manipulator. In Proceedings of the 2013 13th International Conference on Control, Automation and Systems (ICCAS 2013), Gwangju, Republic of Korea, 20–23 October 2013; pp. 1794–1798. [Google Scholar]
- Choi, J.; Kang, S. External force estimation using joint torque sensors for a robot manipulator. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St. Paul, MN, USA, 14–18 May 2012; pp. 4507–4512. [Google Scholar]
- He, W.; Yan, Z.; Sun, C.; Chen, Y. Adaptive neural network control of a flapping wing micro aerial vehicle with disturbance observer. IEEE Trans. Cybern. 2017, 47, 3452–3465. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Meng, T.; He, X.; Sun, C. Iterative learning control for a flapping wing micro aerial vehicle under distributed disturbances. IEEE Trans. Cybern. 2018, 49, 1524–1535. [Google Scholar] [CrossRef]
- Leboutet, Q.; Roux, J.; Janot, A.; Guadarrama-Olvera, J.R.; Cheng, G. Inertial parameter identification in robotics: A survey. Appl. Sci. 2021, 11, 4303. [Google Scholar] [CrossRef]
- Lutter, M. A differentiable newton–euler algorithm for real-world robotics. In Inductive Biases in Machine Learning for Robotics and Control; Siciliano, B., Khatib, O., Eds.; Springer Tracts in Advanced Robotics; Springer Nature: Cham, Switzerland, 2023; pp. 9–34. Available online: https://link.springer.com/chapter/10.1007/978-3-031-37832-4_2 (accessed on 24 October 2025).
- Huang, W.; Min, H.; Guo, Y.; Liu, M. A review of dynamic parameters identification for manipulator control. Cobot 2022, 1, 5. [Google Scholar] [CrossRef]
- Xie, K.; Cao, Q.; Luan, N.; Zhu, X. External Forces/Torques perception of robot endeffector tip based on a 6-axis force sensor. In Proceedings of the 2021 International Conference on Intelligent Computing, Automation and Systems (ICICAS), Chongqing, China, 29–31 December 2021; pp. 440–444. [Google Scholar]
- Zhang, L.-J.; Hu, R.-Q.; Yi, W.-M. Research on force sensing for the end-load of industrial robot based on a 6-axis force/torque sensor. Acta Autom. Sin. 2017, 43, 439–447. [Google Scholar] [CrossRef]
- Farsoni, S.; Bonfè, M. Complete and consistent payload identification during human-robot collaboration: A safety-oriented procedure. In Proceedings of the Human-Friendly Robotics 2021: HFR: 14th International Workshop on Human-Friendly Robotics, Bologna, Italy, 28–29 October 2021; pp. 15–28. [Google Scholar]
- Nadeau, P.; Giamou, M.; Kelly, J. Fast object inertial parameter identification for collaborative robots. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 3560–3566. [Google Scholar]
- Duan, J.; Liu, Z.; Bin, Y.; Cui, K.; Dai, Z. Payload identification and gravity/inertial compensation for six-dimensional force/torque sensor with a fast and robust trajectory design approach. Sensors 2022, 22, 439. [Google Scholar] [CrossRef] [PubMed]
- Su, H.; Yang, C.; Mdeihly, H.; Rizzo, A.; Ferrigno, G.; De Momi, E. Neural network enhanced robot tool identification and calibration for bilateral teleoperation. IEEE Access 2019, 7, 122041–122051. [Google Scholar] [CrossRef]
- Su, H.; Qi, W.; Yang, C.; Sandoval, J.; Ferrigno, G.; De Momi, E. Deep neural network approach in robot tool dynamics identification for bilateral teleoperation. IEEE Robot. Autom. Lett. 2020, 5, 2943–2949. [Google Scholar] [CrossRef]
- Cao, M.Y.; Laws, S.; Ferdinando, R.y.B. Six-axis force/torque sensors for robotics applications: A review. IEEE Sens. J. 2021, 21, 27238–27251. [Google Scholar] [CrossRef]
- Kebede, G.A.; Ahmad, A.R.; Lee, S.-C.; Lin, C.-Y. Decoupled six-axis force–moment sensor with a novel strain gauge arrangement and error reduction techniques. Sensors 2019, 19, 3012. [Google Scholar] [CrossRef]
- Chavez, F.J.A.; Nava, G.; Traversaro, S.; Nori, F.; Pucci, D. Model based in situ calibration with temperature compensation of 6 axis force torque sensors. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 5397–5403. [Google Scholar]
- Zhao, Y.; Liu, Y.; Li, Y.; Hao, Q. Development and application of resistance strain force sensors. Sensors 2020, 20, 5826. [Google Scholar] [CrossRef] [PubMed]
- Xue, X.; Huang, H.; Zuo, L.; Wang, N. A compliant force control scheme for industrial robot interactive operation. Front. Neurorobot. 2022, 16, 865187. [Google Scholar] [CrossRef]
- Yu, Y.; Shi, R.; Lou, Y. Bias estimation and gravity compensation for wrist-mounted force/torque sensor. IEEE Sens. J. 2021, 22, 17625–17634. [Google Scholar] [CrossRef]
- Shin, J.; Shin, J.; Jung, H.-r.; Won, J.; Auh, E.; Moon, H. On-Site Implementation of External Wrench Measurement via Non-Linear Optimization in Six-Axis Force–Torque Sensor Calibration and Crosstalk Compensation. Appl. Sci. 2025, 15, 1510. [Google Scholar] [CrossRef]
- Yao, L.; Gao, Q.; Zhang, D.; Zhang, W.; Chen, Y. An integrated compensation method for the force disturbance of a six-axis force sensor in complex manufacturing scenarios. Sensors 2021, 21, 4706. [Google Scholar] [CrossRef]
- Liu, M.; Li, P.; Duan, J.; Liu, L.; Shen, Y.; Tian, W.; Ji, Y. A two-stage payload dynamic parameter identification method for interactive industrial robots with large components. IEEE Trans. Autom. Sci. Eng. 2025. [Google Scholar] [CrossRef]
- Wu, J.; Huang, T.; Zhu, Z.; Song, K. Cold starting temperature time-related compensation model of inertial sensors based on particle swarm optimization algorithm. Rev. Sci. Instrum. 2021, 92, 065106. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Y.; Liu, H. Temperature compensation for a six-axis force/torque sensor based on the particle swarm optimization least square support vector machine for space manipulator. IEEE Sens. J. 2015, 16, 798–805. [Google Scholar] [CrossRef]
- Gao, Z.; Wen, Y.; Li, P.; Lei, H.; Xiao, Q.; Fan, Y. Creep compensation for mechanical sensors: Considering historical loading memory. Measurement 2025, 249, 116901. [Google Scholar] [CrossRef]
- Sousa, C.D.; Cortesao, R. Physical feasibility of robot base inertial parameter identification: A linear matrix inequality approach. Int. J. Robot. Res. 2014, 33, 931–944. [Google Scholar] [CrossRef]
- Lotfi Rezaabad, A.; Vishwanath, S. Long short-term memory spiking networks and their applications. In Proceedings of the International Conference on Neuromorphic Systems, Oak Ridge, TN, USA, 28–30 July 2020; pp. 1–9. [Google Scholar]
- Jiangtao, X.; Yu, X.; Renpeng, W.; Jinhui, Z.; Wei, Z.; Yi, Z. A Novel Robot Tool Manipulation Method for Battery Degumming Task. In Proceedings of the 2024 7th International Symposium on Autonomous Systems (ISAS), Chongqing, China, 7–9 May 2024; pp. 1–5. [Google Scholar]

| 0.89 kg | 1.81 kg | 2.60 kg | 3.51 kg | |||||
|---|---|---|---|---|---|---|---|---|
| Identified | Theoretical | Identified | Theoretical | Identified | Theoretical | Identified | Theoretical | |
| m (kg) | 0.95 | 0.89 | 1.86 | 1.81 | 2.66 | 2.60 | 3.61 | 3.51 |
| cx (mm) | −81.8 | −89 | −127.4 | −130 | −0.9 | 0 | −132.4 | −137 |
| cy (mm) | −0.35 | 0 | −0.95 | 0 | −153.5 | −156 | 0.66 | 0 |
| cz (mm) | 2.66 | 2.9 | 6.93 | 6.50 | 8.63 | 9.80 | 16.1 | 15 |
| Ixx (kg·cm2) | 3.34 | 3.94 | −72.25 | −523.6 | 499.80 | 753.58 | −123.3 | −965.21 |
| Ixy (kg·cm2) | 1.76 | 0 | −130.56 | 0 | 19.08 | 0 | −419.01 | 0 |
| Ixz (kg·cm2) | −2.58 | −2.27 | −11.47 | −38.28 | 41.91 | 0 | −140.8 | −96.46 |
| Iyy (kg·cm2) | 144.50 | 119.16 | −517.74 | −156.74 | 26.76 | 41.73 | −882.71 | −526.64 |
| Iyz (kg·cm2) | 4.10 | 0 | −39.29 | 0 | 43.04 | −45.41 | 31.403 | 0 |
| Izz (kg·cm2) | 154.78 | 122.91 | −486.99 | −146.79 | 73.94 | 773.39 | −804.65 | −426.39 |
| Identification time (s) | 5.6 | 5.8 | 6.1 | 5.6 | ||||
| Reading of Sensor | After Decoupling | After SNN Compensation | Resolution of Wrist Sensor | |
|---|---|---|---|---|
| (N) | 8.41 | 0.75 | 0.27 | 0.2 |
| (N) | 5.70 | 0.74 | 0.31 | 0.2 |
| (N) | 12.84 | 1.02 | 0.49 | 0.8 |
| (N*m) | 0.477 | 0.057 | 0.023 | 0.01 |
| (N*m) | 0.791 | 0.081 | 0.028 | 0.01 |
| (N*m) | 0.049 | 0.031 | 0.008 | 0.002 |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| Ours | 0.27 | 0.31 | 0.49 | 0.023 | 0.028 | 0.008 | SNN-LSM |
| [16] | 0.593 | 0.751 | 0.822 | 0.013 | 0.301 | 0.003 | Double-LSM |
| [28] | 0.693 | 1.069 | 1.285 | 0.095 | 0.110 | 0.022 | Bias with Non-liner Optimization |
| [29] | 0.377 | 0.583 | 0.629 | 0.0082 | 0.0138 | 0.003 | DL-LSM |
| (%FS) | (%FS) | (%FS) | (%FS) | (%FS) | (%FS) | Method | Sensor Resolution | |
|---|---|---|---|---|---|---|---|---|
| Ours | 0.135 | 0.155 | 0.245 | 0.230 | 0.280 | 0.123 | SNN-LSM | HEX-E OnRobot ( 0.2, 0.8, 0.01, 0.002) |
| [16] | 0.473 | 0.571 | 0.328 | 0.218 | 0.428 | 0.049 | Double-LSM | Omega190 ( 0.375, 0.628, 0.05, 0.03) |
| [28] | 0.347 | 0.535 | 0.643 | 0.633 | 0.733 | 0.147 | Bias with Non-liner Optimization | AFT200 ( 0.15, 0.015) |
| [29] | 0.377 | 0.583 | 0.315 | 0.164 | 0.276 | 0.060 | DL-LSM | Self-developed tandem force sensor ( 0.003, 0.006, 0.00015) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, D.; Xiao, J.; Xie, Y.; Luo, T.; Zhang, J.; Zhou, W. A Universal Tool Interaction Force Estimation Approach for Robotic Tool Manipulation. Sensors 2025, 25, 6619. https://doi.org/10.3390/s25216619
Wen D, Xiao J, Xie Y, Luo T, Zhang J, Zhou W. A Universal Tool Interaction Force Estimation Approach for Robotic Tool Manipulation. Sensors. 2025; 25(21):6619. https://doi.org/10.3390/s25216619
Chicago/Turabian StyleWen, Diyun, Jiangtao Xiao, Yu Xie, Tao Luo, Jinhui Zhang, and Wei Zhou. 2025. "A Universal Tool Interaction Force Estimation Approach for Robotic Tool Manipulation" Sensors 25, no. 21: 6619. https://doi.org/10.3390/s25216619
APA StyleWen, D., Xiao, J., Xie, Y., Luo, T., Zhang, J., & Zhou, W. (2025). A Universal Tool Interaction Force Estimation Approach for Robotic Tool Manipulation. Sensors, 25(21), 6619. https://doi.org/10.3390/s25216619







