Calibration and Validation of an Autonomous, Novel, Low-Cost, Dynamic Flux Chamber for Measuring Landfill Methane Emissions
Highlights
- Low-cost air quality sensors can be leveraged in the development and optimization of an affordable and portable methane flux chamber.
- A calibration system for low-cost sensors was developed to operate in a laboratory setting and achieve measurements capable of covering a wide dynamic range of methane emissions from landfills.
- Low-cost flux chambers can be deployed in large numbers across a landfill to support simultaneous and continuous measurements achieving spatially and temporally broad information about emissions.
- Low-cost sensors can be effectively calibrated across a very wide range of methane concentrations while mitigating the confounding influence of ambient temperature and humidity variations.
Abstract
1. Introduction
1.1. Techniques to Measure Emissions from Landfills
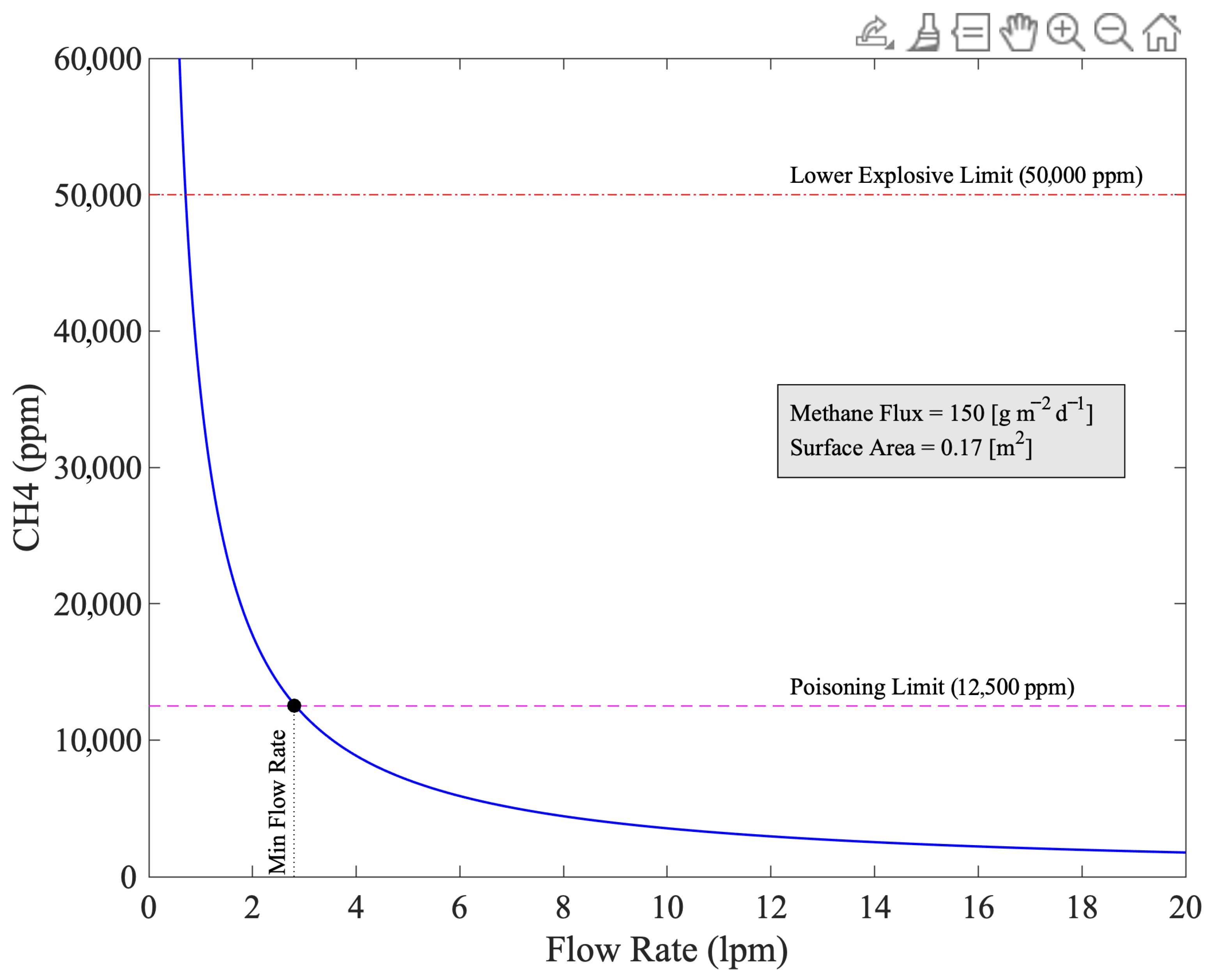
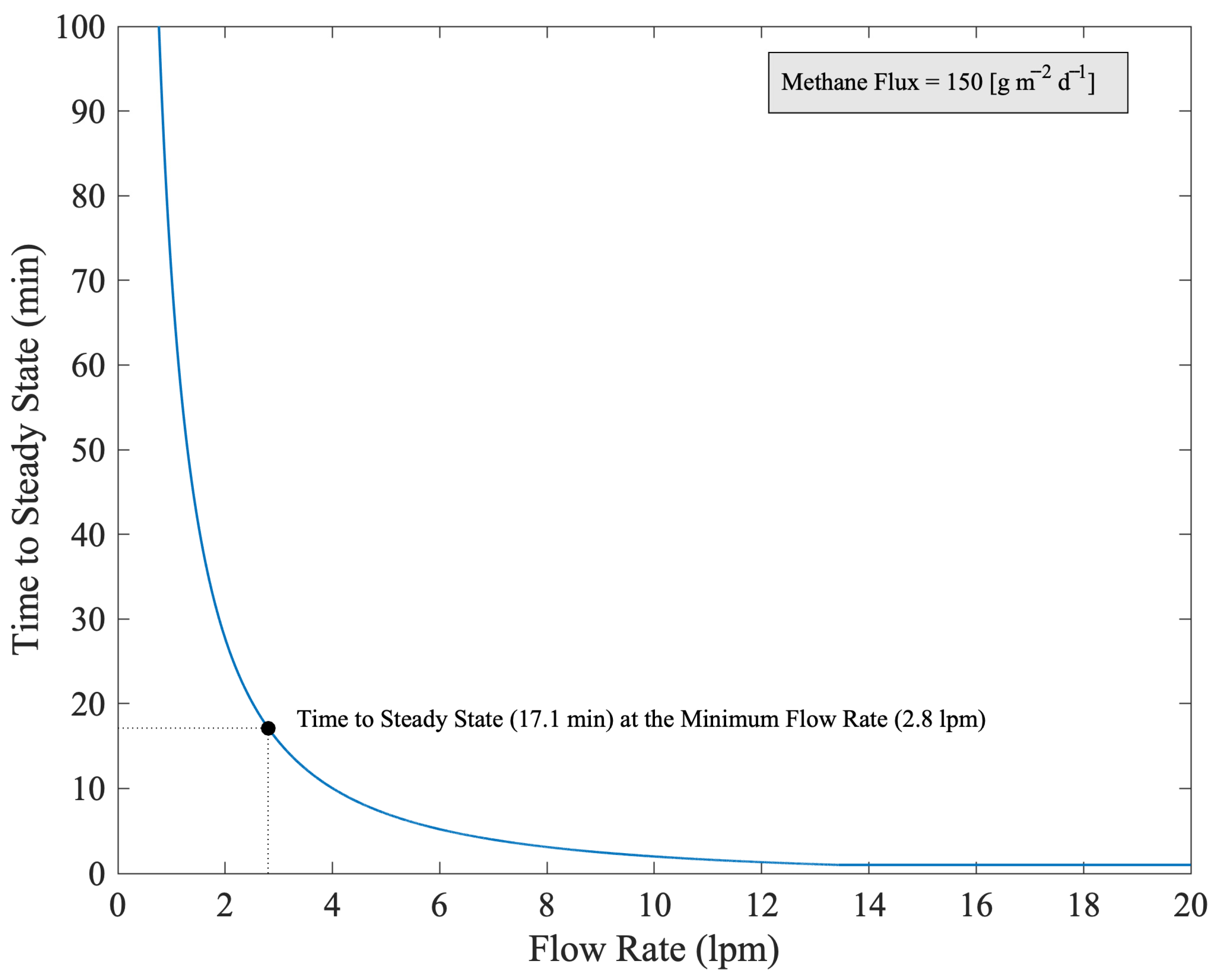
1.2. Design Considerations for a Dynamic Flux Chamber
1.3. Measuring Methane with Low-Cost Sensors
2. Materials and Methods
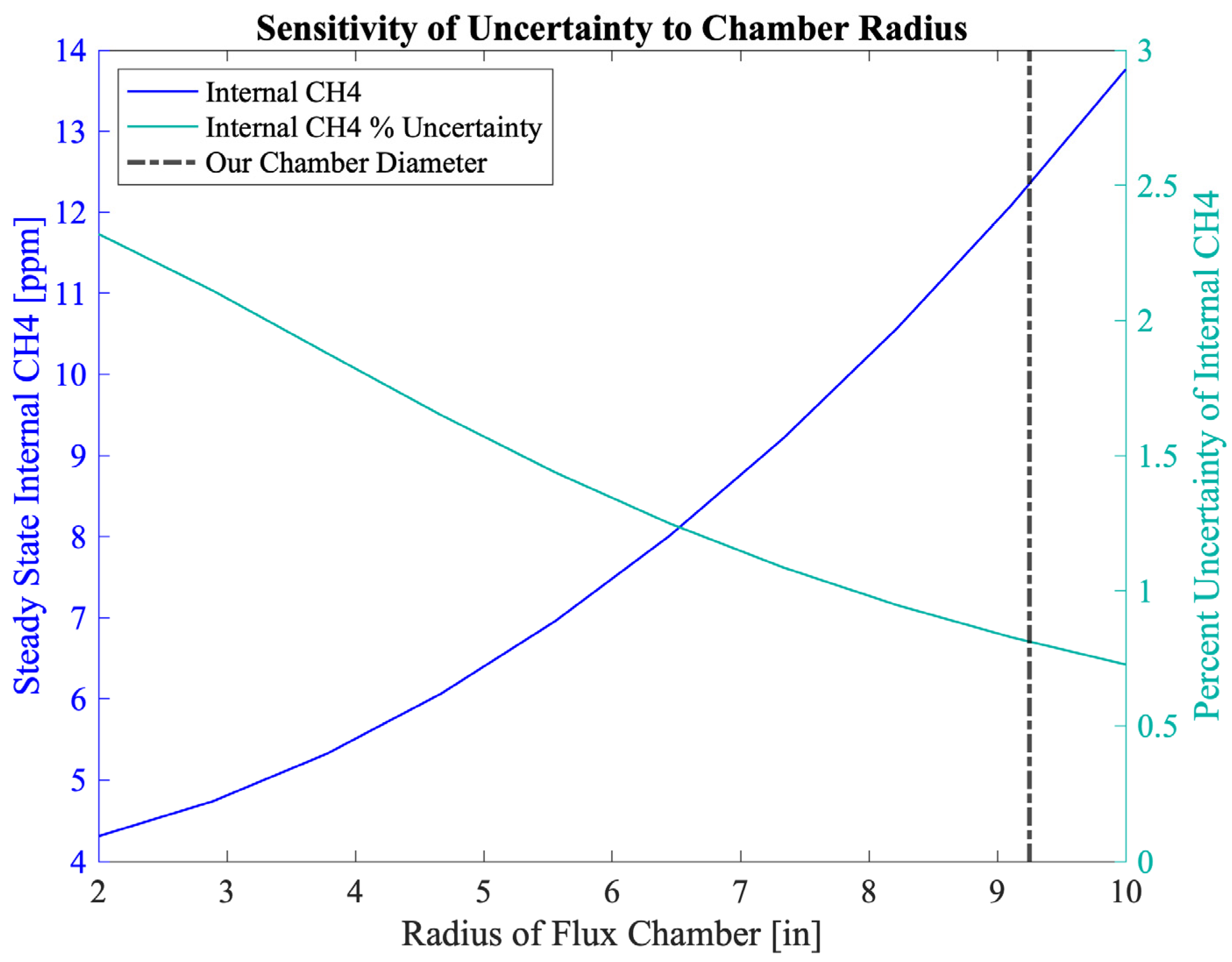
2.1. Flux Chamber Design and Optimization
2.2. Printed Circuit Board Design
2.3. Internal Chamber Sensor Calibration
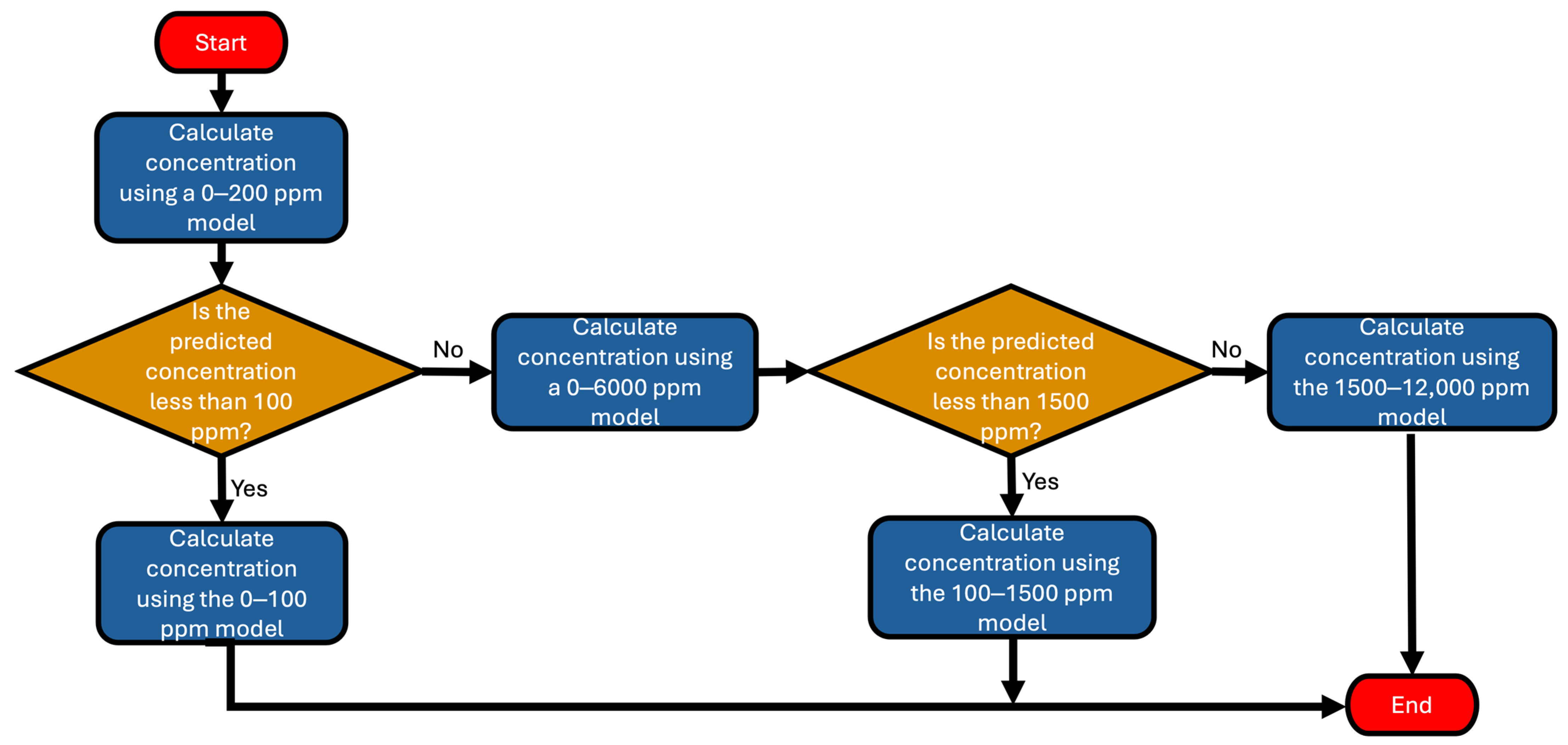
2.3.1. Predictor Selection
2.3.2. Piecewise
2.4. Ambient Sensor Calibration
2.5. Flux Chamber Validation
2.5.1. Flux Laboratory Validation
2.5.2. Field Validation of Chamber Concentration
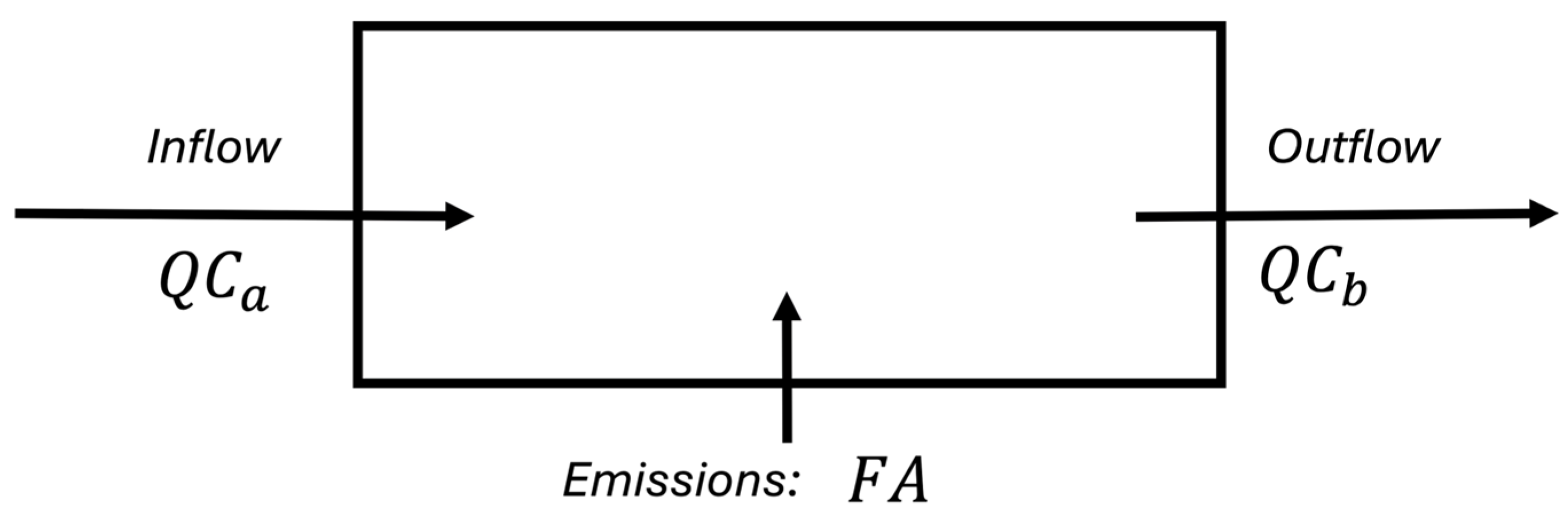
2.6. Flux Quantification
3. Results and Discussion
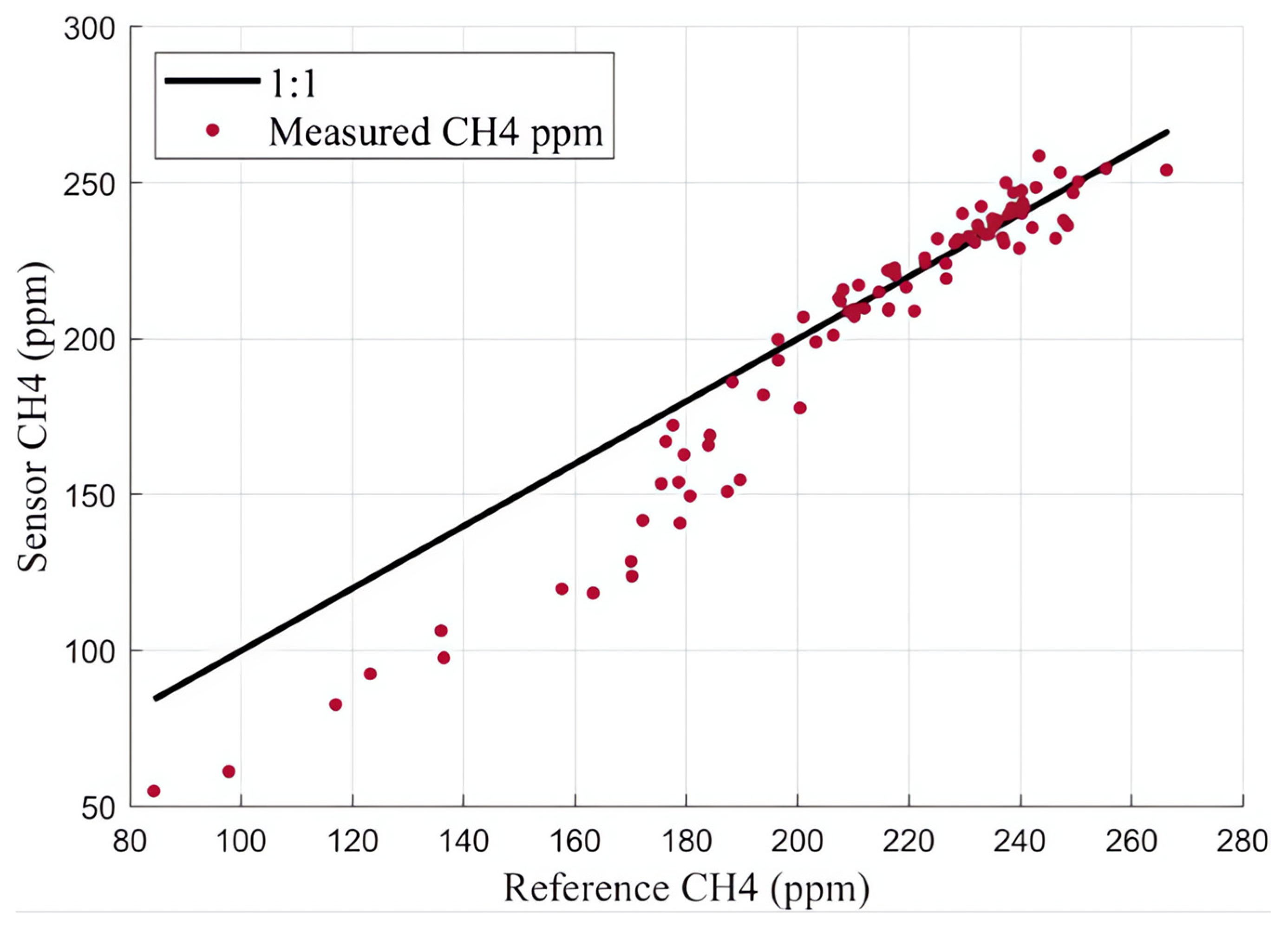
3.1. Methane Sensor Calibration
3.2. Flux Quantification and Validation
3.3. Field Validation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CH4 | Methane |
| VOC | Volatile Organic Compound |
| H2S | Hydrogen Sulfide |
| MOX | Metal Oxide |
| IR | Infrared |
| PCB | Printed Circuit Board |
| RMSE | Root Mean Squared Error |
| MBE | Mean Biased Error |
| PPM | Parts Per Million |
References
- IPCC. IPCC, 2023: Summary for Policymakers. In Climate Change 2023: Synthesis Report. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Lee, H., Romero, J., Eds.; IPCC: Geneva, Switzerland, 2023. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2021: The Physical Science Basis. In Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021. [Google Scholar]
- EPA. Inventory of US Greenhouse Gas Emissions and Sinks: 1990–2020. Available online: https://www.epa.gov/ghgemissions/inventory-us-greenhouse-gas-emissions-and-sinks (accessed on 1 October 2025).
- Moghadam, M.A.; Feizi, R.; Panahi Fard, M.; Haghighi Fard, N.J.; Omidinasab, M.; Faraji, M.; Shenavar, B. Estimating Greenhouse Emissions from Sanitary Landfills Using Land-GEM and IPCC Model Based on Realistic Scenarios of Different Urban Areas: A Case Study of Iran. J. Environ. Health Sci. Eng. 2021, 19, 819–830. [Google Scholar] [CrossRef] [PubMed]
- Fjelsted, L.; Christensen, A.G.; Larsen, J.E.; Kjeldsen, P.; Scheutz, C. Assessment of a Landfill Methane Emission Screening Method Using an Unmanned Aerial Vehicle Mounted Thermal Infrared Camera—A Field Study. Waste Manag. 2019, 87, 893–904. [Google Scholar] [CrossRef] [PubMed]
- Gasbarra, D.; Toscano, P.; Famulari, D.; Finardi, S.; Di Tommasi, P.; Zaldei, A.; Carlucci, P.; Magliulo, E.; Gioli, B. Locating and Quantifying Multiple Landfills Methane Emissions Using Aircraft Data. Environ. Pollut. 2019, 254, 112987. [Google Scholar] [CrossRef] [PubMed]
- Allen, G.; Hollingsworth, P.; Kabbabe, K.; Pitt, J.R.; Mead, M.I.; Illingworth, S.; Roberts, G.; Bourn, M.; Shallcross, D.E.; Percival, C.J. The Development and Trial of an Unmanned Aerial System for the Measurement of Methane Flux from Landfill and Greenhouse Gas Emission Hotspots. Waste Manag. 2019, 87, 883–892. [Google Scholar] [CrossRef]
- Erland, B.M.; Thorpe, A.K.; Gamon, J.A. Recent Advances Toward Transparent Methane Emissions Monitoring: A Review. Environ. Sci. Technol. 2022, 56, 16567–16581. [Google Scholar] [CrossRef]
- Matacchiera, F.; Manes, C.; Beaven, R.P.; Rees-White, T.C.; Boano, F.; Mønster, J.; Scheutz, C. AERMOD as a Gaussian Dispersion Model for Planning Tracer Gas Dispersion Tests for Landfill Methane Emission Quantification. Waste Manag. 2019, 87, 924–936. [Google Scholar] [CrossRef]
- Pliszka, H.O. Characterizing Landfill Methane Through a Low-Cost Ground-Based Sensor Network: Preliminary Studies at a Colorado Landfill. Master’s Thesis, University of Colorado at Boulder, Boulder, CO, USA, 2023. [Google Scholar]
- Castro Gámez, A.F.; Rodríguez Maroto, J.M.; Vadillo Pérez, I. Quantification of Methane Emissions in a Mediterranean Landfill (Southern Spain). A Combination of Flux Chambers and Geostatistical Methods. Waste Manag. 2019, 87, 937–946. [Google Scholar] [CrossRef]
- Reinhart, D.R.; Cooper, D.C.; Walker, B.L. Flux Chamber Design and Operation for the Measurement of Municipal Solid Waste Landfill Gas Emission Rates. J. Air Waste Manag. Assoc. 1992, 42, 1067–1070. [Google Scholar] [CrossRef]
- Jeong, S.; Park, J.; Kim, Y.M.; Park, M.H.; Kim, J.Y. Innovation of Flux Chamber Network Design for Surface Methane Emission from Landfills Using Spatial Interpolation Models. Sci. Total Environ. 2019, 688, 18–25. [Google Scholar] [CrossRef]
- Maasakkers, J.D.; Varon, D.J.; Elfarsdóttir, A.; McKeever, J.; Jervis, D.; Mahapatra, G.; Pandey, S.; Lorente, A.; Borsdorff, T.; Foorthuis, L.R.; et al. Using Satellites to Uncover Large Methane Emissions from Landfills. Sci. Adv. 2022, 8, eabn9683. [Google Scholar] [CrossRef]
- Schroth, M.H.; Eugster, W.; Gómez, K.E.; Gonzalez-Gil, G.; Niklaus, P.A.; Oester, P. Above- and below-Ground Methane Fluxes and Methanotrophic Activity in a Landfill-Cover Soil. Waste Manag. 2012, 32, 879–889. [Google Scholar] [CrossRef]
- Mønster, J.; Kjeldsen, P.; Scheutz, C. Methodologies for Measuring Fugitive Methane Emissions from Landfills—A Review. Waste Manag. 2019, 87, 835–859. [Google Scholar] [CrossRef] [PubMed]
- Bekin, N.; Agam, N. Rethinking the Deployment of Static Chambers for CO2 Flux Measurement in Dry Desert Soils. Biogeosciences 2023, 20, 3791–3802. [Google Scholar] [CrossRef]
- Jeong, J.H.; Kang, S.J.; Lim, J.M.; Lee, J.-H. Comparison and Optimization of Flux Chamber Methods of Methane Emissions from Landfill Surface Area. J. Korean Soc. Environ. Eng. 2016, 38, 535–542. [Google Scholar] [CrossRef]
- Draughon, G.T.S.; Lynch, J.P.; Zekkos, D.; O’Laughlin, S. Development of an Autonomous Flux Chamber for Continuous Methane Measurements at Msw Landfills. In Proceedings of the 17th International Waste Managment and Landfill Symposium, Cagliari, Italy, 30 September–4 October 2019. [Google Scholar]
- Bastviken, D.; Nygren, J.; Schenk, J.; Parellada Massana, R.; Thanh Duc, N. Technical Note: Facilitating the Use of Low-Cost Methane (Ch4) Sensors in Flux Chambers-Calibration, Data Processing, and an Open-Source Make-It-Yourself Logger. Biogeosciences 2020, 17, 3659–3667. [Google Scholar] [CrossRef]
- ELT Sensors. CH4/C2H4/C3H8/C4H10-D3 Sensor Modules. Available online: https://www.eltsensor.co.kr/2016/products/oem_modules/CH4-D3.html (accessed on 1 October 2025).
- Kwaśny, M.; Bombalska, A. Optical Methods of Methane Detection. Sensors 2023, 23, 2834. [Google Scholar] [CrossRef]
- SGX Sensortech. INIR2-ME100 Methane Sensor Datasheet; SGX Sensortech: Katowice, Poland, 2025. [Google Scholar]
- Figaro. TGS 2600 Data Sheet; Figaro Engineering Inc.: Osaka, Japan, 2013; pp. 1–2. [Google Scholar]
- Figaro. TGS 2611 Data Sheet; Figaro Engineering Inc.: Osaka, Japan, 2017; pp. 1–2. [Google Scholar]
- Collier-oxandale, A.; Casey, J.G.; Piedrahita, R.; Ortega, J.; Halliday, H.; Johnston, J.; Hannigan, M.P. Assessing a Low-Cost Methane Sensor Quantification System for Use in Complex Rural and Urban Environments. Atmos. Meas. Tech. 2018, 11, 3569–3594. [Google Scholar] [CrossRef]
- Casey, J.G.; Collier-Oxandale, A.; Hannigan, M. Performance of Artificial Neural Networks and Linear Models to Quantify 4 Trace Gas Species in an Oil and Gas Production Region with Low-Cost Sensors. Sens. Actuators B Chem. 2019, 283, 504–514. [Google Scholar] [CrossRef]
- Eugster, W.; Laundre, J.; Eugster, J.; Kling, G.W. Long-Term Reliability of the Figaro TGS 2600 Solid-State Methane Sensor under Low-Arctic Conditions at Toolik Lake, Alaska. Atmos. Meas. Tech. 2020, 13, 2681–2695. [Google Scholar] [CrossRef]
- Furuta, D.; Sayahi, T.; Li, J.; Wilson, B.; Presto, A.A.; Li, J. Characterization of Inexpensive Metal Oxide Sensor Performance for Trace Methane Detection. Atmos. Meas. Tech. 2022, 15, 5117–5128. [Google Scholar] [CrossRef]
- Martinez, R.R.; Santaren, D.; Laurent, O.; Cropley, F.; Mallet, C.; Ramonet, M.; Caldow, C.; Rivier, L.; Broquet, G.; Bouchet, C.; et al. The Potential of Low-Cost Tin-Oxide Sensors Combined with Machine Learning for Estimating Atmospheric CH4 Variations around Background Concentration. Atmosphere 2021, 12, 107. [Google Scholar] [CrossRef]
- Silberstein, J.; Wellbrook, M.; Hannigan, M. Utilization of a Low-Cost Sensor Array for Mobile Methane Monitoring. Sensors 2024, 24, 519. [Google Scholar] [CrossRef] [PubMed]
- Furst, L.; Feliciano, M.; Frare, L.; Igrejas, G. A Portable Device for Methane Measurement Using a Low-Cost Semiconductor Sensor: Development, Calibration and Environmental Applications. Sensors 2021, 21, 7456. [Google Scholar] [CrossRef]
- Riddick, S.N.; Mauzerall, D.L.; Celia, M.; Allen, G.; Pitt, J.; Kang, M.; Riddick, J.C. The Calibration and Deployment of a Low-Cost Methane Sensor. Atmos. Environ. 2020, 230, 117440. [Google Scholar] [CrossRef]
- van den Bossche, M.; Rose, N.T.; De Wekker, S.F.J. Potential of a Low-Cost Gas Sensor for Atmospheric Methane Monitoring. Sens. Actuators B Chem. 2017, 238, 501–509. [Google Scholar] [CrossRef]
- Shah, A.; Laurent, O.; Broquet, G.; Philippon, C.; Kumar, P.; Allegrini, E.; Ciais, P. Determining Methane Mole Fraction at a Landfill Site Using the Figaro Taguchi Gas Sensor 2611-C00 and Wind Direction Measurements. Environ. Sci. Atmos. 2024, 4, 362–386. [Google Scholar] [CrossRef]
- Almand-Hunter, B.B.; Walker, J.T.; Masson, N.P.; Hafford, L.; Hannigan, M.P. Development and Validation of Inexpensive, Automated, Dynamic Flux Chambers. Atmos. Meas. Tech. 2015, 8, 267–280. [Google Scholar] [CrossRef]
- Camarda, M.; Gurrieri, S.; Valenza, M. Effects of Soil Gas Permeability and Recirculation Flux on Soil CO2 Flux Measurements Performed Using a Closed Dynamic Accumulation Chamber. Chem. Geol. 2009, 265, 387–393. [Google Scholar] [CrossRef]
- Rayment, M.B.; Jarvis, P.G. An Improved Open Chamber System for Measuring Soil CO2 Effluxes in the Field. J. Geophys. Res. Atmos. 1997, 102, 28779–28784. [Google Scholar] [CrossRef]
- Kuhn, J.N.; Elwell, A.C.; Elsayed, N.H.; Joseph, B. Requirements, Techniques, and Costs for Contaminant Removal from Landfill Gas. Waste Manag. 2017, 63, 246–256. [Google Scholar] [CrossRef] [PubMed]
- Berger, S.; Dun, S.; Gavrelis, N.; Helmick, J.; Mann, J.; Nickle, R.; Perlman, G.; Warner, S.; Wilhelmi, J.; Williams, R.; et al. Landfill Gas Basics. In Landfill Gas Primer: An Overview for Environmental Health Professionals; Agency for Toxic Substances and Disease Registry: Atlanta, GA, USA, 2001; pp. 3–14. [Google Scholar]




| Technology/Tool | Strengths | Weaknesses |
|---|---|---|
| Aerial Remote Sensing [5] | Rapid, direct detection of methane plumes; identification of leaks and hotspots; relatively low-cost with use of UAVs | Limited spatial coverage; sensitive to weather and operator technique; typically qualitative; snapshot in time |
| Aerial Mass Balance [6,7] | Large area coverage; detection of major emission zones quickly; quantification of emissions of overall landfill area and hotspots in some cases | Expensive; snapshot in time; accuracy affected by wind and atmospheric conditions |
| Eddy Covariance [8,15] | Quantitative flux estimation; continuous measurements that can capture temporal variability; minimal site disturbance | Complex data analysis; requires specific meteorology; high-cost and technical expertise needed; relies on installation of tower infrastructure; limited spatial resolution of emissions |
| Fence-line Surveys with Gaussian Plume Modeling [9] | Tracer gas enhances accuracy; comprehensive spatial coverage and resolution possible | Model assumptions may not capture complex terrain or variable meteorology |
| Sensor Networks with Inverse Modeling [10] | Continuous monitoring over long periods; relatively low-cost | Indirect flux estimates with model uncertainty; requires dense, well-calibrated sensor network |
| Static Flux Chamber [11,13,17] | Simple, low-cost and direct measurement; portable | Labor-intensive; very limited spatial coverage; can alter local pressure and flux dynamics |
| Dynamic Flux Chamber [12,16,18] | Better accuracy relative to static chambers since concentrations build up in the chamber to a lesser extent; allows for continuous near-real-time flux determination; direct measurement | More complex systems relative to static chambers; limited spatial representativeness; requires stable setup and calibration; potential to alter flux dynamics related to pressure, temperature, and CH4 concentration |
| Targeted Satellite Observations [14,15] | Very broad spatial coverage; enables regional or global methane tracking; useful for identifying super-emitters | Limited spatial resolution; cloud interference; retrieval accuracy lower for small or variable sites |
| Maker | Sensor | Manufacturer Specified Sensitivities | Cost Per Unit | Ambient Sensor Array | Chamber Sensor Array |
|---|---|---|---|---|---|
| Figaro | TGS2600 | air, methane, CO, iso-butane, ethanol, hydrogen, temperature, humidity | 11.00 USD | 1 | 1 |
| Figaro | TGS2602 | air, hydrogen, ammonia, ethanol, hydrogen sulfide, toluene, temperature, humidity | 12.20 USD | 1 | 1 |
| Figaro | TGS2611 | air, hydrogen, ethanol, methane, temperature, humidity | 11.20 USD | 1 | 1 |
| Bosch Sensortec | BME680-Gas | ethane, isoprene, ethanol, acetone, CO, temperature, humidity | 10.76 USD | 1 | 1 |
| BME680-Pressure | pressure | ||||
| BME680-Temperature | temperature | ||||
| BME680-Humidity | relative humidity |
| Regression Range | Coefficient | Predictor | p-Value | Intercept |
|---|---|---|---|---|
| 0–100 ppm | C00 = −0.00129 | TGS2600 | 0.9634 | B = −217.237 |
| C02 = 0.00501 | TGS2602 | 3.013 × 10−6 | ||
| C11 = 0.124537 | TGS2611 | 7.872 × 10−11 | ||
| CBME = 1.443659 | BME | 3.921 × 10−265 | ||
| CT = −1.12251 | Temperature | 6.959 × 10−21 | ||
| CH = −0.15887 | Relative Humidity | 8.961 × 10−5 | ||
| CR1 = −301.944 | 0 | |||
| CR2 = −77.486 | 3.249 × 10−65 | |||
| CR3 = 66.68535 | 1.076 × 10−18 | |||
| CR4 = 1581.711 | 1.948 × 10−67 | |||
| CR5 = 72.63999 | 3.847 × 10−10 | |||
| CR6 = −207.449 | 3.514 × 10−7 |
| Regression Range | Coefficient | Predictor | p-Value | Intercept |
|---|---|---|---|---|
| 100–1500 ppm | C00 = −2.01822 | TGS2600 | 1.753 × 10−255 | B = 768.135 |
| C02 = 0.106666 | TGS2602 | 8.978 × 10−109 | ||
| C11 = 1.159243 | TGS2611 | 0 | ||
| CBME = 0.374516 | BME | 8.780 × 10−14 | ||
| CT = 12.47826 | Temperature | 1.220 × 10−75 | ||
| CH = 3.837942 | Relative Humidity | 3.673 × 10−62 | ||
| CR1 = 361.3001 | 3.960 × 10−46 | |||
| CR2 = −9359.08 | 1.185 × 10−134 | |||
| CR3 = −765.343 | 0 | |||
| CR4 = 0.467051 | 2.519 × 10−304 | |||
| CR5 = −0.09559 | 2.356 × 10−302 | |||
| CR6 = 902.1457 | 2.880 × 10−58 |
| Regression Range | Coefficient | Predictor | p-Value | Intercept |
|---|---|---|---|---|
| 1500–12,000 ppm | C00 = −2.84299 | TGS2600 | 6.607 × 10−169 | B = 2952.922 |
| C02 = 0.033676 | TGS2602 | 0.0825 | ||
| C11 = 4.499467 | TGS2611 | 0 | ||
| CBME = −1.11855 | BME | 3.927 × 10−10 | ||
| CT = −189.655 | Temperature | 0 | ||
| Chum = −180.961 | Relative Humidity | 0 | ||
| CR1 = −434,102 | 0 | |||
| CR2 = −39.383 | 0 | |||
| CR3 = −3907.23 | 0 | |||
| CR4 = 387,837.2 | 0 | |||
| CR5 = 293,553.9 | 1.284 × 10−246 | |||
| CR6 = 5562.674 | 7.929 × 10−184 |
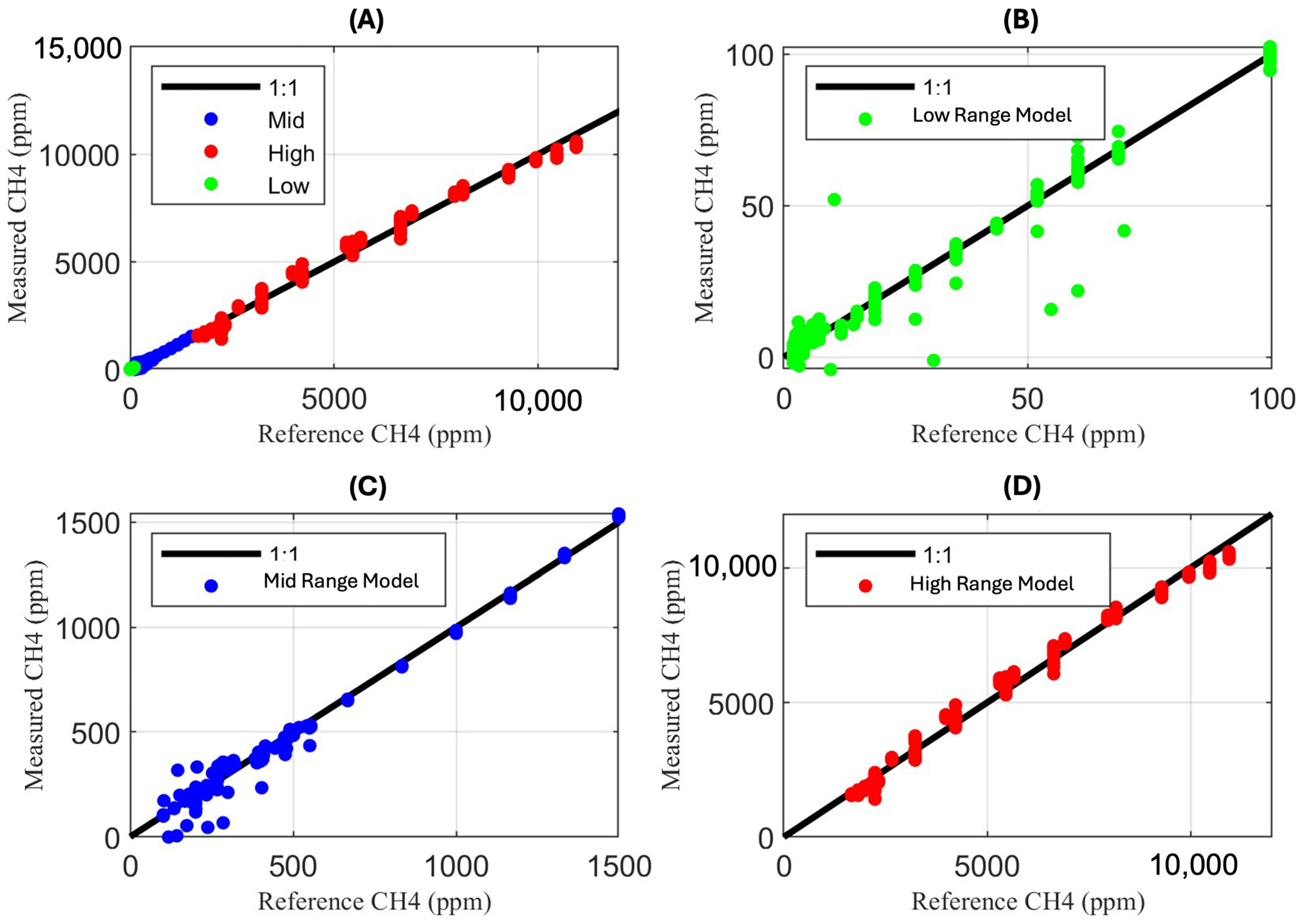
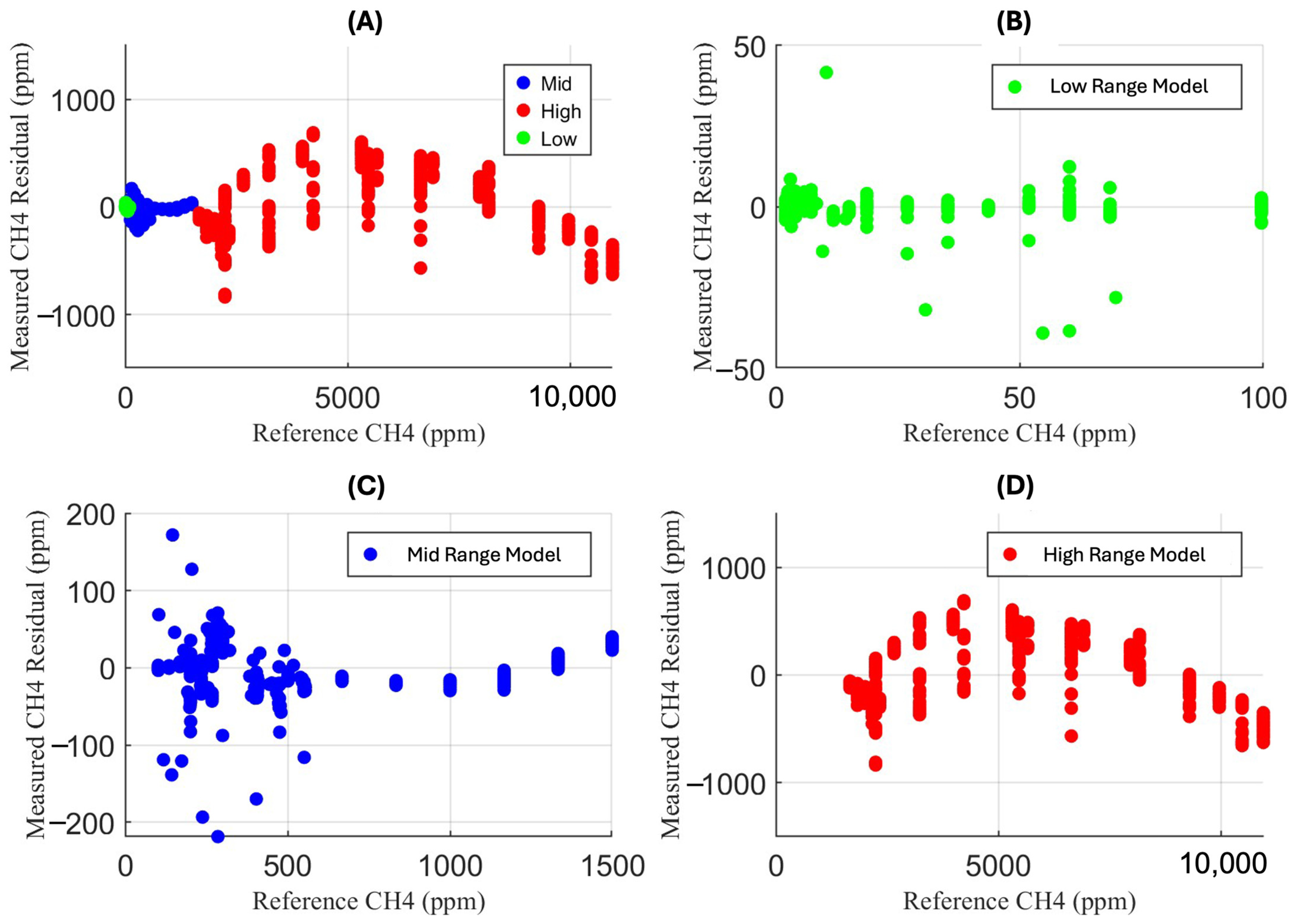
| Piecewise Range | RMSE (ppm) | MBE | R^2 | Max Percent Error (%) |
|---|---|---|---|---|
| 10–100 | 3.1 | 2.9 × 10−14 | 0.994 | 31.0 |
| 100–1500 | 21 | −0.38 | 0.997 | 21.1 |
| 1500–12,000 | 307 | 1.1 | 0.991 | 20.5 |
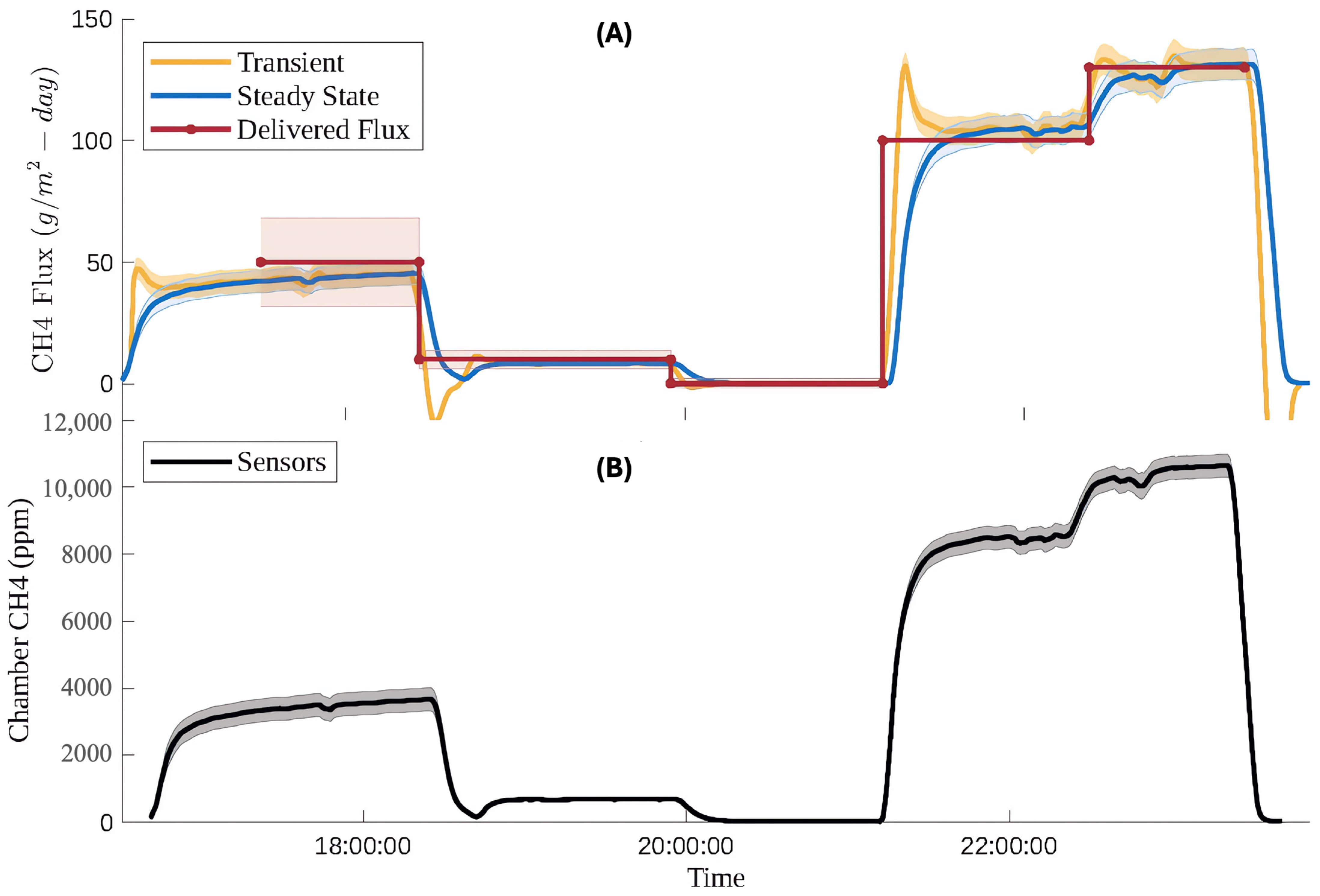
| Quantification Method | RMSE (g/m2-Day) | MBE (g/m2-Day) |
|---|---|---|
| Transient Model (Continuous) | 50 | −4.9 |
| Steady State Model (Continuous) | 10.8 | −1.6 |
| Setpoint Average (Discrete) | 7.3 | −2.2 |
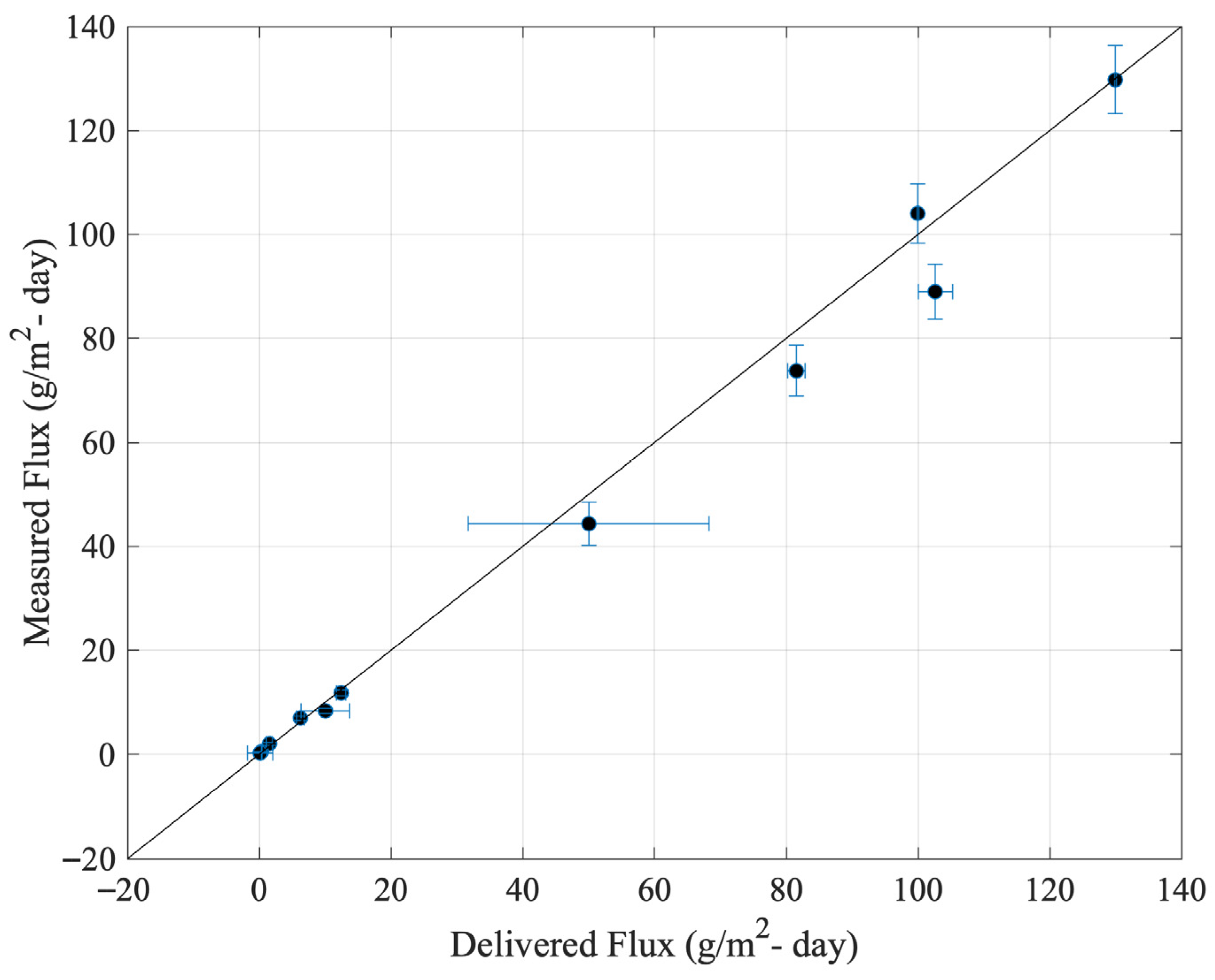
| Delivered Flux (g/m2-Day) | Measured Flux (g/m2-Day) | % Uncertainty of Measured Flux |
|---|---|---|
| 0.11 ± 2 | 0.26 ± 0.04 | 15 |
| 0.33 ± 0.06 | 0.44 ± 0.04 | 10 |
| 1.6 ± 0.5 | 2.03 ± 0.3 | 13 |
| 6.3 ± 0.5 | 6.9 ± 0.4 | 6 |
| 10.0 ± 4 | 8.3 ± 0.4 | 5 |
| 12.5 ± 0.7 | 11.8 ± 0.6 | 5 |
| 50 ± 20 | 44 ± 4 | 9 |
| 82 ± 1 | 74 ± 5 | 7 |
| 100.0 ± 0.1 | 104 ± 6 | 5 |
| 103 ± 3 | 89 ± 6 | 6 |
| 130.0 ± 0.2 | 129 ± 7 | 5 |
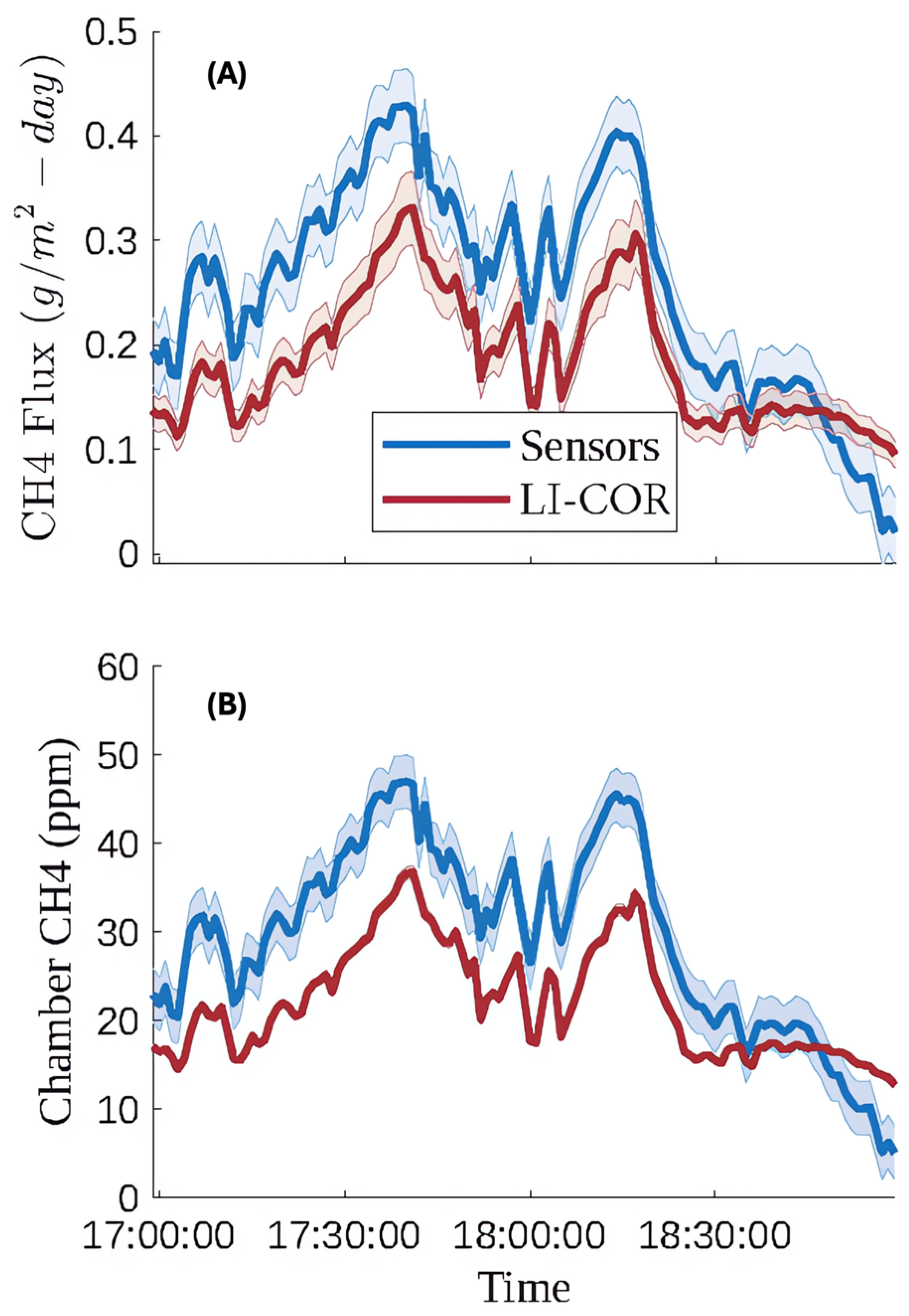
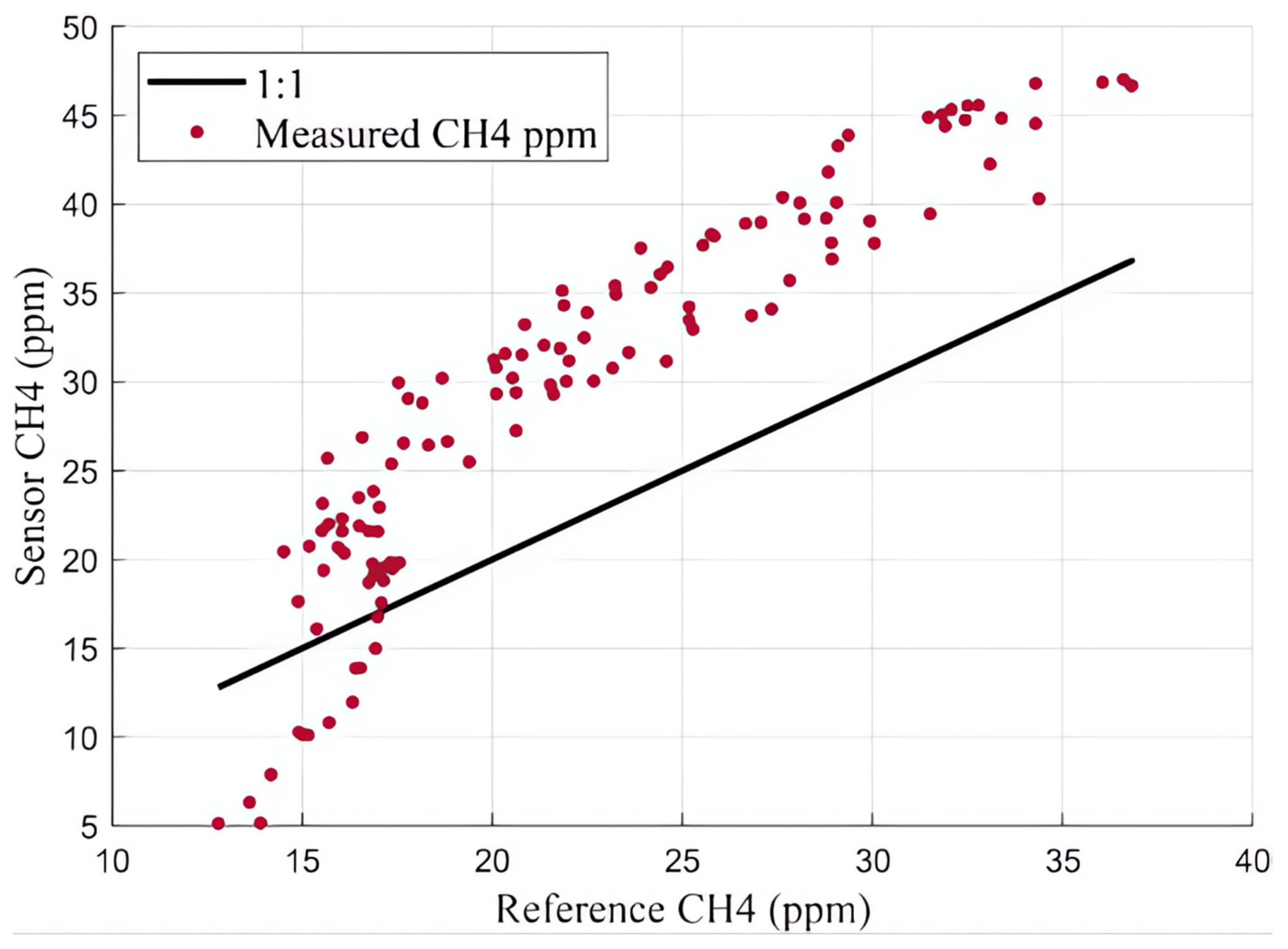
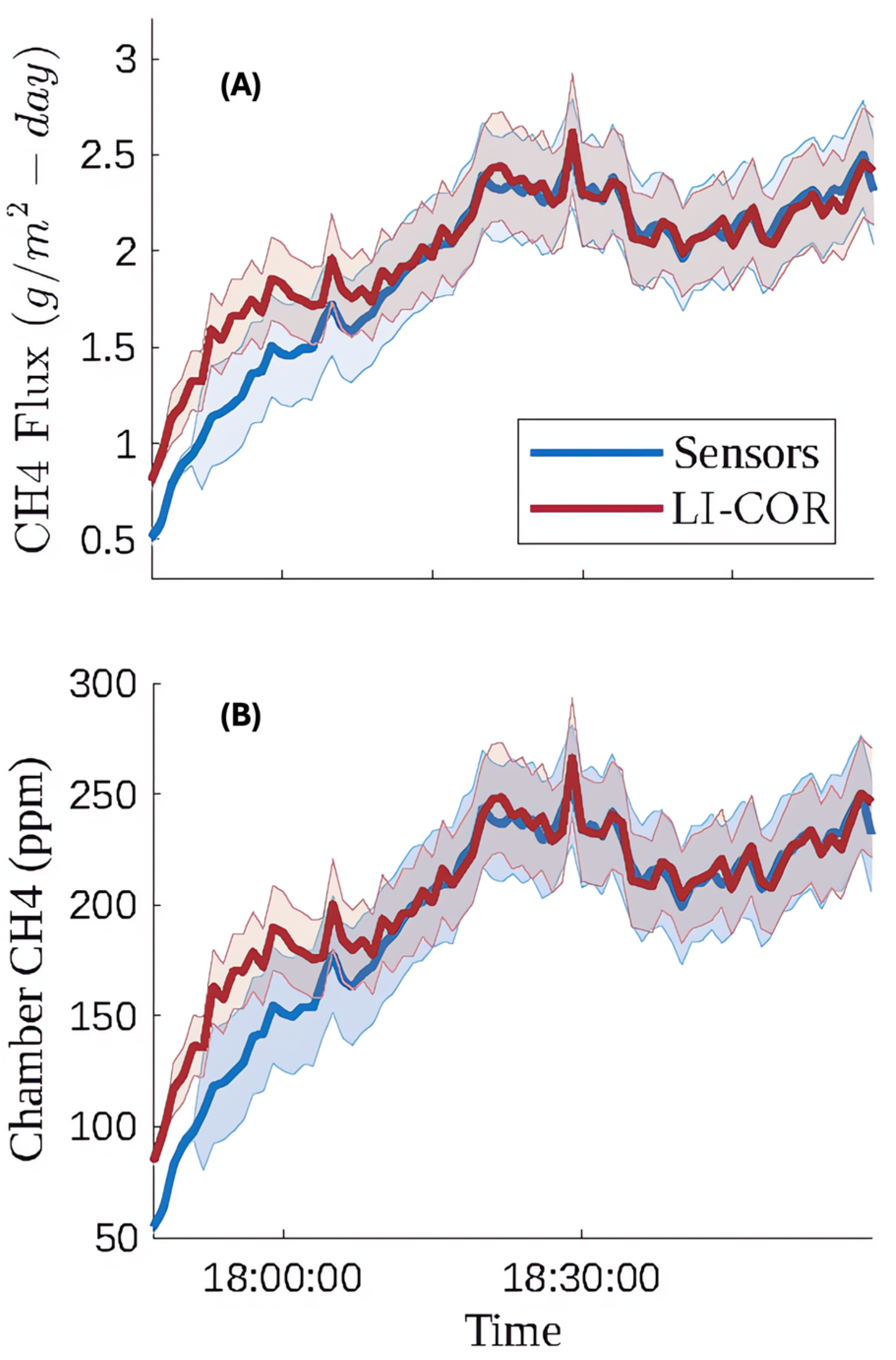
| Test Date | RMSE (ppm) | MBE (ppm) | Mean % Error |
|---|---|---|---|
| April 9th | 9.0 | 7.2 | 37.0 |
| April 12th | 16.9 | −7.6 | 6.74 |
| Test Date | RMSE (g/m2-Day) | MBE (g/m2-Day) | Mean % Error |
|---|---|---|---|
| April 9th | 0.08 | 0.05 | 30.1 |
| April 12th | 0.47 | −0.31 | 11.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brown, A.G.; Rousseau, N.G.; Doskocil, D.; O’Neill, C.T.; VanMatre, S.G.; Kane, J.J.; Casey, J.G.; Hannigan, M.P.; Coffey, E.R. Calibration and Validation of an Autonomous, Novel, Low-Cost, Dynamic Flux Chamber for Measuring Landfill Methane Emissions. Sensors 2025, 25, 6613. https://doi.org/10.3390/s25216613
Brown AG, Rousseau NG, Doskocil D, O’Neill CT, VanMatre SG, Kane JJ, Casey JG, Hannigan MP, Coffey ER. Calibration and Validation of an Autonomous, Novel, Low-Cost, Dynamic Flux Chamber for Measuring Landfill Methane Emissions. Sensors. 2025; 25(21):6613. https://doi.org/10.3390/s25216613
Chicago/Turabian StyleBrown, Avery G., Nikona G. Rousseau, Dylan Doskocil, Cullen T. O’Neill, Seth G. VanMatre, Justin J. Kane, Joanna G. Casey, Michael P. Hannigan, and Evan R. Coffey. 2025. "Calibration and Validation of an Autonomous, Novel, Low-Cost, Dynamic Flux Chamber for Measuring Landfill Methane Emissions" Sensors 25, no. 21: 6613. https://doi.org/10.3390/s25216613
APA StyleBrown, A. G., Rousseau, N. G., Doskocil, D., O’Neill, C. T., VanMatre, S. G., Kane, J. J., Casey, J. G., Hannigan, M. P., & Coffey, E. R. (2025). Calibration and Validation of an Autonomous, Novel, Low-Cost, Dynamic Flux Chamber for Measuring Landfill Methane Emissions. Sensors, 25(21), 6613. https://doi.org/10.3390/s25216613









