Method for Suppressing Non-Stationary Interference in the Main-Lobe Based on a Multi-Polarized Array
Abstract
1. Introduction
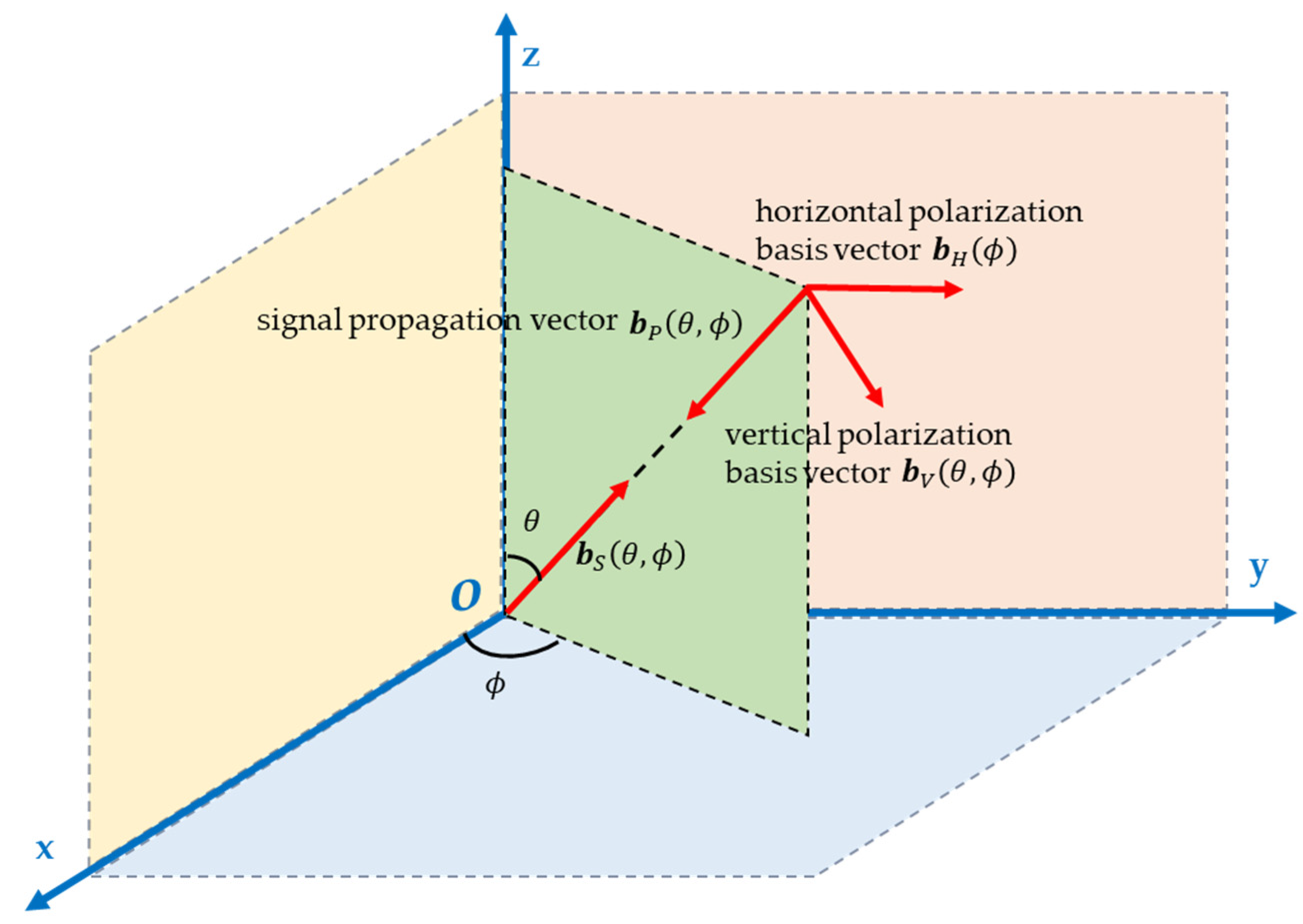
2. Received Signal Model
3. Interference Suppression Method
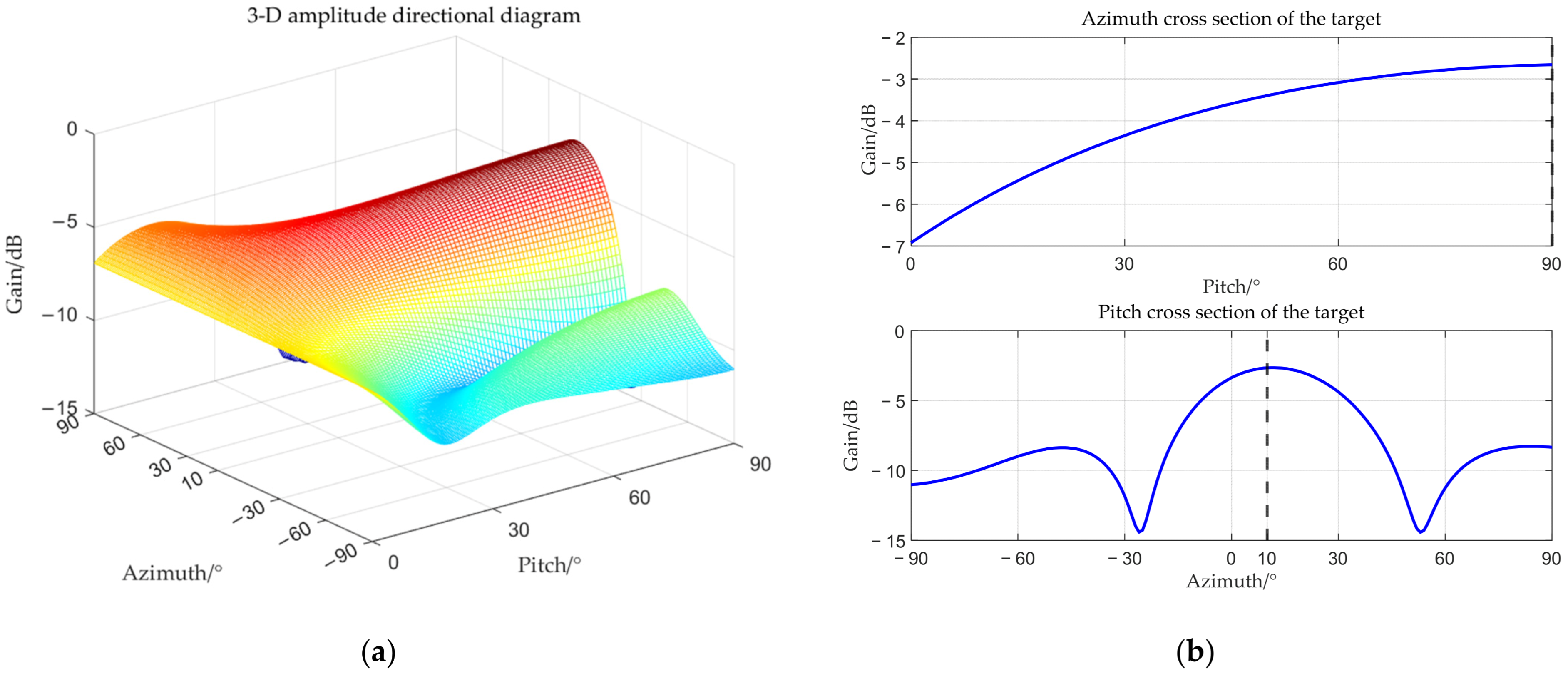
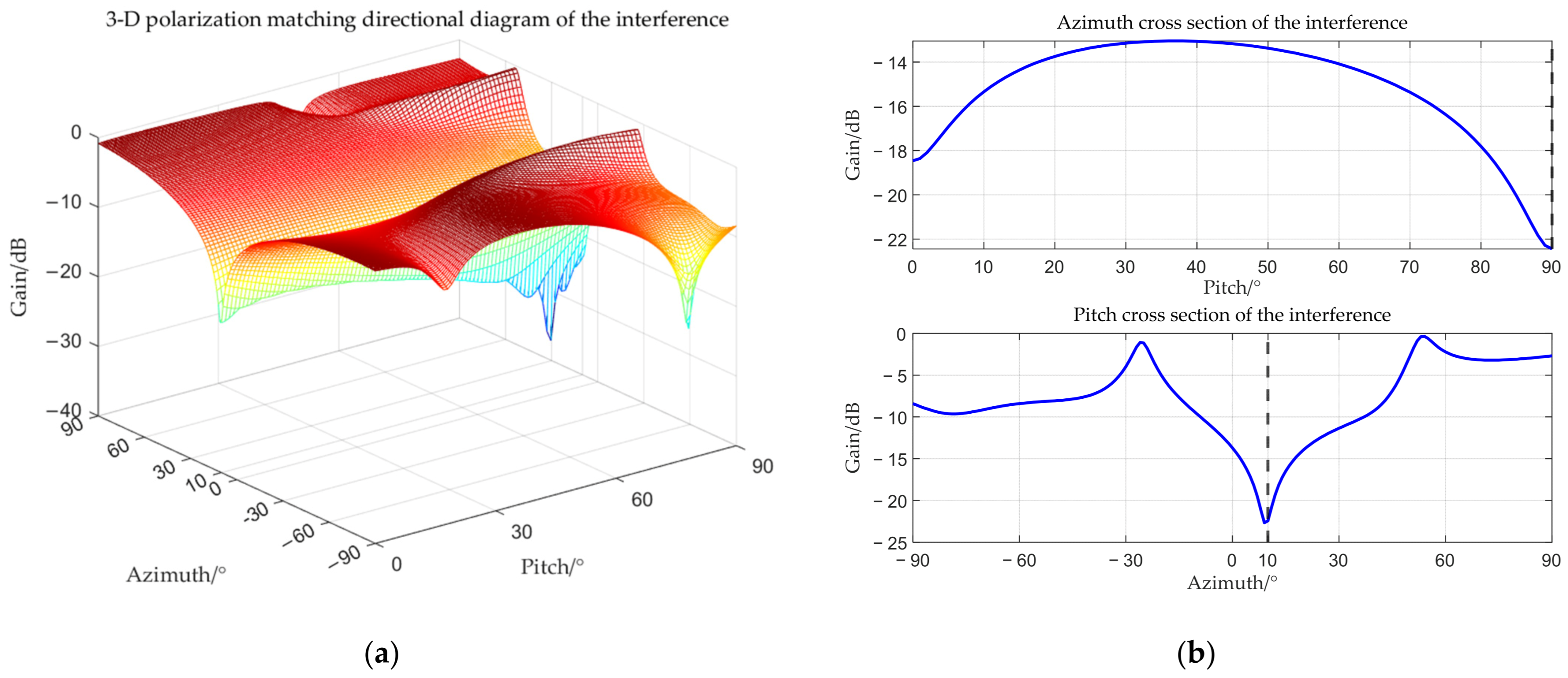
3.1. Calculating Target Steering Vector
3.2. Constructing Time–Frequency Covariance Matrix
3.3. Beamforming
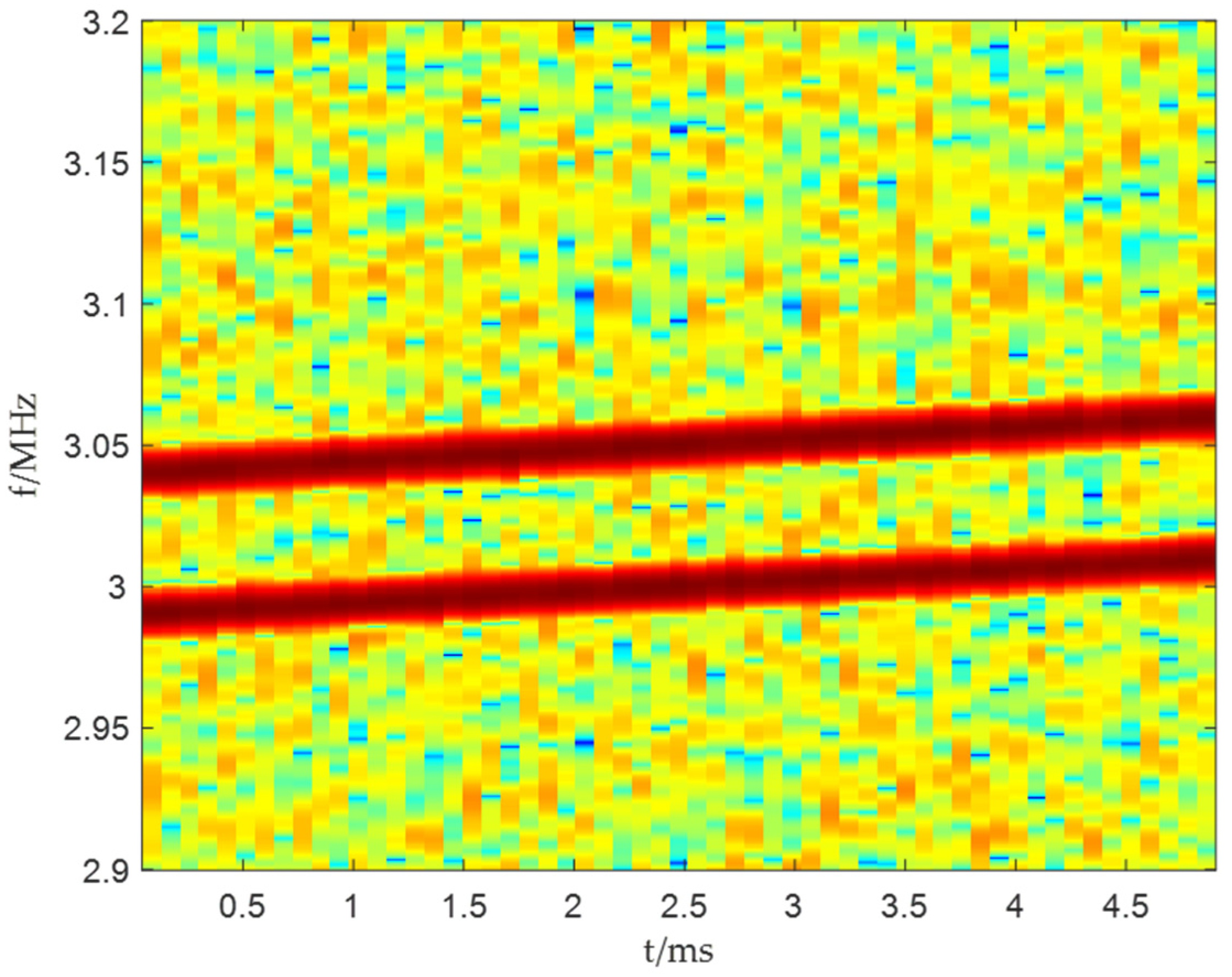
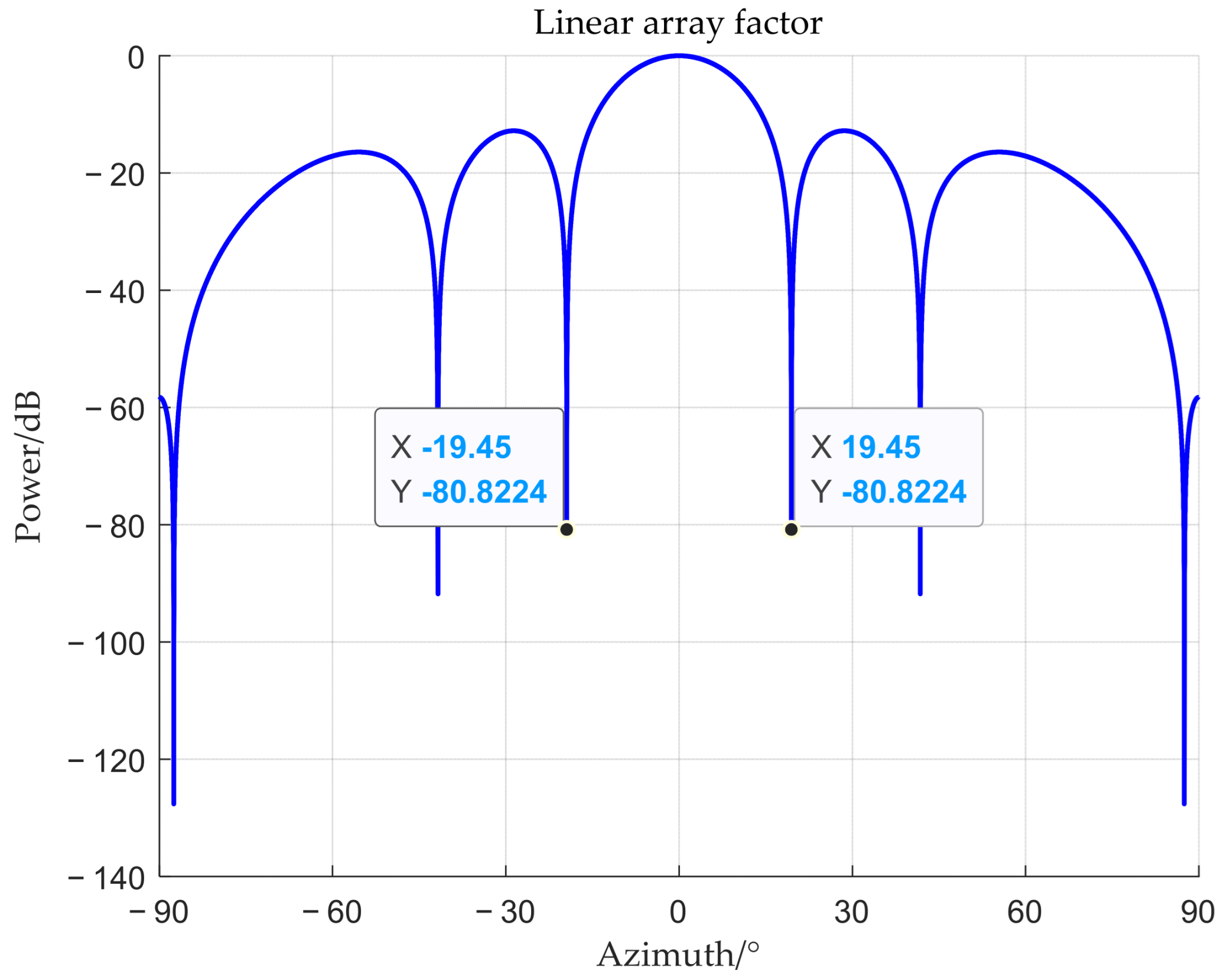
4. Simulation Analysis
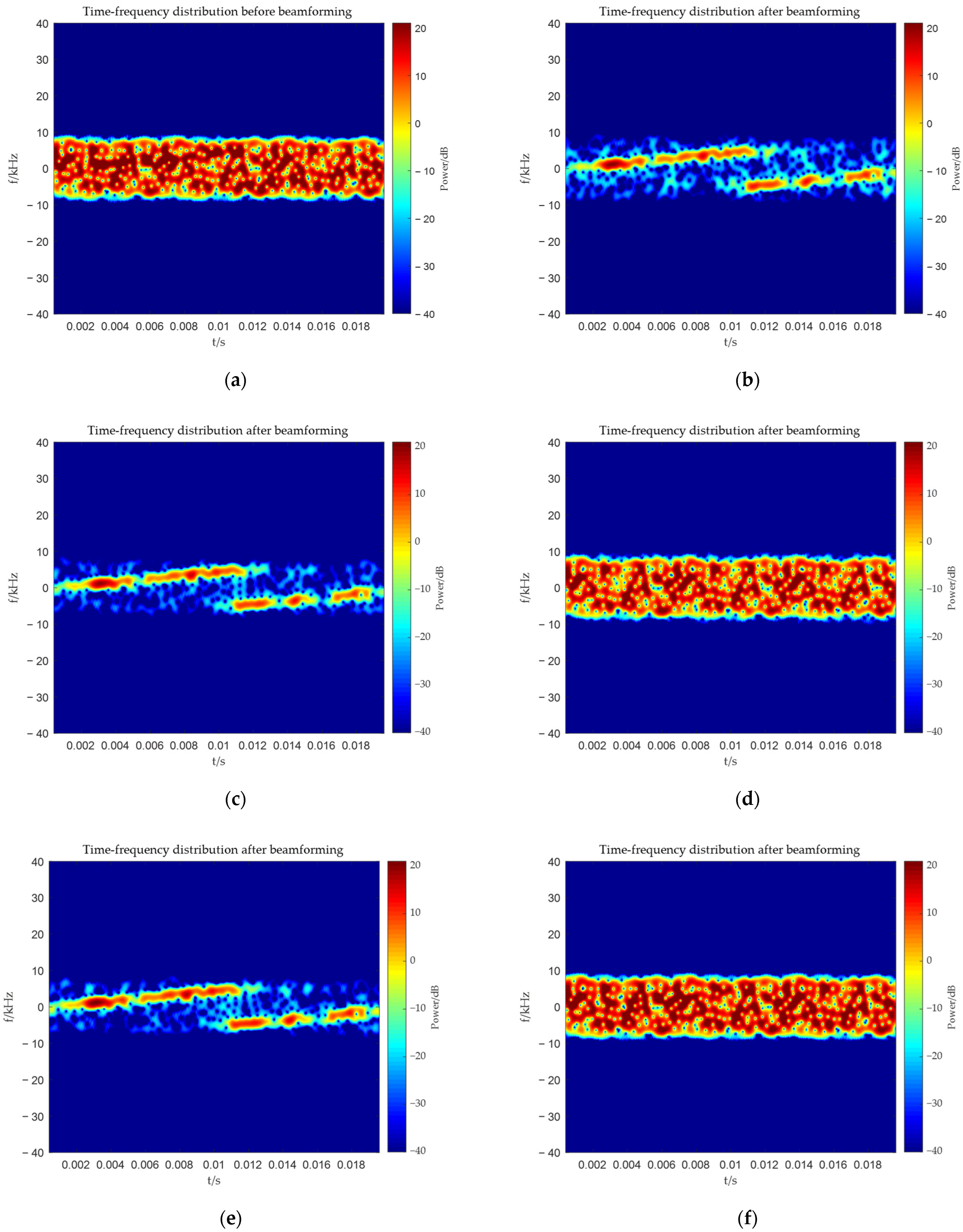
4.1. The Interference Is Located Within the Main-Lobe
4.2. Interference Coincides with the Target
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Duan, B.W.; Bai, Z.D.; Chen, Q.Y. Real-time modeling and analysis of ionosphere in the China region. Eng. Surv. Mapp. 2025, 34, 22–29+38. [Google Scholar]
- Ji, Y.F.; Dong, Z.; Zhang, Y.S.; Xiong, C.; Mao, W.F.; Wang, C. Research overview on ionospheric probing based on spaceborne synthetic aperture radars. J. Radars 2025, 14, 1323–1342. [Google Scholar] [CrossRef]
- Zhen, W.M.; Ou, M.; Zhu, Q.L.; Dong, X.; Liu, D. Review on ionospheric sounding and modeling. Chin. J. Radio Sci. 2023, 38, 625–645. [Google Scholar] [CrossRef]
- Zhen, W.M.; Ou, M.; Yu, X.; Feng, J.; Wu, J. Ionospheric Measurement and Application Technology Based on Satellite Beacon Signal; National Defense Industry Press: Beijing, China, 2022. [Google Scholar]
- Shi, S.; Yang, G.; Jiang, C.; Zhang, Y.; Zhao, Z. Wuhan Ionospheric Oblique Backscattering Sounding System and Its Applications—A Review. Sensors 2017, 17, 1430. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.P. Ground Wave Radar Ionospheric Clutter Interference and Suppression Measures. Sci. Technol. Innov. 2020, 15, 112–113. [Google Scholar]
- Han, S.; Guo, W.; Liu, P.; Wang, T.; Wang, C.; Fang, Q.; Yang, J.; Li, L.; Liu, D.; Huang, J. Chaotic Coding for Interference Suppression of Digital Ionosonde. Remote Sens 2023, 15, 3747. [Google Scholar] [CrossRef]
- Chen, Z.; Xie, F.; Zhao, C.; He, C. An Orthogonal Projection Algorithm to Suppress Interference in High-Frequency Surface Wave Radar. Remote Sens. 2018, 10, 403. [Google Scholar] [CrossRef]
- Zhang, C.F.; Jiao, P.N.; Li, Q.; Zheng, R.Q. An Approach of Interference Mitigation in Backscatter Sounding of Ionosphere. J. China Acad. Electron. Inf. Technol. 2011, 6, 630–633. [Google Scholar]
- Lao, C.Z.; Yang, G.B.; Liu, T.X.; Jiang, C.H.; Li, H.; Tian, R. An Adaptive Eigen-Subspace Filtering Method for Interference Suppression in Wuhan Ionospheric Oblique Backscatter Sounding System. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Zhang, X.; Yao, D.; Yang, Q.; Dong, Y.; Deng, W. Knowledge-Based Generalized Side-Lobe Canceller for Ionospheric Clutter Suppression in HFSWR. Remote Sens. 2018, 10, 104. [Google Scholar] [CrossRef]
- Guo, Y.Y.; Wei, Y.S.; Xu, R.Q. Fast-Time STAP Based on BSS for Heterogeneous Ionospheric Clutter Mitigation in HFSWR. IET Radar Sonar Navig. 2020, 14, 927–934. [Google Scholar] [CrossRef]
- Huang, L.; Wen, B.Y.; Wu, L.M.; Yao, M. Ionospheric Interference Mitigation in HFSWR. Chin. J. Radio Sci. 2007, 22, 626–630. [Google Scholar]
- Guo, X.; Sun, H.B.; Yeo, T.S. Interference Cancellation for High-Frequency Surface Wave Radar. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1879–1891. [Google Scholar]
- Chen, G.; Zhao, Z.Y.; Zhu, G.Q.; Huang, Y.J.; Li, T. HF Radio-Frequency Interference Mitigation. IEEE Geosci. Remote Sens. Lett. 2010, 7, 479–482. [Google Scholar] [CrossRef]
- Wang, B.D. Polarization of Electromagnetic Waves and Its Applications. Chin. J. Radio Sci. 1999, 3, 347–356. [Google Scholar] [CrossRef]
- Zhao, C.Y. Polarization Ways of Electromagnetic Wave and Its Applications. Sci. Technol. Innov. Her. 2013, 24, 11–12. [Google Scholar]
- Quan, B.; Liang, X.H.; Ji, G.B.; Cheng, Y.; Liu, W.; Ma, J.N.; Zhang, Y.A.; Li, D.R.; Xu, G.Y. Dielectric Polarization in Electromagnetic Wave Absorption: Review and Perspective. J. Alloys Compd. 2017, 728, 1065–1075. [Google Scholar] [CrossRef]
- Chen, J. Theoretical Analysis and Application of Antenna Polarization Mismatch. Space Electron. Technol. 1998, 4, 48–53+63. [Google Scholar]
- Tian, W.R.; Li, J.N. Transmission Efficiency of Two Arbitrary-Polarization Waves and Its Effects on Antenna Measurements. Radar Sci. Technol. 2008, 6, 305–310. [Google Scholar]
- Xie, Q.P.; Pan, X.Y.; Chen, J.Y.; Xiao, S.P. Efficient angle and polarization parameter estimaiton for electromagnetic vector sensors multiple-input multiple-output radar by using sparse array. Acta Phys. Sin. 2020, 69, 074302. [Google Scholar] [CrossRef]
- Liang, H.; Cui, C.; Yu, J.; Hao, T.D. Joint Estimation of Two Dimensional DOA with High Accuracy and Polarization for MIMO Radar Using Electromagnetic Vector Sensor Arrays. J. Electron. Inf. Technol. 2016, 38, 2437–2444. [Google Scholar]
- Xu, Y.G.; Liu, Z.W. Simultaneous estimation of 2-D DOA and polarization of multiple coherent sources using an electromagnetic vector sensor array. J. Commun. 2004, 5, 28–38. [Google Scholar]
- Zhang, X.R.; Yang, J.J.; Xu, Y.G.; Liu, Z.W. GSC-beamformer based on electromagnetic vector-Sensor arrays. Aerosp. Electron. Warf. 2011, 27, 58–61. [Google Scholar]
- Liu, J.; Liu, W.J.; Liu, H.W.; Chen, B.; Xia, X.G.; Dai, F.Z. Average SINR calculation of a persymmetric sample matrix inversion beamformer. IEEE Trans. Signal Process. 2016, 64, 2135–2145. [Google Scholar] [CrossRef]
- Vorobyov, S.A.; Gershman, A.B.; Luo, Z.Q. Robust adaptive beamforming using worst-case performance optimization: A solution to the signal mismatch problem. IEEE Trans. Signal Process. 2003, 51, 313–324. [Google Scholar] [CrossRef]
- Vorobyov, S.A. Principles of minimum variance robust adaptive beamforming design. Signal Process. 2013, 93, 3264–3277. [Google Scholar] [CrossRef]
- Wang, H.Y.; Yao, Z.C.; Fan, Z.L.; Liu, G.B. Interference mitigation for GNSS receivers with dual-polarised sensitive arrays in the joint space–frequency–polarisation domain. IET Radar Sonar Navig. 2019, 13, 700–711. [Google Scholar] [CrossRef]
- Lin, Z.Y.; Tao, J.W. MVDR beamforming for correlated signal with vector smoothing. J. Commun. 2013, 34, 94–104. [Google Scholar]
- Li, H.T.; Li, Z.Z.; Song, Z.J.; Wang, L. A new algorithm for vector sensor line array beamforming. Transducer Microsyst. Technol. 2015, 34, 144–146, 150. [Google Scholar]
- Yue, Y.X.; Zhou, C.W.; Xing, F.Y.; Choo, K.K.R.; Shi, Z.G. Adaptive Beamforming for Cascaded Sparse Diversely Polarized Planar Array. IEEE Trans. Veh. Technol. 2023, 72, 15648–15664. [Google Scholar] [CrossRef]
- Dai, H.Y.; Li, Y.Z.; Liu, Y.; Wang, X.S. Novel research on main-lobe jamming polarization suppression technology. Sci. China Inf. Sci. 2012, 55, 368–376. [Google Scholar] [CrossRef]
- Ji, Y.; Lu, Y.; Wei, S.; Li, Z. Multiple Mainlobe Interferences Suppression Based on Eigen-Subspace and Eigen-Oblique Projection. Sensors 2022, 22, 8494. [Google Scholar] [CrossRef]
- Yang, X.P.; Zhang, Z.A.; Zeng, T.; Long, T.; Tapan, K.S. Mainlobe Interference Suppression Based on Eigen-Projection Processing and Covariance Matrix Reconstruction. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 1369–1372. [Google Scholar] [CrossRef]
- Zhang, L.; Su, L.H.; Wang, D.; Luo, Y.; Zhang, Q. Mainlobe Interference Suppression for Radar Network via RPCA-Based Covariance Matrix Reconstruction. IEEE Sens. J. 2023, 23, 5094–5108. [Google Scholar] [CrossRef]
- Li, R.; He, H.; Liu, X.; Wang, L.; You, Y.; Li, Z.; Han, X. An Anti-Mainlobe Suppression Jamming Method Based on Improved Blind Source Separation Using Variational Mode Decomposition and Wavelet Packet Decomposition. Sensors 2025, 25, 3404. [Google Scholar] [CrossRef]
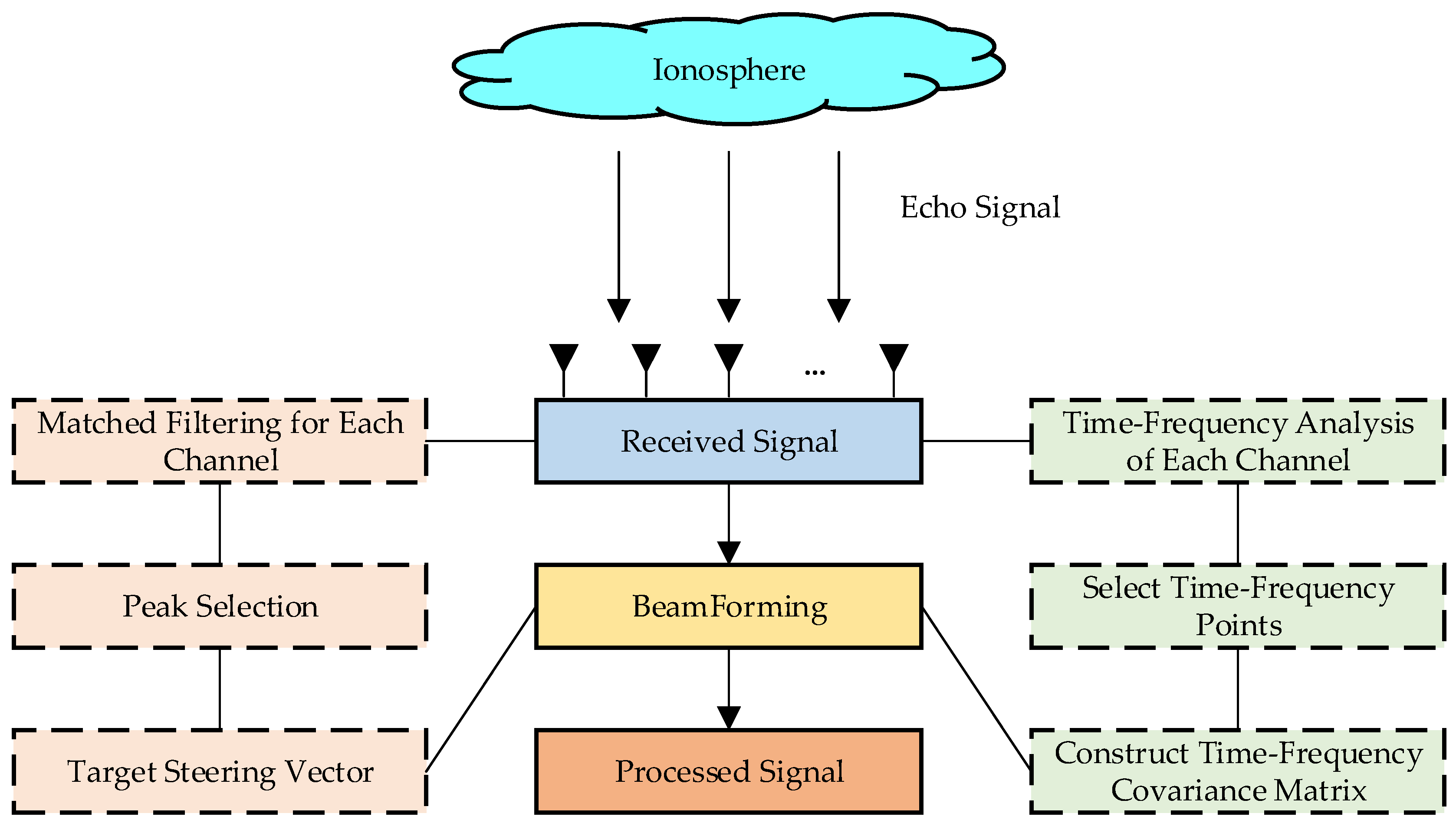
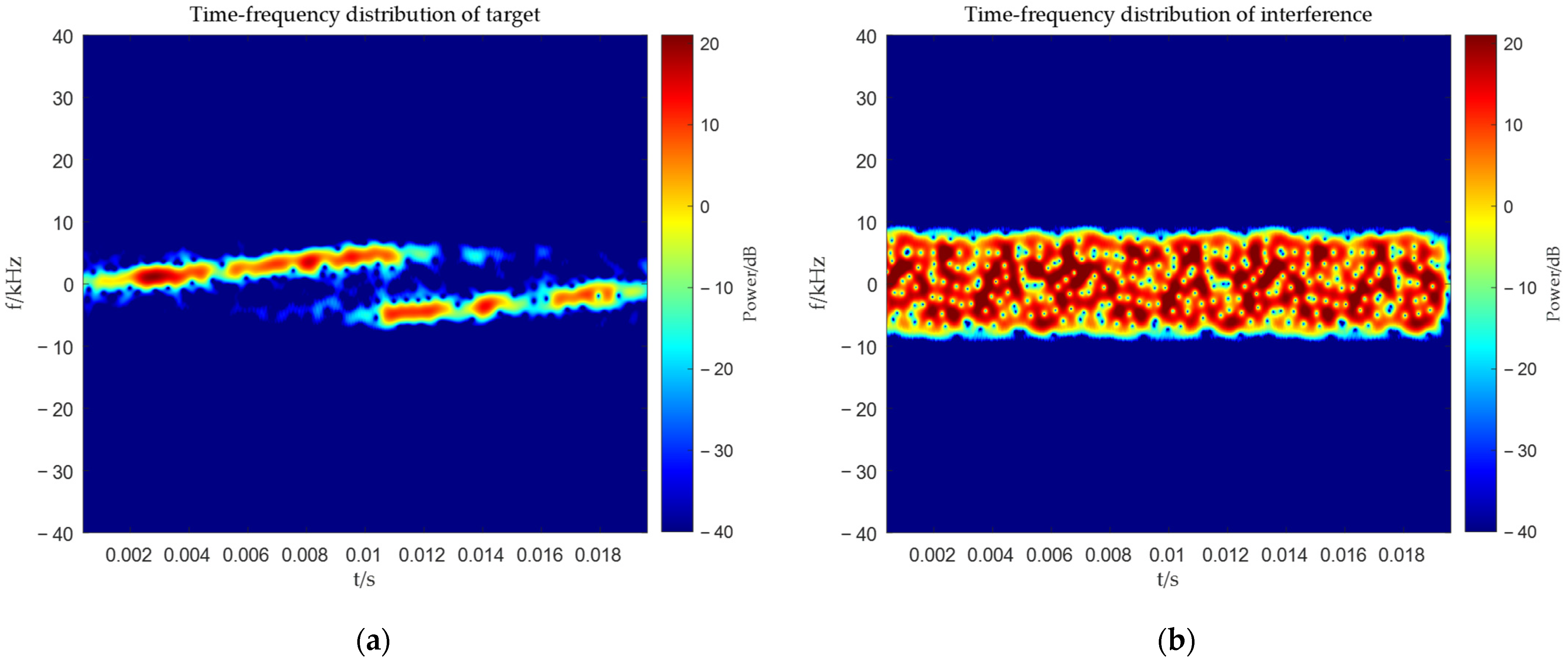
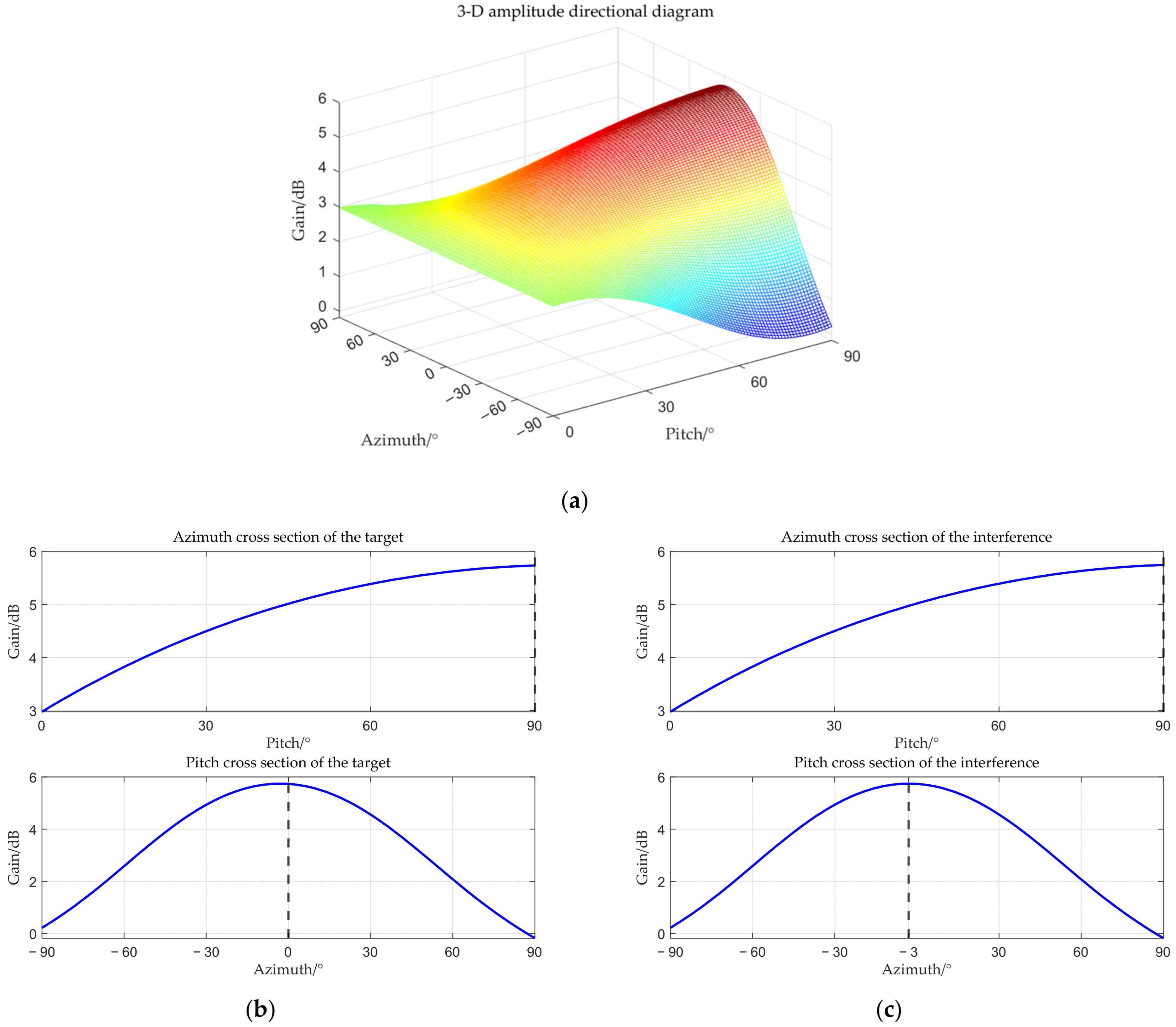
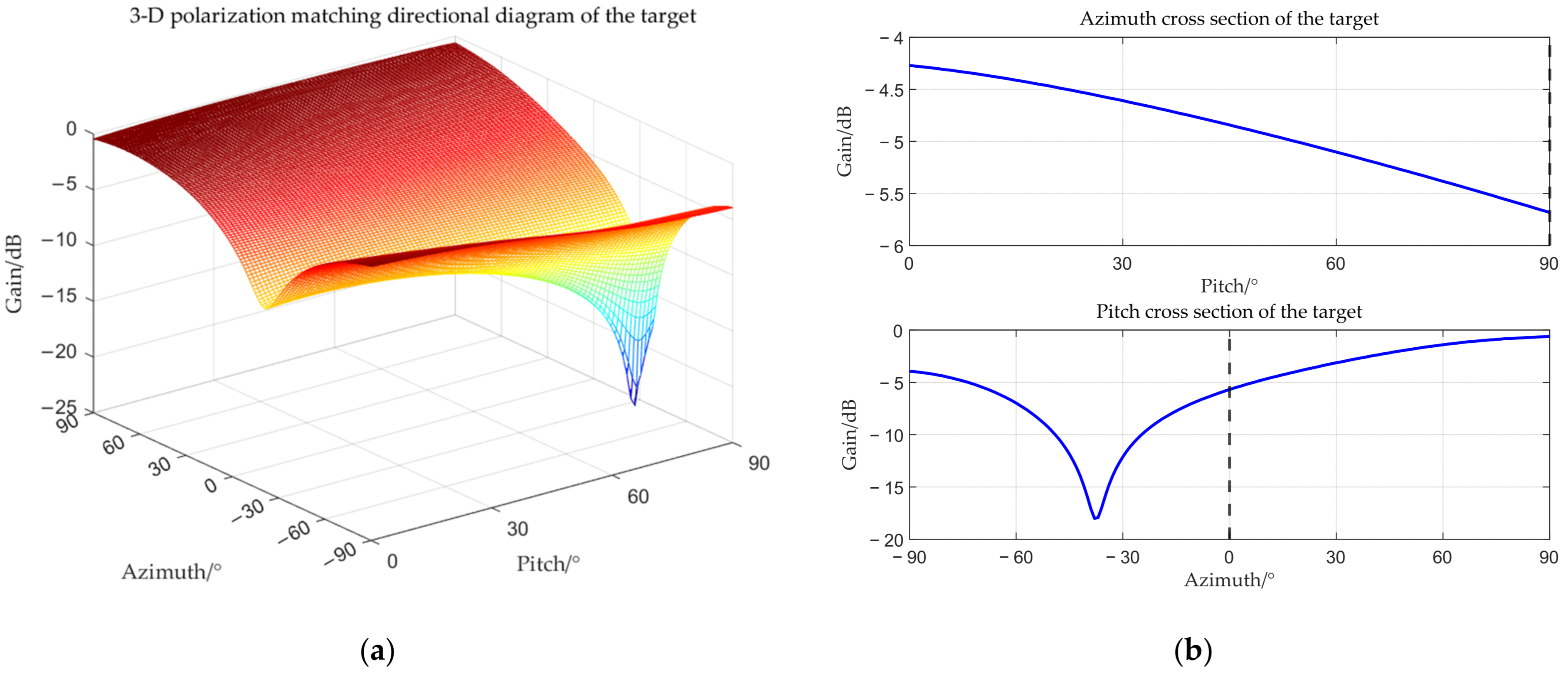
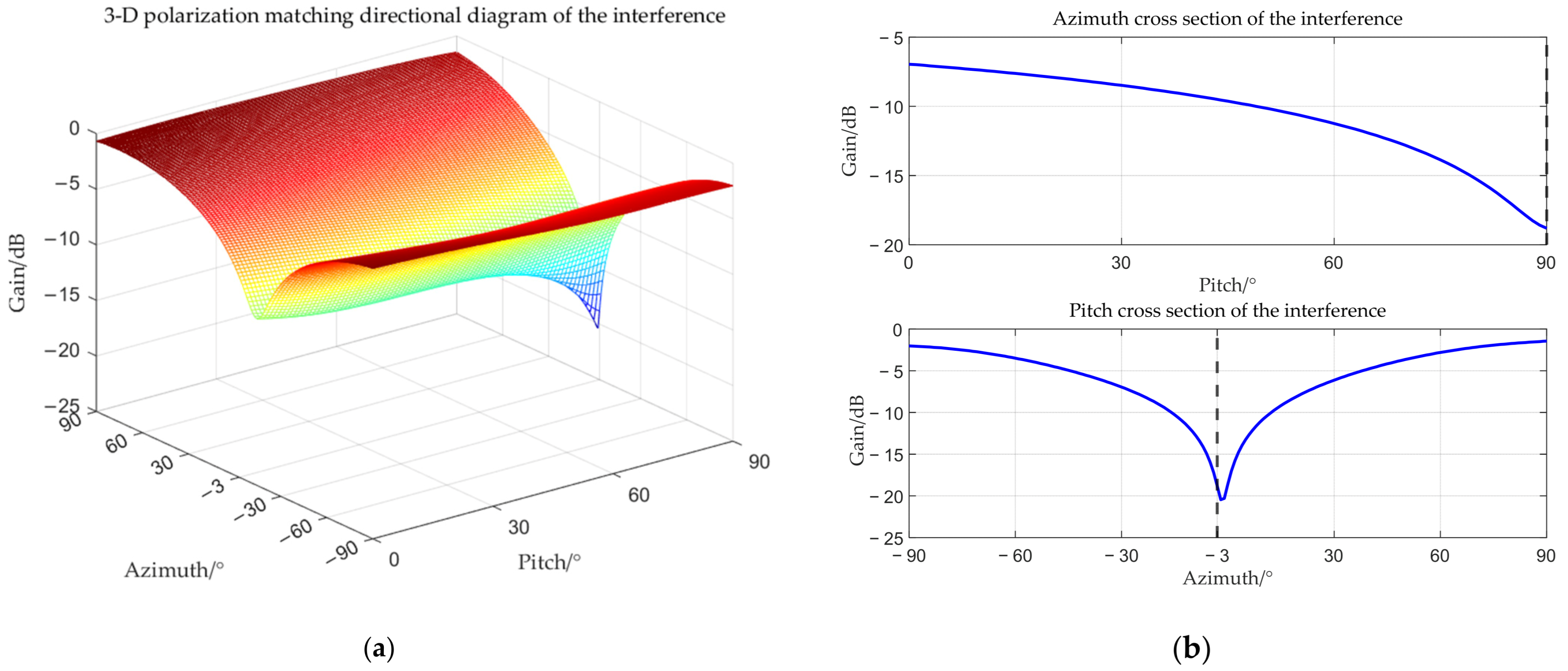



| Beamforming Method for Non-Stationary Interference in the Main-Lobe Based on a Multi-Polarized Array |
|---|
| 1) According to Equation (13), perform matched filtering on the outputs of each channel and select the peak points at the same position to obtain the estimated target steering vector . |
| 2) Based on Equations (17), (19) and (22), perform time–frequency analysis on the output of each channel of the array to obtain |
| 3) Calculating spatial time–frequency distribution matrix by Equations (26) and (27). |
| 4) Determine frequency point judgment matrix according to Equation (28), and then calculate the time–frequency covariance matrix according to Equation (29). |
| 5) Calculating the beamforming weight vector according to Equation (36). |
| 6) The beamforming result is |
| 7) Calculating amplification coefficient by Equations (37) and (38), The final result of beamforming is |
| Parameter Name | Parameter Value |
|---|---|
| Carrier Frequency | 16,320 kHz |
| Sampling Frequency | 80 kHz |
| Band-Width | 10 kHz |
| Time-Width | 20 ms |
| Sampling Points | 1600 |
| Spacing between Array Elements | 6.9 m |
| Number of Array Elements | 8 |
| SNR | 10 dB |
| Fully Polarized Parameters (Target) | (20°, 10°) |
| Fully Polarized Parameters (Interference) | (30°, 40°) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Ding, S.; Wei, N.; Bi, J.; Zheng, R. Method for Suppressing Non-Stationary Interference in the Main-Lobe Based on a Multi-Polarized Array. Sensors 2025, 25, 6587. https://doi.org/10.3390/s25216587
Wang J, Ding S, Wei N, Bi J, Zheng R. Method for Suppressing Non-Stationary Interference in the Main-Lobe Based on a Multi-Polarized Array. Sensors. 2025; 25(21):6587. https://doi.org/10.3390/s25216587
Chicago/Turabian StyleWang, Jie, Shujuan Ding, Na Wei, Jinzhi Bi, and Rongqiu Zheng. 2025. "Method for Suppressing Non-Stationary Interference in the Main-Lobe Based on a Multi-Polarized Array" Sensors 25, no. 21: 6587. https://doi.org/10.3390/s25216587
APA StyleWang, J., Ding, S., Wei, N., Bi, J., & Zheng, R. (2025). Method for Suppressing Non-Stationary Interference in the Main-Lobe Based on a Multi-Polarized Array. Sensors, 25(21), 6587. https://doi.org/10.3390/s25216587





