Improved Quadtree-Based Selection of Single Images for 3D Generation
Abstract
1. Introduction
- We introduce a novel quadtree model that incorporates multiple visual features—including region size, pixel variance, edge density, and gradient direction consistency—into a unified splitting criterion. This multi-feature fusion mechanism overcomes the limitations of conventional single-feature quadtree methods, enabling more robust image content analysis.
- We develop a comprehensive scoring function that quantitatively assesses images along three critical dimensions: information richness, structural complexity, and edge preservation. This metric provides a holistic evaluation of an image’s suitability for 3D reconstruction, improving selection accuracy while mitigating overfitting.
- We establish a fully automated image screening pipeline and conduct extensive validation on real-world datasets. Results show that our method consistently selects images that enhance the reconstruction quality of Tencent’s Hunyuan 3D model, outperforming existing screening approaches on key metrics such as Accuracy and Completeness.
2. Related Work
2.1. Quadtree Structure
2.2. Single-View Reconstruction
2.3. AI-Based 3D Model Generation
3. Method
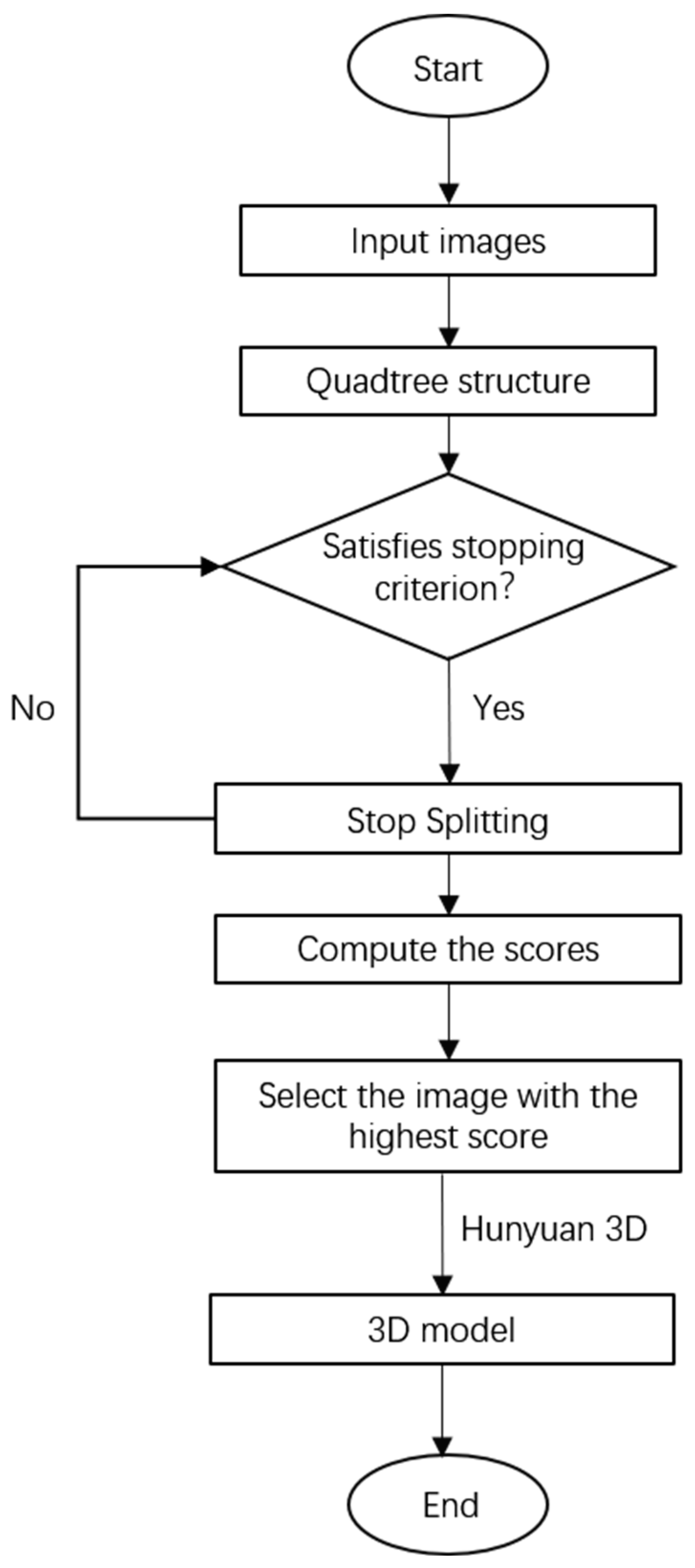
3.1. Image Screening Framework Based on Multi-Feature Fusion and Quadtree
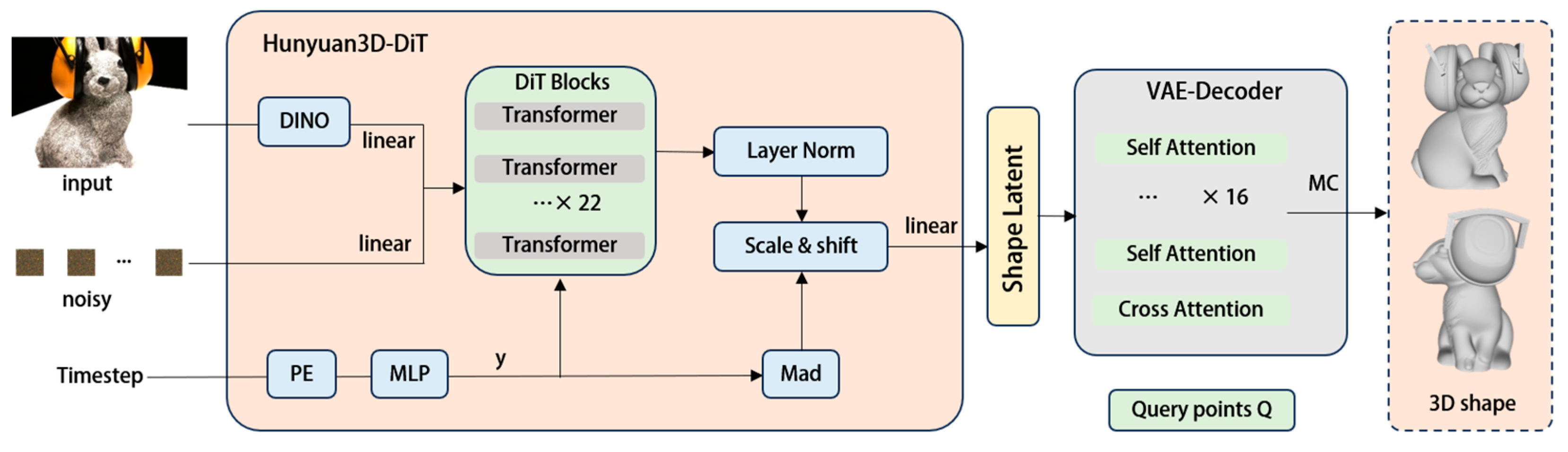
3.2. Hunyuan3D 2.1
4. Experiment and Discussion
4.1. Test Design
4.2. Evaluation and Analysis
4.3. Ablation Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, M.; Zhou, P.; Liu, J.-W.; Keppo, J.; Lin, M.; Yan, S.; Xu, X. Instant3D: Instant Text-to-3D Generation. Int. J. Comput. Vis. 2024, 132, 4456–4472. [Google Scholar] [CrossRef]
- Li, J.; Tan, H.; Zhang, K.; Xu, Z.; Luan, F.; Xu, Y.; Hong, Y.; Sunkavalli, K.; Shakhnarovich, G.; Bi, S. Instant3D: Fast Text-to-3D with Sparse-View Generation and Large Reconstruction Model. arXiv 2023, arXiv:2311.06214. [Google Scholar] [CrossRef]
- Choy, C.B.; Xu, D.F.; Gwak, J.Y.; Chen, K.; Savarese, S. 3D-R2N2: A Unified Approach for Single and Multi-view 3D Object Reconstruction. In Proceedings of the 14th European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 628–644. [Google Scholar]
- Fan, H.Q.; Su, H.; Leonidas, G. A Point Set Generation Network for 3D Object Reconstruction from a Single Image. In Proceedings of the 2017 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; IEEE: New York, NY, USA, 2017; pp. 2463–2471. [Google Scholar]
- Zhou, W.; Shi, X.; She, Y.; Liu, K.; Zhang, Y. Semi-supervised single-view 3D reconstruction via multi shape prior fusion strategy and self-attention. Comput. Graph. 2025, 126, 104142. [Google Scholar] [CrossRef]
- Zhang, L.; Xie, C.; Kitahara, I. DP-AMF: Depth-Prior-Guided Adaptive Multi-Modal and Global-Local Fusion for Single-View 3D Reconstruction. J. Imaging 2025, 11, 246. [Google Scholar] [CrossRef] [PubMed]
- Shen, Q.; Wu, Z.; Yi, X.; Zhou, P.; Zhang, H.; Yan, S.; Wang, X. Gamba: Marry Gaussian Splatting With Mamba for Single-View 3D Reconstruction. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Shrestha, P.; Zhou, Y.; Xie, C.; Kitahara, I. M3D: Dual-Stream Selective State Spaces and Depth-Driven Framework for High-Fidelity Single-View 3D Reconstruction. arXiv 2024, arXiv:2411.12635. [Google Scholar] [CrossRef]
- Stathopoulou, E.K.; Battisti, R.; Cernea, D.; Georgopoulos, A.; Remondino, F. Multiple View Stereo with quadtree-guided priors. ISPRS J. Photogramm. Remote Sens. 2023, 196, 197–209. [Google Scholar] [CrossRef]
- Braun, D.; Morel, O.; Demonceaux, C.; Vasseur, P. N-QGNv2: Predicting the optimum quadtree representation of a depth map from a monocular camera. Pattern Recognit. Lett. 2024, 179, 94–100. [Google Scholar] [CrossRef]
- Xu, C.; Wang, B.; Ye, Z.; Mei, L. ETQ-Matcher: Efficient Quadtree-Attention-Guided Transformer for Detector-Free Aerial–Ground Image Matching. Remote Sens. 2025, 17, 1300. [Google Scholar] [CrossRef]
- Zhou, Y.; Lin, P.; Liu, H.; Zheng, W.; Li, X.; Zhang, W. Fast and flexible spatial sampling methods based on the Quadtree algorithm for ocean monitoring. Front. Mar. Sci. 2024, 11, 1365366. [Google Scholar] [CrossRef]
- Scholefield, A.; Dragotti, P.L. Quadtree structured image approximation for denoising and interpolation. IEEE Trans. Image Process. 2014, 23, 1226–1239. [Google Scholar] [CrossRef] [PubMed]
- Hernandez-Lopez, F.J.; Muñiz-Pérez, O. Parallel fractal image compression using quadtree partition with task and dynamic parallelism. J. Real-Time Image Process. 2022, 19, 391–402. [Google Scholar] [CrossRef]
- Chen, R.; Zhang, J.; Liang, Y.; Luo, G.; Li, W.; Liu, J.; Li, X.; Long, X.; Feng, J.; Tan, P. Dora: Sampling and Benchmarking for 3D Shape Variational Auto-Encoders. In Proceedings of the 2025 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 10–17 June 2025; IEEE: New York, NY, USA, 2024; pp. 16251–16261. [Google Scholar]
- Li, W.; Liu, J.; Chen, R.; Liang, Y.; Chen, X.; Tan, P.; Long, X. CraftsMan: High-fidelity Mesh Generation with 3D Native Generation and Interactive Geometry Refiner. In Proceedings of the 2025 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 10–17 June 2025; IEEE: New York, NY, USA, 2024; pp. 5307–5317. [Google Scholar]
- Xiang, J.; Lv, Z.; Xu, S.; Deng, Y.; Wang, R.; Zhang, B.; Chen, D.; Tong, X.; Yang, J. Structured 3D Latents for Scalable and Versatile 3D Generation. arXiv 2024. [Google Scholar] [CrossRef]
- Hunyuan3d, T.; Yang, S.; Yang, M.; Feng, Y.; Huang, X.; Zhang, S.; He, Z.; Luo, D.; Liu, H.; Zhao, Y.; et al. Hunyuan3D 2.1: From Images to High-Fidelity 3D Assets with Production-Ready PBR Material. arXiv 2025, arXiv:2506.15442. [Google Scholar]
- Tochilkin, D.; Pankratz, D.; Liu, Z.; Huang, Z.; Letts, A.; Li, Y.; Liang, D.; Laforte, C.; Jampani, V.; Cao, Y.P. TripoSR: Fast 3D Object Reconstruction from a Single Image. arXiv 2024, arXiv:2403.02151. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, B.; Zhang, T.; Gu, S.; Bao, J.; Baltrusaitis, T.; Shen, J.; Chen, D.; Wen, F.; Chen, Q.; et al. RODIN: A Generative Model for Sculpting 3D Digital Avatars Using Diffusion. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; IEEE: New York, NY, USA, 2023; pp. 4563–4573. [Google Scholar]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. In Proceedings of the 16th European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; Springer: Berlin/Heidelberg, Germany, 2020; pp. 99–106. [Google Scholar]
- Yang, X.; Shi, H.; Zhang, B.; Yang, F.; Wang, J.; Zhao, H.; Liu, X.; Wang, X.; Lin, Q.; Yu, J.; et al. Hunyuan3D 1.0: A Unified Framework for Text-to-3D and Image-to-3D Generation. arXiv 2024, arXiv:2411.02293. [Google Scholar] [CrossRef]
- Zibo, Z.; Zeqiang, L.; Qingxiang, L.; Yunfei, Z.; Haolin, L.; Shuhui, Y.; Yifei, F.; Mingxin, Y.; Sheng, Z.; Xianghui, Y.; et al. Hunyuan3D 2.0: Scaling Diffusion Models for High Resolution Textured 3D Assets Generation. arXiv 2025, arXiv:2501.12202. [Google Scholar] [CrossRef]
- Zhang, B.; Tang, J.; Nießner, M.; Wonka, P. 3DShape2VecSet: A 3D Shape Representation for Neural Fields and Generative Diffusion Models. ACM Trans. Graph. 2023, 42, 92. [Google Scholar] [CrossRef]
- Feng, Y.; Yang, M.; Yang, S.; Zhang, S.; Yu, J.; Zhao, Z.; Liu, Y.; Jiang, J.; Guo, C. RomanTex: Decoupling 3D-aware Rotary Positional Embedded Multi-Attention Network for Texture Synthesis. arXiv 2025, arXiv:2503.19011. [Google Scholar]
- Burley, B. Physically-Based Shading at Disney. ACM Siggraph 2012, 2012, 1–7. [Google Scholar]
- Jensen, R.; Dahl, A.; Vogiatzis, G.; Tola, E.; Aanaes, H. Large Scale Multi-view Stereopsis Evaluation. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; IEEE: New York, NY, USA, 2014; pp. 406–413. [Google Scholar]



| Scan2 | Scan4 | Scan12 | Scan31 | Scan33 | |||||||||||
| Acc | Comp | Overall | Acc | Comp | Overall | Acc | Comp | Overall | Acc | Comp | Overall | Acc | Comp | Overall | |
| QT | 7.657 | 7.862 | 7.759 | 3.619 | 3.716 | 3.667 | 8.716 | 8.970 | 8.843 | 8.235 | 10.459 | 9.347 | 6.370 | 5.711 | 6.040 |
| Ours | 3.369 | 6.480 | 4.924 | 2.859 | 6.517 | 4.688 | 7.172 | 6.358 | 6.765 | 4.814 | 7.713 | 6.263 | 4.830 | 6.277 | 5.554 |
| Scan48 | Scan75 | Scan77 | Scan114 | Scan118 | |||||||||||
| Acc | Comp | Overall | Acc | Comp | Overall | Acc | Comp | Overall | Acc | Comp | Overall | Acc | Comp | Overall | |
| QT | 6.356 | 8.358 | 7.357 | 8.303 | 8.942 | 8.622 | 3.862 | 2.781 | 3.322 | 6.935 | 8.593 | 7.764 | 3.513 | 4.275 | 3.894 |
| Ours | 4.799 | 3.611 | 4.205 | 5.705 | 4.208 | 4.956 | 3.011 | 2.561 | 2.786 | 2.093 | 2.560 | 2.327 | 3.731 | 5.370 | 4.551 |
| Method | Acc | Comp | Overall |
|---|---|---|---|
| Baline QT (N) | 6.935 | 8.593 | 7.764 |
| Ours-D (N + ) | 3.475 | 4.066 | 3.770 |
| Ours-E (N + ) | 5.623 | 6.772 | 6.198 |
| Ours-Full (N + ) | 2.093 | 2.560 | 2.327 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Liu, Y.; Fang, Y.; Zhang, Y.; Lu, Y.; Sun, G. Improved Quadtree-Based Selection of Single Images for 3D Generation. Sensors 2025, 25, 6559. https://doi.org/10.3390/s25216559
Li W, Liu Y, Fang Y, Zhang Y, Lu Y, Sun G. Improved Quadtree-Based Selection of Single Images for 3D Generation. Sensors. 2025; 25(21):6559. https://doi.org/10.3390/s25216559
Chicago/Turabian StyleLi, Wanyun, Yue Liu, Yuqiang Fang, Yasheng Zhang, Yao Lu, and Gege Sun. 2025. "Improved Quadtree-Based Selection of Single Images for 3D Generation" Sensors 25, no. 21: 6559. https://doi.org/10.3390/s25216559
APA StyleLi, W., Liu, Y., Fang, Y., Zhang, Y., Lu, Y., & Sun, G. (2025). Improved Quadtree-Based Selection of Single Images for 3D Generation. Sensors, 25(21), 6559. https://doi.org/10.3390/s25216559





