GeoAssemble: A Geometry-Aware Hierarchical Method for Point Cloud-Based Multi-Fragment Assembly
Abstract
1. Introduction
- Geometry-Enhanced Feature Encoder: We develop a DGCNN-based feature extractor that integrates centroid-relative position features to construct a multi-dimensional feature representation. This innovation effectively addresses the challenge of multi-scale adaptability on irregular fracture surfaces.
- Global-Local Hierarchical Matching Mechanism: We design a two-stage matching strategy that integrates global geometry-guided coarse matching with local geometry-constrained fine matching. This strategy incorporates differentiable optimization and dynamic weight learning mechanisms, significantly reducing combinatorial ambiguity.
- Geometry-Aware Auxiliary Transformation Generation: We propose a physically plausible approach for generating an auxiliary transformation, specifically aimed at revising initial pose transformation. This approach effectively prevents error accumulation from random initialization.
2. Related Work
2.1. Feature Matching
2.2. Semantics-Based Assembly
2.3. Geometry-Based Learning Methods
2.4. Low-Overlap Point Cloud Registration
2.5. Summary
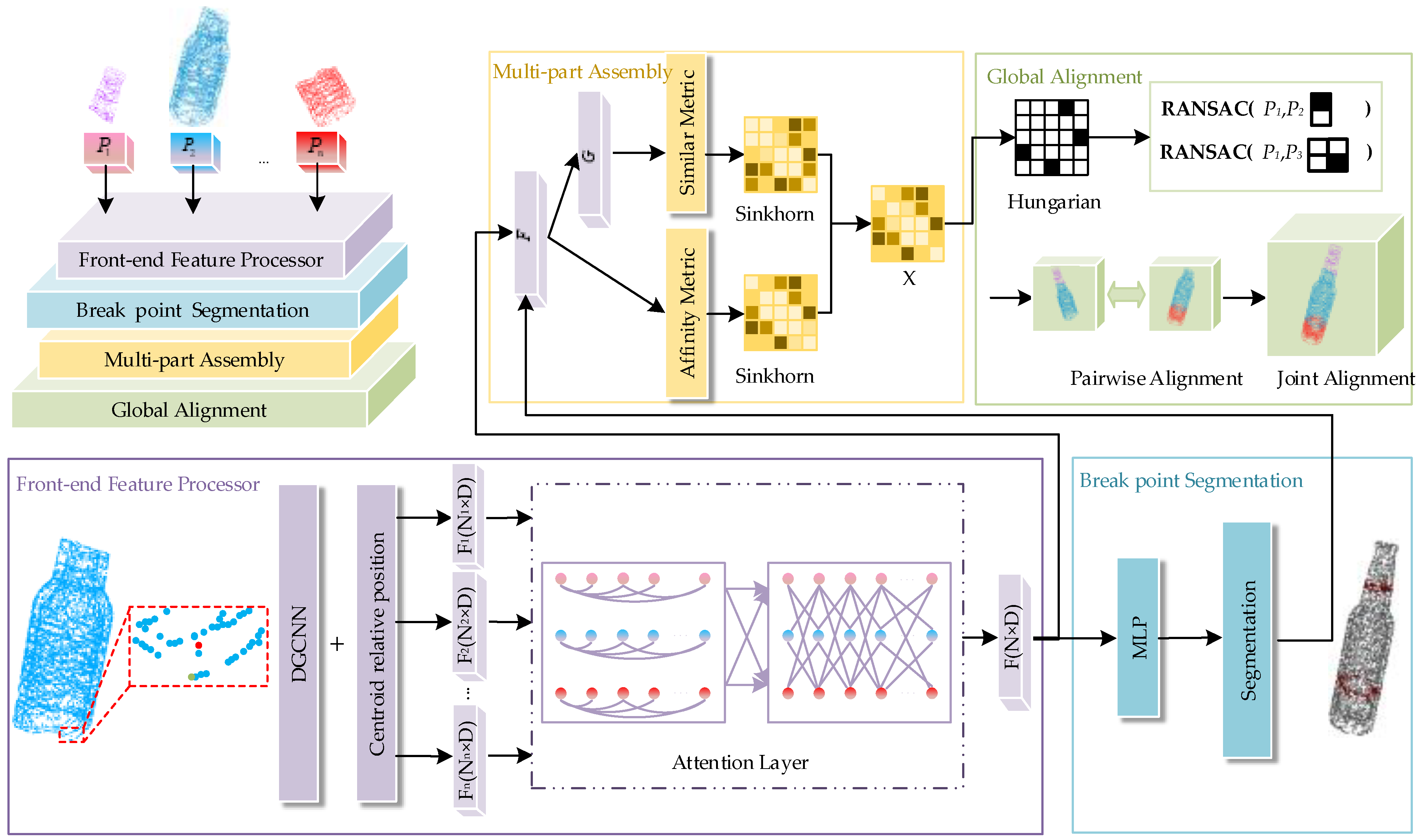
3. Methods
3.1. Front-End Feature Extractor
3.2. Break Point Segmentation
3.3. Multi-Fragment Assembly
3.4. Global Alignment
4. Experiment
4.1. Protocol
4.1.1. Datasets
4.1.2. Evaluation Metrics
4.1.3. Baseline Methods
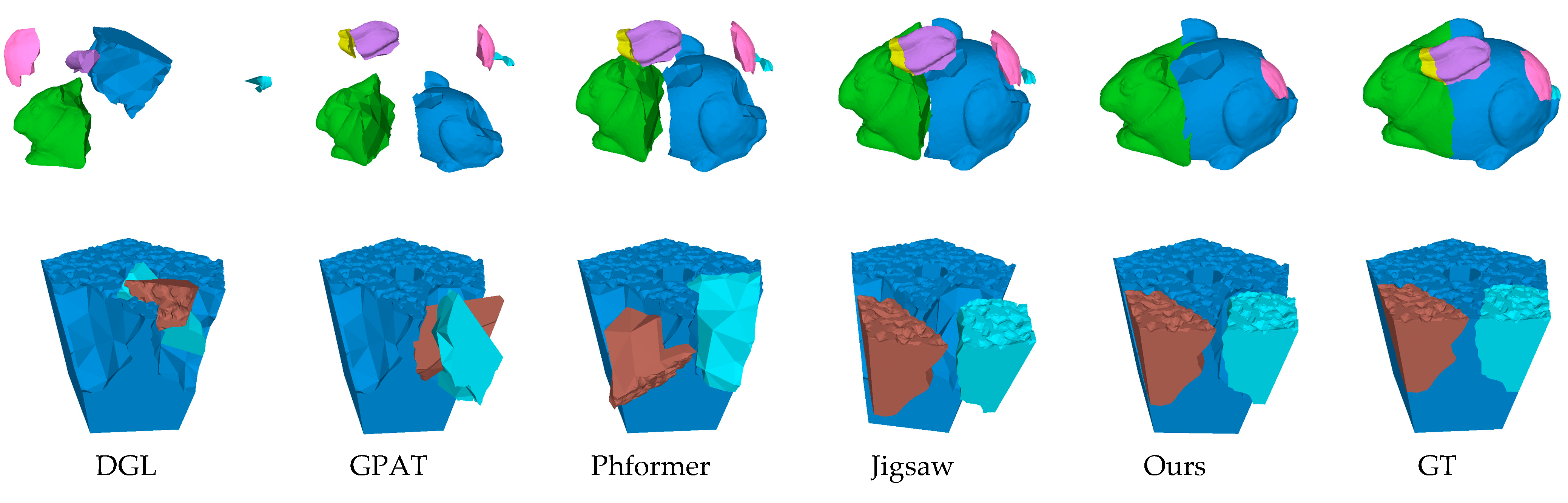
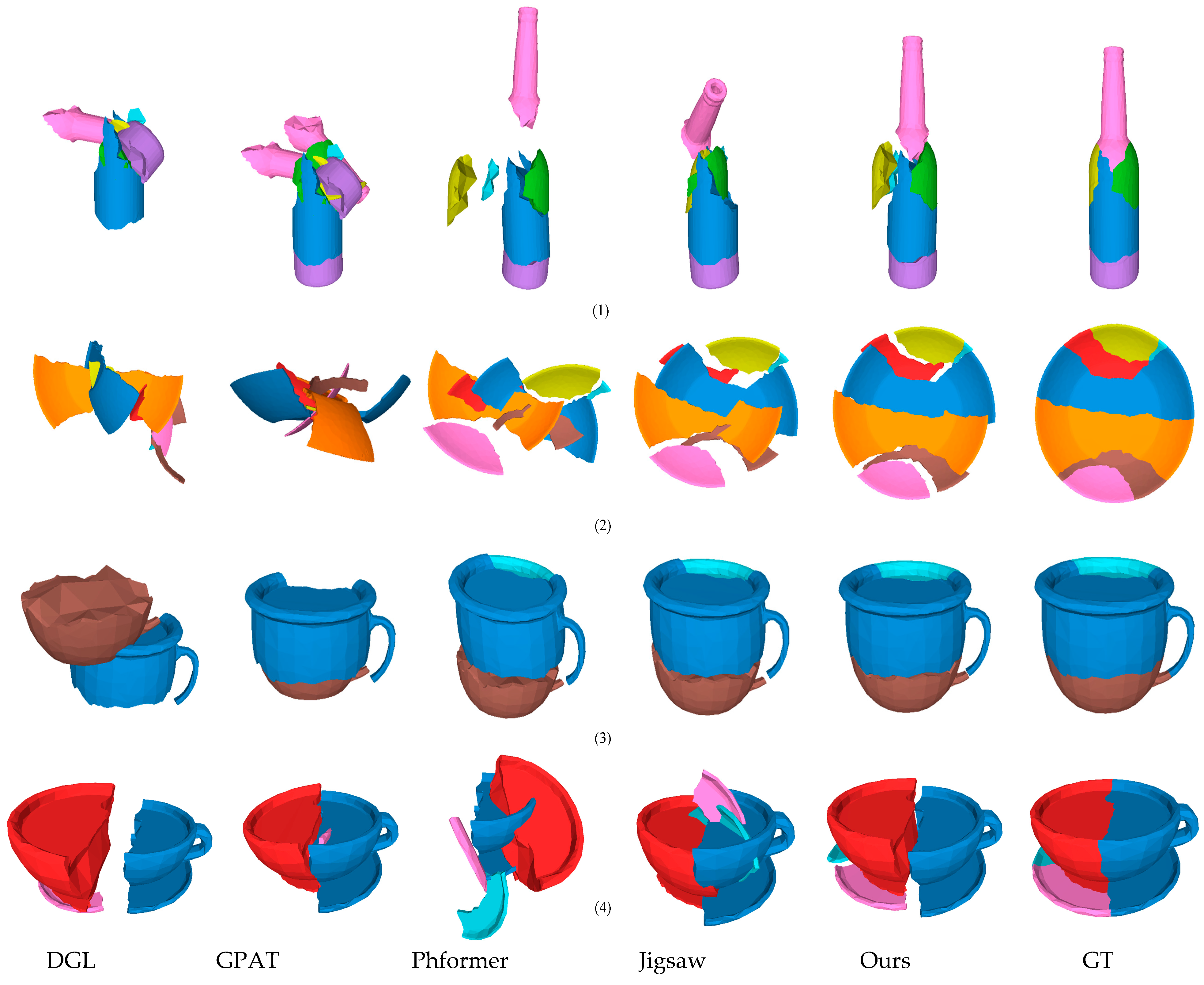
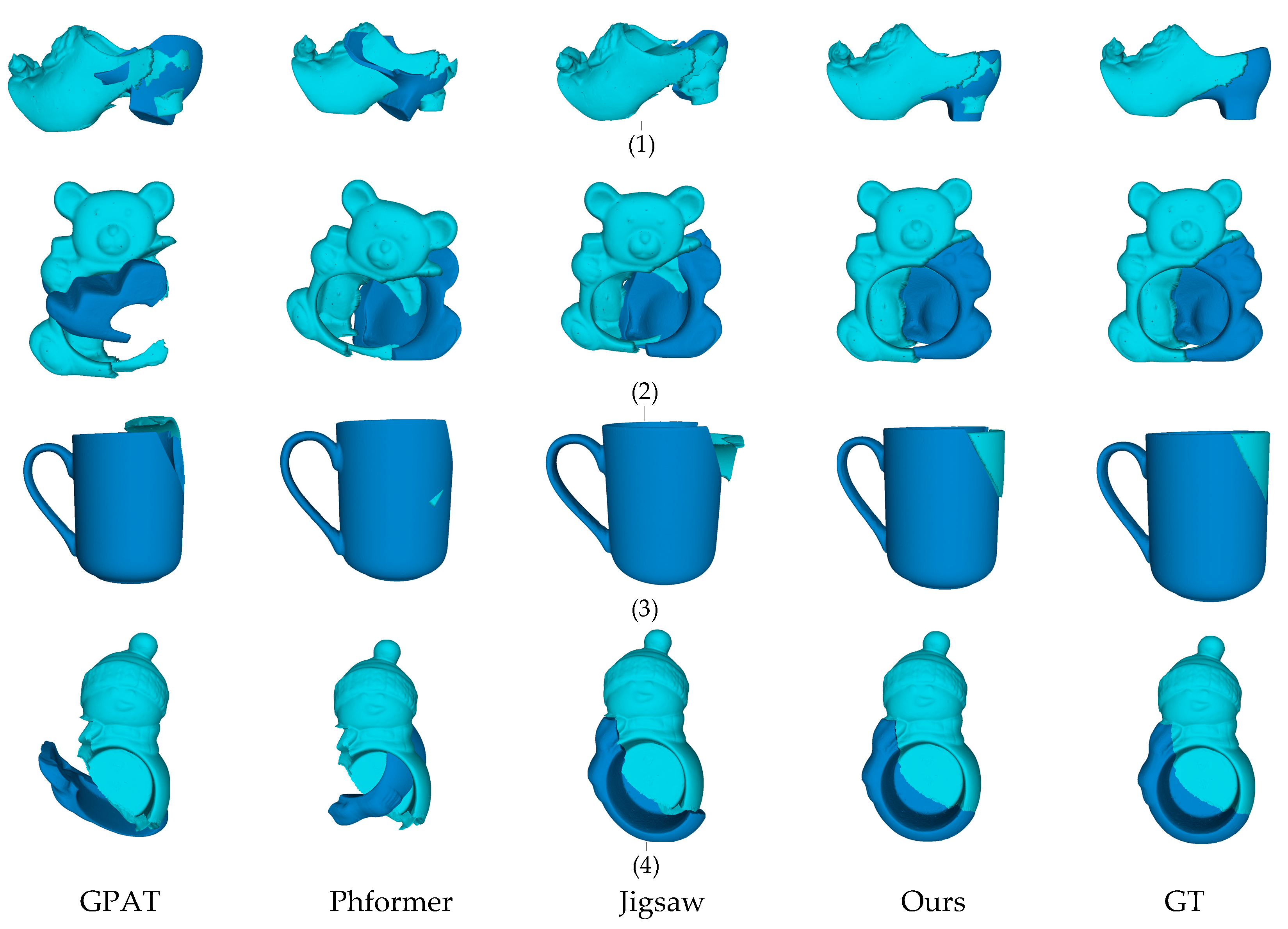
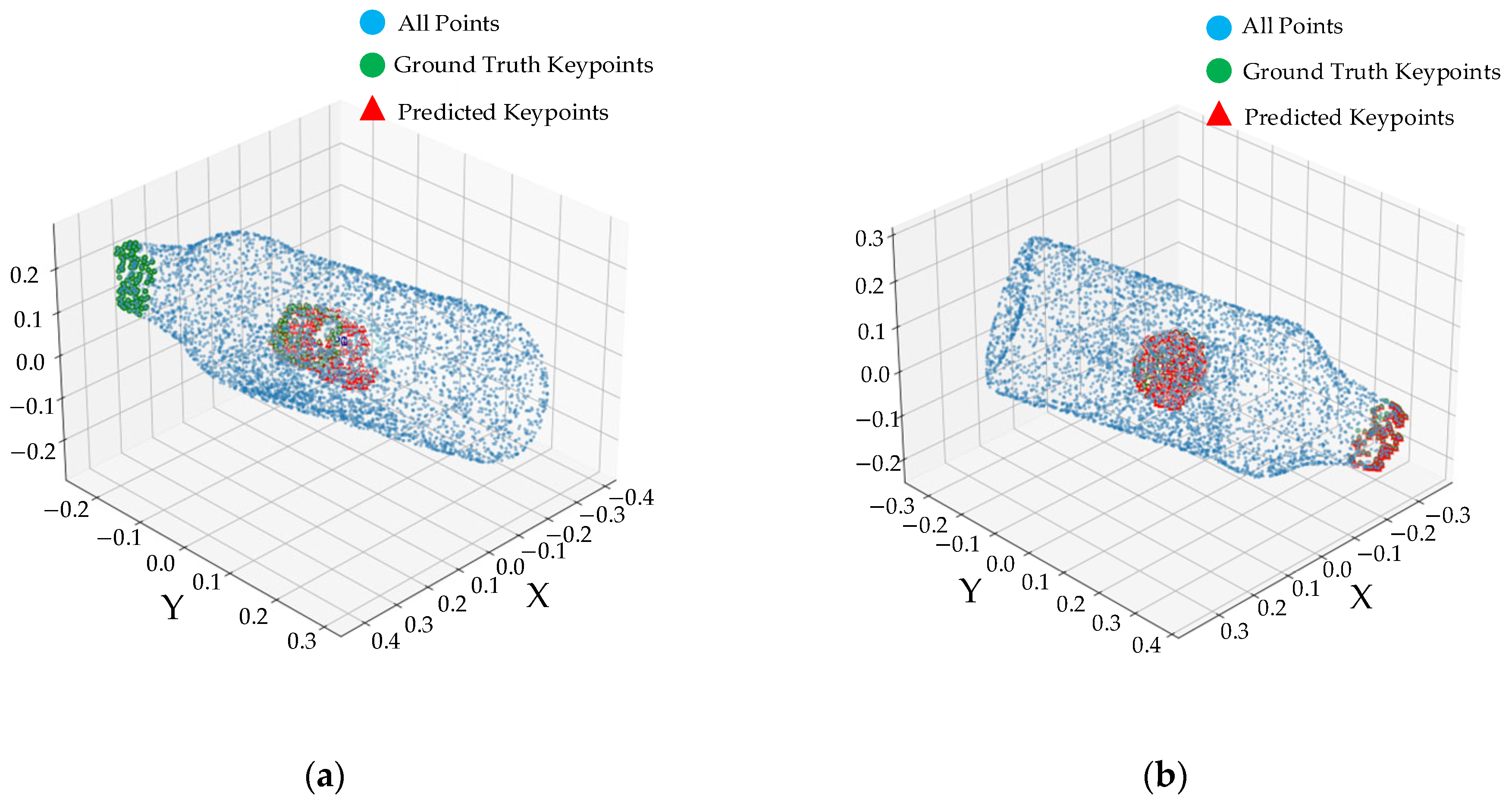
4.2. Multi-Fragment Assembly
4.2.1. Breaking Bad
4.2.2. Fantastic Breaks
4.2.3. Ablation Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, R.; Zhang, Z.; Zhang, W.; He, L.; Zhu, C. Deep learning-driven semantic segmentation and spatial analysis of quarry relic landscapes using point cloud data: Insights from the Shaoxing quarry relics. Npj Herit. Sci. 2025, 13, 77. [Google Scholar] [CrossRef]
- Nasiri, S.M.; Hosseini, R.; Moradi, H. Multiple-solutions RANSAC for finding axes of symmetry in fragments of objects. Pattern Recognit. 2022, 131, 108805. [Google Scholar] [CrossRef]
- Bolourian, N.; Nasrollahi, M.; Bahreini, F.; Hammad, A. Point cloud-based concrete surface defect semantic segmentation. J. Comput. Civ. Eng. 2023, 37, 04022056. [Google Scholar] [CrossRef]
- Wei, X.; Wang, F.; He, D.; Liu, C.; Xu, D. Coal gangue image recognition model based on CSPNet-YOLOv7 target detection algorithm. Coal Sci. Technol. 2024, 52, 238–248. [Google Scholar]
- Li, Y.; Mo, K.; Duan, Y.; Wang, H.; Zhang, J.; Shao, L. Category-level multi-part multi-joint 3d shape assembly. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 3281–3291. [Google Scholar]
- Wu, D.; Yan, Z.; Zha, H. PanoRecon: Real-time panoptic 3D reconstruction from monocular video. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 21507–21518. [Google Scholar]
- Mo, K.; Zhu, S.; Chang, A.X.; Yi, L.; Tripathi, S.; Guibas, L.J.; Su, H. Partnet: A large-scale benchmark for fine-grained and hierarchical part-level 3d object understanding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 909–918. [Google Scholar]
- Sellán, S.; Chen, Y.C.; Wu, Z.; Garg, A.; Jacobson, A. Breaking bad: A dataset for geometric fracture and reassembly. Adv. Neural Inf. Process. Syst. 2022, 35, 38885–38898. [Google Scholar]
- Lee, J.; Kim, J.; Chung, H.; Park, J.; Cho, M. Learning to assemble geometric shapes. arXiv 2022, arXiv:2205.11809. [Google Scholar] [CrossRef]
- Li, J.; Cheng, C.; Ma, J.; Liu, G. Geometric Point Attention Transformer for 3D Shape Reassembly. arXiv 2024, arXiv:2411.17788. [Google Scholar] [CrossRef]
- Chen, Y.C.; Li, H.; Turpin, D.; Jacobson, A.; Garg, A. Neural shape mating: Self-supervised object assembly with adversarial shape priors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12724–12733. [Google Scholar]
- Zhao, B.; Wang, Z.; Jia, Z.; Liang, D.; Liu, Q. Three-Dimensional Local Feature Descriptor based on Dynamic Graph Convolution and PointNet. J. Comput.-Aided Des. Comput. Graph. 2025, 37, 89–99. [Google Scholar]
- Dao, T. Flashattention-2: Faster attention with better parallelism and work partitioning. arXiv 2023, arXiv:2307.08691. [Google Scholar] [CrossRef]
- Huguet, G.; Vuckovic, J.; Fatras, K.; Thibodeau-Laufer, E.; Lemos, P.; Islam, R.; Liu, C.; Rector-Brooks, J.; Akhound-Sadegh, T.; Bronstein, M.; et al. Sequence-augmented SE (3)-flow matching for conditional protein generation. Adv. Neural Inf. Process. Syst. 2024, 37, 33007–33036. [Google Scholar]
- Tropsha, A.; Isayev, O.; Varnek, A.; Schneider, G.; Cherkasov, A. Integrating QSAR modelling and deep learning in drug discovery: The emergence of deep QSAR. Nat. Rev. Drug Discov. 2024, 23, 141–155. [Google Scholar] [CrossRef]
- You, Y.; Lou, Y.; Li, C.; Cheng, Z.; Li, L.; Ma, L.; Lu, C.; Wang, W. Keypointnet: A large-scale 3d keypoint dataset aggregated from numerous human annotations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 13647–13656. [Google Scholar]
- Qin, Z.; Yu, H.; Wang, C.; Guo, Y.; Peng, Y.; Xu, K. Geometric transformer for fast and robust point cloud registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11143–11152. [Google Scholar]
- Cardarelli, L. From fragments to digital wholeness: An AI generative approach to reconstructing archaeological vessels. J. Cult. Herit. 2024, 70, 250–258. [Google Scholar] [CrossRef]
- Modolo, M.; Delpiano, D.; Martellotta, E.F.; Peresani, M. Bone refits and implications for the reconstruction of a Late Middle Palaeolithic Context: Unit A9 of Fumane Cave. J. Paleolit. Archaeol. 2024, 8, 1. [Google Scholar] [CrossRef]
- Sun, J.; Shen, Z.; Wang, Y.; Bao, H.; Zhou, X. LoFTR: Detector-free local feature matching with transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 8922–8931. [Google Scholar]
- Liu, S.; Wei, G.; Fan, Y.; Chen, L.; Zhang, Z. Multimodal registration network with multi-scale feature-crossing. Int. J. Comput. Assist. Radiol. Surg. 2024, 19, 2269–2278. [Google Scholar] [CrossRef]
- Wu, Y.; Luo, C.; Gong, M.; Ding, H.; Sheng, J.; Miao, Q.; Li, H.; Ma, W.; He, H. Multi-task multi-scale feature selection for point cloud registration. IEEE Trans. Evol. Comput. 2025. [Google Scholar] [CrossRef]
- Wang, R.; Yan, J.; Yang, X. Neural graph matching network: Learning lawler’s quadratic assignment problem with extension to hypergraph and multiple-graph matching. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 5261–5279. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Lu, J.; Wang, T.; Yan, J. Learning universe model for partial matching networks over multiple graphs. arXiv 2022, arXiv:2210.10374. [Google Scholar] [CrossRef]
- Sörman, A.; Noterman, A.A.; Fjellström, M. Fragmentation in archaeological context: Studying the incomplete. In Broken Bodies, Places and Objects: New Perspectives on Fragmentation in Archaeology; Routledge: Abingdon, UK, 2023; pp. 1–22. [Google Scholar]
- Jones, B.; Hildreth, D.; Chen, D.; Baran, I.; Kim, V.G.; Schulz, A. Automate: A dataset and learning approach for automatic mating of cad assemblies. ACM Trans. Graph. (TOG) 2021, 40, 1–18. [Google Scholar] [CrossRef]
- Xu, X.; Wang, Y.; Zheng, Y.; Rao, Y.; Zhou, J.; Lu, J. Back to reality: Weakly-supervised 3d object detection with shape-guided label enhancement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8438–8447. [Google Scholar]
- Schor, N.; Katzir, O.; Zhang, H.; Cohen-Or, D. Componet: Learning to generate the unseen by part synthesis and composition. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 8759–8768. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Wang, H.; Liu, Y.; Hu, Q.; Wang, B.; Chen, J.; Dong, Z.; Guo, Y.; Wang, W.; Yang, B. RoReg: Pairwise point cloud registration with oriented descriptors and local rotations. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10376–10393. [Google Scholar] [CrossRef]
- Wu, R.; Tie, C.; Du, Y.; Zhao, Y.; Dong, H. Leveraging se (3) equivariance for learning 3d geometric shape assembly. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 14311–14320. [Google Scholar]
- Lu, J.; Hua, G.; Huang, Q. Jigsaw++: Imagining complete shape priors for object reassembly. arXiv 2024, arXiv:2410.11816. [Google Scholar]
- Xu, Q.C.; Chen, H.X.; Hua, J.; Zhan, X.; Yang, Y.L.; Mu, T.J. Fragmentdiff: A diffusion model for fractured object assembly. In Proceedings of the SIGGRAPH Asia 2024 Conference Papers, Tokyo, Japan, 3–6 December 2024; pp. 1–12. [Google Scholar]
- Niu, X.; Wang, Q.; Liu, B.; Zhang, J. An automatic chinaware fragments reassembly method framework based on linear feature of fracture surface contour. ACM J. Comput. Cult. Herit. 2022, 16, 1–22. [Google Scholar] [CrossRef]
- Qin, Z.; Yu, H.; Wang, C.; Guo, Y.; Peng, Y.; Ilic, S.; Hu, D.; Xu, K. Geotransformer: Fast and robust point cloud registration with geometric transformer. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 9806–9821. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Furukawa, Y. Puzzlefusion++: Auto-agglomerative 3d fracture assembly by denoise and verify. arXiv 2024, arXiv:2406.00259. [Google Scholar]
- Lamb, N.; Palmer, C.; Molloy, B.; Banerjee, S.; Banerjee, N.K. Fantastic breaks: A dataset of paired 3d scans of real-world broken objects and their complete counterparts. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 4681–4691. [Google Scholar]
- Lu, J.; Sun, Y.; Huang, Q. Jigsaw: Learning to assemble multiple fractured objects. Adv. Neural Inf. Process. Syst. 2023, 36, 14969–14986. [Google Scholar]
- Cui, W.; Yao, R.; Du, S. Phformer: Multi-fragment assembly using proxy-level hybrid transformer. Proc. AAAI Conf. Artif. Intell. 2024, 38, 1408–1416. [Google Scholar] [CrossRef]
- Zhan, G.; Fan, Q.; Mo, K.; Shao, L.; Chen, B.; Guibas, L.J.; Dong, H. Generative 3d part assembly via dynamic graph learning. Adv. Neural Inf. Process. Syst. 2020, 33, 6315–6326. [Google Scholar]

| Configuration Name | Parameter |
|---|---|
| CPU | Intel(R) Core(TM)i9-14900K |
| GPU | NVIDIA GeForce RTX 3090 |
| CUDA | 11.3 |
| Pytorch | 1.10.1 + cu113 |
| Method | RMSE(R) Degree ↓ | MAE(R) Degree ↓ | RMSE(T) | MAE(T) | PA% ↑ |
|---|---|---|---|---|---|
| Tested on the Everyday dataset | |||||
| DGL [40] | 82.3 | 68.7 | 16.2 | 13.6 | 23.7 |
| GPAT [10] | 79.3 | 66.4 | 14.4 | 11.1 | 30.2 |
| Phformer [39] | 34.4 | 29.4 | 10.0 | 8.1 | 47.4 |
| Jigsaw [38] | 41.2 | 35.6 | 7.7 | 6.12 | 63.6 |
| GeoAssemble | 34.0 | 29.4 | 6.3 | 4.98 | 71.1 |
| Tested on the Artifact dataset | |||||
| DGL [40] | 85.4 | 76.2 | 18.7 | 15.4 | 7.2 |
| GPAT [10] | 78.7 | 73.4 | 16.2 | 13.6 | 9.3 |
| Phformer [39] | 36.5 | 31.8 | 13.2 | 11.4 | 21.9 |
| Jigsaw [38] | 57.9 | 50.2 | 16.9 | 13.8 | 36.5 |
| GeoAssemble | 50.3 | 43.4 | 14.1 | 11.5 | 46.6 |
| Method | RMSE (R) Degree ↓ | MAE (R) Degree ↓ | RMSE(T) | MAE(T) | PA% ↑ |
|---|---|---|---|---|---|
| GPAT [10] | 72.7 | 62.3 | 15.6 | 13.4 | 37.2 |
| Phformer [39] | 39.3 | 32.2 | 14.4 | 11.7 | 45.7 |
| Jigsaw [38] | 43.1 | 37.8 | 9.7 | 7.8 | 54.6 |
| GeoAssemble | 26.0 | 22.1 | 6.2 | 4.9 | 71.3 |
| Components | RMSE (R) | MAE (R) | RMSE (T) | MAE (T) | PA | |||
|---|---|---|---|---|---|---|---|---|
| DGCNN | Centroid Position | Matching | Auxiliary Edges | Degree ↓ | Degree ↓ | % ↑ | ||
| 41.2 | 35.6 | 7.77 | 6.12 | 63.6 | ||||
| √ | 35.6 | 31.2 | 6.98 | 5.54 | 65.2 | |||
| √ | √ | 34.8 | 29.9 | 6.77 | 5.31 | 66.7 | ||
| √ | √ | √ | 34.5 | 29.8 | 6.69 | 5.29 | 67.9 | |
| √ | √ | √ | √ | 34.0 | 29.4 | 6.31 | 4.98 | 71.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, C.; Ren, Y.; Wang, Z.; Zhang, Y. GeoAssemble: A Geometry-Aware Hierarchical Method for Point Cloud-Based Multi-Fragment Assembly. Sensors 2025, 25, 6533. https://doi.org/10.3390/s25216533
Jia C, Ren Y, Wang Z, Zhang Y. GeoAssemble: A Geometry-Aware Hierarchical Method for Point Cloud-Based Multi-Fragment Assembly. Sensors. 2025; 25(21):6533. https://doi.org/10.3390/s25216533
Chicago/Turabian StyleJia, Caiqin, Yali Ren, Zhi Wang, and Yuan Zhang. 2025. "GeoAssemble: A Geometry-Aware Hierarchical Method for Point Cloud-Based Multi-Fragment Assembly" Sensors 25, no. 21: 6533. https://doi.org/10.3390/s25216533
APA StyleJia, C., Ren, Y., Wang, Z., & Zhang, Y. (2025). GeoAssemble: A Geometry-Aware Hierarchical Method for Point Cloud-Based Multi-Fragment Assembly. Sensors, 25(21), 6533. https://doi.org/10.3390/s25216533





