Fault Diagnosis Method for Pumping Station Units Based on the tSSA-Informer Model
Abstract
Highlights
- The proposed tSSA-Informer model achieves 90.85% diagnostic accuracy under strong noise (SNR = −9 dB) and 61.32% accuracy with only 10% labeled samples, outperforming SSA-Informer, GA-Informer, and other comparative models.
- The tSSA algorithm optimizes Informer hyperparameters 7.74% faster than the original SSA, and the integrated data preprocessing (IQR + CWT + KPCA) effectively enhances the representation of non-stationary vibration features.
- The model’s anti-noise and small-sample adaptability precisely addresses the “multi-interference, scarce samples” dilemma of pumping station unit fault diagnosis in practical engineering.
- The tSSA-optimized Informer framework provides a referable paradigm for hyperparameter tuning and time-series feature mining in mechanical fault diagnosis fields.
Abstract
1. Introduction
2. Research Methods
2.1. Improved Sparrow Search Algorithm
2.1.1. Adaptive T-Distribution Strategy Improves the Sparrow Search Algorithm
2.1.2. Analysis of the Time Complexity of the Improved Sparrow Search Algorithm
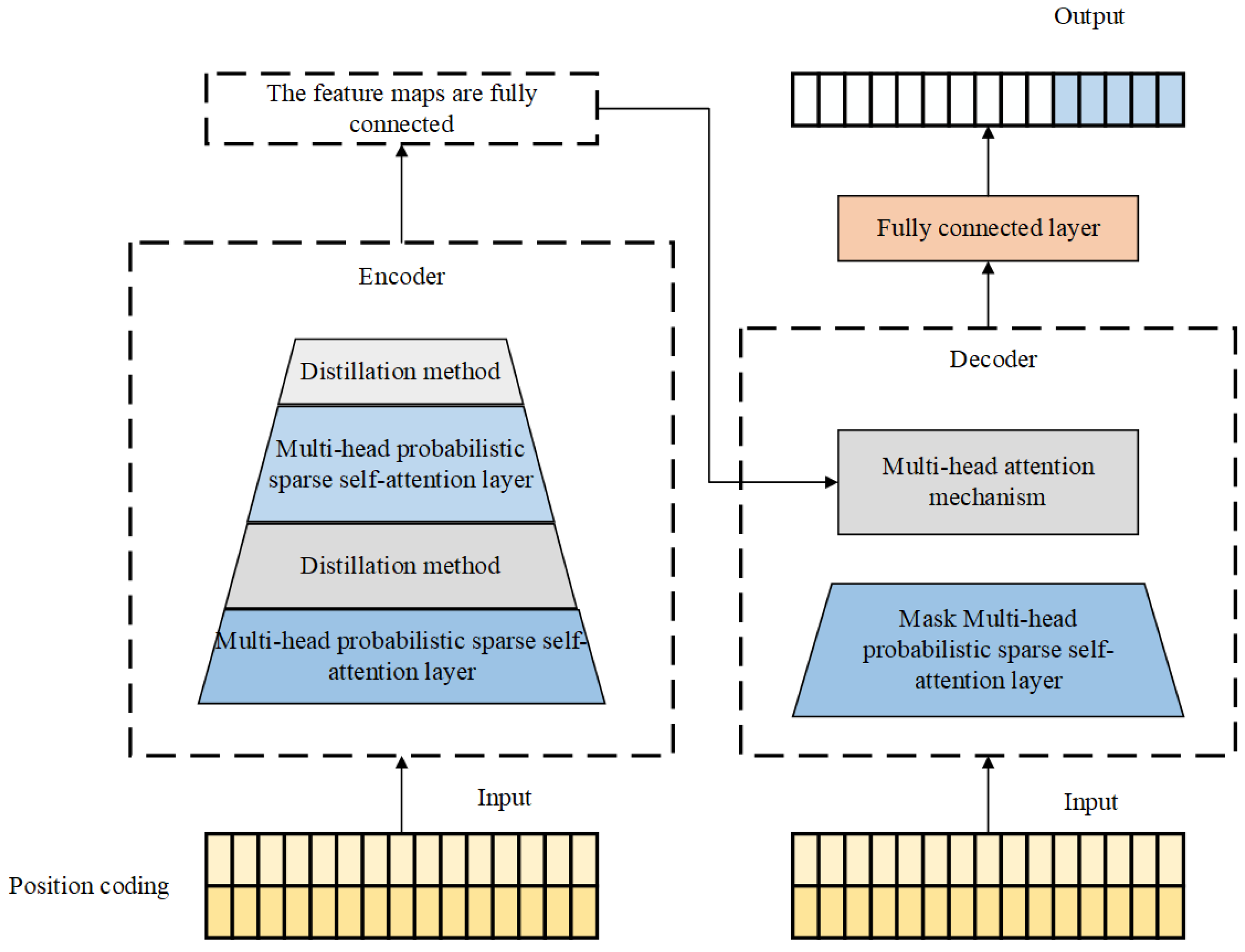
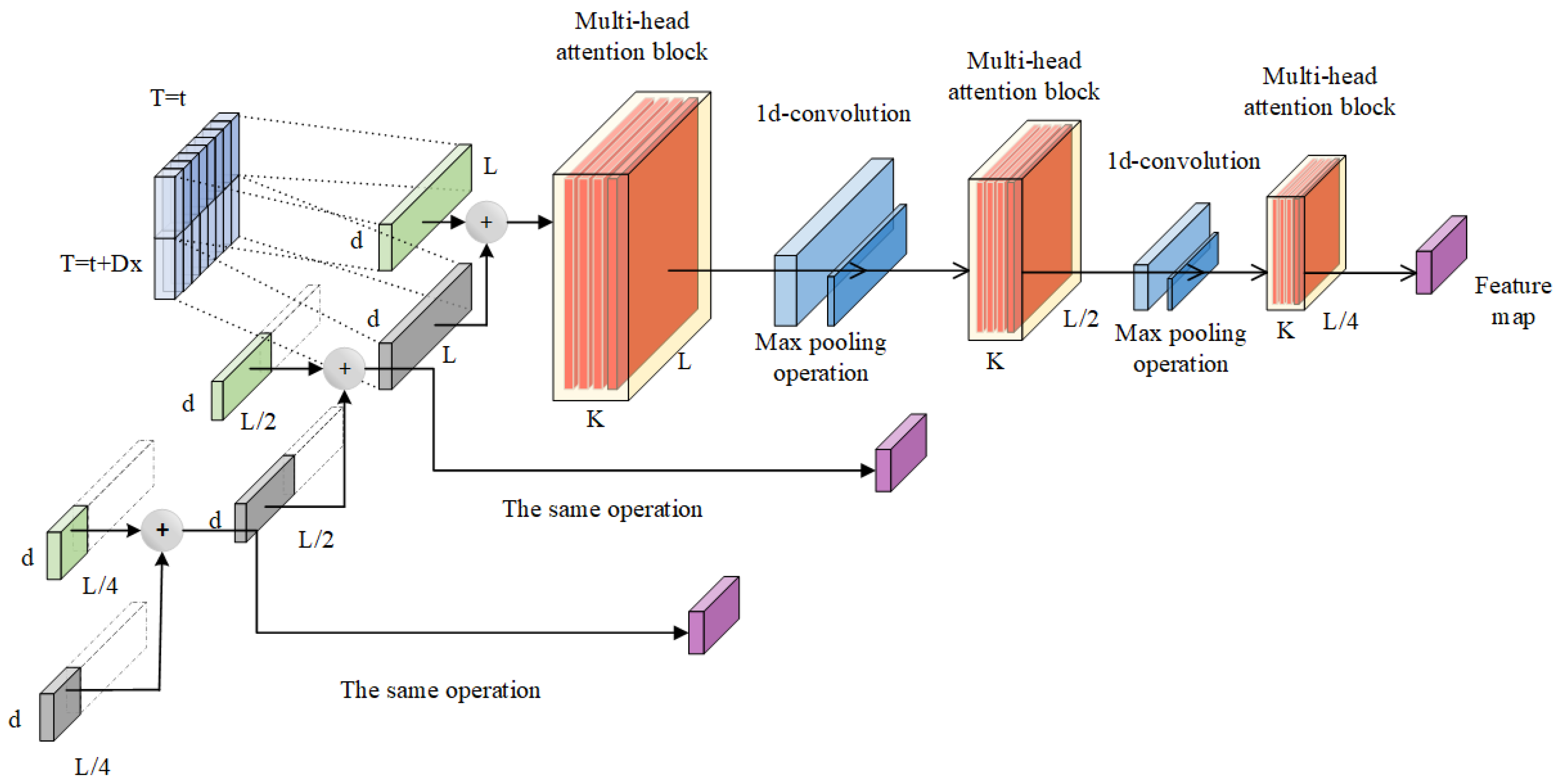
2.2. The Principle of Informer Model
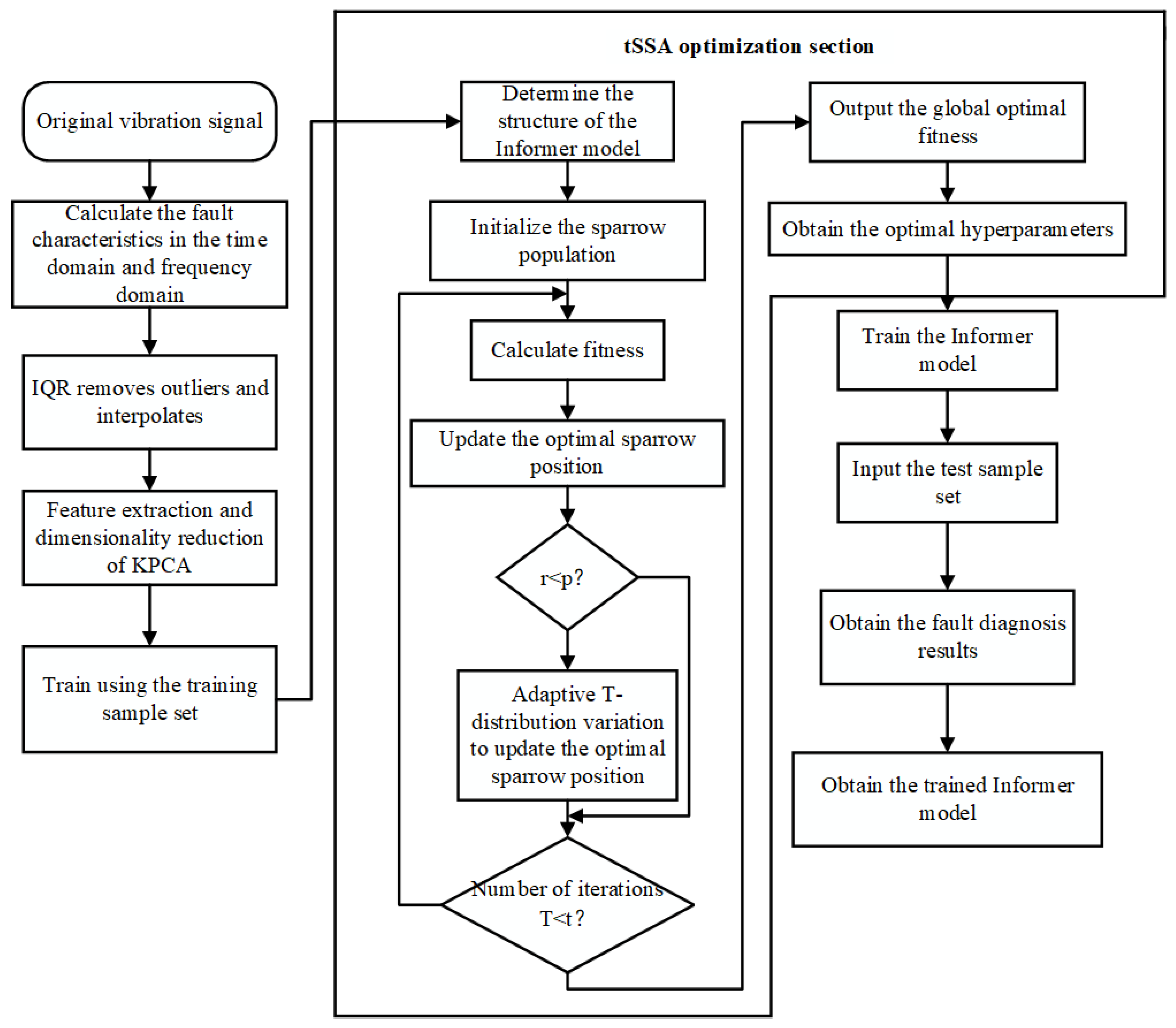
2.3. tSSA-Informer Model
- (1)
- Data processing: First, clarify the input and output of the tSSA-Informer fault diagnosis model. The feature parameters extracted from the vibration signals of pumping station units serve as the model input, and the fault categories of pumping station units are used as the model output. When inputting data, it is first necessary to identify and remove outliers from the data using the interquartile range (IQR) method, then correct the data via spline interpolation. The KPCA method is applied for feature extraction and dimensionality reduction, and finally, the input format of the data is adjusted to a 3D tensor suitable for the Informer model. Ultimately, the experimental data are divided into a 70% training set and a 30% test set.
- (2)
- Set the corresponding parameters of the tSSA algorithm: population size N, proportion of discoverers PD, proportion of sentinels SD, warning value R2, and total number of iterations T; initialize the sparrow population using the initialization function; construct the Informer fault diagnosis model and determine the range of hyperparameters to be optimized.
- (3)
- Optimize Informer hyperparameters using the tSSA algorithm: Input the experimental samples into the fault diagnosis model for classification training, take the error rate during training as the fitness value in the optimization process, and obtain the optimal Informer hyperparameters after T iterations.
- (4)
- Perform fault diagnosis using the optimized model: The sample labels correspond to the fault types of pumping station units. The adaptability and effectiveness of the model are evaluated by comparing the model’s predicted output results with the true labels.
3. Fault Diagnosis of the Pump Station Unit Dataset
3.1. Experimental Configuration
3.2. Data Collection and Data Processing
3.2.1. Data Collection
3.2.2. Data Processing
3.2.3. Simulated Noise
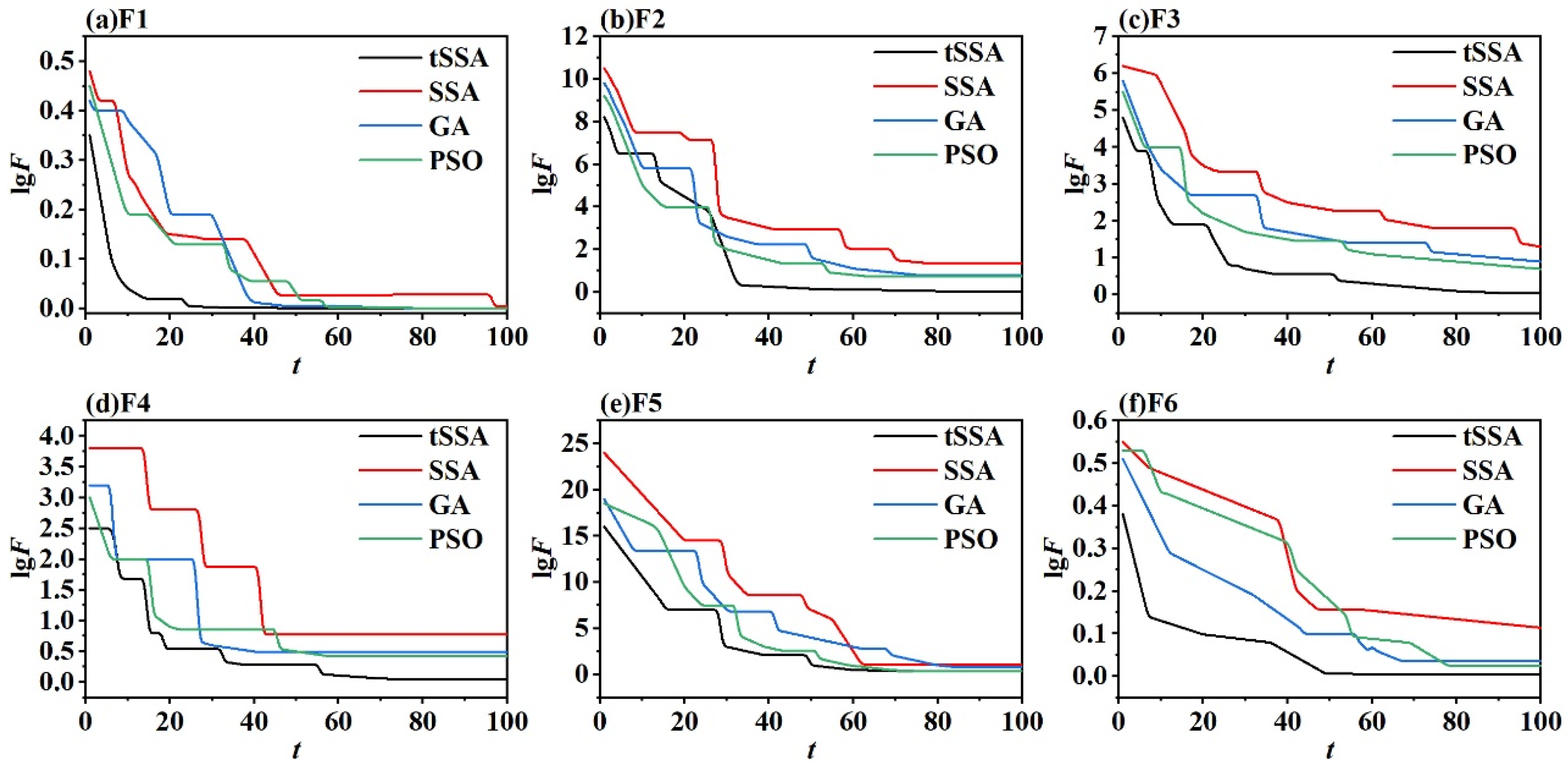
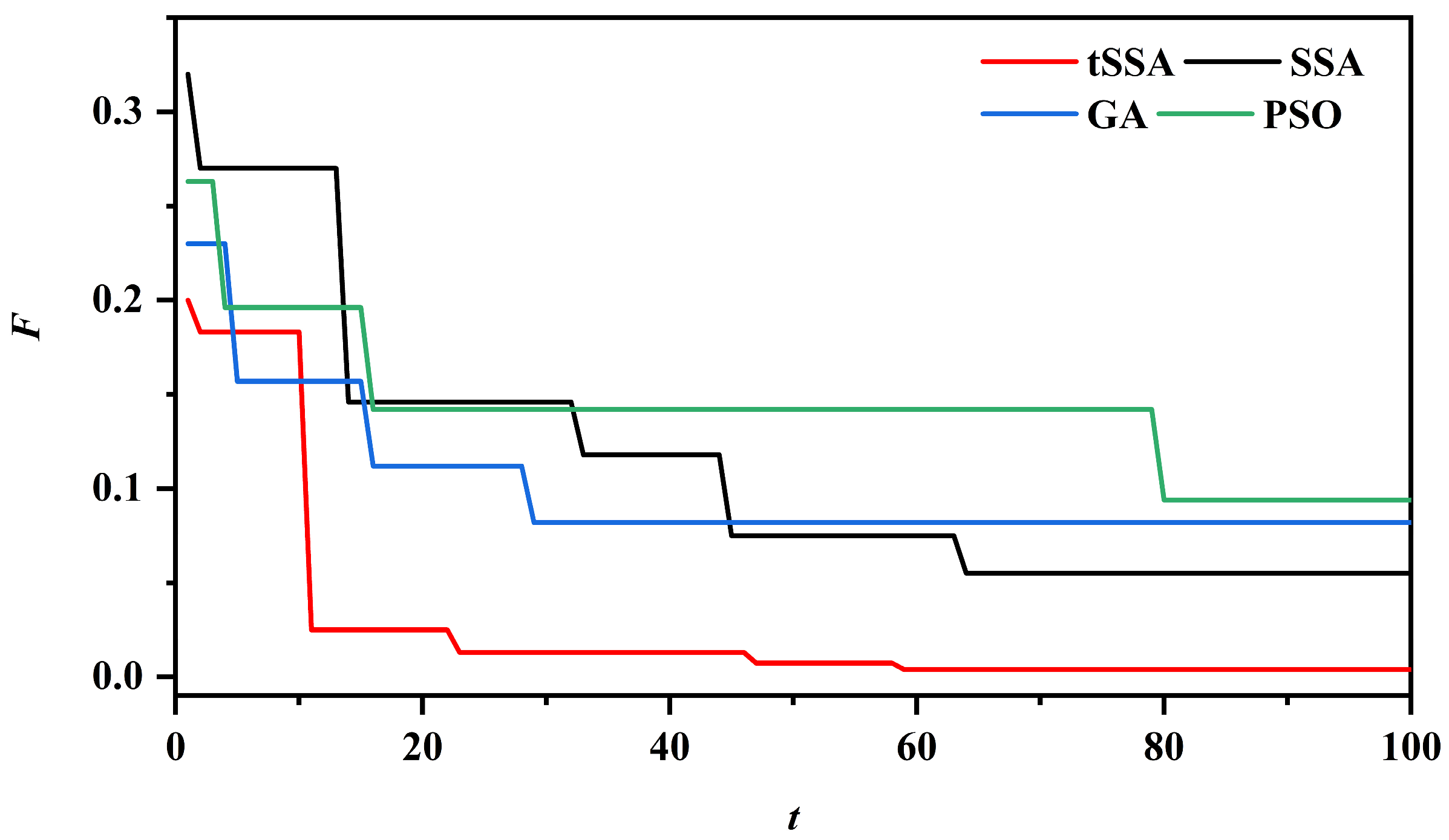
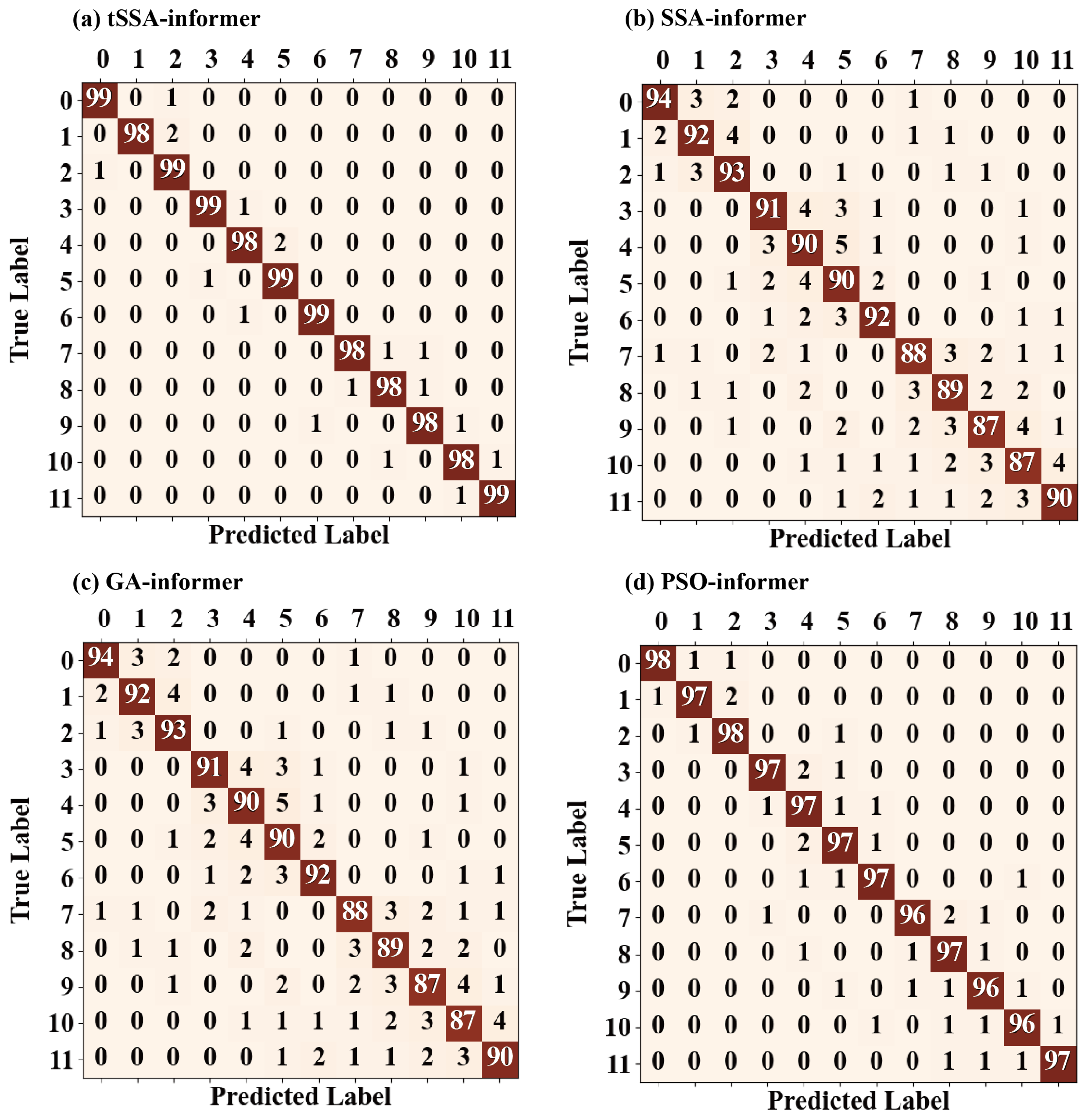
3.3. Comparison of Optimization Algorithms
3.4. Comparison of Model Diagnostic Performance
3.5. Comparison Under Different Sample Sizes of Labels
3.6. Model Ablation Experiment
4. Discussion
4.1. Advantages of the tSSA-Informer Model
4.2. The tSSA-Informer Model Is Insufficient
4.3. Outlook of the tSSA-Informer Model
5. Conclusions
- (1)
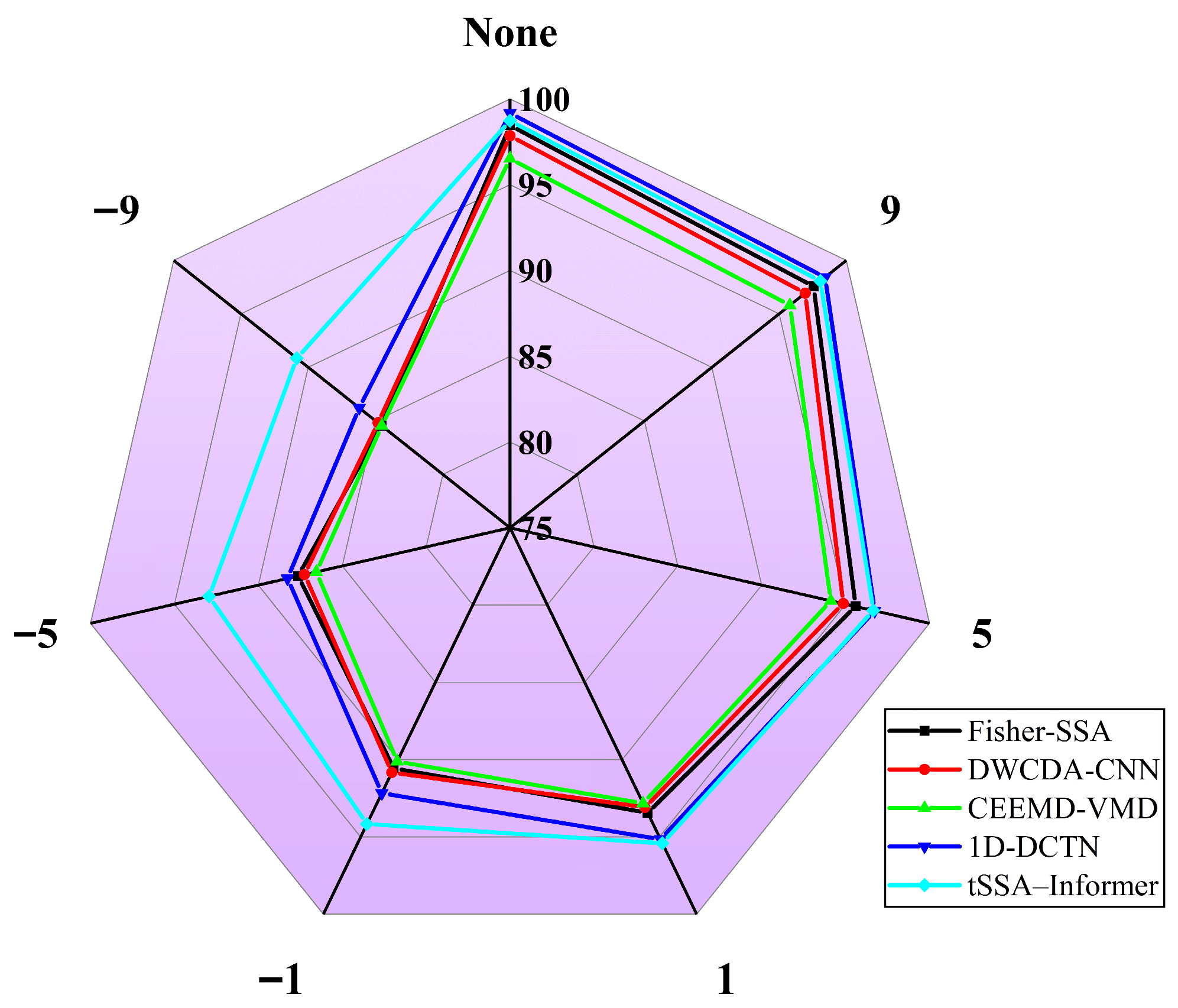
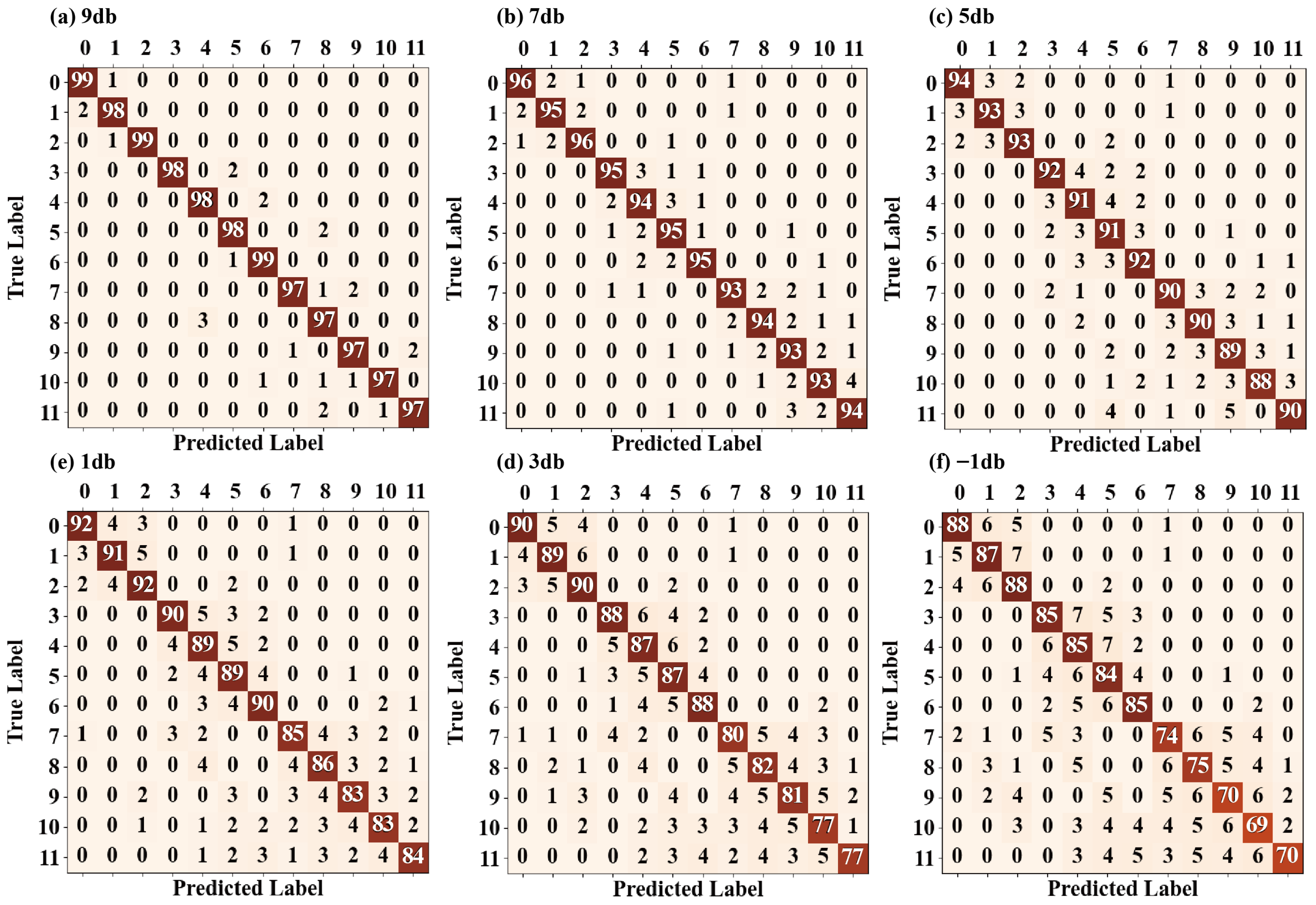
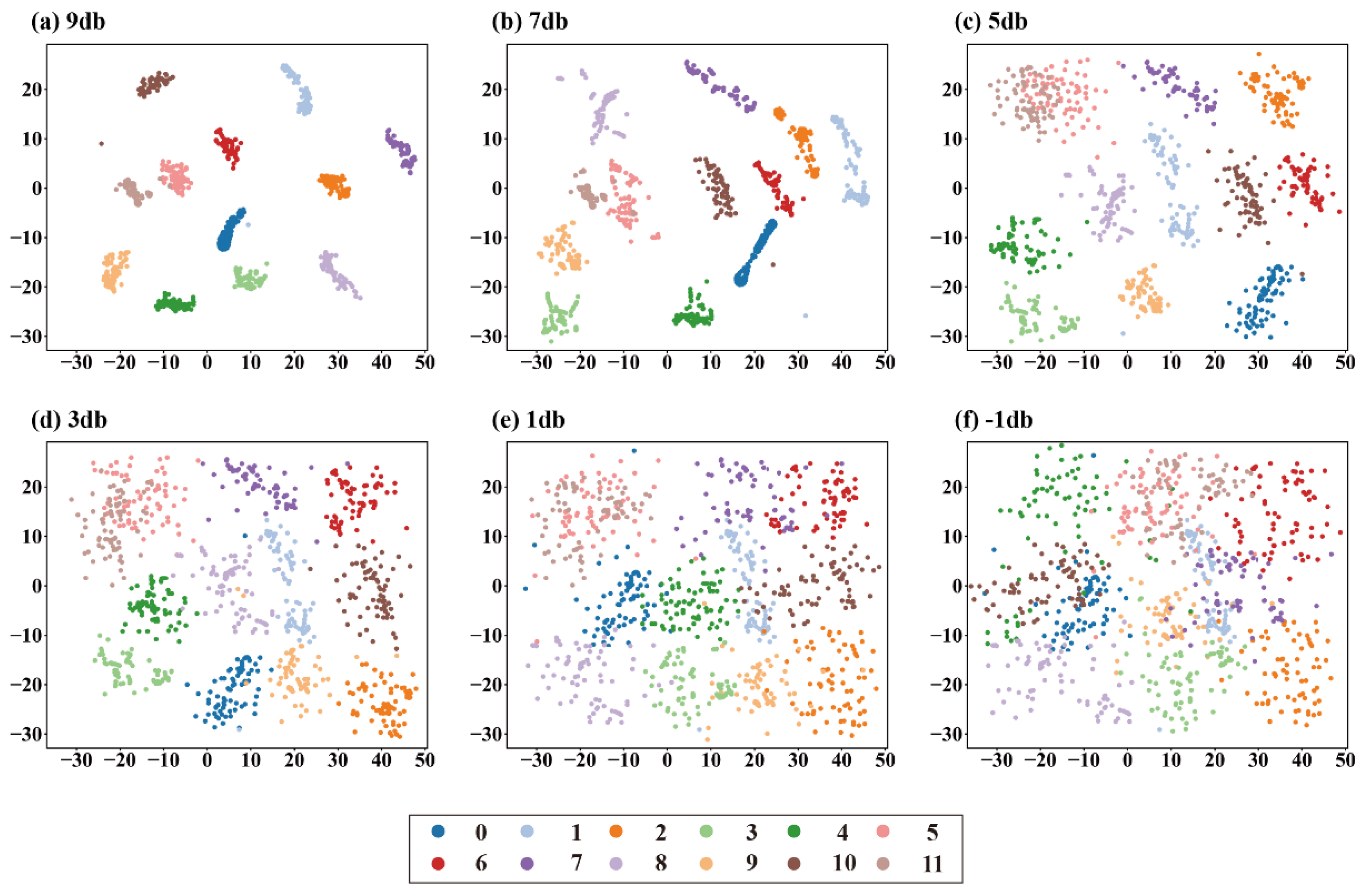
- It has outstanding anti-noise interference capability and is suitable for complex working conditions. The “long-tail anti-outliers” feature of SSA and the sparse self-attention mechanism of Informer form a synergistic effect, effectively solving the problem that the fault features of traditional models are easily submerged under strong noise. Experiments show that under the strong noise condition of SNR = −1 dB, the diagnostic accuracy rate of the model reaches 87.47%, which is more than 12% higher than that of comparison models such as 1D-DCTN. Even in an extreme noise environment with SNR = −9 dB, the accuracy rate remains at 90.85%, and 90% of the error samples are concentrated in similar working conditions. There are fewer than eight cross-category misjudgments, fully verifying its reliable adaptability in multi-source interference scenarios of pumping stations.
- (2)
- It has excellent adaptability to small samples and lowers the threshold for labeling costs. To address the issue of scarce labeled data in actual operation and maintenance, the model achieves core feature mining with a small number of samples through tSSA global optimization and Informer information distillation mechanisms. When the labeled sample size is reduced to 10%, its accuracy rate still reaches 61.32%, which is nearly 26 percentage points higher than that of the suboptimal DWCDA-CNN. It is much higher than traditional models such as Fisher-SSA and 1D-DCTN, significantly reducing the reliance on large-scale labeled data and adapting to scenarios where the data accumulation of new monitoring stations is insufficient.
- (3)
- The diagnostic accuracy and optimization efficiency are synergistically optimized, and the performance is comprehensively leading. The efficient optimization of Informer hyperparameters by tSSA has achieved a dual improvement in accuracy and efficiency: in a noise-free environment, the average diagnostic accuracy of the model reaches 98.73%, with the highest accuracy reaching 99.36%, which is 5.17% higher than that of SSA-Informer. Hyperparameter optimization only takes 10 min and 44 s, which is 40% faster than the genetic algorithm and has better search accuracy than PSO-Informer. The error rate is reduced by 12% under similar parameter configurations. Both the confusion matrix and t-SNE visualization show that the model has clear feature clustering for the 12 types of faults, with closely clustered samples of the same type and high boundary discrimination.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, W.; Chen, J.; Li, J.; Xia, K. Derivative and enhanced discrete analytic wavelet algorithm for rolling bearing fault diagnosis. Microprocess. Microsyst. 2021, 82, 103872. [Google Scholar] [CrossRef]
- Ting, L.; ShuangLin, L.; Ze, M. Analysis of Fault Diagnosis Methods for Electromechanical Equipment in Pumping Stations of Water Conservancy Projects. Mach. China 2023, 96–100. [Google Scholar]
- Shunchao, Z.; Jianrong, Z. Typical failures and hydraulic optimization research for large-axis inclined pump stations. Water Conserv. Constr. Manag. 2024, 44, 37–42. [Google Scholar]
- Yu, H.T.; Kim, H.J.; Park, S.H.; Kim, M.H.; Jeon, I.S.; Choi, B.K. Classification of rotary machine fault considering signal differences. J. Mech. Sci. Technol. 2022, 36, 517–525. [Google Scholar] [CrossRef]
- Huo, Z.; Zhang, Y.; Jombo, G.; Shu, L. Adaptive multiscale weighted permutation entropy for rolling bearing fault diagnosis. IEEE Access 2020, 8, 87529–87540. [Google Scholar] [CrossRef]
- Cai, B.; Zhao, Y.; Liu, H.; Xie, M. A data-driven fault diagnosis methodology in three-phase inverters for PMSM drive systems. IEEE Trans. Power Electron. 2017, 32, 5590–5600. [Google Scholar] [CrossRef]
- Lv, Y.; Yuan, R.; Song, R. Multivariate empirical mode decomposition and its application to fault diagnosis of rolling bearing. Mech. Syst. Signal Process. 2016, 81, 219–234. [Google Scholar] [CrossRef]
- Hassan, M.F.B.; Bonello, P. A Neural Network Identification Technique for a Foil-Air Bearing Under Variable Speed Conditions and Its Application to Unbalance Response Analysis. J. Tribol. 2017, 139, 021501. [Google Scholar] [CrossRef]
- Kumar, P.; Khalid, S.; Kim, H.S. Prognostics and Health Management of Rotating Machinery of Industrial Robot with Deep Learning Applications—A Review. Mathematics 2023, 11, 3008. [Google Scholar] [CrossRef]
- Demassey, S.; Sessa, V.; Tavakoli, A. Alternating Direction Method and Deep Learning for Discrete Control with Storage. Comb. Optim. 2024, 14594. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, G.; Li, C.; Chen, Y.; Zhang, Z. A New Deep Learning Model for Fault Diagnosis with Good Anti-Noise and Domain Adaptation Ability on Raw Vibration Signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep learning and its applications to machine health monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 5998–6008. [Google Scholar]
- Bao, Z.; Du, J.; Zhang, W.; Wang, J.; Qiu, T.; Cao, Y. A Transformer Model-Based Approach to Bearing Fault Diagnosis. Data Sci. 2021, 17, 5678–5686. [Google Scholar]
- Wang, R.; Dong, E.; Cheng, Z.; Liu, Z.; Jia, X. Transformer-based intelligent fault diagnosis methods of mechanical equipment: A survey. Open Phys. 2024, 22, 20240015. [Google Scholar] [CrossRef]
- Sun, W.; Yan, R.; Jin, R.; Xu, J.; Yang, Y.; Chen, Z. LiteFormer: A Lightweight and Efficient Transformer for Rotating Machine Fault Diagnosis. IEEE Trans. Reliab. 2024, 73, 1258–1269. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, K.; Zheng, L. Transformer Fault Diagnosis Method Based on TimesNet and Informer. Actuators 2024, 13, 74. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. AAAI Conf. Artif. Intell. 2021, 35, 11106–11114. [Google Scholar] [CrossRef]
- Wang, Y. Deepening Intelligent Microgrid Management: A Study on Improving Load Forecasting Accuracy Based on Informer Models. IEEE Trans. Smart Grid 2024, 15, 1234–1245. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, Q.; Chang, W.; Xiao, P.; Li, M. EGFormer: An Enhanced Transformer Model with Efficient Attention Mechanism for Traffic Flow Forecasting. Vehicles 2024, 6, 120–139. [Google Scholar] [CrossRef]
- Rao, Z.; Wu, J.; Li, G.; Wang, H. Voltage abnormity prediction method of lithium-ion energy storage power station using informer based on Bayesian optimization. Sci. Rep. 2024, 15, 1234–1245. [Google Scholar] [CrossRef] [PubMed]
- Wei, D.; Wang, Z.; Qiu, M.; Yu, J.; Jin, Y.; Sha, X.; Ouyang, K. Multiple objectives escaping bird search optimization and its application in stock market prediction based on transformer model. Sci. Rep. 2025, 15, 5730. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Liu, Y. Explainable AI for Hyperparameter Optimization. IEEE Trans. Artif. Intell. 2023, 12, 1234–1245. [Google Scholar]
- Nie, J.; Liu, S.; Xiang, C.; Xu, J.; Li, Y. Life Prediction of Railway Relays Based on TPE-Informer Model. J. Electr. Eng. 2024, 19, 98–106. [Google Scholar]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Lu, X.; Mu, X.; Zhang, J.; Wang, Z. Chaotic Sparrow Search Optimization Algorithm. J. Beijing Univ. Aeronaut. Astronaut. 2021, 47, 1712–1720. [Google Scholar]
- Chen, Z.-G.; Zhan, Z.H. Two-Layer Collaborative Differential Evolution Algorithm forMultimodal Optimization Problems. Chin. J. Comput. 2021, 44, 1806–1823. [Google Scholar]
- Gao, S.; Hao, W.; Wang, Q.; Zhang, Y. Missing-Data Filling Method Based on Improved Informer Model for Mechanical-Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2024, 73, 1–10. [Google Scholar] [CrossRef]
- Zhang, K.; Zhu, E.; Zhang, Y.; Gao, Y.; Tang, M.; Huang, Q. A multi-fault diagnosis method for rolling bearings. Signal Image Video Process. 2024, 18, 8413–8426. [Google Scholar] [CrossRef]
- Ren, S.; Lou, X. Rolling Bearing Fault Diagnosis Method Based on SWT and Improved Vision Transformer. Sensors 2025, 25, 2090. [Google Scholar] [CrossRef]
- Yang, X.; Liu, B.; Xiang, L.; Hu, A.; Xu, Y. A novel intelligent fault diagnosis method of rolling bearings with small samples. Measurement 2022, 203, 111899. [Google Scholar] [CrossRef]
- Jiang, Q. Research on mechanical fault diagnosis and maintenance strategy of aero engines based on flight line maintenance experience. Eng. Technol. Manag. 2025, 10, 183–186. [Google Scholar]
- Han, Q.; Liu, J.; He, G.; Li, W. Multi-source fusion perception intelligent fault diagnosis methods for critical components of industrial robots. J. Vib. Eng. 2025, 38, 1252–1259. [Google Scholar]

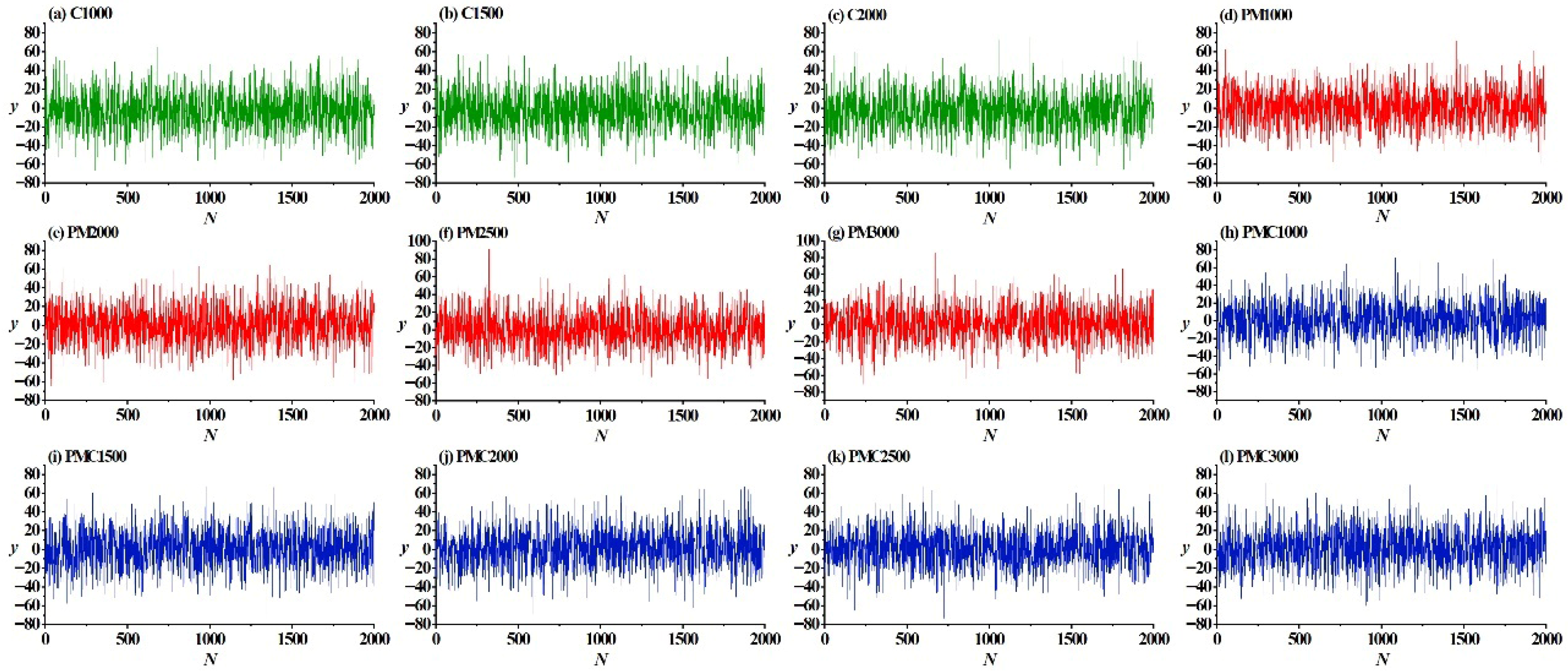
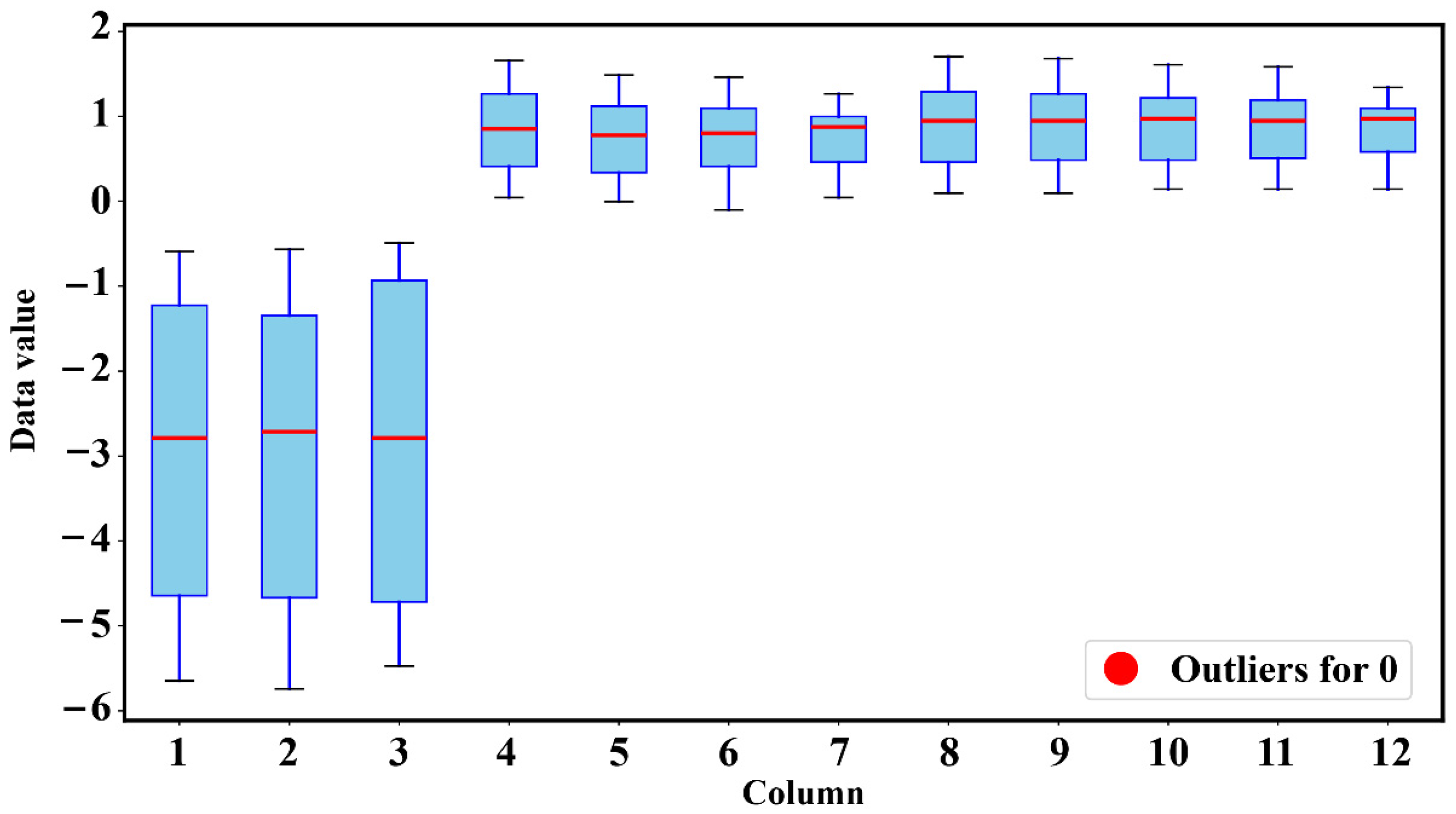
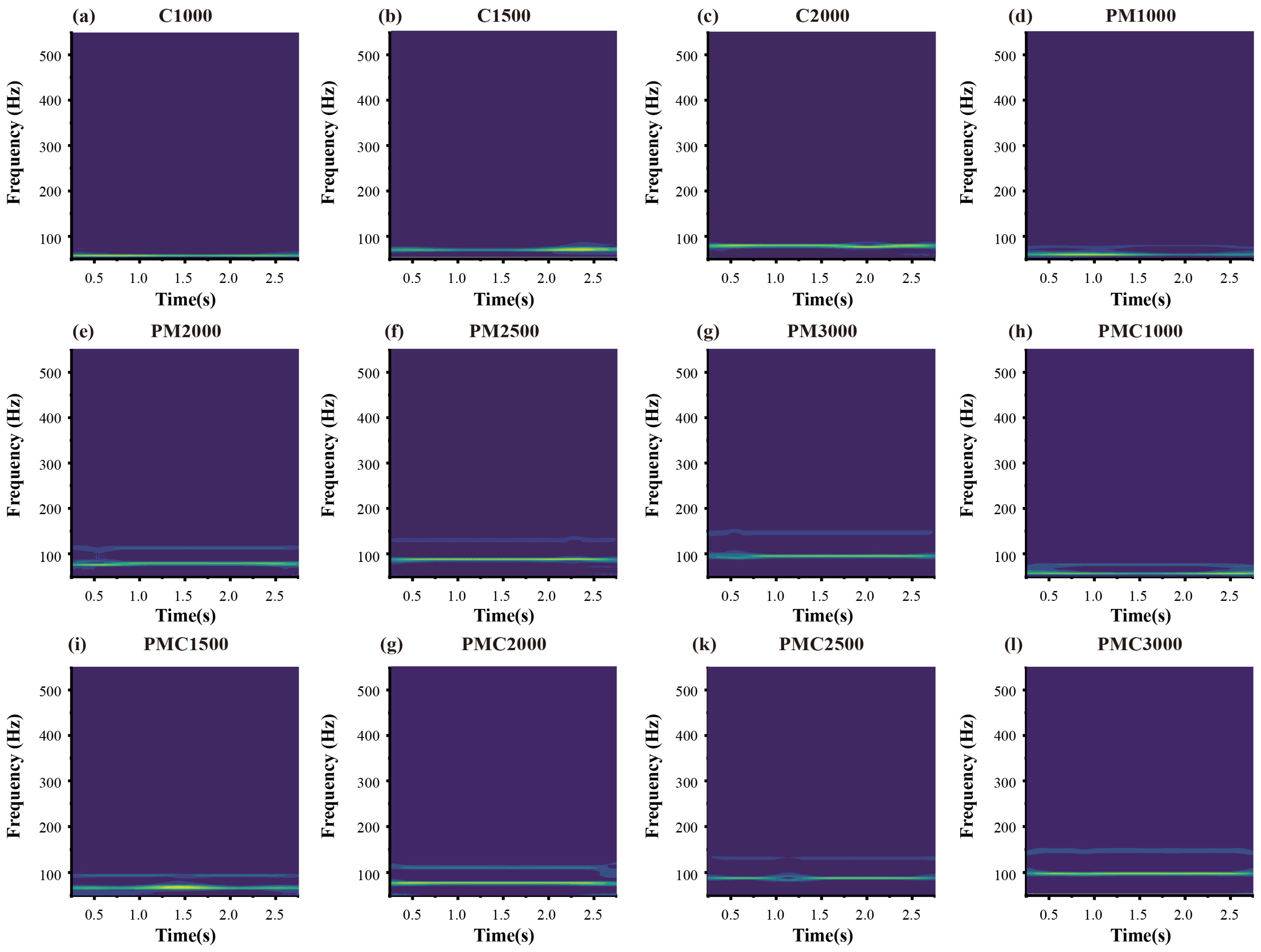
| Fault Type | Rotational Speed | Number of Samples | Degree of Failure | Category |
|---|---|---|---|---|
| Parallel misalignment (C) | 1000 | 400 | 0.07 | 0 |
| 1500 | 400 | 0.14 | 1 | |
| 2000 | 400 | 0.21 | 2 | |
| Rotor–stator friction fault (PM) | 1000 | 400 | 0.07 | 3 |
| 2000 | 400 | 0.14 | 4 | |
| 2500 | 400 | 0.21 | 5 | |
| 3000 | 400 | 0.28 | 6 | |
| Misalignment—rubbing coupling fault (PMC) | 1000 | 400 | 0.07 | 7 |
| 1500 | 400 | 0.14 | 8 | |
| 2000 | 400 | 0.21 | 9 | |
| 2500 | 400 | 0.28 | 10 | |
| 3000 | 400 | 0.35 | 11 |
| Dimension Numbering | Cumulative Contribution Rate | Dimension Numbering | Cumulative Contribution Rate |
|---|---|---|---|
| 1 | 0.1384 | 13 | 0.8070 |
| 2 | 0.2621 | 14 | 0.8289 |
| 3 | 0.3767 | 15 | 0.8503 |
| 4 | 0.4841 | 16 | 0.8706 |
| 5 | 0.5352 | 17 | 0.8904 |
| 6 | 0.5795 | 18 | 0.9076 |
| 7 | 0.6220 | 19 | 0.9246 |
| 8 | 0.6633 | 20 | 0.9410 |
| 9 | 0.7026 | 21 | 0.9568 |
| 10 | 0.7308 | 22 | 0.9722 |
| 11 | 0.7573 | 23 | 0.9868 |
| 12 | 0.7826 | 24 | 1.0000 |
| Model | Parameter | Value | Time Consumed | |
|---|---|---|---|---|
| tSSA–Informer | Core architecture parameters | e_layers | 3 | 10 min 44 s |
| d_layers | 1 | |||
| n_head | 4 | |||
| distillationlayers | 2 | |||
| Hyperparameter | d_model | 192 | ||
| d_ff | 155 | |||
| Activation function | Feedforward network activation function | RELU | ||
| Output layer activation function | Softmax | |||
| SSA–Informer | Core architecture parameters | e_layers | 2 | 11 min 38 s |
| d_layers | 1 | |||
| n_head | 4 | |||
| distillationlayers | 1 | |||
| Hyperparameter | d_model | 176 | ||
| d_ff | 137 | |||
| Activation function | Feedforward network activation function | RELU | ||
| Output layer activation function | Softmax | |||
| GA–Informer | Core architecture parameters | e_layers | 4 | 18 min 53 s |
| d_layers | 1 | |||
| n_head | 5 | |||
| distillationlayers | 2 | |||
| Hyperparameter | d_model | 217 | ||
| d_ff | 143 | |||
| Activation function | Feedforward network activation function | RELU | ||
| Output layer activation function | Softmax | |||
| PSO–Informer | Core architecture parameters | e_layers | 3 | 10 min 17 s |
| d_layers | 1 | |||
| n_head | 4 | |||
| distillationlayers | 2 | |||
| Hyperparameter | d_model | 194 | ||
| d_ff | 171 | |||
| Activation function | Feedforward network activation function | RELU | ||
| Output layer activation function | Softmax |
| Model | tSSA-Informer | SSA-Informer | GA-Informer | PSO-Informer | |
|---|---|---|---|---|---|
| Training resource consumption | Total time consumption (h) | 2.8 | 4.2 | 3.6 | 3.1 |
| Peak GPU memory (GB) | 10.2 | 13.7 | 12.5 | 11.8 | |
| Peak CPU memory (GB) | 28.5 | 32.8 | 30.1 | 29.7 | |
| Inference performance indicators | GPU side latency (ms) | 9.6 | 13.2 | 11.8 | 10.3 |
| Edge CPU latency (ms) | 42.3 | 58.7 | 51.2 | 45.6 | |
| Accelerate module end delay (ms) | 18.7 | 25.4 | 22.6 | 20.1 | |
| Inference GPU memory usage (MB) | 850 | 1050 | 920 | 880 | |
| Inference CPU memory usage (MB) | 480 | 620 | 550 | 510 | |
| Model | Average Diagnostic Accuracy % | Max Diagnostic Accuracy % |
|---|---|---|
| tSSA-Informer | 98.73 | 99.36 |
| SSA-Informer | 93.56 | 94.35 |
| GA-Informer | 96.34 | 97.51 |
| PSO-Informer | 97.36 | 97.69 |
| Informer | 91.75 | 92.92 |
| Combination of Comparative Models | tSSA—Average Accuracy Rate of Informer (%) | Average Accuracy Rate of the Comparison Model (%) | Standard Deviation | Paired t-Test p Value | 95% Confidence Interval (Difference in Accuracy Rate, %) |
|---|---|---|---|---|---|
| tSSA-Informer vs. SSA-Informer | 98.73 | 93.56 | 0.42 | <0.001 | [4.72, 5.62] |
| tSSA-Informer vs. GA-Informer | 98.73 | 96.34 | 0.38 | <0.001 | [2.05, 2.73] |
| tSSA-Informer vs. PSO-Informer | 98.73 | 97.36 | 0.35 | 0.002 | [1.01, 1.73] |
| Model | SNR | Accuracy Rate | Macro-P | Macro-R | Macro-F1 |
|---|---|---|---|---|---|
| Fisher-SSA | None | 98.46 | 98.23 | 98.35 | 98.29 |
| 9 dB | 97.57 | 97.31 | 97.42 | 97.36 | |
| 5 dB | 95.60 | 95.34 | 95.47 | 95.40 | |
| 1 dB | 93.44 | 93.18 | 93.30 | 93.24 | |
| −1 dB | 90.56 | 90.29 | 90.41 | 90.35 | |
| −5 dB | 87.63 | 87.35 | 87.48 | 87.41 | |
| −9 dB | 84.54 | 84.26 | 84.39 | 84.32 | |
| DWCDA-CNN | None | 97.85 | 97.61 | 97.72 | 97.66 |
| 9 dB | 96.94 | 96.68 | 96.80 | 96.74 | |
| 5 dB | 94.87 | 94.60 | 94.73 | 94.66 | |
| 1 dB | 93.08 | 92.81 | 92.94 | 92.87 | |
| −1 dB | 90.83 | 90.55 | 90.68 | 90.61 | |
| −5 dB | 87.25 | 86.97 | 87.10 | 87.03 | |
| −9 dB | 84.81 | 84.52 | 84.65 | 84.58 | |
| CEEMD-VMD | None | 96.52 | 96.27 | 96.39 | 96.33 |
| 9 dB | 95.81 | 95.55 | 95.68 | 95.61 | |
| 5 dB | 94.13 | 93.86 | 93.99 | 93.92 | |
| 1 dB | 92.83 | 92.55 | 92.68 | 92.61 | |
| −1 dB | 90.12 | 89.84 | 89.97 | 89.90 | |
| −5 dB | 86.54 | 86.25 | 86.38 | 86.31 | |
| −9 dB | 84.53 | 84.24 | 84.37 | 84.30 | |
| 1 D-DCTN | None | 99.17 | 98.92 | 99.05 | 98.98 |
| 9 dB | 98.42 | 98.16 | 98.29 | 98.22 | |
| 5 dB | 96.74 | 96.47 | 96.60 | 96.53 | |
| 1 dB | 95.15 | 94.88 | 95.01 | 94.94 | |
| −1 dB | 92.16 | 91.87 | 92.00 | 91.93 | |
| −5 dB | 88.26 | 87.96 | 88.09 | 88.02 | |
| −9 dB | 86.20 | 85.90 | 86.03 | 86.01 |
| Model | Accuracy With Different Sample Sizes of Labels | |||
|---|---|---|---|---|
| 70% | 50% | 30% | 10% | |
| Fisher-SSA | 90.37 | 73.54 | 46.54 | 21.62 |
| DWCDA-CNN | 91.83 | 77.19 | 52.73 | 35.41 |
| CEEMD-VMD | 90.11 | 75.38 | 49.72 | 32.54 |
| 1D-DCTN | 93.42 | 79.68 | 45.42 | 18.29 |
| tSSA-Informer | 93.17 | 87.25 | 73.84 | 61.32 |
| Model Variant | Full Sample Scenarios (Acc/Relative Improvement) | Small Sample Scenario (10% Marking, Acc/Relative Improvement) | Strong Noise Scene (SNR = −9 dB, Acc/Relative Improvement) |
|---|---|---|---|
| Informer | 91.75/0.0 | 61.32/0.0 | 75.40/0.0 |
| Informer + trend cycle separation | 94.20/+2.45 | 67.30/+5.80 | 81.60/+6.20 |
| Informer + trend cycle separation + sparse attention | 96.53/+4.78 | 74.40/+13.30 | 85.35/+9.95 |
| tSSA-Informer | 98.73/+6.98 | 61.32/+24.50 | 90.85/+15.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Q.; Yang, H.; Tian, Y.; Guo, L. Fault Diagnosis Method for Pumping Station Units Based on the tSSA-Informer Model. Sensors 2025, 25, 6458. https://doi.org/10.3390/s25206458
Tian Q, Yang H, Tian Y, Guo L. Fault Diagnosis Method for Pumping Station Units Based on the tSSA-Informer Model. Sensors. 2025; 25(20):6458. https://doi.org/10.3390/s25206458
Chicago/Turabian StyleTian, Qingqing, Hongyu Yang, Yu Tian, and Lei Guo. 2025. "Fault Diagnosis Method for Pumping Station Units Based on the tSSA-Informer Model" Sensors 25, no. 20: 6458. https://doi.org/10.3390/s25206458
APA StyleTian, Q., Yang, H., Tian, Y., & Guo, L. (2025). Fault Diagnosis Method for Pumping Station Units Based on the tSSA-Informer Model. Sensors, 25(20), 6458. https://doi.org/10.3390/s25206458




