Analysis Method for the Spatial Layout Equilibrium of Highway Transportation Network Based on Community Detection
Abstract
1. Introduction
2. Materials and Methods
2.1. Methodological Framework
2.2. Case Study
2.3. Highway Network Construction Method
2.4. Description of Community Structure
2.5. Expression of Connectivity Component
2.6. Detecting Community Structure by Using the C-Louvain Algorithm
| Algorithm 1: C-Louvain Algorithm |
| Input: G = (V, E, W): graph representation. Output: C: community sets at each level; Q: modularity at each level. Var: ĉ: vertex u’s best candidate community set. 1 Identify network G connectivity, if it is not connected, find the connected components , and community detection. Sorting by node degree within the connected component. 2 Loop outer |
| Output: C, Q |
2.7. Identifying Key Communities by Using DFS
- (1)
- Select any community within the connected component to start the traversal and record its parent community, and check if it is a root community.
- (2)
- If the currently visited community is a root community and has more than two child communities, it is a key community.
- (3)
- If it is not a root community and has a child community, and in the subgraph with the child community as the root, no community has an edge pointing to the DFS graph’s upper-level node of the current community, then it is a key community.
- (4)
- Repeat steps (2)–(3) until no communities can be visited.
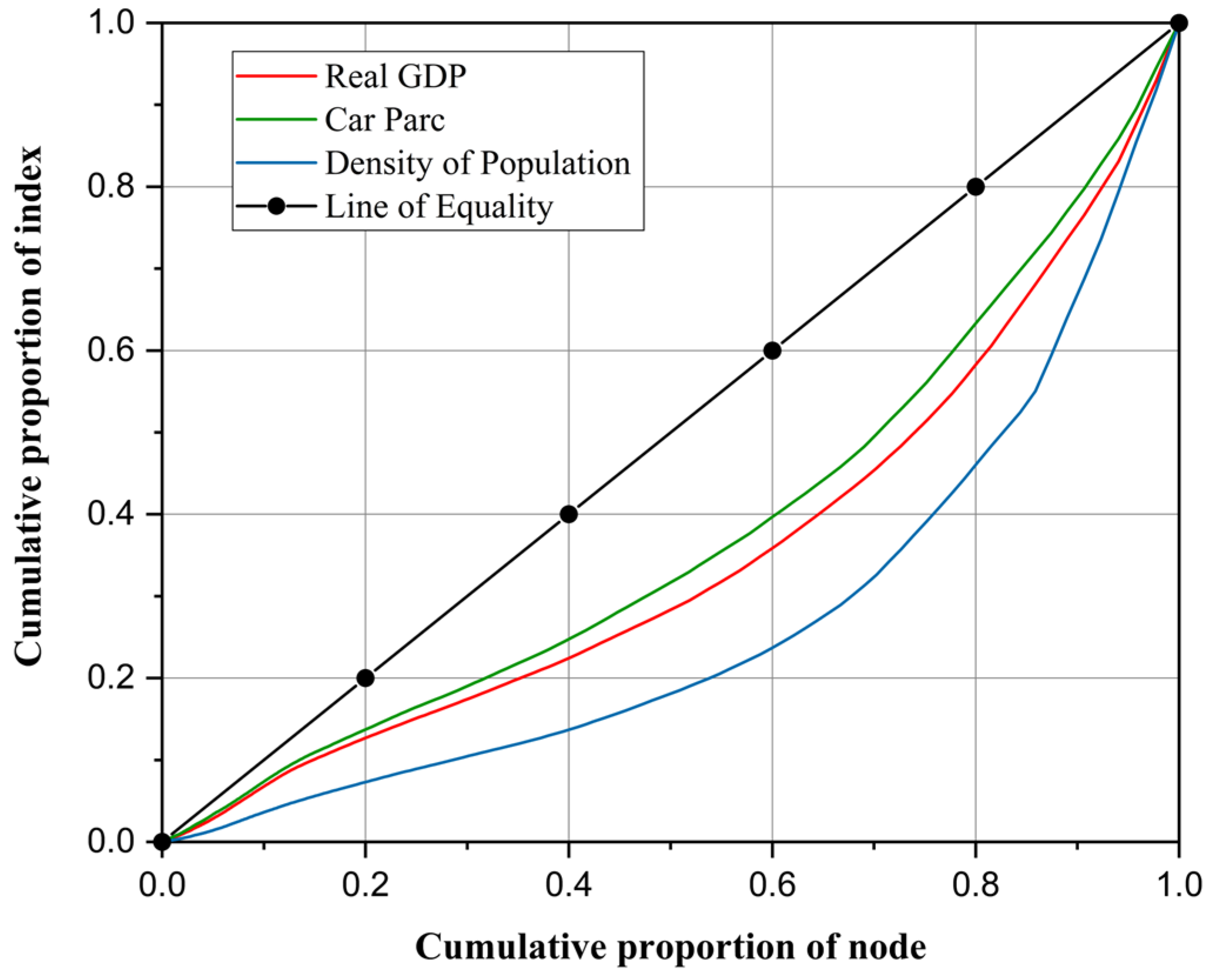
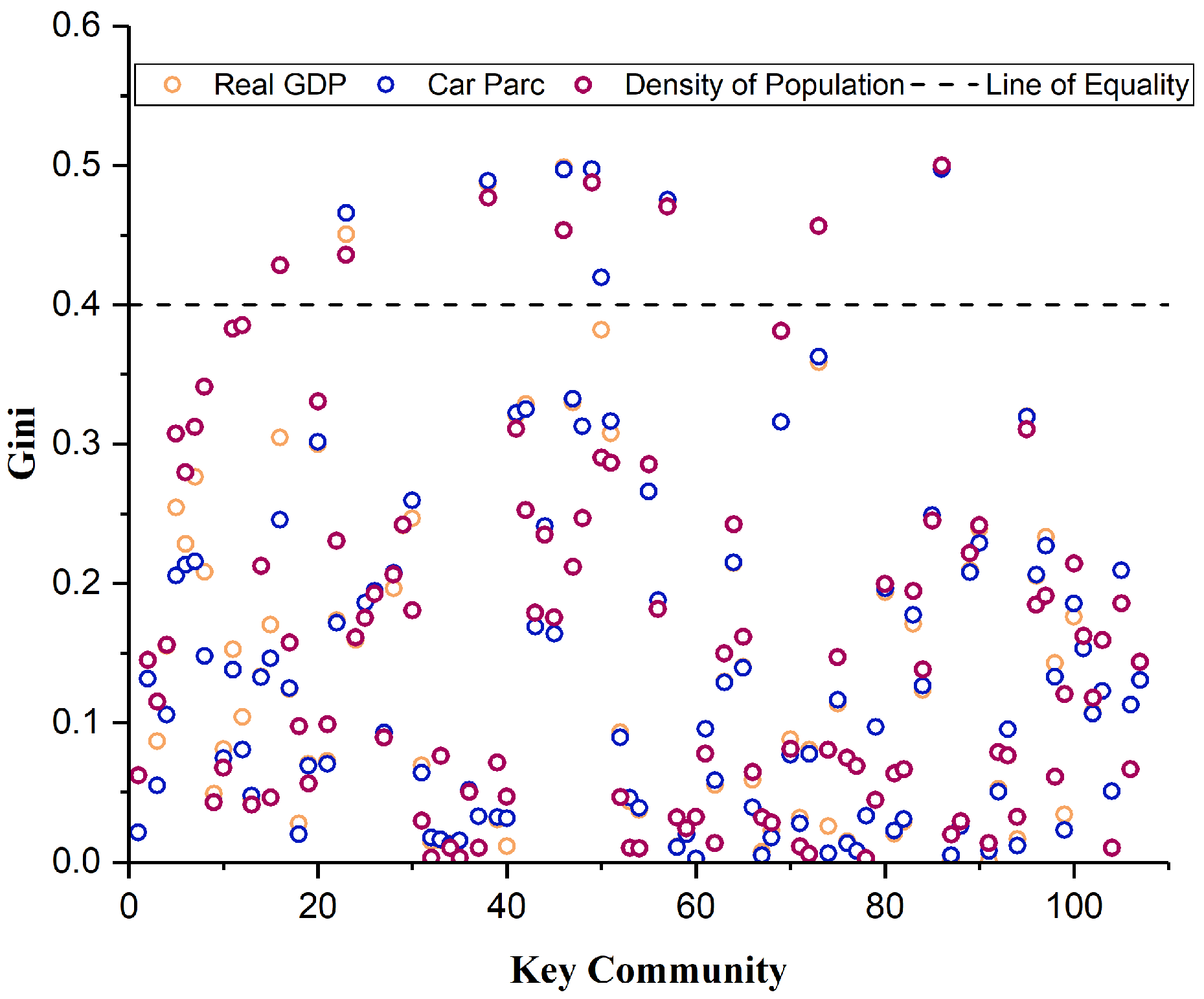
2.8. Evaluating Spatial Layout Equilibrium Using the Gini Coefficient
3. Results
3.1. Highway Network Modeling
3.1.1. Shenyang Highway Network Modeling
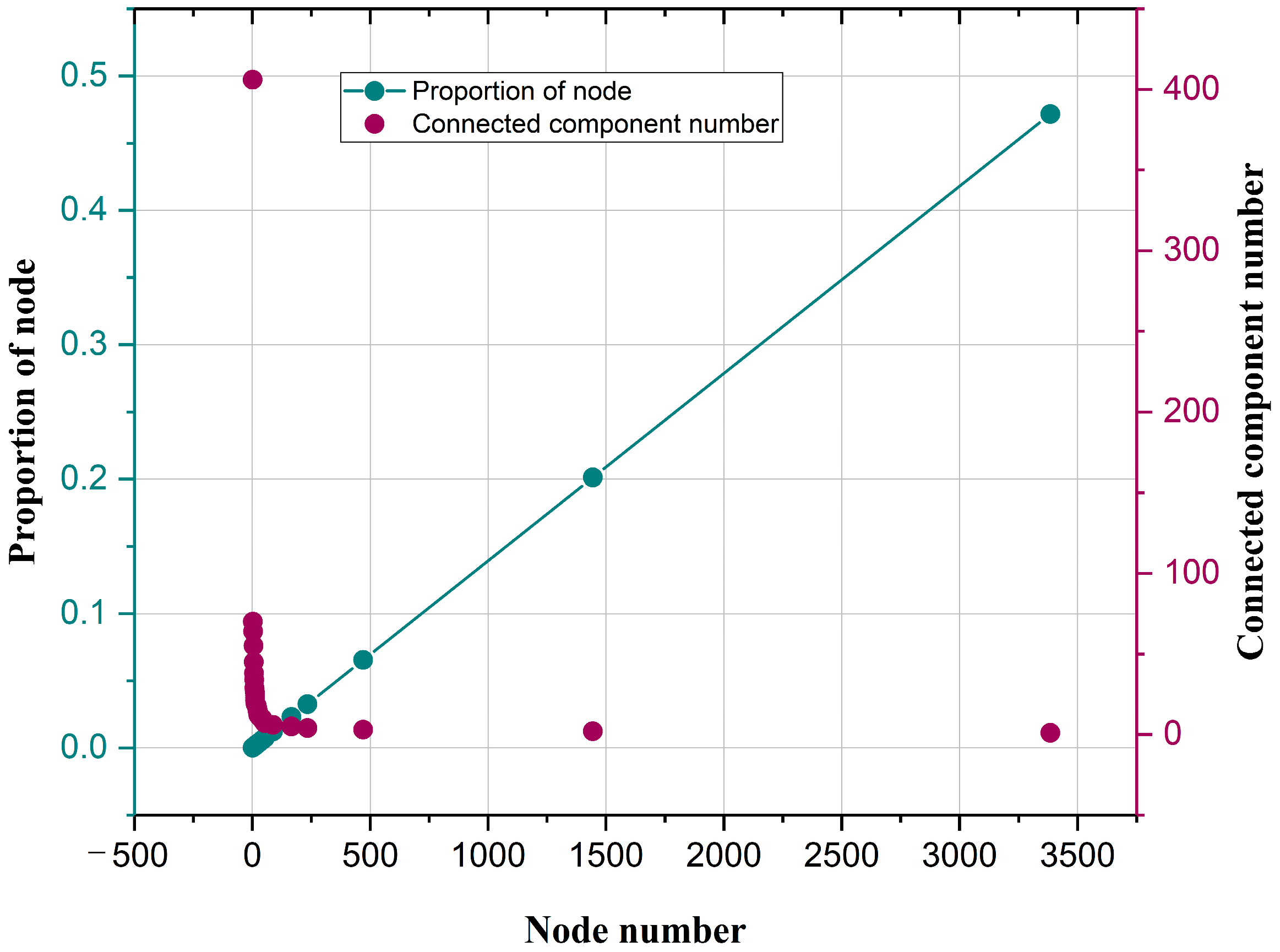
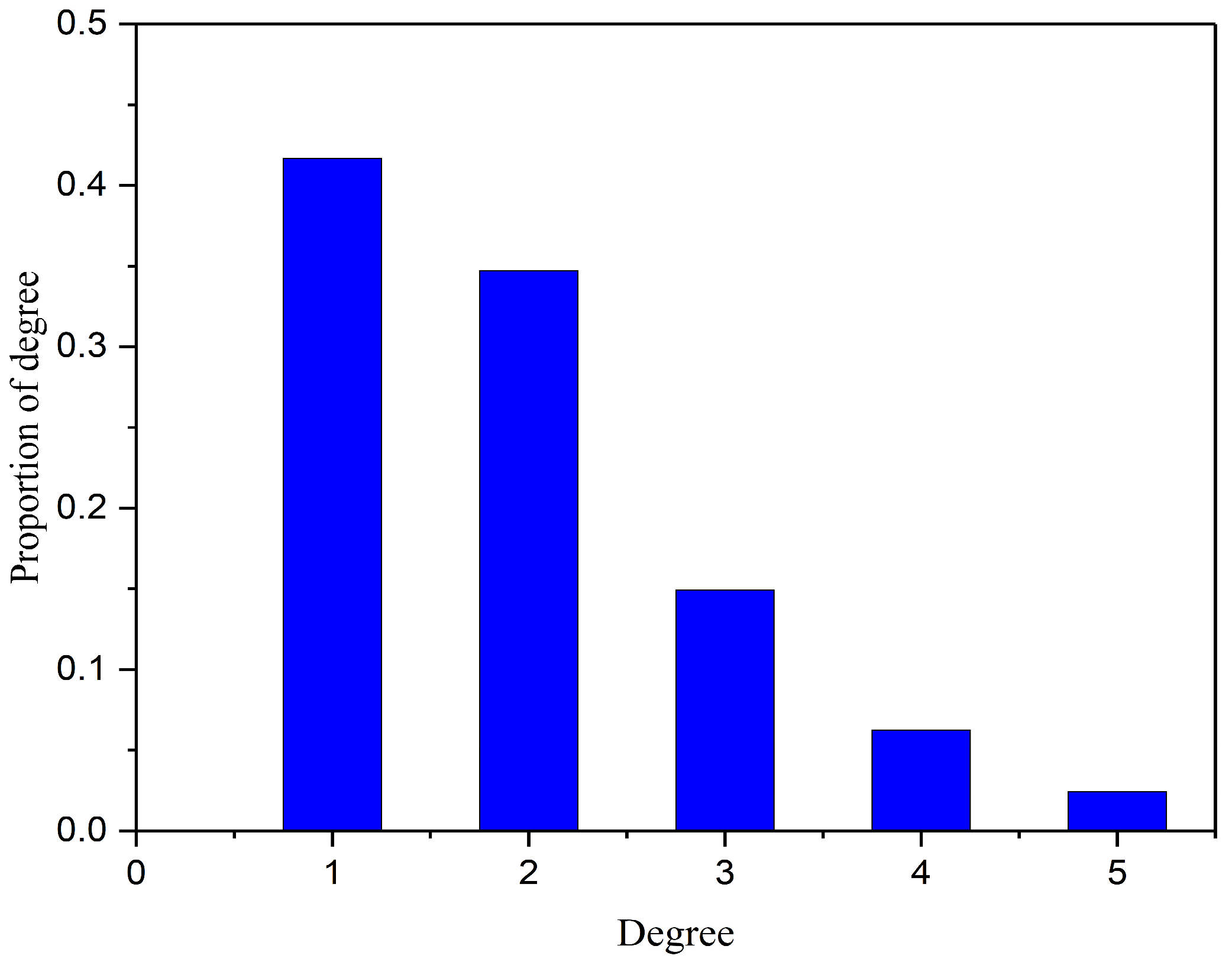
3.1.2. Network Connectivity Analysis
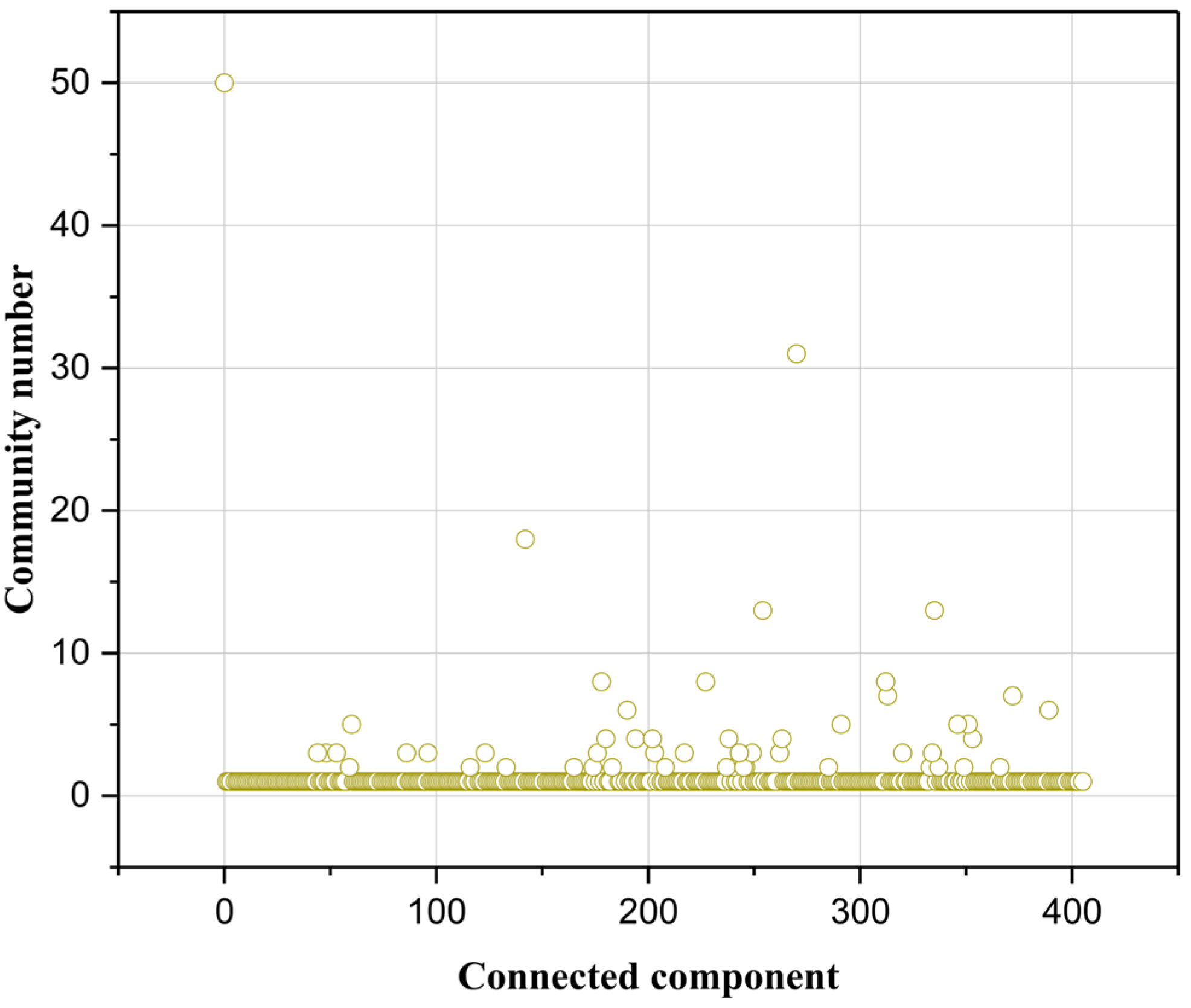
3.2. Community Detection Results
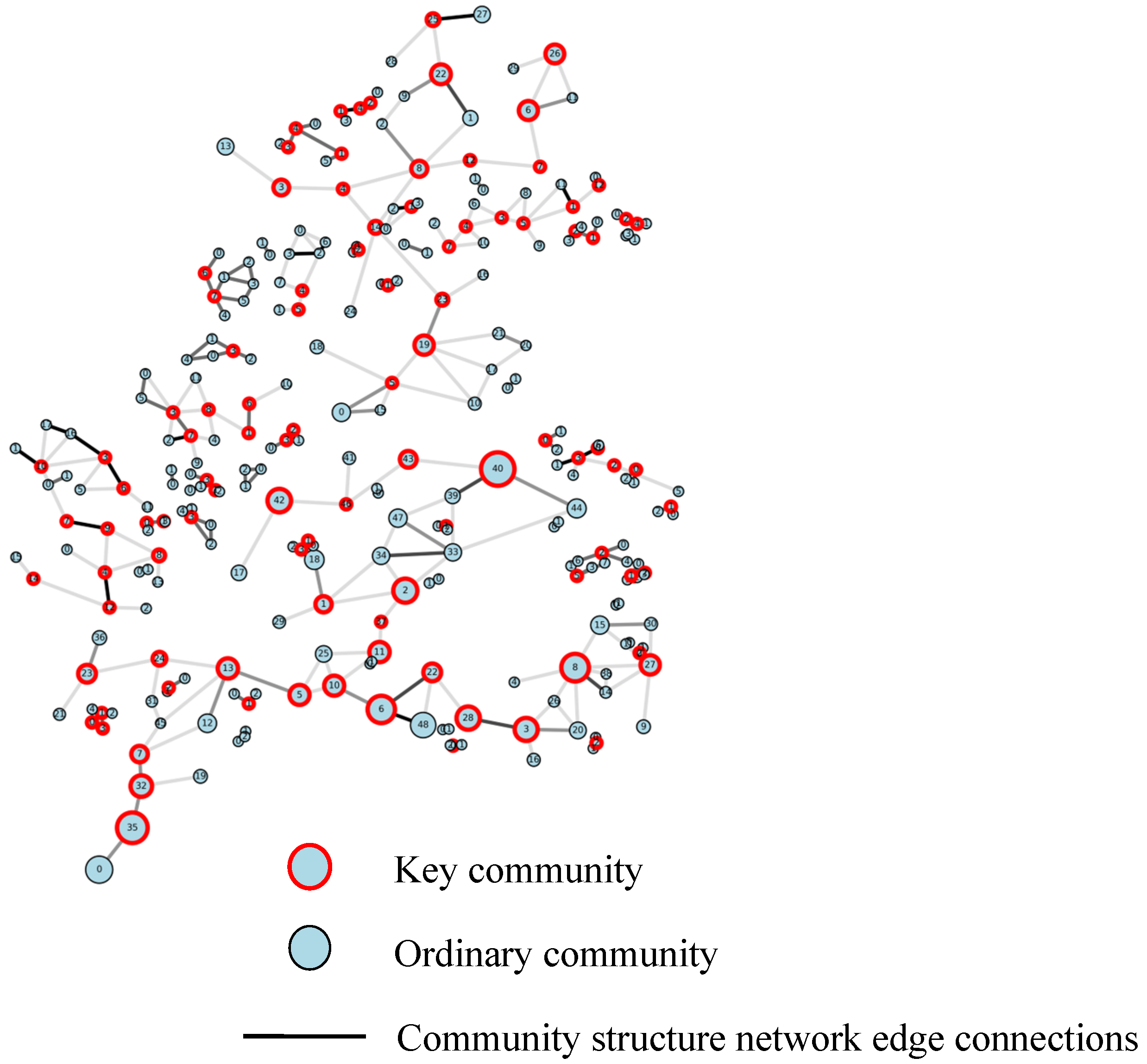
3.3. Key Community Identification
3.3.1. Community Structure Network Analysis
3.3.2. Key Community Identification Results
3.4. Gini Coefficient Equalization Evaluation Results
3.5. Algorithm Comparison
4. Discussion
4.1. Algorithm Discussion
4.2. Traffic Policy Implication
- (1)
- The policy should shift from “efficiency first” to “efficiency and equity equally.” While investment in high-demand corridors is important, attention must be paid to areas marginalized by inadequate infrastructure. Policymakers should introduce a framework for assessing transport equity to ensure that people in different income groups and in urban, rural, and remote areas enjoy basic mobility rights. This means that projects that improve “service gaps” should be given higher weight in investment decisions to avoid transport networks becoming tools that exacerbate social stratification.
- (2)
- Equilibrium should be used as a lever to achieve sustainable development goals. Areas with low infrastructure utilization are often accompanied by extensive land development and ecological pressure. Through equilibrium analysis, investment can be guided to stock optimization rather than incremental expansion. It can not only improve efficiency but also reduce the occupation of land and environment. At the same time, optimizing high-demand corridors can reduce congestion and carbon emissions across the entire road network, directly contributing to the “double carbon” goal.
- (3)
- A resilient regional economy should be built through balanced planning. A balanced network implies multiple growth poles and connecting channels within a region, rather than a single central dependency. This multicentric, networked structure exhibits greater resilience in the face of external shocks. Policies should encourage the cultivation of characteristic industrial nodes in surrounding areas and connect them with core cities through efficient road networks to form regional economies with complementary functions and coordinated development, thus supporting long-term and sustainable regional integration.
5. Conclusions
- (1)
- There are significant differences in the number of communities within different connected components, which reflects the heterogeneity of the network’s structure.
- (2)
- Using the Gini coefficient to quantitatively evaluate the supply–demand balance of key communities, the results show that in the study area, the proportion of county highway mileage is 7.07%, that of township highway mileage is 49.40%, and that of village highway mileage is 43.53%, mainly concentrated on township highways and village highways.
- (3)
- The originality of this work lies in its integration of complex network theory with transportation engineering, providing both methodological innovation and practical implications for urban planning. Community detection has opened up new avenues for research in traffic management systems.
- (4)
- Future work should involve on-site verification to enhance expert knowledge and validate the accuracy of the constructed network data. Results may differ when employing other community detection algorithms, necessitating an analysis of various influencing factors to achieve more precise community detection outcomes. We will study the advantages and disadvantages of the C-Louvain method in comparison with the hybrid methods or multi-criteria equilibrium analysis. We will also study dynamic or temporal analyses of the adaptability of the research methods. Concurrently, the influence of interpolating socioeconomic indicators into the research results is analyzed. To enhance the versatility and real-world applicability of C-Louvain, studies should focus on conducting case studies in multiple cities with diverse geographic and socioeconomic contexts to evaluate the transferability of C-Louvain. Additional data sources should be integrated to enrich the multimodal network representation and improve the accuracy of community detection.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- OECD. Reinforcing Rural Resilience; OECD Rural Studies; OECD Publishing: Paris, France, 2025. [Google Scholar] [CrossRef]
- World Bank. Kyrgyz Republic Country Economic Memorandum; World Bank Publications: Washington, DC, USA, 2020. [Google Scholar] [CrossRef]
- Diez, J. Sustainable and Smart Mobility Strategy. World Highw. 2020, 10, 29. [Google Scholar]
- Tacoli, C. The links between urban and rural development. Environ. Urban. 2003, 15, 3–12. [Google Scholar] [CrossRef]
- Ma, C.; Jiang, Y.; Qi, K. Investigating the urban–rural integrated town development strategy on the basis of the study of rural forms in Nantong, China. Front. Archit. Res. 2021, 10, 190–201. [Google Scholar] [CrossRef]
- The State Council of China. Outline Development Plan for the Guangdong-Hong Kong-Macao Greater Bay Area; Chinese Government Network: Beijing, China, 2019. Available online: https://www.gov.cn/zhengce/2019-02/18/content_5366593.htm#1 (accessed on 25 May 2025).
- China Highway Engineering Consultants Corporation. “The Feasibility Study of Shen Zhong Link”, Report; China Highway Engineering Consultants Corporation: Beijing, China, 2015; Available online: https://www.bridgeweb.com/Design-com...d-for-major-coastto-coast-link-in-China/3975 (accessed on 25 May 2025).
- Ministry of Transport of the People’s Republic of China. National Highway Network Planning; Ministry of Transport of the People’s Republic of China: Beijing, China, 2022.
- Zhang, C.S.; Ma, R.G. Equilibrium Evaluation and Development Strategies for Highway Network in Plateau Mountainous Area. D Highw. Transp. Res. Dev. 2010, 8, 114–119. [Google Scholar]
- Fan, S.G.; Connie, C.-K. Regional road development rural and urban poverty Evidence from China. Transp. Policy 2008, 15, 305–314. [Google Scholar] [CrossRef]
- Pei, Y.L.; Jin, Y.Q.; Cheng, Z. Equilibrium of Topology and Layout of Urban Multimode Public Transit Network. China J. Highw. Transp. 2021, 34, 127–138. [Google Scholar] [CrossRef]
- Newman, M.E.J. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef] [PubMed]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 10, 10008. [Google Scholar] [CrossRef]
- Crucitti, P.; Latora, V.; Porta, S. Centrality measures in spatial networks of urban streets. Phys. Rev. E 2006, 73, 036125. [Google Scholar] [CrossRef]
- Porta, S.; Crucitti, P.; Latora, V. The network analysis of urban streets: A primal approach. Environ. Plan. B Urban Anal. City Sci. 2006, 33, 705–725. [Google Scholar] [CrossRef]
- Porta, S.; Crucitti, P.; Latora, V. The network analysis of urban streets: A dual approach. Phys. A Stat. Mech. Its Appl. 2006, 369, 853–866. [Google Scholar] [CrossRef]
- Boeing, G. OSMnx: New methods for acquiring, constructing, analyzing, and visualizing complex street networks. Comput. Environ. Urban Syst. 2017, 65, 126–139. [Google Scholar] [CrossRef]
- Wang, Y.J.; Deng, Y.; Ren, F.; Zhu, R.X.; Wang, P.; Du, T.; Da, Q.Y. Analysing the spatial configuration of urban bus networks based on the geospatial network analysis method. Cities 2020, 96, 102406. [Google Scholar] [CrossRef]
- Radicchi, F.; Castellano, C.; Cecconi, F.; Loreto, V.; Parisi, D. Defining and identifying communities in networks. Proc. Natl. Acad. Sci. USA 2004, 9, 2658–2663. [Google Scholar] [CrossRef] [PubMed]
- Gui, Q.; Deng, R.; Xue, P.F.; Cheng, X.H. A community discovery algorithm based on boundary nodes and label propagation. Pattern Recognit. Lett. 2018, 109, 103–109. [Google Scholar] [CrossRef]
- Sharma, R.; Oliveira, S. Community detection algorithm for big social networks using hybrid architecture. Big Data Res. 2017, 10, 44–52. [Google Scholar] [CrossRef]
- Song, Q.; Wang, X.F. Efficient routing on large road networks using hierarchical communities. IEEE Trans. Intell. Transp. Syst. 2011, 12, 132–140. [Google Scholar] [CrossRef]
- Aldecoa, R.; Marín, I. Exploring the limits of community detection strategies in complex networks. Sci. Rep. 2013, 3, 2216. [Google Scholar] [CrossRef]
- Fortunato, S.; Hric, D. Community detection in networks: A user guide. Phys. Rep. 2016, 659, 1–44. [Google Scholar] [CrossRef]
- Javed, M.A.; Younis, M.S.; Latif, S.; Qadir, J.; Baig, A. Community detection in networks: A multidisciplinary review. J. Netw. Comput. Appl. 2018, 108, 87–111. [Google Scholar] [CrossRef]
- AI, F.J. Research on a large-scale community detection algorithm based on non-weighted graph. Clust. Comput. 2019, 22, 2555–2562. [Google Scholar] [CrossRef]
- Mohammadi, M.; Fazlali, M.; Hosseinzadeh, M. Accelerating Louvain community detection algorithm on graphic processing unit. J. Supercomput. 2020, 77, 6056–6077. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Even, S.; Even, G. Graph Algorithms; Cambridge University Press: Cambridge, UK, 2011; pp. 63–74. [Google Scholar]
- Wang, H.; Zhang, J. Line-Constrained k-Median, k-Means, and k-Center Problems in the Plane. In Algorithms and Computation; Ahn, H.K., Shin, C.S., Eds.; Springer: Cham, Switzerland, 2014; pp. 3–14. [Google Scholar]
- Li, Z.X.; Ren, S.; Hu, N.; Liu, Y.; Qin, Z.; Rick, S.M.G. Equality of public transit connectivity: The influence of mass rapid transit services on individual buildings for Singapore. Transp. B Transp. Dyn. 2018, 7, 576–595. [Google Scholar] [CrossRef]
- Cao, X.S.; Chen, H.L.; Liang, F.W.; Wang, W.L. Measurement and spatial differentiation characteristics of transit equity: A case study of Guangzhou, China. Sustainability 2018, 10, 1069. [Google Scholar] [CrossRef]
- Song, Y.; Kim, H.; Lee, K.; Ahn, K. Subway network expansion and transit equity: A case study of Gwangju metropolitan area. South Korea. Transp. Policy 2018, 72, 148–158. [Google Scholar] [CrossRef]
- Nocera, S.; Fabio, A.; Cavallaro, F. The adoption of grid transit networks in non-metropolilan contexts. Transp. Res. Part A Policy Pract. 2020, 132, 256–272. [Google Scholar] [CrossRef]
- Zhang, M.Y.; Huang, T.; Guo, Z.X.; He, Z.G. Complex-network-based traffic network analysis and dynamics: A comprehensive review. Phys. A Stat. Mech. Its Appl. 2022, 607, 128063. [Google Scholar] [CrossRef]
- Tanuja, S.; Ho, I.W.H.; Tse, C.K. Spatial analysis of bus transport networks using network theory. Phys. A Stat. Mech. Its Appl. 2018, 502, 295–314. [Google Scholar] [CrossRef]
- Linovski, O.; Baker, D.M.; Manaugh, K. Equity in practice? Evaluations of equity in planning for bus rapid transit. Transp. Res. Part A Policy Pract. 2018, 113, 75–87. [Google Scholar] [CrossRef]
- Zhong, H.L.; Feng, K.S.; Sun, L.X.; Cheng, L.; Hubacek, K. Household carbon and energy inequality in Latin American and Caribbean countries. J. Environ. Manag. 2020, 273, 110979. [Google Scholar] [CrossRef]
- Huang, Y.; Hong, X.J.; Zheng, Y.; Zhang, Y.W.; Li, Z.R. Assessment and optimization of spatial equity for urban parks: A case study in Nanjing, China. Ecol. Indic. 2024, 166, 112449. [Google Scholar] [CrossRef]
- Albert-László, B. Scale-free networks: A decade and beyond. Science 2009, 325, 412–413. [Google Scholar] [CrossRef]
- Barabasi, A.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
- Newman, M.E.J. Fast algorithm for detecting community structure in networks. Phys. Rev. E 2004, 69, 066133. [Google Scholar] [CrossRef] [PubMed]
- Traag, V.A.; Waltman, L.; van Eck, N.J. From Louvain to Leiden: Guaranteeing well-connected communities. Sci. Rep. 2019, 9, 5233. [Google Scholar] [CrossRef]
- Raghavan, U.N.; Albert, R.; Kumara, S. Near linear time algorithm to detect community structures in large-scale networks. Phys. Rev. E 2007, 76, 036106. [Google Scholar] [CrossRef] [PubMed]
- Bagrow, J.P.; Bolt, E.M. Local method for detecting communities. Phys. Rev. E 2005, 72, 046108. [Google Scholar] [CrossRef] [PubMed]
- Gregory, S. Finding overlapping communities in networks by label propagation. New J. Phys. 2010, 12, 103018. [Google Scholar] [CrossRef]
- Yang, B.; Cheung, W.K.; Liu, J. Community mining from signed social networks. IEEE Trans. Knowl. Data Eng. 2007, 19, 1333–1348. [Google Scholar] [CrossRef]
- Rosvall, M.; Bergstrom, C.T. Maps of random walks on complex networks reveal community structure. Proc. Natl. Acad. Sci. USA 2008, 105, 1118–1123. [Google Scholar] [CrossRef] [PubMed]
- Ronhovde, P.; Nussinov, Z. Multiresolution community detection for megascale networks by information-based replica correlations. Phys. Rev. E 2009, 80, 016109. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Pu, P.; Han, D.D.; Tang, M. Self-adaptive Louvain algorithm: Fast and stable community detection algorithm based on the principle of small probability event. Phys. A Stat. Mech. Its Appl. 2018, 506, 975–986. [Google Scholar] [CrossRef]

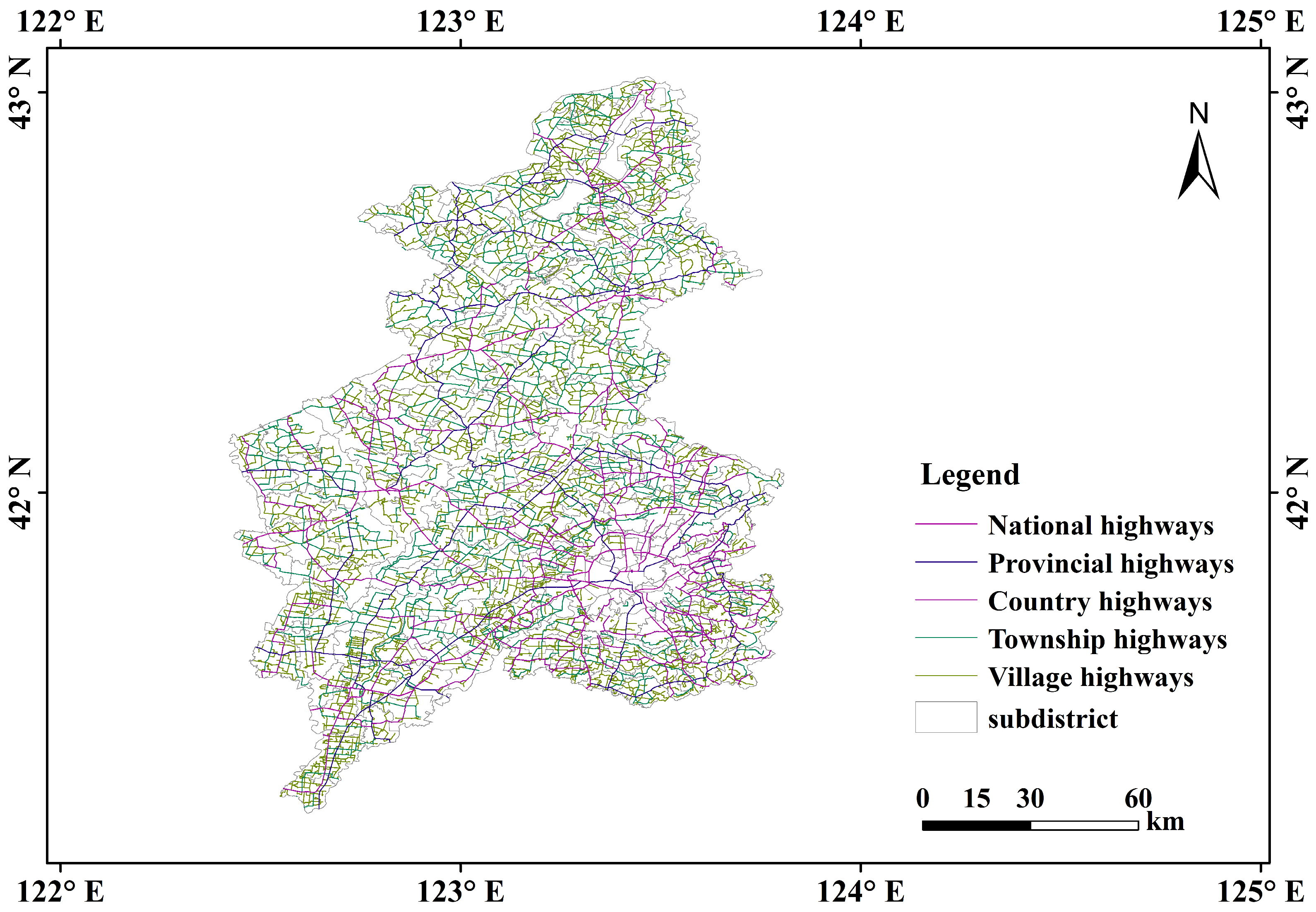
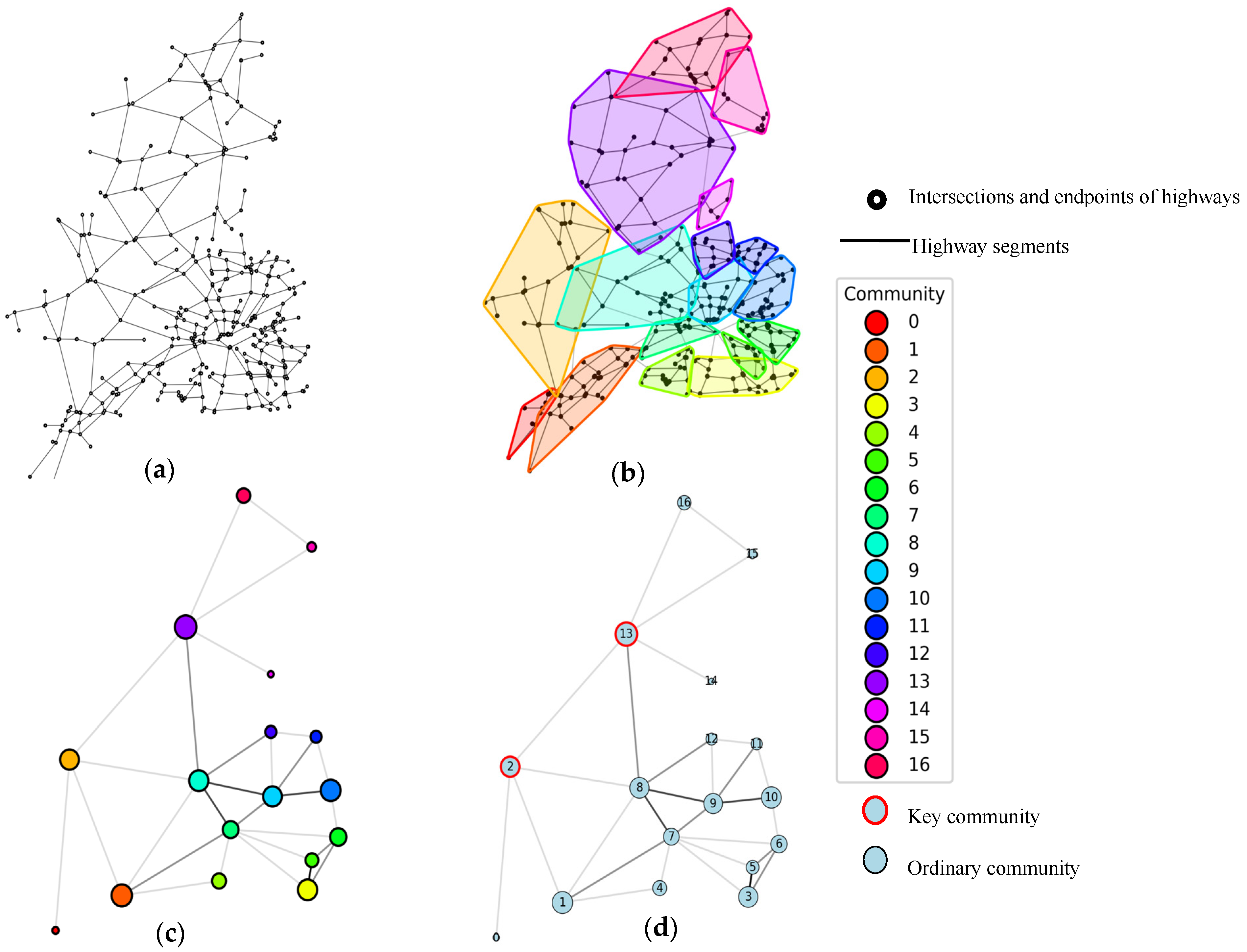
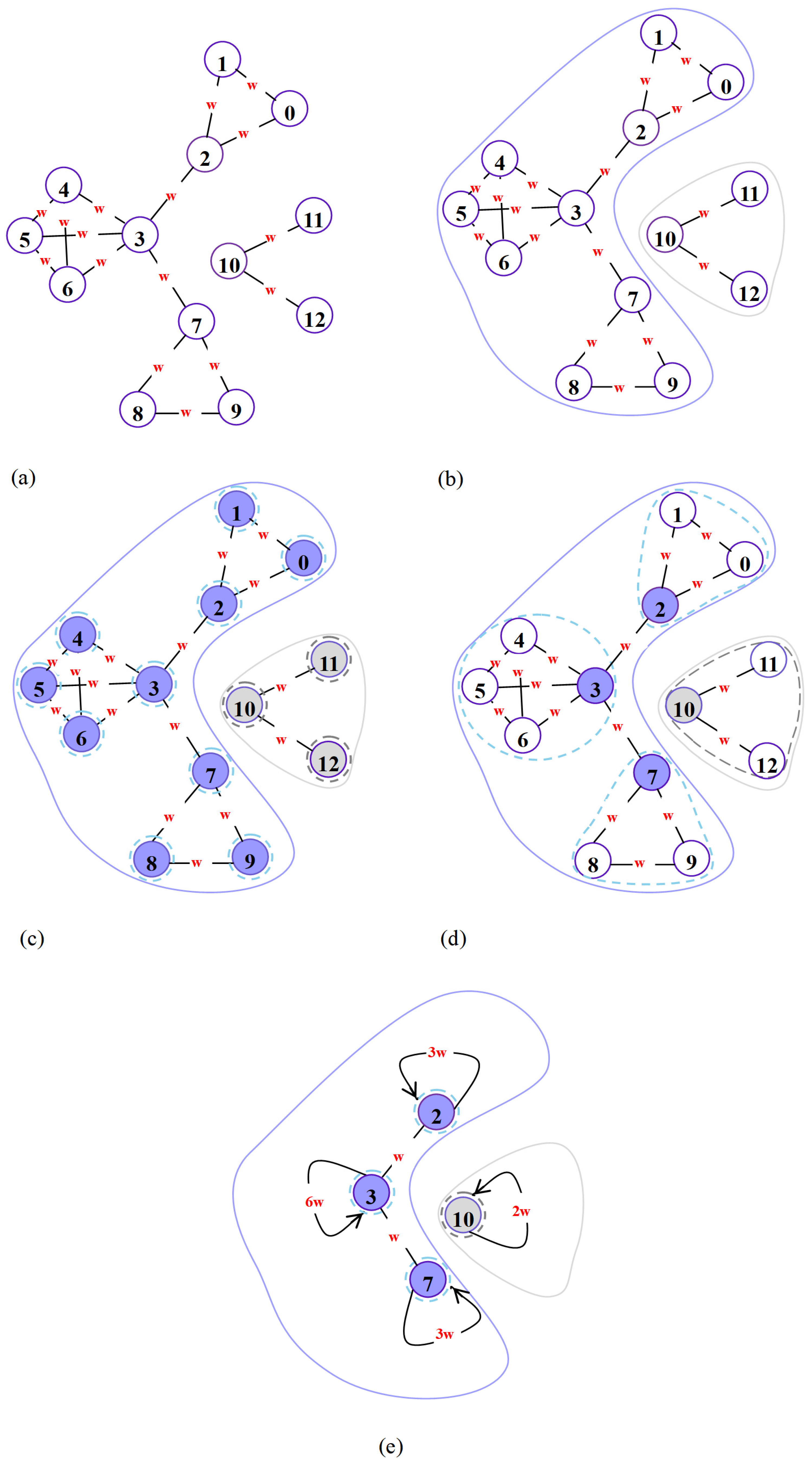
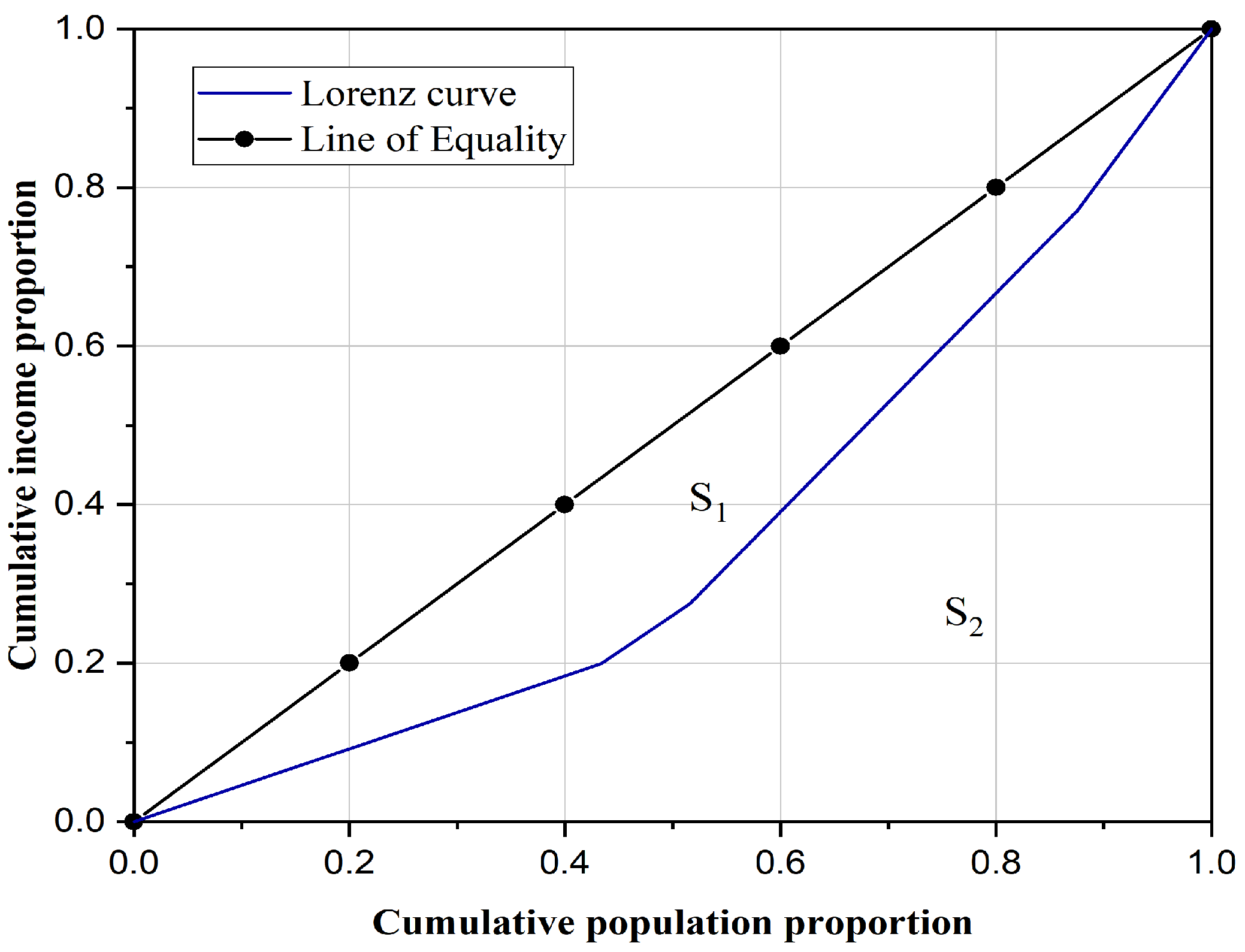


| Highway Class | Number of Highways | Length (km) |
|---|---|---|
| National highways | 8 | 799.33 |
| Provincial highways | 14 | 1058.28 |
| County highways | 86 | 1427.02 |
| Township highways | 442 | 3382.83 |
| Village highways | 2070 | 5853.09 |
| Model | Q | CV | O |
|---|---|---|---|
| FN | 0.9734 | 3.4216 | O(n2 log n) |
| Louvain | 0.9537 | 0.0006 | O(n log n) |
| Leiden | 0.9561 | 0.4374 | O(n log n) |
| C-Louvain | 0.9739 | 0.0003 | ) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Song, W.; Sun, J.; Dai, P. Analysis Method for the Spatial Layout Equilibrium of Highway Transportation Network Based on Community Detection. Sensors 2025, 25, 6366. https://doi.org/10.3390/s25206366
Zhang Y, Song W, Sun J, Dai P. Analysis Method for the Spatial Layout Equilibrium of Highway Transportation Network Based on Community Detection. Sensors. 2025; 25(20):6366. https://doi.org/10.3390/s25206366
Chicago/Turabian StyleZhang, Yuanyuan, Weidong Song, Jinguang Sun, and Peng Dai. 2025. "Analysis Method for the Spatial Layout Equilibrium of Highway Transportation Network Based on Community Detection" Sensors 25, no. 20: 6366. https://doi.org/10.3390/s25206366
APA StyleZhang, Y., Song, W., Sun, J., & Dai, P. (2025). Analysis Method for the Spatial Layout Equilibrium of Highway Transportation Network Based on Community Detection. Sensors, 25(20), 6366. https://doi.org/10.3390/s25206366






