Decentralized Cycle-Free Game-Theoretic Adaptive Traffic Signal Control: Model Enhancement and Testing on Isolated Signalized Intersections
Abstract
1. Introduction
1.1. Related Work
1.2. Study Contribution
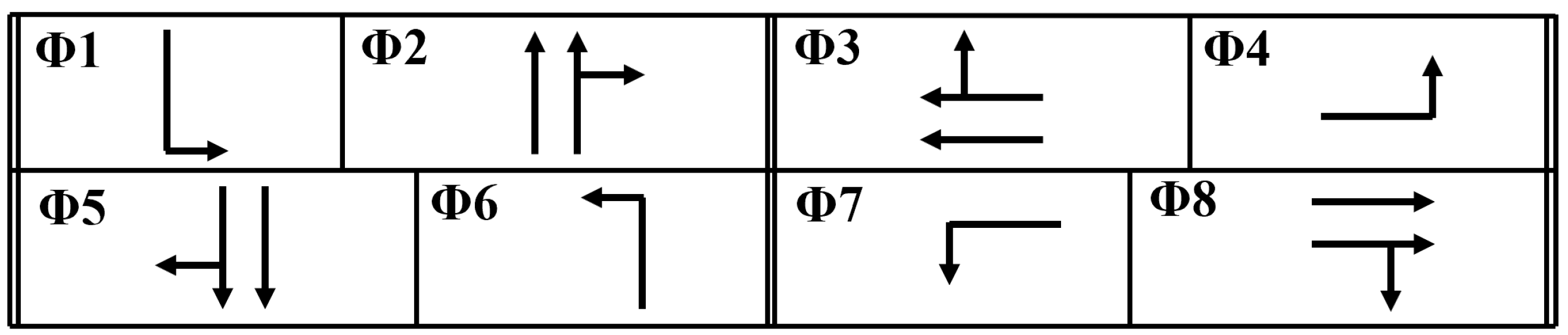
- Integration with full NEMA eight-phase control: Unlike most prior game-theoretic controllers, which were limited to simplified two-phase or four-phase configurations, we implement the controller within the widely used NEMA eight-phase framework. This extension is critical for real-world applicability, as it allows the method to directly interface with existing traffic controller architectures in the US.
- Explicit consideration of phase transition penalties: We incorporate yellow and all-red clearance intervals into the payoff evaluation process. This addition corrects a common limitation in earlier studies, which ignored intergreen times and consequently overstated potential benefits.
- Density-based payoff evaluation: We redefine the bargaining utility function using the approach of traffic density rather than queue length. This methodological enhancement captures lane utilization more effectively, ensuring that approaches with high but dispersed demand are not undervalued, which is an issue that has affected previous NB implementations.
- Adaptive evaluation horizon and minimum green enforcement: We introduce a dynamic control horizon that adjusts to the current queue discharge time across all phases. This ensures that each green interval is long enough to clear existing queues and meet driver expectancy, avoiding unrealistic or erratic phase changes while maintaining flexibility.
- Comprehensive benchmarking: We benchmark the enhanced DNB controller not only against conventional pretimed (Webster and Laguna-Du-Rakha) and actuated controller strategies but also against a reinforcement learning-based controller reported in the literature. The results demonstrate that the DNB controller achieves significant improvements without the need for pre-training, highlighting its scalability and transferability across intersections.
2. Traffic Signal Control Strategy
2.1. Overview of the DNB Algorithm
2.2. The DNB Players
2.3. The Disagreement Point
2.4. The Payoff Evaluation Process
2.5. Traffic Density Prediction
2.6. The Solution Procedure
| Algorithm 1 The DNB Algorithm |
|
2.7. The DNB Evaluation Horizon
3. The DNB Algorithm Experimental Setup
- The vehicle dynamics model for light-duty vehicles developed by Rakha et al. [26,27] is used to model vehicle motion. Maximum acceleration is determined by the maximum tractive force and instantaneous resisting forces, with the tractive force calculated from the vehicle’s maximum power. Resisting forces include rolling, aerodynamic, and grade resistance forces. These calculations are done at every time step ().
- The Van Aerde steady-state car-following and traffic stream model [28], which is a single-regime model that combines the Greenshields and Pipes functional forms, is used to simulate the vehicle’s steady-state car-following behavior. The speed-density relationship is modeled using Equations (9)–(12).
- The Fadhloun–Rakkha car-following model [29] is used to simulate human-driven vehicles, incorporating vehicle dynamics, steady-state car-following behavior, and collision avoidance strategies to maintain safe following distances. The model includes acceleration and collision avoidance regions, where throttle and deceleration levels are adjusted based on the current speed, spacing, and the lead vehicle’s behavior. Vehicle acceleration is expressed as a proportion of the maximum allowable acceleration (Equation (6)) using the throttle level (). This model governs the dynamics of vehicles, ensuring collision avoidance by calculating the required deceleration using a vehicle kinematics model.
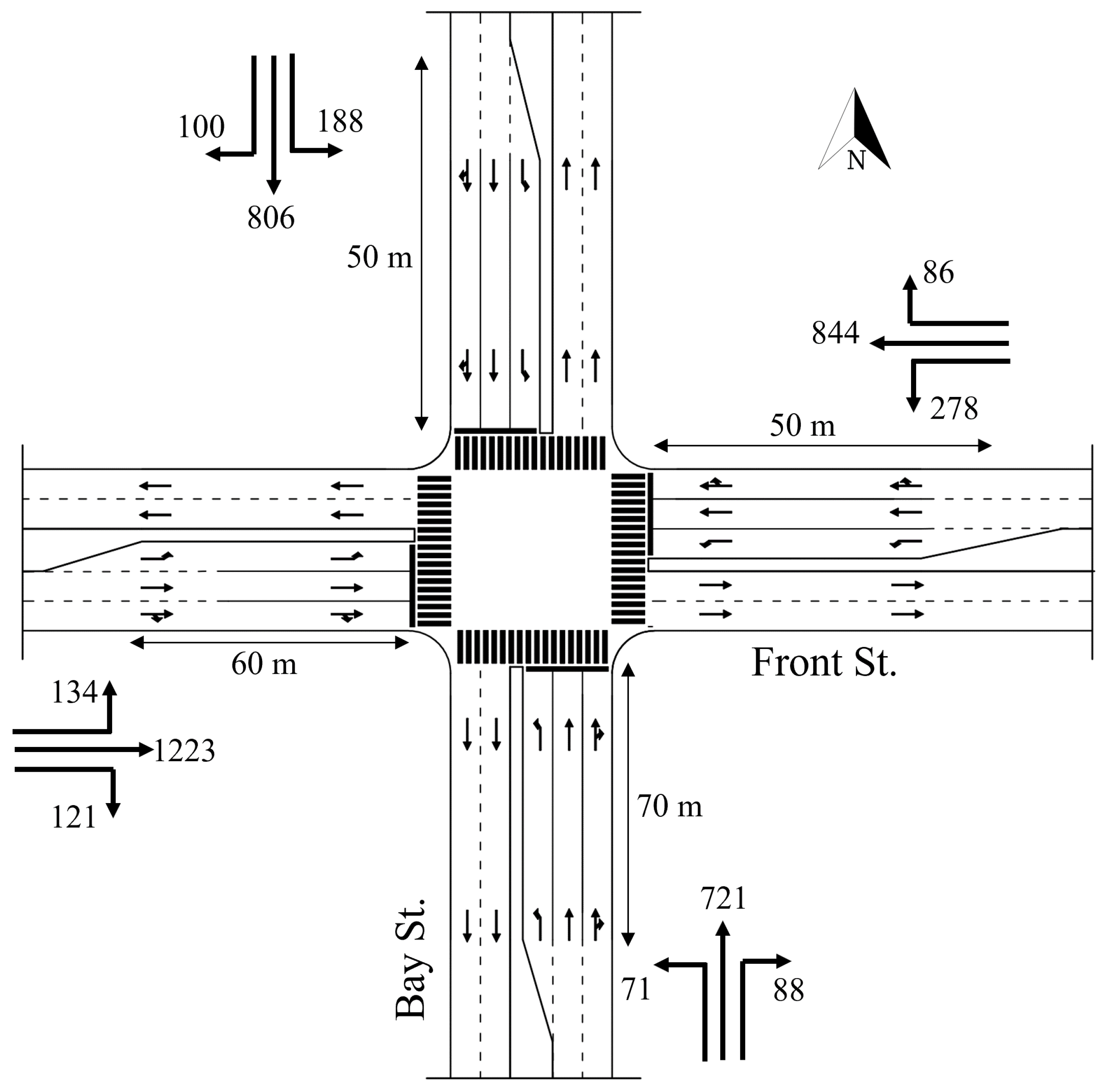
3.1. Case Studies
3.1.1. Case Study 1
3.1.2. Case Study 2
3.2. Model Calibration and Validation
3.2.1. Calibration of Model Parameters
- The free-flow speed is the speed at or below which 85% of the vehicles are observed to travel under free-flow conditions, which is observed in this case to be 54.8 mph (88.3 km/h), where the posted speed limit is 45 mph.
- The saturation flow rate is computed using the average vehicle flow rate when discharging from a queue.
- The speed-at-capacity is obtained by measuring the average vehicle speeds when discharging from a queue.
- The jam density is obtained by measuring the traffic stream density when vehicles are queued during the red signal indication.
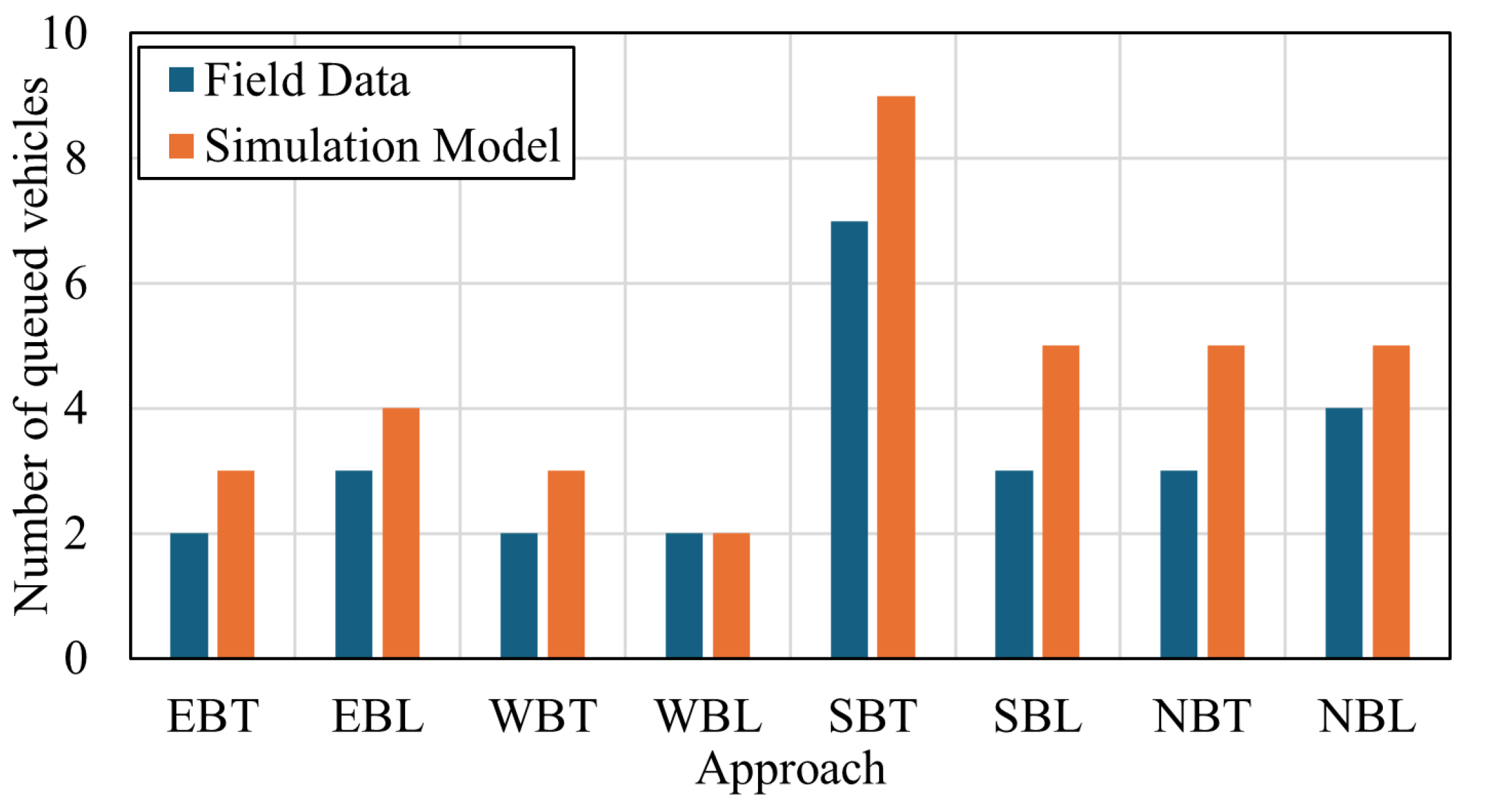
3.2.2. Model Validation
3.3. Benchmarks
4. Results and Analysis
4.1. Results of Case Study 1
4.1.1. Optimal Cycle Length Computation
4.1.2. Vehicle Delay
4.1.3. Fuel Consumption
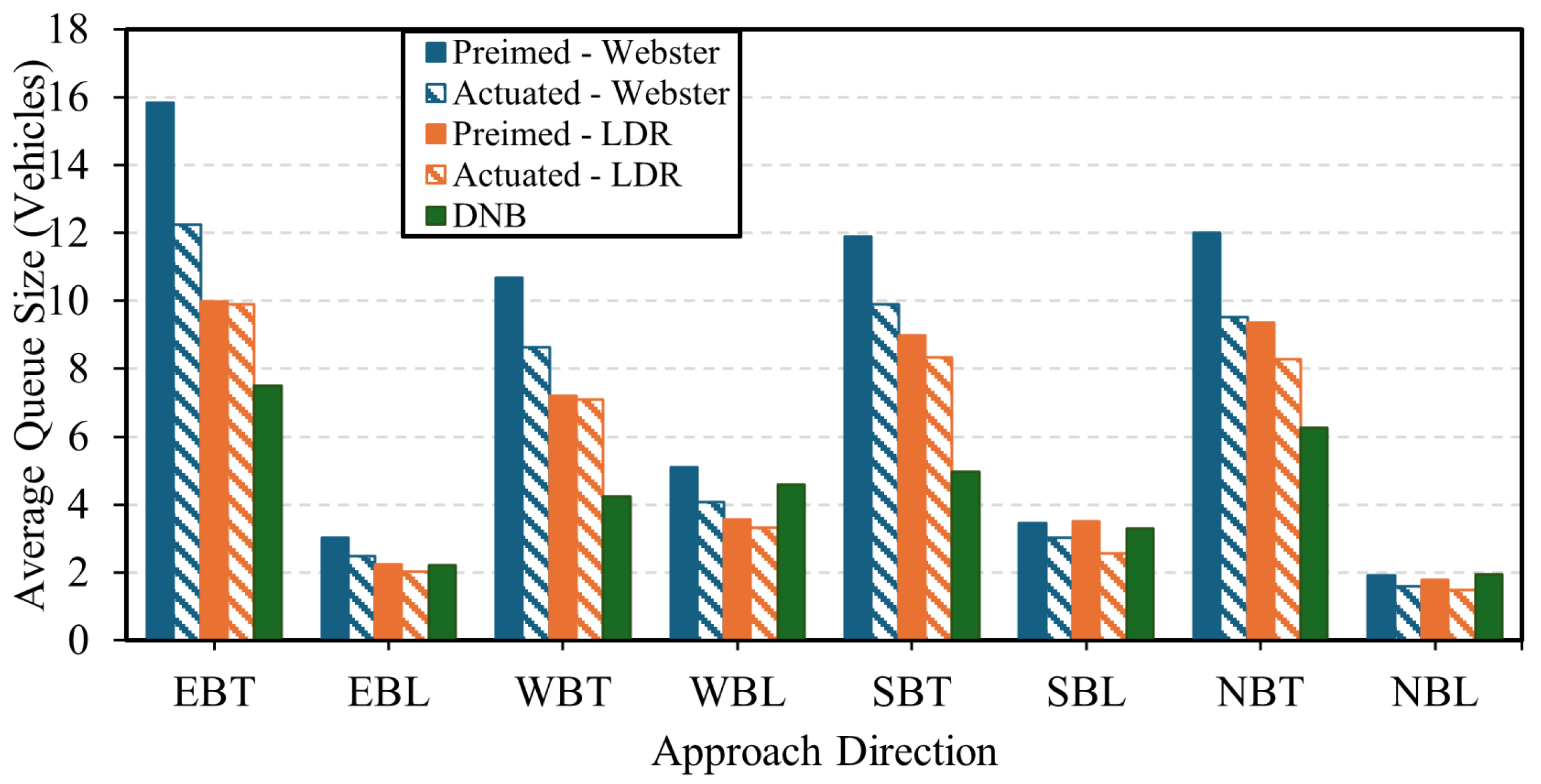
4.1.4. Queue Size
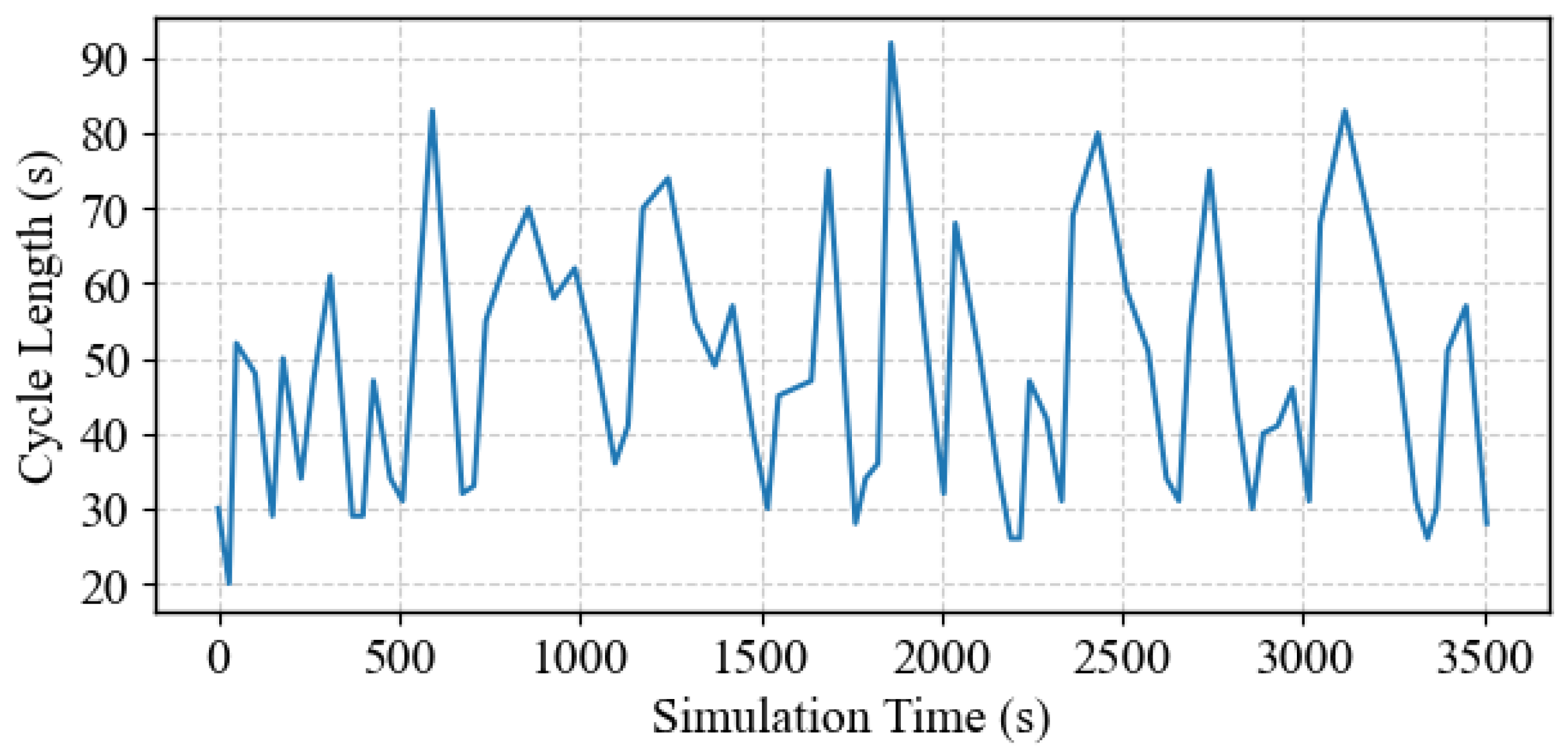
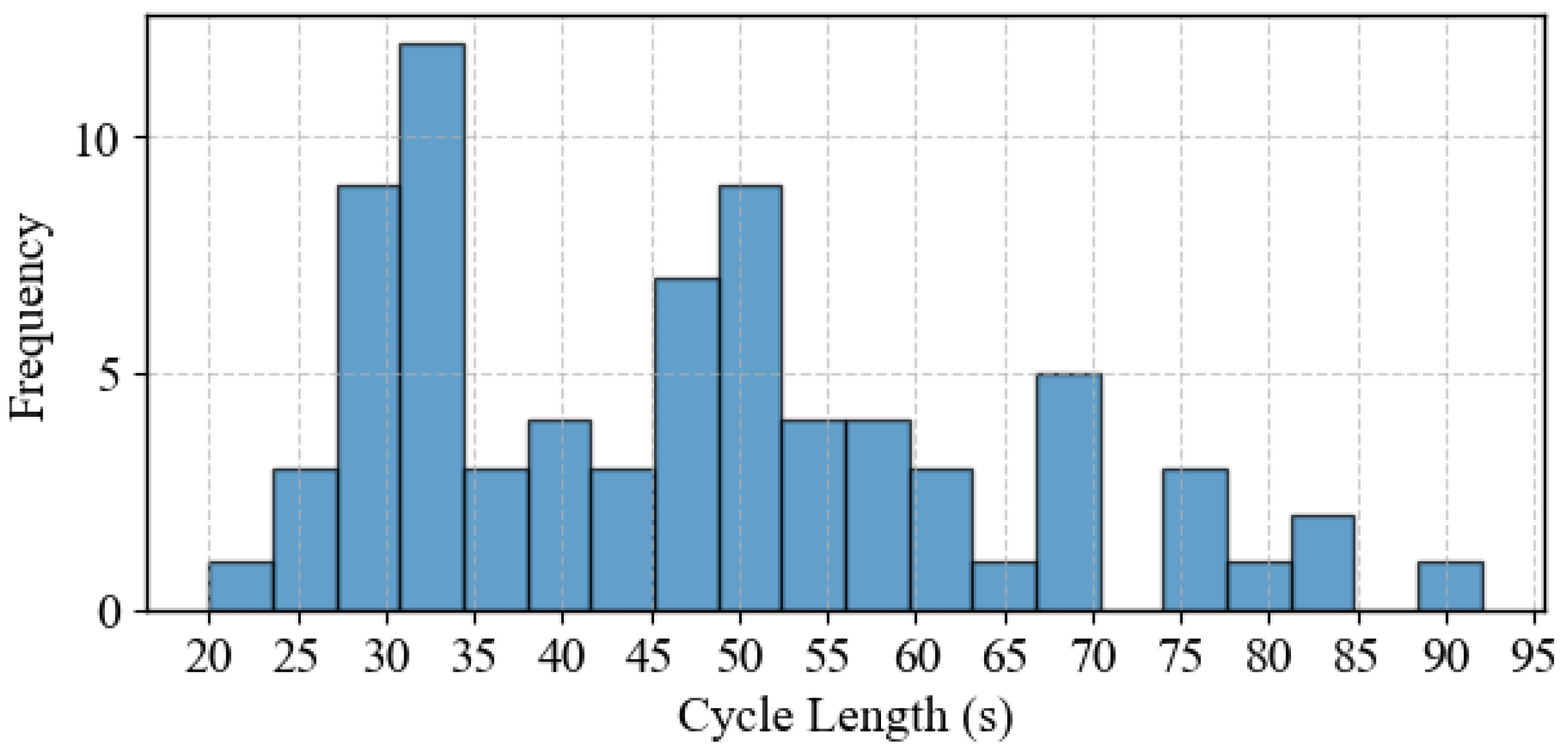
4.1.5. Variation of the Cycle Length and Phase Splits
4.1.6. Number of Vehicles in the System
4.2. Results of Case Study 2
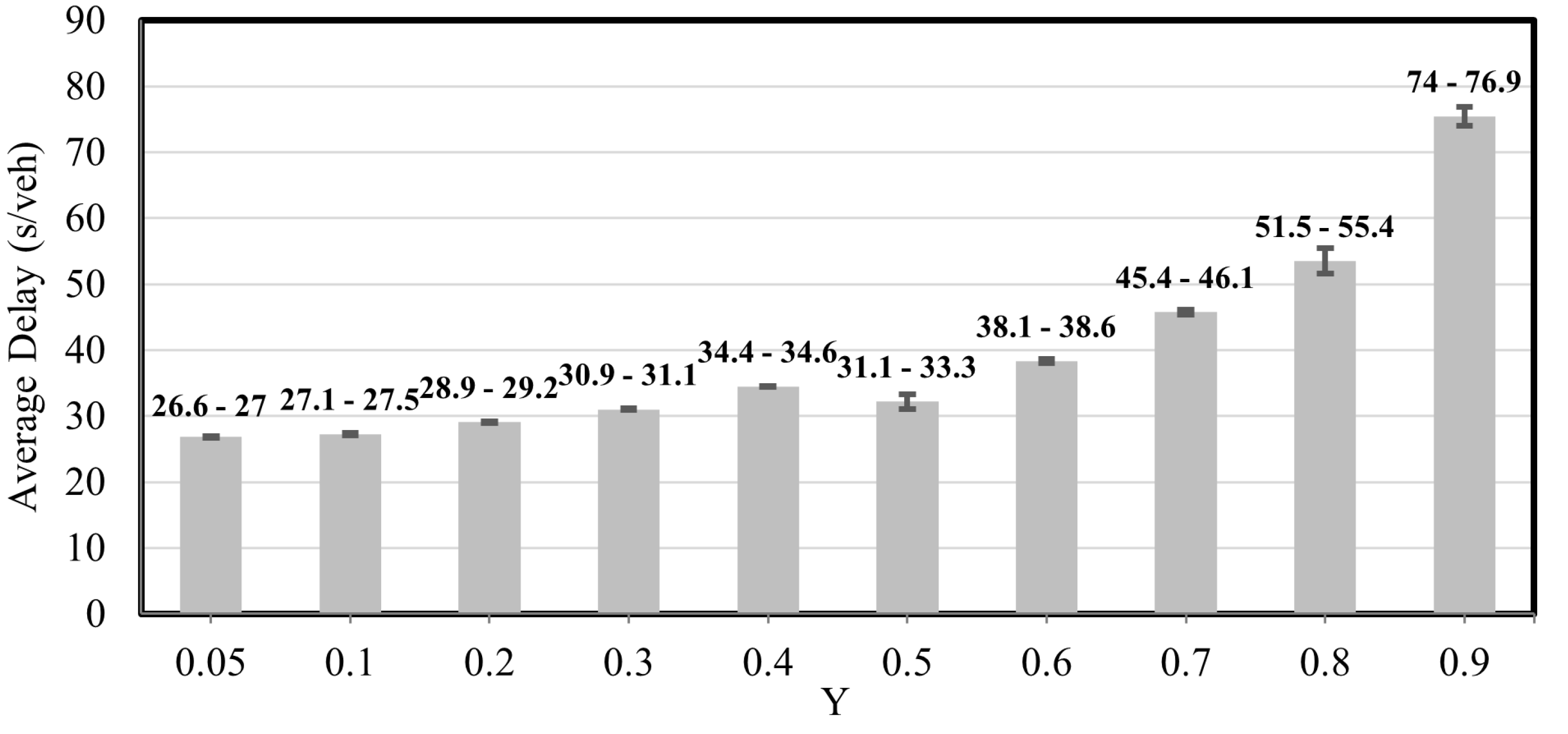
4.2.1. Optimal Cycle Length Computation
4.2.2. Vehicle Delay
4.2.3. Queue Size
4.3. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DNB | Decentralized Nash Bargaining |
| VOC | Volume-to-Capacity Ratio |
| NB | Nash Bargaining |
| NEMA | National Electrical Manufacturers Association |
| TSC | Traffic Signal Controller |
References
- Papageorgiou, M.; Diakaki, C.; Dinopoulou, V.; Kotsialos, A.; Wang, Y. Review of road traffic control strategies. Proc. IEEE 2003, 91, 2043–2067. [Google Scholar] [CrossRef]
- Webster, F.; Cobbe, B. A Controlled Experiment on the Capacity of Junctions with Traffic Signals; Note No. RN/3313/FVW. BR587; Road Research Lab.: Londaon, UK, 1958. [Google Scholar]
- Calle-Laguna, A.J.; Du, J.; Rakha, H.A. Computing optimum traffic signal cycle length considering vehicle delay and fuel consumption. Transp. Res. Interdiscip. Perspect. 2019, 3, 100021. [Google Scholar] [CrossRef]
- Mirchandani, P.; Head, L. A real-time traffic signal control system: Architecture, algorithms, and analysis. Transp. Res. Part C Emerg. Technol. 2001, 9, 415–432. [Google Scholar] [CrossRef]
- Akopov, A.S.; Beklaryan, L.A.; Thakur, M. Improvement of Maneuverability Within a Multiagent Fuzzy Transportation System With the Use of Parallel Biobjective Real-Coded Genetic Algorithm. IEEE Trans. Intell. Transp. Syst. 2022, 23, 12648–12664. [Google Scholar] [CrossRef]
- Nam, D.; Lavanya, R.; Jayakrishnan, R.; Yang, I.; Jeon, W.H. A Deep Learning Approach for Estimating Traffic Density Using Data Obtained from Connected and Autonomous Probes. Sensors 2020, 20, 4824. [Google Scholar] [CrossRef] [PubMed]
- Kell, J.H.; Fullerton, I.J. Manual of Traffic Signal Design, 2nd ed.; Institute of Transportation Engineers (ITE): Washington, DC, USA, 1991. [Google Scholar]
- Skabardonis, A.; Deakin Skabardonis, H. Progression Through a Series of Intersections with Traffic Actuated Controllers; Federal Highway Administration, Offices of Research & Development: Washington, DC, USA, 1988.
- Srinivasan, D.; Choy, M.; Cheu, R. Neural Networks for Real-Time Traffic Signal Control. IEEE Trans. Intell. Transp. Syst. 2006, 7, 261–272. [Google Scholar] [CrossRef]
- El-Tantawy, S.; Abdulhai, B.; Abdelgawad, H. Design of Reinforcement Learning Parameters for Seamless Application of Adaptive Traffic Signal Control. J. Intell. Transp. Syst. 2014, 18, 227–245. [Google Scholar] [CrossRef]
- Ahmad, F.; Almarri, O.; Shah, Z.; Al-Fagih, L. Game theory applications in traffic management: A review of authority-based travel modelling. Travel Behav. Soc. 2023, 32, 100585. [Google Scholar] [CrossRef]
- Ahmad, F.; Al-Fagih, L. Travel behaviour and game theory: A review of route choice modeling behaviour. J. Choice Model. 2024, 50, 100472. [Google Scholar] [CrossRef]
- Raghothama, J.; Meijer, S.A. A Review of Gaming Simulation in Transportation. In Frontiers in Gaming Simulation; Meijer, S.A., Smeds, R., Eds.; Springer: Cham, Switzerland, 2014; pp. 237–244. [Google Scholar] [CrossRef]
- Zhang, H.; Su, Y.; Peng, L.; Yao, D. A review of game theory applications in transportation analysis. In Proceedings of the 2010 International Conference on Computer and Information Application, Perth, Australia, 20–23 April 2010; pp. 152–157. [Google Scholar] [CrossRef]
- Linglong, T.; Xiaohua, Z.; Dunli, H.; Yanzhang, S.; Ren, W. A Study of Single Intersection Traffic Signal Control Based on Two-player Cooperation Game Model. In Proceedings of the 2010 WASE International Conference on Information Engineering, Qinhuangdao, China, 14–15 August 2010; Volume 2, pp. 322–327. [Google Scholar] [CrossRef]
- Bazzan, A.L.C. A Distributed Approach for Coordination of Traffic Signal Agents. Autonomous Agents and Multi-Agent Systems 2005, 10, 131–164. [Google Scholar] [CrossRef]
- Alvarez, I.; Poznyak, A. Game theory applied to urban traffic control problem. In Proceedings of the ICCAS 2010, Gyeonggi-do, Republic of Korea, 27–30 October 2010; pp. 2164–2169. [Google Scholar] [CrossRef]
- Bui, K.H.N.; Jung, J.E.; Camacho, D. Game theoretic approach on Real-time decision making for IoT-based traffic light control. Concurr. Comput. Pract. Exp. 2017, 29, e4077. [Google Scholar] [CrossRef]
- Guo, J.; Harmati, I. Optimization of Traffic Signal Control with Different Game Theoretical Strategies. In Proceedings of the 2019 23rd International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 9–11 October 2019; pp. 750–755. [Google Scholar] [CrossRef]
- Guo, J.; Harmati, I. Comparison of Game Theoretical Strategy and Reinforcement Learning in Traffic Light Control. Period. Polytech. Transp. Eng. 2020, 48, 313–319. [Google Scholar] [CrossRef]
- Abdelghaffar, H.M.; Rakha, H.A. Development and Testing of a Novel Game Theoretic De-Centralized Traffic Signal Controller. IEEE Trans. Intell. Transp. Syst. 2021, 22, 231–242. [Google Scholar] [CrossRef]
- Abdelghaffar, H.M.; Rakha, H.A. A Novel Decentralized Game-Theoretic Adaptive Traffic Signal Controller: Large-Scale Testing. Sensors 2019, 19, 2282. [Google Scholar] [CrossRef] [PubMed]
- Shafik, A.K.; Rakha, H.A. Enhancing and Evaluating a Decentralized Cycle-Free Game-Theoretic Adaptive Traffic Signal Controller on an Isolated Signalized Intersection. In Proceedings of the 2024 IEEE International Conference on Smart Mobility (SM), Niagara Falls, ON, Canada, 16–18 September 2024; pp. 216–221. [Google Scholar] [CrossRef]
- NEMA Standards Publication TS 2-2021: Traffic Controller Assemblies with NTCIP Requirements. 2003. Available online: https://www.nema.org/docs/default-source/standards-document-library/nema-ts-2-2021-contents-and-scopeb71294ae-eb9a-45e2-a501-e5c0672dbd6b.pdf?sfvrsn=ef98a362_3 (accessed on 1 September 2025).
- Shafik, A. PyTrafficSimulator. 2024. Available online: https://github.com/akshafik/PyTrafficSimulator_CSM (accessed on 1 September 2025).
- Rakha, H.; Snare, M.; Dion, F. Vehicle Dynamics Model for Estimating Maximum Light-Duty Vehicle Acceleration Levels. Transp. Res. Rec. J. Transp. Res. Board 2004, 1883, 40–49. [Google Scholar] [CrossRef]
- Rakha, H.A.; Ahn, K.; Moran, K.; Saerens, B.; Bulck, E.V.D. Virginia Tech Comprehensive Power-Based Fuel Consumption Model: Model development and testing. Transp. Res. Part D Transp. Environ. 2011, 16, 492–503. [Google Scholar] [CrossRef]
- Van Aerde, M.; Rakha, H. Multivariate calibration of single regime speed-flow-density relationships [road traffic management]. In Proceedings of the Pacific Rim TransTech Conference. 1995 Vehicle Navigation and Information Systems Conference Proceedings. 6th International VNIS. A Ride into the Future, Seattle, WA, USA, 30 July–2 August 1995; pp. 334–341. [Google Scholar] [CrossRef]
- Fadhloun, K.; Rakha, H. A novel vehicle dynamics and human behavior car-following model: Model development and preliminary testing. Int. J. Transp. Sci. Technol. 2020, 9, 14–28. [Google Scholar] [CrossRef]
- Zheng, O.; Abdel-Aty, M.; Yue, L.; Abdelraouf, A.; Wang, Z.; Mahmoud, N. CitySim: A Drone-Based Vehicle Trajectory Dataset for Safety-Oriented Research and Digital Twins. In Transportation Research Record; SAGE Publications Ltd.: Thousand Oaks, CA, USA, 2023. [Google Scholar] [CrossRef]
- Almannaa, M.H.; Chen, H.; Rakha, H.A.; Loulizi, A.; El-Shawarby, I. Field implementation and testing of an automated eco-cooperative adaptive cruise control system in the vicinity of signalized intersections. Transp. Res. Part D Transp. Environ. 2019, 67, 244–262. [Google Scholar] [CrossRef]
- Urbanik, T.; Tanaka, A.; Lozner, B.; Lindstrom, E.; Lee, K.; Quayle, S.; Beaird, S.; Tsoi, S.; Ryus, P.; Gettman, D.; et al. Signal Timing Manual, 2nd ed.; Transportation Research Board: Washington, DC, USA, 2015. [Google Scholar] [CrossRef]
- Shafik, A.K.; Rakha, H.A. Kalman Filter-based Real-Time Traffic State Estimation and Prediction using Vehicle Probe Data. In Proceedings of the 2024 IEEE International Conference on Smart Mobility (SM), Niagara Falls, ON, Canada, 16–18 September 2024; pp. 110–115. [Google Scholar] [CrossRef]
- Shafik, A.K.; Rakha, H.A. Integrated Back of Queue Estimation and Vehicle Trajectory Optimization Considering Uncertainty in Traffic Signal Timings. IEEE Trans. Intell. Transp. Syst. 2024, 25, 21393–21403. [Google Scholar] [CrossRef]
- Shafik, A.K.; Eteifa, S.; Rakha, H.A. Optimization of Vehicle Trajectories Considering Uncertainty in Actuated Traffic Signal Timings. IEEE Trans. Intell. Transp. Syst. 2023, 24, 7259–7269. [Google Scholar] [CrossRef]










| Scenario | Players | Total Payoff | |||
|---|---|---|---|---|---|
| 1 | 2 | … | J | ||
| Scenario 1 | Green | Red | … | Red | |
| Scenario 2 | Red | Green | … | Red | |
| … | … | … | … | … | … |
| Scenario I | Red | Red | … | Green | |
| Notation | Description |
|---|---|
| Vehicle Dynamics | |
| Throttle input | |
| Driveline efficiency | |
| Constant accounting for gear shift impacts | |
| Vehicle mass acting on the tractive axle | |
| Road friction or adhesion coefficient | |
| Air density at sea level and 25 °C | |
| Drag coefficient | |
| Altitude correction factor | |
| Vehicle frontal area | |
| , , | Rolling resistance constants |
| Van Aerde Traffic Stream Model | |
| Traffic density, and the jam density. | |
| Vehicle speed, the free-flow speed, and the speed at capacity. | |
| Fixed distance headway constant | |
| First variable headway constant | |
| Second variable distance headway constant | |
| Car-Following Model | |
| Car-following model parameters | |
| Steady-state spacing, current vehicle spacing, and jam spacing, respectively | |
| Steady-state speed, follower speed, and leader vehicle speed, respectively | |
| Kinematic (required) and desired deceleration levels, respectively | |
| Parameter | Case Study 1 | Case Study 2 |
|---|---|---|
| Saturation Flow Rate (veh/h/ln) | 1900 | 1800 |
| Free-flow Speed (km/h) | 40.0 | 88.3 |
| Speed-at-Capacity (km/h) | 25.0 | 40.0 |
| Jam Density (veh/km) | 160 | 114 |
| Control Type | Average Delay (s/veh) | Improvement | |
|---|---|---|---|
| Pretimed | Webster | 48.5 | - |
| LDR | 36.0 | 25.8% | |
| Actuated | Webster | 38.7 | 20.3% |
| LDR | 33.0 | 32.0% | |
| DNB | 30.1 | 37.9% |
| Control Type | Average FC (mL) | Improvement | |
|---|---|---|---|
| Pretimed | Webster | 77.2 | - |
| LDR | 70.5 | 8.6% | |
| Actuated | Webster | 71.7 | 7.1% |
| LDR | 68.7 | 11.0% | |
| DNB | 68.8 | 10.9% |
| Y | Cycle Length (s) | |
|---|---|---|
| LDR | Webster | |
| 0.05 | 60 | 60 |
| 0.1 | 60 | 60 |
| 0.2 | 60 | 60 |
| 0.3 | 60 | 60 |
| 0.4 | 65 | 60 |
| 0.5 (Actual Demand) | 75 | 75 |
| 0.6 | 85 | 105 |
| 0.7 | 100 | 140 |
| 0.8 | 115 | 205 |
| 0.9 | 140 | 415 |
| Y Ratio | Mean | SD | p-Value | ||
|---|---|---|---|---|---|
| DNB | Actuated-LDR | DNB | Actuated-LDR | ||
| 0.05 | 26.80 | 32.62 | 0.323 | 0.215 | |
| 0.10 | 27.28 | 33.42 | 0.331 | 0.305 | |
| 0.20 | 29.06 | 33.83 | 0.244 | 0.106 | |
| 0.30 | 31.03 | 35.31 | 0.169 | 0.089 | |
| 0.40 | 34.48 | 36.80 | 0.198 | 0.126 | |
| 0.50 | 32.20 | 42.69 | 0.607 | 0.021 | |
| 0.60 | 38.33 | 44.56 | 0.506 | 0.008 | |
| 0.70 | 45.75 | 50.21 | 0.757 | 0.028 | |
| 0.80 | 53.49 | 57.50 | 3.736 | 0.349 | |
| 0.90 | 75.47 | 95.50 | 2.759 | 11.247 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shafik, A.K.; Rakha, H.A. Decentralized Cycle-Free Game-Theoretic Adaptive Traffic Signal Control: Model Enhancement and Testing on Isolated Signalized Intersections. Sensors 2025, 25, 6339. https://doi.org/10.3390/s25206339
Shafik AK, Rakha HA. Decentralized Cycle-Free Game-Theoretic Adaptive Traffic Signal Control: Model Enhancement and Testing on Isolated Signalized Intersections. Sensors. 2025; 25(20):6339. https://doi.org/10.3390/s25206339
Chicago/Turabian StyleShafik, Amr K., and Hesham A. Rakha. 2025. "Decentralized Cycle-Free Game-Theoretic Adaptive Traffic Signal Control: Model Enhancement and Testing on Isolated Signalized Intersections" Sensors 25, no. 20: 6339. https://doi.org/10.3390/s25206339
APA StyleShafik, A. K., & Rakha, H. A. (2025). Decentralized Cycle-Free Game-Theoretic Adaptive Traffic Signal Control: Model Enhancement and Testing on Isolated Signalized Intersections. Sensors, 25(20), 6339. https://doi.org/10.3390/s25206339







