Implementation of an SS-Compensated LC-Thermistor Topology for Passive Wireless Temperature Sensing
Abstract
Highlights
- A passive wireless temperature sensor is implemented using SS-compensated magnetically coupled LC tanks.
- The thermistor’s resistance is directly reflected in the input impedance at split resonance frequencies.
- Enables accurate, battery-free, and contactless temperature sensing through impedance monitoring.
- Suitable for applications requiring simple and reliable wireless sensing topologies.
Abstract
1. Introduction
2. Mathematical Modeling of the SS-Compensated LC-Thermistor Sensor Topology
| Solutions for ZPA Resonance Frequencies | Bifurcation Conditions | |
|---|---|---|
| (17) | is real if | |
| (18) | is always real | |
| (19) | is real if |
3. Practical Implementation of the SS-Compensated LC-Thermistor Sensor Topology
3.1. RF-Modeling of Utilized Components
3.2. LC-Thermistor Sensor Implementation
3.3. Comparison with Various Sensors
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moya, A.; García, C.; Vázquez, M.; Hernando, B.; Zhukova, V.; Zhukov, A. Scattering of microwaves by a passive array antenna based on amorphous ferromagnetic microwires for wireless sensors with biomedical applications. Sensors 2019, 19, 3060. [Google Scholar] [CrossRef]
- Li, C.; Wu, J.; Yuan, H.; Yin, W.; Wang, G.; Wang, H. Overview of recent development on wireless sensing circuits and systems for healthcare and biomedical applications. IEEE J. Emerg. Sel. Top. Circ. Syst. 2018, 8, 165–177. [Google Scholar] [CrossRef]
- Huang, Q.-A.; Dong, L.; Wang, L.-F. LC passive wireless sensors toward a wireless sensing platform: Status, prospects, and challenges. J. Microelectromech. Syst. 2016, 25, 822–841. [Google Scholar] [CrossRef]
- Yeon, P.; Kim, M.-G.; Brand, O.; Ghovanloo, M. Optimal design of passive resonating wireless sensors for wearable and implantable devices. IEEE Sens. J. 2019, 19, 7460–7470. [Google Scholar] [CrossRef]
- He, D.; Cui, Y.; Ming, F.; Wu, W. Advancements in passive wireless sensors, materials, devices, and applications. Sensors 2023, 23, 8200. [Google Scholar] [CrossRef]
- Lu, D.; Yan, Y.; Avila, R.; Kandela, I.; Stepien, I.; Seo, M.H.; Song, Y.M.; Rogers, J.A. Bioresorbable, wireless, passive sensors as temporary implants for monitoring regional body temperature. Adv. Healthc. Mater. 2020, 9, 2000942. [Google Scholar] [CrossRef]
- Yue, W.; Yin, M.; Li, C.; Wu, Y.; Wang, Z.; Zhu, Y. Advancements in passive wireless sensing systems in monitoring harsh environment and healthcare applications. Nano-Micro Lett. 2025, 17, 106. [Google Scholar] [CrossRef]
- Tan, Q.; Wei, T.; Chen, X.; Luo, T.; Wu, G.; Li, C.; Xiong, J. Antenna-resonator integrated wireless passive temperature sensor based on low-temperature co-fired ceramic for harsh environment. Sens. Actuators A Phys. 2015, 236, 299–308. [Google Scholar] [CrossRef]
- Li, W.; Liang, T.; Liu, W.; Jia, P.; Chen, Y.; Xiong, J.; Li, Y. Wireless passive pressure sensor based on sapphire direct bonding for harsh environments. Sens. Actuators A Phys. 2018, 280, 406–412. [Google Scholar] [CrossRef]
- Wang, L.; Chen, J.; Yang, Y.; Li, Y.; Zhao, X.; Zhu, W. Passive wireless multi-parameter LC sensing system for in situ health monitoring of bearings. Sens. Actuators A Phys. 2024, 379, 115934. [Google Scholar] [CrossRef]
- Strader, N.; Jordan, B.R.; Bilac, O.; Tennant, K.M.; Reynolds, D.S.; Sabolsky, E.M.; Daniszewski, A.C. Near-field passive wireless sensor for high-temperature metal corrosion monitoring. Sensors 2024, 24, 7806. [Google Scholar] [CrossRef]
- Dong, Z.; Tu, J.; Xu, Q.; Zhu, Y.; Li, J.; Hu, Y.; Zhang, Y.; Xue, Z. A dual-sensitive element wireless passive LC temperature sensor and application in bearing monitoring. Meas. Sci. Technol. 2025, 36, 075105. [Google Scholar] [CrossRef]
- Idhaiam, K.S.V.; Caswell, J.A.; Pozo, P.D.; Sabolsky, K.; Sierros, K.A.; Reynolds, D.S.; Sabolsky, E.M. All-ceramic LC resonator for chipless temperature sensing within high temperature systems. IEEE Sens. J. 2021, 21, 19771–19779. [Google Scholar] [CrossRef]
- Varadharajan Idhaiam, K.S.; Caswell, J.A.; Pozo, P.D.; Sabolsky, K.; Sierros, K.A.; Reynolds, D.S.; Sabolsky, E.M. All-ceramic passive wireless temperature sensor realized by tin-doped indium oxide (ITO) electrodes for harsh environment applications. Sensors 2022, 22, 2165. [Google Scholar] [CrossRef]
- Lin, B.; Tan, Q.; Zhang, G.; Zhang, L.; Wang, Y.; Xiong, J. Temperature and pressure composite measurement system based on wireless passive LC sensor. IEEE Trans. Instrum. Meas. 2020, 70, 9502811. [Google Scholar] [CrossRef]
- Dutta, P.P.; Benken, A.C.; Li, T.; Ordonez-Varela, J.R.; Gianchandani, Y.B. Passive wireless pressure gradient measurement system for fluid flow analysis. Sensors 2023, 23, 2525. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, W.; Chen, H.; Li, H.; Xue, Z.; Shen, S. Flexible LC sensor array for wireless multizone pressure monitoring. IEEE Sens. J. 2023, 24, 2628–2636. [Google Scholar] [CrossRef]
- Ma, M.; Wang, Y.; Liu, F.; Zhang, F.; Liu, Z.; Li, Y. Passive wireless LC proximity sensor based on LTCC technology. Sensors 2019, 19, 1110. [Google Scholar] [CrossRef]
- Wu, T.; Bhadra, S. A printed LC resonator-based flexible RFID for remote potassium ion detection. IEEE J. Flex. Electron. 2021, 1, 47–57. [Google Scholar] [CrossRef]
- Bona, M.; Serpelloni, M.; Sardini, E.; Lombardo, C.O.; Andò, B. Telemetric technique for wireless strain measurement from an inkjet-printed resistive sensor. IEEE Trans. Instrum. Meas. 2016, 66, 583–591. [Google Scholar] [CrossRef]
- Yang, M.; Ye, Z.; Farhat, M.; Chen, P.Y. Ultrarobust wireless interrogation for sensors and transducers: A non-Hermitian telemetry technique. IEEE Trans. Instrum. Meas. 2021, 70, 1504709. [Google Scholar] [CrossRef]
- Sandra, K.R.; George, B.; Kumar, V.J. A nonintrusive magnetically coupled sensor for measuring liquid level. IEEE Trans. Instrum. Meas. 2020, 69, 7716–7724. [Google Scholar] [CrossRef]
- Al Jarrah, A.M.; Aljabarin, N. Magnetic coupling of two coils due to flow of pure water inside them–double coil volumetric flow sensor. Adv. Sci. Technol. Res. J. 2022, 16, 47–53. [Google Scholar] [CrossRef]
- Zhou, B.B.; Wang, L.F.; Dong, L.; Huang, Q.A. Observation of the perturbed eigenvalues of PT-symmetric LC resonator systems. J. Phys. Commun. 2021, 5, 045010. [Google Scholar] [CrossRef]
- Zhou, B.B.; Chen, D.; Zhang, C.; Dong, L. Realizing multi-parameter measurement using PT-symmetric LC sensors. Sensors 2024, 24, 6570. [Google Scholar] [CrossRef]
- Chen, P.Y.; Sakhdari, M.; Hajizadegan, M.; Cui, Q.; Cheng, M.M.C.; El-Ganainy, R.; Alù, A. Generalized parity–time symmetry condition for enhanced sensor telemetry. Nat. Electron. 2018, 1, 297–304. [Google Scholar] [CrossRef]
- Dong, Z.; Li, Z.; Yang, F.; Qiu, C.W.; Ho, J.S. Sensitive readout of implantable microsensors using a wireless system locked to an exceptional point. Nat. Electron. 2019, 2, 335–342. [Google Scholar] [CrossRef]
- Hajizadegan, M.; Sakhdari, M.; Liao, S.; Chen, P.Y. High-sensitivity wireless displacement sensing enabled by PT-symmetric telemetry. IEEE Trans. Antennas Propag. 2019, 67, 3445–3449. [Google Scholar] [CrossRef]
- Zhou, B.B.; Deng, W.J.; Wang, L.F.; Dong, L.; Huang, Q.A. Enhancing the remote distance of LC passive wireless sensors by parity-time symmetry breaking. Phys. Rev. Appl. 2020, 13, 064022. [Google Scholar] [CrossRef]
- Takamatsu, T.; Yu, S.; Miyake, T. Wearable, implantable, parity-time symmetric bioresonators for extremely small biological signal monitoring. Adv. Mater. Technol. 2023, 8, 2201704. [Google Scholar] [CrossRef]
- Sis, S.A. Comprehensive closed-form analysis of bifurcation in inductive wireless power transfer systems. J. Comput. Appl. Math. 2026, 473, 116847. [Google Scholar] [CrossRef]
- Thomas, E.M.; Heebl, J.D.; Pfeiffer, C.; Grbic, A. A power link study of wireless non-radiative power transfer systems using resonant shielded loops. IEEE Trans. Circ. Syst. I Regul. Pap. 2012, 59, 2125–2136. [Google Scholar] [CrossRef]
- Sis, S.A.; Kavut, S. A frequency-tuned magnetic resonance-based wireless power transfer system with near-constant efficiency up to 24 cm distance. Turk. J. Electr. Eng. Comput. Sci. 2018, 26, 3168–3180. [Google Scholar] [CrossRef]
- Sis, S.A. A circuit model-based analysis of magnetically coupled resonant loops in wireless power transfer systems. Electrica 2018, 18, 159–166. [Google Scholar] [CrossRef]
- Wang, C.-S.; Covic, G.A.; Stielau, O.H. Power transfer capability and bifurcation phenomena of loosely coupled inductive power transfer systems. IEEE Trans. Ind. Electron. 2004, 51, 148–157. [Google Scholar] [CrossRef]
- Yan, D.; Yan, J.; Wang, G.; Zhao, Y.; Zhang, L.; Gao, X. Low-Cost Wireless Temperature Measurement: Design, Manufacture, and Testing of a PCB-Based Wireless Passive Temperature Sensor. Sensors 2018, 18, 532. [Google Scholar] [CrossRef]
- Wang, L.-F.; Lu, J.-J.; Dong, L.; Huang, Q.-A. A Biocompatible and Biodegradable LC Temperature Sensor Based on Dual-Layer Inductors. IEEE Sens. J. 2024, 24, 3766–3775. [Google Scholar] [CrossRef]
- Ren, Q.-Y.; Huang, J.-Q.; Wang, L.-F.; Wan, S.; Sun, L.-T.; Huang, Q.-A. Temperature Sensing Properties of the Passive Wireless Sensor Based on Graphene Oxide Films. In Proceedings of the IEEE SENSORS 2014, Valencia, Spain, 2–5 November 2014; pp. 432–435. [Google Scholar]
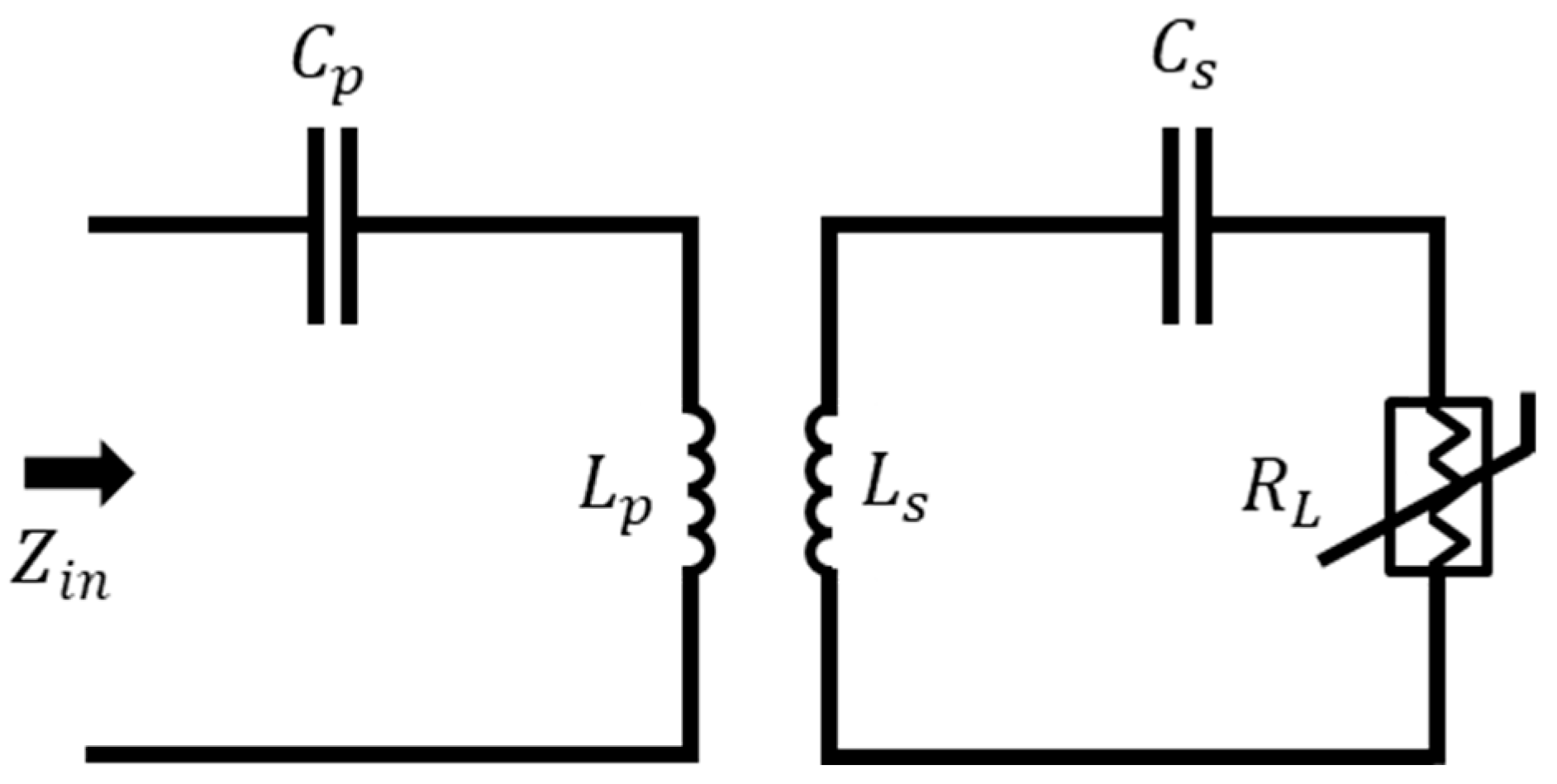

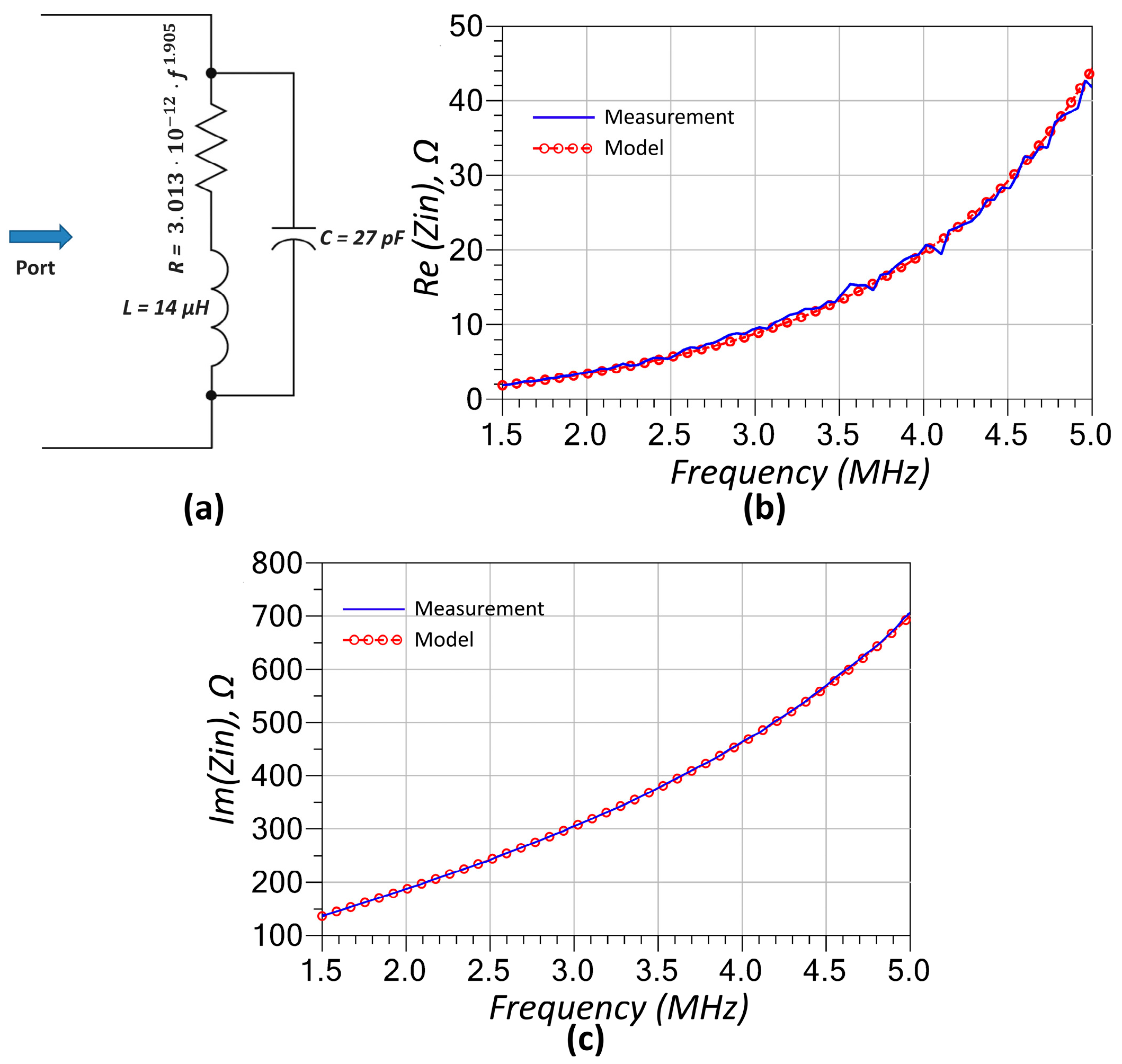
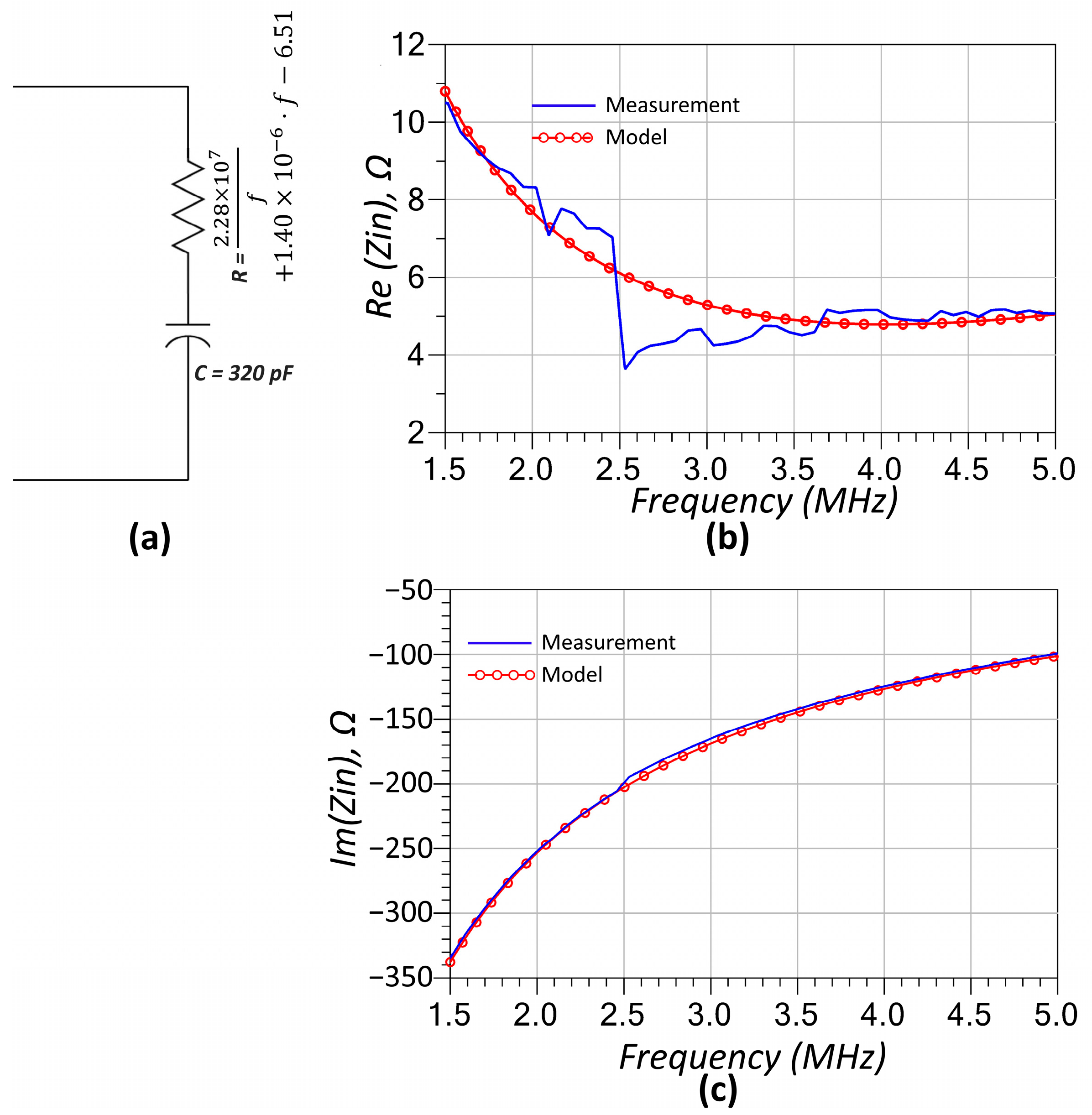
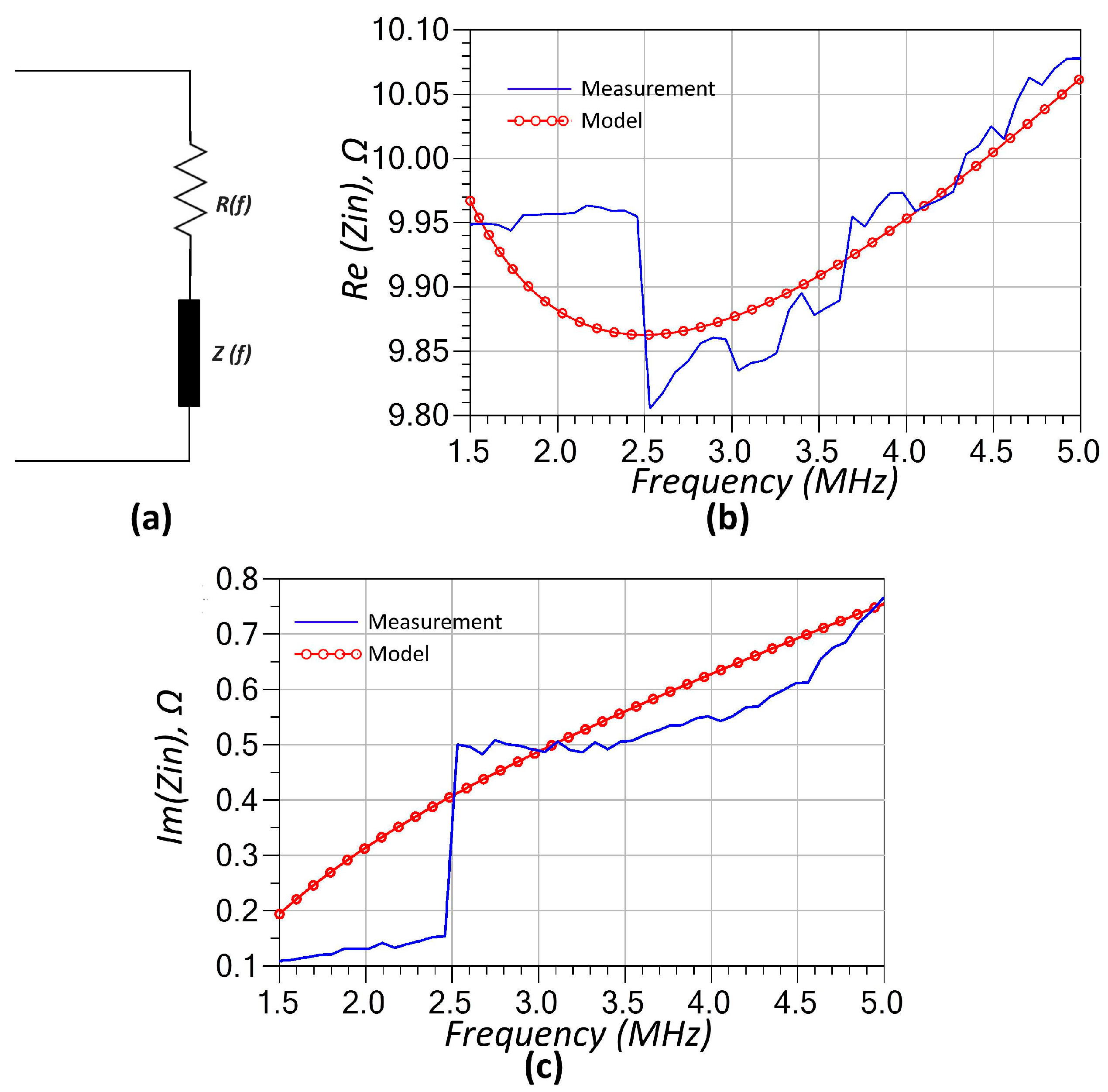
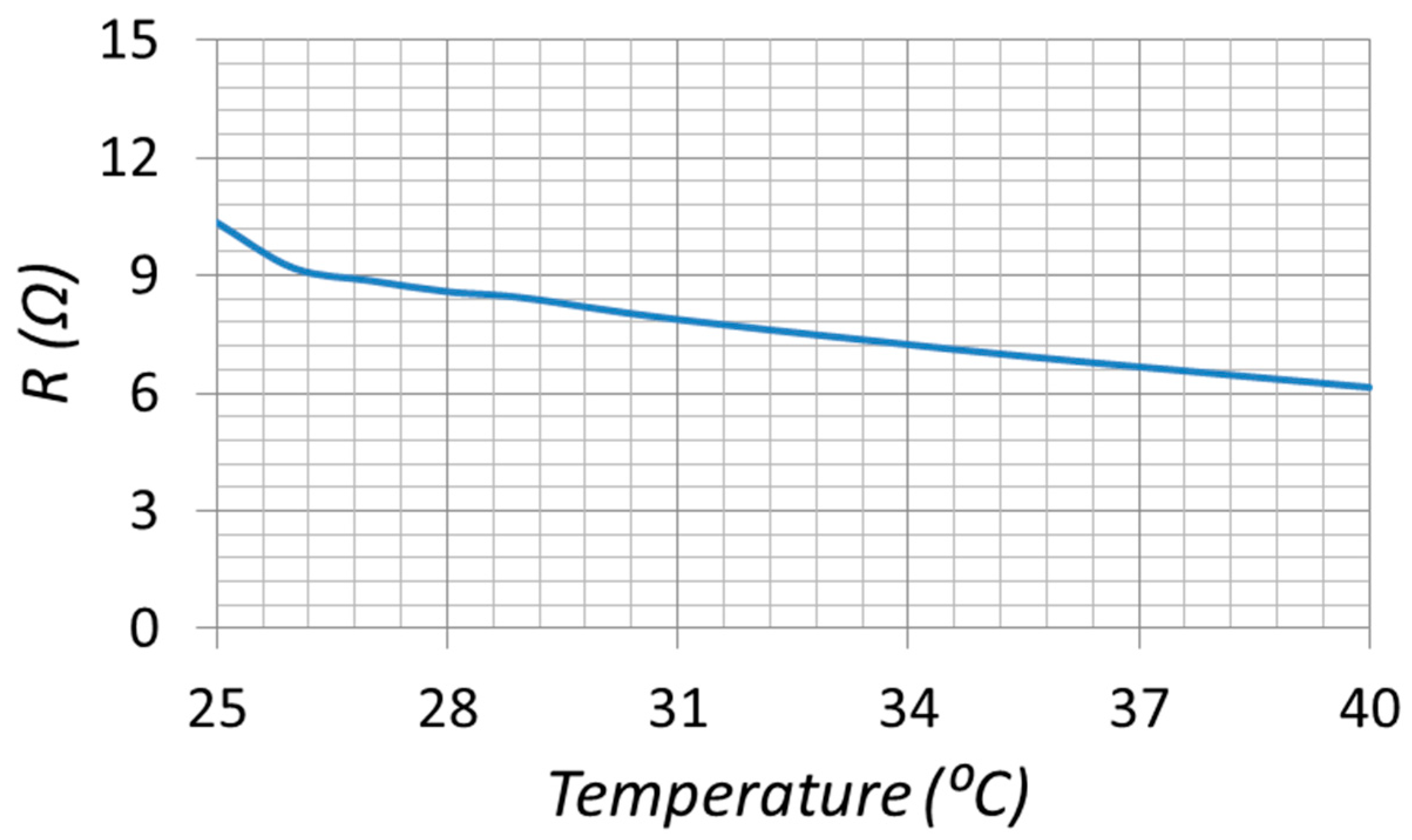

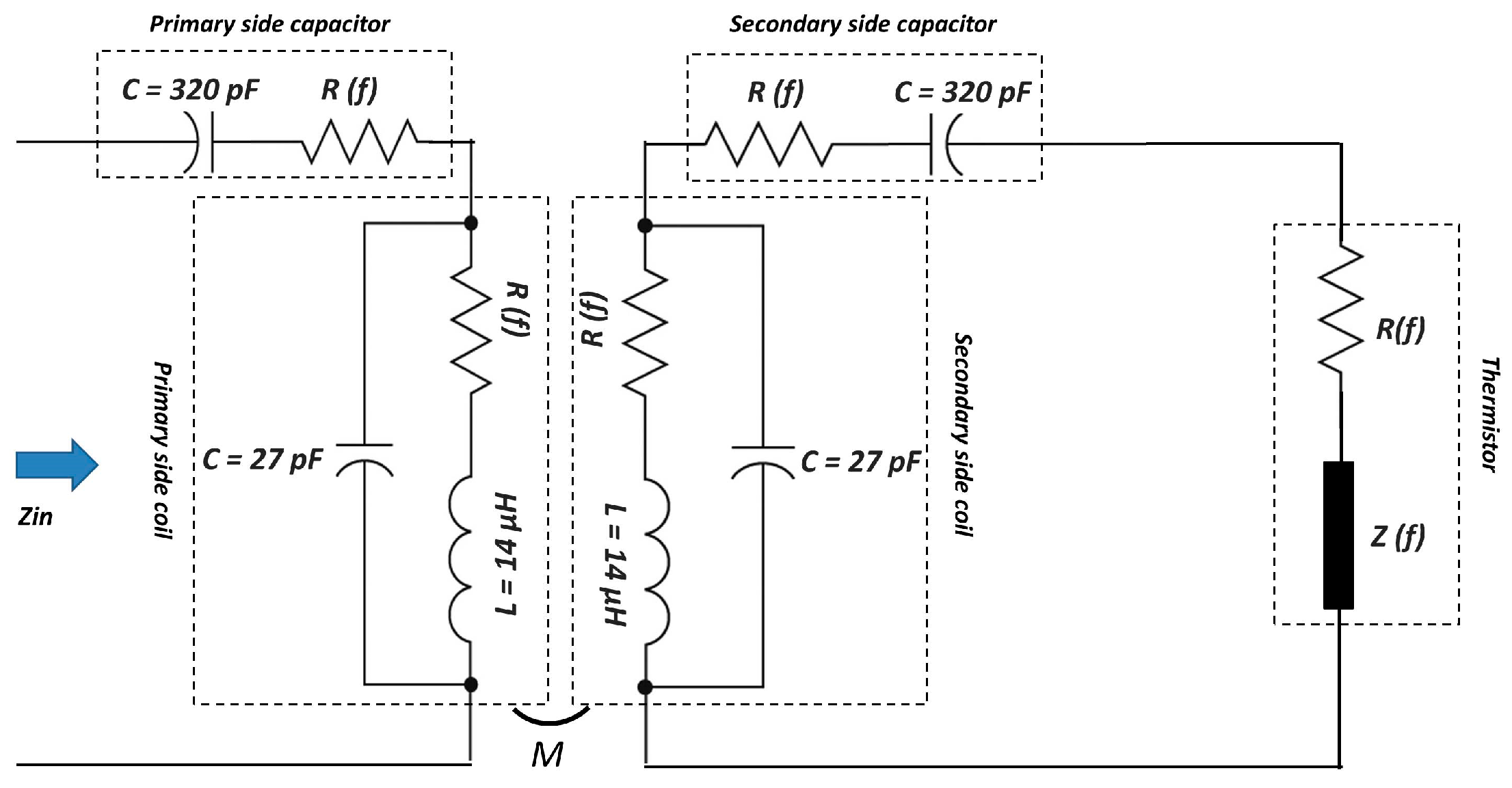

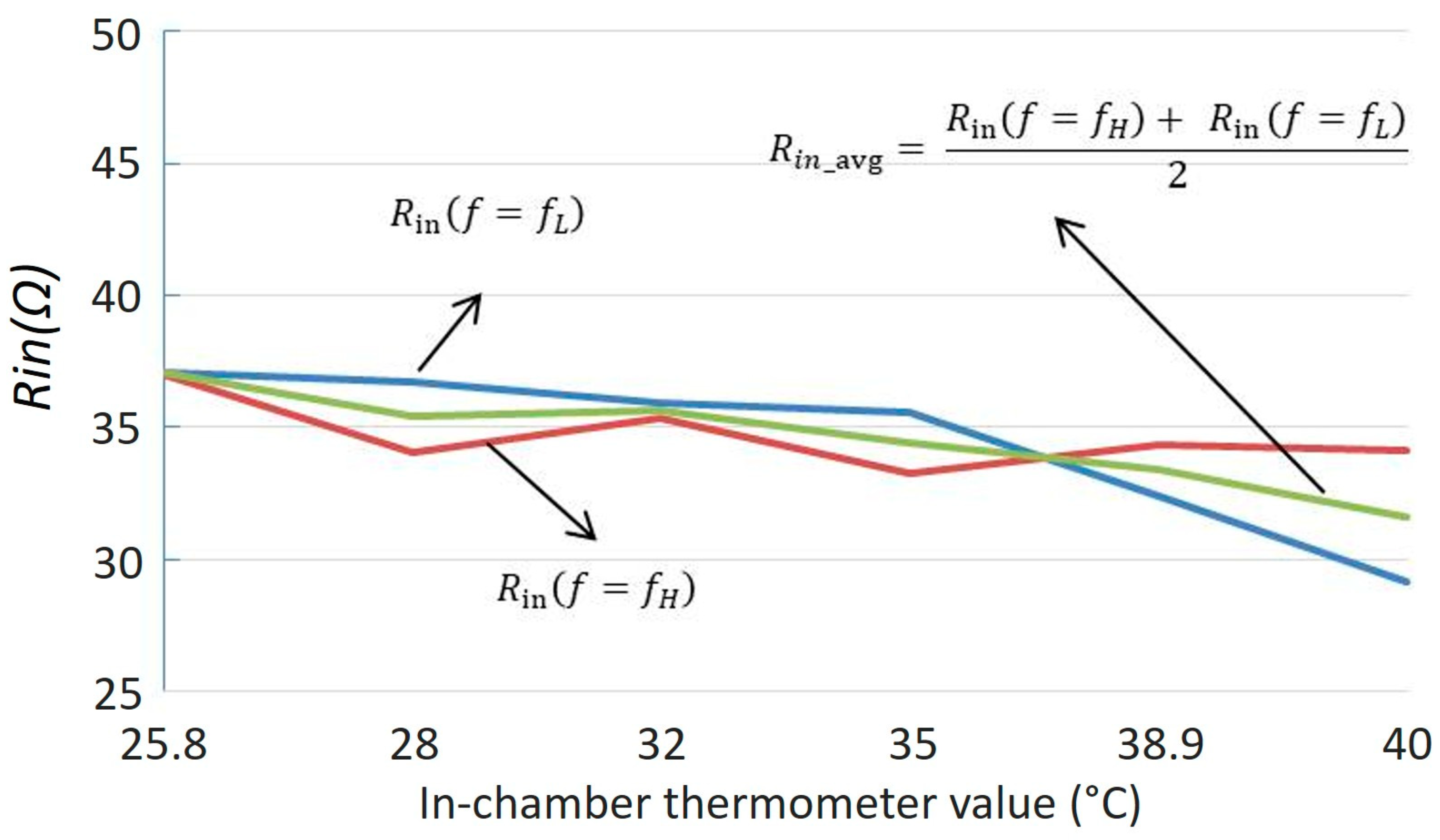

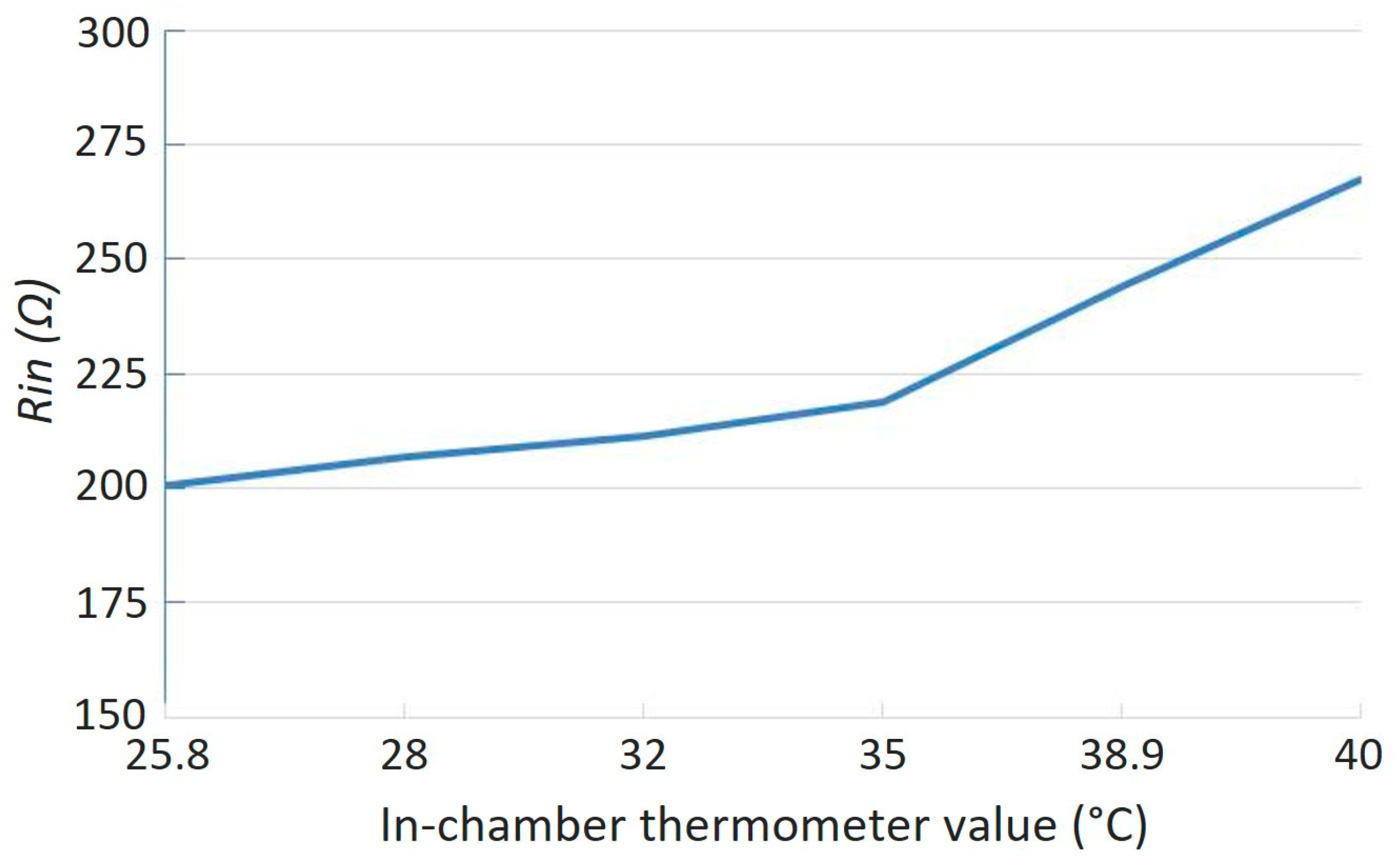
| Solutions for ZPA Resonance Frequencies | Bifurcation Conditions | |
|---|---|---|
| (11) | is real if | |
| (12) | is always real | |
| (13) | is real if |
| Case | ||||
|---|---|---|---|---|
| Nominal | 330 pF | |||
| Ref | Topology/Readout | Sensing Element | Range (°C) | Sensitivity | Reader Complexity |
|---|---|---|---|---|---|
| [36] | Near field coupling of RF antenna link. | PCB patch antenna | −40 to 125 | Sweep/PLL or VNA | |
| [37] | LC passive, dual-layer inductor (L) | PEG dielectric between dual inductors (biocompatible/biodegradable) | 36 to 40 | Sweep/PLL or VNA; | |
| [38] | Single-LC, frequency-shift | Graphene-oxide capacitive film | −40 to 0 and 10 to 60 | (−40–0), 46.1 (10–60) | Sweep/PLL or VNA; |
| [12] | Passive LC (dual-sensitive element), bearing apps | Dual sensing elements (both C and L) | −40 to 140 | No ferrite: −40 °C–40 °C: −14.91 kHz/°C 40 °C–100 °C: +37.59 kHz/°C ------------------ With ferrite: −40 °C–40 °C: −17.12 kHz/°C 40–100 °C: +139.32 kHz/°C 100–140 °C: +72.23 kHz/°C | Sweep/PLL or VNA; |
| This work | Impedance mirroring | NTC thermistor | 25–40 | (from ) | Single tone or two-tone source or VNA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sis, S.A.; Dikerler Kozar, Y. Implementation of an SS-Compensated LC-Thermistor Topology for Passive Wireless Temperature Sensing. Sensors 2025, 25, 6316. https://doi.org/10.3390/s25206316
Sis SA, Dikerler Kozar Y. Implementation of an SS-Compensated LC-Thermistor Topology for Passive Wireless Temperature Sensing. Sensors. 2025; 25(20):6316. https://doi.org/10.3390/s25206316
Chicago/Turabian StyleSis, Seyit Ahmet, and Yeliz Dikerler Kozar. 2025. "Implementation of an SS-Compensated LC-Thermistor Topology for Passive Wireless Temperature Sensing" Sensors 25, no. 20: 6316. https://doi.org/10.3390/s25206316
APA StyleSis, S. A., & Dikerler Kozar, Y. (2025). Implementation of an SS-Compensated LC-Thermistor Topology for Passive Wireless Temperature Sensing. Sensors, 25(20), 6316. https://doi.org/10.3390/s25206316





