Inversion of Soil Parameters and Deformation Prediction for Deep Excavation Based on PSO-SVM Model
Abstract
1. Introduction
2. Soil Parameters Inversion Method Based on PSO-SVM Model
2.1. Support Vector Machine Model
2.2. Particle Swarm Optimization Algorithm
2.3. Soil Parameters Inversion Process Based on PSO-SVM Model
- The value range of soil parameters is determined. Soil parameter samples are constructed based on the orthogonal experimental design. Each set of soil parameters is input into the ABAQUS finite element software to calculate the horizontal displacements of the deep excavation retaining structures. Training samples are obtained and divided into training and testing sets.
- Using the MATLAB software, the velocity and position of each particle in the particle swarm are initialized randomly. The learning factor is set to 1.50 and to 1.70. The maximum evolution number is configured as 100. The termination iteration number is assigned a value of 100. The maximum population size M is designated as 10. The penalty parameter C and kernel function parameter g are constrained within the interval [0.1, 100].
- The particle fitness of the SVM model under different parameter combinations is evaluated by the PSO algorithm using five-fold cross-validation on the training set (22 groups), The separate testing set (five groups) is strictly reserved for the final evaluation of the model’s generalization performance. When the global optimum is superior to the fitness of the particle itself, the velocity and position of the local optimum particle and the global optimum particle are updated. The updated particle fitness is computed by the SVM model.
- Whether the maximum iteration number is reached is checked. If “No”, the process is returned to Step (3). If “Yes”, the optimal penalty parameter C and kernel function parameter g are output.
- The output optimal penalty parameter C and kernel function parameter g are input into the SVM model. A nonlinear relationship between the horizontal displacements of deep excavation retaining structures and soil parameters is established using the input sample sets. An optimized SVM model is obtained.
- The monitoring data of the horizontal displacements of deep excavation retaining structures are input into the optimized SVM model, and inverted parameter values are obtained. The inverted soil parameters are brought into the ABAQUS finite element software. The horizontal displacement values of the retaining structures after inversion are calculated and compared with the monitorings for verification.
3. Soil Parameters Inversion Based on PSO-SVM Model
3.1. Deep Excavation and Monitoring Points
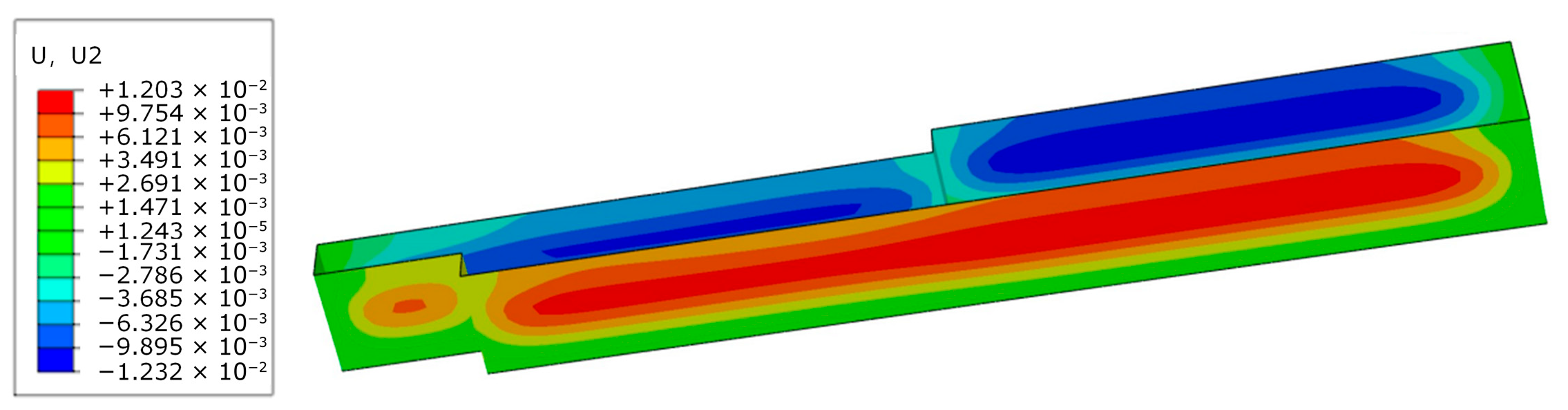
3.2. Establishment of Finite Element Model for Deep Excavation
3.3. Establishment of Initial Finite Element Model for Deep Excavation
3.4. Sample Construction and Soil Parameters Inversion
3.5. Establishment of Inversion Finite Element Model for Deep Excavation
3.6. Prediction of Retaining Structure Deformation During Subsequent Cases
4. Conclusions
- Based on orthogonal experimental design and finite element simulation, training samples are obtained. Optimal parameters for the PSO-SVM model are determined, and an optimal mapping relationship between the mechanical parameters of deep excavation soils and the horizontal displacements of retaining structures is established. A soil parameter inversion method for deep excavations is formed.
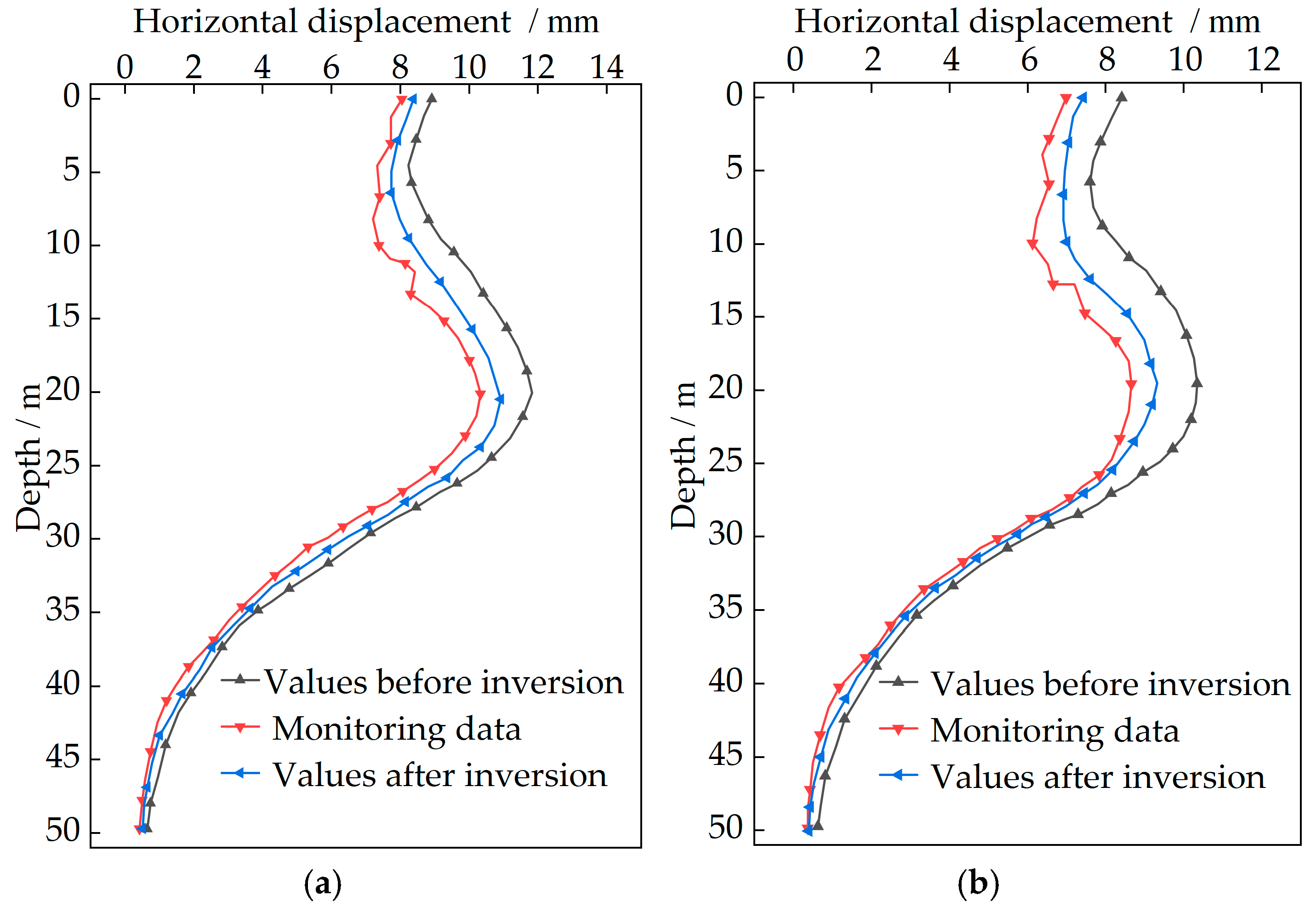
- The accuracy of the finite element model is validated by monitoring data from the Wuhan Zhongyi Road Metro Station deep excavation. The soil parameter inversion can be performed with the optimized PSO-SVM model, and the deformation simulation results of retaining structures demonstrate greater consistency with monitoring trends. At monitoring point CX1, the maximum relative error of simulated horizontal displacement can be reduced from 14.53% to 5.72%. At CX2, this error can be decreased from 18.96% to 7.63%. These results indicate smaller errors and significantly improved accuracy for finite element simulations with inverted soil parameters.
- During Case 2, the maximum horizontal displacements at CX1 and CX2 are recorded as 13.42 mm and 11.80 mm, respectively. During Case 3, these values reach 15.66 mm and 14.22 mm, respectively. All values remain below the project warning threshold of 30.00 mm. The practical applicability and safety reliability of the model are confirmed, which provides a reference for deep excavation analysis and evaluation during the construction period.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BP | Back Propagation Neural Network |
| CNN | Convolutional Neural Network |
| LSTM | Long Short-Term Memory |
| SVM | Support Vector Machine |
| PSO | Particle Swarm Optimization |
References
- Huang, J.; Shen, G.; Zheng, H. Is insufficient land supply the root cause of housing shortage? Empirical evidence from Hong Kong. Habitat Int. 2015, 49, 538–546. [Google Scholar] [CrossRef]
- Satterthwaite, D. How Urban Societies Can Adapt to Resource Shortage and Climate Change. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 1762–1783. [Google Scholar] [CrossRef]
- Liu, T.; Su, H. Intelligent prediction method of urban road traffic congestion based on knowledge graph technology. Adv. Transp. Stud. 2024. [Google Scholar] [CrossRef]
- Yang, H.; Wu, N.; Zhang, W.; Liu, Z.; Fan, J.; Wang, C. Dynamic response of spatial train-track-bridge interaction system due to unsupported track using virtual work principle. Appl. Sci. 2022, 12, 6156. [Google Scholar] [CrossRef]
- Feltynowski, M.; Kronenberg, J.; Bergier, T.; Kabisch, N. Challenges of urban green space management in the face of using inadequate data. Urban For. Urban Green. 2018, 31, 56–66. [Google Scholar] [CrossRef]
- Piovani, C. The “Greening” of China: Progress, limitations, and contradictions. J. Contemp. Asia 2017, 47, 93–115. [Google Scholar] [CrossRef]
- Cui, J.; Nelson, J. Underground transport: An overview. Tunn. Undergr. Space Technol. 2019, 87, 122–126. [Google Scholar] [CrossRef]
- Cui, J.; Broere, W.; Lin, D. Underground space utilization for urban renewal. Tunn. Undergr. Space Technol. 2021, 108, 103726. [Google Scholar] [CrossRef]
- Broere, W. Urban underground space: Solving the problems of today’s cities. Tunn. Undergr. Space Technol. 2016, 55, 245–248. [Google Scholar] [CrossRef]
- Peng, T.; Ren, D.; Kang, C.; Liu, H.; Xue, P.; Huang, H. Deformation Characteristics of Soft Soil Induced by Deep Excavation and Its Impact on Adjacent Tunnels: A Case Study in Shanghai. KSCE J. Civ. Eng. 2024, 28, 14. [Google Scholar] [CrossRef]
- Lin, P.; Liu, P.; Ankit, G.; Singh, Y. Deformation monitoring analysis and numerical simulation in a deep foundation pit. Soil Mech. Found. Eng. 2021, 58, 56–62. [Google Scholar] [CrossRef]
- Li, Y.J.; Zhou, Z.; Alcalá, J.; Yepes, V. Research on spatial deformation monitoring and numerical coupling of deep foundation pit in soft soil. J. Build. Eng. 2025, 99, 111636. [Google Scholar] [CrossRef]
- Wang, W.; Han, Z.; Deng, J.; Zhang, X.; Zhang, Y. Study on soil reinforcement param in deep foundation pit of marshland metro station. Heliyon 2019, 5, e02814. [Google Scholar] [CrossRef]
- Levasseur, S.; Malécot, Y.; Boulon, M.; Garnier, J. Soil parameter identification using a genetic algorithm. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 189–213. [Google Scholar] [CrossRef]
- Hu, A.; Xie, S.; Li, T.; Zhang, Y.; Yang, D. Soil parameter inversion modeling using deep learning algorithms and its application to settlement prediction: A comparative study. Acta Geotech. 2023, 18, 5597–5618. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, H.; Cao, H.; Zhang, X.; Zhang, A.; Wu, N.; Liu, Z. Separation of Temperature-Induced Response for Bridge Long-Term Monitoring Data Using Local Outlier Correction and Savitzky–Golay Convolution Smoothing. Sensors 2023, 23, 2632. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Jiang, L.; Xu, F.; Gu, J.; Ye, Z.; Peng, Y.; Liu, Z.; Cheng, R. Safety Evaluation for Fabricated Small Box Girder Bridges Based on Fuzzy Analytic Hierarchy Process and Monitoring Data. Sensors 2024, 24, 4592. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Yang, H.; Liu, W.; Ye, Z.; Pei, J.; Liu, Z.; Fan, J. Early Warning for Continuous Rigid Frame Bridges Based on Nonlinear Modeling for Temperature-Induced Deflection. Sensors 2024, 4, 3587. [Google Scholar] [CrossRef]
- Wu, N.; Yang, H.; Afsar, H.; Wang, B.; Fan, J. Analysis of Train–Track–Bridge Coupling Vibration Characteristics for Heavy-Haul Railway Based on Virtual Work Principle. Sensors 2023, 23, 8550. [Google Scholar] [CrossRef]
- Yang, H.; Wu, N.; Cao, H.; Zhang, W. Two-stage stochastic model updating approach based on Bayesian framework and hybrid multi-population migrant genetic-metropolis-hastings algorithm for heavy-haul railway bridges. Eng. Optim. 2025, 57, 1343–1366. [Google Scholar] [CrossRef]
- Zentar, R.; Hicher, P.; Moulin, G. Identification of soil parameters by inverse analysis. Comput. Geotech. 2001, 28, 129–144. [Google Scholar] [CrossRef]
- Li, H.; Zhao, Z.; Du, X. Research and application of deformation prediction model for deep foundation pit based on LSTM. Wirel. Commun. Mob. Comput. 2022, 2022, 9407999. [Google Scholar] [CrossRef]
- Wu, X.; Feng, Z.; Liu, J.; Zhang, Y.; Li, M. Predicting existing tunnel deformation from adjacent foundation pit construction using hybrid machine learning. Autom. Constr. 2024, 165, 105516. [Google Scholar] [CrossRef]
- Li, Q.; Cheng, F.; Zhang, X. Numerical simulation and deformation prediction of deep pit based on PSO-BP neural network inversion of soil parameters. Sensors 2024, 24, 2959. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.; Cheng, S.; Chen, R.; Guo, Y.; Liu, W. ANN deformation prediction model for deep foundation pit with considering the influence of rainfall. Sci. Rep. 2023, 13, 22664. [Google Scholar] [CrossRef]
- Wang, X.; Qin, Z.; Bai, X.; Wang, L.; Chen, Y. Research progress of machine learning in deep foundation pit deformation prediction. Buildings 2025, 15, 852. [Google Scholar] [CrossRef]
- Chen, C.; Li, S.; Ye, J.; Chen, F.; Wu, Y.; Yu, J.; Cai, Y.; Lin, J.; Zhou, X. Soil Parameter Inversion in Dredger Fill Strata Using GWO-MLSSVR for Deep Foundation Pit Engineering. Buildings 2025, 15, 1864. [Google Scholar] [CrossRef]
- Li, X.; Liu, X.; Li, C.; Hu, Z.; Shen, G.; Huang, Z. Foundation pit displacement monitoring and prediction using least squares support vector machines based on multi-point measurement. Struct. Health Monit. 2019, 18, 715–724. [Google Scholar] [CrossRef]
- Bowen, X.; Xinjiang, L. Spatiotemporal LS-SVM inverse control for nonlinear distributed parameter systems with application to heating process. Nonlinear Dyn. 2023, 111, 17229–17246. [Google Scholar] [CrossRef]
- Le, T.C.; Nghia, N.T.; Khatir, S. An efficient approach for damage identification based on improved machine learning using PSO-SVM. Eng. Comput. 2022, 38, 3069–3084. [Google Scholar] [CrossRef]
- Ayat, N.; Cheriet, M.; Suen, C. Automatic model selection for the optimization of SVM kernels. Pattern Recognit. 2005, 38, 1733–1745. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, H. Bounded quantile loss for robust support vector machines-based classification and regression. Expert Syst. Appl. 2024, 242, 19. [Google Scholar] [CrossRef]
- Li, G.; You, J.; Liu, X. Support vector machine (SVM) based prestack AVO inversion and its applications. J. Appl. Geophys. 2015, 120, 60–68. [Google Scholar] [CrossRef]
- Freitas, D.; Lopes, L.; Morgado-Dias, F. Particle swarm optimization: A historical review up to the current developments. Entropy 2020, 22, 362. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Jain, M.; Saihjpal, V.; Singh, N.; Arora, A. An overview of variants and advancements of PSO algorithm. Appl. Sci. 2022, 12, 8392. [Google Scholar] [CrossRef]
- Wang, W. Research on Automatic Monitoring of Deep and Large Foundation Pit Construction and Deformation Prediction of Enclosure Structure. Master’s Thesis, Wuhan Institute of Technology, Wuhan, China, 2023. [Google Scholar] [CrossRef]
- Tian, A.; Ju, J.; Zhang, H.; Yin, P.; Tang, Q.; Li, W. Soil and structure deformation during deep foundation pit excavation in soft clay: Case study and sensitivity analysis. Arab. J. Geosci. 2022, 15, 926. [Google Scholar] [CrossRef]
- Niu, Y.; Wang, Q.; Ma, F. Study on the Influence of Foundation Pit Excavation on the Deformation of Adjacent Subway Tunnel in the Affected Area of Fault Zones. Sustainability 2023, 15, 9462. [Google Scholar] [CrossRef]
- GB 50497-2019; Technical Standard for Monitoring of Building Excavation Engineering. Ministry of Housing and Urban-Rural Development of the People’s Republic of China, China Planning Press: Beijing, China, 2020.

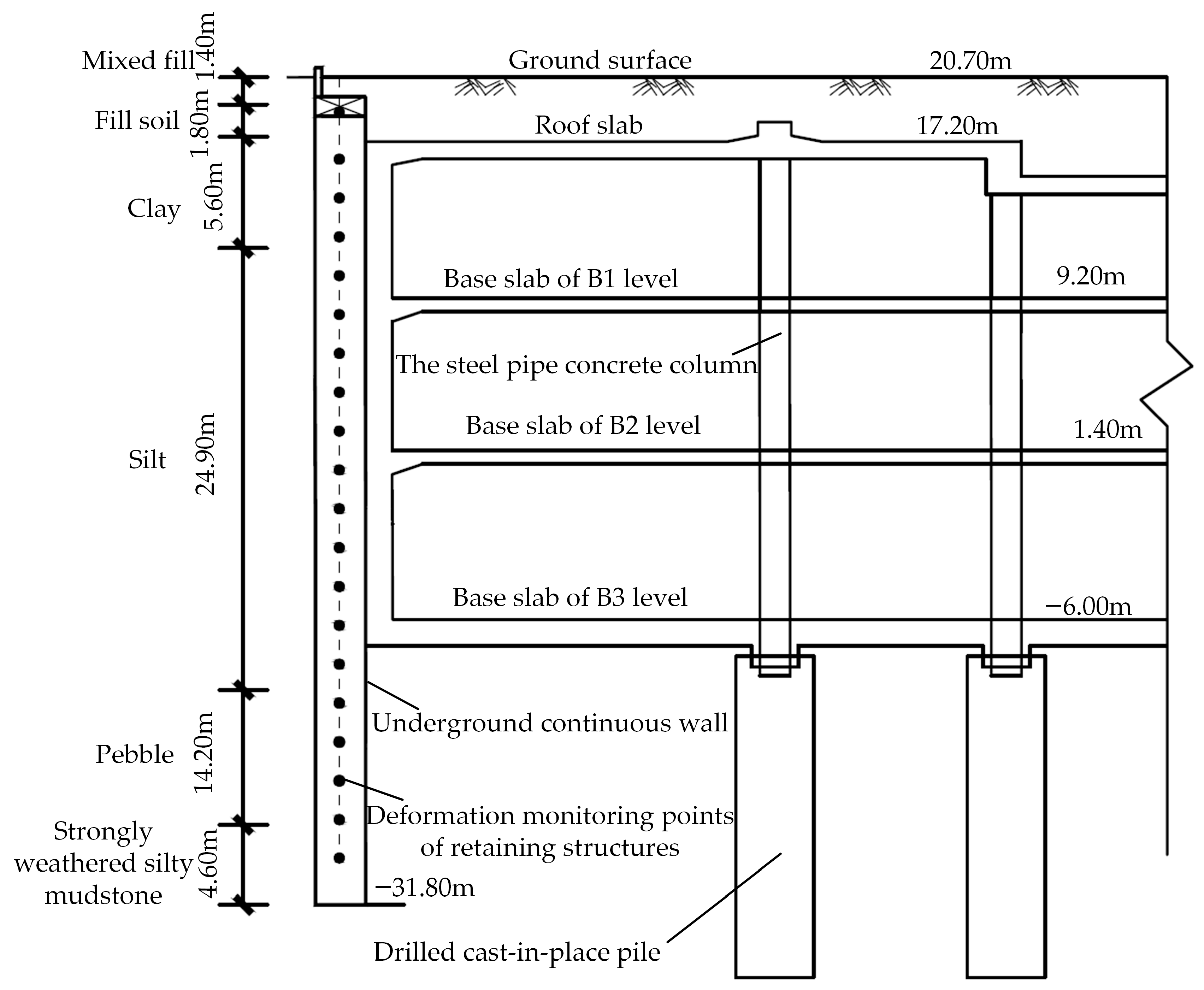
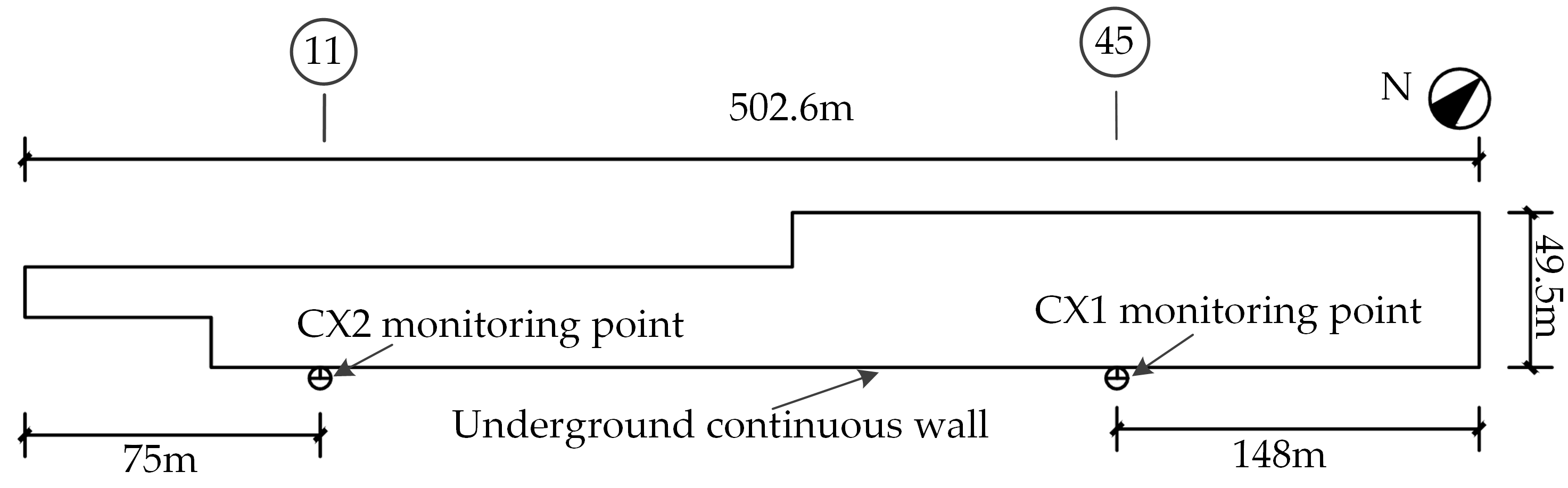







| Thickness h (m) | Soil Layer | Severe γ (kN/m3) | Modulus of Elasticity E (MPa) | Poisson Ratio | Cohesion (kPa) | Internal Friction Angle (°) |
|---|---|---|---|---|---|---|
| 1.40 | Mixed fill | 0 | 5.40 | 0.35 | 5.00 | 19.0 |
| 1.80 | Fill soil | 18.20 | 7.00 | 0.34 | 9.00 | 7.00 |
| 5.60 | Clay | 18.80 | 12.00 | 0.25 | 18.00 | 11.00 |
| 24.90 | Silt | 19.00 | 27.00 | 0.32 | 12.00 | 12.00 |
| 14.20 | Pebble | 20.00 | 114.00 | 0.28 | 0 | 35.00 |
| 6.20 | Strongly weathered silty mudstone | 23.50 | 215.00 | 0.27 | 111.00 | 26.00 |
| 25.90 | Moderately weathered silty mudstone | 24.80 | 260.00 | 0.24 | 220.00 | 31.00 |
| Horizontal | (MPa) | (kPa) | (°) | (MPa) | (kPa) | (°) | (MPa) | (kPa) | (°) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 5.60 | 7.20 | 5.60 | 9.60 | 14.40 | 8.80 | 21.60 | 9.60 | 9.60 |
| 2 | 7.00 | 9.00 | 7.00 | 12.00 | 18.00 | 11.00 | 27.00 | 12.00 | 12.00 |
| 3 | 8.40 | 10.80 | 8.40 | 14.40 | 21.60 | 13.20 | 32.40 | 14.40 | 14.40 |
| Experiment | (MPa) | (kPa) | (°) | (MPa) | (kPa) | (°) | (MPa) | (kPa) | (°) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 5.60 | 7.20 | 5.60 | 9.60 | 14.40 | 8.80 | 21.60 | 9.60 | 9.60 |
| 2 | 5.60 | 7.20 | 5.60 | 9.60 | 18.00 | 11.00 | 27.00 | 12.00 | 12.00 |
| 3 | 5.60 | 7.20 | 5.60 | 9.60 | 21.60 | 13.20 | 32.40 | 14.40 | 14.40 |
| 4 | 5.60 | 9.00 | 7.00 | 12.00 | 14.40 | 8.80 | 21.60 | 12.00 | 12.00 |
| 5 | 5.60 | 9.00 | 7.00 | 12.00 | 18.00 | 11.00 | 27.00 | 14.40 | 14.40 |
| 6 | 5.60 | 9.00 | 7.00 | 12.00 | 21.60 | 13.20 | 32.40 | 9.60 | 9.60 |
| 7 | 5.60 | 10.80 | 8.40 | 14.40 | 14.40 | 8.80 | 21.60 | 14.40 | 14.40 |
| 8 | 5.60 | 10.80 | 8.40 | 14.40 | 18.00 | 11.00 | 27.00 | 9.60 | 9.60 |
| 9 | 5.60 | 10.80 | 8.40 | 14.40 | 21.60 | 13.20 | 32.40 | 12.00 | 12.00 |
| 10 | 7.00 | 7.20 | 5.60 | 14.40 | 14.40 | 11.00 | 32.40 | 9.60 | 12.00 |
| 11 | 7.00 | 7.20 | 7.00 | 14.40 | 18.00 | 13.20 | 21.60 | 12.00 | 14.40 |
| 12 | 7.00 | 7.20 | 8.40 | 14.40 | 21.60 | 8.80 | 27.00 | 14.40 | 9.60 |
| 13 | 7.00 | 9.00 | 5.60 | 9.60 | 14.40 | 11.00 | 32.40 | 12.00 | 14.40 |
| 14 | 7.00 | 9.00 | 7.00 | 9.60 | 18.00 | 13.20 | 21.60 | 14.40 | 9.60 |
| 15 | 7.00 | 9.00 | 8.40 | 9.60 | 21.60 | 8.80 | 27.00 | 9.60 | 12.00 |
| 16 | 7.00 | 10.80 | 5.60 | 12.00 | 14.40 | 11.00 | 32.40 | 14.40 | 9.60 |
| 17 | 7.00 | 10.80 | 7.00 | 12.00 | 18.00 | 13.20 | 21.60 | 9.60 | 12.00 |
| 18 | 7.00 | 10.80 | 8.40 | 12.00 | 21.60 | 8.80 | 27.00 | 12.00 | 14.40 |
| 19 | 8.40 | 7.20 | 8.40 | 12.00 | 14.40 | 13.20 | 27.00 | 9.60 | 14.40 |
| 20 | 8.40 | 7.20 | 8.40 | 12.00 | 18.00 | 8.80 | 32.40 | 12.00 | 9.60 |
| 21 | 8.40 | 7.20 | 8.40 | 12.00 | 21.60 | 11.00 | 21.60 | 14.40 | 12.00 |
| 22 | 8.40 | 9.00 | 5.60 | 14.40 | 14.40 | 13.20 | 27.00 | 12.00 | 9.60 |
| 23 | 8.40 | 9.00 | 5.60 | 14.40 | 18.00 | 8.80 | 32.40 | 14.40 | 12.00 |
| 24 | 8.40 | 9.00 | 5.60 | 14.40 | 21.60 | 11.00 | 21.60 | 9.60 | 14.40 |
| 25 | 8.40 | 10.80 | 7.00 | 9.60 | 14.40 | 13.20 | 27.00 | 14.40 | 12.00 |
| 26 | 8.40 | 10.80 | 7.00 | 9.60 | 18.00 | 8.80 | 32.40 | 9.60 | 14.40 |
| 27 | 8.40 | 10.80 | 7.00 | 9.60 | 21.60 | 11.00 | 21.60 | 12.00 | 9.60 |
| Experiment | J1 | J2 | J3 | J4 | J5 | J6 | J7 | J8 | J9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 7.79 | 6.67 | 6.58 | 7.65 | 9.01 | 10.24 | 11.39 | 8.92 | 8.56 |
| 2 | 8.45 | 7.75 | 7.63 | 8.72 | 9.20 | 11.07 | 11.23 | 10.11 | 8.06 |
| 3 | 7.87 | 7.65 | 6.76 | 8.89 | 8.92 | 10.04 | 10.78 | 10.05 | 8.13 |
| 4 | 7.67 | 7.16 | 6.81 | 8.68 | 9.11 | 10.24 | 10.93 | 9.11 | 7.61 |
| 5 | 8.70 | 7.31 | 7.18 | 8.03 | 10.21 | 10.48 | 11.41 | 10.01 | 8.44 |
| 6 | 8.91 | 7.25 | 7.12 | 8.22 | 8.64 | 10.06 | 10.86 | 9.16 | 7.10 |
| 7 | 8.26 | 8.07 | 7.35 | 8.14 | 8.51 | 9.65 | 9.71 | 9.24 | 8.31 |
| 8 | 8.01 | 6.82 | 6.77 | 9.05 | 9.50 | 11.31 | 10.46 | 10.23 | 9.31 |
| 9 | 8.69 | 7.71 | 7.25 | 8.86 | 9.61 | 9.94 | 11.47 | 10.16 | 8.50 |
| 10 | 8.87 | 7.80 | 7.49 | 8.98 | 9.69 | 10.24 | 10.93 | 10.65 | 8.90 |
| 11 | 8.31 | 7.88 | 6.43 | 7.59 | 9.44 | 10.79 | 11.20 | 9.87 | 8.54 |
| 12 | 7.83 | 7.41 | 6.46 | 8.14 | 8.58 | 9.88 | 11.39 | 9.28 | 8.75 |
| 13 | 8.27 | 8.13 | 7.59 | 8.62 | 9.13 | 10.01 | 10.49 | 9.62 | 7.66 |
| 14 | 7.59 | 7.31 | 6.68 | 8.63 | 9.12 | 10.95 | 10.16 | 8.21 | 7.69 |
| 15 | 8.27 | 7.75 | 7.25 | 7.49 | 8.14 | 9.14 | 10.98 | 9.47 | 8.77 |
| 16 | 8.47 | 7.83 | 7.13 | 9.06 | 9.58 | 9.65 | 10.31 | 9.51 | 8.52 |
| 17 | 8.75 | 7.74 | 6.80 | 8.62 | 9.78 | 10.84 | 11.43 | 8.71 | 8.40 |
| 18 | 7.78 | 7.21 | 6.51 | 8.73 | 9.12 | 9.60 | 9.72 | 8.54 | 7.62 |
| 19 | 7.79 | 7.54 | 7.26 | 8.45 | 8.83 | 9.44 | 9.01 | 8.23 | 7.81 |
| 20 | 8.16 | 7.72 | 7.03 | 8.43 | 8.54 | 9.96 | 10.10 | 9.04 | 8.12 |
| 21 | 9.27 | 8.21 | 7.11 | 8.34 | 9.14 | 10.57 | 11.74 | 10.45 | 9.04 |
| 22 | 8.33 | 7.36 | 6.98 | 8.48 | 9.23 | 10.13 | 10.82 | 9.23 | 8.50 |
| 23 | 7.83 | 7.30 | 7.21 | 8.85 | 8.29 | 8.99 | 9.15 | 8.66 | 7.44 |
| 24 | 8.01 | 7.88 | 7.43 | 8.41 | 9.25 | 9.65 | 10.33 | 8.59 | 7.04 |
| 25 | 8.23 | 7.79 | 7.06 | 8.42 | 9.18 | 10.08 | 10.64 | 9.76 | 8.48 |
| 26 | 7.60 | 6.68 | 6.46 | 8.12 | 8.43 | 9.55 | 9.87 | 8.95 | 7.35 |
| 27 | 8.07 | 7.76 | 7.21 | 8.28 | 9.80 | 10.28 | 10.41 | 8.66 | 7.42 |
| Horizontal | (MPa) | (kPa) | (°) | (MPa) | (kPa) | (°) | (MPa) | (kPa) | (°) |
|---|---|---|---|---|---|---|---|---|---|
| Before inversion | 7.00 | 9.00 | 7.00 | 12.00 | 18.00 | 11.00 | 27.00 | 12.00 | 12.00 |
| After inversion | 7.52 | 9.43 | 6.31 | 11.76 | 19.21 | 11.34 | 27.54 | 11.12 | 12.89 |
| Correction range | 7.40% | 4.80% | −9.90% | −2.00% | 6.70% | 3.10% | 2.00% | −7.30% | 7.40% |
| Monitoring Point | Before Inversion | After Inversion | |||||
|---|---|---|---|---|---|---|---|
| Horizontal Displacement | Maximum Horizontal Displacement/mm | Absolute Error/mm | Relative Error/% | Maximum Horizontal Displacement/mm | Absolute Error/mm | Relative Error/% | |
| CX1 | 10.32 | 11.82 | 1.50 | 14.53% | 10.91 | 0.59 | 5.72% |
| CX2 | 8.65 | 10.29 | 1.64 | 18.96% | 9.31 | 0.66 | 7.63% |
| Measuring Point | Case | Depth of Maximum Horizontal Displacement | Maximum Horizontal Displacement |
|---|---|---|---|
| CX1 | 2 | 24.48 m | 13.42 mm |
| 3 | 26.85 m | 15.66 mm | |
| CX2 | 2 | 23.06 m | 11.80 mm |
| 3 | 26.15 m | 14.22 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Chen, L.; Yang, H.; Li, B.; Yang, L.; Peng, H.; Cao, H. Inversion of Soil Parameters and Deformation Prediction for Deep Excavation Based on PSO-SVM Model. Sensors 2025, 25, 6281. https://doi.org/10.3390/s25206281
Zhao J, Chen L, Yang H, Li B, Yang L, Peng H, Cao H. Inversion of Soil Parameters and Deformation Prediction for Deep Excavation Based on PSO-SVM Model. Sensors. 2025; 25(20):6281. https://doi.org/10.3390/s25206281
Chicago/Turabian StyleZhao, Jing, Longhui Chen, Hongyin Yang, Bin Li, Linlong Yang, Hao Peng, and Hongyou Cao. 2025. "Inversion of Soil Parameters and Deformation Prediction for Deep Excavation Based on PSO-SVM Model" Sensors 25, no. 20: 6281. https://doi.org/10.3390/s25206281
APA StyleZhao, J., Chen, L., Yang, H., Li, B., Yang, L., Peng, H., & Cao, H. (2025). Inversion of Soil Parameters and Deformation Prediction for Deep Excavation Based on PSO-SVM Model. Sensors, 25(20), 6281. https://doi.org/10.3390/s25206281







