Research on Lateral Stability Control of Four-Wheel Independent Drive Electric Vehicle Based on State Estimation
Abstract
1. Introduction
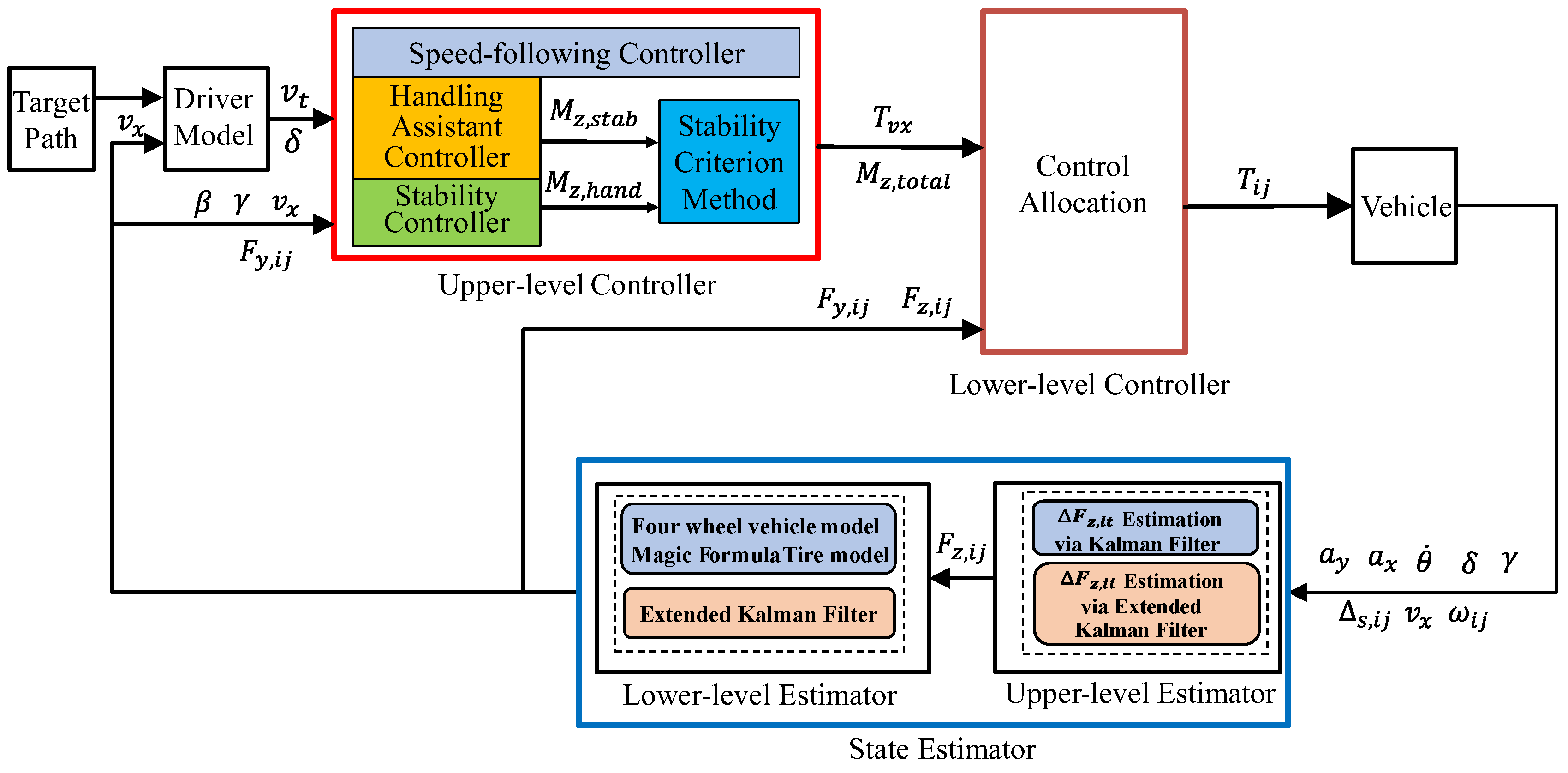
- A hierarchical estimation method. The upper layer uses KF and EKF observers to estimate the vertical loads on all four wheels based on data collected by low-cost onboard sensors. The lower layer focuses on a three-degrees-of-freedom four-wheel vehicle model combined with the nonlinear MF-T, utilizing an EKF observer to estimate the lateral forces on all four wheels and the vehicle centroid sideslip angle.
- A layered architecture for vehicle lateral stability control. When the vehicle is stable, the control system provides additional yaw moments to enhance the vehicle handling performance. In contrast, when the vehicle becomes unstable, the control system generates additional yaw moments to restore stability.
2. Driver Model and Vehicle Dynamics Model
2.1. Driver Model
2.2. Vehicle Dynamics Model
2.2.1. Magic Formula Tire Model
2.2.2. Four-Wheel Vehicle Dynamics Model
2.2.3. Linear Two-Degrees-of-Freedom Vehicle Dynamics Model
3. Vehicle State Estimation
3.1. Vehicle Vertical Load Estimation
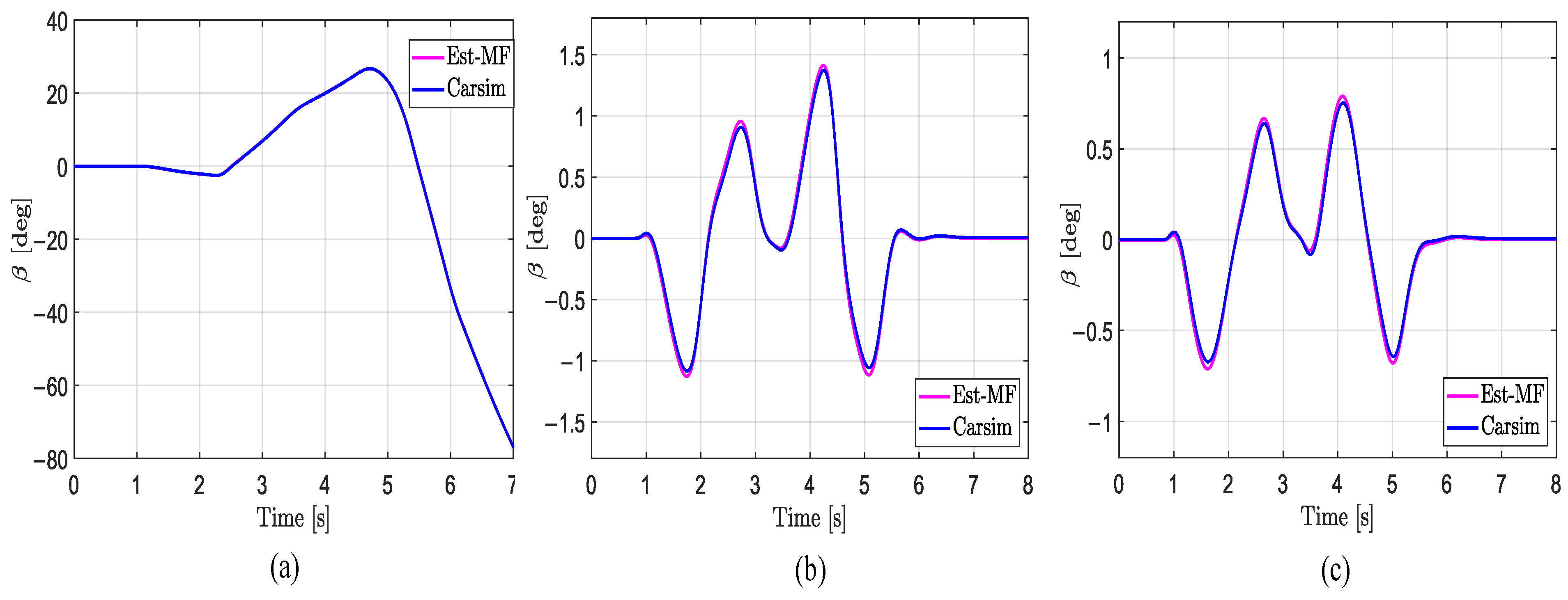
3.2. Vehicle Lateral Force and Sideslip Angle Estimation
3.3. Cornering Stiffness Estimation
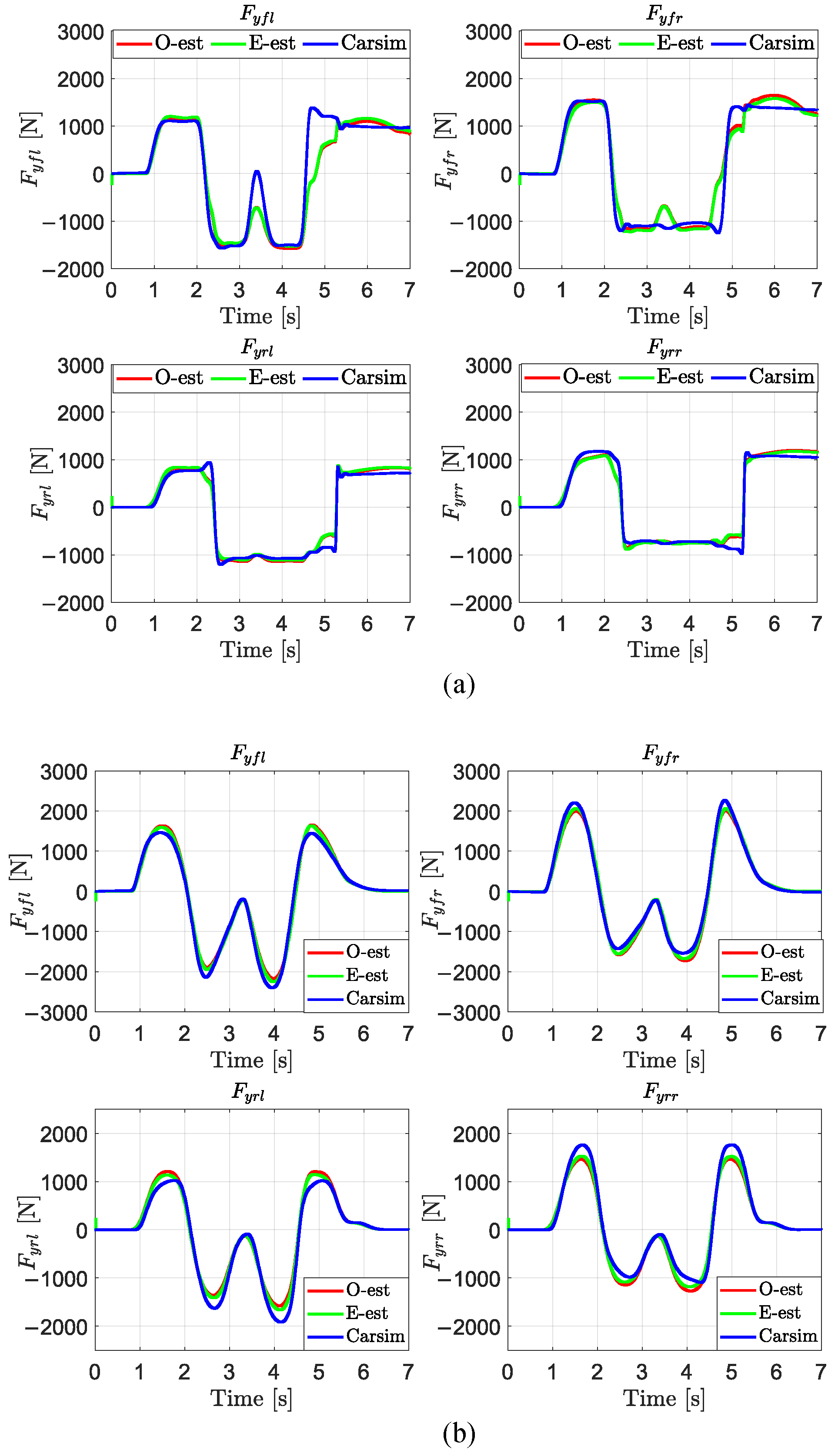
3.4. Estimation Results
3.4.1. Estimation Results of
3.4.2. Estimation Results of and
3.4.3. Estimation Results of Cornering Stiffness
4. Controller Design
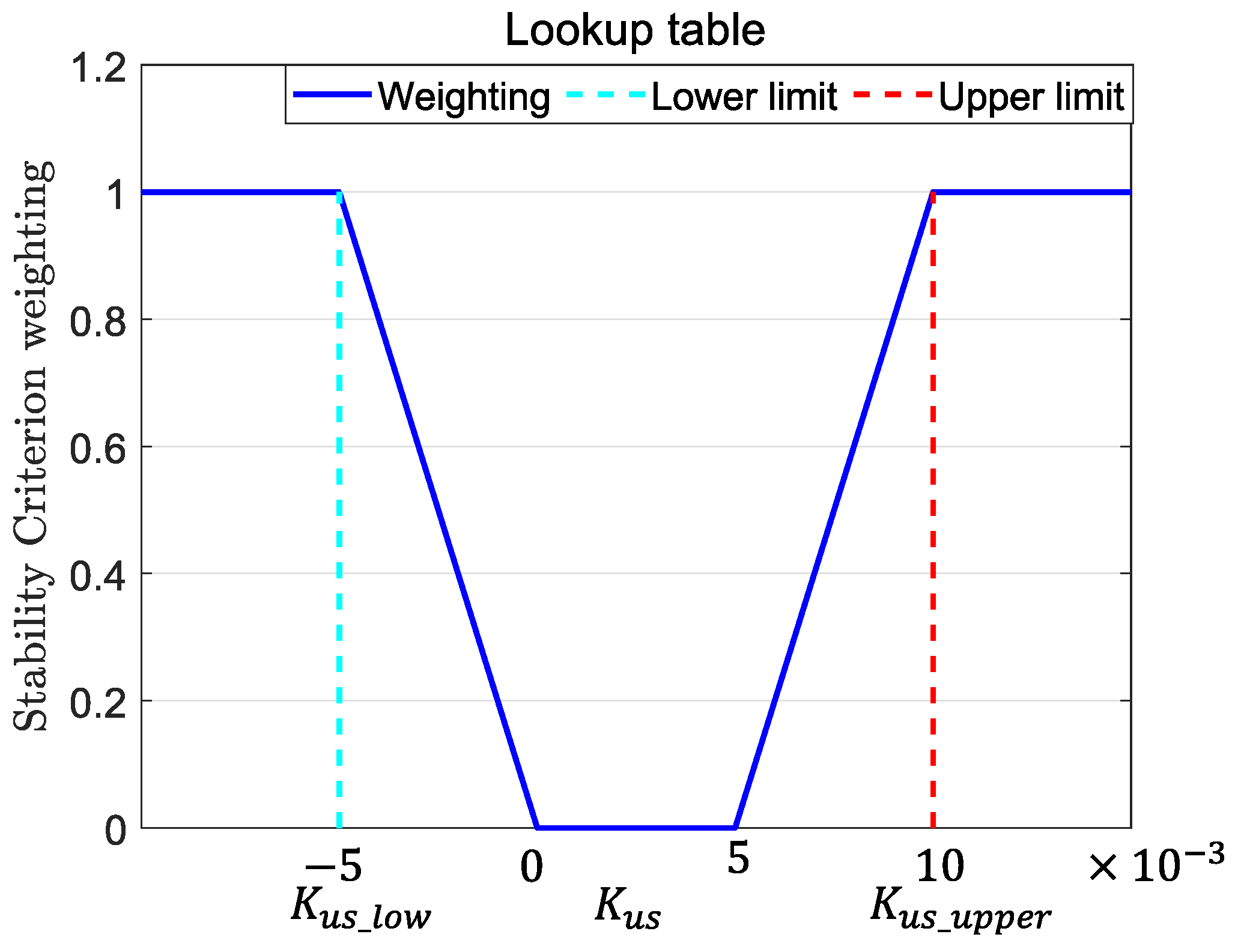
4.1. Stability Criterion Method
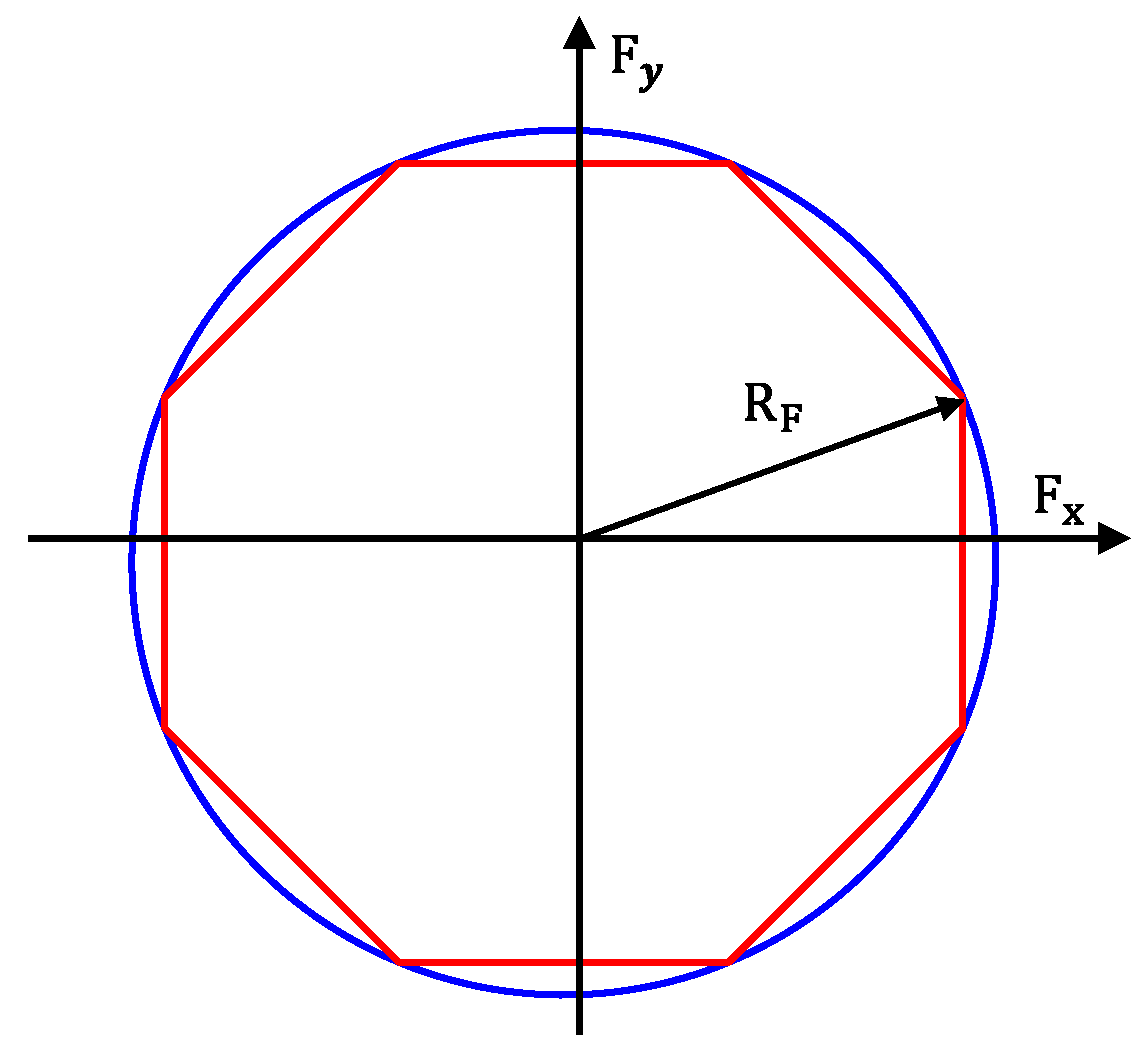
4.2. Control Allocation
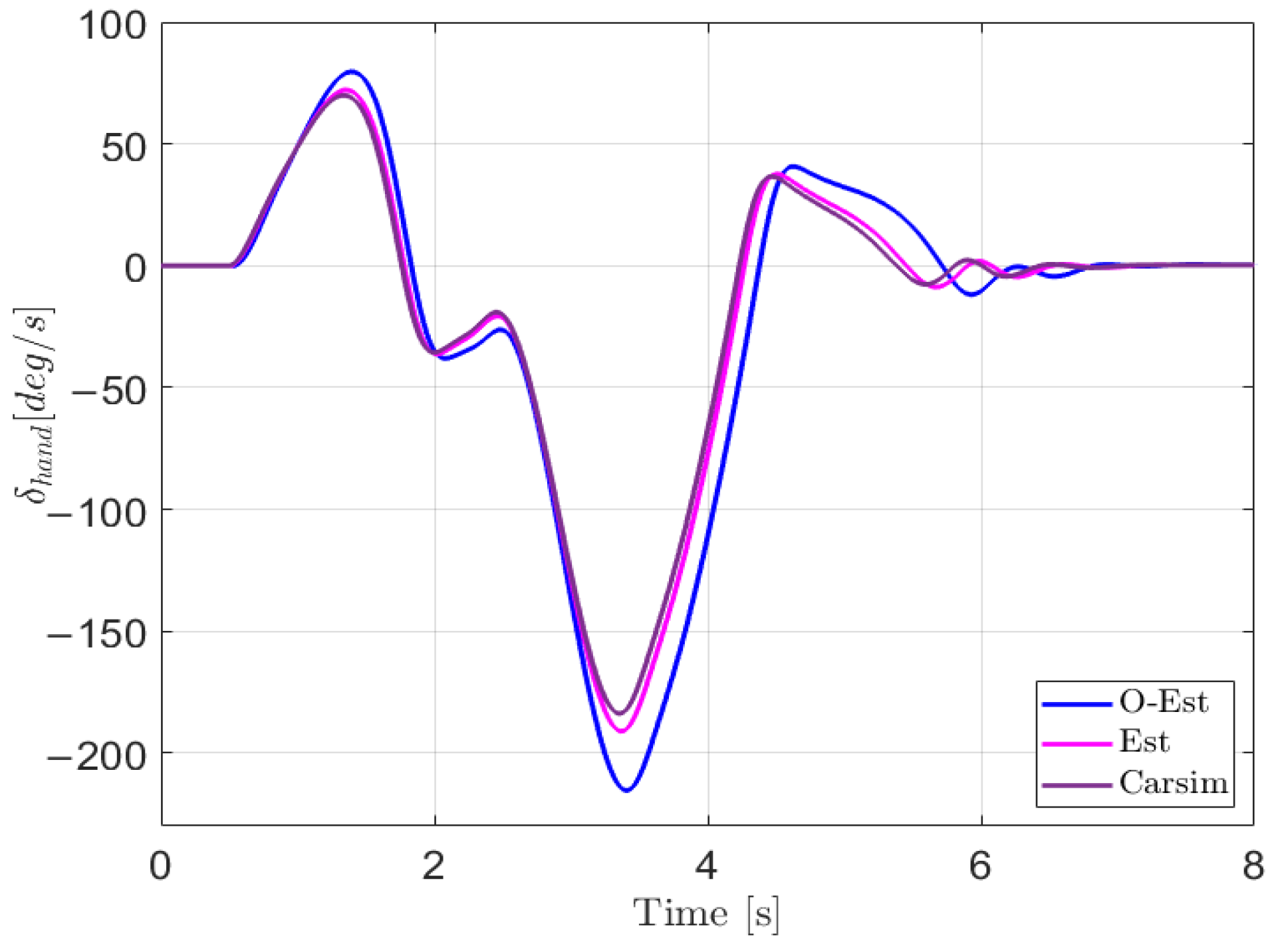
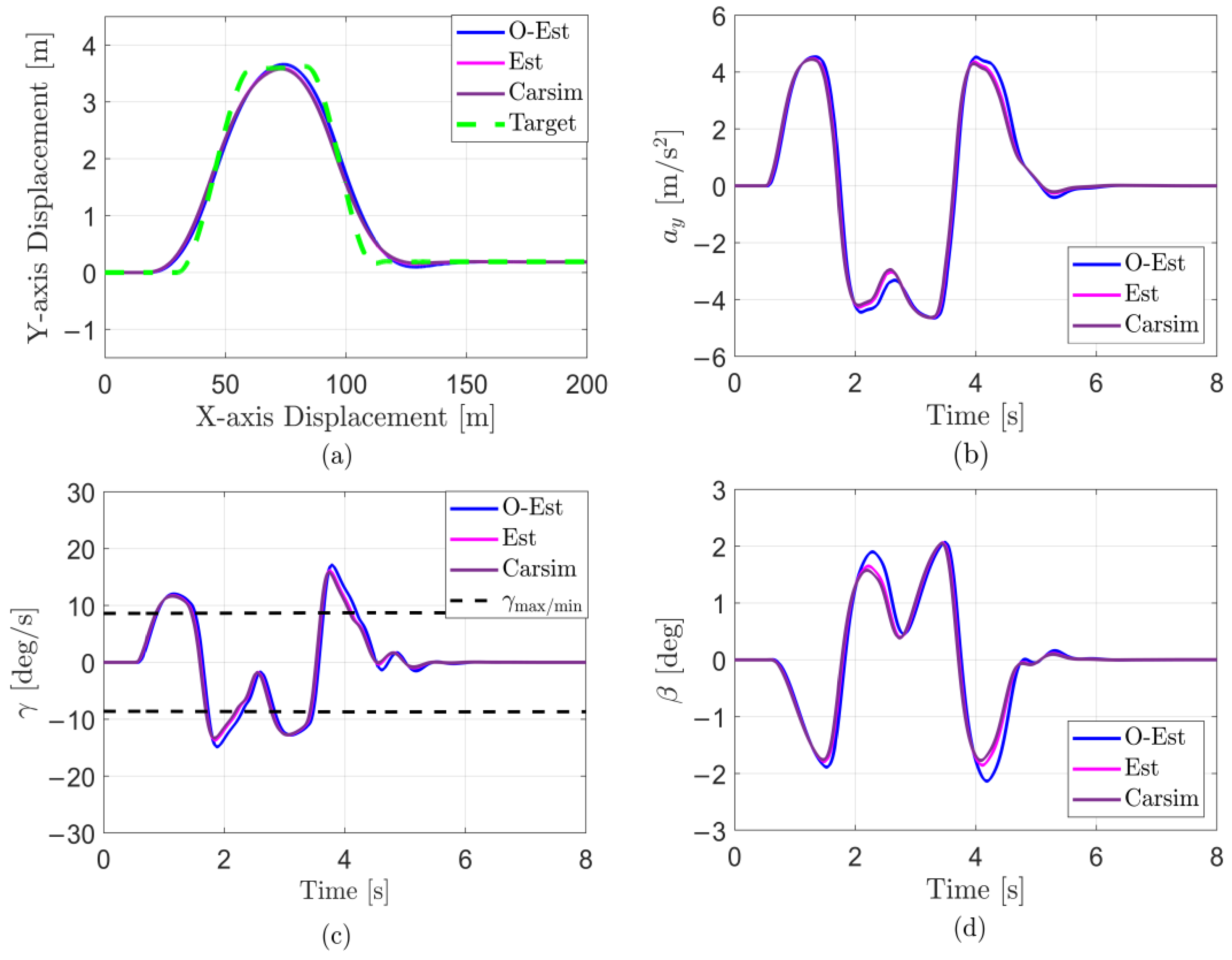
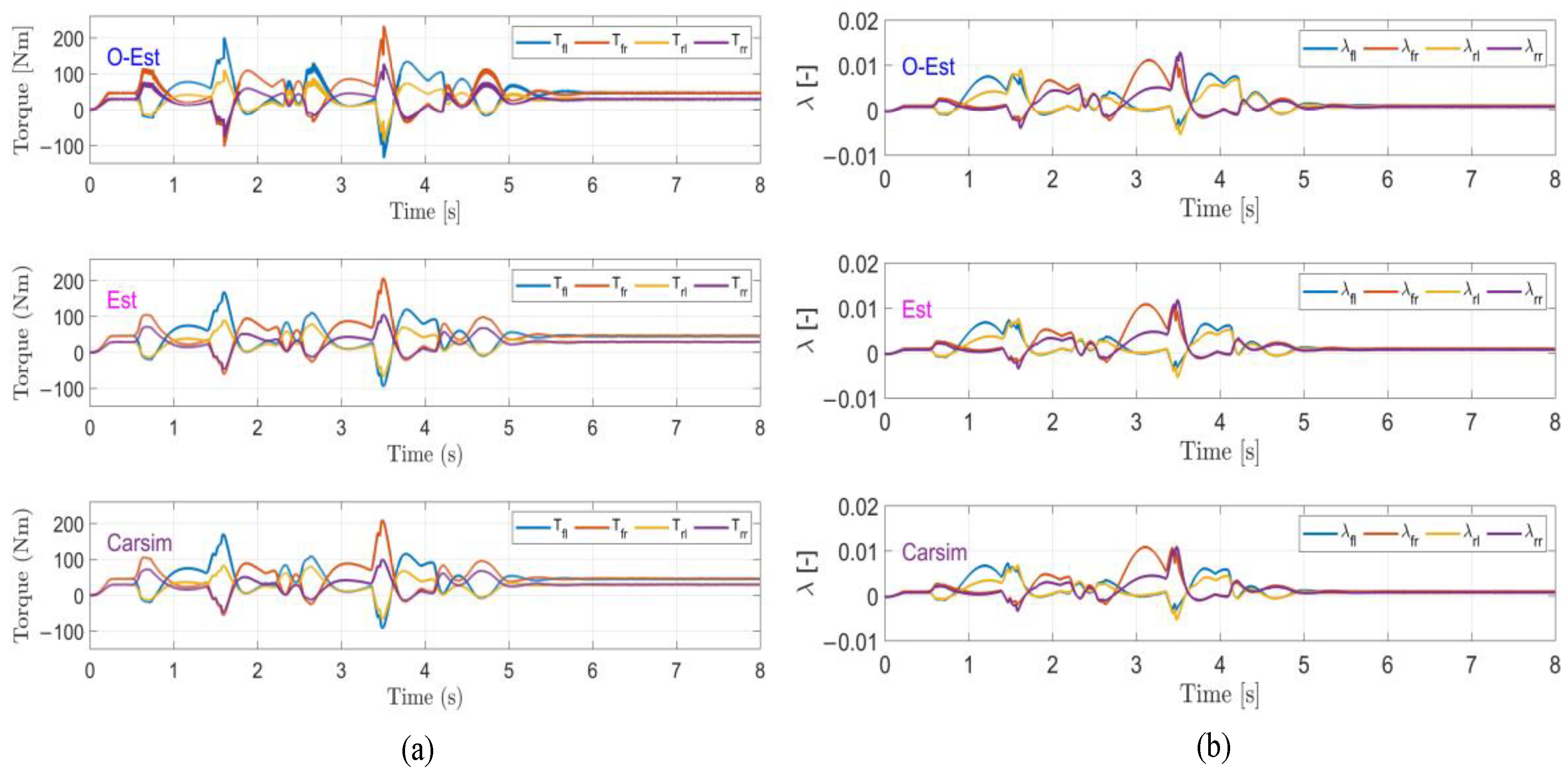
5. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Skrickij, V.; Kojis, P.; Sabanovic, E.; Shyrokau, B.; Ivanov, V. Review of Integrated Chassis Control Techniques for Automated Ground Vehicles. Sensors 2024, 24, 600. [Google Scholar] [CrossRef] [PubMed]
- Ahangarnejad, A.H.; Radmehr, A.; Ahmadian, M. A review of vehicle active safety control methods: From antilock brakes to semiautonomy. J. Vib. Control 2020, 27, 1683–1712. [Google Scholar] [CrossRef]
- Magalhaes Junior, Z.R.; Murilo, A.; Lopes, R.V. Vehicle Stability Upper-Level-Controller Based on Parameterized Model Predictive Control. IEEE Access 2022, 10, 21048–21065. [Google Scholar] [CrossRef]
- Peng, S.-T.; Chen, C.-K.; Sheu, Y.-R.; Chang, Y.-C. Enhancement of Yaw Moment Control for Drivers with Excessive Steering in Emergency Lane Changes. Appl. Sci. 2024, 14, 5984. [Google Scholar] [CrossRef]
- Li, J.-T.; Chen, C.-K.; Ren, H. Time-Optimal Trajectory Planning and Tracking for Autonomous Vehicles. Sensors 2024, 24, 3281. [Google Scholar] [CrossRef] [PubMed]
- Puscul, D.; Lex, C.; Vignati, M.; Shao, L. A Literature Survey on Sideslip Angle Estimation Using Vehicle Dynamics Based Methods. IEEE Access 2024, 12, 70263–70277. [Google Scholar] [CrossRef]
- Ao, D.; Wong, P.K.; Huang, W. Model predictive control allocation based on adaptive sliding mode control strategy for enhancing the lateral stability of four-wheel-drive electric vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 238, 1514–1534. [Google Scholar] [CrossRef]
- Stano, P.; Montanaro, U.; Tavernini, D.; Tufo, M.; Fiengo, G.; Novella, L.; Sorniotti, A. Model predictive path tracking control for automated road vehicles: A review. Annu. Rev. Control 2023, 55, 194–236. [Google Scholar] [CrossRef]
- Bessafa, H.; Delattre, C.; Belkhatir, Z.; Khemmar, R.; Zemouche, A. A New Discrete-Time Interval Estimator for Vehicle Side-Slip Angle Estimation. IFAC-Pap. 2022, 55, 85–90. [Google Scholar] [CrossRef]
- Bascetta, L.; Ferretti, G. LFT-Based Identification of Lateral Vehicle Dynamics. IEEE Trans. Veh. Technol. 2022, 71, 1349–1362. [Google Scholar] [CrossRef]
- Xu, G.; Qiao, Y.; Chen, X.; Peng, T.; Zhao, C. Enhanced Vehicle Sideslip Angle Estimation through Multi-Source Information Fusion. In Proceedings of the 2023 7th CAA International Conference on Vehicular Control and Intelligence (CVCI), Changsha, China, 27–29 October 2023; pp. 1–6. [Google Scholar]
- Napolitano Dell’Annunziata, G.; Ruffini, M.; Stefanelli, R.; Adiletta, G.; Fichera, G.; Timpone, F. Four-Wheeled Vehicle Sideslip Angle Estimation: A Machine Learning-Based Technique for Real-Time Virtual Sensor Development. Appl. Sci. 2024, 14, 1036. [Google Scholar] [CrossRef]
- Ziaukas, Z.; Busch, A.; Wielitzka, M. Estimation of Vehicle Side-Slip Angle at Varying Road Friction Coefficients Using a Recurrent Artificial Neural Network. In Proceedings of the 2021 IEEE Conference on Control Technology and Applications (CCTA), San Diego, CA, USA, 9–11 August 2021; pp. 986–991. [Google Scholar]
- Bertipaglia, A.; Alirezaei, M.; Happee, R.; Shyrokau, B. An Unscented Kalman Filter-Informed Neural Network for Vehicle Sideslip Angle Estimation. IEEE Trans. Veh. Technol. 2024, 73, 12731–12746. [Google Scholar] [CrossRef]
- Dong, X.; Tao, S.; Zhang, H. Robust Lateral and Longitudinal Tire Force Estimation Based on PMI Observer for Intelligent Vehicle. In Proceedings of the 2022 IEEE 5th International Conference on Industrial Cyber-Physical Systems (ICPS), Coventry, UK, 24–26 May 2022; pp. 1–6. [Google Scholar]
- Xu, N.; Askari, H.; Huang, Y.; Zhou, J.; Khajepour, A. Tire Force Estimation in Intelligent Tires Using Machine Learning. IEEE Trans. Intell. Transp. Syst. 2022, 23, 3565–3574. [Google Scholar] [CrossRef]
- Meng, D.; Jiang, Y.; Chu, H.; Tian, M.; Gao, B. Data-Driven Tire Forces Estimation for Autonomous Vehicle Applications. In Proceedings of the 2024 43rd Chinese Control Conference (CCC), Kunming, China, 28–31 July 2024; pp. 6421–6426. [Google Scholar]
- Cheng, S.; Li, L.; Yan, B.; Liu, C.; Wang, X.; Fang, J. Simultaneous estimation of tire side-slip angle and lateral tire force for vehicle lateral stability control. Mech. Syst. Signal Process. 2019, 132, 168–182. [Google Scholar] [CrossRef]
- Mosconi, L.; Farroni, F.; Sakhnevych, A.; Timpone, F.; Gerbino, F.S. Adaptive vehicle dynamics state estimator for onboard automotive applications and performance analysis. Veh. Syst. Dyn. 2022, 61, 3244–3268. [Google Scholar] [CrossRef]
- Baffet, G.; Charara, A.; Lechner, D.; Thomas, D. Experimental evaluation of tire-road forces and sideslip angle observers. In Proceedings of the 2007 European Control Conference (ECC), Kos, Greece, 2–5 July 2007; pp. 625–631. [Google Scholar]
- Doumiati, M.; Charara, A.; Victorino, A.; Lechner, D. Vehicle Dynamics Estimation Using Kalman Filtering: Experimental Validation; Wiley-ISTE: London, UK, 2012; p. 304. [Google Scholar]
- Ren, H.; Li, Y.; Wang, Y.; Chen, C.-K.; Yang, L.; Zhao, Y. Learning-based model predictive control for safe path planning and control. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024, 09544070241265763. [Google Scholar] [CrossRef]
- Stocco, D.; Biral, F.; Bertolazzi, E. A physical tire model for real-time simulations. Math. Comput. Simul. 2024, 223, 654–676. [Google Scholar] [CrossRef]
- Ma, Y.-J.; Chen, C.-K.; Zhang, X.-D. On the Lateral Stability System of Four-Wheel Driven Electric Vehicles Based on Phase Plane Method. Electronics 2024, 13, 4569. [Google Scholar] [CrossRef]
- Chien, P.-C.; Chen, C.-K. Integrated Chassis Control and Control Allocation for All Wheel Drive Electric Cars with Rear Wheel Steering. Electronics 2021, 10, 2885. [Google Scholar] [CrossRef]
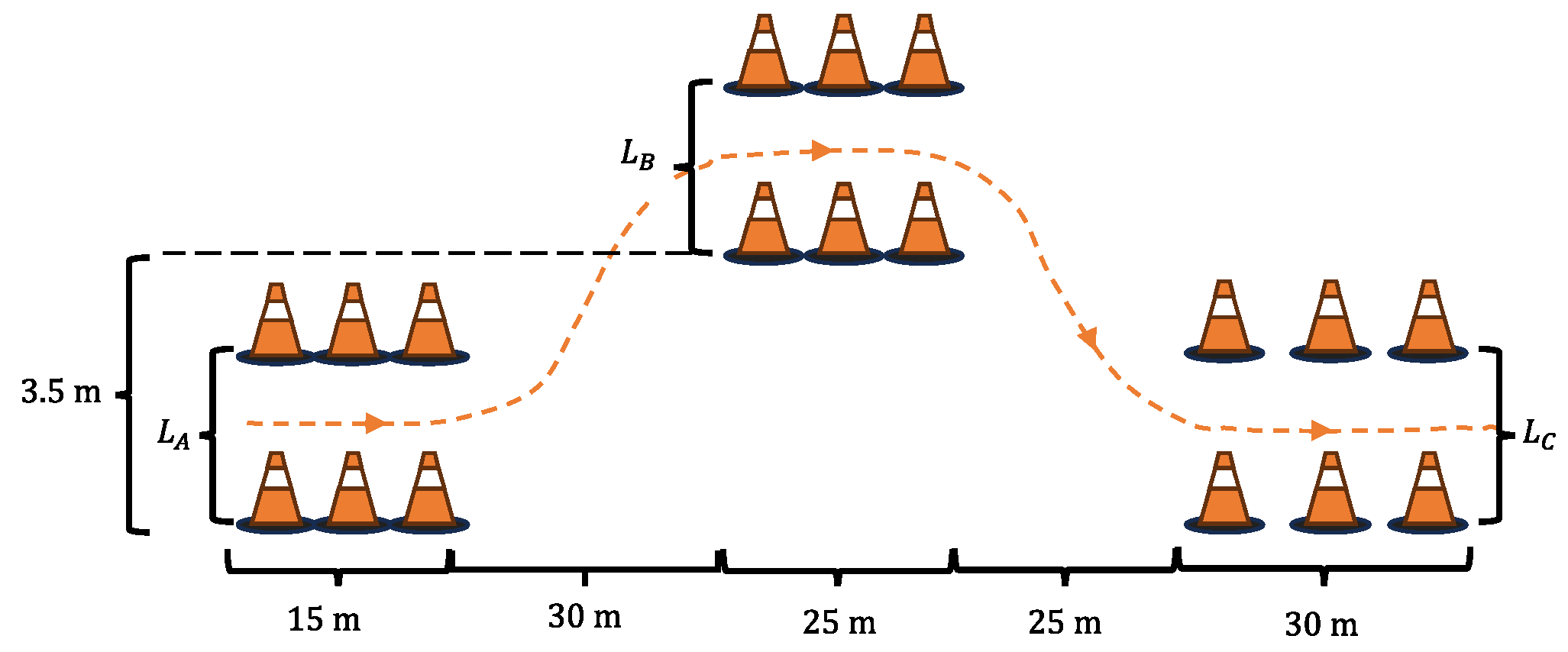
- ISO 3888-1:2018; Passenger Cars—Test Track for a Severe Lane-Change Manoeuvre—Part 1: Double Lane-Change. International Organization for Standardization: Geneva, Switzerland, 2018.


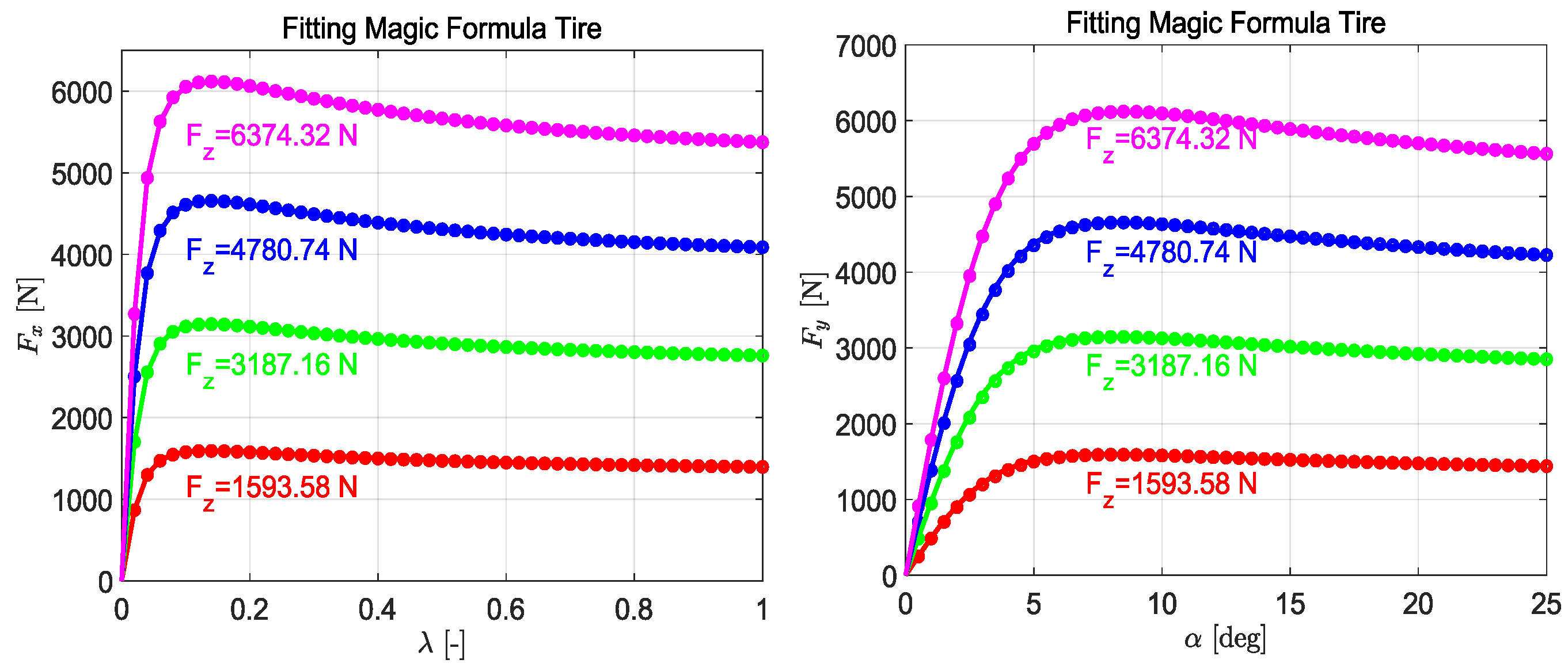



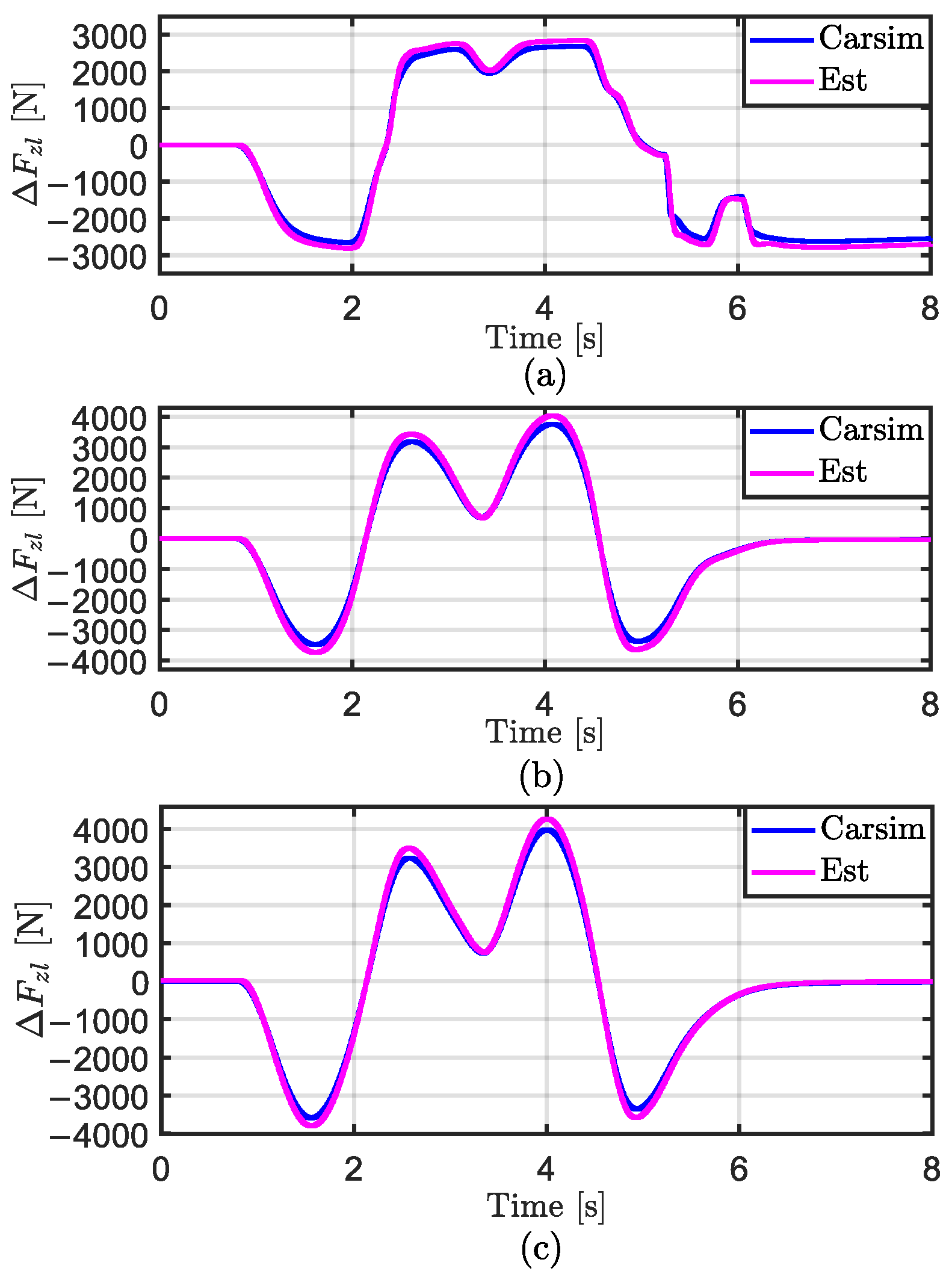

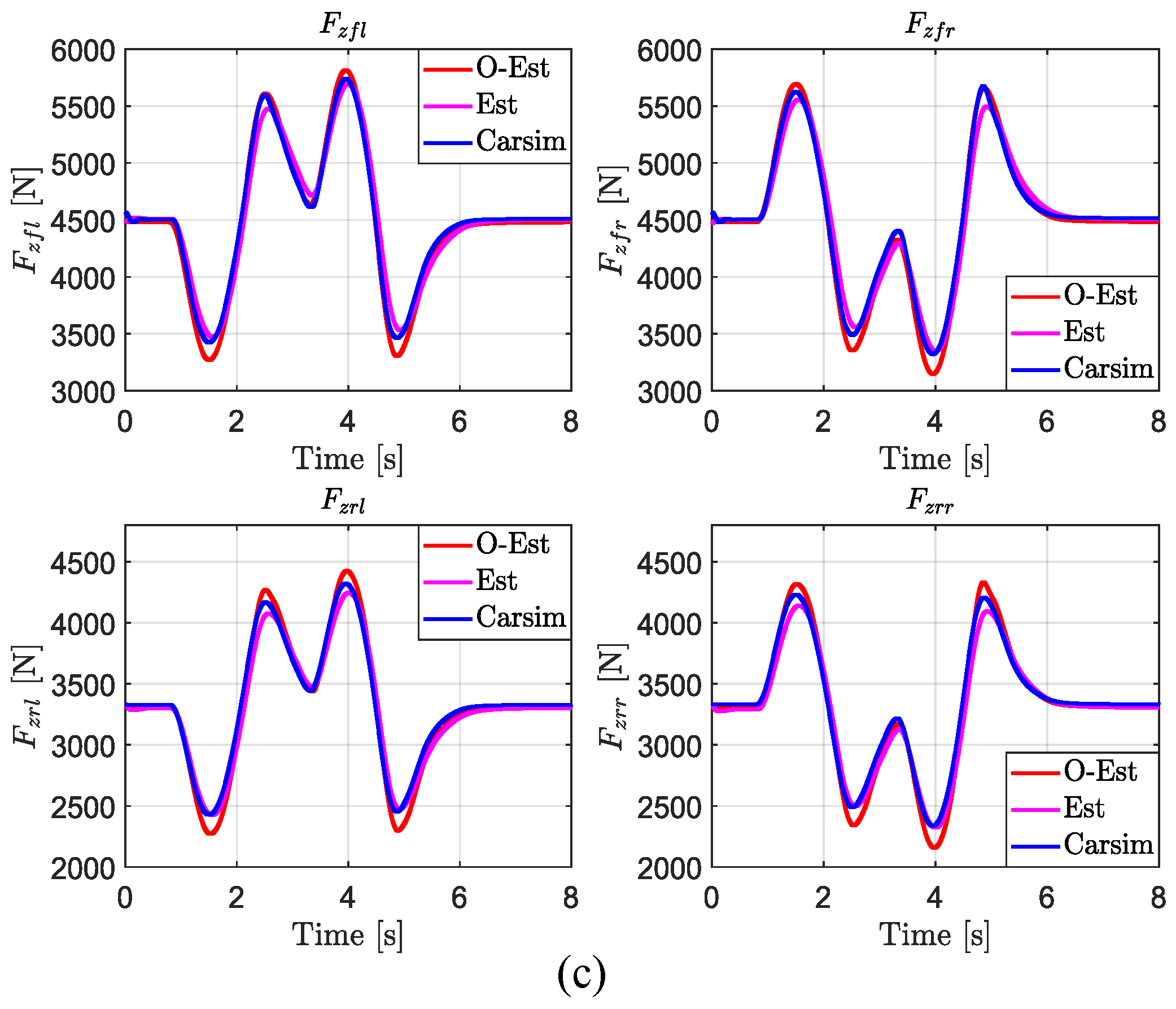


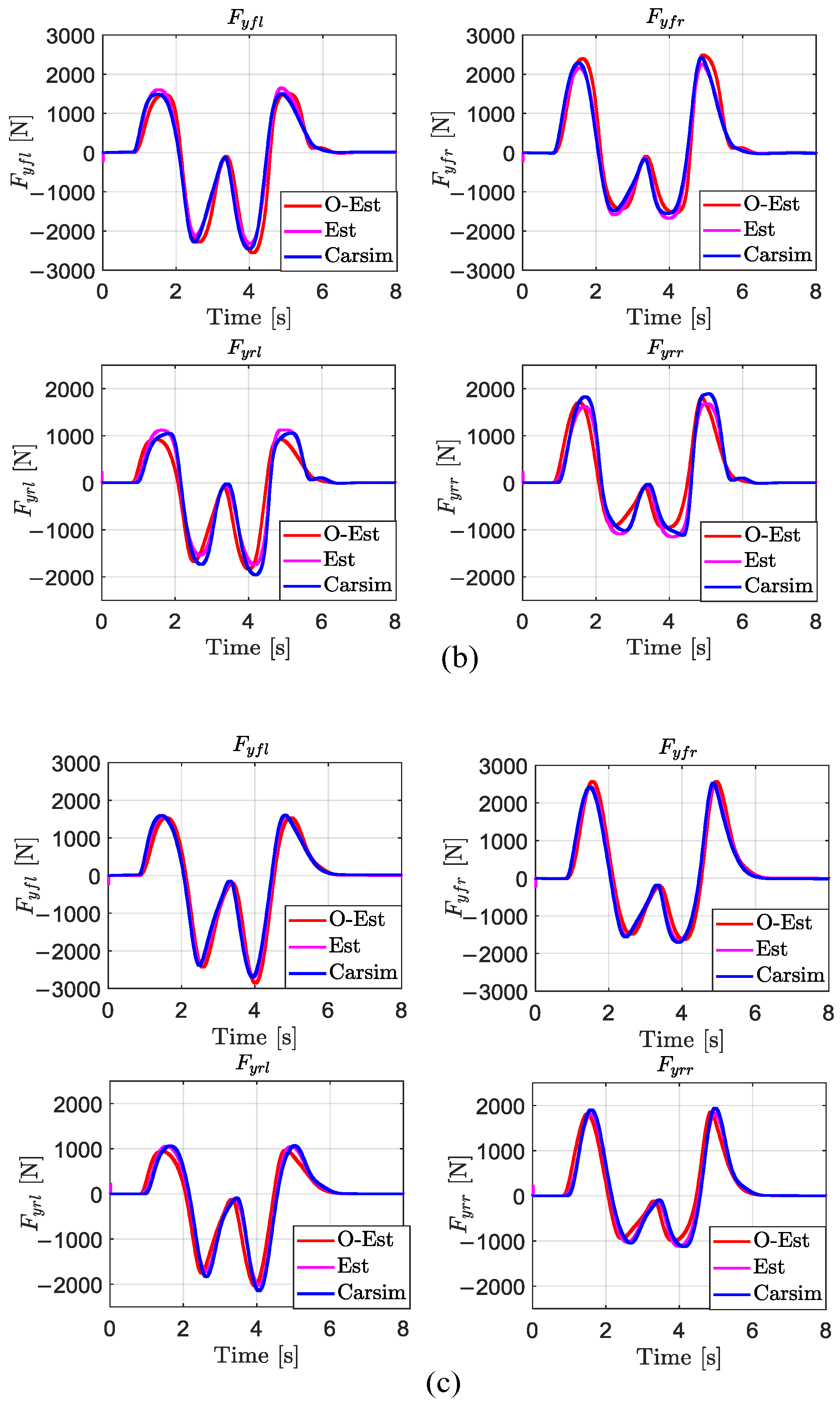






| 1017 | 969.3 | 0.55 | 1.4 | ||||||
| 1017 | 9730 | 0.3505 | 0.09514 | −0.2752 | 1.413 |
| Parameter | Value |
|---|---|
| Total vehicle weight (kg) | 1592.00 |
| Sprung mass (kg) | 1230.00 |
| Vehicle track width (mm) | 1675.00 |
| Wheelbase (mm) | 2600.00 |
| Distance from the CG to the front axle (mm) | 1065.00 |
| Distance from the CG to the rear axle (mm) | 1535.00 |
| Height of the CG above the ground (mm) | 540.00 |
| Yaw moment of inertia | 1520.00 |
| MAE (N) | ME (N) | RMSE (N) | |
|---|---|---|---|
| 0.3 | 124.535 | 534.431 | 145.243 |
| 0.5 | 106.282 | 297.750 | 150.768 |
| 0.85 | 92.349 | 285.897 | 126.757 |
| MAE (N) | ME (N) | RMSE (N) | Total Time (s) | ||
|---|---|---|---|---|---|
| 0.3 | O-Est | 163.28 | 372.66 | 184.70 | 0.042 |
| Est | 66.40 | 206.51 | 87.69 | 0.095 | |
| 0.5 | O-Est | 72.27 | 324.86 | 102.88 | 0.044 |
| Est | 49.15 | 166.73 | 61.68 | 0.096 | |
| 0.85 | O-Est | 56.69 | 280.15 | 101.41 | 0.042 |
| Est | 36.98 | 112.91 | 50.23 | 0.096 |
| MAE (N) | ME (N) | RMSE (N) | Total Time (s) | ||
|---|---|---|---|---|---|
| 0.3 | O-Est | 143.03 | 1282.69 | 274.26 | 0.069 |
| Est | 70.56 | 512.96 | 109.94 | 0.188 | |
| 0.5 | O-Est | 163.31 | 1019.84 | 262.42 | 0.073 |
| Est | 62.17 | 349.07 | 95.92 | 0.187 | |
| 0.85 | O-Est | 172.31 | 784.44 | 251.82 | 0.068 |
| Est | 57.06 | 199.02 | 78.60 | 0.189 |
| MAE (N) | ME (N) | RMSE (N) | Total Time (s) | ||
|---|---|---|---|---|---|
| 0.3 | O-est | 132.317 | 857.882 | 214.054 | 0.135 |
| E-est | 70.564 | 512.962 | 109.938 | 0.188 | |
| 0.5 | O-est | 88.625 | 387.789 | 130.725 | 0.137 |
| E-est | 62.170 | 349.067 | 95.924 | 0.187 | |
| 0.85 | O-est | 60.040 | 223.918 | 82.959 | 0.135 |
| E-est | 57.061 | 199.022 | 78.601 | 0.189 |
| MAE (deg) | ME (deg) | RMSE (deg) | Total Time (s) | |
|---|---|---|---|---|
| 0.3 | 0.28 | 0.188 | ||
| 0.5 | 0.06 | 0.187 | ||
| 0.85 | 0.05 | 0.189 |
| Total Time (s) | ||||||
|---|---|---|---|---|---|---|
| O-Est | 2.07 | 11.64 | 170.93 | 215.21 | 7.554 | |
| Est | 1.98 | 11.28 | 149.68 | 190.91 | 7.726 | |
| Carsim | 1.96 | 11.22 | 145.25 | 183.61 | 7.446 |
| Total Time (s) | ||||||
|---|---|---|---|---|---|---|
| O-Est | 2.13 | 17.09 | 233.34 | 61.83 | 7.554 | |
| Est | 2.06 | 16.14 | 206.63 | 57.9 | 7.726 | |
| Carsim | 2.05 | 15.81 | 203.56 | 56.77 | 7.443 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.-J.; Chen, C.-K.; Ren, H. Research on Lateral Stability Control of Four-Wheel Independent Drive Electric Vehicle Based on State Estimation. Sensors 2025, 25, 474. https://doi.org/10.3390/s25020474
Ma Y-J, Chen C-K, Ren H. Research on Lateral Stability Control of Four-Wheel Independent Drive Electric Vehicle Based on State Estimation. Sensors. 2025; 25(2):474. https://doi.org/10.3390/s25020474
Chicago/Turabian StyleMa, Yu-Jie, Chih-Keng Chen, and Hongbin Ren. 2025. "Research on Lateral Stability Control of Four-Wheel Independent Drive Electric Vehicle Based on State Estimation" Sensors 25, no. 2: 474. https://doi.org/10.3390/s25020474
APA StyleMa, Y.-J., Chen, C.-K., & Ren, H. (2025). Research on Lateral Stability Control of Four-Wheel Independent Drive Electric Vehicle Based on State Estimation. Sensors, 25(2), 474. https://doi.org/10.3390/s25020474






