Superimposed CSI Feedback Assisted by Inactive Sensing Information
Abstract
1. Introduction
- We introduce the inactive sensing information into the superimposed CSI feedback, opening up a new mode of sensing information-assisted superimposed CSI feedback. Thus, the forgotten sensing information is utilized in the superimposed CSI feedback. To the best of our knowledge, this work presents the first leverage of inactive sensing information to assist superimposed CSI feedback. Moreover, this mode can be easily extended to other inactive sensing information-assisted communication.
- We derive prior information for interference suppression in superimposed CSI feedback by leveraging the inactive sensing information. In the paper, we take the UE and BS embedded global navigation satellite system (GNSS) chips as an example to derive prior information in both delay and Doppler dimensions. As a result, a new modal data different from communication signals can be obtained for CSI feedback, forming additional prior information for SIS.
- We propose a sensing information-assisted superimposed CSI feedback method. Based on the introduction of sensing information and the derivation of prior information, the CSI recovery in superimposed CSI feedback can be further denoised in the delay–Doppler (DD) domain. In this method, a denoising process is developed by leveraging sensing prior information. This only requires simple processing and slightly increased computational complexity, while achieving a significant performance improvement in the SIS.
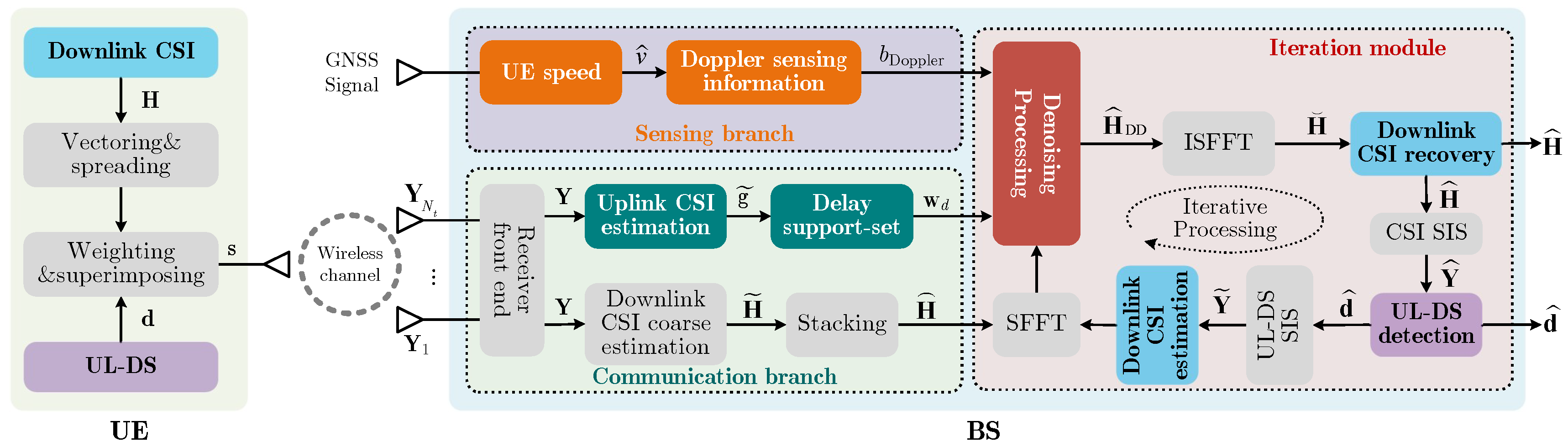
2. CSI Feedback System
3. Sensing Information-Assisted CSI Feedback
3.1. Doppler Shift Prior Using Speed Sensing
3.2. Path Delay Prior from Uplink CSI
| Algorithm 1 Doppler shift and path delay prior derivations. |
|
3.3. Downlink CSI Recovery and UL-DS Detection
| Algorithm 2 Downlink CSI and UL-DS recoveries. |
|
4. Computational Complexity Analysis
5. Experiment Results
5.1. Parameters Setting
5.2. Effectiveness Analysis
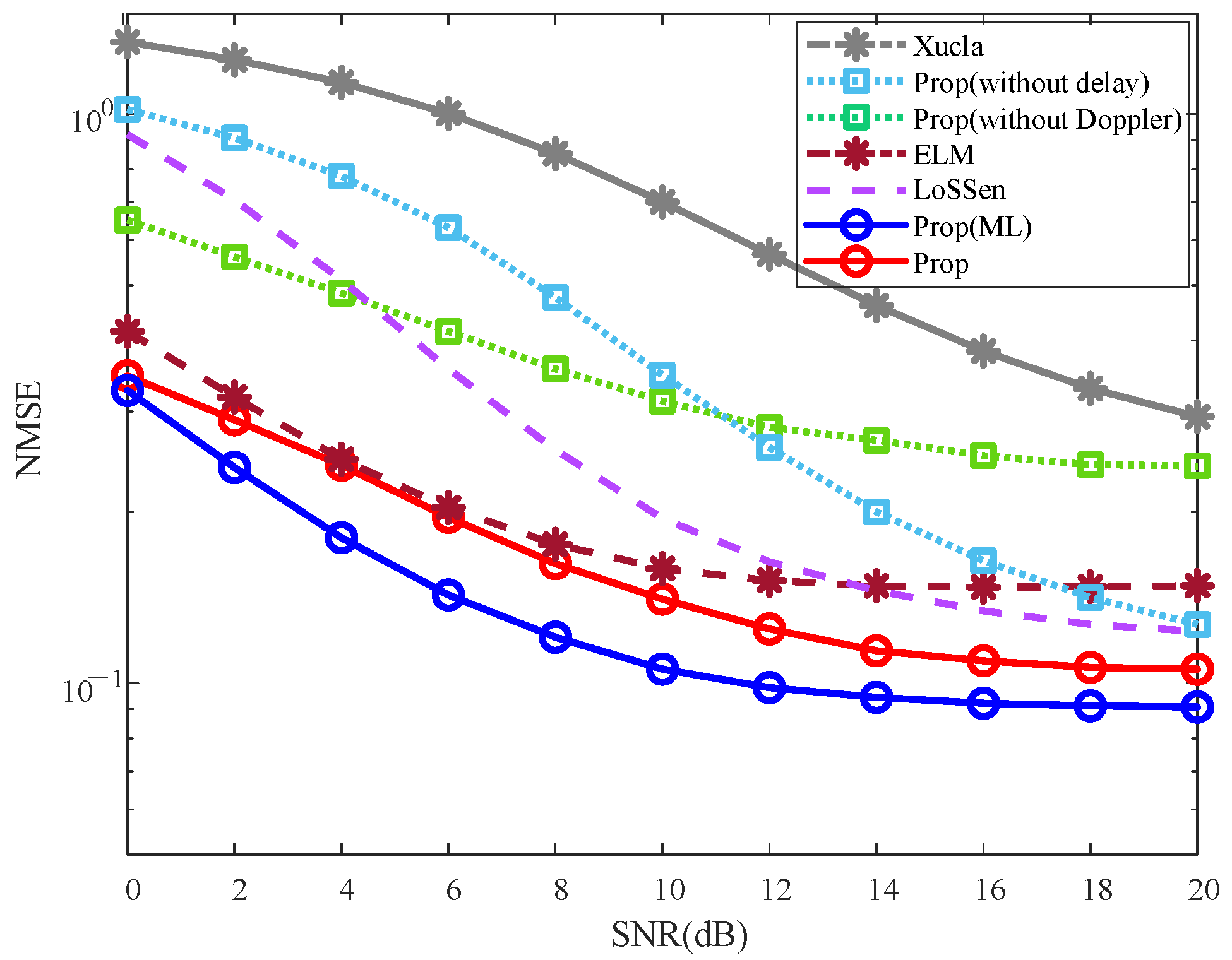
5.2.1. NMSE Effectiveness Analysis
5.2.2. BER Effectiveness Analysis
5.3. Robustness Analysis
5.3.1. Robustness Against
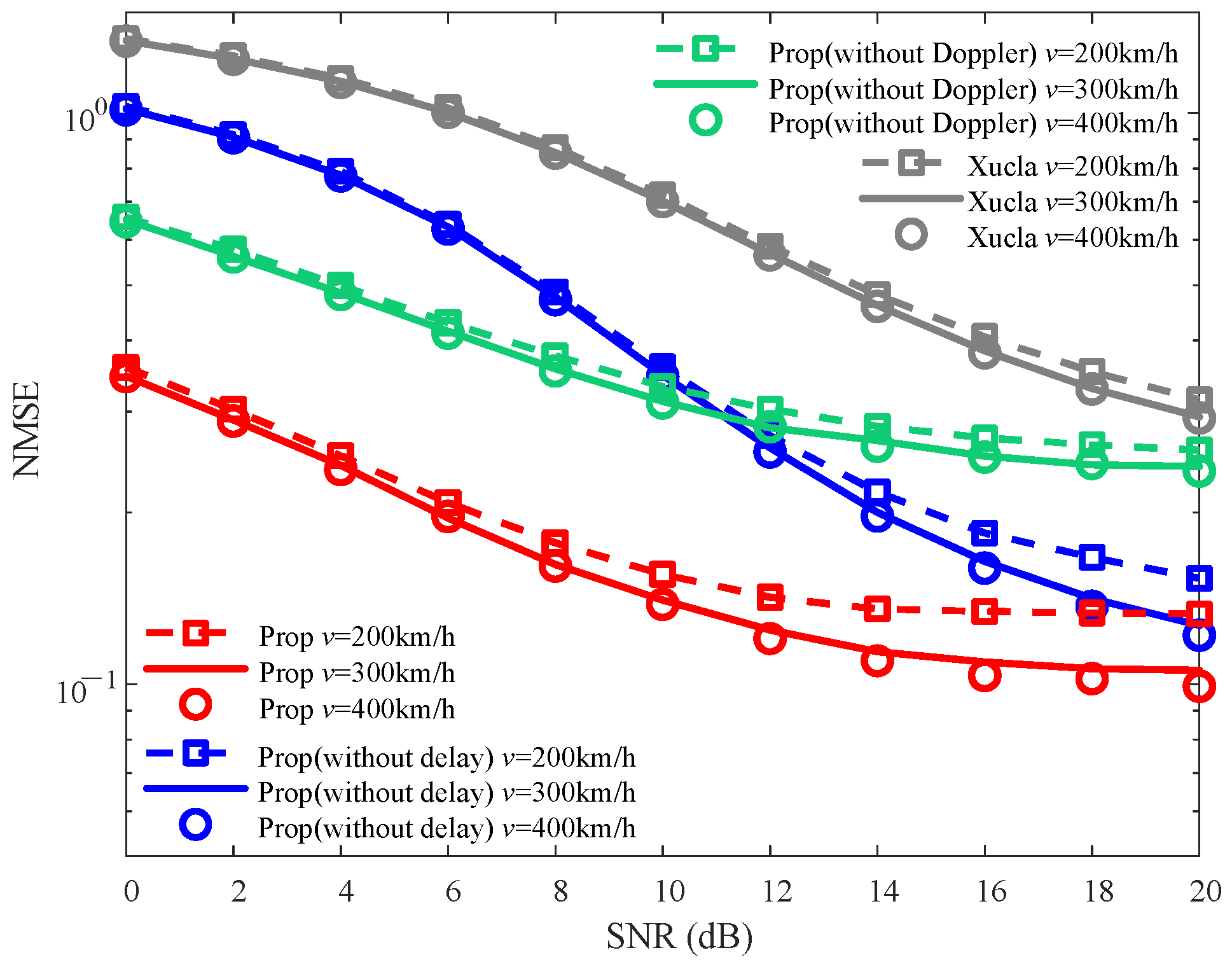
5.3.2. Robustness Against v
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fu, S.; Su, Z.; Jia, Y.; Zhou, H.; Jin, Y.; Ren, J.; Wu, B.; Huq, K. Interference Cooperation via Distributed Game in 5G Networks. IEEE Internet Things J. 2019, 6, 311–320. [Google Scholar] [CrossRef]
- Carrera, D.; Zabala-Blanco, D.; Vargas-Rosales, C.; Azurdia-Meza, C. Extreme learning machine-based receiver for multi-user massive MIMO systems. IEEE Commun. Lett. 2021, 25, 484–488. [Google Scholar] [CrossRef]
- Cui, Y.; Guo, J.; Wen, C.; Jin, S. Communication-Efficient Personalized Federated Edge Learning for Massive MIMO CSI Feedback. IEEE Trans. Wirel. Commun. 2024, 23, 7362–7375. [Google Scholar] [CrossRef]
- Guo, J.; Zuo, Y.; Wen, C.; Jin, S. User-Centric Online Gossip Training for Autoencoder-Based CSI Feedback. IEEE J. Sel. Top. Signal Process. 2022, 16, 559–572. [Google Scholar] [CrossRef]
- Wen, C.; Shih, W.; Jin, S. Deep Learning for Massive MIMO CSI Feedback. IEEE Wirel. Commun. Lett. 2018, 7, 748–751. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, Y.; Gui, G.; Zhao, H.; Gacanin, H.; Sari, H. Interacting Federated and Transfer Learning-Aided CSI Prediction for Intelligent Cellular Networks. IEEE Trans. Veh. Technol. 2023, 72, 15776–15787. [Google Scholar] [CrossRef]
- Song, G.; Wang, Z.; Du, Y.; Xiao, L.; Jiang, T. Enabling Affordable Implicit Channel Feedback for Internet of Things. IEEE Internet Things J. 2022, 9, 16606–16618. [Google Scholar] [CrossRef]
- Xu, D.; Huang, Y.; Yang, L. Feedback of Downlink Channel State Information Based on Superimposed Coding. IEEE Commun. Lett. 2007, 11, 240–242. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, H.; Fu, Y.; Yang, G.; Ma, S.; Hou, F.; Tsiftsis, T. Zero-Forcing-Based Downlink Virtual MIMO–NOMA Communications in IoT Networks. IEEE Internet Things J. 2020, 7, 2716–2737. [Google Scholar] [CrossRef]
- Cao, J.; Lian, L.; Mao, Y.; Clerckx, B. Adaptive CSI Feedback with Hidden Semantic Information Transfer. In Proceedings of the 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Qing, C.; Cai, B.; Yang, Q.; Wang, J.; Huang, C. Deep Learning for CSI Feedback Based on Superimposed Coding. IEEE Access 2019, 7, 93723–93733. [Google Scholar] [CrossRef]
- Qing, C.; Cai, B.; Yang, Q.; Wang, J.; Huang, C. ELM-Based Superimposed CSI Feedback for FDD Massive MIMO System. IEEE Access 2020, 8, 53408–53418. [Google Scholar] [CrossRef]
- Guo, J.; Wen, C.; Jin, S. Eliminating CSI Feedback Overhead via Deep Learning-Based Data Hiding. IEEE J. Sel. Areas Commun. 2022, 40, 2267–2281. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, R. Deep data hiding-based channel state information feedback within audio signals. Electron. Lett. 2023, 59, e12854. [Google Scholar] [CrossRef]
- He, Z.; Zhang, X.; Wang, Y.; Lin, Y.; Gui, G.; Gacanin, H.; Sari, H.; Adachi, F. A Robust CSI-Based Wi-Fi Passive Sensing Method Using Attention Mechanism Deep Learning. IEEE Internet Things J. 2023, 10, 17490–17499. [Google Scholar] [CrossRef]
- Zaidi, S.; Manalastas, M.; Farooq, H.; Imran, A. Mobility Management in Emerging Ultra-Dense Cellular Networks: A Survey, Outlook, and Future Research Directions. IEEE Access 2020, 8, 183505–183533. [Google Scholar] [CrossRef]
- Qin, Z.; Gao, F.; Lin, B.; Tao, X.; Liu, G.; Pan, C. A Generalized Semantic Communication System: From Sources to Channels. IEEE Wirel. Commun. 2023, 30, 18–26. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, M.; Gao, Y.; Feng, Z. MIMO Radar Aided mmWave Time-Varying Channel Estimation in MU-MIMO V2X Communications. IEEE Trans. Wirel. Commun. 2021, 20, 7581–7594. [Google Scholar] [CrossRef]
- Liu, A.; Huang, Z.; Li, M.; Wan, Y.; Li, W.; Han, T.; Liu, C.; Du, R.; Tan, D.; Lu, J.; et al. A Survey on Fundamental Limits of Integrated Sensing and Communication. IEEE Commun. Surv. Tutor. 2022, 24, 994–1034. [Google Scholar] [CrossRef]
- Ali, A.; Gonzalez-Prelcic, N.; Heath, R.; Ghosh, A. Leveraging Sensing at the Infrastructure for mmWave Communication. IEEE Commun. Mag. 2020, 58, 84–89. [Google Scholar] [CrossRef]
- Liu, F.; Yuan, W.; Masouros, C.; Yuan, J. Radar-Assisted Predictive Beamforming for Vehicular Links: Communication Served by Sensing. IEEE Trans. Wirel. Commun. 2020, 19, 7704–7719. [Google Scholar] [CrossRef]
- Qing, C.; Liu, Z.; Hu, W.; Zhang, Y.; Cai, X.; Du, P. LoS Sensing-Based Channel Estimation in UAV-Assisted OFDM Systems. IEEE Wirel. Commun. Lett. 2024, 13, 1320–1324. [Google Scholar] [CrossRef]
- Varshney, N.; Berweger, S.; Chuang, J.; Blandino, S.; Wang, J.; Pazare, N.; Gentile, C.; Golmie, N. Adaptive Channel-State-Information Feedback in Integrated Sensing and Communication Systems. IEEE Internet Things J. 2023, 10, 22469–22486. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Wen, C.; Wang, H.; Gao, F.; Jiang, T.; Jin, S. Deep learning for wireless physical layer: Opportunities and challenges. China Commun. 2017, 14, 92–111. [Google Scholar] [CrossRef]
- Ali, M.; Li, Y.; Jewel, M.; Famoriji, O.; Lin, F. Channel estimation and peak-to-average power ratio analysis of narrowband internet of things uplink systems. Wirel. Commun. Mob. Comput. 2018, 2018, 2570165. [Google Scholar] [CrossRef]
- Shi, Q.; Liu, L.; Zhang, S.; Cui, S. Device-Free Sensing in OFDM Cellular Network. IEEE J. Sel. Areas Commun. 2022, 40, 1838–1853. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, P.; Feng, J.; Zhang, Y.; Mumtaz, S.; Rodriguez, J. Computation Resource Allocation and Task Assignment Optimization in Vehicular Fog Computing: A Contract-Matching Approach. IEEE Trans. Veh. Technol. 2019, 68, 3113–3125. [Google Scholar] [CrossRef]
- Angelis, G.; Baruffa, G.; Cacopardi, S. GNSS/Cellular Hybrid Positioning System for Mobile Users in Urban Scenarios. IEEE Trans. Intell. Transp. Syst. 2013, 14, 313–321. [Google Scholar] [CrossRef]
- Feng, J.; Liu, Z.; Wu, C.; Ji, Y. AVE: Autonomous Vehicular Edge Computing Framework with ACO-Based Scheduling. IEEE Trans. Veh. Technol. 2017, 66, 10660–10675. [Google Scholar] [CrossRef]
- Leeuwen, S. GPS Point Position Calculation. GPS Solut. 2002, 6, 115–117. [Google Scholar] [CrossRef]
- Rappaport, T. Wireless Communications: Principles and Practice; Prentice Hall PTR: Englewood Cliffs, NJ, USA, 1996. [Google Scholar]
- Hong, Y.; Thaj, T.; Viterbo, E. Delay-Doppler Communications: Principles and Applications; Academic Press: London, UK, 2022. [Google Scholar]
- Raviteja, P.; Phan, K.; Hong, Y. Embedded Pilot-Aided Channel Estimation for OTFS in Delay–Doppler Channels. IEEE Trans. Veh. Technol. 2019, 68, 4906–4917. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, L.; Ding, Z. Exploiting Bi-Directional Channel Reciprocity in Deep Learning for Low Rate Massive MIMO CSI Feedback. IEEE Wirel. Commun. Lett. 2019, 8, 889–892. [Google Scholar] [CrossRef]
- Guo, J.; Wen, C.; Jin, S. CAnet: Uplink-Aided Downlink Channel Acquisition in FDD Massive MIMO Using Deep Learning. IEEE Trans. Commun. 2022, 70, 199–214. [Google Scholar] [CrossRef]
- Qing, C.; Yang, Q.; Cai, B.; Pan, B.; Wang, J. Superimposed Coding-Based CSI Feedback Using 1-Bit Compressed Sensing. IEEE Commun. Lett. 2020, 24, 193–197. [Google Scholar] [CrossRef]
- Han, Y.; Liu, Q.; Wen, C.; Jin, S.; Wong, K. FDD Massive MIMO Based on Efficient Downlink Channel Reconstruction. IEEE Trans. Commun. 2019, 67, 4020–4034. [Google Scholar] [CrossRef]
- Srivastava, S.; Singh, R.; Jagannatham, A.; Hanzo, L. Delay-Doppler and Angular Domain 4D-Sparse CSI Estimation in OTFS Aided MIMO Systems. IEEE Trans. Veh. Technol. 2022, 71, 13447–13452. [Google Scholar] [CrossRef]
- Qing, C.; Tang, S.; Cai, X.; Wang, J. Lightweight 1-D CNN-Based Timing Synchronization for OFDM Systems With CIR Uncertainty. IEEE Wirel. Commun. Lett. 2022, 11, 2375–2379. [Google Scholar] [CrossRef]
- Qing, C.; Ye, Q.; Liu, W.; Wang, Z.; Wang, J.; Chen, J. LoS sensing-based superimposed CSI feedback for UAV-assisted mmWave systems. Chin. J. Aeronaut. 2023, 36, 349–360. [Google Scholar] [CrossRef]
- Zohra, S.; Abdelhafid, A.; Yassine, N.I.; Fadela, B. Performance Evaluation of a Broadband MIMO-CP-OFDM Communication System in the context of 5G-and-Beyond-3GPP defined Fading Channels. In Proceedings of the 2022 2nd International Conference on Innovative Research in Applied Science, Engineering and Technology (IRASET), Meknes, Morocco, 3–4 March 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Charrada, A. SVM based on LMMSE for high-speed coded OFDM channel with normal and extended cyclic prefix. Phys. Commun. 2018, 29, 288–295. [Google Scholar] [CrossRef]




| Method | Computational Complexity | Computational Complexity Case | Increased Complexity |
|---|---|---|---|
| Xucla | 824,202,356 | − | |
| ELM | 643,323,158 | − | |
| LoSSen | 840,979,572 | − | |
| Prop(ML) | 643,456,278 | 0.0207% | |
| Prop | 824,601,716 | 0.0485% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Jiang, H.; Wang, Z.; He, L.; Yang, Y.; Ye, M.; Qing, C. Superimposed CSI Feedback Assisted by Inactive Sensing Information. Sensors 2025, 25, 6156. https://doi.org/10.3390/s25196156
Zhang M, Jiang H, Wang Z, He L, Yang Y, Ye M, Qing C. Superimposed CSI Feedback Assisted by Inactive Sensing Information. Sensors. 2025; 25(19):6156. https://doi.org/10.3390/s25196156
Chicago/Turabian StyleZhang, Mintao, Haowen Jiang, Zilong Wang, Linsi He, Yuqiao Yang, Mian Ye, and Chaojin Qing. 2025. "Superimposed CSI Feedback Assisted by Inactive Sensing Information" Sensors 25, no. 19: 6156. https://doi.org/10.3390/s25196156
APA StyleZhang, M., Jiang, H., Wang, Z., He, L., Yang, Y., Ye, M., & Qing, C. (2025). Superimposed CSI Feedback Assisted by Inactive Sensing Information. Sensors, 25(19), 6156. https://doi.org/10.3390/s25196156






