Numerical and Experimental Study of Mode Coupling Due to Localised Few-Mode Fibre Bragg Gratings and a Spatial Mode Multiplexer
Abstract
1. Introduction
2. Achieving FBG Spectral Control
2.1. Proposed Setup
2.2. Localised FBG Realisation
2.3. System Simulation
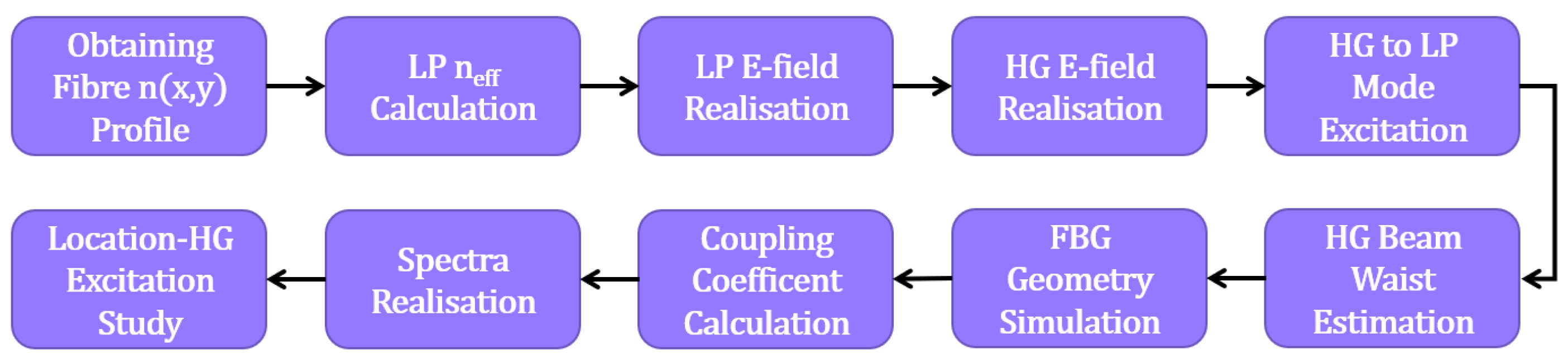
3. Numerical Study Theory
3.1. Output Fibre Specifications and Modelling
3.2. Linearly Polarised Fibre Modes
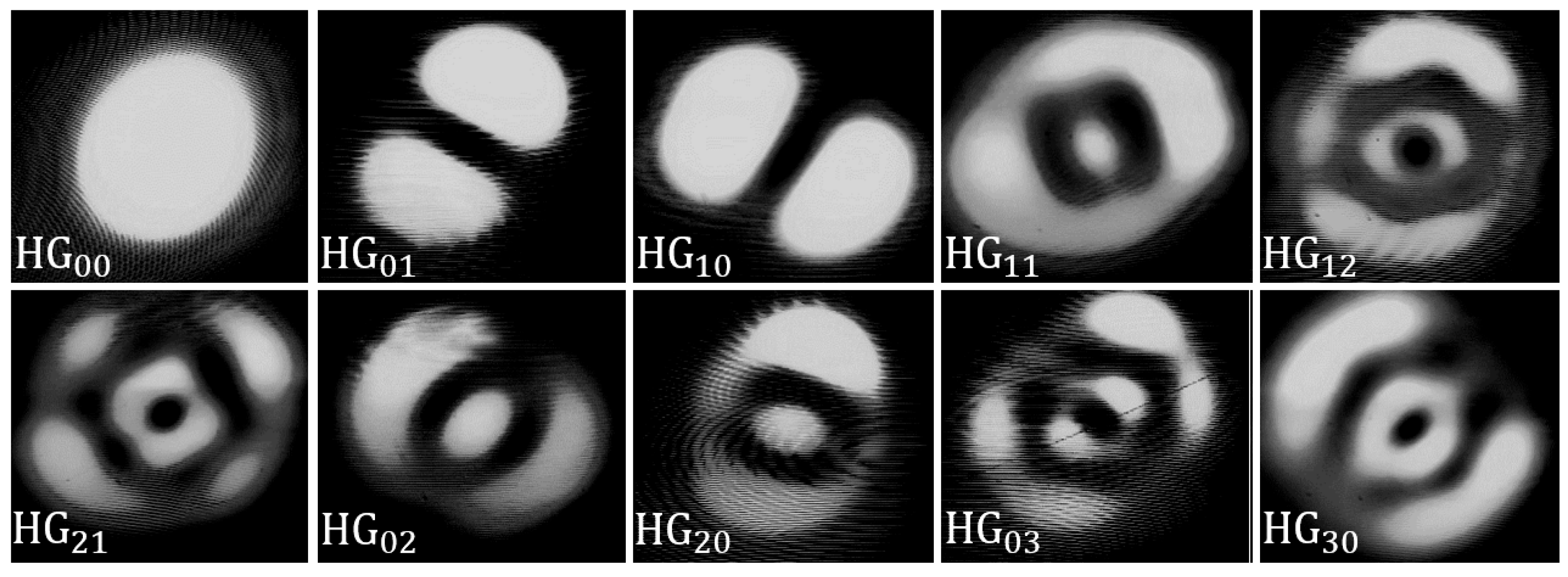
3.3. MUX Hermitian Gauss Modes
3.4. HG Model Experimental Verification
3.5. Ince–Gauss Approximation
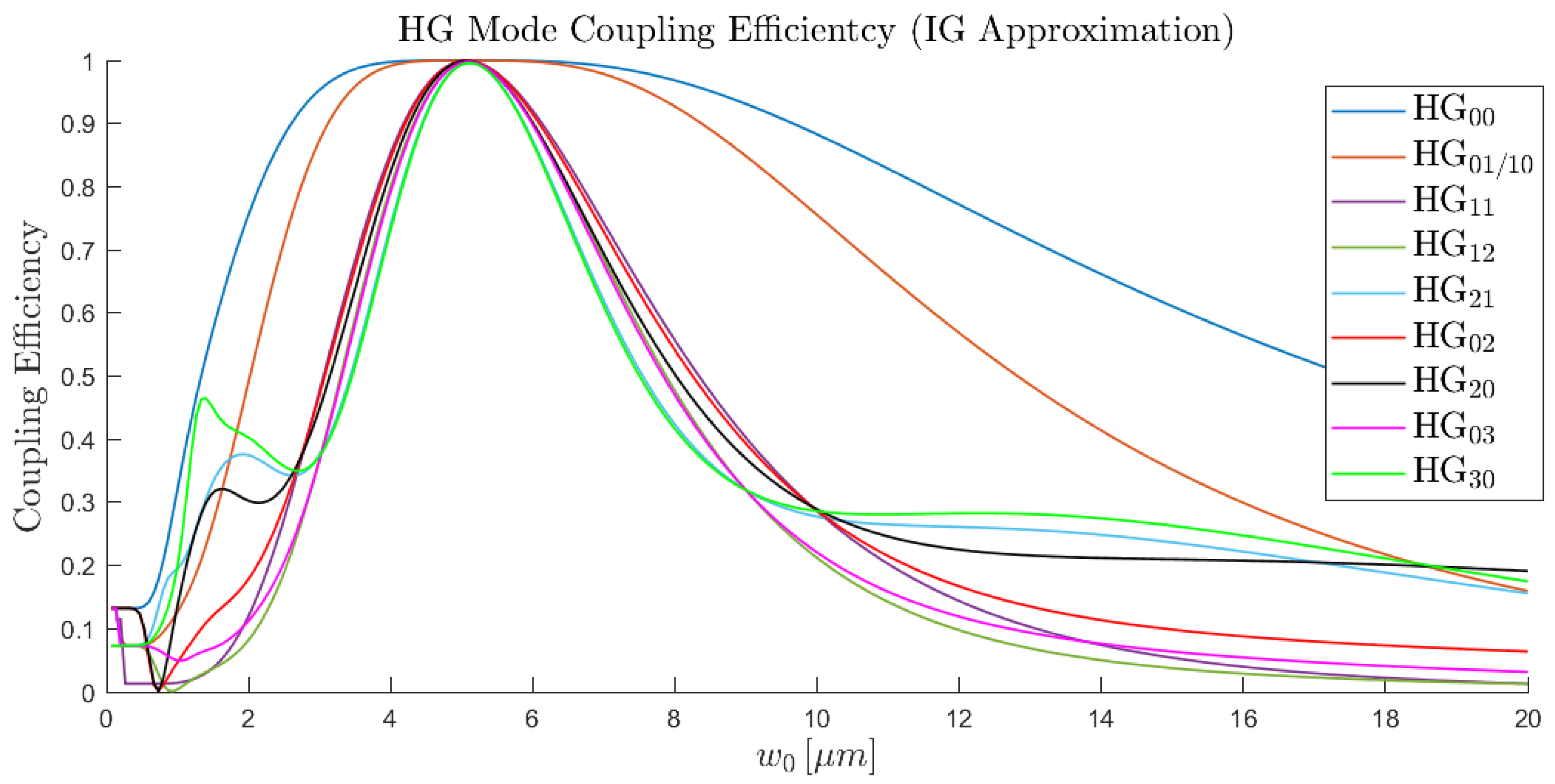
3.6. Free-Space to Fibre-Mode Coupling
3.7. Beam Waist Estimation
4. Localised FBG Modelling
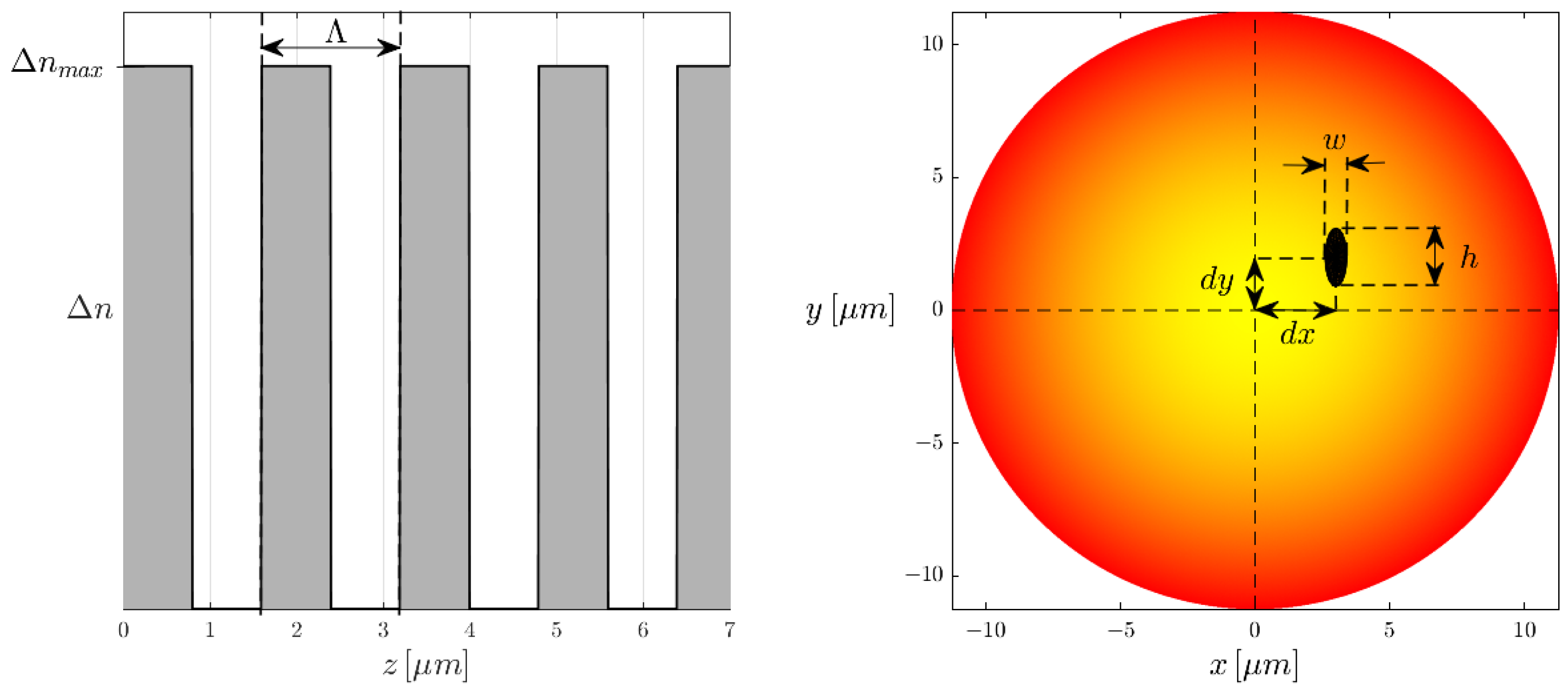
4.1. FBG Refractive Index Modification Geometry
4.2. Coupling Coefficients
4.3. Spectra Realisation
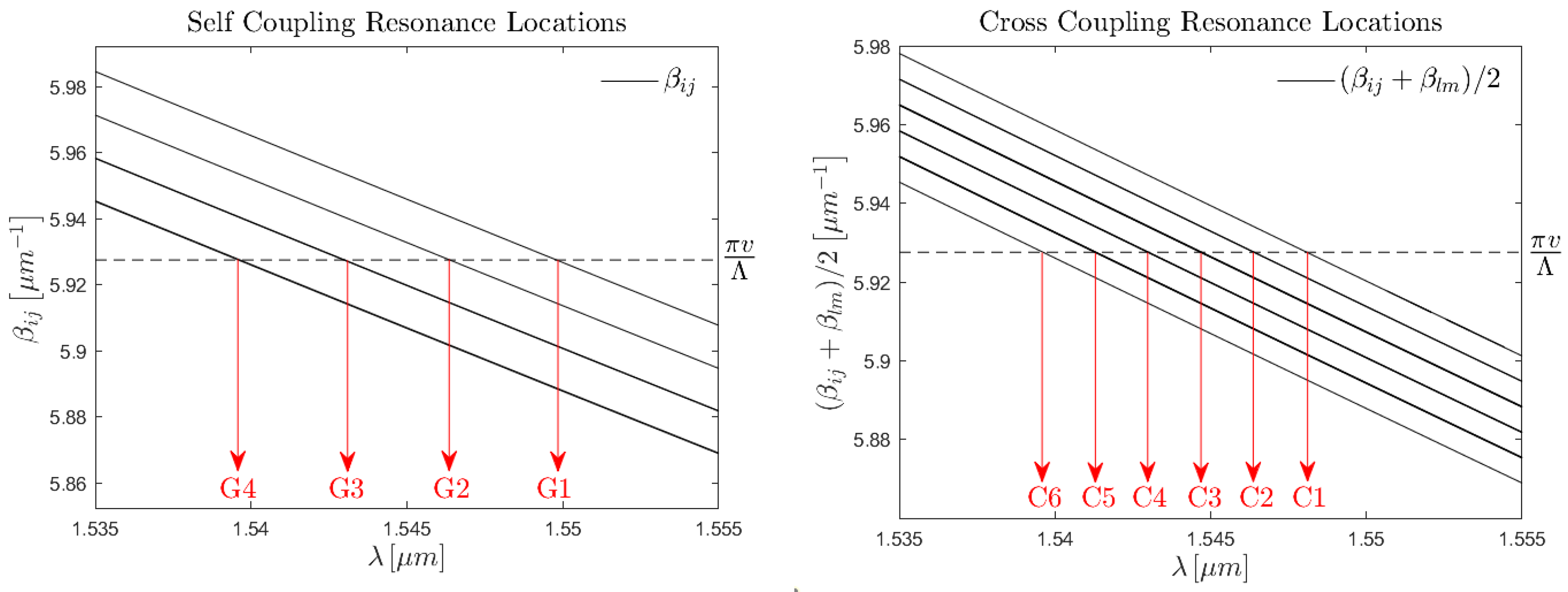
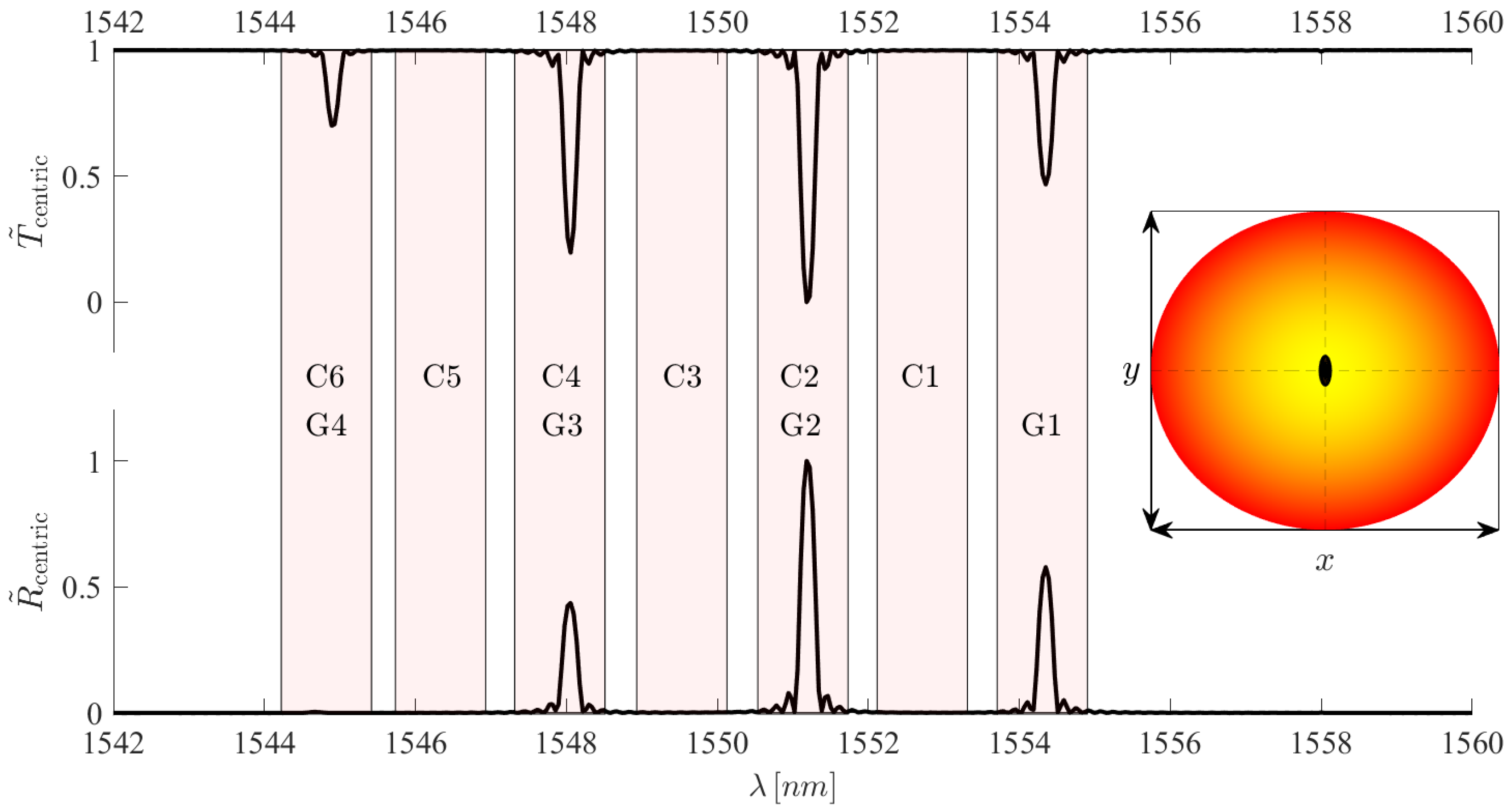
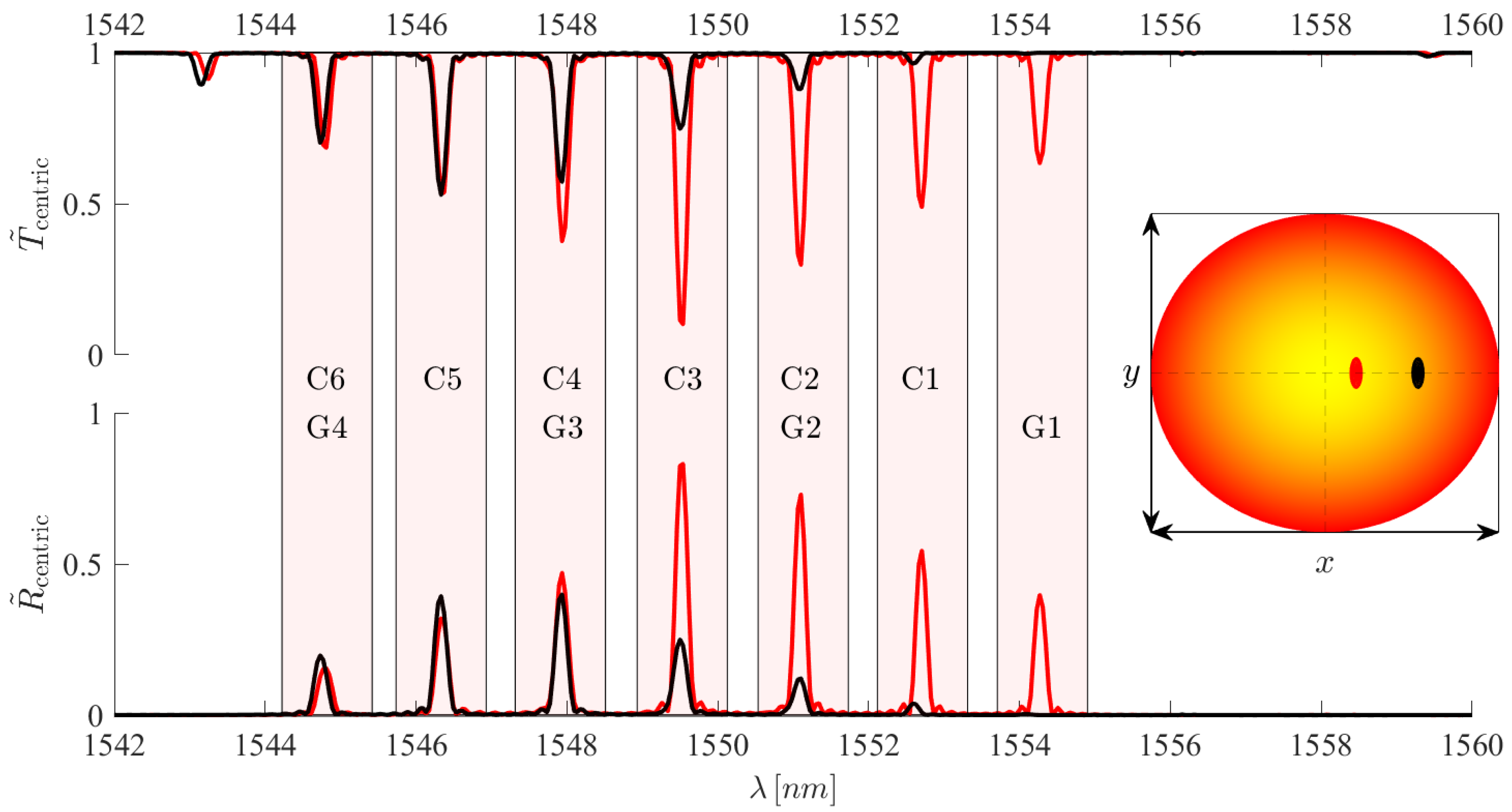
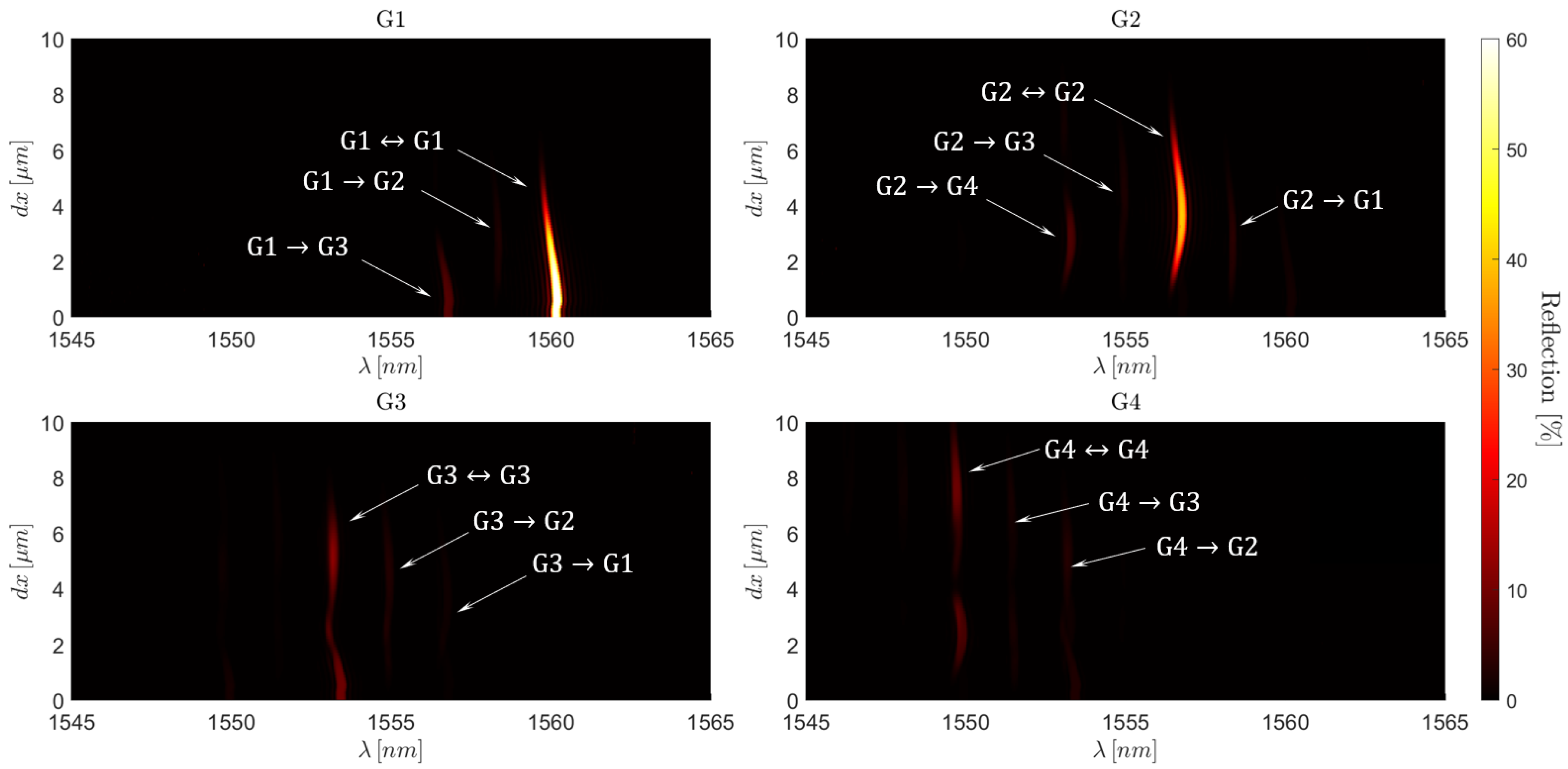
4.4. Features of the Few-Mode Localised FBG Spectrum
- Self-coupling resonance compositions:
- -
- -
- -
- -
- Cross-coupling resonance compositions:
- -
- -
- -
- -
- -
- -
5. Results and Discussion
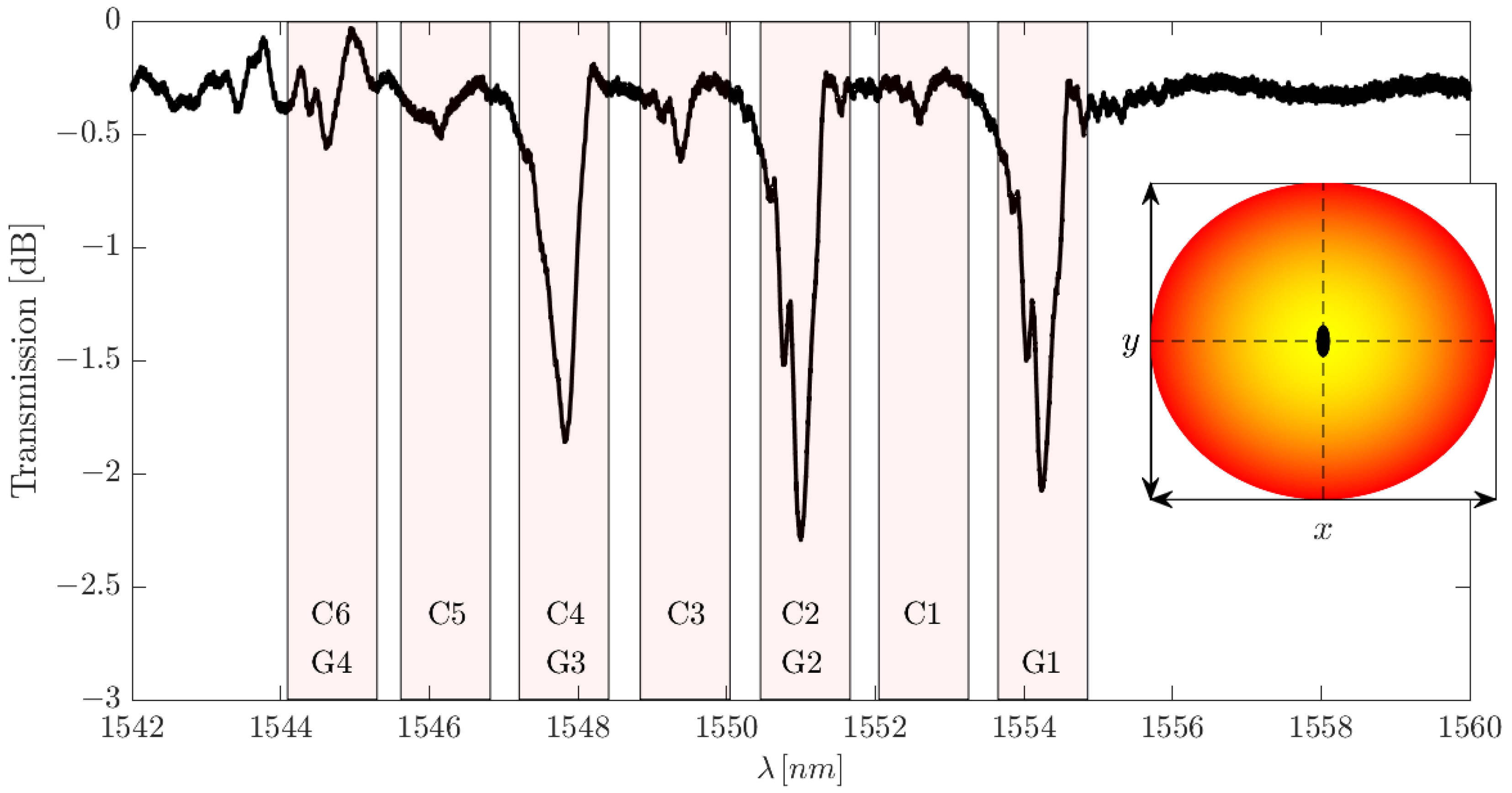
5.1. Validation of the Numerical Model
5.2. Transmission Spectral Control
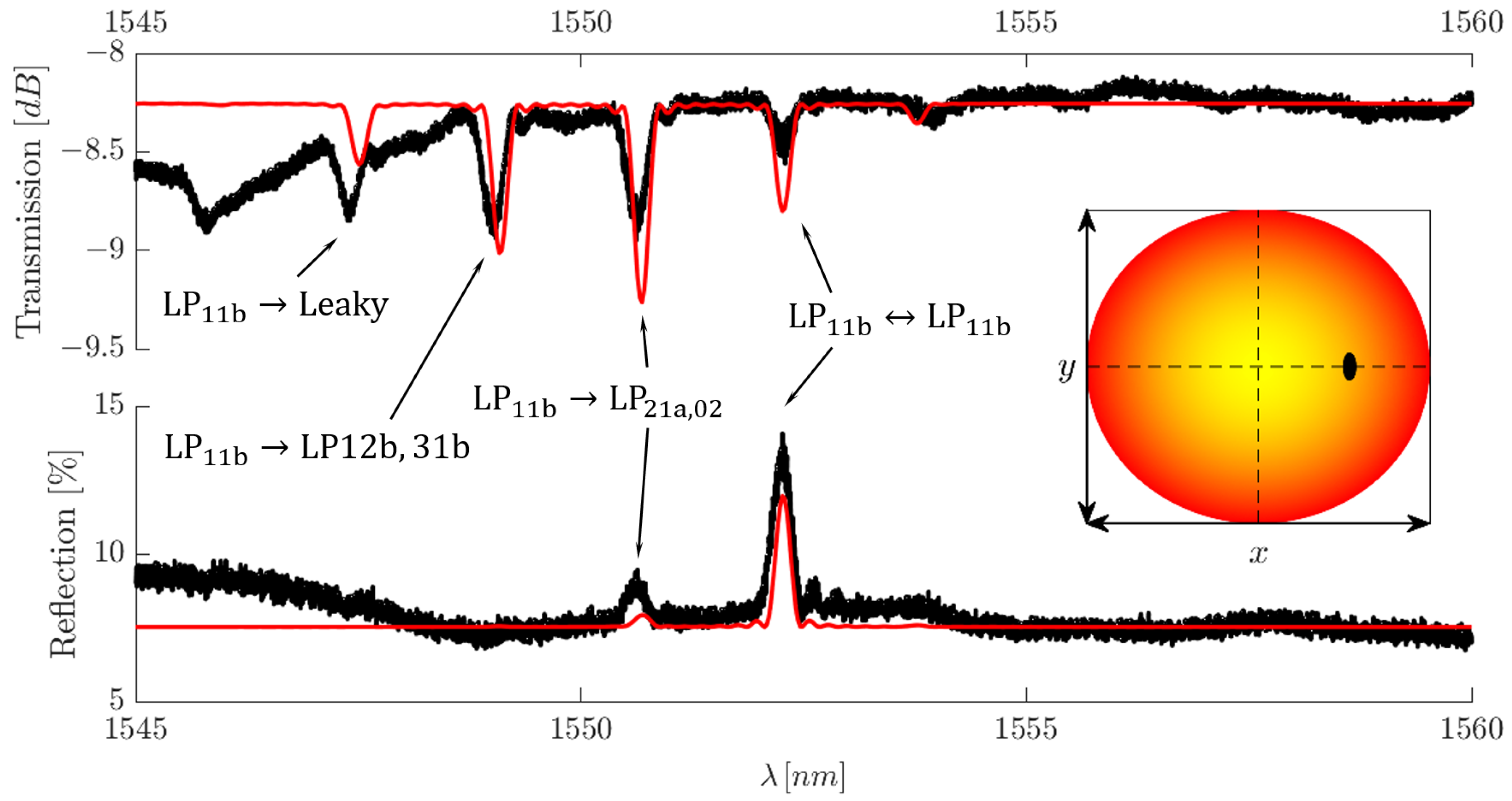
5.3. Wave Division Multiplexing
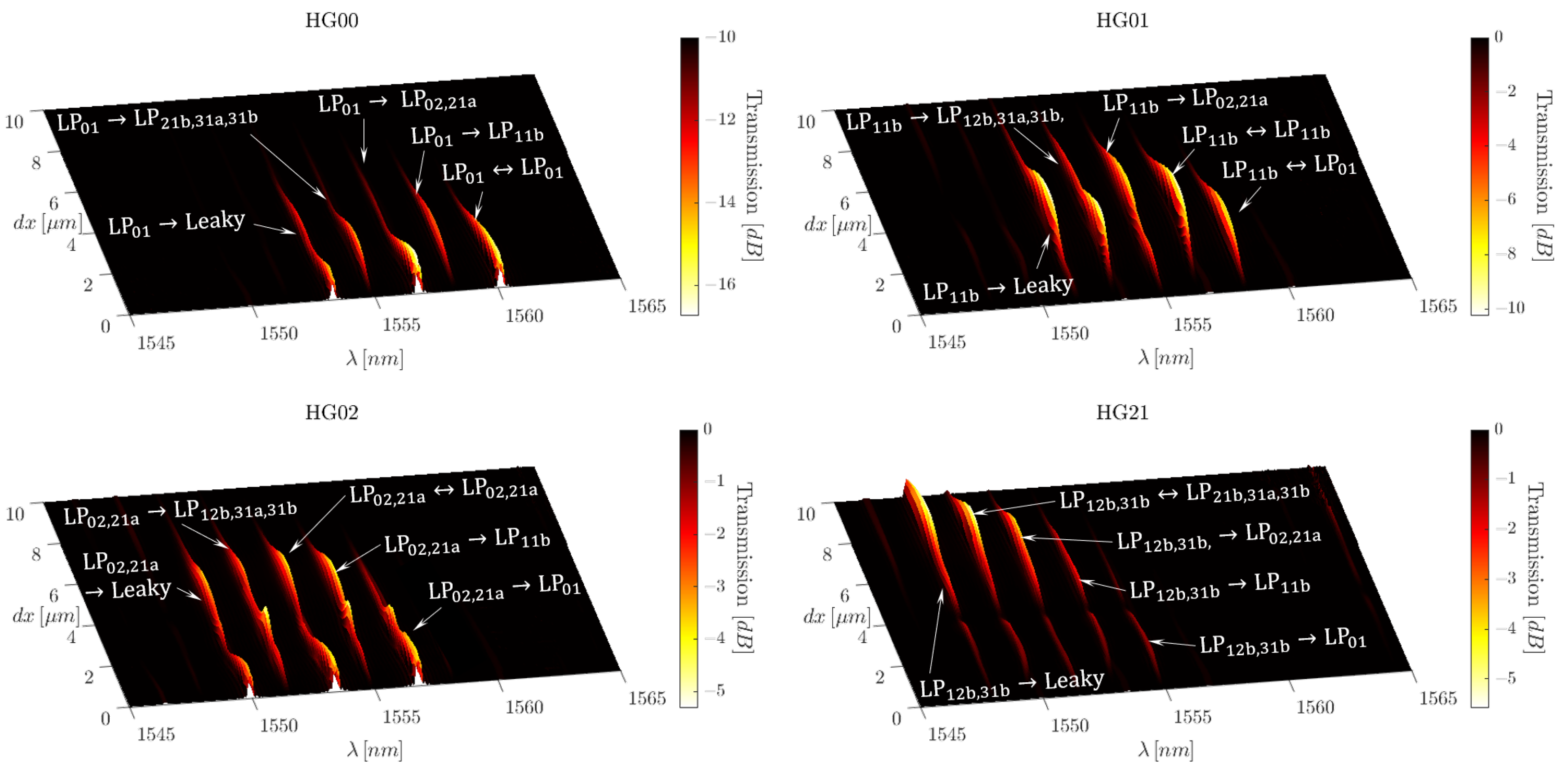
5.4. Spatial Mode Division Multiplexing
5.5. Discussion on Localised FBG Optimisation
6. Conclusions
Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kashyap, R. Fiber Bragg Gratings; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Sun, Y.; Yao, Y.; Niu, H.; Zha, H.; Zhang, L.; Tian, Z.; Chen, N.K.; Ren, Y. Peak wavelength and bandwidth tunable fiber Bragg grating notch filter induced by femtosecond laser point by point inscription. Opt. Commun. 2022, 521, 128583. [Google Scholar] [CrossRef]
- Sahota, J.K.; Gupta, N.; Dhawan, D. Fiber Bragg grating sensors for monitoring of physical parameters: A comprehensive review. Opt. Express 2020, 59, 060901. [Google Scholar] [CrossRef]
- Qiu, Y.; Wang, Q.; Zhao, H.; Chen, J.; Wang, Y. Review on composite structural health monitoring based on fiber Bragg grating sensing principle. J. Shanghai Jiaotong Univ. (Sci.) 2013, 18, 129–139. [Google Scholar] [CrossRef]
- Kinet, D.; Mégret, P.; Goossen, K.W.; Qiu, L.; Heider, D.; Caucheteur, C. Fiber Bragg Grating Sensors toward Structural Health Monitoring in Composite Materials: Challenges and Solutions. Sensors 2014, 14, 7394–7419. [Google Scholar] [CrossRef]
- Hegde, G.; Asokan, S.; Hegde, G. Fiber Bragg grating sensors for aerospace applications: A review. ISSS J. Micro Smart Syst. 2022, 11, 257–275. [Google Scholar] [CrossRef]
- Guo, T.; Liu, F.; Guan, B.O.; Albert, J. [INVITED] Tilted fiber grating mechanical and biochemical sensors. Opt. Laser Technol. 2016, 78, 19–33. [Google Scholar] [CrossRef]
- Fasseaux, H.; Caucheteur, C.; Loyez, M. Unraveling Plasmonic Tilted Fiber Bragg Gratings (TFBG): A Journey From “Anomalous Resonances” to Refined Refractometry. Laser Photonics Rev. 2025, 19, 2400833. [Google Scholar] [CrossRef]
- Thomas, J.; Jovanovic, N.; Becker, R.G.; Marshall, G.D.; Withford, M.J.; Tünnermann, A.; Nolte, S.; Steel, M.J. Cladding mode coupling in highly localized fiber Bragg gratings: Modal properties and transmission spectra. Opt. Express 2011, 19, 325–341. [Google Scholar] [CrossRef]
- Thomas, J.U.; Jovanovic, N.; Krämer, R.G.; Marshall, G.D.; Withford, M.J.; Tünnermann, A.; Nolte, S.; Steel, M.J. Cladding mode coupling in highly localized fiber Bragg gratings II: Complete vectorial analysis. Opt. Express 2012, 20, 21434–21449. [Google Scholar] [CrossRef]
- Shen, F.; Zhang, T. Numerical Analyses of the Polarization Dependent Cladding Mode Coupling in Localized Fiber Bragg Gratings. IEEE Access 2021, 9, 6689–6695. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Zhu, H.; Hu, G. Mode add-drop technology based on few-mode fiber Bragg gratings. Opt. Express 2023, 31, 10007–10018. [Google Scholar] [CrossRef]
- Wang, S.; Liu, X.; Wang, H.; Hu, G. High-order mode fiber laser based on few-mode fiber gratings. Opt. Laser Technol. 2022, 155, 108416. [Google Scholar] [CrossRef]
- Ashry, I.; Mao, Y.; Trichili, A.; Wang, B.; Ng, T.K.; Alouini, M.S.; Ooi, B.S. A Review of Using Few-Mode Fibers for Optical Sensing. IEEE Access 2020, 8, 179592–179605. [Google Scholar] [CrossRef]
- Dostovalov, A.V.; Wolf, A.A.; Zlobina, E.A.; Kablukov, S.I.; Babin, S.A. Femtosecond-pulse inscription of fiber Bragg gratings in multimode graded index fiber. In Proceedings of the Laser Applications in Microelectronic and Optoelectronic Manufacturing (LAMOM) XXII, San Francisco, CA, USA, 30 January–2 February 2017; Volume 10091, pp. 121–126. [Google Scholar] [CrossRef]
- Ali, M.M.; Jung, Y.; Lim, K.S.; Islam, M.R.; Alam, S.U.; Richardson, D.J.; Ahmad, H. Characterization of Mode Coupling in Few-Mode FBG With Selective Mode Excitation. IEEE Photonics Technol. Lett. 2015, 27, 1713–1716. [Google Scholar] [CrossRef]
- Cailabs. PROTEUS|Inventing the Optical Networks of the Future. Available online: https://www.cailabs.com/fiber-networks/optical-networks-of-the-future/proteus/ (accessed on 10 July 2025).
- Labroille, G.; Denolle, B.; Jian, P.; Genevaux, P.; Treps, N.; Morizur, J.F. Efficient and mode selective spatial mode multiplexer based on multi-plane light conversion. Opt. Express 2014, 22, 15599–15607. [Google Scholar] [CrossRef] [PubMed]
- Bhatia, N.; John, J. Multimode interference devices with single-mode–multimode–multimode fiber structure. Appl. Opt. 2014, 53, 5179–5186. [Google Scholar] [CrossRef]
- Leon-Saval, S.; Fontaine, N.; Salazar-Gil, J.; Ercan, B.; Ryf, R.; Bland-Hawthorn, J. Mode-selective photonic lanterns for space-division multiplexing. Opt. Express 2014, 22, 1036–1044. [Google Scholar] [CrossRef]
- Ryf, R.; Randel, S.; Gnauck, A.H.; Bolle, C.; Sierra, A.; Mumtaz, S.; Esmaeelpour, M.; Burrows, E.C.; Essiambre, R.J.; Winzer, P.J.; et al. Mode-Division Multiplexing Over 96 km of Few-Mode Fiber Using Coherent 6 ×6 MIMO Processing. J. Light. Technol. 2012, 30, 521–531. [Google Scholar] [CrossRef]
- Sugioka, K. Femtosecond laser three-dimensional micro- and nanofabrication. J. Appl. Phys. 2014, 1, 041303. [Google Scholar] [CrossRef]
- Alda, J. Laser and Gaussian Beam Propagation and Transformation. In Encyclopedia of Optical Engineering; Driggers, R.G., Ed.; Marcel Dekker: New York, NY, USA, 2003; pp. 1000–1012. [Google Scholar] [CrossRef]
- He, W.; Zhu, L.; Zhang, W.; Liu, F.; Dong, M. Point-by-Point Femtosecond-Laser Inscription of 2-μm-Wavelength-Band FBG Through Fiber Coating. IEEE Photonics J. 2019, 11, 1–8. [Google Scholar] [CrossRef]
- Chen, R.; He, J.; Xu, X.; Wu, J.; Wang, Y.; Wang, Y. High-Quality Fiber Bragg Gratings Inscribed by Femtosecond Laser Point-by-Point Technology. Micromachines 2022, 13, 1808. [Google Scholar] [CrossRef]
- Sillard, P.; Molin, D.; Bigot-Astruc, M.; Jongh, K.d.; Achten, F. Micro-Bend-Resistant Low-DMGD 6-LP-Mode Fiber. In Proceedings of the Optical Fiber Communication Conference (2016), Anaheim, CA, USA, 20–22 March 2016. paper Th1J.5. [Google Scholar] [CrossRef]
- Vassallo, C. Optical Waveguide Concepts; Elsevier Science: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Zhou, Y.; Zhao, J.; Shi, Z.; Rafsanjani, S.M.H.; Mirhosseini, M.; Zhu, Z.; Willner, A.E.; Boyd, R.W. Hermite–Gaussian mode sorter. Opt. Lett. OL 2018, 43, 5263–5266. [Google Scholar] [CrossRef]
- Gizatulin, A.R.; Lyubopytov, V.S.; Sultanov, A.K. Influence of fiber bends on mode-dependent loss and mode coupling in mode division multiplexing systems. In Proceedings of the Optical Technologies for Telecommunications, Samara, Russia, 22–24 November 2016; Volume 10342, pp. 33–39. [Google Scholar] [CrossRef]
- Yuan, Y.; Wu, G.; Li, X.; Fan, Y.; Wu, X. Effects of twisting and bending on LP21 mode propagation in optical fiber. Opt. Lett. OL 2011, 36, 4248–4250. [Google Scholar] [CrossRef]
- Winzer, P.J.; Ryf, R.; Randel, S. Chapter 10—Spatial Multiplexing Using Multiple-Input Multiple-Output Signal Processing. In Optical Fiber Telecommunications, 6th ed.; Kaminow, I.P., Li, T., Willner, A.E., Eds.; Optics and Photonics; Academic Press: Boston, MA, USA, 2013; pp. 433–490. [Google Scholar] [CrossRef]
- Kogelnik, H.; Winzer, P.J. Modal Birefringence in Weakly Guiding Fibers. J. Light. Technol. JLT 2012, 30, 2240–2245. [Google Scholar] [CrossRef]
- Bandres, M.A.; Gutiérrez-Vega, J.C. Ince—Gaussian modes of the paraxial wave equation and stable resonators. J. Opt. Soc. Am. A 2004, 21, 873–880. [Google Scholar] [CrossRef]
- Erdogan, T. Fiber grating spectra. J. Light. Technol. 1997, 15, 1277–1294. [Google Scholar] [CrossRef]
- Lu, C.; Cui, Y. Fiber Bragg grating spectra in multimode optical fibers. J. Light. Technol. 2006, 24, 598–604. [Google Scholar] [CrossRef]


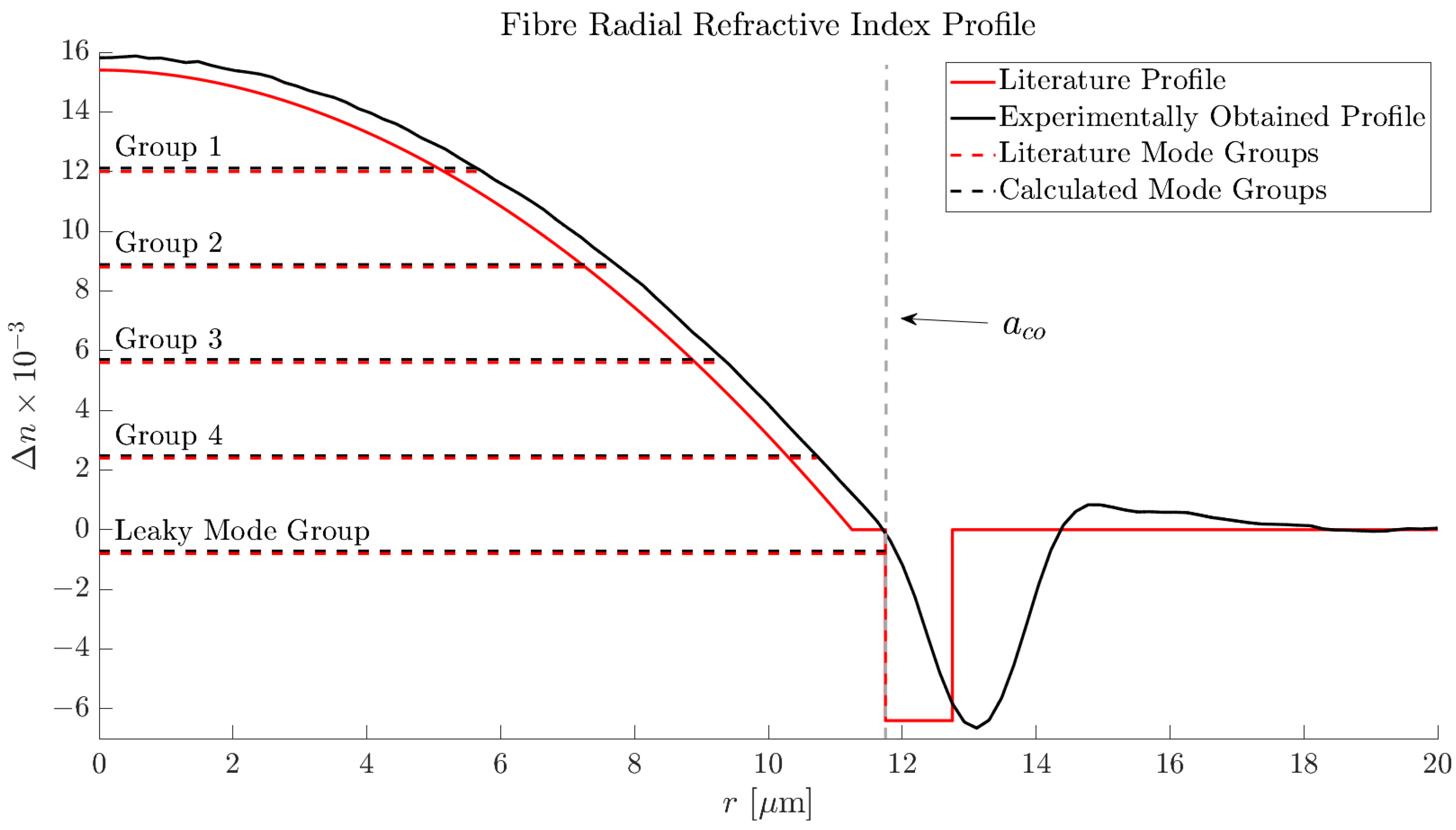

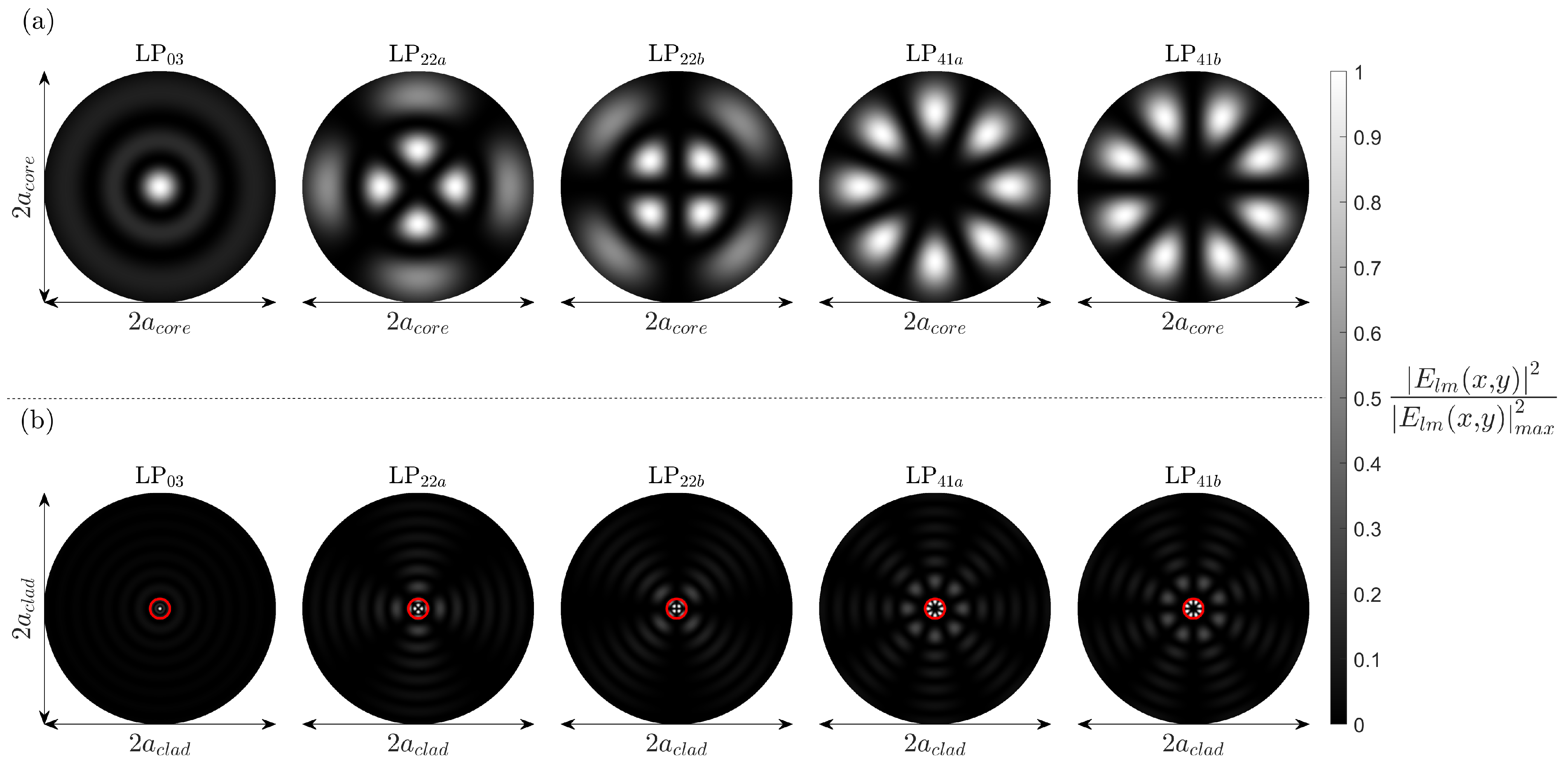



| Group Number | HG Output Modes | LP Fibre Modes |
|---|---|---|
| , | , | |
| , , | , , | |
| , , , | , , , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hainsworth, J.; Morana, A.; Lescure, L.; Veyssiere, P.; Girard, S.; Marin, E. Numerical and Experimental Study of Mode Coupling Due to Localised Few-Mode Fibre Bragg Gratings and a Spatial Mode Multiplexer. Sensors 2025, 25, 6087. https://doi.org/10.3390/s25196087
Hainsworth J, Morana A, Lescure L, Veyssiere P, Girard S, Marin E. Numerical and Experimental Study of Mode Coupling Due to Localised Few-Mode Fibre Bragg Gratings and a Spatial Mode Multiplexer. Sensors. 2025; 25(19):6087. https://doi.org/10.3390/s25196087
Chicago/Turabian StyleHainsworth, James, Adriana Morana, Lucas Lescure, Philippe Veyssiere, Sylvain Girard, and Emmanuel Marin. 2025. "Numerical and Experimental Study of Mode Coupling Due to Localised Few-Mode Fibre Bragg Gratings and a Spatial Mode Multiplexer" Sensors 25, no. 19: 6087. https://doi.org/10.3390/s25196087
APA StyleHainsworth, J., Morana, A., Lescure, L., Veyssiere, P., Girard, S., & Marin, E. (2025). Numerical and Experimental Study of Mode Coupling Due to Localised Few-Mode Fibre Bragg Gratings and a Spatial Mode Multiplexer. Sensors, 25(19), 6087. https://doi.org/10.3390/s25196087







