Temperature Calibration Using Machine Learning Algorithms for Flexible Temperature Sensors
Abstract
1. Introduction
2. Properties of Flexible Temperature Sensors
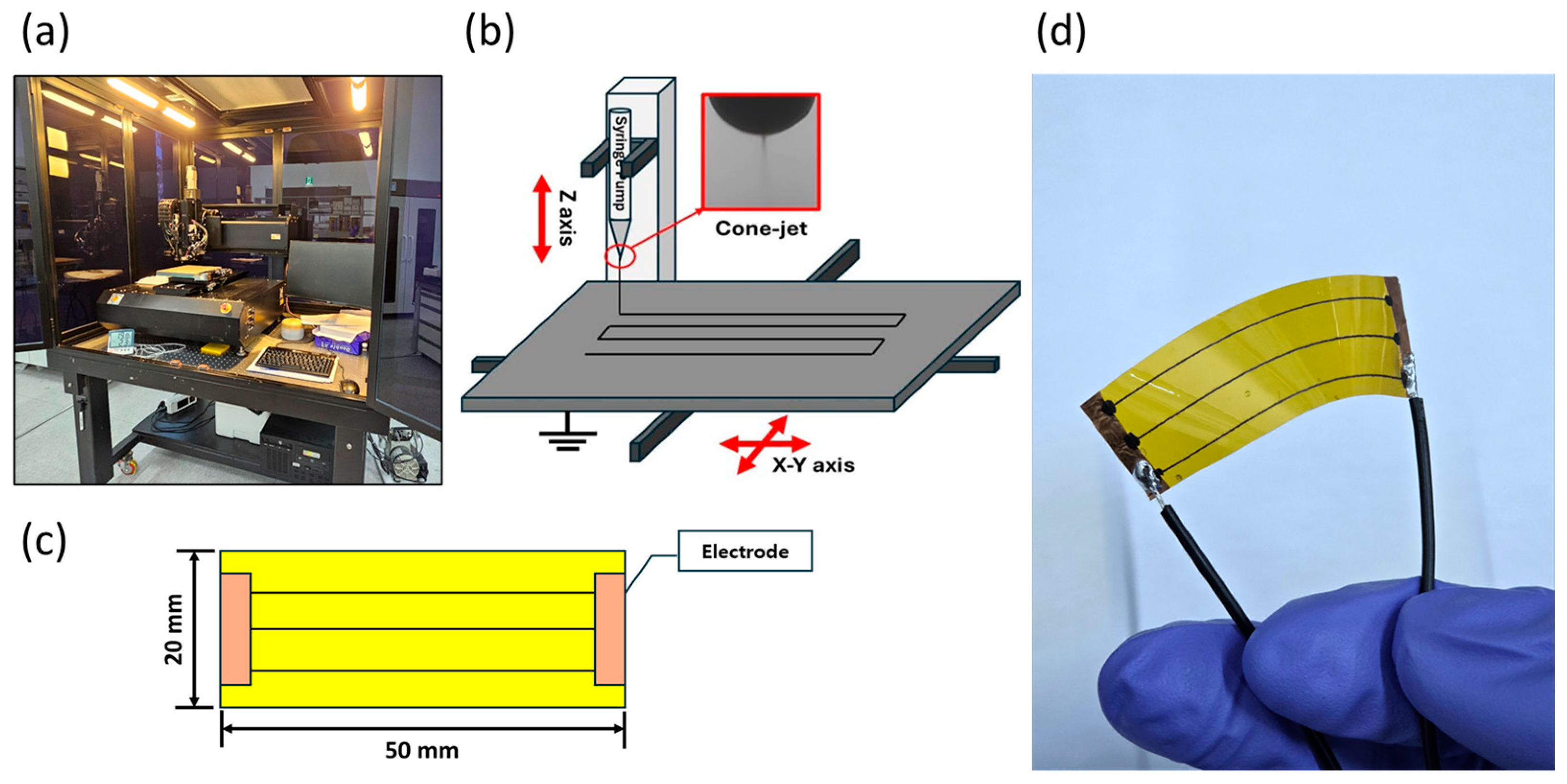
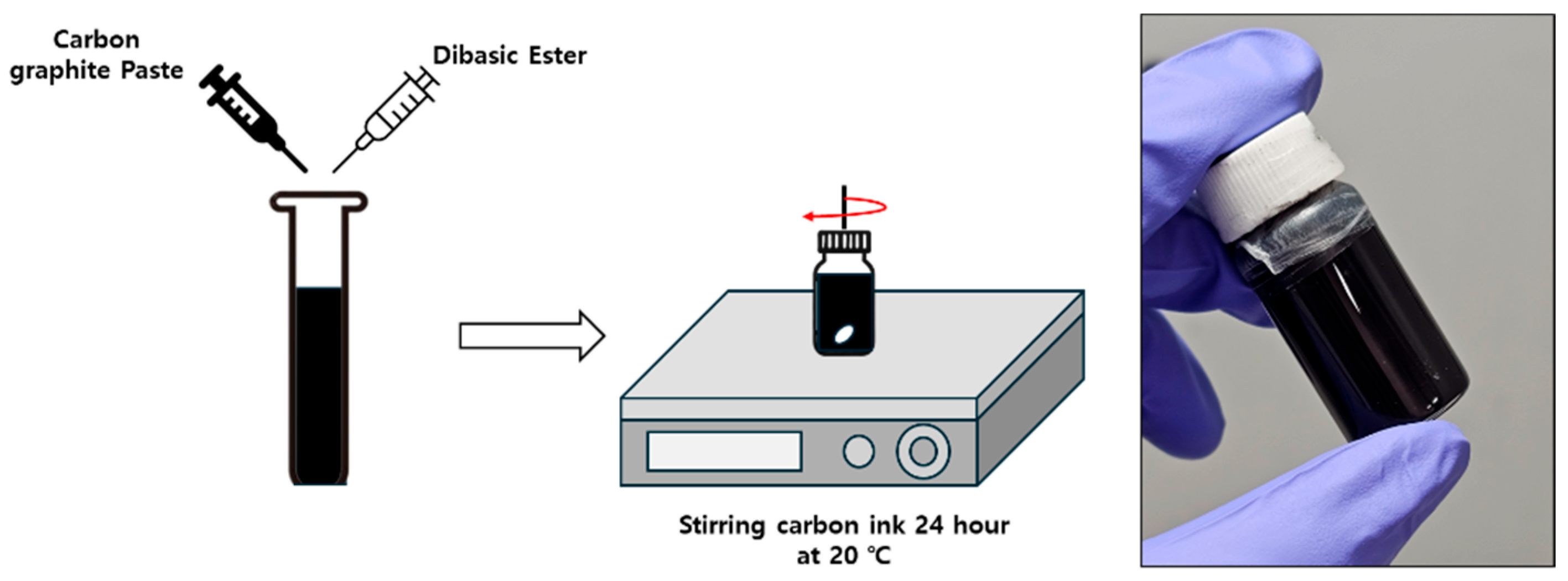
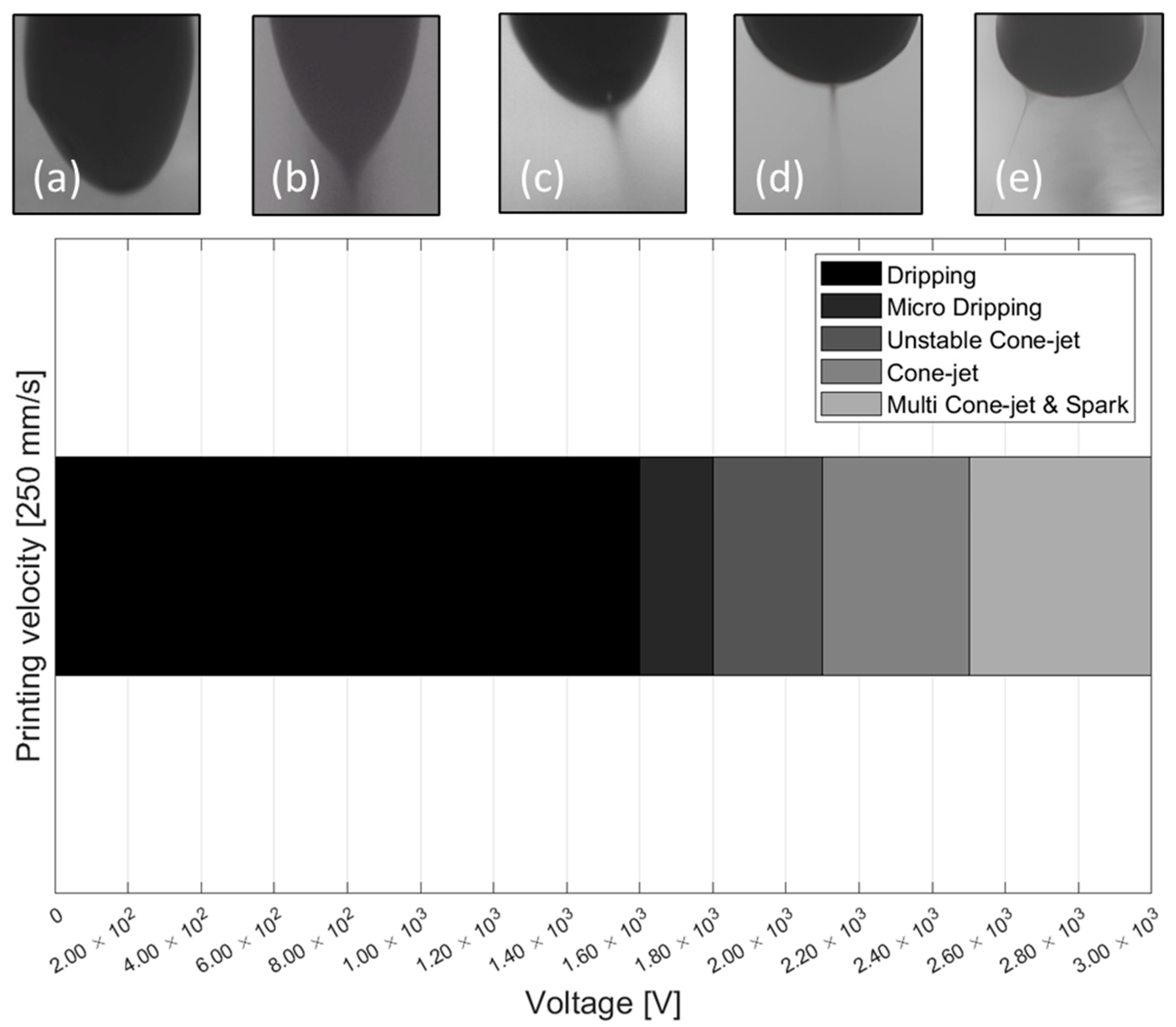
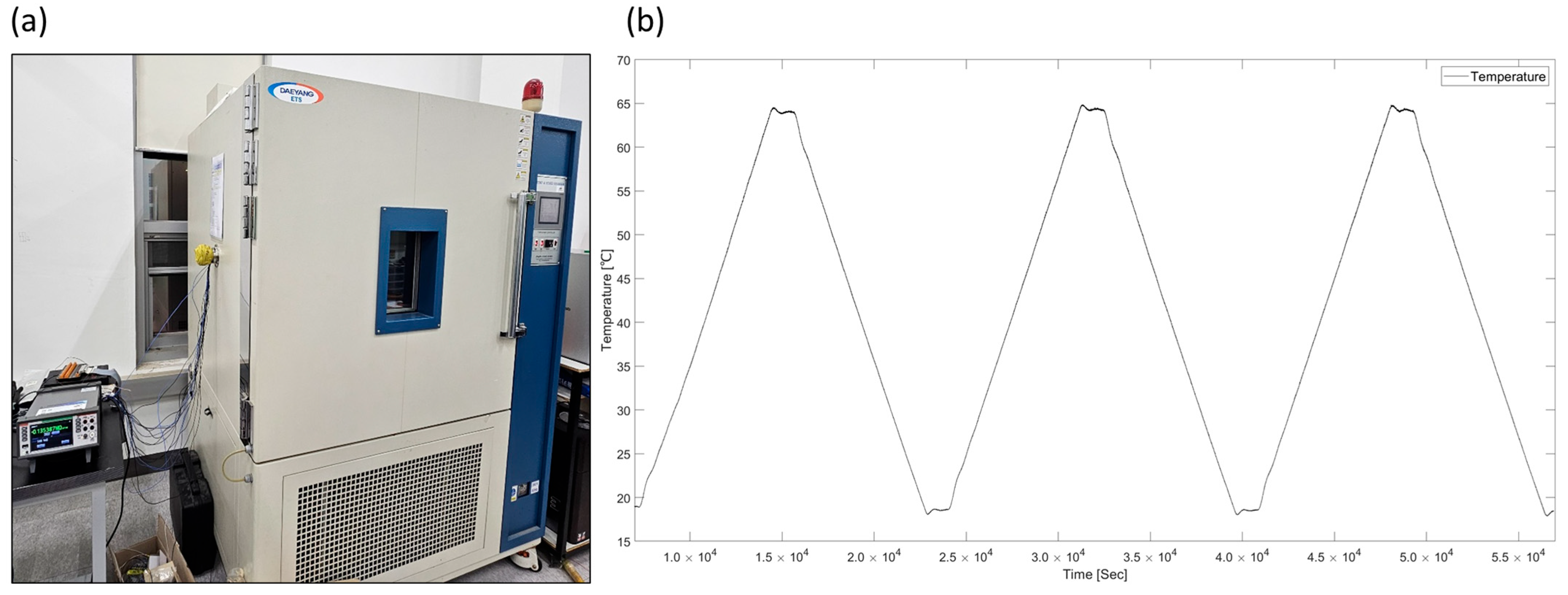
2.1. Ink Manufacturing Process and EHD Inkjet Printing Parameters
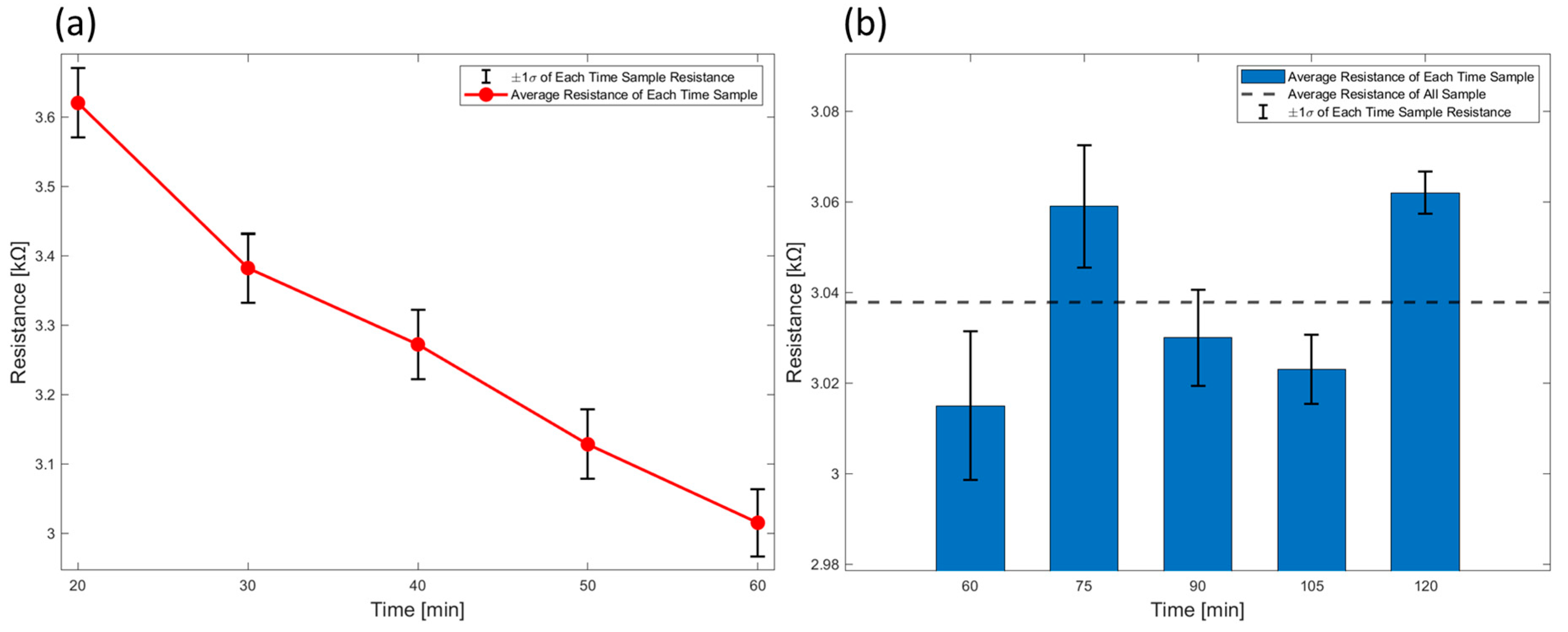
2.2. Initial Resistance Characteristics by Sintering Times
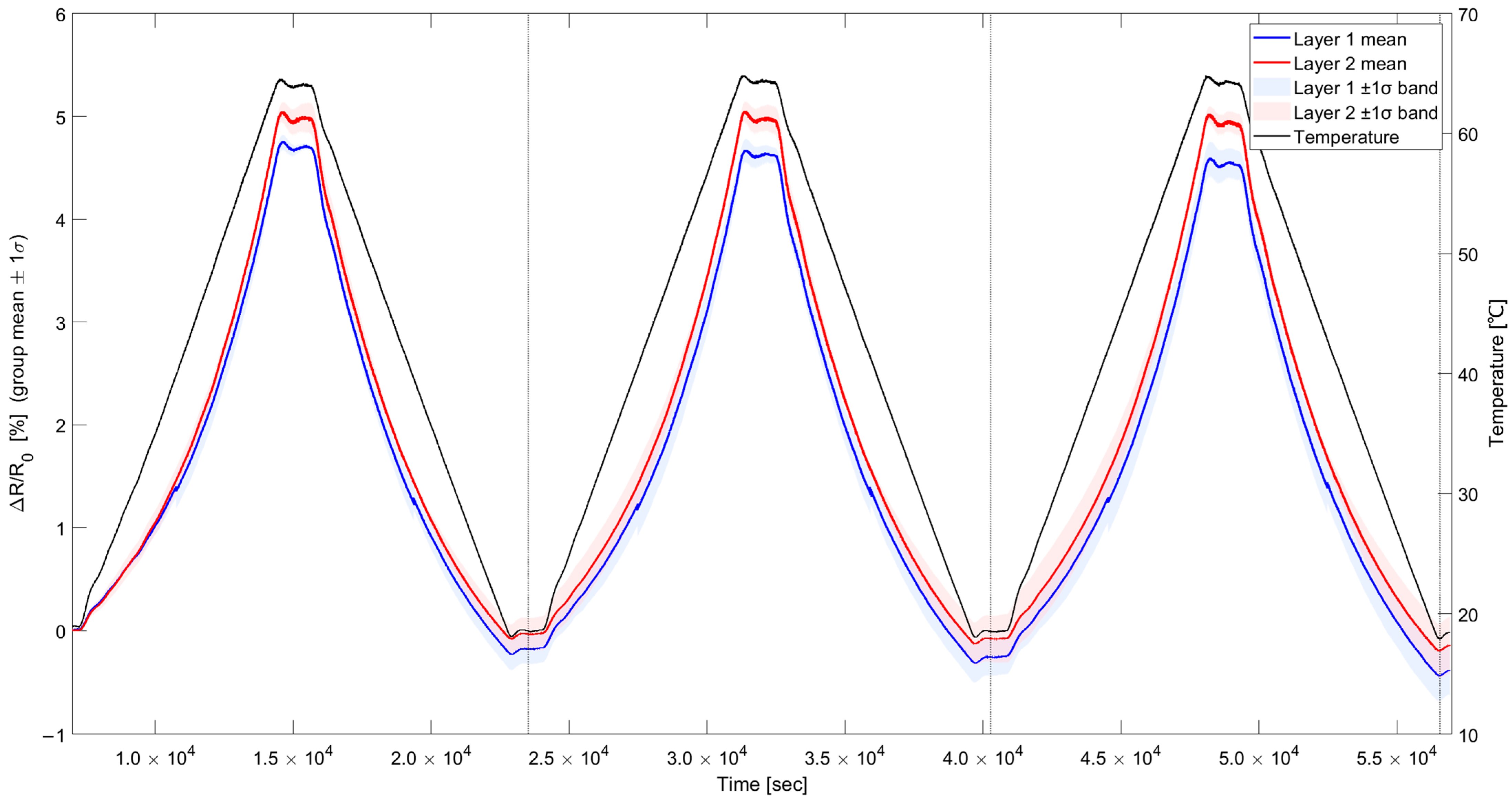
2.3. Differeces of Resistance Change Properties by Printed Layers
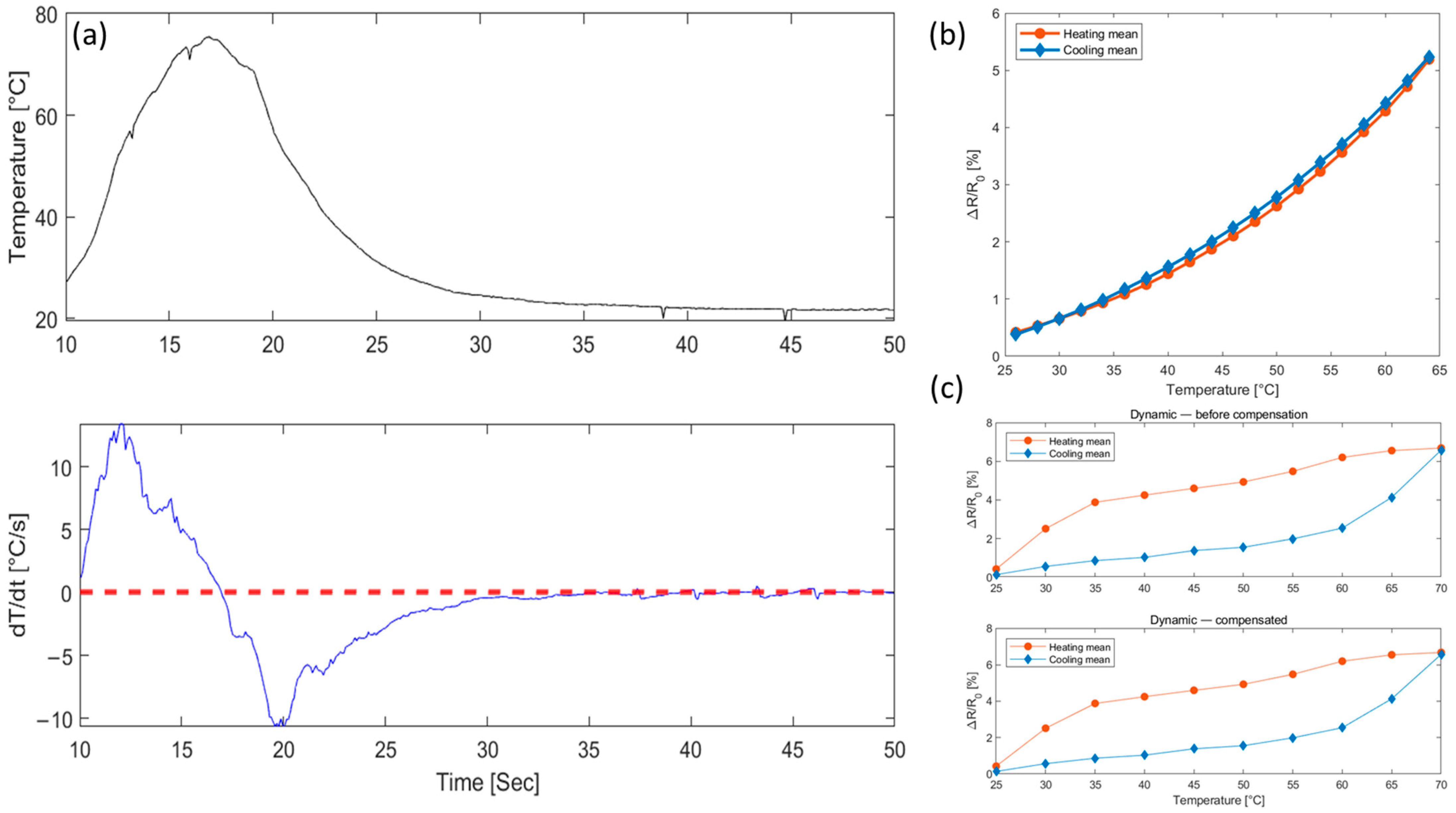
2.4. Analysis of Sensor’s Hysteresis Characteristics
3. Calibrations Sensor Resistance Changes According to Deep Learning
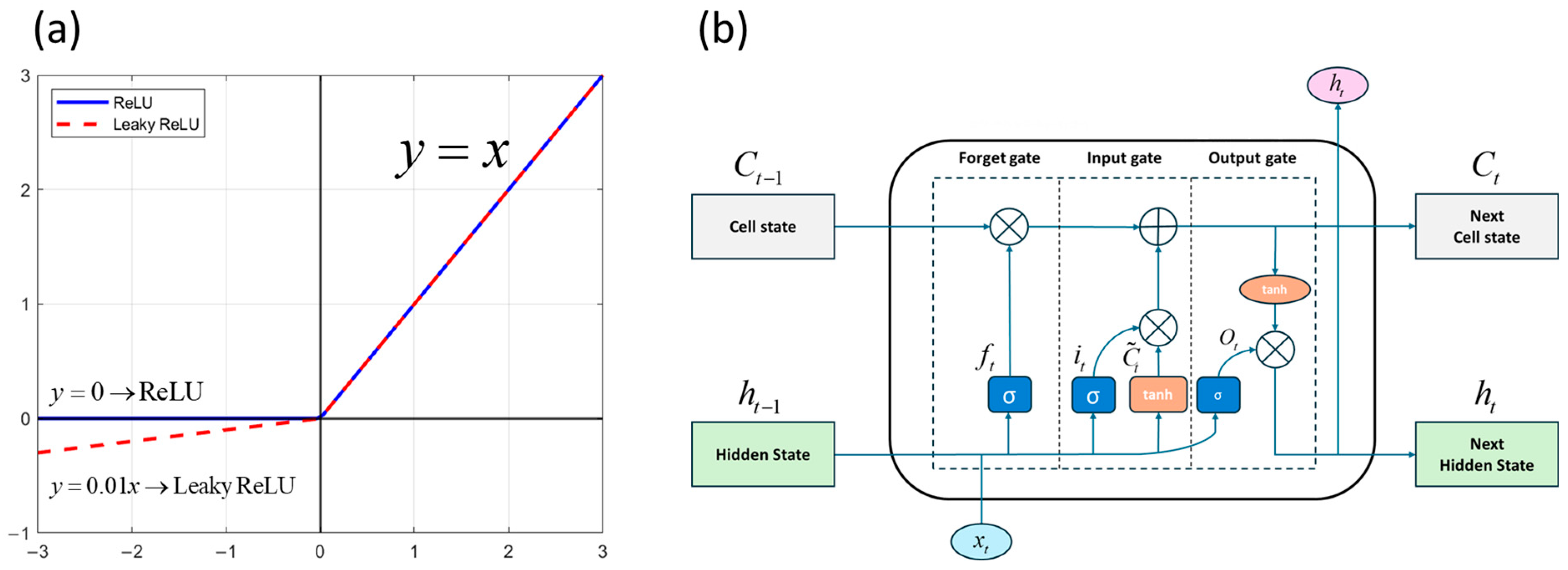
3.1. Basics of DNN and LSTM Models
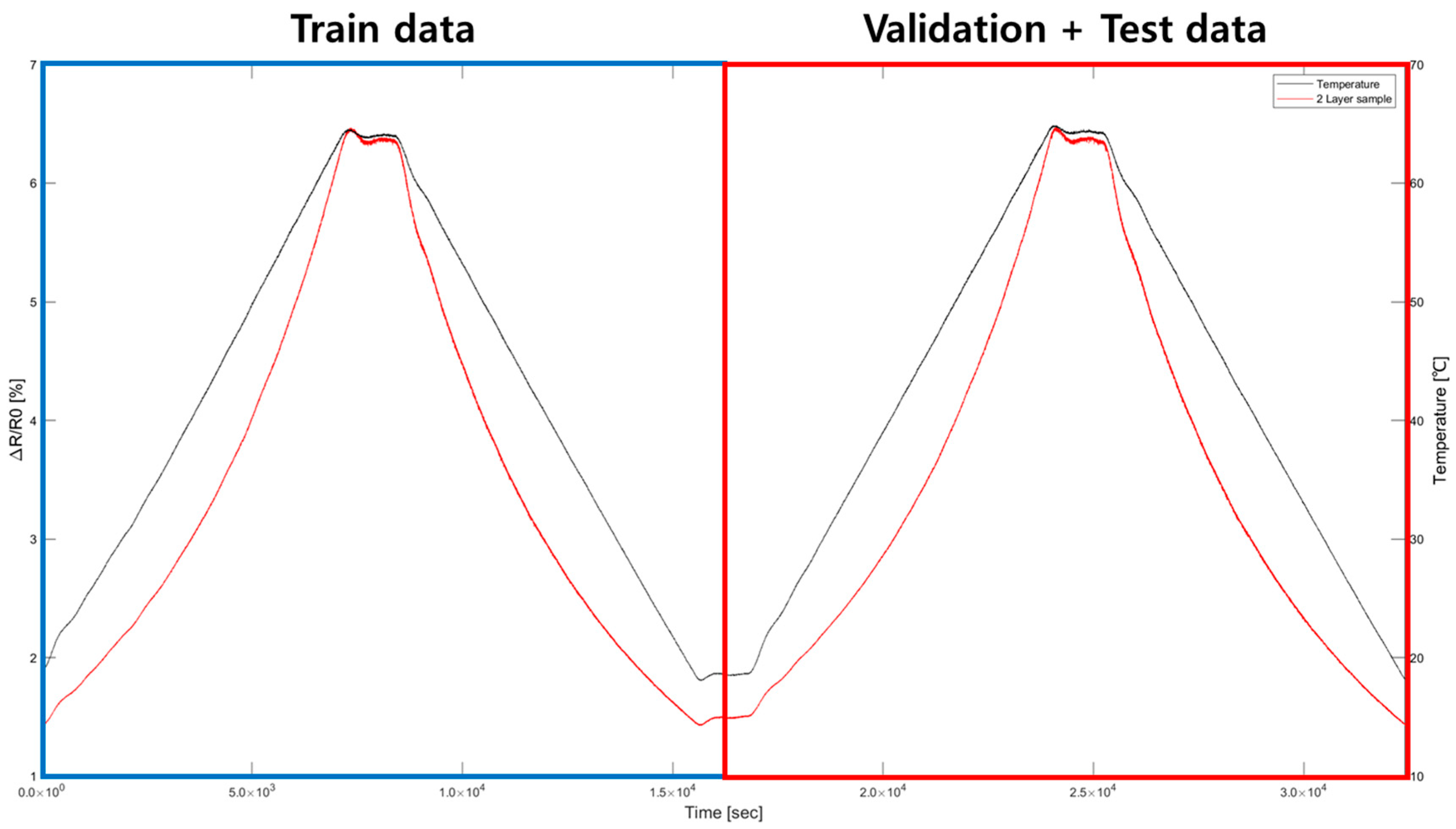
3.2. Preprocess for the Data and Model Performance Evaluation
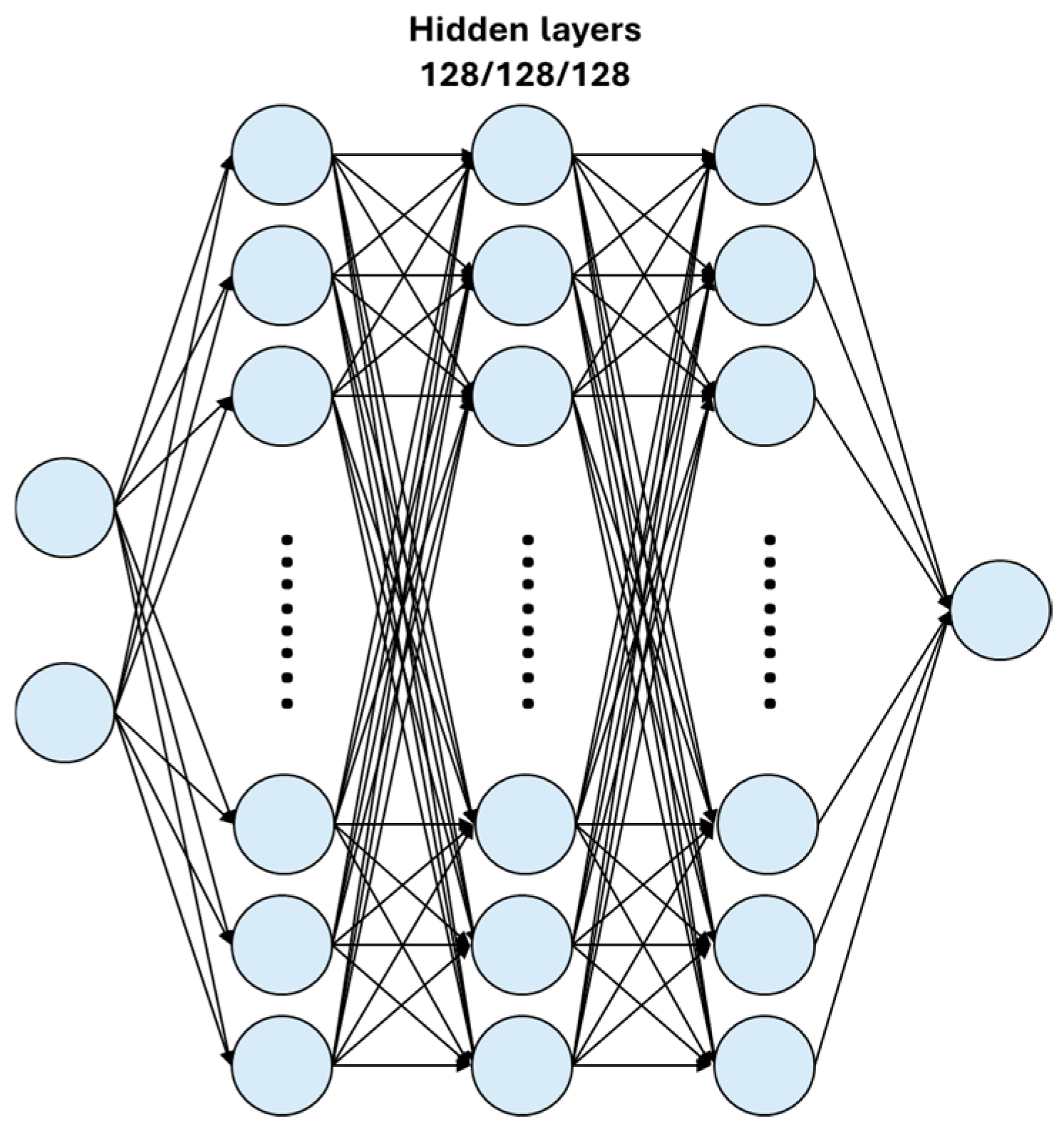
3.3. Dataset for Model Training and the Structure of DNN and LSTM
4. Results and Discussions
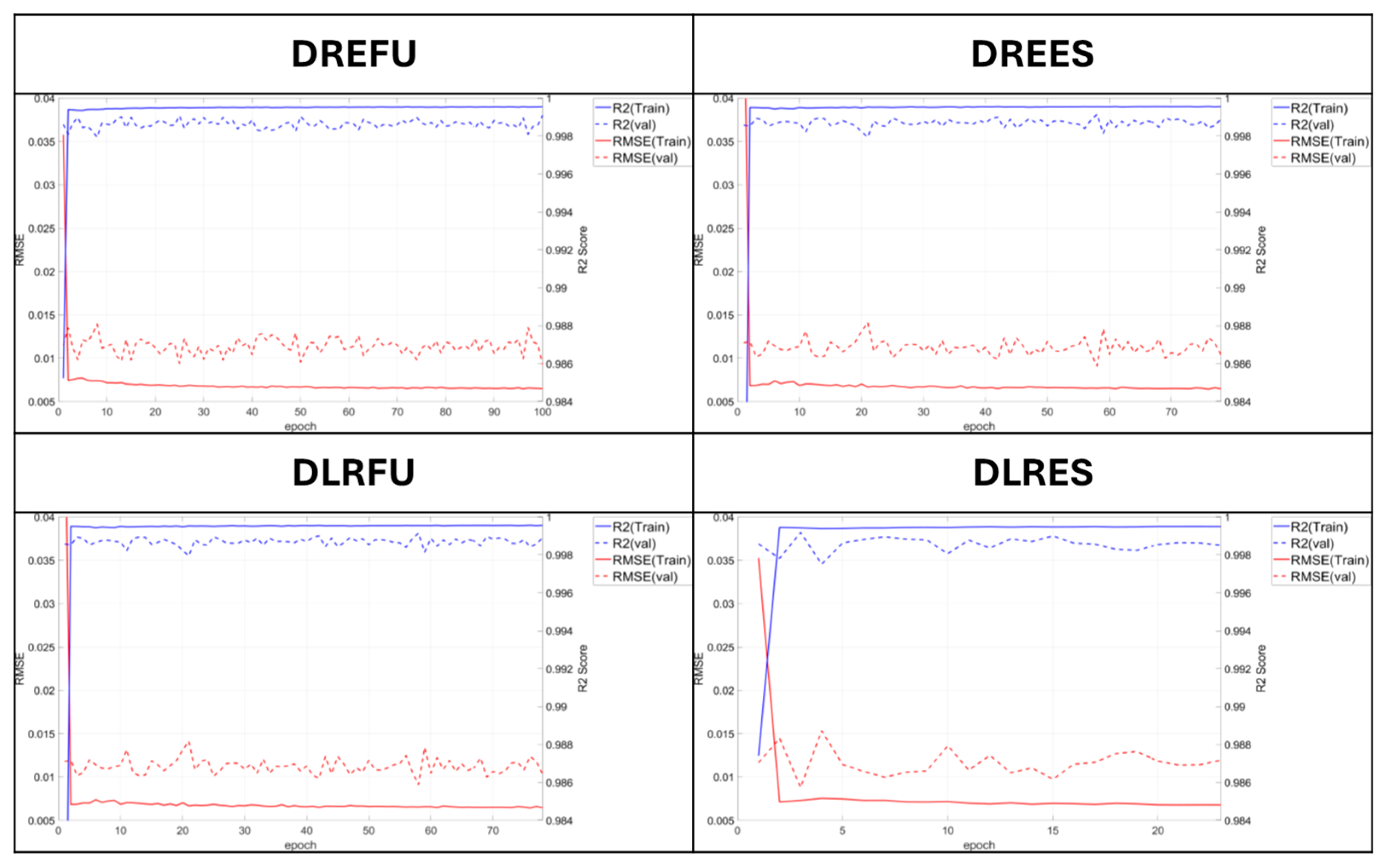
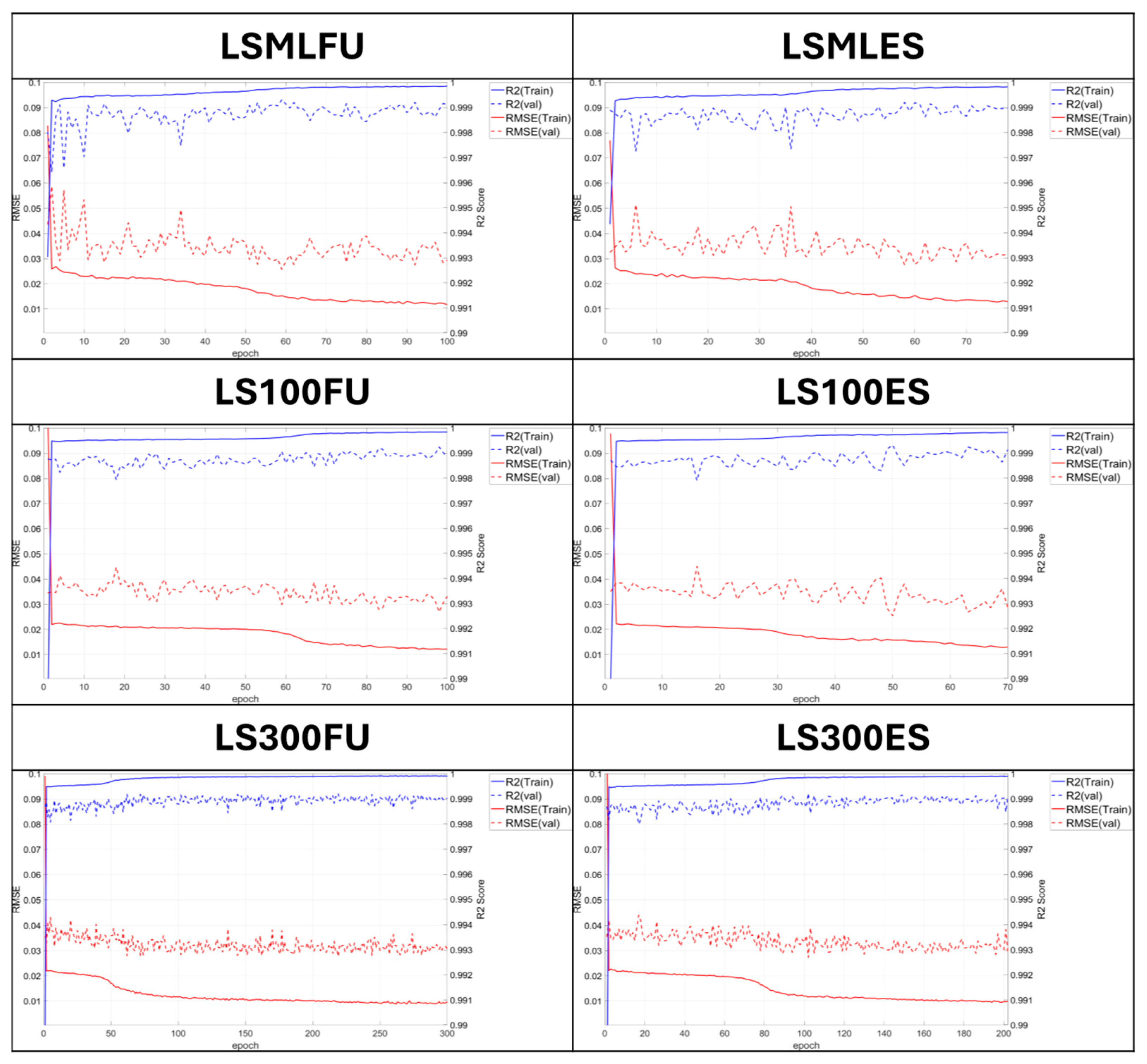
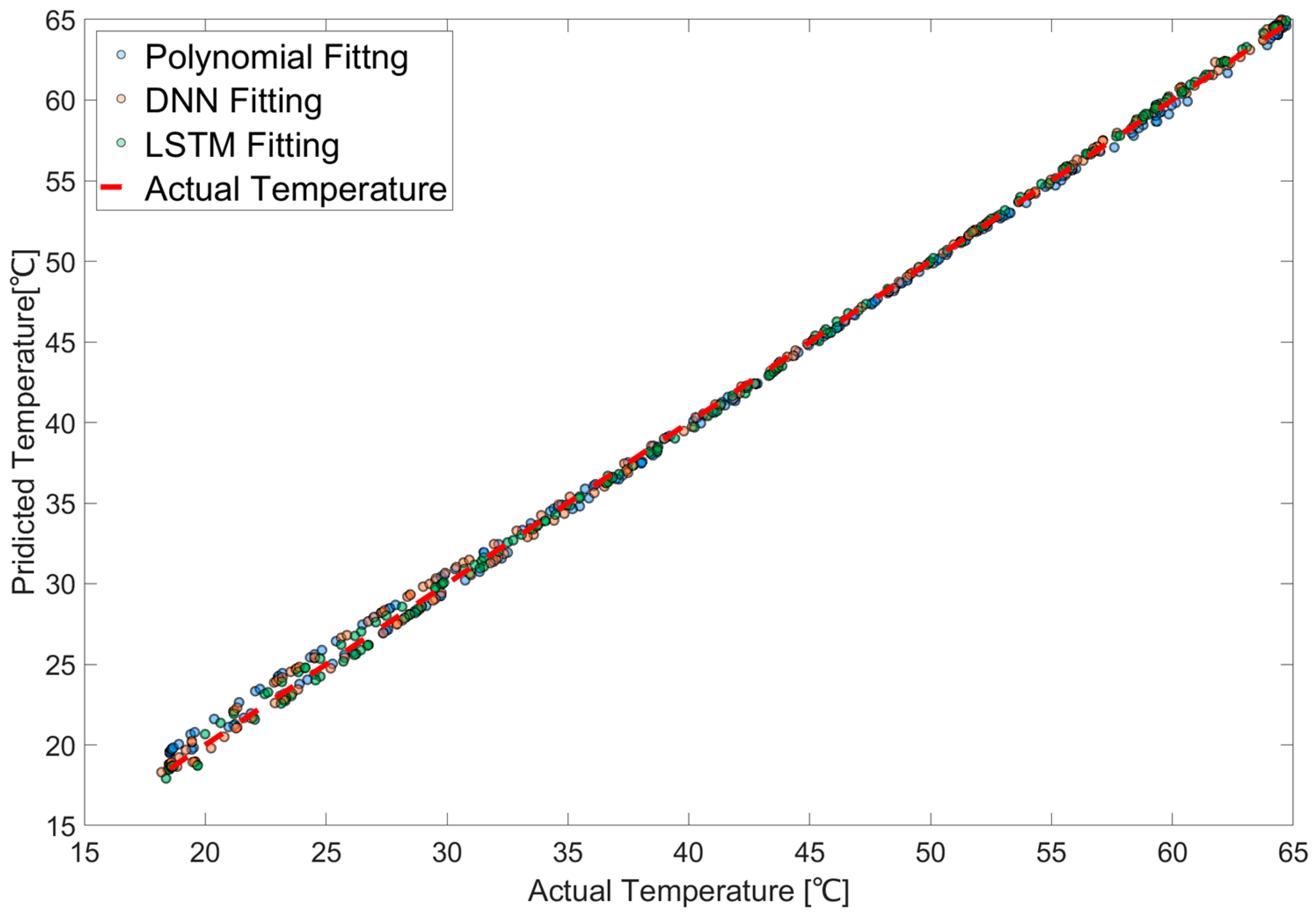
4.1. Model Optimization and Performance on Static Temperature Data
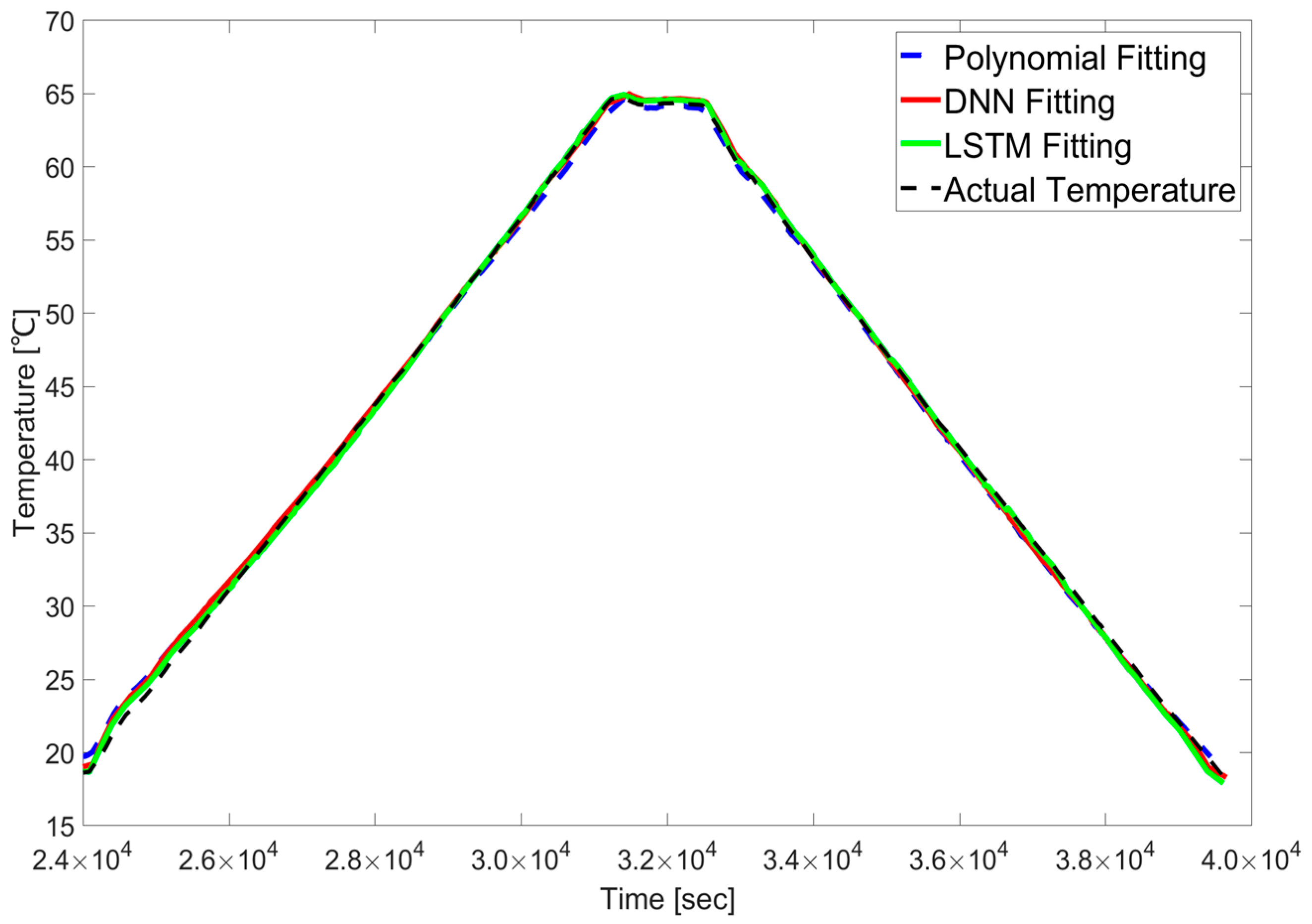
4.2. Generalization to Dynamic Hysteresis Conditions
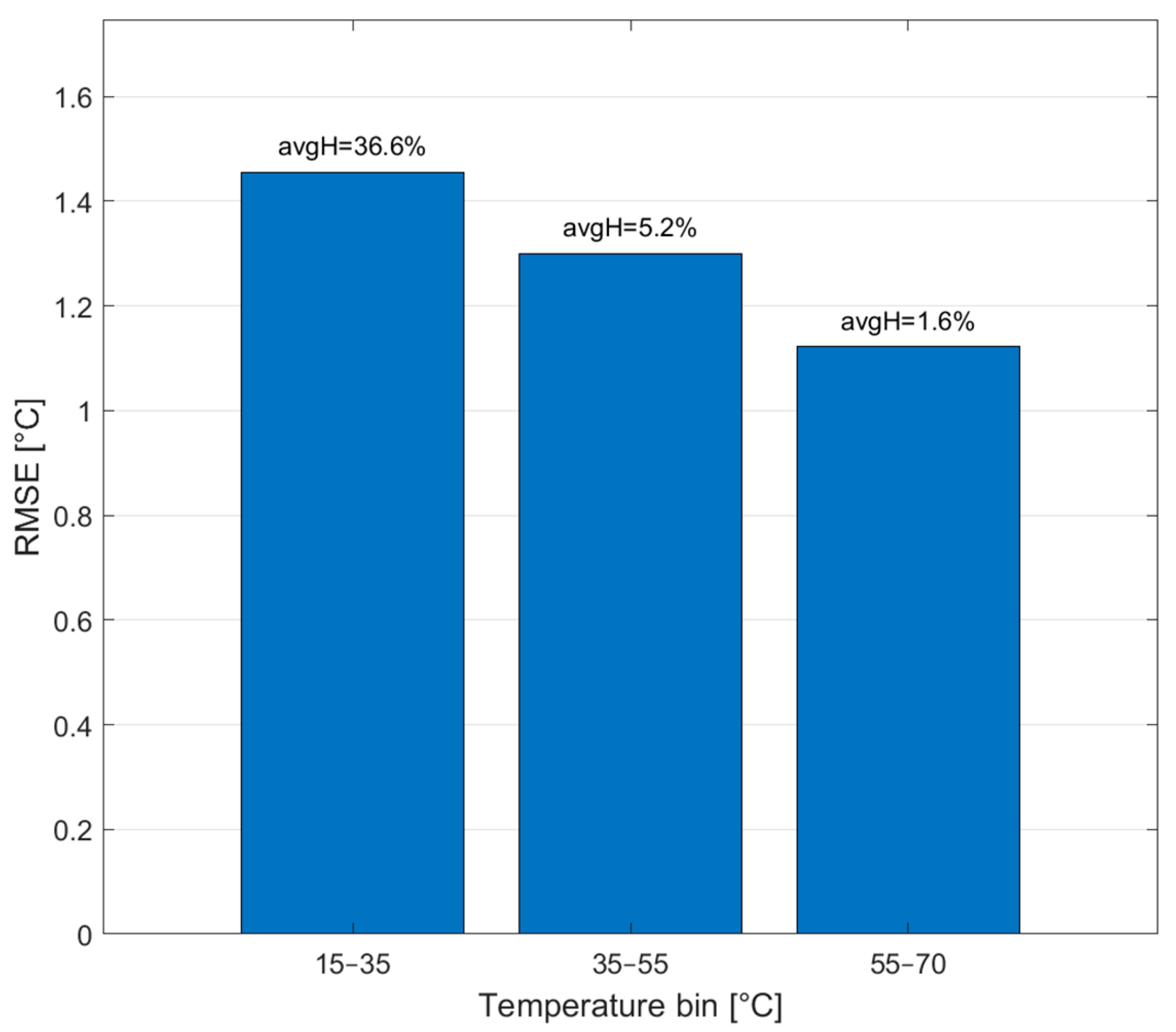
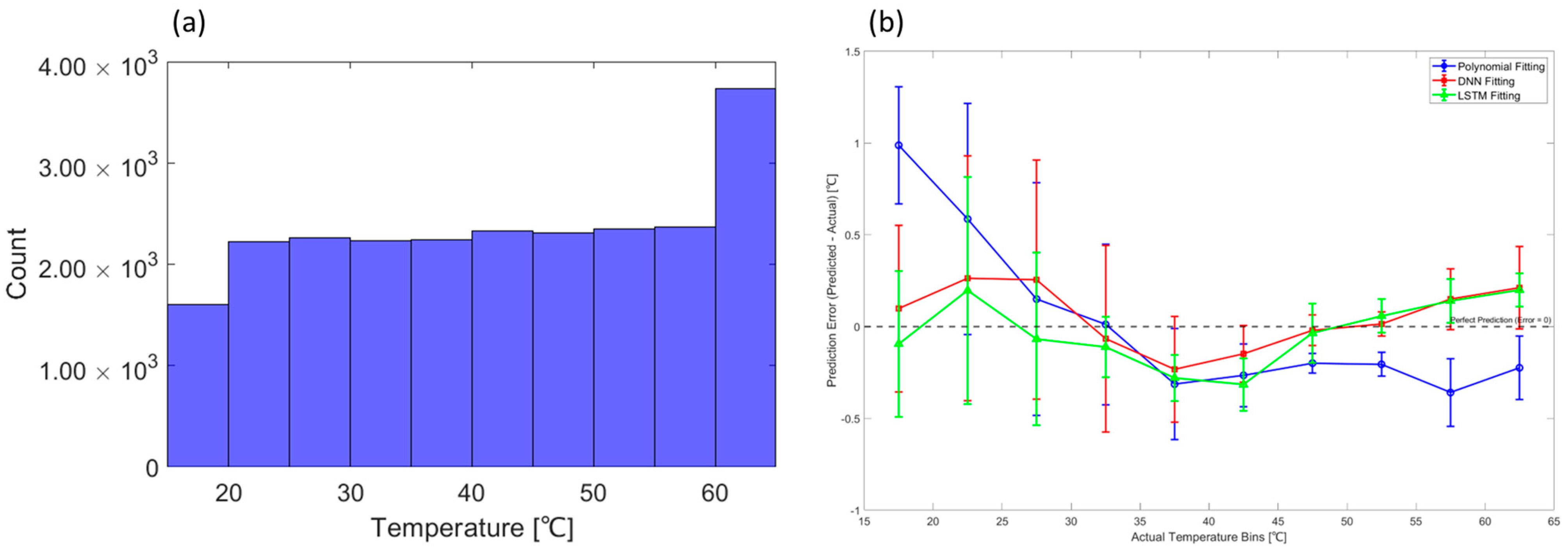
4.3. Analysis of Model Characteristics and Error Sources
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, W.M.; Zhang, Z.H.; Wang, Z.W.; Chen, B. Temperature analysis and prediction for road-rail steel truss cable-stayed bridges based on the structural health monitoring. Eng. Struct. 2024, 315, 118476. [Google Scholar] [CrossRef]
- Lin, Y.; Liu, Y.T.; Chang, Y.W. An Investigation of the Temperature-Drift Effect on Strain Measurement of Concrete Beams. Appl. Sci. 2019, 9, 1662. [Google Scholar] [CrossRef]
- Peng, G.; Nakamura, S.; Zhu, X.; Wu, Q.; Wang, H. An experimental and numerical study on temperature gradient and thermal stress of CFST truss girders under solar radiation. Comput. Concr. 2017, 20, 605–616. [Google Scholar] [CrossRef]
- Farreras-Alcover, I.; Chryssanthopoulos, M.K.; Andersen, J.E. Regression models for structural health monitoring of welded bridge joints based on temperature, traffic and strain measurements. Struct. Health Monit. 2015, 14, 648–662. [Google Scholar] [CrossRef]
- Christoforidou, A.; Pavlovic, M. Fatigue performance of composite-steel injected connectors at room and elevated temperatures. Eng. Struct. 2024, 315, 118421. [Google Scholar] [CrossRef]
- Barmpakos, D.; Kaltsas, G. A Review on Humidity, Temperature and Strain Printed Sensors-Current Trends and Future Perspectives. Sensors 2021, 21, 739. [Google Scholar] [CrossRef]
- Khan, Y.; Thielens, A.; Muin, S.; Ting, J.; Baumbauer, C.; Arias, A.C. A New Frontier of Printed Electronics: Flexible Hybrid Electronics. Adv. Mater. 2020, 32, e1905279. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, S.; Rahman, K.; Cheema, T.A.; Shakeel, M.; Khan, A.; Bermak, A. Fabrication of Low-Cost Resistance Temperature Detectors and Micro Heaters by Electrohydrodynamic Printing. Sensors 2022, 13, 1419. [Google Scholar] [CrossRef]
- Arman Kuzubasoglu, B.; Kursun Bahadir, S. Flexible temperature sensors: A review. Sens. Actuator A-Phys. 2020, 315, 112282. [Google Scholar] [CrossRef]
- Ahn, J.H.; Kim, H.N.; Lee, C.Y. Thin-film temperature sensors with grid-type circuits for temperature distribution measurements. Sens. Actuator A-Phys. 2024, 365, 114903. [Google Scholar] [CrossRef]
- He, Y.; Li, L.; Su, Z.; Xu, L.; Guo, M.; Duan, B.; Wang, W.; Cheng, B.; Sun, D.; Hai, Z. Electrohydrodynamic Printed Ultra-Micro AgNPs Thin Film Temperature Sensors Array for High-Resolution Sensing. Micromachines 2023, 14, 1621. [Google Scholar] [CrossRef]
- Kamal, W.; Rahman, K.; Ahmad, S.; Shakeel, M.; Ali, T. Electrohydrodynamic printed nanoparticle-based resistive temperature sensor. Flex. Print. Electron. 2022, 7, aca48a. [Google Scholar] [CrossRef]
- Lungulescu, E.M.; Stancu, C.; Setnescu, R.; Notingher, P.V.; Badea, T.A. Electrical and Electro-Thermal Characteristics of (Carbon Black-Graphite)/LLDPE Composites with PTC Effect. Materials 2024, 17, 1224. [Google Scholar] [CrossRef]
- Xu, J.; Mu, B.; Zhang, L.; Chai, R.; He, Y.; Zhang, X. Fabrication and optimization of passive flexible ammonia sensor for aquatic supply chain monitoring based on adaptive parameter adjustment artificial neural network (APA-ANN). Comput. Electron. Agric 2023, 212, 82. [Google Scholar] [CrossRef]
- Azad, A.K.; Wang, L.; Guo, N.; Lu, C.; Tam, H.Y. Temperature sensing in BOTDA system by using artificial neural network. Electron. Lett. 2015, 51, 1578–1580. [Google Scholar] [CrossRef]
- Bak, J.S.; Tai, M.S.; Park, D.H.; Jeong, S.K. Subsonic Wind Tunnel Wall Interference Correction Method Using Data Mining and Multi-Layer Perceptron. Int. J. Aeronaut. Space Sci. 2024, 25, 861–880. [Google Scholar] [CrossRef]
- Chesnokova, M.; Nurmukhametov, D.; Ponomarev, R.; Agliullin, T.; Kuznetsov, A.; Sakhabutdinov, A.; Morozov, O.; Makarov, R. Microscopic Temperature Sensor Based on End-Face Fiber-Optic Fabry–Perot Interferometer. Photonics 2024, 11, 712. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; He, X.; Ji, H.; Li, Y.; Duan, X.; Guo, F. Prediction of Vehicle Driver’s Facial Air Temperature With SVR, ANN, and GRU. IEEE Access 2022, 10, 20212–20222. [Google Scholar] [CrossRef]
- Almassri, A.M.M.; Wan Hasan, W.Z.; Ahmad, S.A.; Shafie, S.; Wada, C.; Horio, K. Self-Calibration Algorithm for a Pressure Sensor with a Real-Time Approach Based on an Artificial Neural Network. Sensors 2018, 18, 2561. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Zhao, C.; Wang, Y.; Wang, H. Machine-Learning-Based Calibration of Temperature Sensors. Sensors 2023, 23, 7347. [Google Scholar] [CrossRef]
- Koziel, S.; Pietrenko-Dabrowska, A.; Wojcikowski, M.; Pankiewicz, B. Field calibration of low-cost particulate matter sensors using artificial neural networks and affine response correction. Measurement 2024, 230, 114529. [Google Scholar] [CrossRef]
- Nan, J.; Chen, J.; Li, M.; Li, Y.; Ma, Y.; Fan, X. A Temperature Prediction Model for Flexible Electronic Devices Based on GA-BP Neural Network and Experimental Verification. Micromachines 2024, 15, 430. [Google Scholar] [CrossRef]
- Ren, L.; Zhao, J.; Zhou, Y.; Li, L.; Zhang, Y.-n. Artificial neural network-assisted optical fiber sensor for accurately measuring salinity and temperature. Sens. Actuator A-Phys. 2024, 366, 114958. [Google Scholar] [CrossRef]
- Yu, Y.; Cui, S.; Yang, G.; Xu, L.; Chen, Y.; Cao, K.; Wang, L.; Yu, Y.; Zhang, X. ANN-Assisted High-Resolution and Large Dynamic Range Temperature Sensor Based on Simultaneous Microwave Photonic and Optical Measurements. IEEE Sens. J. 2023, 23, 1105–1114. [Google Scholar] [CrossRef]
- Shi, H.; Hu, S.; Zhang, J. LSTM based prediction algorithm and abnormal change detection for temperature in aerospace gyroscope shell. Int. J. Intell. Comput. Cybern. 2019, 12, 274–291. [Google Scholar] [CrossRef]
- Paul, A.; Shekhar Roy, S. Numerical simulation to predict printed width in EHD inkjet 3D printing process. Mater. Today Proc. 2022, 62, 373–379. [Google Scholar] [CrossRef]
- Mkhize, N.; Bhaskaran, H. Electrohydrodynamic Jet Printing: Introductory Concepts and Considerations. Small Sci. 2021, 2, 73. [Google Scholar] [CrossRef]
- VijayaSekhar, K.; Acharyya, S.G.; Debroy, S.; Miriyala, V.P.K.; Acharyya, A. Self-healing phenomena of graphene: Potential and applications. Open Phys. 2016, 14, 364–370. [Google Scholar] [CrossRef]
- Jung, E.M.; Lee, S.W.; Kim, S.H. Printed ion-gel transistor using electrohydrodynamic (EHD) jet printing process. Org. Electron. 2018, 52, 123–129. [Google Scholar] [CrossRef]
- Ail, S.; Hassan, A.; Hassan, G.; Bae, J.H.; Lee, C.H. All-printed humidity sensor based on graphene/methyl-red composite with high sensitivity. Carbon NY 2016, 105, 23–32. [Google Scholar] [CrossRef]
- Du, F.; Scogna, R.C.; Zhou, W.; Brand, S.; Fischer, J.E.; Winey, K.I. Nanotube Networks in Polymer Nanocomposites: Rheology and Electrical Conductivity. Macromolecules 2004, 37, 9048–9055. [Google Scholar] [CrossRef]
- Rogers, J.A.; Someya, T.; Huang, Y. Materials and Mechanics for Stretchable Electronics. Science 2010, 327, 1603–1607. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.M.; Khoshgoftaar, T.M. Survey on deep learning with class imbalance. J. Big Data 2019, 6, 27. [Google Scholar] [CrossRef]
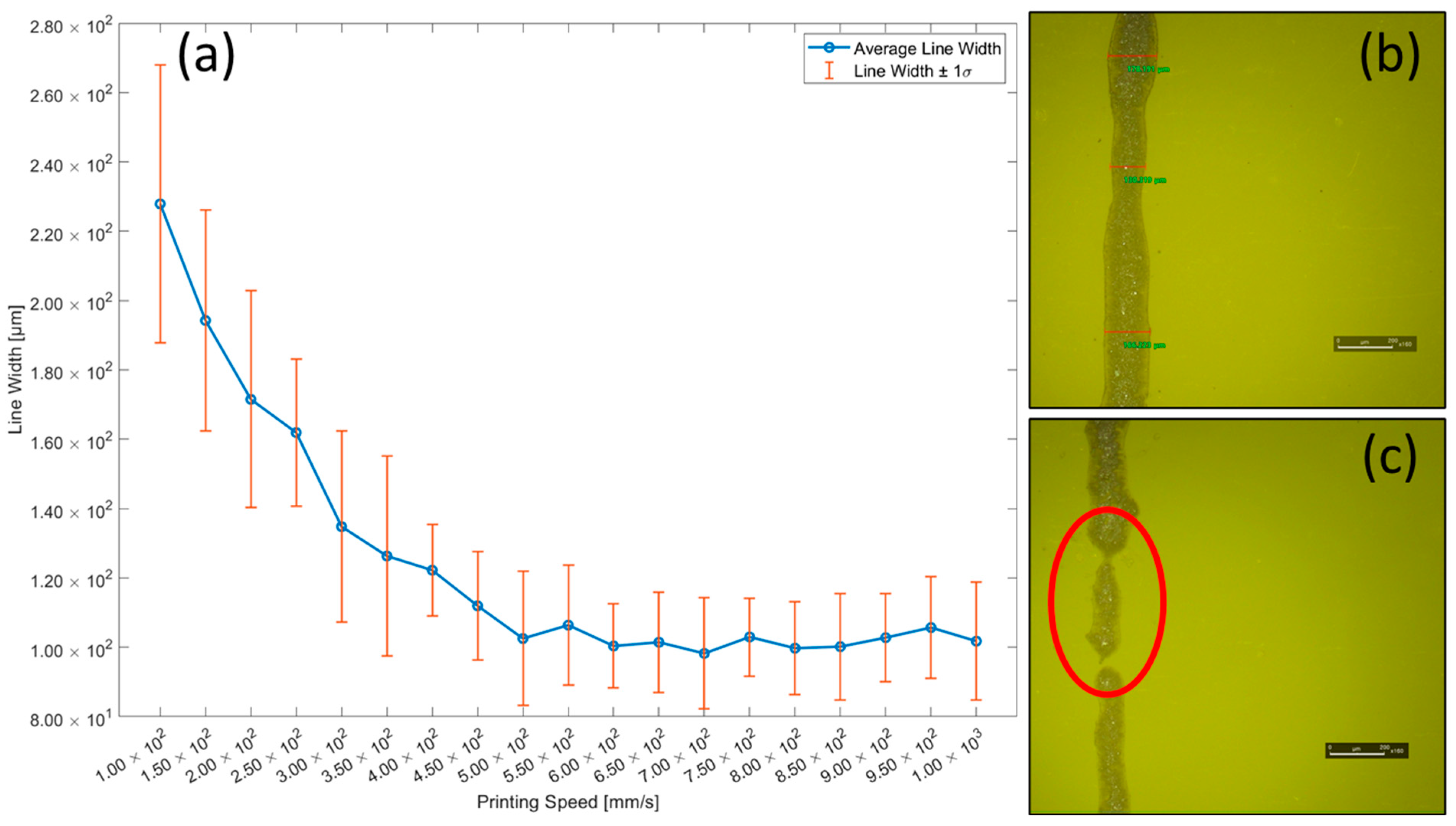
| Printing Speed [mm/s] | Average Line Width [μm] | STD of Line Width [μm] |
|---|---|---|
| 100 | 227.905 | 40.014 |
| 150 | 194.258 | 31.908 |
| 200 | 171.500 | 31.282 |
| 250 | 161.917 | 21.147 |
| 300 | 134.793 | 27.542 |
| 350 | 126.329 | 28.752 |
| 400 | 122.213 | 13.211 |
| 450 | 111.955 | 15.631 |
| 500 | 102.520 | 19.366 |
| 550 | 106.382 | 17.277 |
| 600 | 100.367 | 12.141 |
| 650 | 101.443 | 14.434 |
| 700 | 98.214 | 16.020 |
| 750 | 102.963 | 11.233 |
| 800 | 99.733 | 13.358 |
| 850 | 100.177 | 15.366 |
| 900 | 102.773 | 12.790 |
| 950 | 105.686 | 14.728 |
| 1000 | 101.760 | 16.996 |
| Parameter | Value [Unit] |
|---|---|
| Move acceleration [X, Y axis] | 250 [mm/s2] |
| Print speed [X, Y axis] | 250 [mm/s] |
| Printing position [Z axis] | 1000 [μm] |
| Printing voltage [DC] | 2.3 [kV] |
| L1 STD [%] | L1 TCR [/°C] | L1 NET [°C] | L2 STD [%] | L2 TCR [/°C] | L2 NET [°C] | ||
|---|---|---|---|---|---|---|---|
| Cycle 1 | 0.105 | 0.107 | 1.970 | 0.0226 | 0.112 | 1.892 | |
| Cycle 2 | 0.171 | 0.108 | 2.015 | 0.0801 | 0.113 | 1.986 | |
| Cycle 3 | 0.218 | 0.108 | 1.984 | 0.1223 | 0.113 | 1.971 | |
| Static Thermal Condition | Dynamic Thermal Condition | |
|---|---|---|
| NET_Heating [°C] | 2.313 | 14.065 |
| NET_Cooling [°C] | 2.053 | 18.446 |
| Hysteresis_Area [%] | 0.077 | 2.604 |
| Before Compensation | After Compensation | |
|---|---|---|
| NET_Heating [°C] | 14.065 | 14.059 |
| NET_Cooling [°C] | 18.446 | 18.457 |
| Hysteresis_Area [%] | 2.604 | 2.605 |
| Total Data | Train Data | Validation Data | Test Data | Input Data | Output Data |
|---|---|---|---|---|---|
| 94,580 [100%] | 47,290 [50%] | 23,645 [25%] | 23,645 [25%] | Resistance, Resistance ratio | Temperature |
| Model | Activation Function | Epoch | Early Stopping | Layers |
|---|---|---|---|---|
| DREFU | ReLU | 100 | None | 128/128/128 (Hidden layers) |
| DREES | 78 | O | ||
| DLRFU | Leaky ReLU | 100 | None | |
| DLRES | 23 | O |
| Model | Time Step | Epoch | Early Stopping | Layers |
|---|---|---|---|---|
| LSMLFU | 100 | 100 | None | 32/32 (LSTM layers) 128/128/128 (Hidden layers) |
| LSMLES | 78 | O | ||
| LS100FU | 100 | None | 16 (LSTM layer) 128 (Hidden layer) | |
| LS100ES | 70 | O | ||
| LS300FU | 300 | None | ||
| LS300ES | 202 | O |
| Model | RMSE [°C] | R2 Score |
|---|---|---|
| Lasso—Poly | 0.5077 | 0.9988 |
| DREFU | 0.4602 | 0.9990 |
| DREES | 0.4140 | 0.9992 |
| DLRFU | 0.4336 | 0.9991 |
| DLRES | 0.4031 | 0.9992 |
| Model | RMSE [°C] | R2 Score |
|---|---|---|
| LSMLFU | 0.4279 | 0.9991 |
| LSMLES | 0.4126 | 0.9992 |
| LS100FU | 0.3616 | 0.9994 |
| LS100ES | 0.3792 | 0.9993 |
| LS300FU | 0.3680 | 0.9994 |
| LS300ES | 0.3373 | 0.9995 |
| Model | R2 Score | RMSE [°C] | MAE [°C] |
|---|---|---|---|
| LSTM | 0.7989 | 4.8987 | 4.0880 |
| DNN | 0.4199 | 9.3089 | 7.0781 |
| Lasso-Poly | −0.4407 | 12.4510 | 10.2030 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, U.-J.; Ahn, J.-H.; Lee, J.-H.; Lee, C.-Y. Temperature Calibration Using Machine Learning Algorithms for Flexible Temperature Sensors. Sensors 2025, 25, 5932. https://doi.org/10.3390/s25185932
Kim U-J, Ahn J-H, Lee J-H, Lee C-Y. Temperature Calibration Using Machine Learning Algorithms for Flexible Temperature Sensors. Sensors. 2025; 25(18):5932. https://doi.org/10.3390/s25185932
Chicago/Turabian StyleKim, Ui-Jin, Ju-Hun Ahn, Ji-Han Lee, and Chang-Yull Lee. 2025. "Temperature Calibration Using Machine Learning Algorithms for Flexible Temperature Sensors" Sensors 25, no. 18: 5932. https://doi.org/10.3390/s25185932
APA StyleKim, U.-J., Ahn, J.-H., Lee, J.-H., & Lee, C.-Y. (2025). Temperature Calibration Using Machine Learning Algorithms for Flexible Temperature Sensors. Sensors, 25(18), 5932. https://doi.org/10.3390/s25185932







