Receiver Location Optimization for Heterogeneous S-Band Marine Transmitters in Passive Multistatic Radar Networks via NSGA-II
Abstract
1. Introduction
2. Materials and Methods
2.1. Analysis of Detection Performance of Non-Cooperative Multistatic Radar Systems
- (1)
- The detection probability of the target by the detection system within a specific direction and distance range, with a focus on analyzing the influence of environmental factors and disturbances on the detection effect of the target—by comprehensively considering these factors, the target detection capability of radars in complex environments can be evaluated more accurately.
- (2)
- The maximum detection distance that the detection system can achieve under the given false alarm rate and detection probability—this method starts from the perspective of radar layout and configuration to analyze the overall performance of the system. By setting reasonable false alarm rates and detection probability thresholds, it assesses the maximum detection distance that the radar can achieve while maintaining high performance.
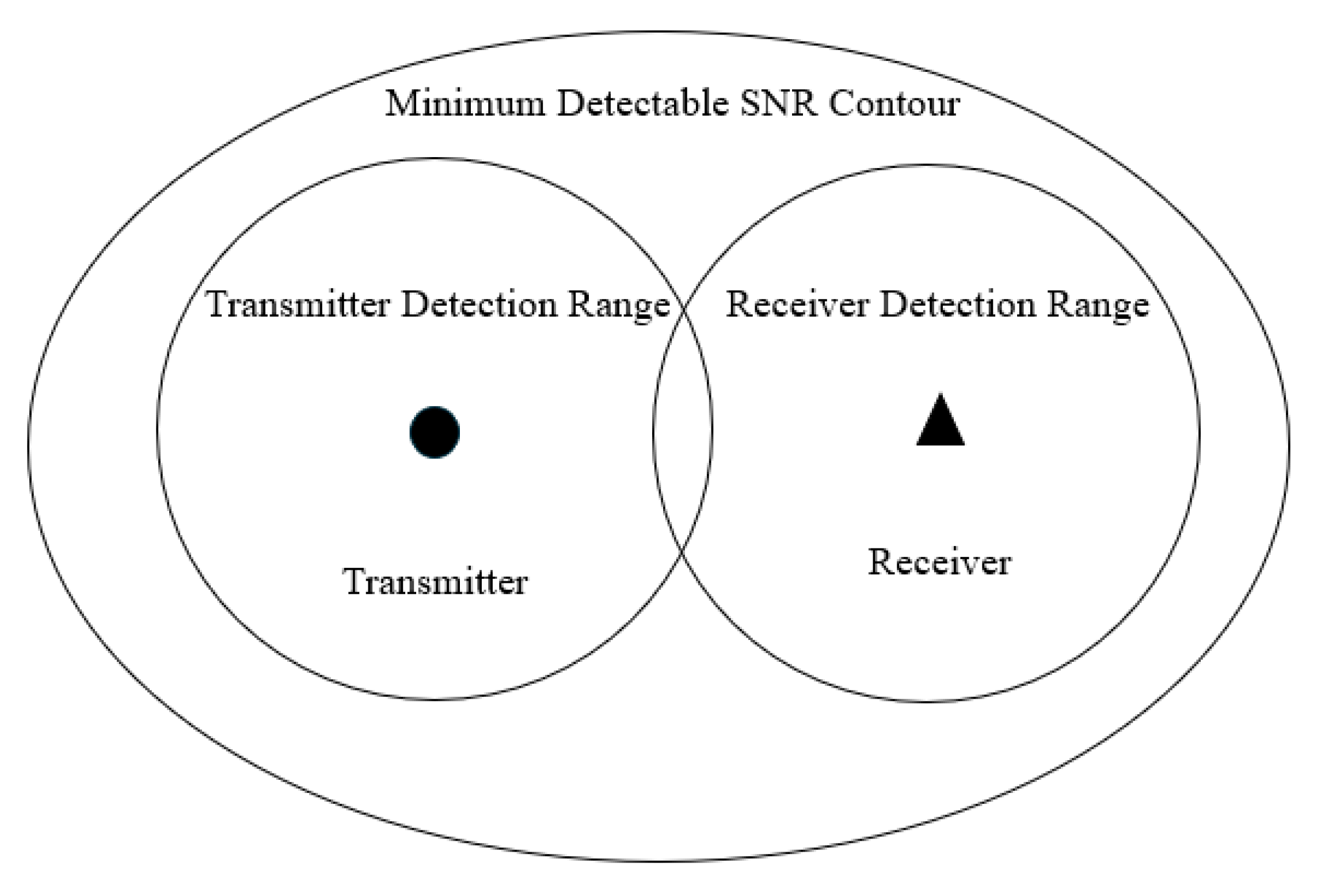
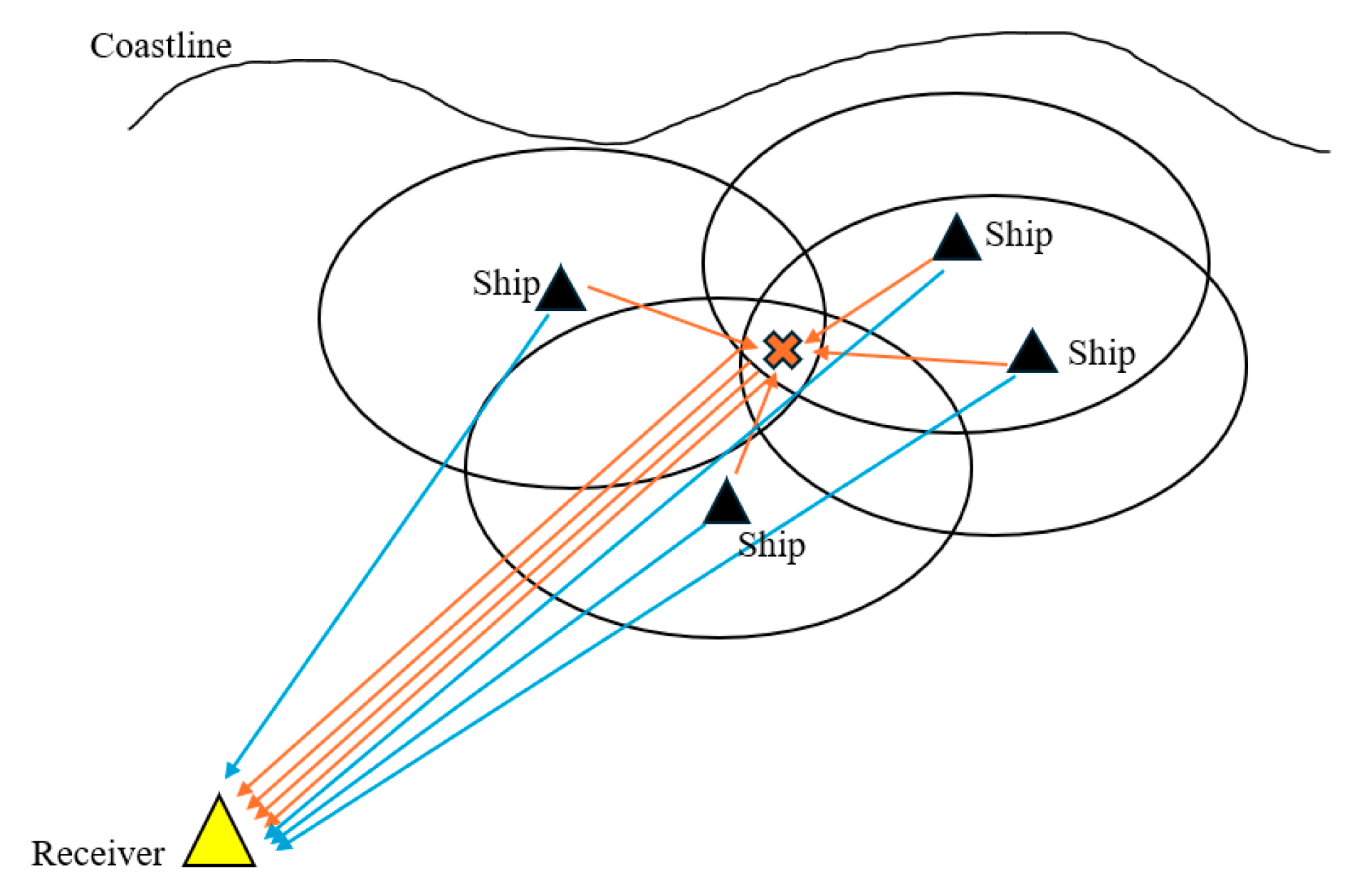
2.1.1. Multistatic Radar Detection Range
2.1.2. Multistatic Radar Positioning Method
- (1)
- Positioning methods based on time information, which measure time information such as the Time Difference of Arrival (TDOA) and the distance between two bases through multistatic radar systems. In TDOA, the time difference of signal arrival is measured by multiple receiving stations, and the intersection point of the hyperbola is formed to determine the target position. This method requires high-precision time synchronization and is suitable for distributed radar systems. In the bistatic distance and method, the total distance from the transmitting station to the target and then to the receiving station (bistatic distance) is utilized. Multiple bistatic distances form an elliptical trajectory, and the target is located through the intersection of the ellipses [11].
- (2)
- Angle of Arrival (AOA) and other angular information-based positioning techniques use the intersection of geometric triangles to estimate the position of each receiving station, which measures the incident angle of the target signal. High-precision direction-finding devices, including phased array antennas, are necessary for this technique [12].
- (3)
- The Doppler frequency shift-based positioning technique uses data from several receiving stations along with the difference in Doppler frequency shift brought on by the target’s movement to determine the target’s position and speed. This method is mostly applicable to the dynamic target tracking of radar transmission [13].
- (4)
- By integrating TDOA with AOA and combining temporal information with angular information for hybrid positioning, the robustness of positioning is enhanced and geometric dilution errors are reduced [14].
- (1)
- Time error
- (2)
- Baseline error:
- (3)
- Azimuth error:
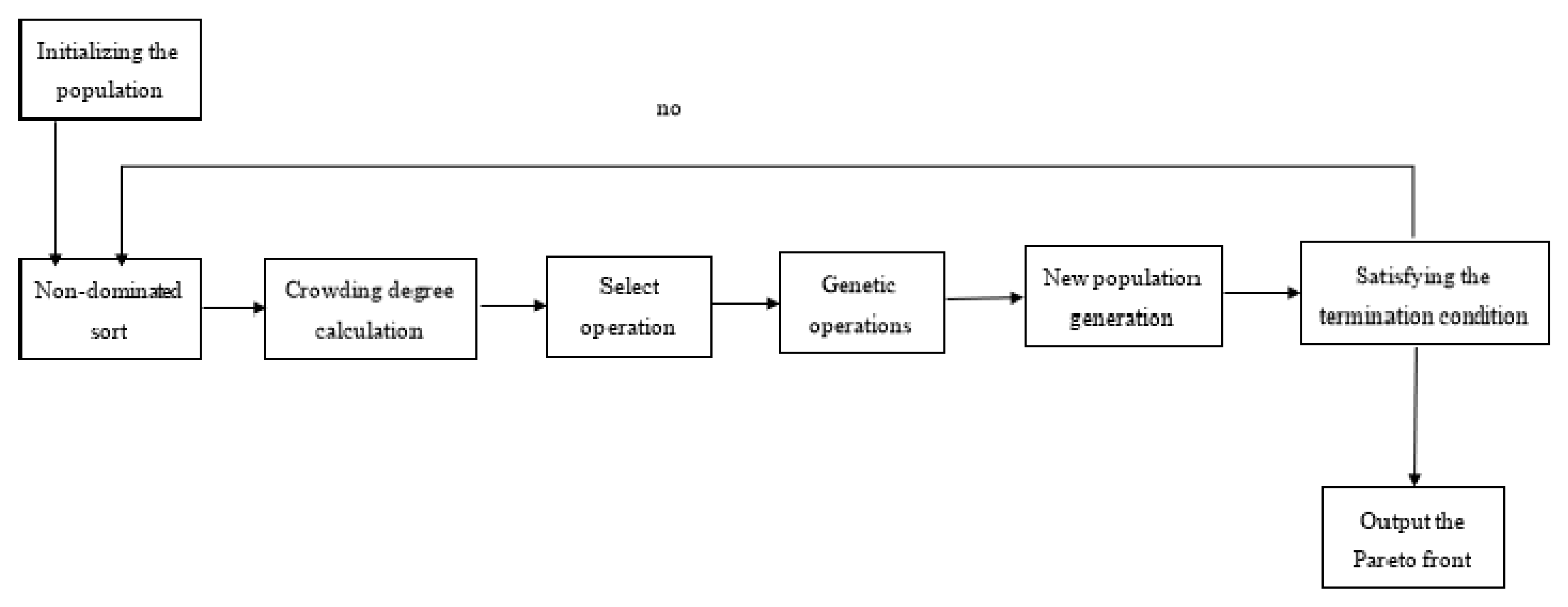
2.2. Non-Dominated Sorting Genetic Algorithm
2.2.1. The Core Principle of Non-Dominated Sorting Genetic Algorithm
2.2.2. Multistatic Radar Optimization
3. Results
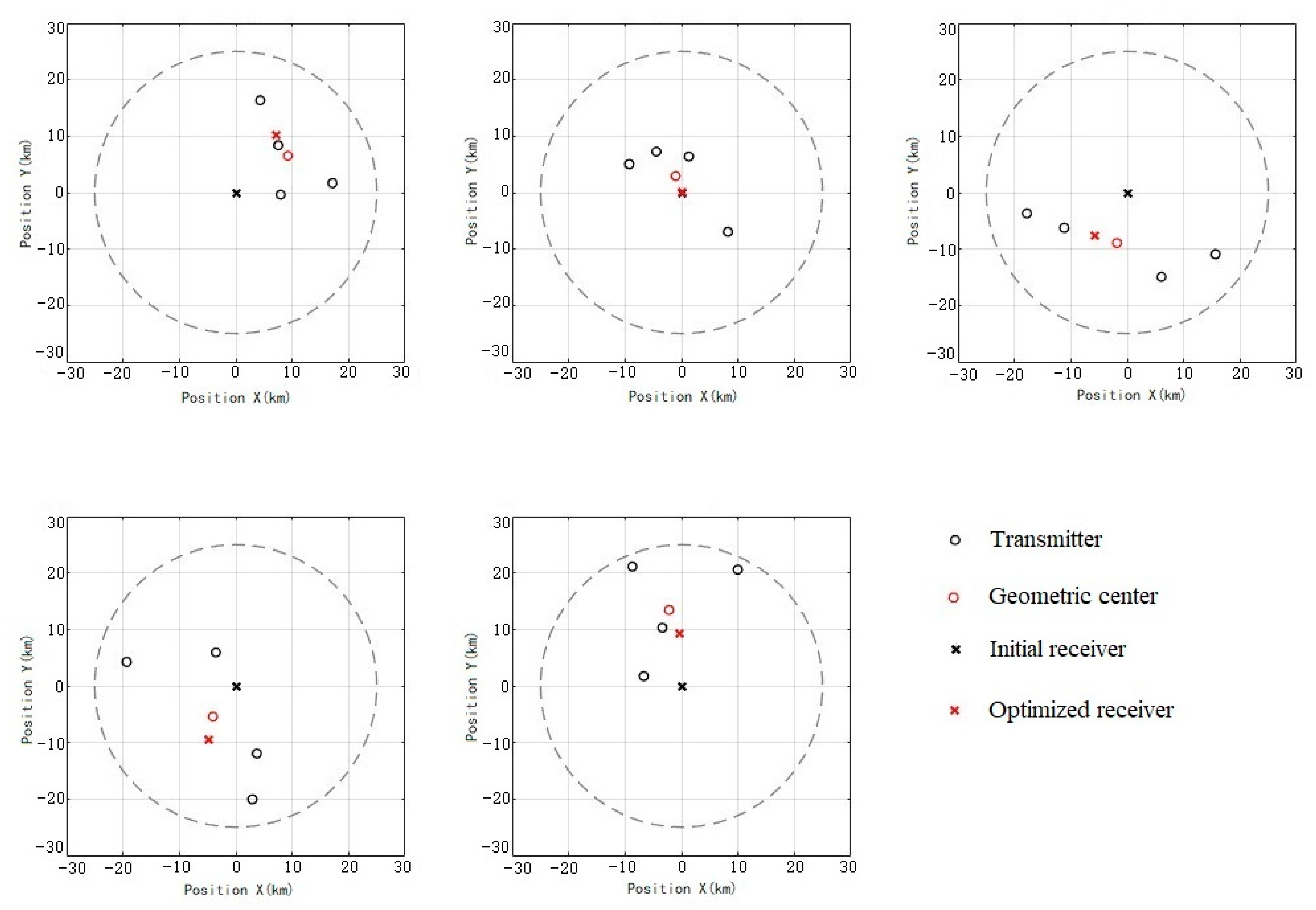
3.1. Simulation Process
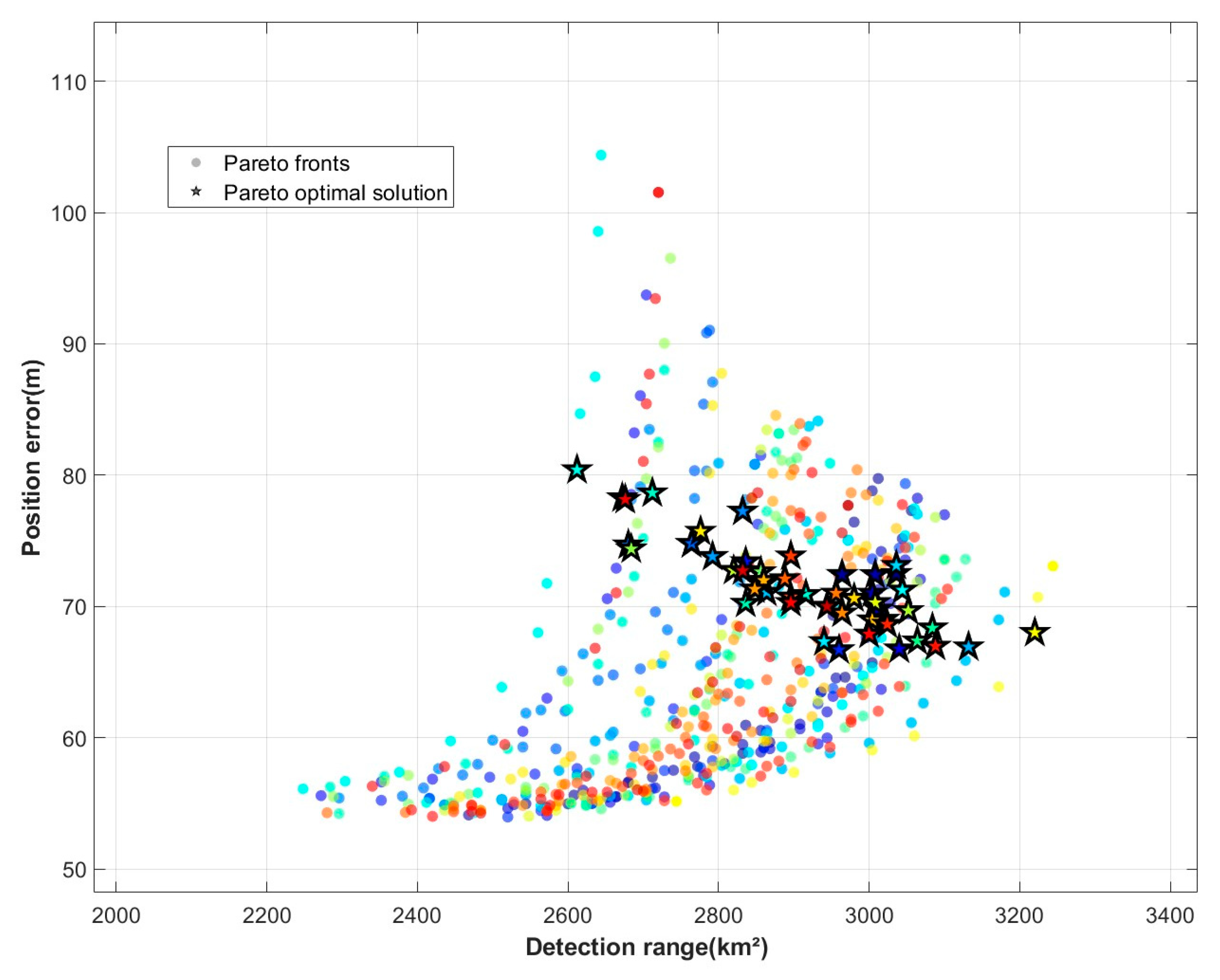
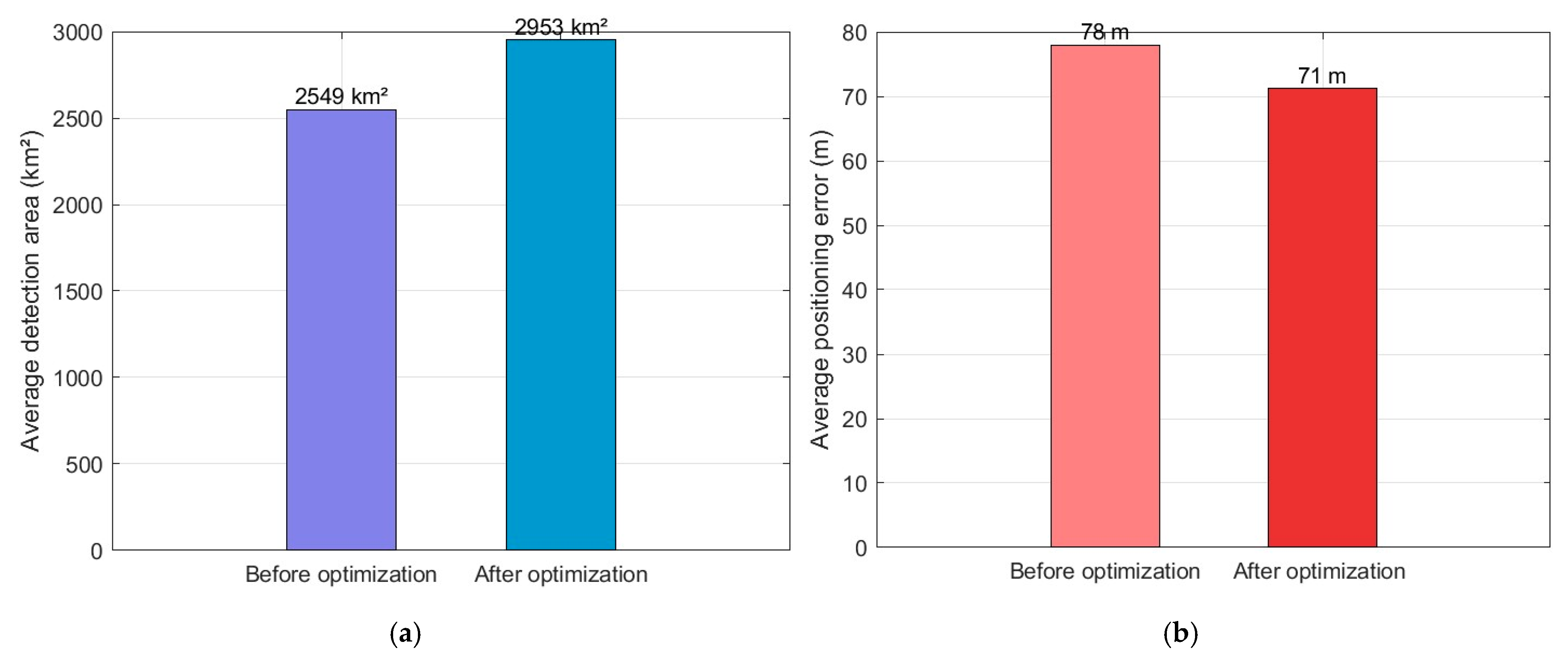
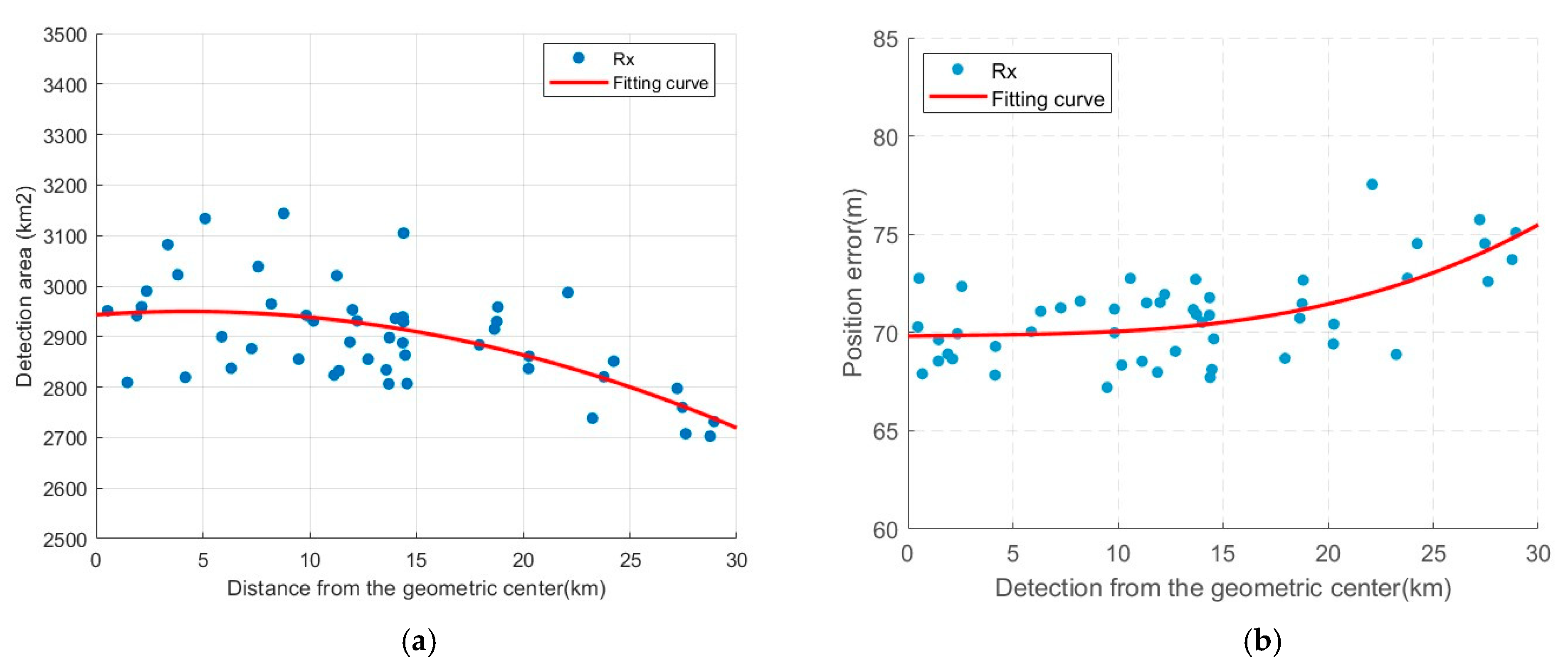
3.2. Analysis of Simulation Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ananya, D.; Aradhana, M.; Surajit, D.; Kandarpa, K.S. Artificial Intelligence in Radar Technology and Communication Network. In Proceedings of the 2024 MIT Art, Design and Technology School of Computing International Conference (MITADTSoCiCon), Pune, India, 25–27 April 2024; pp. 1–8. [Google Scholar] [CrossRef]
- Santos, J.; Pedersen, M.L.; Ulusoy, B.; Weinell, C.E.; Pedersen, H.C.; Petersen, P.M.; Dam-Johansen, K.; Pedersen, C. A Tunable Hyperspectral Imager for Detection and Quantification of Marine Biofouling on Coated Surfaces. Sensors 2022, 22, 7074. [Google Scholar] [CrossRef] [PubMed]
- Si, M.; Song, J.; Yang, F. Performance simulation analysis of non-cooperative multi-base radar system. Radar Sci. Technol. 2024, 22, 69–76+86. [Google Scholar]
- Griffiths, H.D.; Baker, C.J. An Introduction to Passive Radar; Artech House: Norwood, MA, USA, 2017. [Google Scholar]
- Zhuan, J.; Song, J.; Xiong, W.; Wang, Z. Overview of Non-cooperative Radar Illuminator Passive Bistatic Radar. J. Detect. Control 2023, 45, 35–45+69. [Google Scholar]
- Sing, C.S. Passive Multistatic Detection of Maritime Targets Using Opportunistic Radar. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 2014. [Google Scholar]
- Tan, Q.J.O. Passive Coherent Detection and Target Location with Multiple Non-Cooperative Transmitters. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 2015. [Google Scholar]
- Saillant, S.; Bok, D.; Molinié, J.P.; Leventis, A.; Samczynski, P.; Brouar, P. iFURTHER Project-A Cognitive Network of HF Radars for Europe Defence. In Proceedings of the 2023 IEEE International Radar Conference (RADAR), Sydney, Australia, 6–10 November 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Księżyk, A.; Płotka, M.; Abratkiewicz, K.; Maksymiuk, R.; Wszołek, J.; Samczyńs, J. Opportunities and Limitations in Radar Sensing Based on 5G Broadband Cellular Networks. IEEE Aerosp. Electron. Syst. Mag. 2023, 38, 4–21. [Google Scholar] [CrossRef]
- Bao, Q.; Wang, S.; Pan, J.; Zhu, Q. Key technology analysis of target detection system based on non-cooperative radar illuminator. Chin. J. Radio Sci. 2020, 35, 496–503. [Google Scholar]
- Fatima, G.; Stoica, P.; Aubry, A.; De Maio, A.; Babu, P. Optimal Placement of the Receivers for Multistatic Target Localization. IEEE Trans. Radar Syst. 2024, 2, 391–403. [Google Scholar] [CrossRef]
- Al-Sadoon, M.A.G.; Patwary, M.N.; Rahman, M.A.; Abd-Alhameed, R.A. Efficient Small Angle-of-Arrival Array Sensor for Intelligent Localisation and Tracking Systems. In Proceedings of the 2021 IEEE 4th 5G World Forum (5GWF), Montreal, QC, Canada, 13–15 October 2021; pp. 475–480. [Google Scholar]
- Shiraki, N.; Honma, N.; Murata, K.; Nakayama, T.; Iizuka, S. Experimental Evaluation of Multi-Target Localization Accuracy Using Multistatic MIMO Radar. IEEE Sens. J. 2023, 23, 28863–28871. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, J. Analytical evaluation of geometric dilution of precision for three-dimensional angle-of-arrival target localization in wireless sensor networks. Int. J. Distrib. Sens. Netw. 2020, 16, 1550147720920471. [Google Scholar] [CrossRef]
- Nasso, I.; Santi, F.; Pastina, D. Maritime Targets Velocity Estimation in Space-Based Passive Multistatic Radar Using Long Integration Times. IEEE Access 2021, 9, 163764–163779. [Google Scholar] [CrossRef]
- Pant, M.; Snasel, V.; Verma, S. A Comprehensive Review on NSGA-II for Multi-Objective Combinatorial Optimization Problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Xue, L.; Zeng, P.; Yu, H. SETNDS: A SET-Based Non-Dominated Sorting Algorithm for Multi-Objective Optimization Problems. Appl. Sci. 2020, 10, 6858. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, Y.; Sun, S.; Ting, L.; Yu, S. A comprehensive survey on NSGA-II for multi-objective optimization and applications. Artif. Intell. Rev. 2023, 56, 15217–15270. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, B.M.; Lee, T.H. Optimal deployment of mobile sensors for target tracking in 2D and 3D spaces. IEEE/CAA J. Autom. Sin. 2014, 1, 24–30. [Google Scholar] [CrossRef][Green Version]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength Pareto evolutionary algorithm. TIK Rep. 2001, 103. [Google Scholar] [CrossRef]
- Oguz-Ekim, P.; Gomes, J.P.; Xavier, J.; Oliveira, P. Robust Localization of Nodes and Time-Recursive Tracking in Sensor Networks Using Noisy Range Measurements. IEEE Trans. Signal Process. 2011, 59, 3930–3942. [Google Scholar] [CrossRef]


| Serial Number | Radar Parameters | Measurement Value |
|---|---|---|
| 1 | Width of beam | 1.8° |
| 2 | Scan rate | 30 rpm |
| 3 | Power output | 30 kw |
| 4 | Frequency | 3000 MHz |
| 5 | Gain of antenna | 28 dB |
| 6 | Wavelength | 0.0995 m |
| 7 | Bandwidth of noise | 5 MHz |
| 8 | Pulse repetition frequency | 1000 Hz |
| Serial Number | Algorithm Parameters | Measurement Value |
|---|---|---|
| 1 | Population size | 50 |
| 2 | Generations | 50 |
| 3 | Crossover rates | 0.8 |
| 4 | Migration rates | 0.2 |
| 5 | Bounds | Geometric center ± 25 km |
| 6 | Encoding | Real encoding |
| 7 | Penalty coefficient | 50 |
| Method | Optimization Objectives | Constraints | Gains |
|---|---|---|---|
| Convex Relaxation [19] | GDOP minimization | Linear/Convex | ~15–20% GDOP reduction |
| MOEA/D [20] | Coverage, Accuracy | Geometric | ~15–20% coverage improvement |
| SPEA2 [21] | Detection probability, Positioning error | Energy, Geometric | ~10–16% error reduction |
| Gradient-based [22] | CRLB minimization | Differentiable constraints | ~12–18% CRLB improvement |
| Proposed NSGA-II | Coverage area, Localization accuracy | Bistatic angle, Baseline distance | 15.8% coverage gain, 8.9% error reduction |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; He, P.; Song, J.; Wang, Z. Receiver Location Optimization for Heterogeneous S-Band Marine Transmitters in Passive Multistatic Radar Networks via NSGA-II. Sensors 2025, 25, 5861. https://doi.org/10.3390/s25185861
Li X, He P, Song J, Wang Z. Receiver Location Optimization for Heterogeneous S-Band Marine Transmitters in Passive Multistatic Radar Networks via NSGA-II. Sensors. 2025; 25(18):5861. https://doi.org/10.3390/s25185861
Chicago/Turabian StyleLi, Xinpeng, Pengfei He, Jie Song, and Zhongxun Wang. 2025. "Receiver Location Optimization for Heterogeneous S-Band Marine Transmitters in Passive Multistatic Radar Networks via NSGA-II" Sensors 25, no. 18: 5861. https://doi.org/10.3390/s25185861
APA StyleLi, X., He, P., Song, J., & Wang, Z. (2025). Receiver Location Optimization for Heterogeneous S-Band Marine Transmitters in Passive Multistatic Radar Networks via NSGA-II. Sensors, 25(18), 5861. https://doi.org/10.3390/s25185861






