Strain Sensor-Based Fatigue Prediction for Hydraulic Turbine Governor Servomotor in Complementary Energy Systems
Abstract
1. Introduction
2. Materials and Methods
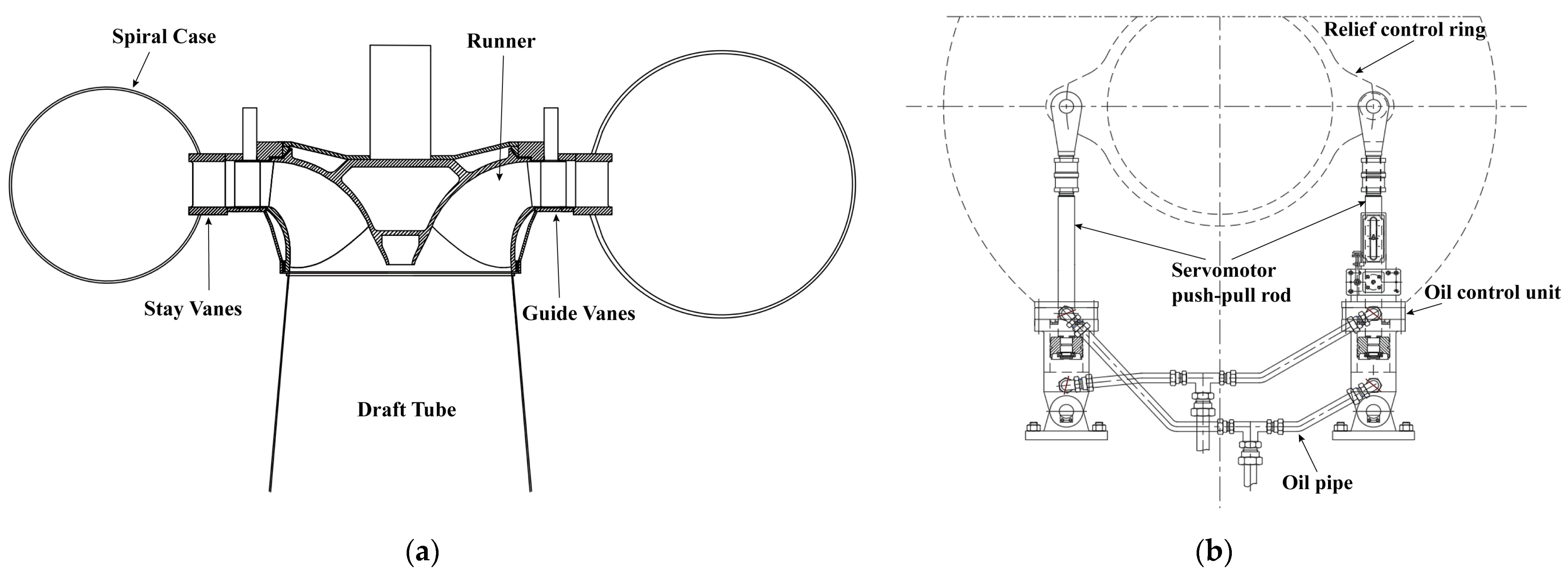
2.1. Test Power Station and Equipment Parameters
2.2. Strain Testing System Configuration
2.3. Data Acquisition and Processing
- (1)
- Zero drift correction (controlled within ±2 με);
- (2)
- Noise filtering using 5-point moving average combined with 50 Hz notch filter;
- (3)
- Signal conditioning to improve SNR from 45 dB to 65 dB;
- (4)
- Strain-to-stress conversion (based on material elastic modulus E = 206 GPa);
- (5)
- Load calculation (based on rod cross-sectional area A = 0.785 × 10−2 m2).
2.4. Finite Element Modeling
2.5. Fatigue Life Prediction Model
3. Results
3.1. Sensor Performance Validation
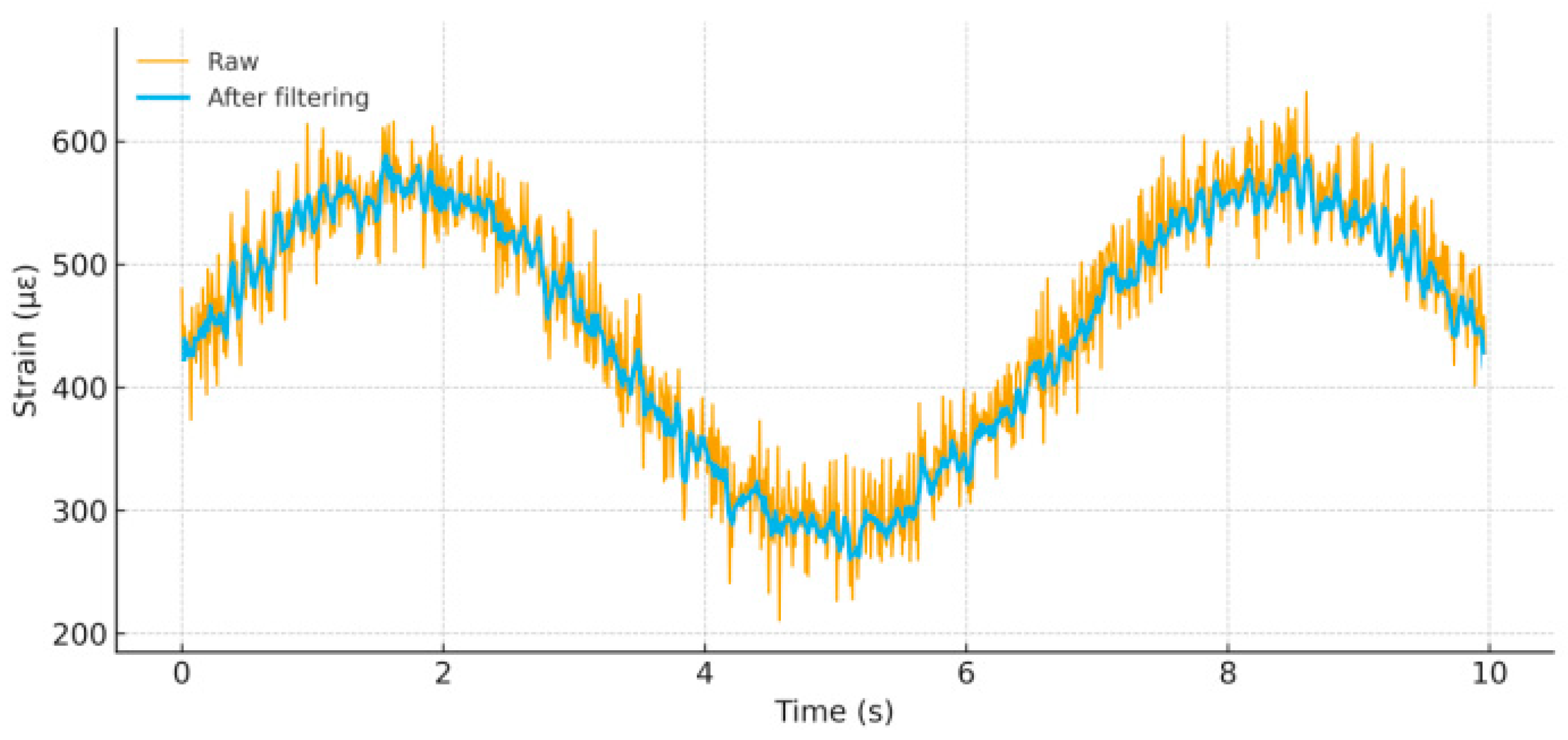
3.2. Strain Response Characteristics Analysis
3.3. Load Strain Relationship Analysis
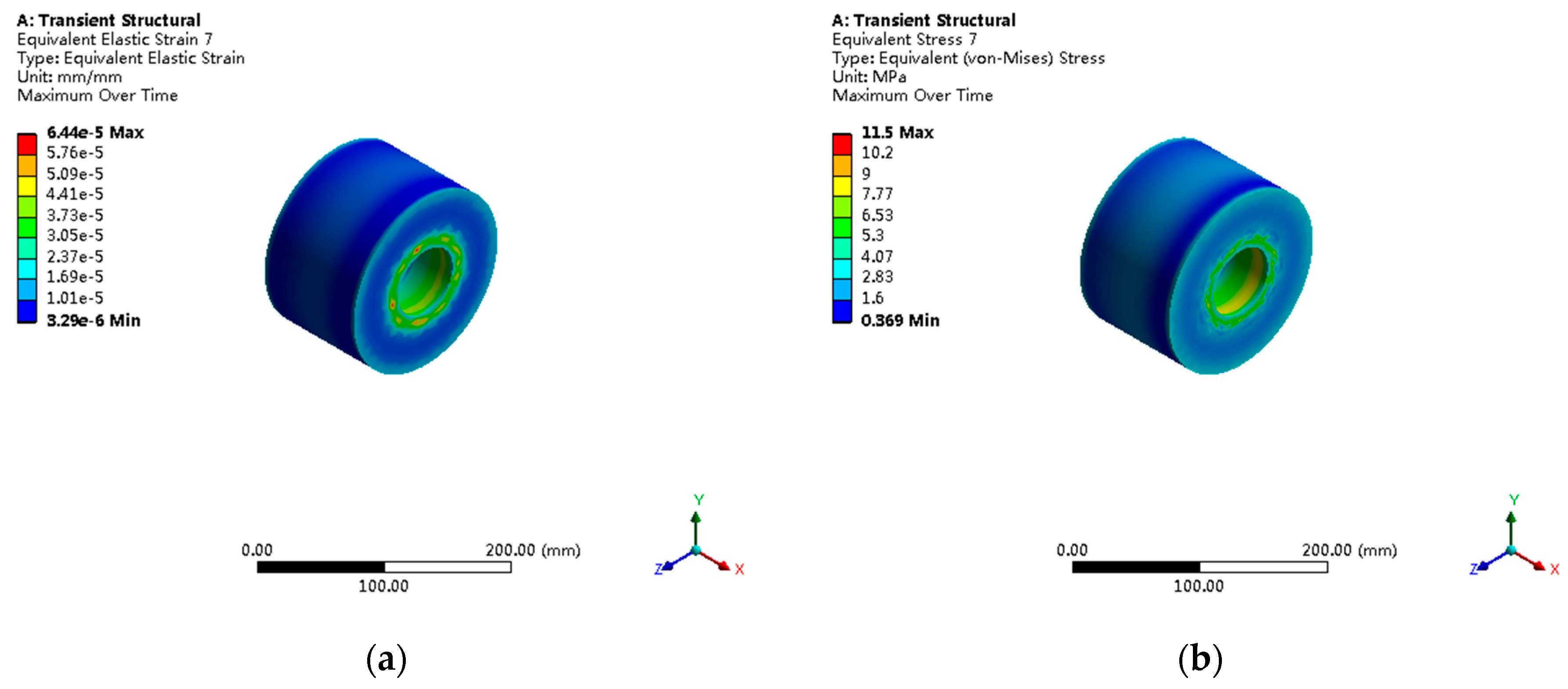
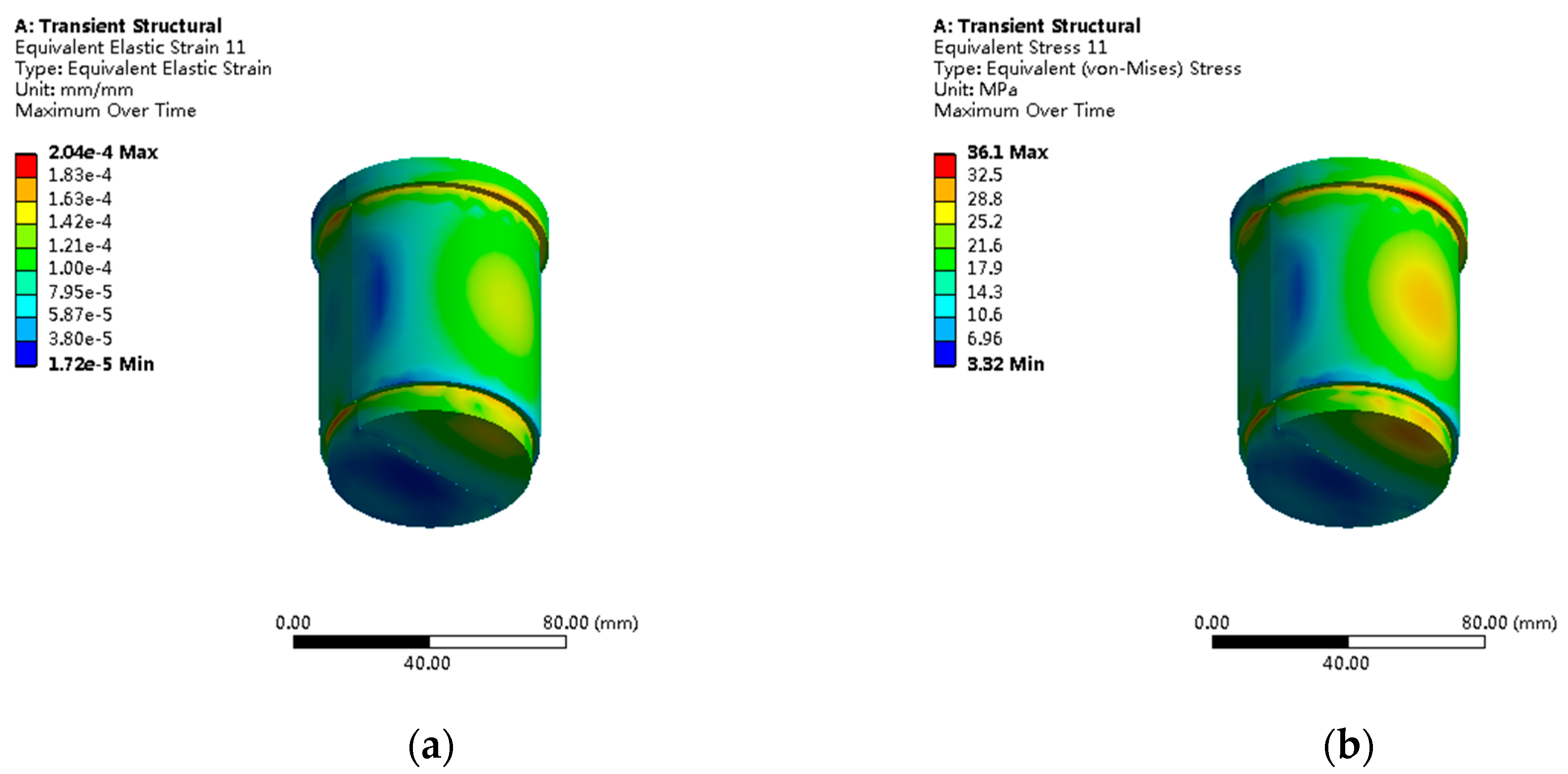
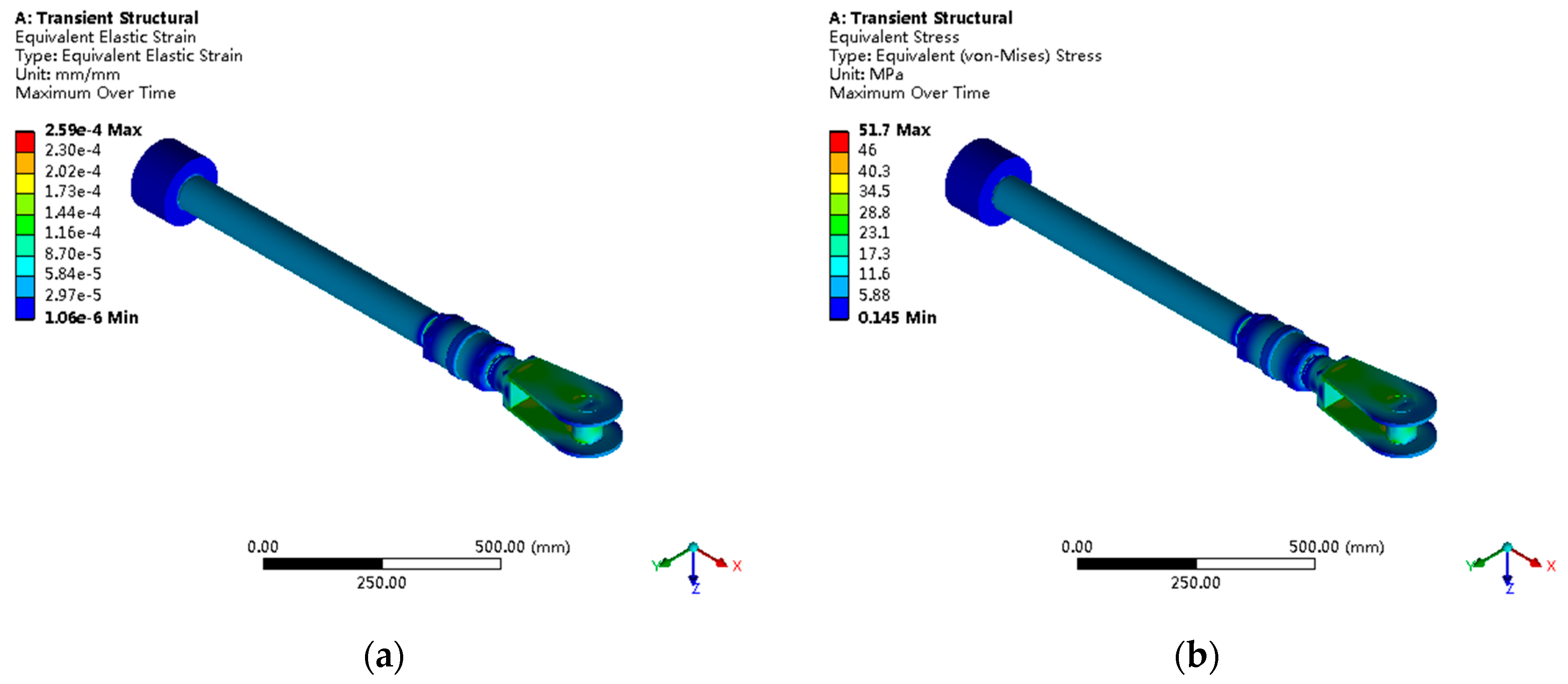
3.4. Finite Element Analysis Results
3.5. Fatigue Life Prediction Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Jia, H.; Li, H.; Zhang, Z.; Sun, W. Complementary Analysis and Performance Improvement of a Hydro-Wind Hybrid Power System. Water 2024, 16, 2912. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, J.; Yuan, S.; Li, H.; Chen, D.; Zhang, J. Comprehensive Regulation Benefits of Hydropower Generation System in Reducing Wind Power Fluctuation. Water 2021, 13, 2987. [Google Scholar] [CrossRef]
- Adamantiades, A.; Kessides, I. Nuclear power for sustainable development: Current status and future prospects. Energy Policy 2009, 37, 5149–5166. [Google Scholar] [CrossRef]
- Mai, V.; Pham, Q.H.; Favrel, A.; Gauthier, J.-P.; Gagnon, M. Active learning-based optimization of hydroelectric turbine startup to minimize fatigue damage. Renew. Energy 2025, 256. [Google Scholar] [CrossRef]
- Liu, X.; Luo, Y.; Wang, Z. A review on fatigue damage mechanism in hydro turbines. Renew. Sustain. Energy Rev. 2016, 54, 1–14. [Google Scholar] [CrossRef]
- Muser, T.; Krymova, E.; Morabito, A.; Seydoux, M.; Vagnoni, E. Fatigue damage reduction in hydropower startups with machine learning. Nat. Commun. 2025, 16, 2961. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, P.; Xiao, H.; Liu, Z.; Liu, W. A study on heat transfer enhancement for solar air heaters with ripple surface. Renew. Energy 2021, 172, 477–487. [Google Scholar] [CrossRef]
- Amini, A.; Rey-Mermet, S.; Crettenand, S.; Münch-Alligné, C. A hybrid methodology for assessing hydropower plants under flexible operations: Leveraging experimental data and machine learning techniques. Appl. Energy 2025, 383. [Google Scholar] [CrossRef]
- Vlentín, D.; Egusquiza, E.; Presas, A.; Valero, C.; Egusquiza, M.; Egusquiza, E. Detection of Hydraulic Phenomena in Francis Turbines with Different Sensors. Sensors 2019, 19, 4053. [Google Scholar] [CrossRef]
- Liu, P.; Huang, X.; Yang, T.; Wang, Z. Flow-Induced Fatigue Damage of Large Francis Turbines Under Multiple Operating Loads. Appl. Sci. 2024, 14, 12003. [Google Scholar] [CrossRef]
- Rivas, E.Y.; Vyacheslavov, A.; Gogolinskiy, K.V.; Sapozhnikova, K.; Taymanov, R. Deformation Monitoring Systems for Hydroturbine Head-Cover Fastening Bolts in Hydroelectric Power Plants. Sensors 2025, 25, 2548. [Google Scholar] [CrossRef]
- Kong, L.; Ma, L.; Wang, K.; Peng, X.; Geng, N. Three-Dimensional-Scanning of Pipe Inner Walls Based on Line Laser. Sensors 2024, 24, 3554. [Google Scholar] [CrossRef]
- Zhang, N.; Davis, C.; Chiu, W.K.; Boilard, T.; Bernier, M. Fatigue Performance of Type I Fibre Bragg Grating Strain Sensors. Sensors 2019, 19, 3524. [Google Scholar] [CrossRef]
- Doujak, E.; Maly, A.; Unterluggauer, J.; Haller, F.; Maier, M.; Blasbichler, C.; Stadler, S. Fatigue Strength Analysis of a Prototype Francis Turbine in a Multilevel Lifetime Assessment Procedure Part III: Instrumentation and Prototype Site Measurement. Energies 2023, 16, 6072. [Google Scholar] [CrossRef]
- Mantilla, C.A.; Valdés, J.A.; Casanova, F. Multiaxial fatigue analysis for the shaft of a 100 MW hydro-power generator. J. Mech. Eng. Sci. 2019, 13, 4928–4945. [Google Scholar] [CrossRef]
- Lin, J.; Wu, N.; Li, L.; Xie, M.; Xie, S.; Wang, X.; Brandon, N.; Sun, Y.; Chen, J.; Zhao, Y. Performance and parameter optimization of a capacitive salinity/heat engine for harvesting salinity difference energy and low grade heat. Renew. Energy 2021, 183, 283–293. [Google Scholar] [CrossRef]
- Gagnon, M.; Tahan, A.; Bocher, P.; Thibault, D. Influence of load spectrum assumptions on the expected reliability of hydroelectric turbines: A case study. Struct. Saf. 2014, 50, 1–8. [Google Scholar] [CrossRef]
- Marticorena, M.; Mayer, R.; Vignolo, J.; Vaccaro, D.; Peyrano, O.G. Virtual Sensor Implementation in Hydroelectric Turbines: A Digital Twin Approach for Clearance Violation Analysis. International Conference on the Efficiency and Performance Engineering Network; Springer Nature: Cham, Switzerland, 2023; pp. 63–77. [Google Scholar] [CrossRef]
- Mohammed, Z.; Gill, W.A.; Rasras, M. Double-Comb-Finger Design to Eliminate Cross-Axis Sensitivity in a Dual-Axis Accelerometer. IEEE Sens. Lett. 2017, 1, 1–4. [Google Scholar] [CrossRef]
- Doujak, E.; Unterluggauer, J.; Fillinger, G.; Nocker, A.; Haller, F.; Maier, M.; Stadler, S. Fatigue Strength Analysis of a Prototype Francis Turbine in a Multilevel Lifetime Assessment Procedure Part II: Method Application and Numerical Investigation. Energies 2022, 15, 1165. [Google Scholar] [CrossRef]
- Kinne, M.; Thöns, S. Fatigue Reliability Based on Predicted Posterior Stress Ranges Determined from Strain Measurements of Wind Turbine Support Structures. Energies 2023, 16, 2225. [Google Scholar] [CrossRef]
- Ren, G.; Liu, J.; Wan, J.; Wang, W.; Fang, F.; Hong, F.; Yu, D. Investigating the Complementarity Characteristics of Wind and Solar Power for Load Matching Based on the Typical Load Demand in China. IEEE Trans. Sustain. Energy 2021, 13, 778–790. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, J.; Egusquiza, M.; Chen, D.; Li, F.; Behrens, P.; Egusquiza, E. A review of dynamic models and stability analysis for a hydro-turbine governing system. Renew. Sustain. Energy Rev. 2021, 144, 110880. [Google Scholar] [CrossRef]
- Unterluggauer, J.; Doujak, E.; Bauer, C. Fatigue analysis of a prototype Francis turbine based on strain gauge measurements. Wasserwirtschaft 2019, 109, 66–71. [Google Scholar] [CrossRef]
- Seydoux, M.; Vagnoni, E.; Nicolet, C.; Alligné, S.; Paolone, M. Experimental Investigation of the Fatigue-Induced Damage in Hydroelectric Units During Start-Up. Available at SSRN 4788376. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4788376 (accessed on 1 September 2025).
- Raju, S.K.; Periyasamy, M.; Alhussan, A.A.; Kannan, S.; Raghavendran, S.; El-Kenawy, E.-S.M. Machine learning boosts wind turbine efficiency with smart failure detection and strategic placement. Sci. Rep. 2025, 15, 1485. [Google Scholar] [CrossRef] [PubMed]
- Pacheco, J.; Pimenta, F.; Pereira, S.; Cunha, Á.; Magalhães, F. Fatigue Assessment of Wind Turbine Towers: Review of Processing Strategies with Illustrative Case Study. Energies 2022, 15, 4782. [Google Scholar] [CrossRef]
- Bilen, E.; Azzam, B.; Schelenz, R.; Runkel, T.; Raddatz, M.; Jacobs, G. From Strain to Loads: Development of a Measurement Solution for Wind Turbine Transmission Input Loads during Drivetrain Testing. Sensors 2023, 23, 1824. [Google Scholar] [CrossRef]
- Chen, H.; Pan, J.; Wang, S.; Ma, J.; Zhang, W. Fatigue Damage Assessment of Turbine Runner Blades Considering Sediment Wear. Appl. Sci. 2024, 14, 4660. [Google Scholar] [CrossRef]
- Li, X.; Ren, K.; Zheng, X. Exploring the sensitivity of capacity configuration for multi-energy complementary system across multi-temporal scales. Energy 2025, 326. [Google Scholar] [CrossRef]
- Xiong, H.; Egusquiza, M.; Østergaard, P.A.; Pérez-Díaz, J.I.; Sun, G.; Egusquiza, E.; Patelli, E.; Xu, B.; Duan, H.; Chen, D.; et al. Multi-objective optimization of a hydro-wind-photovoltaic power complementary plant with a vibration avoidance strategy. Appl. Energy 2021, 301. [Google Scholar] [CrossRef]
- Roig, R.; Sánchez-Botello, X.; de la Torre, O.; Ayneto, X.; Högström, C.-M.; Mulu, B.; Escaler, X. Fatigue damage analysis of a Kaplan turbine model operating at off-design and transient conditions. Struct. Health Monit. 2023, 23, 1687–1700. [Google Scholar] [CrossRef]
- Guo, Y.; Ming, B.; Huang, Q.; Jiang, J.; Yu, M.; San, M.; Cheng, L.; Jia, R. Evaluating the flexibility supply and demand reliability of hydro–wind–PV–battery complementary systems under different consumption modes. Appl. Energy 2024, 379. [Google Scholar] [CrossRef]
- Salhaoui, M.; Arioua, M.; Guerrero-González, A.; García-Cascales, M.S. An IoT control system for wind power generators. In International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems; Springer International Publishing: Cham, Switzerland, 2018; pp. 469–479. [Google Scholar] [CrossRef]
- Li, Y.; Bi, M.; Gao, W. Theoretical pressure prediction of confined hydrogen explosion considering flame instabilities. J. Loss Prev. Process. Ind. 2019, 57, 320–326. [Google Scholar] [CrossRef]
- Kofler, W.; Schneider, K.; Schuler, X. Guideline for the Assessment of Fatigue Loaded Components in Hydropower Plants. Wasserwirtschaft 2015, 105, 99–103. [Google Scholar] [CrossRef]
- Nasir, J.; Javed, A.; Ali, M.; Ullah, K.; Kazmi, S.A.A. Capacity optimization of pumped storage hydropower and its impact on an integrated conventional hydropower plant operation. Appl. Energy 2022, 323. [Google Scholar] [CrossRef]
- Owebor, K.; Diemuodeke, E.; Briggs, T.; Imran, M. Power Situation and renewable energy potentials in Nigeria—A case for integrated multi-generation technology. Renew. Energy 2021, 177, 773–796. [Google Scholar] [CrossRef]
- Bhatti, B.A.; Hanif, S.; Alam, J.; Mitra, B.; Kini, R.; Wu, D. Using energy storage systems to extend the life of hydropower plants. Appl. Energy 2023, 337. [Google Scholar] [CrossRef]
- Wang, D.; Li, C.; Mao, J.; Yang, Q. What affects the implementation of the renewable portfolio standard? An analysis of the four-party evolutionary game. Renew. Energy 2023, 204, 250–261. [Google Scholar] [CrossRef]










| Parameter | Value | Additional Specifications |
|---|---|---|
| Turbine Type | Francis turbine | Vertical shaft configuration |
| Rated Head | 130 m | Operating range: 115–145 m |
| Rated Flow | 15.47 m3/s | Flow variation: ±20% |
| Rated Speed | 500 rpm | Speed regulation: ±5% |
| Rated Power | 18.56 MW | Power range: 3.7–19.8 MW |
| Runner Diameter | 1.50 m | 6-blade design |
| Efficiency | 93.3% | At rated conditions |
| Guide Vanes | 20 vanes | Opening range: 13–63% |
| Servomotor Type | Hydraulic actuator | Working pressure: 4.0 MPa |
| Regulation Frequency | Average 24/day | Peak: 50/day in complementary mode |
| Material Property | Specification |
|---|---|
| Piston Material | Carbon Steel ASTM A572 Grade 50 |
| Piston Rod Material | Alloy Steel AISI 4140 |
| Connecting Nut Material | High-Strength Steel ASTM A193 B7 |
| Fork Head Material | Forged Steel AISI 4340 |
| Cylindrical Pin Material | Bearing Steel AISI 52100 |
| Elastic Modulus | 206 GPa |
| Poisson’s Ratio | 0.3 |
| Density | 7850 kg/m3 |
| Yield Strength | 355–1380 MPa (varies by component) |
| Component | Max Stress (MPa) | Equivalent Stress (MPa) | Stress Concentration Factor | Fatigue Life (×106 Cycles) | Safety Factor * | Expected Service Life (Years) | Reliability (20-Year) |
|---|---|---|---|---|---|---|---|
| Piston | 18.3 | 15.8 | 1.32 | 15.2 | 4.8 | >25 | 0.9987 |
| Piston Rod | 27.4 | 23.1 | 2.10 | 8.6 | 3.2 | 22–25 | 0.9823 |
| Connecting Nut | 24.2 | 20.7 | 1.85 | 10.8 | 3.8 | >25 | 0.9891 |
| Fork Head | 51.7 | 48.3 | 3.40 | 1.2 | 1.5 | 12–16 | 0.7234 |
| Cylindrical Pin | 36.1 | 31.6 | 2.65 | 3.8 | 2.3 | 16–20 | 0.8756 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, H.; Zhang, Z.; Liu, X.; Deng, W. Strain Sensor-Based Fatigue Prediction for Hydraulic Turbine Governor Servomotor in Complementary Energy Systems. Sensors 2025, 25, 5860. https://doi.org/10.3390/s25185860
Hua H, Zhang Z, Liu X, Deng W. Strain Sensor-Based Fatigue Prediction for Hydraulic Turbine Governor Servomotor in Complementary Energy Systems. Sensors. 2025; 25(18):5860. https://doi.org/10.3390/s25185860
Chicago/Turabian StyleHua, Hong, Zhizhong Zhang, Xiaobing Liu, and Wanquan Deng. 2025. "Strain Sensor-Based Fatigue Prediction for Hydraulic Turbine Governor Servomotor in Complementary Energy Systems" Sensors 25, no. 18: 5860. https://doi.org/10.3390/s25185860
APA StyleHua, H., Zhang, Z., Liu, X., & Deng, W. (2025). Strain Sensor-Based Fatigue Prediction for Hydraulic Turbine Governor Servomotor in Complementary Energy Systems. Sensors, 25(18), 5860. https://doi.org/10.3390/s25185860





