3D-Printed Wearable Sensors for the Identification of Shoulder Movement Planes
Abstract
1. Introduction
- (i)
- design and manufacturing of the wearable systems through 3D printing using two different polymer materials, TPU 95A and 85A;
- (ii)
- metrological characterization of each sensor, evaluating its sensitivity to strain and temperature, and its hysteresis error;
- (iii)
- a pull-out test to determine the strength of the interfacial bond between the optical fiber and the printed polymer structure;
- (iv)
- a preliminary validation conducted on eight healthy subjects, aimed at verifying the system’s ability to detect shoulder joint movements and correctly distinguish the three anatomical planes of motion.
2. The 3D-Printed Wearable Sensors: Sensing Principle, Design, and Fabrication
2.1. Working Principle
2.2. Design
2.3. Fabrication
- Pre-processing
- Production
- Post-processing
3. Metrological Characterization
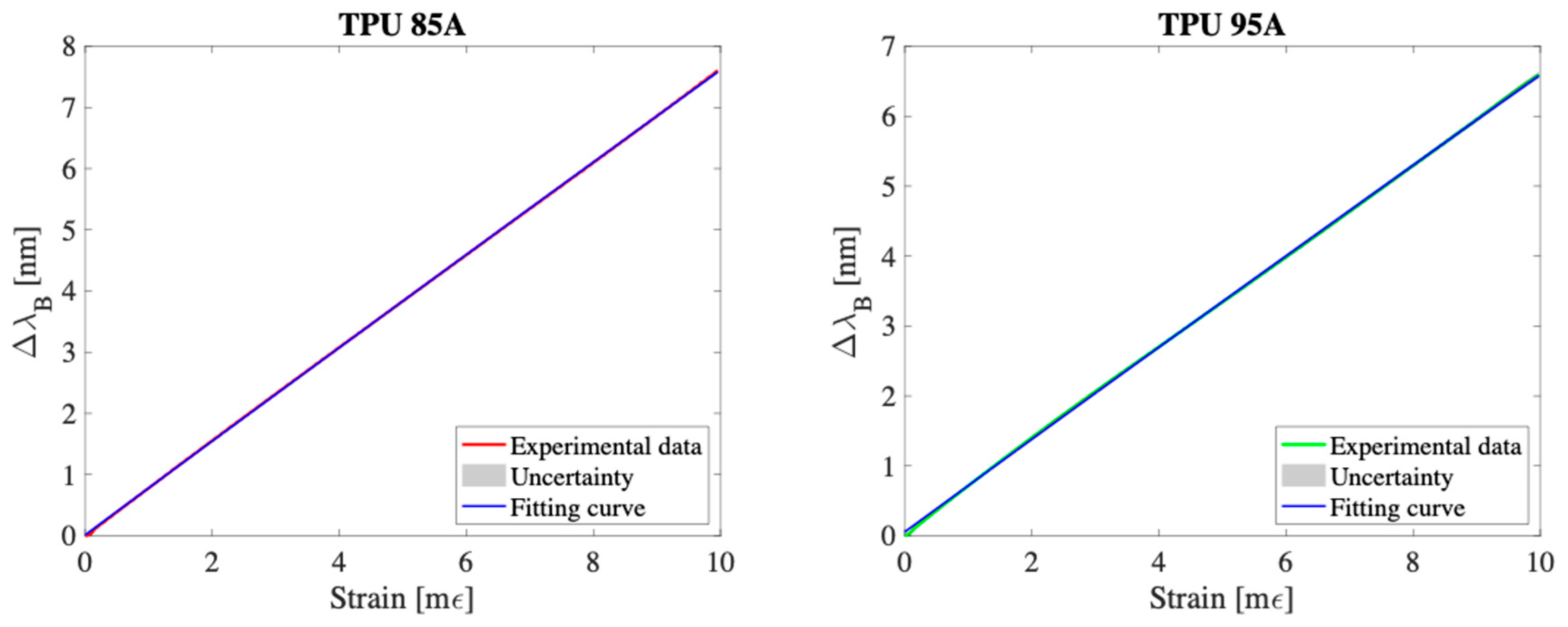
3.1. Response to Strain
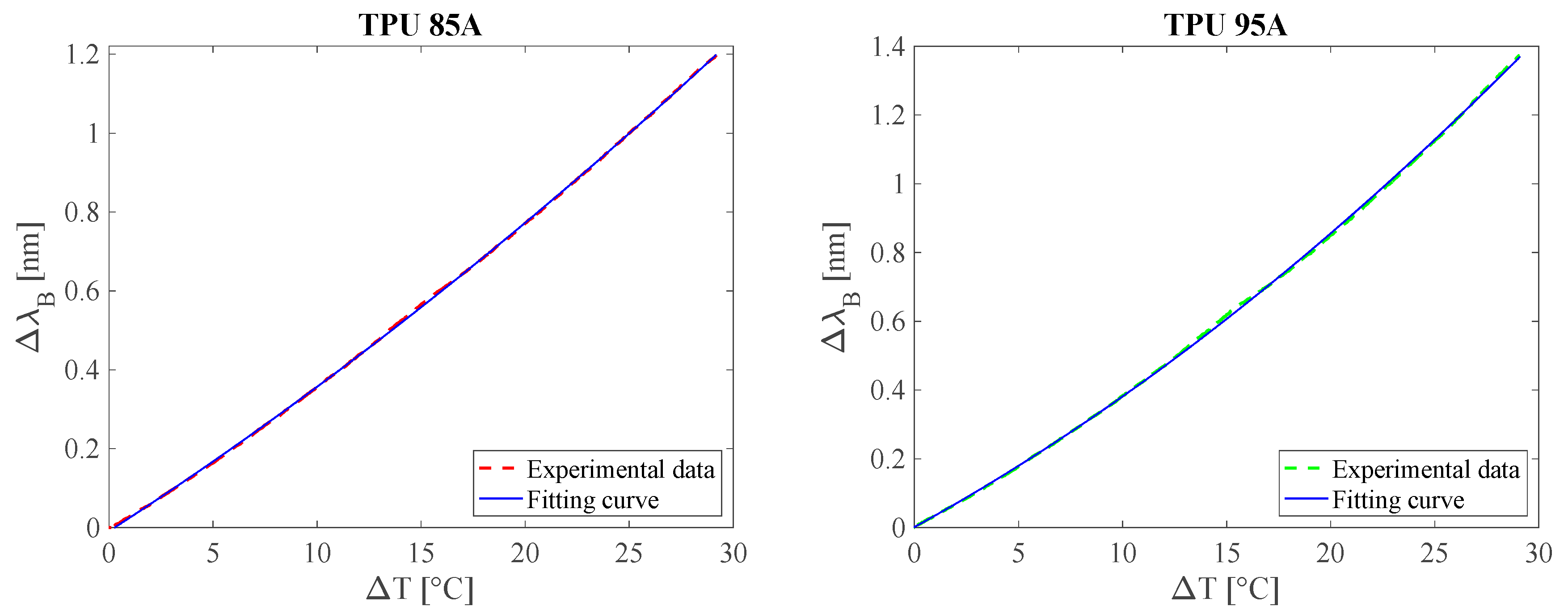
3.2. Response to Temperature
3.3. Hysteresis Cycle
3.4. Pull-Out Test
4. Preliminary Evaluation of the Wearable Sensor Capability of Monitoring Shoulder Movements
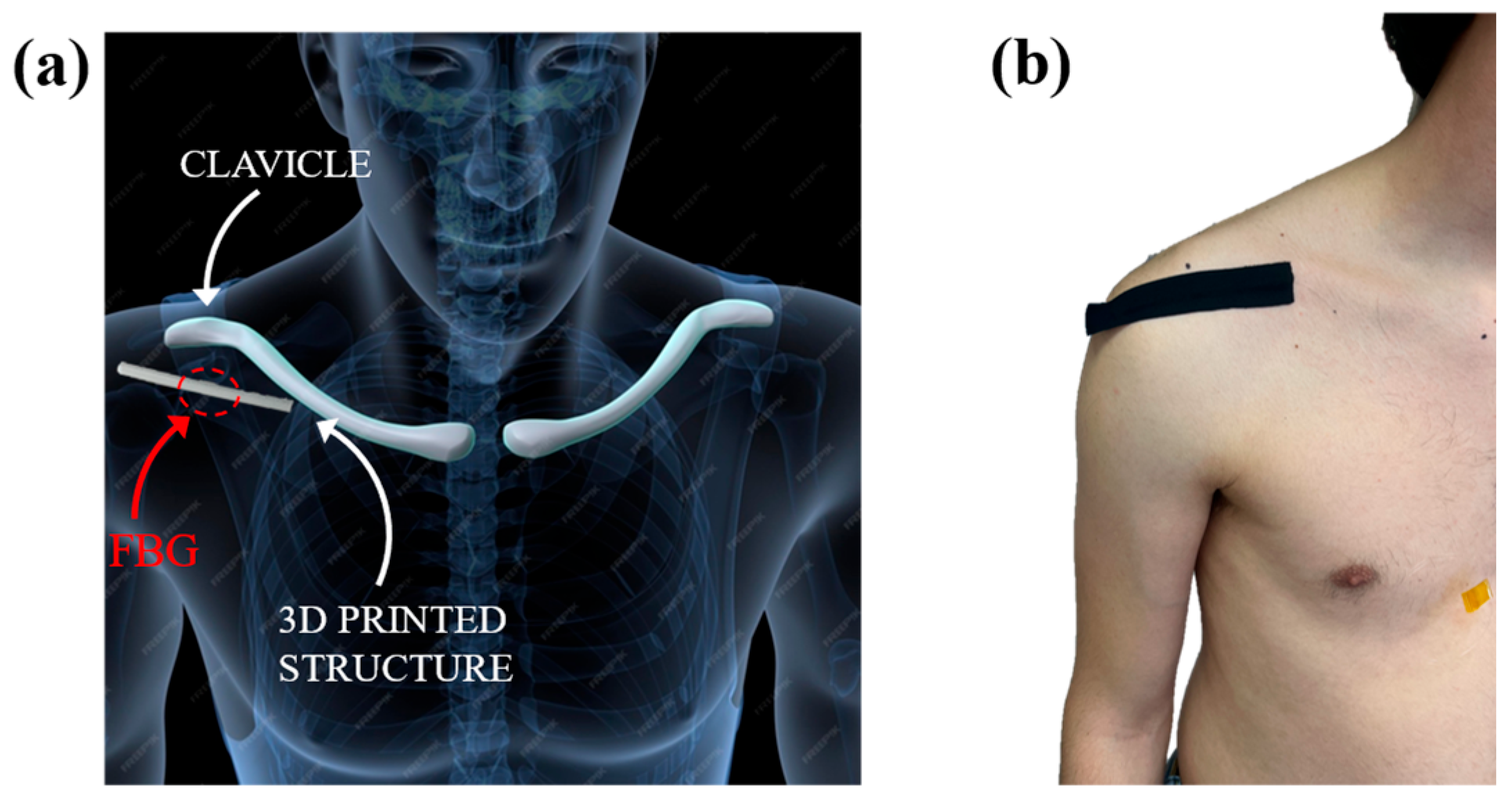
4.1. Experimental Setup and Protocol
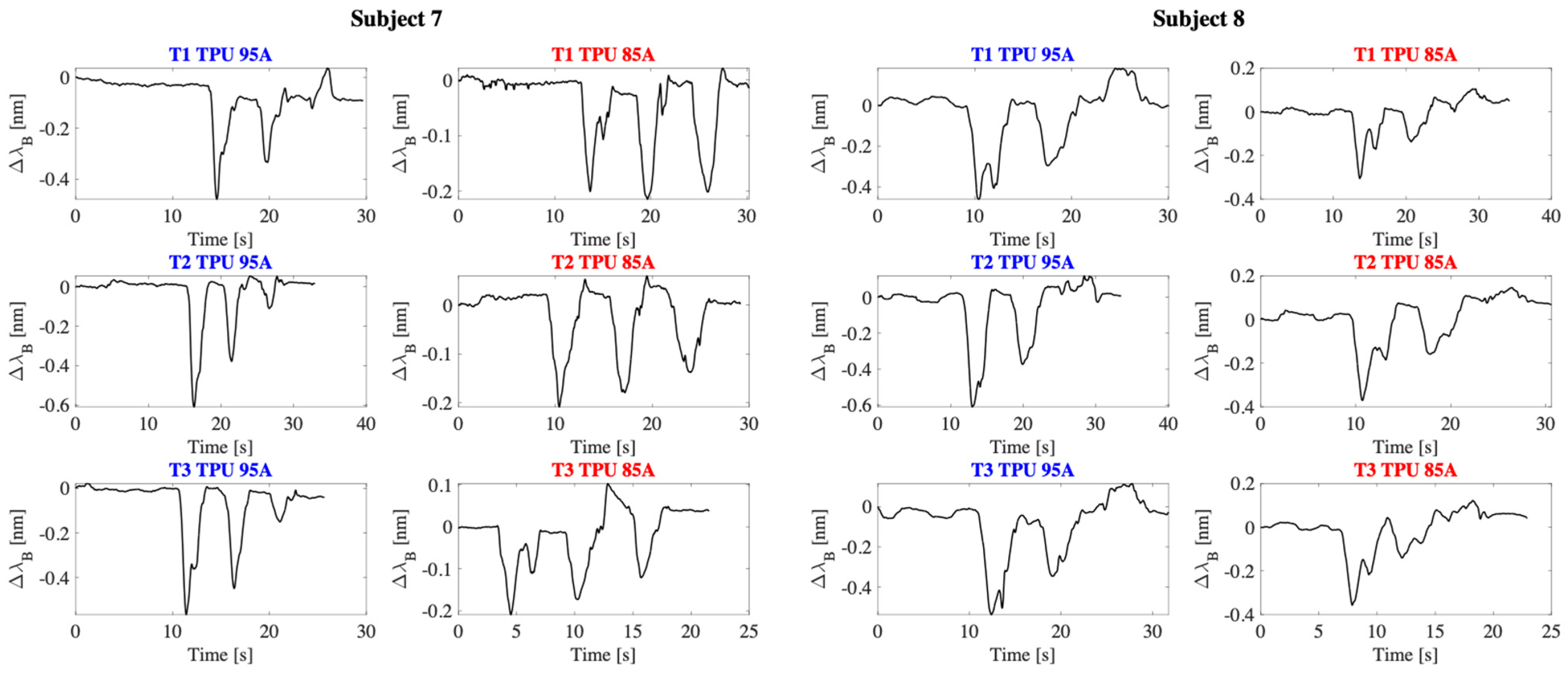
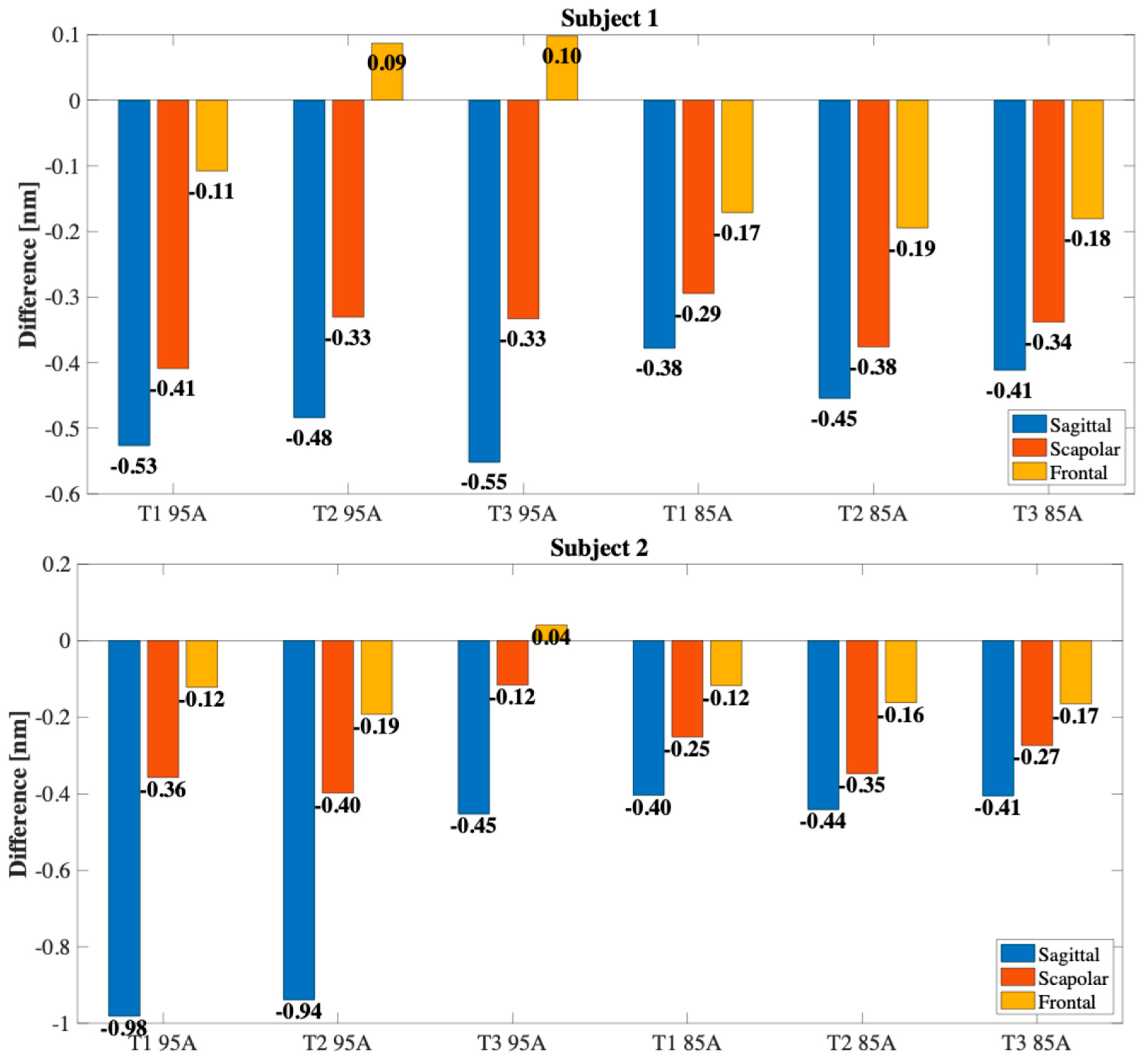
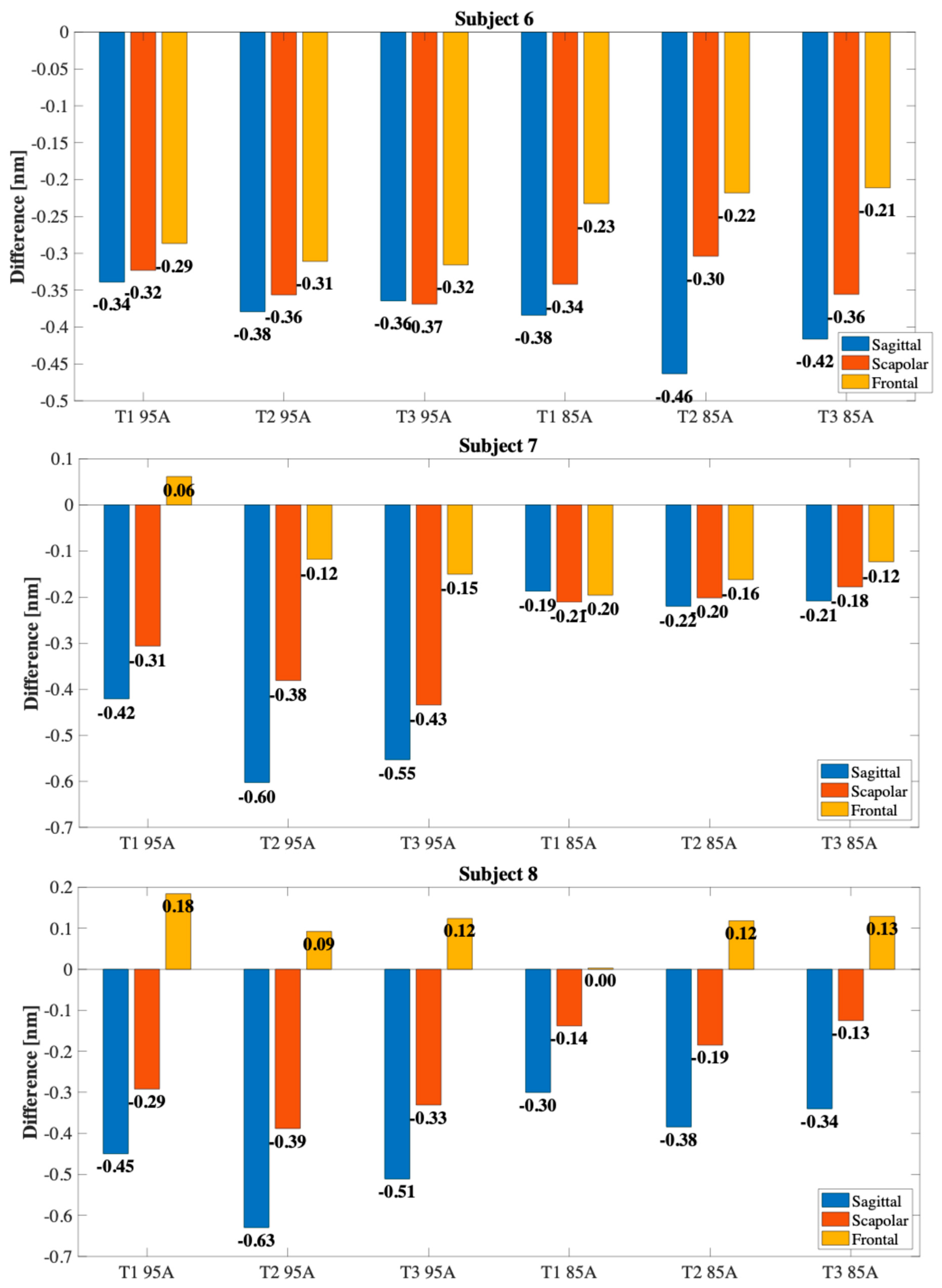
4.2. Results
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Luime, J.J.; Koes, B.W.; Hendriksen, I.J.M.; Burdorf, A.; Verhagen, A.P.; Miedema, H.S.; Verhaar, J.A.N. Prevalence and Incidence of Shoulder Pain in the General Population; a Systematic Review. Scand. J. Rheumatol. 2004, 33, 73–81. [Google Scholar] [CrossRef]
- Van Der Heijden, G.J.M.G. Shoulder Disorders: A State-of-the-Art Review. Best Pract. Res. Clin. Rheumatol. 1999, 13, 287–309. [Google Scholar] [CrossRef]
- Murrell, G.A.C.; Walton, J.R. Diagnosis of Rotator Cuff Tears. Lancet 2001, 357, 769–770. [Google Scholar] [CrossRef]
- Longo, U.G.; Berton, A.; Khan, W.S.; Maffulli, N.; Denaro, V. Histopathology of Rotator Cuff Tears. Sports Med. Arthrosc. Rev. 2011, 19, 227–236. [Google Scholar] [CrossRef] [PubMed]
- Maruvada, S.; Madrazo-Ibarra, A.; Varacallo, M. Anatomy, Rotator Cuff; StatPearls: Treasure Island, FL, USA, 2017. [Google Scholar]
- Lewis, J. Rotator Cuff Related Shoulder Pain: Assessment, Management and Uncertainties. Man. Ther. 2016, 23, 57–68. [Google Scholar] [CrossRef]
- Yamamoto, A.; Takagishi, K.; Osawa, T.; Yanagawa, T.; Nakajima, D.; Shitara, H.; Kobayashi, T. Prevalence and Risk Factors of a Rotator Cuff Tear in the General Population. J. Shoulder Elb. Surg. 2010, 19, 116–120. [Google Scholar] [CrossRef] [PubMed]
- Weber, S.; Chahal, J. Management of Rotator Cuff Injuries. J. Am. Acad. Orthop. Surg. 2020, 28, E193–E201. [Google Scholar] [CrossRef]
- Maffulli, N.; Longo, U.G.; Berton, A.; Loppini, M.; Denaro, V. Biological Factors in the Pathogenesis of Rotator Cuff Tears. Sports Med. Arthrosc. Rev. 2011, 19, 194–201. [Google Scholar] [CrossRef]
- Halder, A.M.; Itoi, E.; An, K.N. Anatomy and Biomechanics of the Shoulder. Orthop. Clin. 2000, 31, 159–176. [Google Scholar] [CrossRef]
- Reinold, M.M.; Escamilla, R.; Wilk, K.E. Current Concepts in the Scientific and Clinical Rationale behind Exercises for Glenohumeral and Scapulothoracic Musculature. J. Orthop. Sports Phys. Ther. 2009, 39, 105–117. [Google Scholar] [CrossRef] [PubMed]
- Bennell, K.; Coburn, S.; Wee, E.; Green, S.; Harris, A.; Forbes, A.; Buchbinder, R. Efficacy and Cost-Effectiveness of a Physiotherapy Program for Chronic Rotator Cuff Pathology: A Protocol for a Randomised, Double-Blind, Placebo-Controlled Trial. BMC Musculoskelet. Disord. 2007, 8, 86. [Google Scholar] [CrossRef]
- Escamilla, R.F.; Yamashiro, K.; Paulos, L.; Andrews, J.R. Shoulder Muscle Activity and Function in Common Shoulder Rehabilitation Exercises. Sports Med. 2009, 39, 663–685. [Google Scholar] [CrossRef]
- Kibler, W.B.; McMullen, J.; Uhl, T. Shoulder Rehabilitation Strategies, Guidelines, and Practice. Orthop. Clin. N. Am. 2001, 32, 527–538. [Google Scholar] [CrossRef]
- Eshoj, H.; Ingwersen, K.G.; Larsen, C.M.; Kjaer, B.H.; Juul-Kristensen, B. Intertester Reliability of Clinical Shoulder Instability and Laxity Tests in Subjects with and without Self-Reported Shoulder Problems. BMJ Open 2018, 8, e018472. [Google Scholar] [CrossRef]
- Leardini, A.; Chiari, A.; Della Croce, U.; Cappozzo, A. Human Movement Analysis Using Stereophotogrammetry. Part 3. Soft Tissue Artifact Assessment and Compensation. Gait Posture 2005, 21, 212–225. [Google Scholar] [CrossRef]
- Heikenfeld, J.; Jajack, A.; Rogers, J.; Gutruf, P.; Tian, L.; Pan, T.; Li, R.; Khine, M.; Kim, J.; Wang, J.; et al. Wearable Sensors: Modalities, Challenges, and Prospects. Lab Chip 2018, 18, 217–248. [Google Scholar] [CrossRef] [PubMed]
- Mukhopadhyay, S.C. Wearable Sensors for Human Activity Monitoring: A Review. IEEE Sens. J. 2015, 15, 1321–1330. [Google Scholar] [CrossRef]
- Shi, C.; Tang, Z.; Zhang, H.; Liu, Y. Development of an FBG-Based Wearable Sensor for Simultaneous Respiration and Heartbeat Measurement. IEEE Trans. Instrum. Meas. 2023, 72, 4000409. [Google Scholar]
- Lo Presti, D.; Bianchi, D.; Massaroni, C.; Coricciati, C.; Rainer, A.; Silvestri, S.; Gizzi, A.; Schena, E. Optimization and Characterization of a 3D-Printed Wearable Strain Sensor for Respiration and Heartbeat Measurements. Measurement 2024, 228, 114377. [Google Scholar] [CrossRef]
- Baig, M.M.; GholamHosseini, H.; Moqeem, A.A.; Mirza, F.; Lindén, M. A Systematic Review of Wearable Patient Monitoring Systems—Current Challenges and Opportunities for Clinical Adoption. J. Med. Syst. 2017, 41, 115. [Google Scholar] [CrossRef] [PubMed]
- Perez, A.J.; Zeadally, S. Recent Advances in Wearable Sensing Technologies. Sensors 2021, 21, 6828. [Google Scholar] [CrossRef]
- Picerno, P.; Cereatti, A.; Cappozzo, A. Joint Kinematics Estimate Using Wearable Inertial and Magnetic Sensing Modules. Gait Posture 2008, 28, 588–595. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Z.; Qiu, S.; Shen, Y.; Wang, J. IMU-Based Gait Analysis for Rehabilitation Assessment of Patients with Gait Disorders. In Proceedings of the 2017 4th International Conference on Systems and Informatics (ICSAI 2017), Hangzhou, China, 11–13 November 2017; pp. 622–626. [Google Scholar] [CrossRef]
- Massaroni, C.; Di Tocco, J.; Lo Presti, D.; Longo, U.G.; Miccinilli, S.; Sterzi, S.; Formica, D.; Saccomandi, P.; Schena, E. Smart Textile Based on Piezoresistive Sensing Elements for Respiratory Monitoring. IEEE Sens. J. 2019, 19, 7718–7725. [Google Scholar] [CrossRef]
- Fiorillo, A.S.; Critello, C.D.; Pullano, A.S. Theory, Technology and Applications of Piezoresistive Sensors: A Review. Sens. Actuators A Phys. 2018, 281, 156–175. [Google Scholar] [CrossRef]
- Kersey, A.D.; Davis, M.A.; Patrick, H.J.; LeBlanc, M.; Koo, K.P.; Askins, C.G.; Putnam, M.A.; Friebele, E.J. Fiber Grating Sensors. J. Light. Technol. 1997, 15, 1442–1462. [Google Scholar] [CrossRef]
- Ngiejungbwen, L.A.; Hamdaoui, H.; Chen, M.Y. Polymer Optical Fiber and Fiber Bragg Grating Sensors for Biomedical Engineering Applications: A Comprehensive Review. Opt. Laser Technol. 2024, 170, 110187. [Google Scholar] [CrossRef]
- Mahmud, S.; Khandakar, A.; Chowdhury, M.E.H.; AbdulMoniem, M.; Bin Ibne Reaz, M.; Bin Mahbub, Z.; Sadasivuni, K.K.; Murugappan, M.; Alhatou, M. Fiber Bragg Gratings Based Smart Insole to Measure Plantar Pressure and Temperature. Sens. Actuators A Phys. 2023, 350, 114092. [Google Scholar] [CrossRef]
- Alhussein, A.N.D.; Qaid, M.R.T.M.; Agliullin, T.; Valeev, B.; Morozov, O.; Sakhabutdinov, A. Fiber Bragg Grating Sensors: Design, Applications, and Comparison with Other Sensing Technologies. Sensors 2025, 25, 2289. [Google Scholar] [CrossRef] [PubMed]
- Koyama, S.; Ohno, Y.; Haseda, Y.; Satou, Y.; Ishizawa, H. Verification of Embedding Conditions for FBG Sensor into Textile Product for the Development of Wearable Healthcare Sensor. Technol. Health Care 2022, 30, 787–798. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zheng, J.; Nie, Q.; Zhao, C.; Wang, Z.; Kumar, S.; Marques, C.; Min, R.; Hu, X. SleepSense: Smart Pillow with Pressure-Sensitive FBG-Embedded Silicone Buttons. IEEE Sens. J. 2023, 23, 19324–19331. [Google Scholar] [CrossRef]
- Majumder, M.; Gangopadhyay, T.K.; Chakraborty, A.K.; Dasgupta, K.; Bhattacharya, D.K. Fibre Bragg Gratings in Structural Health Monitoring—Present Status and Applications. Sens. Actuators A Phys. 2008, 147, 150–164. [Google Scholar] [CrossRef]
- Dimo, A.; Carnevale, A.; Pulcinelli, M.; Massaroni, C.; Longo, U.G.; Schena, E.; Presti, D. Lo Monitoring Shoulder Flexion-Extension Movements Using a 3D-Printed Wearable Sensor Based on Fiber Bragg Grating Technology. In Proceedings of the 2024 IEEE International Workshop on Metrology for Industry 4.0 and IoT, MetroInd4.0 and IoT 2024, Firenze, Italy, 29–31 May 2024; pp. 389–394. [Google Scholar] [CrossRef]
- Fajkus, M.; Nedoma, J.; Siska, P.; Vasinek, V. FBG Sensor of Breathing Encapsulated into Polydimethylsiloxane. Proc. SPIE 2016, 9994, 31–35. [Google Scholar] [CrossRef]
- Di Palma, P.; De Vita, E.; Iadicicco, A.; Campopiano, S. Force Sensor Based on FBG Embedded in Silicone Rubber. IEEE Sens. J. 2023, 23, 1172–1178. [Google Scholar] [CrossRef]
- Presti, D.L.; Leitao, C.; Noccaro, A.; Tavares, C.; Massaroni, C.; Caponero, M.A.; Antunes, P.; Formica, D.; Schena, E. The Effect of Infill Pattern and Density on the Response of 3-D-Printed Sensors Based on FBG Technology. IEEE Sens. J. 2022, 22, 19357–19365. [Google Scholar] [CrossRef]
- Palma, P.D.; Iadicicco, A.; Campopiano, S. Study of Fiber Bragg Gratings Embedded in 3D-Printed Patches for Deformation Monitoring. IEEE Sens. J. 2020, 20, 13379–13386. [Google Scholar] [CrossRef]
- Leal-Junior, A.; Casas, J.; Marques, C.; Pontes, M.J.; Frizera, A. Application of Additive Layer Manufacturing Technique on the Development of High Sensitive Fiber Bragg Grating Temperature Sensors. Sensors 2018, 18, 4120. [Google Scholar] [CrossRef]
- Zhu, Y.; Guo, S.; Ravichandran, D.; Ramanathan, A.; Sobczak, M.T.; Sacco, A.F.; Patil, D.; Thummalapalli, S.V.; Pulido, T.V.; Lancaster, J.N.; et al. 3D-Printed Polymeric Biomaterials for Health Applications. Adv. Heal. Mater. 2025, 14, e2402571. [Google Scholar] [CrossRef] [PubMed]
- Presti, D.L.; Pulcinelli, M.; Massaroni, C.; Nedoma, J.; Schena, E. A 3D-Printed Multi-Parametric Wearable System for Monitoring Breathing Activity and Low Back Movements. In Proceedings of the 2024 IEEE International Workshop on Metrology for Industry 4.0 & IoT (MetroInd4.0 & IoT), Florence, Italy, 29–31 May 2024; pp. 383–388. [Google Scholar] [CrossRef]
- Han, T.; Kundu, S.; Nag, A.; Xu, Y. 3D Printed Sensors for Biomedical Applications: A Review. Sensors 2019, 19, 1706. [Google Scholar] [CrossRef] [PubMed]
- Chekkaramkodi, D.; Ahmed, I.; Al-Rub, R.K.A.; Schiffer, A.; Butt, H. 3D-Printed Multi-Material Optical Fiber Sensor for Dual Sensing Applications. Adv. Compos. Hybrid. Mater. 2025, 8, 107. [Google Scholar] [CrossRef]
- Erdogan, T. Fiber Grating Spectra. J. Light. Technol. 1997, 15, 1277–1294. [Google Scholar] [CrossRef]
- Othonos, A. Fiber Bragg Gratings. Rev. Sci. Instrum. 1997, 68, 4309–4341. [Google Scholar] [CrossRef]
- Carnevale, A.; Longo, U.G.; Schena, E.; Massaroni, C.; Lo Presti, D.; Berton, A.; Candela, V.; Denaro, V. Wearable Systems for Shoulder Kinematics Assessment: A Systematic Review. BMC Musculoskelet. Disord. 2019, 20, 546. [Google Scholar] [CrossRef]
- Carnevale, A.; Massaroni, C.; Presti, D.L.; Formica, D.; Longo, U.G.; Schena, E.; Denaro, V. Wearable Stretchable Sensor Based on Conductive Textile Fabric for Shoulder Motion Monitoring. In Proceedings of the 2020 IEEE International Workshop on Metrology for Industry 4.0 and IoT, MetroInd 4.0 and IoT 2020, Rome, Italy, 3–5 June 2020; pp. 106–110. [Google Scholar] [CrossRef]
- Dimo, A.; Longo, U.G.; Massaroni, C.; Schena, E.; Lo Presti, D. A 3-D-Printed Multiparametric Wearable System Based on Fiber Bragg Gratings for Shoulder Movement and Respiratory Rate Monitoring. IEEE Sens. J. 2024, 24, 34533–34540. [Google Scholar] [CrossRef]
- Frick, A.; Rochman, A. Characterization of TPU-Elastomers by Thermal Analysis (DSC). Polym. Test. 2004, 23, 413–417. [Google Scholar] [CrossRef]
- Gao, X.; Yu, N.; Li, J. Influence of Printing Parameters and Filament Quality on Structure and Properties of Polymer Composite Components Used in the Fields of Automotive. In Structure and Properties of Additive Manufactured Polymer Components; Woodhead Publishing: Sawston, UK, 2020; pp. 303–330. [Google Scholar] [CrossRef]
- Fernandez-Vicente, M.; Calle, W.; Ferrandiz, S.; Conejero, A. Effect of Infill Parameters on Tensile Mechanical Behavior in Desktop 3D Printing. 3D Print. Addit. Manuf. 2016, 3, 183–192. [Google Scholar] [CrossRef]
- Ahmad, H.; Alias, M.A.; Ismail, M.F.; Ismail, N.N.; Zaini, M.K.A.; Lim, K.S.; Brambilla, G.; Grattan, K.T.V.; Rahman, B.M.A. Strain Sensor Based on Embedded Fiber Bragg Grating in Thermoplastic Polyurethane Using the 3D Printing Technology for Improved Sensitivity. Photonic Sens. 2022, 12, 220302. [Google Scholar] [CrossRef]
- Liu, T.; Inoue, Y.; Shibata, K. Measurement of Soft Tissue Deformation to Improve the Accuracy of a Body-Mounted Motion Sensor. J. Med. Devices Trans. ASME 2009, 3, 035001. [Google Scholar] [CrossRef]
- Carnevale, A.; Schena, E.; Formica, D.; Massaroni, C.; Longo, U.G.; Denaro, V. Skin Strain Analysis of the Scapular Region and Wearables Design. Sensors 2021, 21, 5761. [Google Scholar] [CrossRef]
- Cheng-Yu, H.; Ahmed Abro, Z.; Yi-Fan, Z.; Ahmed Lakho, R. An FBG-Based Smart Wearable Ring Fabricated Using FDM for Monitoring Body Joint Motion. J. Ind. Text. 2021, 50, 1660–1673. [Google Scholar] [CrossRef]
- Jin, Y.; Glover, C.M.; Cho, H.; Araromi, O.A.; Graule, M.A.; Li, N.; Wood, R.J.; Walsh, C.J. Soft Sensing Shirt for Shoulder Kinematics Estimation. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 4863–4869. [Google Scholar] [CrossRef]
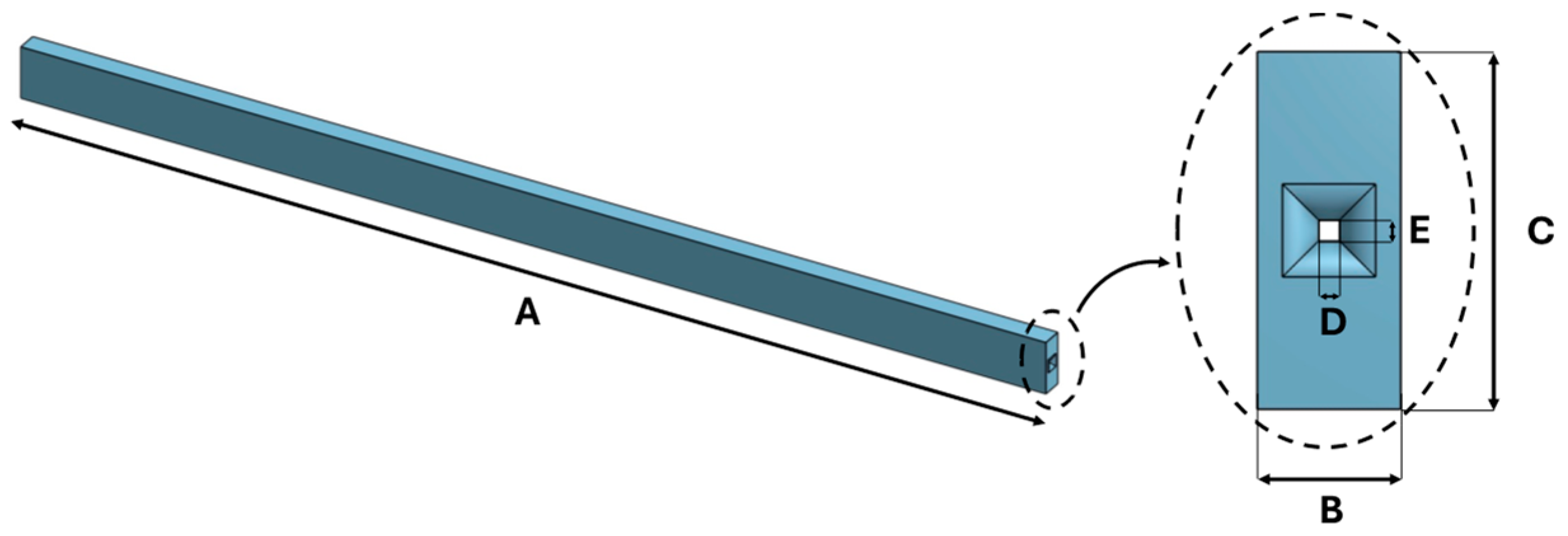






| Dimension [mm] | |
|---|---|
| A | 100 |
| B | 3 |
| C | 5 |
| D | 0.3 |
| E | 0.3 |
| Subjects | Gender | Age (y.o.) * | Height (cm) * | Weight (kg) * |
|---|---|---|---|---|
| S1 * | M * | 24 | 180 | 78 |
| S2 | M | 24 | 174 | 72 |
| S3 | M | 29 | 186 | 90 |
| S4 | M | 26 | 178 | 69 |
| S5 | M | 26 | 177 | 80 |
| S6 | M | 25 | 179 | 70 |
| S7 | M | 24 | 175 | 69 |
| S8 | M | 26 | 186 | 80 |
| Author (Year) | Sensor Type | Strain Sensitivity | Temperature Sensitivity | Hysteresis Error |
|---|---|---|---|---|
| Dimo et al., 2024 [48] | FBG + 3D-printed multiparametric | 0.65 nm/mε | 0.038 nm/°C | 4.1% |
| Carnevale et al., 2021 [54] | Piezoresistive textile | n.a. (relative resistance) | n.a | >10% |
| Cheng-Yu et al., 2021 [55] | FBG + 3D-printed ring (FDM) | 0.42 nm/mε | n.a | 5% |
| Jin et al., 2020 [56] | Capacitive textile (sensing shirt) | n.a | n.a | n.a. (RMSE < 4.5° for kinematics) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimo, A.; Longo, U.G.; D’Hooghe, P.; de Sire, A.; Papalia, R.; Schena, E.; Lo Presti, D. 3D-Printed Wearable Sensors for the Identification of Shoulder Movement Planes. Sensors 2025, 25, 5853. https://doi.org/10.3390/s25185853
Dimo A, Longo UG, D’Hooghe P, de Sire A, Papalia R, Schena E, Lo Presti D. 3D-Printed Wearable Sensors for the Identification of Shoulder Movement Planes. Sensors. 2025; 25(18):5853. https://doi.org/10.3390/s25185853
Chicago/Turabian StyleDimo, Alfredo, Umile Giuseppe Longo, Pieter D’Hooghe, Alessandro de Sire, Rocco Papalia, Emiliano Schena, and Daniela Lo Presti. 2025. "3D-Printed Wearable Sensors for the Identification of Shoulder Movement Planes" Sensors 25, no. 18: 5853. https://doi.org/10.3390/s25185853
APA StyleDimo, A., Longo, U. G., D’Hooghe, P., de Sire, A., Papalia, R., Schena, E., & Lo Presti, D. (2025). 3D-Printed Wearable Sensors for the Identification of Shoulder Movement Planes. Sensors, 25(18), 5853. https://doi.org/10.3390/s25185853










