Control Gain Determination Method for Robust Time-Delay Control of Industrial Robot Manipulators Based on an Improved State Observer
Abstract
1. Introduction
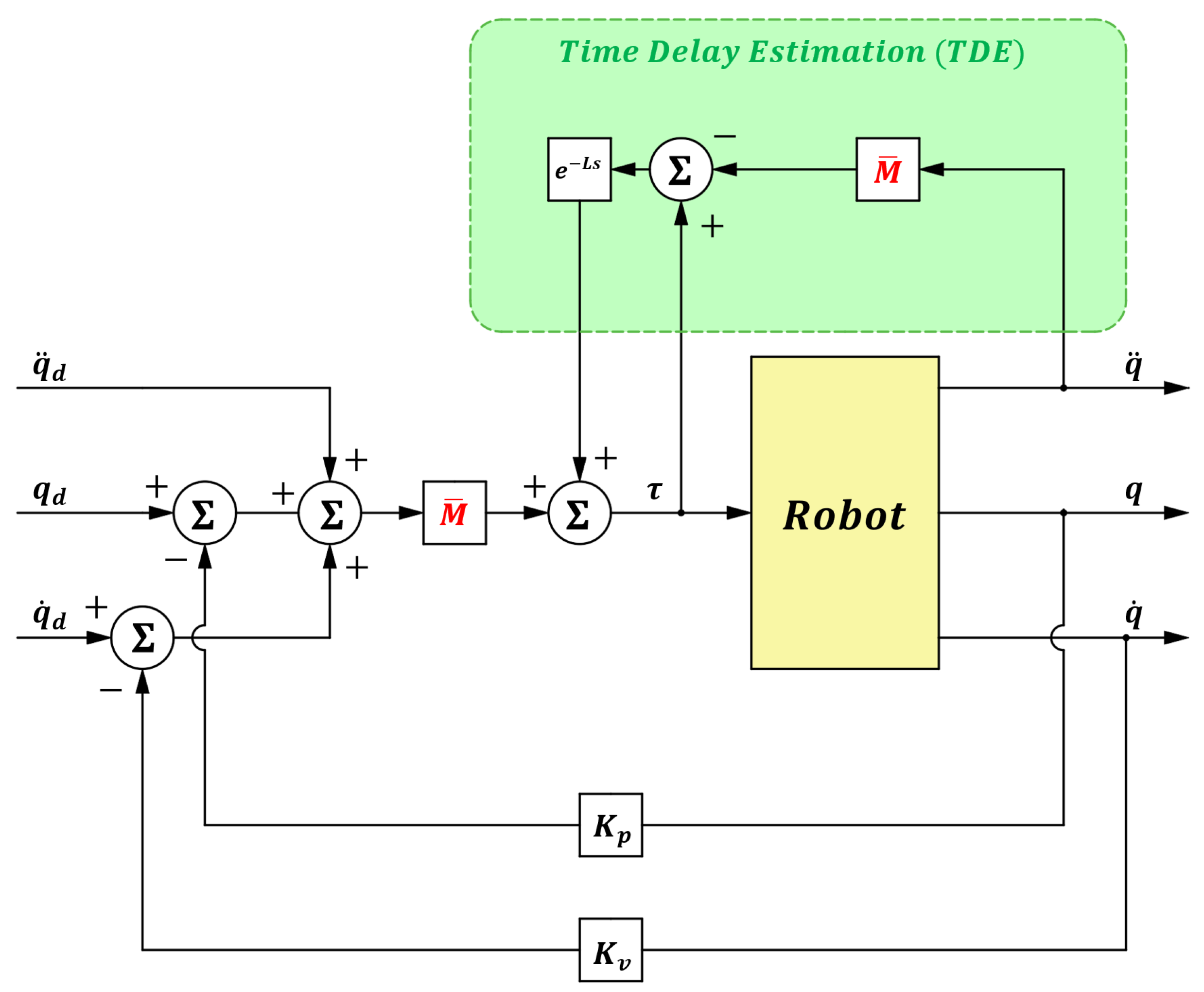
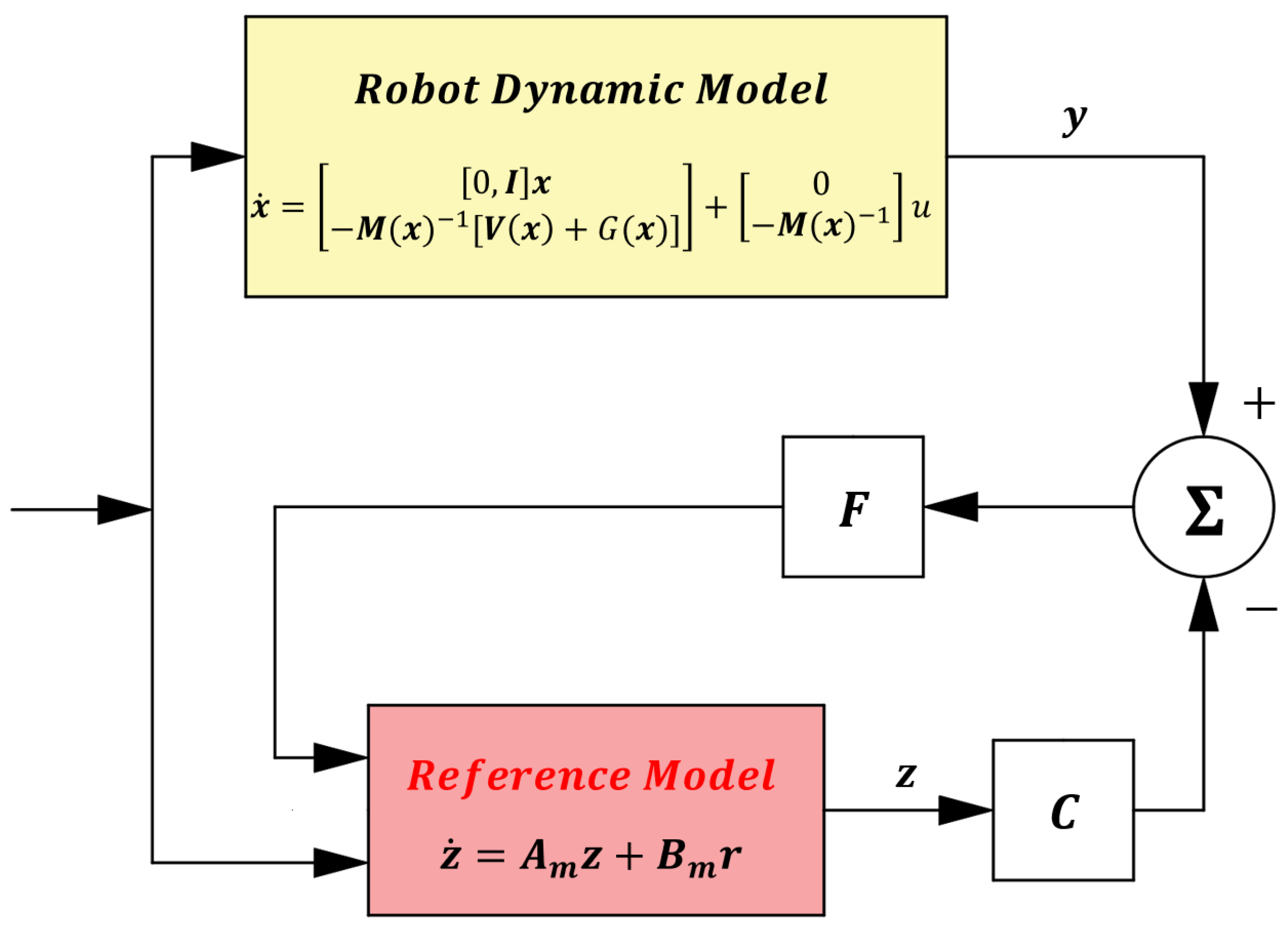
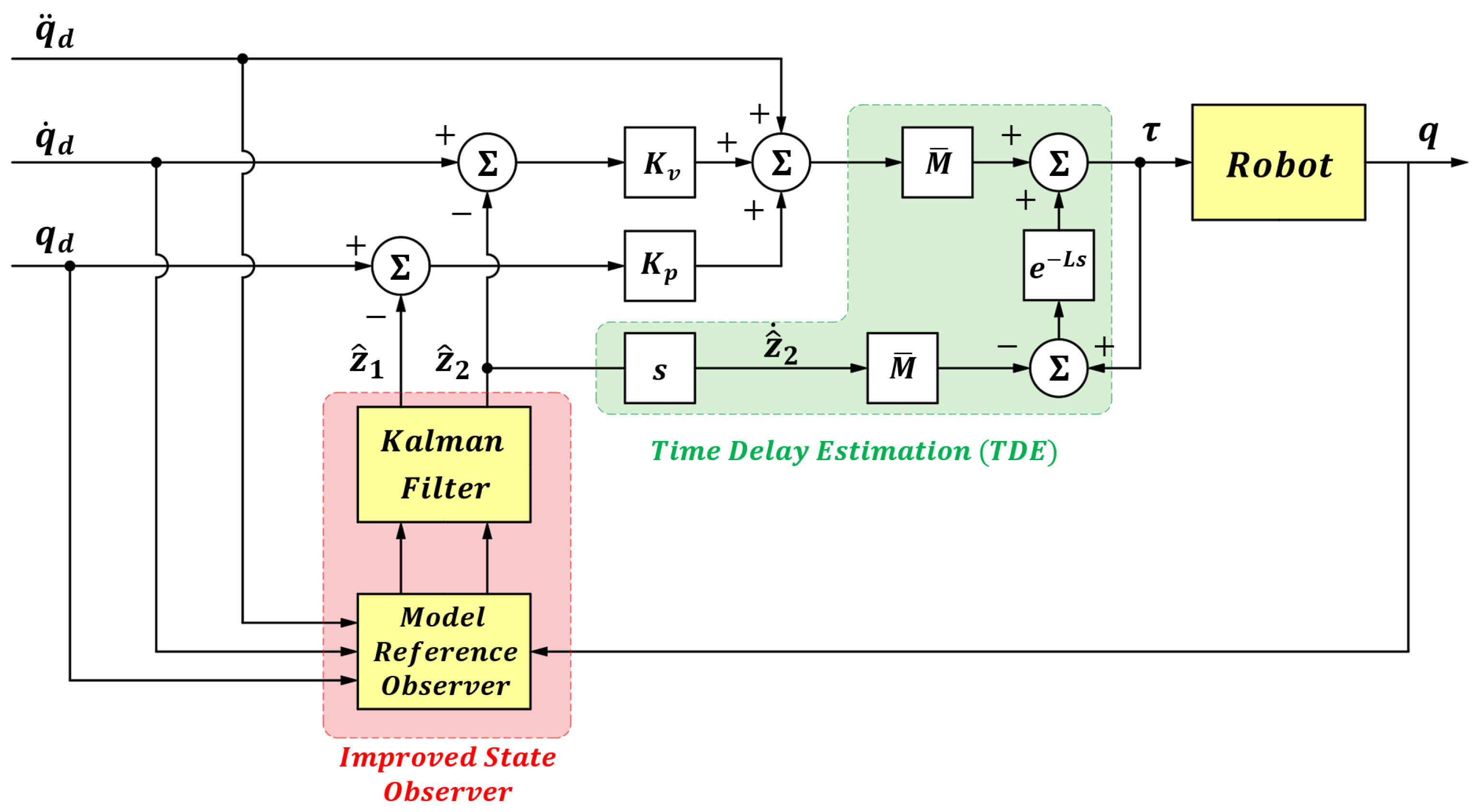
2. Theory and Framework of Time-Delay Control
3. Design Method for Control Gains in Time-Delay Control
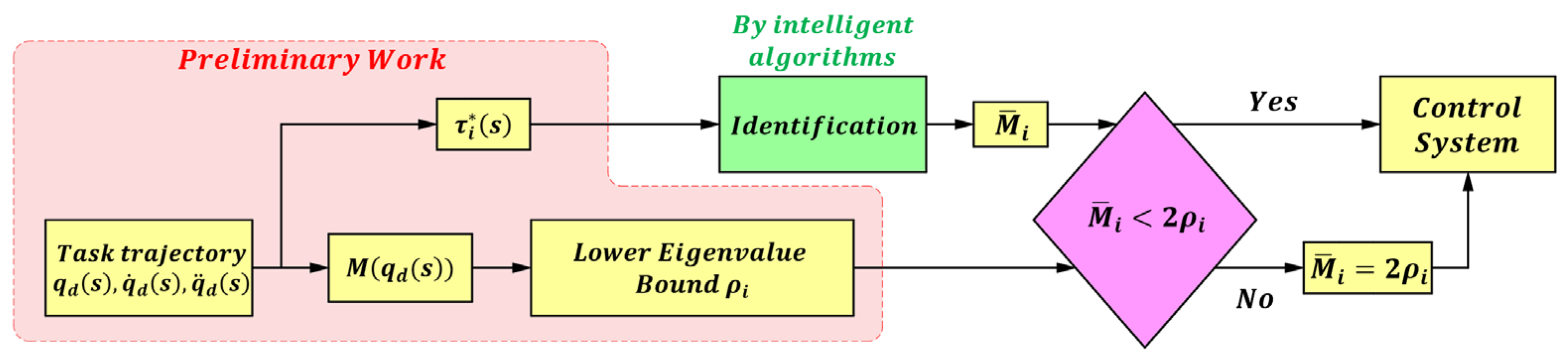
3.1. Linearized Control Gain Matrix Derivation
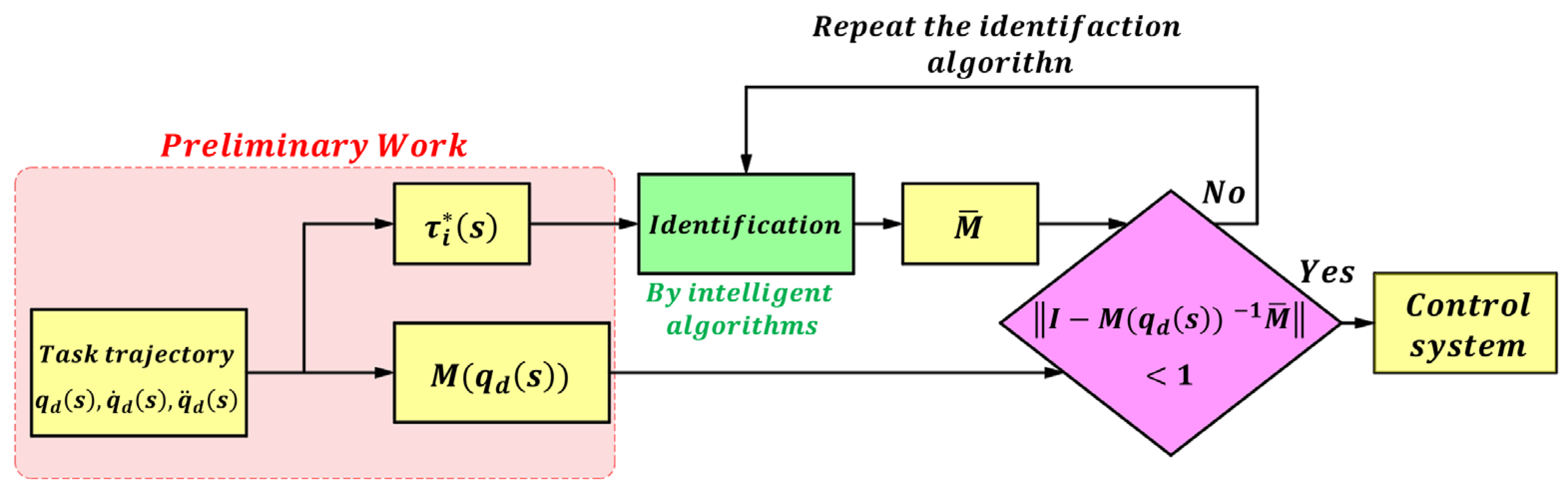
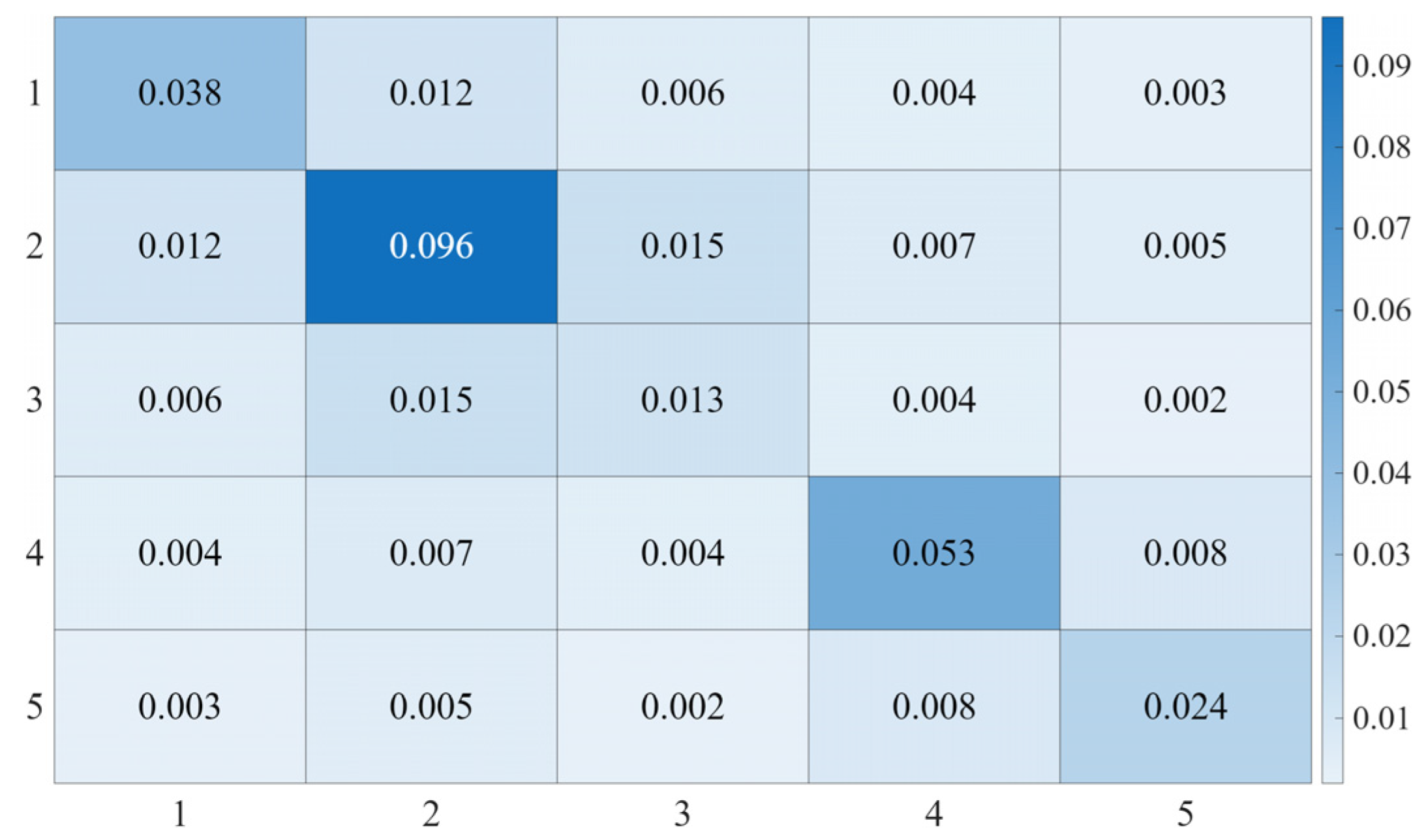
3.2. Identification Method of the Control Gain Matrix
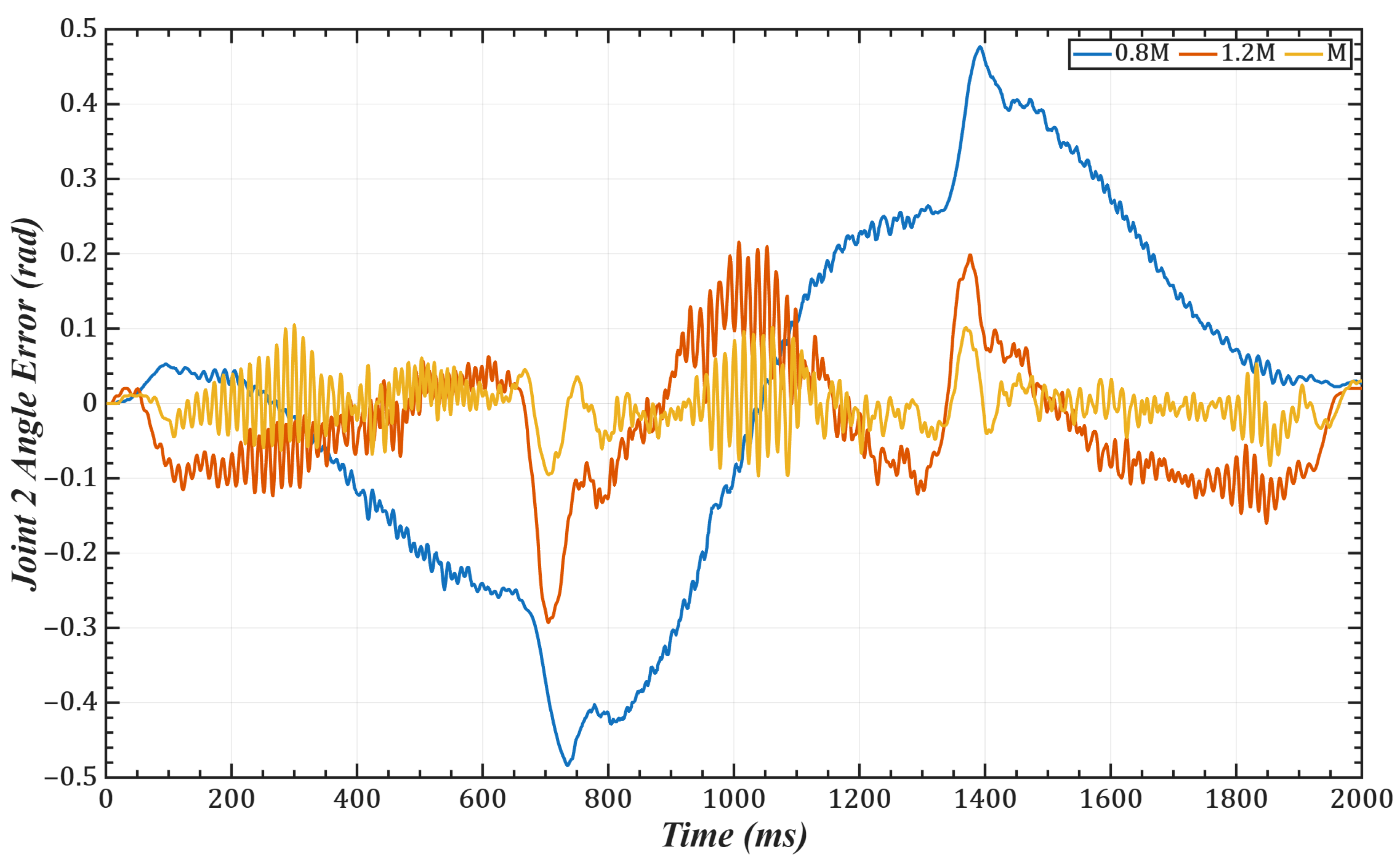
3.3. Simulation Validation of Gain Identification
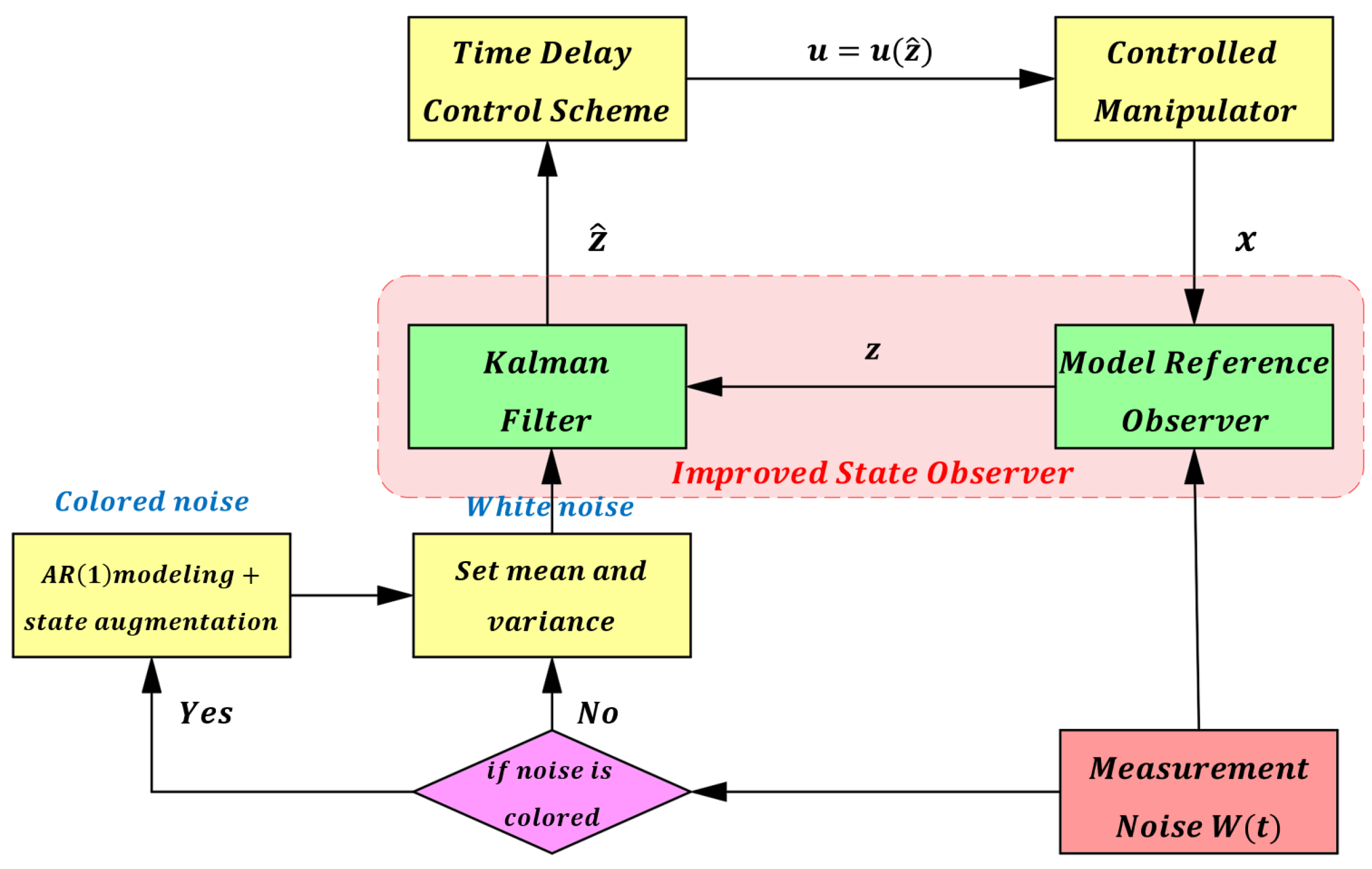
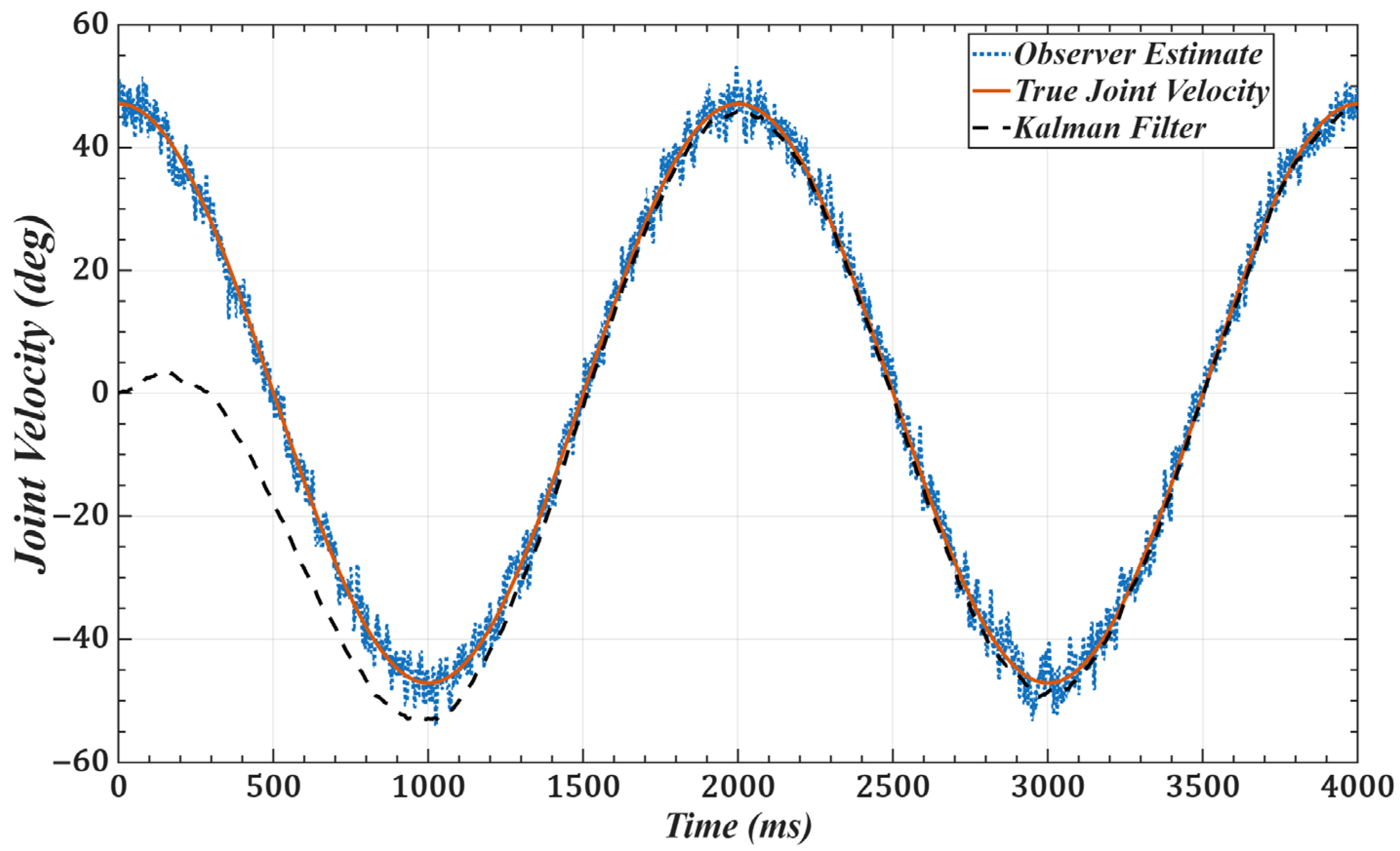
4. Improved State Observer Design
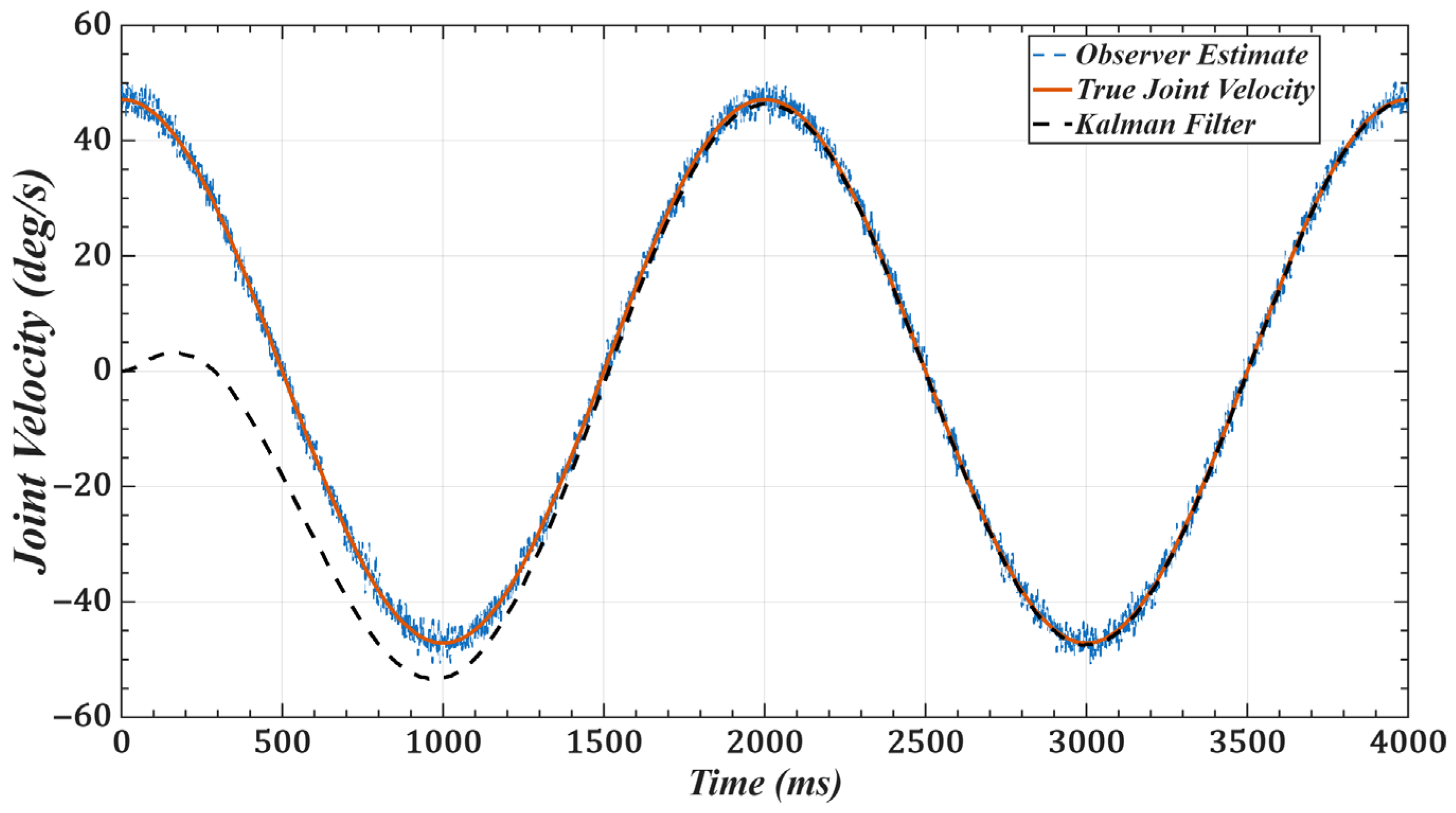
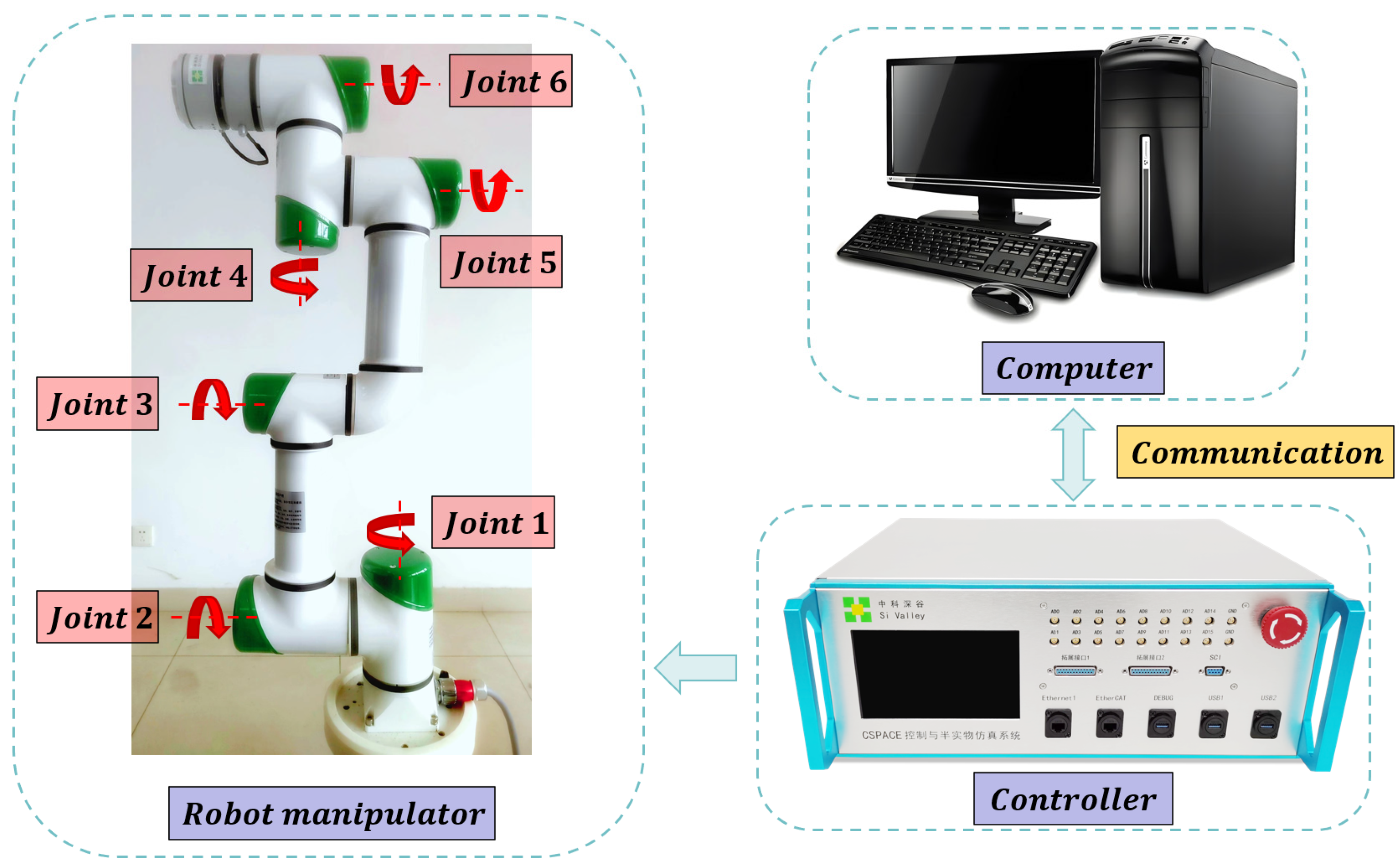
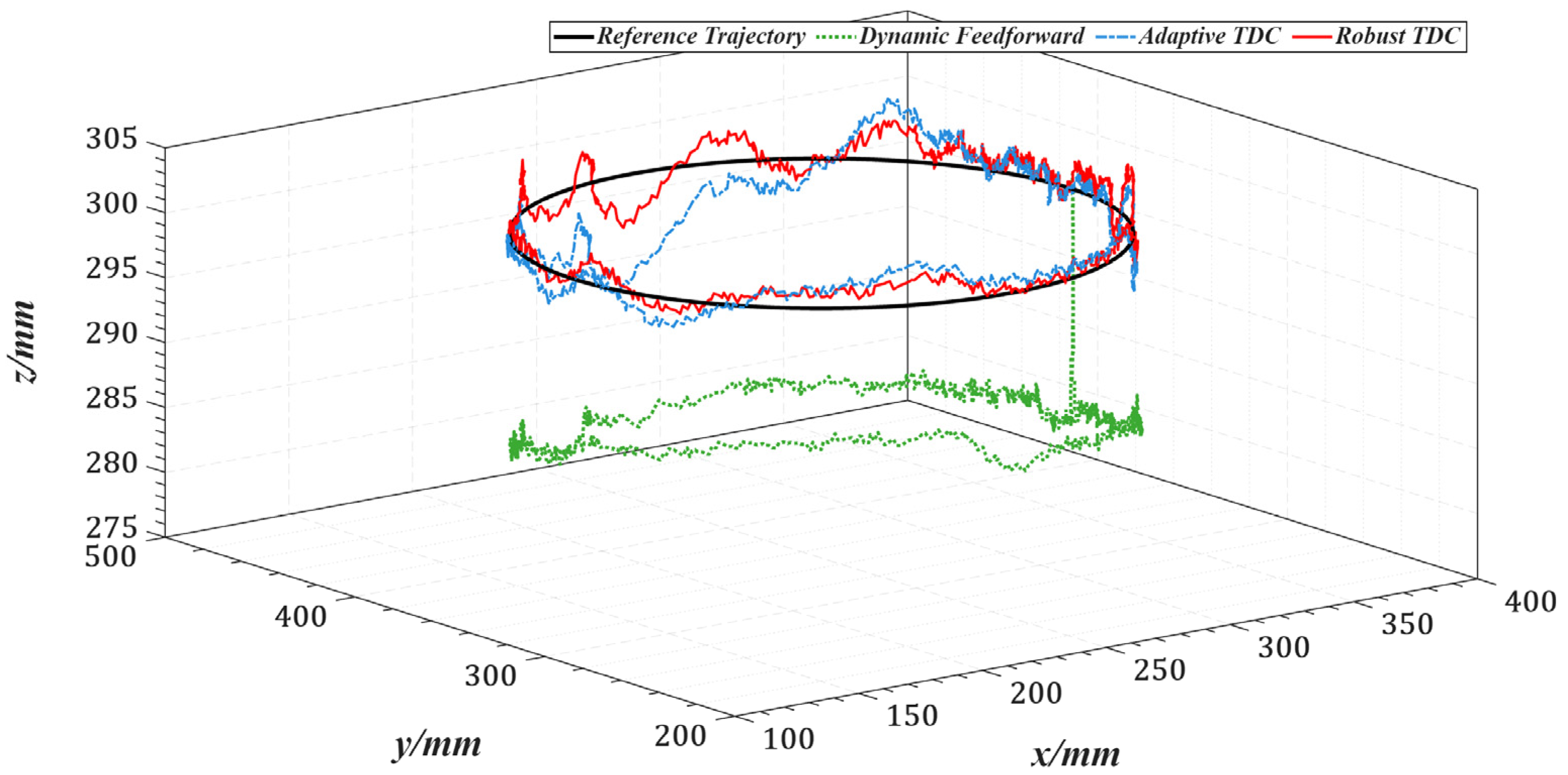
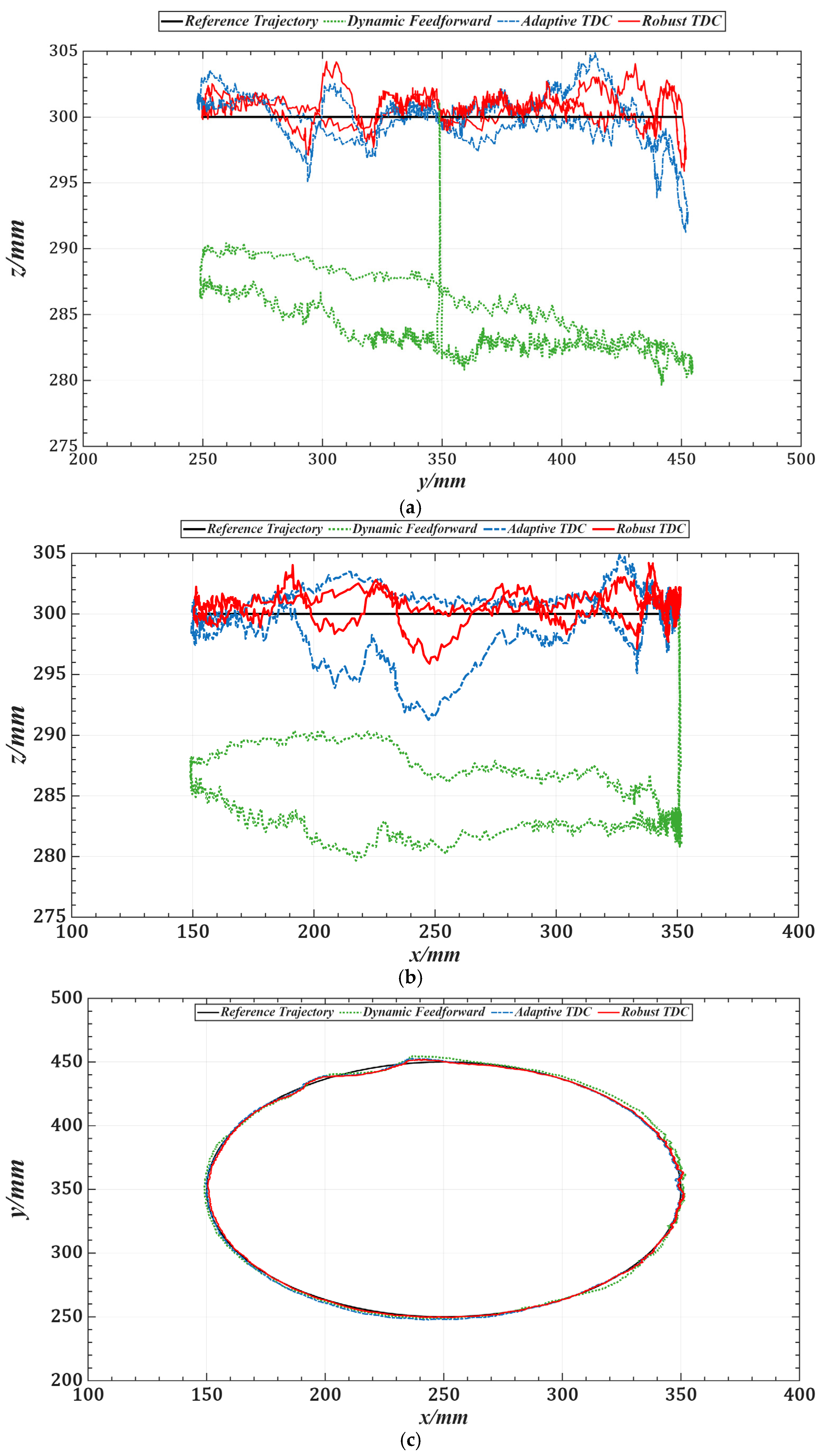
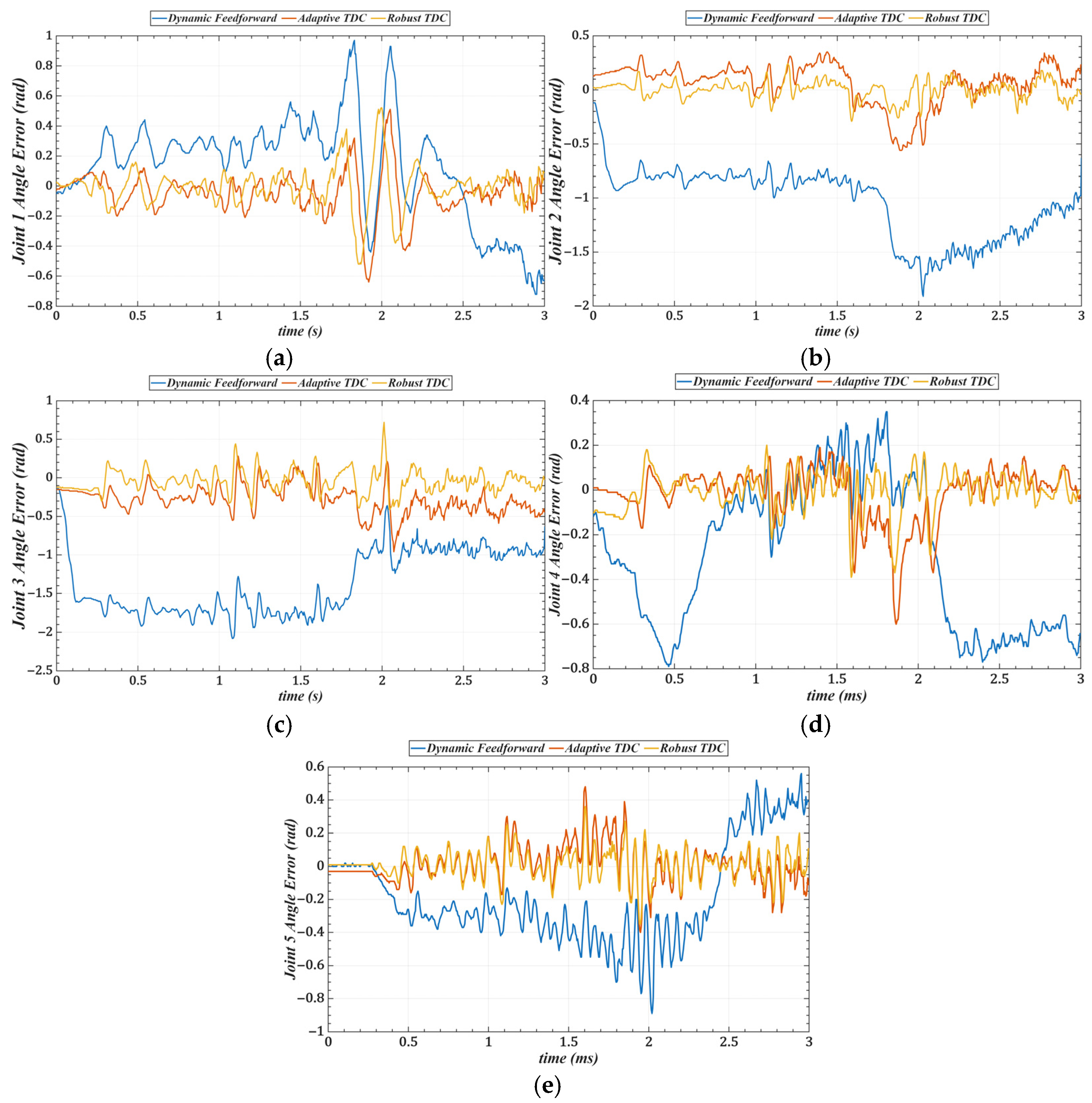
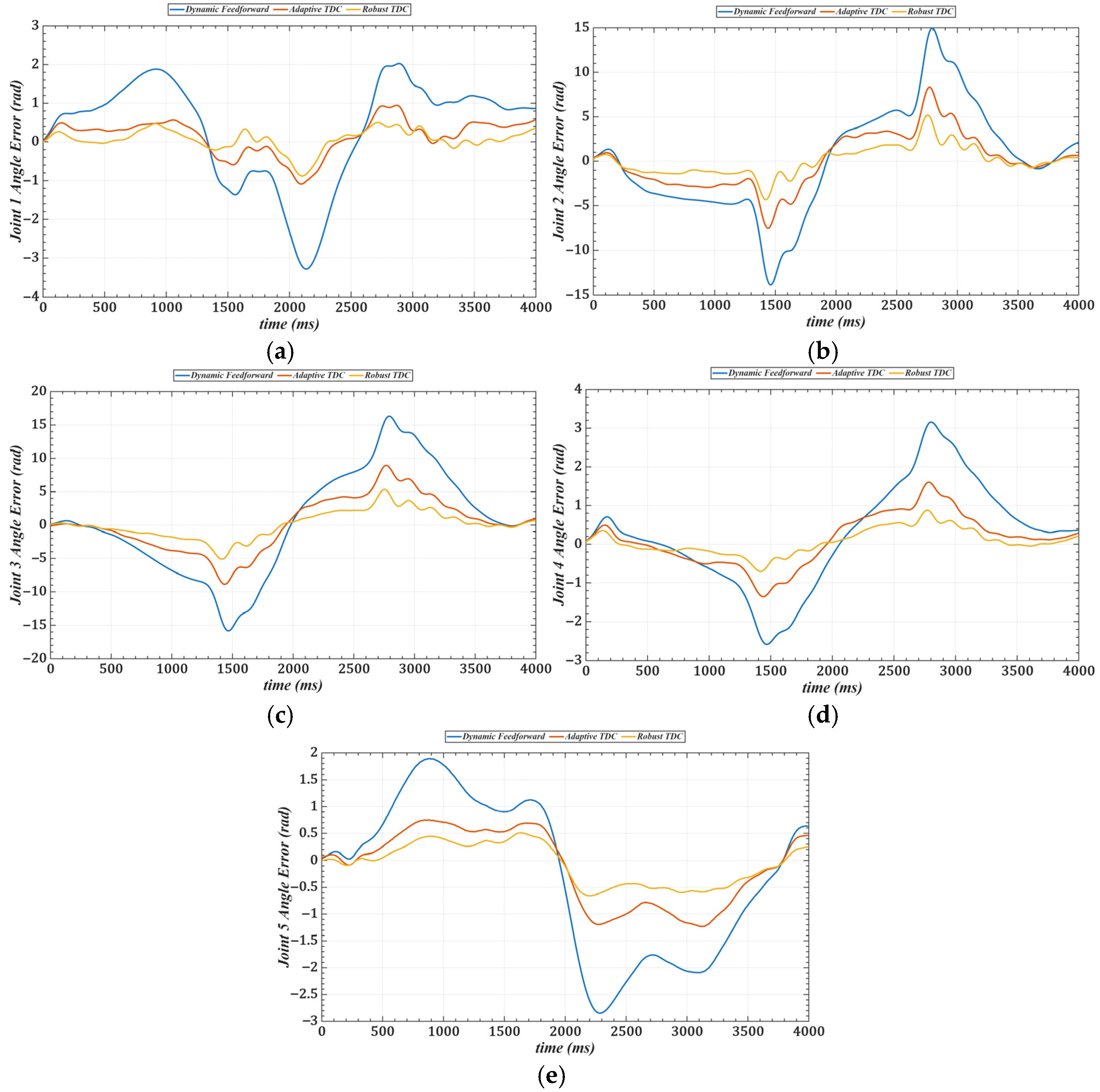
5. Experiments and Results
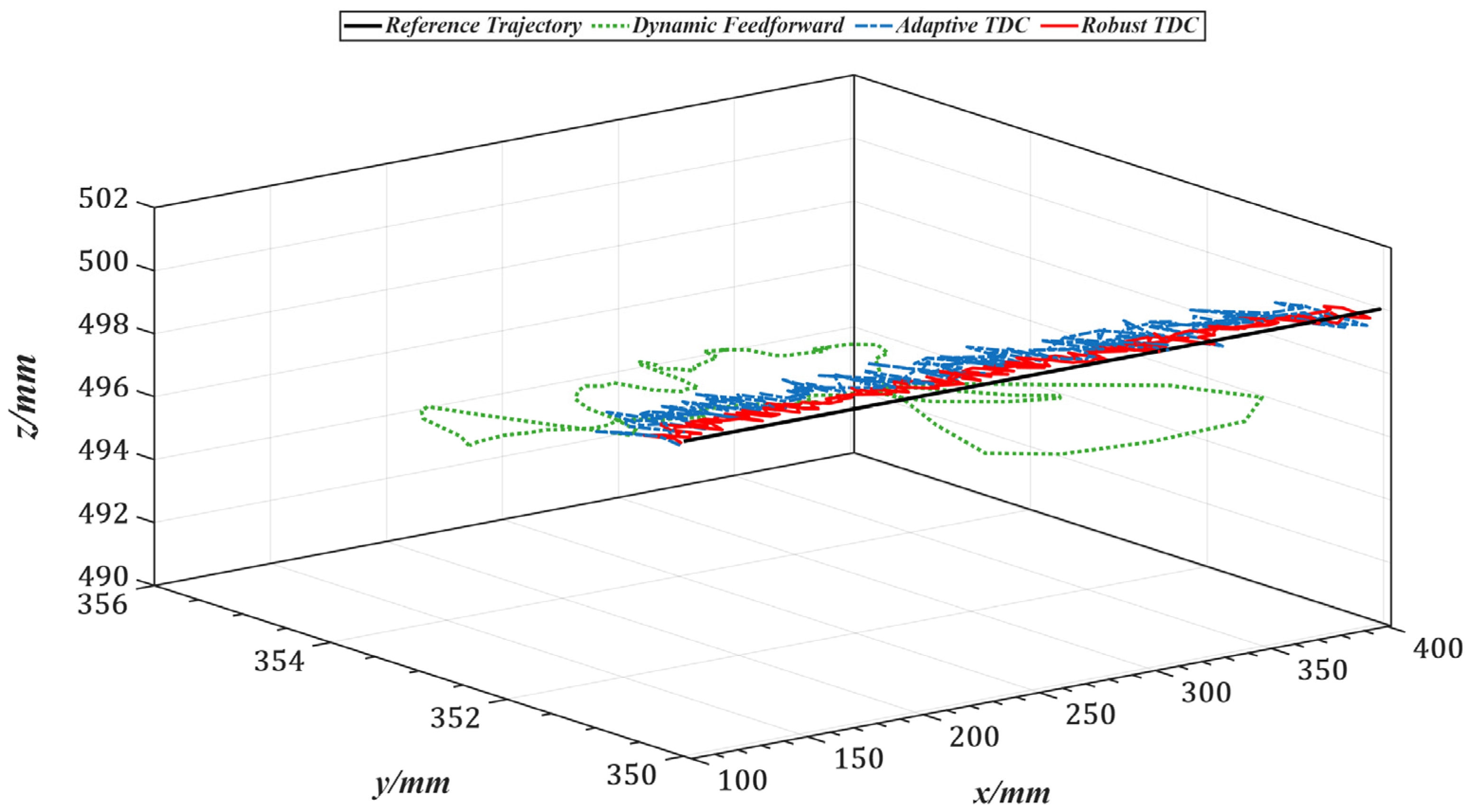
5.1. Trajectory Tracking Without Load
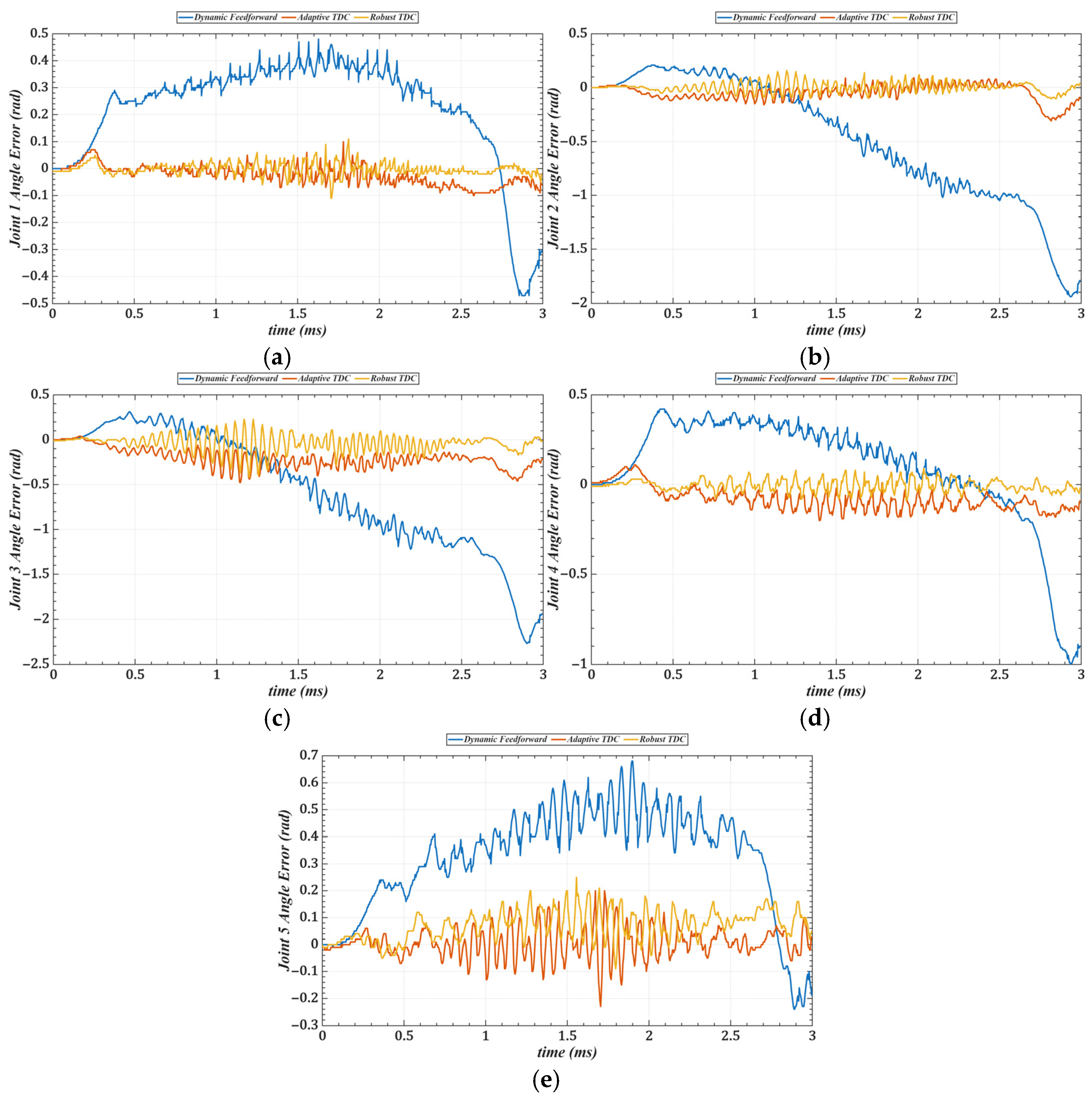
5.2. Trajectory Tracking with Load
6. Discussion
7. Conclusions
- Efficient control gain design: The proposed time-delay control gain determination method can be completed offline, without relying on engineer experience or introducing additional tuning parameters, enabling rapid determination of optimal control gains.
- Accurate state estimation: By integrating a model reference observer with a Kalman filter, measurement noise is effectively suppressed, allowing high-precision estimation of joint states.
- Strong engineering applicability: The method features a simple structure and low computational cost, making it suitable for practical implementation in robotic manipulator systems and offering substantial potential for wider application.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Chen, L.; Ding, J.; Liu, Y. Research on Real-Time Obstacle Avoidance Motion Planning of Industrial Robotic Arm Based on Artificial Potential Field Method in Joint Space. Appl. Sci. 2023, 13, 6973. [Google Scholar] [CrossRef]
- Park, S.H.; Jin, M.; Kang, S.H. Efficient Acceleration-Level Formula of Bias Acceleration Satisfying Time Precedence for Operational Space Formulation. IEEE Access 2022, 10, 65533–65547. [Google Scholar] [CrossRef]
- Huang, A.-C.; Chen, Y.-C. Adaptive sliding control for single-link flexible-joint robot with mismatched uncertainties. IEEE Trans. Control Syst. Technol. 2004, 12, 770–775. [Google Scholar] [CrossRef]
- Chwa, D.; Kwon, H. Nonlinear Robust Control of Unknown Robot Manipulator Systems with Actuators and Disturbances Using System Identification and Integral Sliding Mode Disturbance Observer. IEEE Access 2022, 10, 35410–35421. [Google Scholar] [CrossRef]
- Babaghasabha, R.; Khosravi, M.A.; Taghirad, H.D. Adaptive robust control of fully-constrained cable driven parallel robots. Mechatronics 2015, 25, 27–36. [Google Scholar] [CrossRef]
- Wei, B. A Tutorial on Robust Control, Adaptive Control and Robust Adaptive Control—Application to Robotic Manipulators. Inventions 2019, 4, 49. [Google Scholar] [CrossRef]
- Chatterjee, A.; Chatterjee, R.; Matsuno, F.; Endo, T. Augmented stable fuzzy control for flexible robotic arm using LMI approach and neuro fuzzy state space modeling. IEEE Trans. Ind. Electron. 2008, 55, 1256–1270. [Google Scholar] [CrossRef]
- Kong, L.; He, W.; Dong, Y.; Cheng, L.; Yang, C.; Li, Z. Asymmetric Bounded Neural Control for an Uncertain Robot by State Feedback and Output Feedback. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 1735–1746. [Google Scholar] [CrossRef]
- Yang, C.; Huang, D.; He, W.; Cheng, L. Neural Control of Robot Manipulators with Trajectory Tracking Constraints and Input Saturation. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4231–4242. [Google Scholar] [CrossRef]
- Jin, L.; Li, S.; Hu, B. RNN Models for Dynamic Matrix Inversion: A Control-Theoretical Perspective. IEEE Trans. Ind. Inform. 2018, 14, 189–199. [Google Scholar] [CrossRef]
- Jin, L.; Li, S.; Luo, X.; Li, Y.; Qin, B. Neural Dynamics for Cooperative Control of Redundant Robot Manipulators. IEEE Trans. Ind. Inform. 2018, 14, 3812–3821. [Google Scholar] [CrossRef]
- Jin, M.; Kang, S.H.; Chang, P.H. Robust Compliant Motion Control of Robot with Nonlinear Friction Using Time-Delay Estimation. IEEE Trans. Ind. Electron. 2008, 55, 258–269. [Google Scholar] [CrossRef]
- Kang, S.H.; Jin, M.; Chang, P.H. A Solution to the Accuracy/Robustness Dilemma in Impedance Control. IEEE/ASME Trans. Mechatron. 2009, 14, 282–294. [Google Scholar] [CrossRef]
- Jin, M.; Kang, S.H.; Chang, P.H.; Lee, J. Robust Control of Robot Manipulators Using Inclusive and Enhanced Time Delay Control. IEEE/ASME Trans. Mechatron. 2017, 22, 2141–2152. [Google Scholar] [CrossRef]
- Jin, M.; Lee, J.; Seo, K.-H.; Suh, J.-H. Self-Tuning Control for Articulated Robots Using the Plestan’s Method. Int. J. Precis. Eng. Manuf. 2021, 22, 557–566. [Google Scholar] [CrossRef]
- Chang, P.H.; Lee, J.W. An Observer Design for Time-Delay Control and its Application to DC Servo Motor. In Proceedings of the 1993 American Control Conference, San Francisco, CA, USA, 2–4 June 1993; pp. 1032–1036. [Google Scholar]
- Kim, H.-S.; Kim, K.-H.; Youn, M.-J. On-line dead-time compensation method based on time delay control. IEEE Trans. Control Syst. Technol. 2003, 11, 279–285. [Google Scholar] [CrossRef]
- Lee, J.; Yoo, C.; Park, Y.-S.; Park, B.; Lee, S.-J.; Gweon, D.-G.; Chang, P.-H. An experimental study on time delay control of actuation system of tilt rotor unmanned aerial vehicle. Mechatronics 2012, 22, 184–194. [Google Scholar] [CrossRef]
- Cho, G.R.; Chang, P.H.; Jin, Y. Enhanced feedforward control of non-minimum phase systems for tracking predefined trajectory. In Proceedings of the 2010 IEEE International Symposium on Industrial Electronics, Bari, Italy, 4–7 July 2010; pp. 167–172. [Google Scholar]
- Wang, Y.; Yan, F.; Jiang, S.; Chen, B. Time delay control of cable driven manipulators with adaptive fractional-order nonsingular terminalsliding mode. Adv. Eng. Softw. 2018, 121, 13–25. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, S.; Chen, B.; Wu, H. A new continuous fractional-order nonsingular terminal sliding mode control for cable-driven manipulators. Adv. Eng. Softw. 2018, 119, 21–29. [Google Scholar] [CrossRef]
- Roy, S.; Kar, I.N.; Lee, J.; Jin, M. Adaptive robust time-delay control for a class of uncertain Euler-Lagrange systems. IEEE Trans. Ind. Electron. 2017, 64, 7109–7119. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Gu, L.; Li, X. Time delay control of hydraulic manipulators with continuous nonsingular terminal sliding mode. J. Cent. South Univ. 2015, 22, 4616–4624. [Google Scholar] [CrossRef]
- Wang, Y.; Gu, L.; Xu, Y.; Cao, X. Practical tracking control of robot manipulators with continuous fractional-order nonsingular terminal sliding mode. IEEE Trans. Ind. Electron. 2016, 63, 6194–6204. [Google Scholar] [CrossRef]
- Jin, Y.; Chang, P.H.; Jin, M.; Gweon, D.G. Stability guaranteed time-delay control of manipulators using nonlinear damping and terminal sliding mode. IEEE Trans. Ind. Electron. 2013, 60, 3304–3317. [Google Scholar] [CrossRef]
- Chang, P.H.; Jung, J.H. A systematic method for gain selection of robust PID control for nonlinear plants of second-order controller canonical form. IEEE Trans. Control Syst. Technol. 2009, 17, 473–483. [Google Scholar] [CrossRef]
- Cho, S.J.; Jin, M.; Kuc, T.Y.; Lee, J.S. Stability guaranteed autotuning algorithm of a time-delay controller using a modified nussbaum function. Int. J. Control 2014, 87, 1926–1935. [Google Scholar] [CrossRef]
- Jin, M.; Lee, J.; Tsagarakis, N.G. Model-free robust adaptive control of humanoid robots with flexible joints. IEEE Trans. Ind. Electron. 2017, 64, 1706–1715. [Google Scholar] [CrossRef]
- Baek, J.; Cho, S.; Han, S. Practical time-delay control with adaptive gains for trajectory tracking of robot manipulators. IEEE Trans. Ind. Electron. 2018, 65, 5682–5692. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, F.; Chen, J.; Ju, F.; Chen, B. A New Adaptive Time-Delay Control Scheme for Cable-Driven Manipulators. IEEE Trans. Ind. Inform. 2019, 15, 3469–3481. [Google Scholar] [CrossRef]
- Chang, P.H.; Lee, J.W. A model reference observer for time-delay control and its application to robot trajectory control. IEEE Trans. Control Syst. Technol. 1996, 4, 2–10. [Google Scholar] [CrossRef]
- Lee, J.W.; Chang, P.H. Input/output linearization using time delay control and time delay observer. KSME Int. J. 1999, 13, 546–556. [Google Scholar] [CrossRef]
- Ciria, A.; Schillaci, G.; Pezzulo, G.; Hafner, V.V.; Lara, B. Predictive Processing in Cognitive Robotics: A Review. Neural Comput. 2021, 33, 1402–1432. [Google Scholar] [CrossRef]
- Chen, R.; Jin, X.; Laima, S.; Huang, Y.; Li, H. Intelligent modeling of nonlinear dynamical systems by machine learning. Int. J. Non-Linear Mech. 2022, 142, 103984. [Google Scholar] [CrossRef]
- Peng, Y.; Yang, X.; Li, D.; Ma, Z.; Liu, Z.; Bai, X.; Mao, Z. Predicting flow status of a flexible rectifier using cognitive computing. Expert Syst. Appl. 2025, 264, 125878. [Google Scholar] [CrossRef]
- Hilal, W.; Gadsden, S.A.; Yawney, J. Cognitive Dynamic Systems: A Review of Theory, Applications, and Recent Advances. Proc. IEEE 2023, 111, 575–622. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, B.; Wen, C.; Wang, D.; Wei, G. Model predictive control for complicated dynamic systems: A survey. Int. J. Syst. Sci. 2025, 56, 2168–2193. [Google Scholar] [CrossRef]
- Hsia, T.C.S.; Lasky, T.A.; Guo, Z. Robust independent joint controller design for industrial robot manipulators. IEEE Trans. Ind. Electron. 1991, 38, 21–25. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, S.; Chen, B.; Wu, H. Trajectory tracking control of underwater vehicle-manipulator system using discrete time delay estimation. IEEE Access 2017, 5, 7435–7443. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, L.; Chen, Y.; Ding, J.; Liu, Y.; Yan, D. Control Parameters Design of Spraying Robots Based on Dynamic Feedforward. Electronics 2024, 13, 1583. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, B.; Wang, L.; Yu, G. An iterative learning method for realizing accurate dynamic feedforward control of an industrial hybrid robot. Sci. China Technol. Sci. 2021, 64, 1177–1188. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, J.; Wang, L.; Yu, Z. Accurate dynamic modeling and control parameters design of an industrial hybrid spray-painting robot. Robot. Comput.-Integr. Manuf. 2020, 63, 101923. [Google Scholar] [CrossRef]
- Hsia, T.C.; Gao, L.S. Robot manipulator control using decentralized linear time-invariant time-delayed joint controllers. In Proceedings of the IEEE International Conference on Robotics and Automation, Cincinnati, OH, USA, 13–18 May 1990; Volume 3, pp. 2070–2075. [Google Scholar]
- Open Source Six-Axis Collaborative Robot, Hefei Zhongke Deep Valley Science and Technology Development Co., Ltd. Available online: https://www.vstc.cc/display.php?id=650 (accessed on 23 August 2025).







| Control Gain | |||
|---|---|---|---|
| Mean Error | 3.89 × 10−2 | 1.07 × 10−2 | 2.35 × 10−3 |
| RMS Error | 4.89 × 10−3 | 3.61 × 10−3 | 2.70 × 10−4 |
| Control Gain | |||
|---|---|---|---|
| Mean Error | 2.73 × 10−2 | 1.19 × 10−2 | 2.26 × 10−3 |
| RMS Error | 7.70 × 10−3 | 2.86 × 10−3 | 4.17 × 10−4 |
| RMS/mm | Dynamic Feedforward | Adaptive TDC | Robust TDC |
|---|---|---|---|
| X-direction | 1.5747 | 0.3245 | 0.2430 |
| Y-direction | 2.7832 | 0.5947 | 0.4356 |
| Z-direction | 6.1254 | 1.1361 | 0.8711 |
| Composite RMS | 6.9024 | 1.3485 | 0.9564 |
| RMS/rad | Dynamic Feedforward | Adaptive TDC | Robust TDC |
|---|---|---|---|
| Joint 1 | 0.2775 | 0.1189 | 0.1062 |
| Joint 2 | 0.8428 | 0.1554 | 0.0671 |
| Joint 3 | 1.0997 | 0.2551 | 0.1175 |
| Joint 4 | 0.5303 | 0.1211 | 0.0799 |
| Joint 5 | 0.3398 | 0.1447 | 0.1094 |
| RMS/mm | Dynamic Feedforward | Adaptive TDC | Robust TDC |
|---|---|---|---|
| X-direction | 1.7453 | 0.9738 | 0.5684 |
| Y-direction | 3.1874 | 0.7898 | 0.3949 |
| Z-direction | 3.4349 | 0.4432 | 0.2216 |
| Composite RMS | 5.0004 | 1.3298 | 0.7267 |
| RMS/rad | Dynamic Feedforward | Adaptive TDC | Robust TDC |
|---|---|---|---|
| Joint 1 | 0.3250 | 0.0616 | 0.0257 |
| Joint 2 | 0.9343 | 0.6524 | 0.0451 |
| Joint 3 | 1.0676 | 0.2056 | 0.0927 |
| Joint 4 | 0.5229 | 0.0870 | 0.0392 |
| Joint 5 | 0.3478 | 0.1010 | 0.0702 |
| RMS/rad | Dynamic Feedforward | Adaptive TDC | Robust TDC |
|---|---|---|---|
| Joint 1 | 0.1538 | 0.0829 | 0.0742 |
| Joint 2 | 0.4345 | 0.2596 | 0.1923 |
| Joint 3 | 0.8078 | 0.4397 | 0.2738 |
| Joint 4 | 0.3568 | 0.1924 | 0.1280 |
| Joint 5 | 0.3840 | 0.2065 | 0.1375 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Ding, J.; Xu, T.; Liu, Y. Control Gain Determination Method for Robust Time-Delay Control of Industrial Robot Manipulators Based on an Improved State Observer. Sensors 2025, 25, 5812. https://doi.org/10.3390/s25185812
Chen Y, Ding J, Xu T, Liu Y. Control Gain Determination Method for Robust Time-Delay Control of Industrial Robot Manipulators Based on an Improved State Observer. Sensors. 2025; 25(18):5812. https://doi.org/10.3390/s25185812
Chicago/Turabian StyleChen, Yu, Jianwan Ding, Tianchang Xu, and Yanbing Liu. 2025. "Control Gain Determination Method for Robust Time-Delay Control of Industrial Robot Manipulators Based on an Improved State Observer" Sensors 25, no. 18: 5812. https://doi.org/10.3390/s25185812
APA StyleChen, Y., Ding, J., Xu, T., & Liu, Y. (2025). Control Gain Determination Method for Robust Time-Delay Control of Industrial Robot Manipulators Based on an Improved State Observer. Sensors, 25(18), 5812. https://doi.org/10.3390/s25185812






